Combinatoria y teoría de la probabilidad en el trading (Parte V): Análisis de curvas

Contenido

• Introducción
• Fórmulas útiles de simplificación de datos
• Fundamentos del método de conversión obtenido
• Definiendo los criterios de reducibilidad
• Definiendo los criterios de comparación con el sistema original
• Valoración de un posible corredor para calcular las magnitudes imprescindibles
• Definiendo la probabilidad y el tiempo medio hasta el cruzamiento de los límites superior e inferior del corredor
• Valoración de la efectividad de la conversión simple
• Corrección final y simulación
• Resumiendo
• Conclusión
• Enlaces

Introducción

Vamos a continuar poniendo las bases para ensamblar sistemas comerciales escalables y de múltiples etapas. En el marco del presente artículo, mostraremos cómo podemos usar los desarrollos de los artículos anteriores para acceder a posibilidades más amplias que nos ayuden a describir el proceso de negociación. Esto nos ayudará a evaluar la estrategia desde aquellos puntos de vista que otros métodos de análisis no pueden abordar. En este artículo, exploraremos las posibilidades de convertir muestras complejas de varios estados en muestras de doble estado más simples. Este análisis se ha realizado al estilo de una investigación.

Fórmulas útiles de simplificación de datos

Supongamos que tenemos una estrategia en la que hay muchas ofertas que se suceden sin superponerse, es decir, una estrategia en la que una nueva orden se abre estrictamente después de que se haya cerrado la anterior. Si de repente nos planteamos qué probabilidades tenemos de ganar o perder, además de calcular el tiempo promedio durante el cual se logrará un beneficio o una pérdida en una estrategia dada, entonces automáticamente nos enfrentaremos al hecho de que las órdenes puedan tener un número muy grande de estados (cierre con resultados diferentes).

Para poder aplicar fórmulas fractales a dichas estrategias, primero deberemos reducir estas estrategias a casos que puedan ser considerados en el marco de los fractales. Para hacer esto, solo necesitamos representar nuestra estrategia como una orden con paradas equidistantes donde existe la probabilidad de un salto superior y un salto inferior, exactamente como en nuestro fractal; ya después, se podrán aplicar las fórmulas fractales. Además, el salto hacia arriba y hacia abajo pueden tener diferente tiempo de expiración.

Para reducir cualquier estrategia a una de las estrategias que se pueden describir en el marco de las fórmulas fractales que conseguimos en el artículo anterior, en primer lugar, tendremos que determinar qué magnitudes se deben conocer para poder aplicar las fórmulas fractales. Aquí todo resulta bastante sencillo:

• P[1] – probabilidad de activación del salto superior
• T[1] – tiempo medio de formación de un salto hacia arriba
• T[2] – tiempo medio de formación de un salto hacia abajo

Lo primero que puede resultar útil para comprender este algoritmo son las magnitudes límite cuando el número de saltos tiende a infinito:

1. (P[1] * T[1] + (1 -P[1])*T[2]) * n = T(n)
2. (P[1] * Pr - (1 -P[1])*Pr) * n = P(n)

Para comprender mejor la expresión de arriba, deberemos escribir dos límites de este tipo:

• Lim(n --> +infinity)[P/P0(n)] = 1
• Lim(n --> +infinity)[T/T0(n)] = 1

Los límites indican que, si realizamos los mismos experimentos en la cantidad de "n" unidades, o comerciamos (lo que sea), entonces obtendremos siempre una cantidad diferente de tiempo total invertido por todos los experimentos elementales incluidos en uno general, además de una posición siempre diferente del balance final de nuestro comercio. Por otra parte, queda intuitivamente claro que, con un número infinito de experimentos, el valor real tenderá al límite.  Podemos demostrar este hecho usando generadores de números aleatorios.

• n – número de saltos emulados
• 1-P[1] – probabilidad de activación del salto inferior
• T0(n) – cantidad real de tiempo invertido en “n” saltos
• P0(n) – desplazamiento real del balance o el precio en “n” saltos
• T(n) - tiempo real invertido en “n” saltos
• P(n) – desplazamiento límite en “n” saltos

Podemos ver que, como resultado de esta lógica, hemos obtenido dos ecuaciones; la cantidad de incógnitas en ellas es mayor que su propio número, lo cual no resulta sorprendente, ya que esto es solo el comienzo. Pero estas ecuaciones solo describen un sistema derivado (el que necesitamos obtener). Para el sistema original, las ecuaciones serán semejantes:

1. (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) * m = T(m)
2. (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * m  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * m = P(m)

• P*[1] + P[*2] + … + P*[N2] = 1 – las probabilidades forman un grupo completo

Y exactamente los mismos límites que muestran las mismas magnitudes:

• Lim(m --> +infinity)[P/P0(m)] = 1
• Lim(m --> +infinity)[T/T0(m)] = 1

Las variables utilizadas aquí se describen más abajo:

• m – número de saltos emulados
• T0(m) – cantidad real de tiempo invertido en “m” saltos
• P0(m) – desplazamiento real del balance o el precio en “m” saltos
• T(m) - tiempo real invertido en “m” saltos
• P(m) – desplazamiento real en “m” saltos
• T = Lim(m --> +infinity) [ T(m) ] – tiempo límite
• N1 – número de resultados de transacciones con un beneficio positivo, así como su contador
• N2 - N1 + 1 - número de resultados de transacciones con beneficio negativo (N2 - su contador)

Está claro que necesitamos, usando como base el sistema original, obtener uno nuevo, más simple, compuesto por uno más complejo. La única diferencia es que conocemos todos los parámetros del sistema original, y el segundo no. A las magnitudes conocidas se les han asignado sufijos en forma de “*”.

Si tomamos y equiparamos la segunda y la primera ecuación de ambos sistemas, podremos excluir las variables “P” y “T”:

• (P[1] * T[1] + (1 -P[1])*T[2]) * n = (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) * m
• (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * m  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * m

Como resultado, hemos perdido dos ecuaciones, pero al mismo tiempo hemos eliminado dos incógnitas que no necesitábamos en absoluto. Finalmente, como resultado de estas transformaciones, hemos obtenido una ecuación en la que se desconocen las siguientes magnitudes:

• P [1] - probabilidad de activar el salto (stop) superior
• T [1] - tiempo de expiración del salto superior
• T [2] - tiempo de expiración del salto inferior

Podemos ver que ambas ecuaciones tienen una estructura similar, con el tipo:

1. A1*n = A2*m
2. B1*n = B2*m

Esta estructura sugiere que podemos eliminar una de las variables “n” o “m”, habiendo perdido una ecuación; para ello, deberemos expresar una de las magnitudes, por ejemplo, de la primera ecuación:

• m = ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )* n

Luego podemos sustituir esta expresión en la segunda ecuación y ver qué ocurre:

• (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) ) * n  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) ) * n

Después de realizar esta sustitución, podemos ver que ambos lados de la ecuación han sido multiplicados por “n”; tras dividirlos por una magnitud dada, podemos eliminarla y conseguir una ecuación que depende solo de las magnitudes que necesitamos:

• (P[1] * Pr - (1 -P[1])*Pr) = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )

Consideramos que el valor “Pr” es libre, ya que el número de sistemas posibles a los que podemos reducir todo es igual a infinito. Podemos establecer absolutamente cualquier tamaño de salto, lo esencial es que los saltos hacia arriba y hacia abajo sean iguales en valor absoluto. El resto de las magnitudes se determinarán como resultado de la resolución del sistema de ecuaciones. Hasta ahora, el sistema tiene solo una ecuación, pero nos faltan dos ecuaciones más, que se pueden obtener usando las ecuaciones obtenidas en la sección anterior.

En primer lugar, el sistema deberá tener la misma probabilidad de cruzar los límites superior e inferior del corredor y, en segundo lugar, deberá tener un tiempo promedio idéntico para cruzar uno de los límites. Precisamente estos dos requisitos nos darán las dos ecuaciones restantes. Comenzaremos hablando sobre cómo determinar el tiempo promedio para cruzar uno de los límites. El tiempo promedio para cruzar uno de los límites está determinado por el número promedio de saltos hacia arriba y hacia abajo. Teniendo en cuenta los resultados del artículo anterior, podemos escribir:

• T[U,D] = (S[U,u] * T[1] + S[U,d] * T[2]) * P[U] + (S[D,u] * T[1] + S[D,d] * T[2]) * ( 1 – P[U] )

Esta ecuación nos indica que el tiempo promedio para cruzar uno de los límites depende del número promedio de saltos si se cruza uno de los límites, así como de la probabilidad de cruzar dichos límites. Este criterio nos ofrecerá otra posible ecuación para construir un sistema de ecuaciones que nos permitirá reducir un sistema de comercio complejo a uno más simple. No obstante, podemos dividir esta ecuación aún más, en dos partes:

• T[U] = S[U,u] * T[1] + S[U,d] * T[2]
• T[D] = S[D,u] * T[1] + S[D,d] * T[2]

Estas ecuaciones nos resultarán útiles más abajo. Todos estas estas magnitudes se calculan usando como base el modelo matemático obtenido en el artículo anterior:

• S[U,u], S[U,d], S[D,u], S[D,d], P[U] = f(n,m,p) – todas estas magnitudes son funciones de “n,m,p”
• n = B[U]/ Pr – a su vez, “n” se puede expresar usando la distancia hasta el límite superior y el salto “Pr”
• m = B[D]/ Pr – a su vez “m” se puede expresar usando la distancia hasta el límite superior y el salto "Pr"
• Pr - salto seleccionado
• B[U] - distancia hasta el límite superior
• B[D] - distancia hasta el límite inferior

Fundamentos del método de conversión obtenido

Como ejemplo, podemos tomar una estrategia aleatoria y reducirla al equivalente necesario. Hemos creado una de estas opciones para convertir un sistema multidimensional complejo en uno bidimensional más simple. Intentaremos describir paso a paso el proceso completo de esta reducción. Antes de describir todas estas cosas, hemos implementado todo esto programáticamente y verificado la capacidad de trabajo del método. El programa se adjuntará al artículo. En nuestro programa, hemos usado fórmulas de comparación algo distintas, pero igualmente efectivas. Se basan en el modelo matemático obtenido en el artículo anterior. Usando este como base, podremos obtener los siguientes valores:

• P[U], S[U,u], S[U,d], S[D,u], S[D,d]

A partir de los saltos medios, podemos obtener el tiempo promedio para cruzar el límite superior o inferior. Por el momento, no se entiende por qué necesitamos todo esto, pero ahora todo quedará claro. Para reducir una estrategia con varios estados, primero deberemos generar estas estrategias. Hemos creado un generador de estrategias basado en números aleatorios que nos ayudará con esto. Para mayor claridad, hemos seleccionado cinco curvas generadas aleatoriamente. Este es su aspecto:

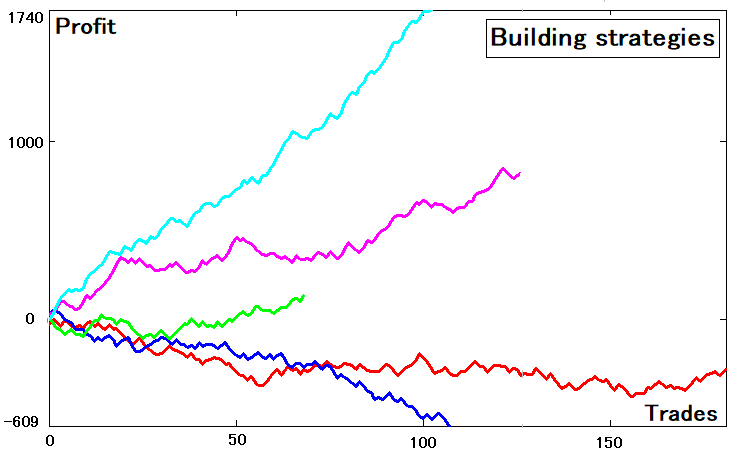
Podemos observar que las estrategias tienen diferentes esperanzas matemáticas, número de transacciones y parámetros de estas. También podemos ver que entre estas curvas también hay curvas no rentables, pero esto no debería preocuparnos, ya que la curva no rentable también es una curva: simplemente no nos gustan sus parámetros. Al fin y al cabo, si algo no nos gusta, no es en absoluto necesario quitarlo.

Ahora, vayamos al grano. Podemos observar que en la figura, los gráficos de los balances que dependen del número de transacción son exactamente los mismos que se verían en el simulador de estrategias del terminal comercial. Partiendo de esto, cada curva se corresponde con una determinada matriz que contiene balances:

• B[i] , i = 0…N
• N - número de transacciones

Podemos obtener esta matriz a partir de la matriz con los parámetros de la orden. En nuestro caso, asumiremos que el contenedor con los datos de las órdenes contiene solo la magnitud de los beneficios o las pérdidas de esta orden, así como su duración:

• Pr[i], T[i]

Asumiremos que el resto de los parámetros no están disponibles para nosotros. Esto parece lo correcto, porque, por ejemplo, si queremos analizar algún backtest o señal, resulta poco probable que este dato esté disponible para nosotros, ya que solo en raras ocasiones alguien guardará estos datos. Más bien, las personas se guiarán por métricas tales como el factor de recuperación, la reducción máxima y métricas similares, donde se concentra solo la información que necesitan. Los únicos datos comerciales que se guardan en todas partes son:

1. El beneficio
2. La hora de apertura de la orden
3. La hora de cierre de la orden

Obviamente, la precisión se verá afectada por esto, pero es inevitable. Ahora podemos escribir cómo obtener una matriz con balances a partir de una matriz con beneficios:

• B[i] = B[i-1] + Pr[i]  if  i > 0
• B[i] = 0  else

Pero para poder analizar las estrategias resultantes relacionadas con el tiempo, de la misma forma, necesitaremos componer una matriz similar con el tiempo:

• TL[i] = TL[i-1] + T[i]  if  i > 0
• TL[i] = 0  else

Una vez que hemos determinado las abscisas y ordenadas de todas esas curvas, podemos realizar la representación gráfica y ver que hay diferencias, dado que ya tenemos funciones de dependencia no según el número de transacción, sino el tiempo:

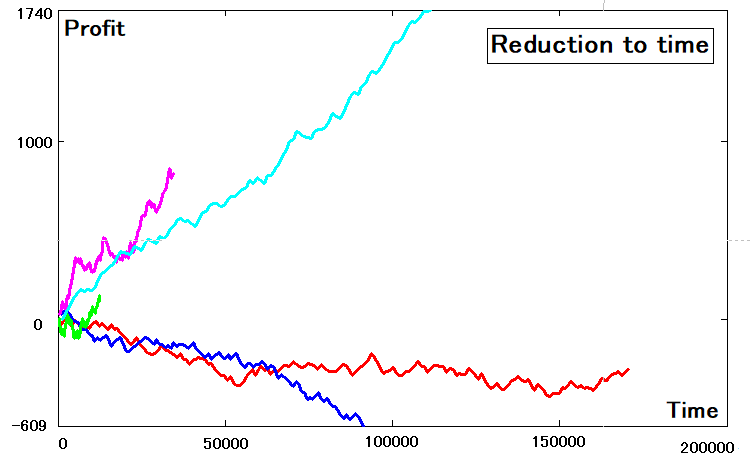
Definiendo los criterios de reducibilidad

Ahora, ya podemos trabajar con estos datos, y también podemos definir los criterios sobre los cuales buscaremos coincidencias entre las curvas con dos estados de beneficio. Desde el punto de vista de la representación en relación al tiempo, nos bastarán tres valores para la información:

1. P[U] - probabilidad de cruzar el límite superior
2. T[U] - tiempo promedio para alcanzar el límite superior
3. T[D] - tiempo promedio para alcanzar el límite inferior

Podemos calcular el segundo y el tercer valor de la forma que sigue:

• T[U] = S[U,u] * T[u] + S[U,d] * T[d]
• T[D] = S[D,u] * T[u] + S[D,d] * T[d]

En cuanto a P[U], esta magnitud ya es proporcionada en su forma terminada por el modelo matemático que hemos obtenido en el artículo anterior. Y no creemos que tenga sentido recordar que “P[D] = 1 - P[U]”. Resulta que, a partir de las cinco magnitudes ofrecidas por el modelo matemático, podemos formar las tres que necesitamos (se describen arriba), y ni siquiera queda nada superfluo. En cuanto a estas dos ecuaciones, se han obtenido arriba: solo hemos cambiado la notación para el tiempo, pues así parece más legible.

Estas magnitudes son calculables y, para ajustarlas a algo, deberemos obtener de alguna forma su valor real a partir de los datos que tenemos. Después de ello, tendremos que seleccionar dichos parámetros de la curva equivalente necesaria con dos estados para que los tres parámetros calculados sean lo más similares posible a los indicadores reales; precisamente así obtendremos nuestros tres criterios. Primero, introducimos la notación para las magnitudes conocidas:

• P*[U] - probabilidad real de cruzar los límites del corredor seleccionado
• T*[U] - tiempo promedio real hasta cruzar el límite superior del corredor
• T*[D] - tiempo promedio real hasta cruzar el límite inferior del corredor

Podemos medir la desviación de los valores reales y calculados en magnitudes relativas o como porcentaje. Si lo hacemos en tanto por ciento, los criterios serán los siguientes:

• KPU = ( | P[U] – P*[U] | / ( P[U] + P*[U] ) ) * 100 %
• KTU = ( | T[U] – T*[U] | / ( T[U] + T*[U] ) ) * 100 %
• KTD = ( | T[D] – T*[D] | / ( T[D] + T*[D] ) ) * 100 %

Definiendo los criterios de comparación con el sistema original

El mejor sistema será el que tenga el mínimo de todos estos indicadores. No obstante, para tener la posibilidad de obtener los valores calculados, primero deberemos determinar el tamaño del corredor a lo largo del cual se determinarán las probabilidades reales y el tiempo real antes de cruzar los límites. Esto se puede representar visualmente:

La figura muestra un ejemplo de definición de dicho corredor para una estrategia rentable. Los triángulos de color púrpura simbolizan el siguiente punto de control para los posibles movimientos hacia arriba y hacia abajo. Nuestro movimiento mínimo requerido se encuentra entre los dos puntos negros. Si tomamos como base el movimiento máximo sucedido para el periodo disponible, entonces la probabilidad P[U] será la unidad. Obviamente, esta será la elección más incorrecta. Por el contrario, necesitaremos un movimiento mínimo que garantice el cruce tanto del corredor inferior como del superior.

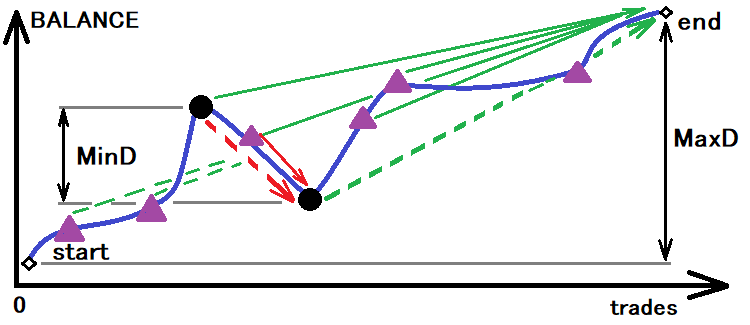
Valoración de un posible corredor para calcular las magnitudes imprescindibles

Pero incluso esto resulta insuficiente. El caso es que si tomamos esta magnitud como base, solo obtendremos un contacto con el límite inferior, lo cual tampoco ofrecerá una gran precisión. En nuestro caso, hemos tomado una magnitud de corredor tres veces inferior a este mínimo. Si hay una muestra suficiente de contactos con el límite, en este caso será suficiente. Bueno, ya hemos decidido el tamaño del corredor, ahora podemos dividir el corredor. Si asumimos que el corredor en sí es un escalón, esto significará que:

• n, m = 1
• p = P[U]
• Pr * n = Pr * m  = 1/3 * MinD – mitad de la amplitud del corredor
• Pr = ( 1/3 * MinD  ) / n = ( 1/3 * MinD  ) / m  – módulo del salto
• T[U,u] = T[U]
• T[D,d] = T[D]
• T[U,d] = 0
• T[D,u] = 0

También podemos usar esta opción si tenemos una muestra comercial muy grande. La ventaja de este enfoque reside en que no tenemos que aplicar un modelo matemático para dividir el corredor, porque en este caso, todo nuestro corredor supone un salto. No obstante, en nuestros cálculos, hemos tomado un ejemplo que usa el modelo matemático, para evitar la monotonía. Si usamos este enfoque, entonces, para seleccionar sus parámetros, deberemos elegir los siguientes rangos de los mismos:

• p = p1 … p2
• N = m = nm1 …. nm2

Hemos tomado para el ejemplo estos intervalos:

• p1 = 0.4, p2 = 0.6, nm1 = 1, nm2 = 3

Claro que podemos tomar rangos más amplios, pero no necesariamente en el número de saltos y en la probabilidad al mismo tiempo. Podemos ampliar uno de los intervalos y dejar el otro sin cambios. Por ejemplo, podemos aumentar "nm2", entonces el método podrá cubrir una gama más amplia de estrategias diferentes, y si el modelo matemático no puede hacer frente a la siguiente opción, podremos cambiar al método sin usar el modelo matemático.

Definiendo la probabilidad y el tiempo medio hasta el cruzamiento de los límites superior e inferior del corredor

Después de seleccionar con éxito todas las magnitudes descritas anteriormente, obtendremos solo la probabilidad "p" para un salto hacia arriba, pero ya podremos partir desde ella para encontrar el tiempo promedio de cruce de los límites. Podemos mostrar claramente cómo se hace esto, transformando para ello ligeramente la ilustración de arriba:

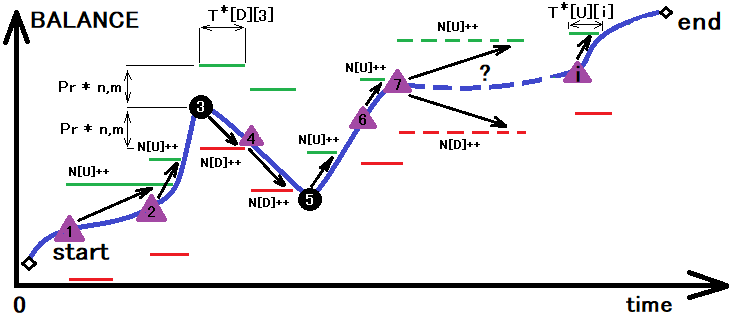
La figura muestra el proceso de suma de los cruces de los límites superior e inferior del corredor, cuyo tamaño se determina como resultado de la transformación anterior. Paralelamente a la suma de estos cruces, se realiza el cálculo del tiempo de permanencia en el cruce. En esta única operación, podemos determinar con un asterisco todas las magnitudes que necesitamos:

• N[U] - número de cruces del límite superior del corredor
• N[D] - número de cruces del límite inferior del corredor
• T[U][i] - matriz con la hora antes de cruzar el límite superior
• T[D][i] - matriz con la hora antes de cruzar el límite inferior

Solo queda usar estos datos para calcular la probabilidad de cruzar el límite superior y el tiempo promedio de cruce de los límites superior e inferior:

• P*[U] = N[U]/ ( N[U] + N[D] )
• T*[U] = Summ( 0…i ) [ T[U][i]  ] / N[U]
• T*[D] = Summ( 0…i ) [ T[D][i]  ] / N[D]

Una vez hayamos encontrado todas las magnitudes en las que debería converger nuestro equivalente bidimensional, deberemos determinar dónde comenzar la búsqueda. Para hacerlo, tendremos que determinar cuál de estas magnitudes posee mayor prioridad en términos de precisión. Hemos tomado como ejemplo la probabilidad de cruzar el límite superior. Este enfoque reduce la potencia de procesamiento necesaria para el análisis. Si hiciéramos una selección de tres valores a la vez en tres intervalos, obtendríamos tres grados de libertad del sistema, lo cual aumentaría el tiempo de cálculo en un orden de magnitud, sobre todo porque con un aumento en la cantidad de datos, esto podría dar un tiempo de cálculo incompatible con la realidad. En cambio, en nuestra lógica, primero hemos realizado una selección de la probabilidad de un salto hacia arriba, y solo entonces hemos hecho una selección del tiempo promedio de saltos hacia arriba y hacia abajo.

Debemos invitar una vez más al lector a que no se confunda: existen muchos saltos en el corredor, y el tiempo antes de cruzar los límites no es el momento de los saltos. Lo mismo ocurre con la probabilidad: la probabilidad de un salto en una determinada dirección no es la probabilidad de cruzar el límite del corredor. La única excepción es la situación “n=m=1”, que describimos al principio.

Como resultado de la selección, obtenemos las siguientes características de salto:

1. p - probabilidad de un salto hacia arriba
2. T[u] - duración media de un salto hacia arriba
3. T[d] - duración media de un salto hacia abajo
4. Pr - módulo de salto en términos de beneficio

Valoración de la efectividad de la conversión simple

Supongamos que se seleccionan todos los parámetros de los saltos, entonces, ¿de qué forma podremos entender como de efectiva ha sido en general dicha operación de conversión? Para valorar la efectividad, podemos trazar líneas rectas hacia las que converjan las estrategias. Su inclinación se puede determinar de la forma siguiente:

• K = EndProfit / EndTime - coeficiente de inclinación de la recta
• P0 = K * t - ecuación de la recta

Este es el aspecto que tendrá:

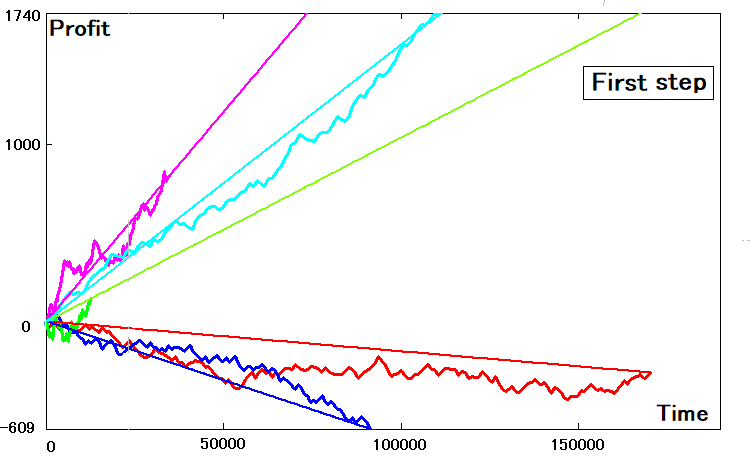
Si los parámetros de las curvas bidimensionales coinciden perfectamente, sus líneas rectas similares tendrán exactamente la misma inclinación y tocarán las curvas de balance en los puntos finales. De forma intuitiva, podemos comprender que, probablemente, tal coincidencia no se dé siempre. Para encontrar el coeficiente de inclinación en el equivalente 2D elegido, podemos usar los datos seleccionados para el salto:

• MP = p * Pr - (1-p) * Pr - esperanza matemática del desplazamiento hacia arriba para cualquier salto
• MT = p * T[u] + (1-p) * T[d] - esperanza matemática del tiempo invertido en la formación de cualquier salto
• K = MP / MT - el mismo coeficiente de inclinación de la recta.

Hemos logrado esto utilizando el mismo programa, y casi siempre sale algo similar a esto:

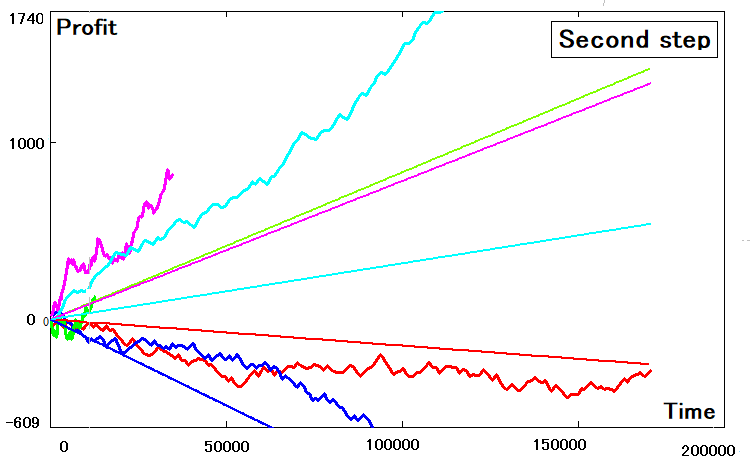
Podemos ver que no todas las estrategias han podido convertirse correctamente en un equivalente bidimensional. Aquellas que no han podido transformarse tienen desviaciones bastante pronunciadas. Estas desviaciones se asocian con las siguientes causas:

1. Un error al calcular las magnitudes con un asterisco
2. Un modelo 2D imperfecto (un modelo menos flexible)
3. La finitud del número posible de intentos de búsqueda (esto resulta también igual a la potencia informática limitada)

Teniendo en cuenta todos estos hechos, podemos realizar ciertos ajustes en el tiempo de salto promedio para al menos igualar los coeficientes de inclinación de los modelos original y derivado. Por supuesto, estas conversiones irán en detrimento de la reducción de las desviaciones de los criterios, pero no podremos conseguirlo de ninguna otra forma. Aún así, a nuestro juicio, el coeficiente de inclinación de la recta es el criterio más importante, porque, como el número de transacciones tiende a infinito, la estrategia original y la derivada deben fusionarse en una línea. Si esto no sucede, entonces tal conversión no tiene mucho sentido. O quizás el asunto no sea el método de conversión, sino ciertas posibilidades ocultas que aún debemos comprender.

Corrección final y simulación

Para hacer tal conversión, podemos utilizar la proporción. Ya que antes de construir estas curvas teníamos las matrices “TL[i]”, “B[i]”, que son equivalentes al tiempo transcurrido desde el inicio de la curva hasta la orden o segmento analizados, podemos tomar los últimos elementos de esta matriz y escribir lo siguiente:

• K = B[n] / TL[n]
• N - índice del último elemento de la matriz de balances (balance final)

A su vez, también podemos calcular dicho coeficiente para las rectas obtenidas en el salto anterior; ya lo consideramos anteriormente:

• K1 = MP / MT

No obstante, está claro que estos coeficientes no son iguales y debemos ajustar este coeficiente. Podemos hacerlo así:

• K = MP / ( KT * MT )
• KT - coeficiente de corrección

Ahora necesitamos introducir este coeficiente dentro de la esperanza matemática para que esta no cambie su sentido, por ejemplo, de la forma siguiente:

• MTK = MT * KT = p * (T[u]* KT) + (1-p) * (T[d]* KT)

Aquí vemos que se han formado entre paréntesis nuevos valores de tiempo corregidos; podemos calcularlos de la forma siguiente:

1. Tn[u] = T[u]* KT
2. Tn[d] = T[d]* KT

Estos serán nuestros tiempos ajustados de salto hacia arriba y hacia abajo. En sí, el factor de corrección se puede calcular equiparando las expresiones para calcular los coeficientes:

• B[n] / TL[n] = MP / ( KT * MT )

Tras resolver la ecuación para "KT", obtenemos una expresión para calcular este valor:

• KT = ( MP / MT ) / ( B[n] / TL[n] ) = ( MP * TL[n] ) / ( MT * B[n] )

Lo único que queda es ajustar el tiempo de salto promedio hacia arriba y hacia abajo. Después de eso, podremos considerar completo el proceso de conversión. Como resultado, obtendremos solo un conjunto de cuatro valores que describen nuestra estrategia al completo, en lugar de enormes matrices que describen más de dos estados:

1. p - probabilidad de un salto hacia arriba
2. Pr – módulo de salto
3. T[u] – tiempo medio de formación de un salto hacia arriba
4. T[d] – tiempo medio de formación de un salto hacia abajo

Estos cuatro parámetros bastan para recrear la propia estrategia usando la simulación. Lo principal es que ahora tenemos acceso a la simulación programática de la estrategia fuera del contexto del mercado y del tiempo. Usando nuestras cinco estrategias como ejemplo, la simulación tendrá el siguiente aspecto:

Las líneas rectas aquí se toman desde el primer salto. Estas líneas se han trazado desde cero hasta el final de la curva de comercio real. Podemos ver que la simulación resulta bastante precisa cerca de las líneas, lo cual confirma la corrección de las conversiones. La única excepción es la línea azul: parece que se trata simplemente de fallos en nuestro algoritmo. Seguro que estas pequeñas cosas se pueden arreglar en poco tiempo.

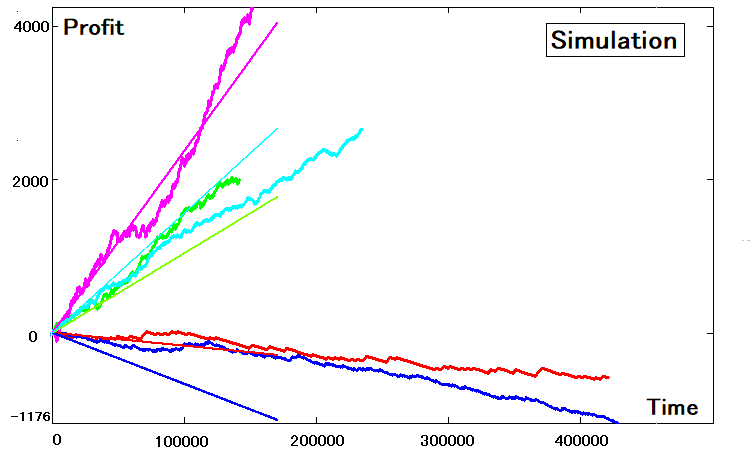
Resumiendo

Durante la investigación de este modelo, han surgido ideas interesantes. Inicialmente, al investigar esquemas en 2D y multiestado, solo queríamos obtener una descripción más simple para sistemas complejos. Como resultado, obtuvimos conclusiones mucho más valiosas y sencillas de los resultados del estudio. Los detalles de todo esto no son fáciles de describir en el artículo, porque hay demasiados matices técnicos y nimiedades. En resumen, qué nos ha dado esta investigación:

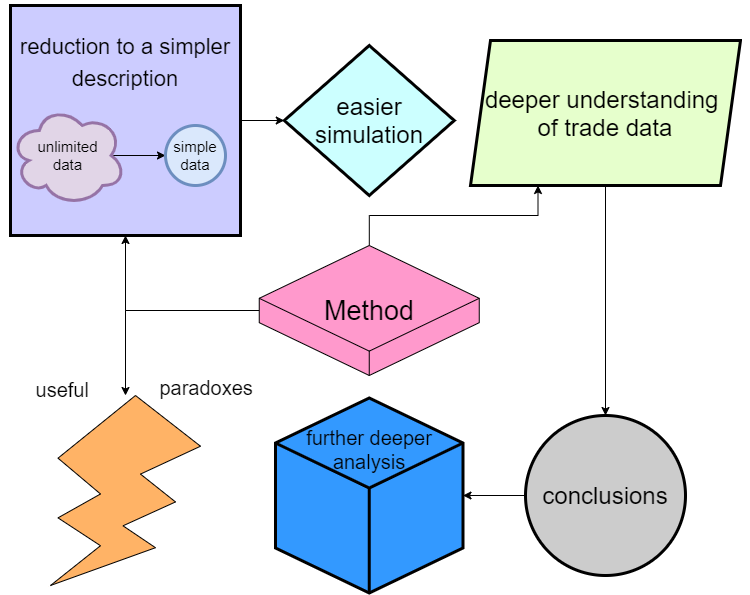
Podemos enumerar todas las ventajas en una lista:

• Muchos sistemas con muchos estados se pueden reducir a dos estados (lo cual significa que también es posible un proceso "n" en "m" estados)
• Podemos usar el proceso de conversión como mecanismo de compresión de los datos comerciales.
• Los datos transformados se pueden devolver mediante simulación, lo cual simplifica simultáneamente la simulación (ya que solo debemos simular dos estados)
• Una comprensión más profunda de los procesos probabilísticos dentro de la fijación de precios permite extraer conclusiones útiles e individuales.
• Usando como base la información obtenida, podemos realizar un análisis más profundo del proceso comercial.
• Ya en este estudio, se han obtenido algunas características útiles para el trading; por el momento, las clasificaremos como paradojas

Como resultado, por supuesto, la idea principal del presente ciclo de artículos es la creación de unas matemáticas simples y útiles que nos permitan crear directamente sistemas ultraestables y multidivisa basados ​​en la teoría de probabilidad. Hasta ahora, esta información no resulta demasiado monolítica, pero un monolito solo se puede construir sobre una buena base, y esto es lo que estamos haciendo.

También conviene decir decir unas palabras aparte sobre las paradojas identificadas durante la investigación. Esas discrepancias obtenidas en la primera etapa de la transformación, que se expresaron en diferentes inclinaciones de la recta equivalente, sugieren que pueden ser usadas para convertir el comercio aleatorio en no aleatorio, u ofrecer varios amplificadores para las señales comerciales.

En otras palabras, podemos obtener de algunas estrategias cero, estrategias con un factor de beneficio positivo, usando solo estos trucos con la transformación de múltiples estados en equivalentes dobles que ya puedan ser procesados ​​por otros métodos y mejorando su calidad. Si bien estos pensamientos están demasiado dispersos para reunirlos, sin duda llegaremos a ello. A nuestro juicio, este es el principal resultado del estudio, porque nos resultará útil más adelante al montar el asesor.

Conclusión

En este artículo, hemos intentado no realizar una descripción exhaustiva, por lo que no nos hemos prodigado en detalles. Obviamente, no hemos podido evitar el uso de matemáticas, pero, teniendo en cuenta la experiencia de artículos anteriores, hemos observado que la información general resulta mucho más útil que los detalles en sí. Si el lector desea comprender con más detalle las complejidades del método, el artículo adjunta al final el programa en el que se ha realizado la investigación. No vamos a describir todos los algoritmos usados allí, porque implican muchas matemáticas aburridas (aunque importantes), y básicamente se trata de trabajar con matrices de datos y otras matrices. Sea como fuere, quien haga algo por el estilo se ceñirá a su propia lógica, pero como punto de partida, podemos tomar algo de ahí.

Si no queremos resolverlo, podemos simplemente jugar con diferentes estrategias y ver cómo se combinarán, ya que hemos desarrollado estos programas específicamente para el artículo, en realidad, como hemos hecho antes. Si hablamos de lo que sucederá a continuación, seguramente iremos pasando de forma gradual a los detalles y comenzaremos a escribir un genial algoritmo de autoadaptación que, esperamos, podrá superar las redes neuronales tanto en calidad como en estabilidad. Ya tenemos algunos desarrollos, pero primero debemos completar la base.

Enlaces

• Combinatoria y teoría de la probabilidad en el trading (Parte I): Fundamentos
  
• Combinatoria y teoría de la probabilidad en el trading (Parte II): Fractal universal
  
• Combinatoria y teoría de la probabilidad en el trading (Parte III): Primer modelo matemático
• Combinatoria y teoría de la probabilidad en el trading (Parte IV): Lógica de Bernoulli