Combinatoria y teoría de la probabilidad en el trading (Parte III): Primer modelo matemático

MetaTrader 5 — Trading | 6 octubre 2021, 11:17

731

Evgeniy Ilin

Contenido

Introducción

En el último artículo, obtuvimos la primera fórmula para fractales, que hizo bastante posible describir todas las magnitudes importantes para describir un fractal usando un modelo matemático. La simulación no pretende describir dichas magnitudes, sino simplemente ayudar a recopilar los primeros datos para poder analizar estas estructuras más profundamente. En este artículo, hemos decidido prestar especial atención a la descripción del proceso completo de desarrollo del primer modelo matemático hasta obtener el modelo matemático en sí, que se puede usar en los más diversos asesores.

Nuevas ideas

Al analizar el fractal simétrico en el artículo anterior, obtuvimos una fórmula general para calcular el número promedio de saltos por los que pasa el precio como resultado del movimiento dentro de un determinado corredor, definido por el número de los mismos corredores simétricos y más pequeños. Aquí está la fórmula mencionada:

S = K^2 - número promedio de saltos del nuevo corredor, basado en que el salto es otro corredor
P = K * P0 --> K = P/P0 - cuántas veces mayor es el corredor conocido que el desconocido
P - anchura del corredor, cuyo número promedio de saltos desconocemos (los saltos son la mitad del tamaño del corredor original)
P0 - anchura del corredor conocido

Para poder describir un corredor asimétrico, deberemos redefinir algunos de los conceptos de arriba, para que resulten más comprensibles. Lo más importante aquí es "K". De hecho, este número muestra el número de saltos por los que debe pasar el precio en un nuevo corredor, siempre que los saltos se realicen solo hacia arriba o solo hacia abajo. Para un corredor simétrico, resulta intuitivamente claro que no importa qué límite analicemos (crucemos), el inferior o el superior: el número dado de saltos adquirirá el mismo valor en vista del carácter especular de este problema, tanto para el límite superior como para el límite inferior. En el caso de la asimetría, como resultado de los experimentos realizados con el código del artículo anterior, hemos obtenido que el número promedio de satos para este caso se determina de la forma siguiente:

S = n * m - número promedio de saltos cuando al darse mitades asimétricas del corredor
n - número de saltos que caben en la mitad superior del corredor
m - número de saltos que caben en la mitad inferior del corredor

De aquí podemos colegir que, en el caso de un corredor simétrico, tendremos: "m = n". Bueno, por supuesto, partiendo de esto:

S = n * n = m * m = m * n = n^2 = m^2 = K^2
K = n = m

Es decir, la primera fórmula que hemos obtenido es solo un caso especial de la anterior, y ya no necesitamos "K".

Una característica interesante de esta función es que S(a*k, b*k) = S(a,b) * S(k,k), lo cual es muy fácil de demostrar:

S(n*k ,m*b) = m*k*n*b = n*m * k*b
S(n ,m) * S(k ,b) = n*m * k*b

Esta propiedad resulta muy interesante si la miramos y pensamos correctamente. Por supuesto, no ofrece ninguna idea directamente, pero si realizamos consideraciones adicionales, puede proporcionar la derivación de todas las fórmulas necesarias para describir el fractal completo. Esta propiedad solo refleja una propiedad muy importante de cualquier fractal: la posibilidad de anidamiento. En otras palabras, cualquier fractal finito de gran complejidad puede representarse como dos o más fractales simples que desempeñan el papel de saltos entre sí. Esta propiedad sigue siendo necesaria para extrapolar esta fórmula a casos más complejos.

Antes de continuar nuestras reflexiones, debemos recordar que las fórmulas anteriormente definidas funcionan solo si “p=0.5”. En cuanto los parámetros del mercado o de nuestro fractal comiencen a desviarse respecto al paseo aleatorio, esta fórmula cambiará de forma muy interesante, a saber:

Ss[n,m,p] es una fórmula más general para el número promedio de saltos (en cualquier dirección)
S(n ,m) = Ss[n,m,0,5] – la fórmula para un paseo aleatorio es un caso especial de la fórmula general

Fórmula general del número medio de saltos y sus consecuencias

Para determinar la forma de una fórmula más general, hemos usado la invariancia del principio de anidación fractal. Resulta interesante que si analizamos algún nivel particular de anidación fractal en relación con el anterior, es posible que no pensemos en qué saltos han tenido lugar en un salto en particular. Esto significa que los saltos primarios hacia arriba y hacia abajo tienen lugar precisamente con las proporciones de frecuencias que se correspondían con la situación del nivel anterior. En otras palabras, la situación en la que se cruza uno de los límites del nivel de anidación correspondiente supone un salto hacia arriba o hacia abajo para el siguiente nivel de anidación aparecido después. Pero también sabemos que la relación de la frecuencia de aparición de los saltos para el nivel de anidación actual no dependerá de la configuración del nivel actual. Esto significa que el principio de anidación de fractales se observa para cualquier probabilidad "p". Esto, a su vez, nos indica que cuando cambia el valor de "p", nuestra fórmula debería cambiar también, pero de alguna manera preservar su propiedad de anidación. Un simple experimento podrá ayudarnos a determinar el tipo de fórmula general. Sabemos que la probabilidad “p” tiene un punto de un paseo aleatorio y dos puntos extremos más con cero y uno. Vamos a ver qué valores tomará nuestra función en estos tres puntos. Después de analizar los resultados de los cálculos, obtendremos lo siguiente:

Ss[n,m,1] = Sn[n] = n
Ss[n,m,0] = Sm[m] = m
Ss[n,m,0.5] = Sn[n] * Sm[m] = m*n
Sn[n,p] – número de saltos en una dirección hasta el límite superior
Sn[m,p] – número de saltos en una dirección hasta el límite inferior

Resulta sencillo adivinar que en el primer caso no tenemos absolutamente ningún salto hacia abajo y todas las cadenas siguen la misma ruta. En el segundo, sin embargo, todo es igual, solo que exactamente al revés: los saltos solo ocurrirán hacia abajo. Podemos ver que en los valores extremos, uno de los multiplicadores parece desaparecer por completo de la fórmula. Esto resulta posible si lo elevamos a cero. El grado cero convierte cualquier número en uno. Además, el grado tiene una invariancia de la forma:

A^X * B^X = (A*B)^X

Si imaginamos nuestros saltos promedio en lugar de estos números, significará que ambos mantendremos el principio de anidación de fractales en funcionamiento, y podremos entender que este grado no depende de “nym”. Como resultado, la fórmula general para el número promedio de saltos tendrá el aspecto que sigue:

Ss[m,n,p] = ( Sn[n] ^ Pn[p] ) * ( S[m] ^ Pm[p] ) = (n ^ Pn[p] ) * ( m ^ Pm[p] )

Si representamos esquemáticamente cómo se verá el principio de anidación de fractales, podremos mostrarlo así:

Cadenas de productos

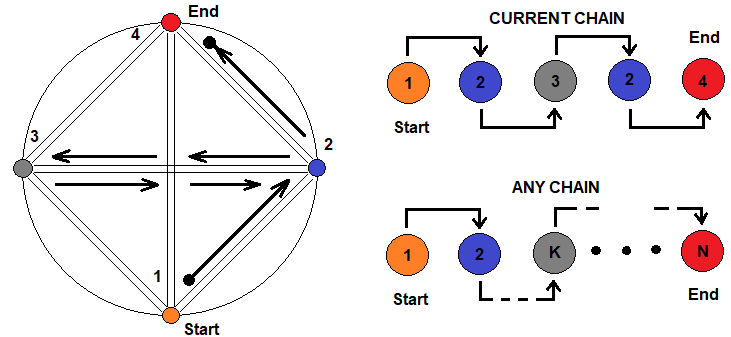
En esta figura, tenemos cuatro estados que simbolizan diferentes fractales, pero que pueden expresarse unos a través de otros. La transición de un estado a otro es posible usando cualquier cadena. A la derecha, se dibuja una cadena elegida arbitrariamente, y un poco más abajo, se muestra que esta cadena puede tener cualquier longitud y complejidad, y que puede pasar por el mismo estado un número ilimitado de veces. Todo esto significa que la fórmula para calcular el número promedio de saltos fractales se puede representar como una cadena de productos que representan los niveles de anidación de los fractales.

Construyendo el prototipo de la función exponencial

Lo que sucederá a continuación, procede de la propiedad de anidación de los fractales y de la invariancia de las funciones de potencia con el mismo grado, en relación con la base. Todos estos principios matemáticos nos ayudarán en el futuro a derivar fórmulas que describan los fractales en mayor profundidad. Resulta que obtenemos dos funciones adicionales cuya forma desconocemos:

Pn [p] - grado para el multiplicador del límite superior
Pm [p] - grado para el multiplicador de límite inferior

Pero sabemos que:

Pn[0.5] = 1 , Pn[1] = 1 , Pn[0] = 0
Pm[0.5] = 1 , Pm[1] = 1 , Pm[0] = 0

Si comprendemos las funciones de potencia, podremos construir un prototipo adecuado para esta función. Hemos elegido este prototipo:

Pn[p] = 1 , if p >= 0.5
Pn[p] = ( (1 – p)/0.5 ) ^ K
Pm[p] = 1 , if p <= 0.5
Pm[p] = ( p/0.5 ) ^ K
K - grado que regula la planitud de la función

En realidad, sería más exacto representar "2" y "4" como polinomios más precisos que puedan describir con mayor precisión la transición suave de un grado dado, pero, en nuestra opinión, esto sería redundante. Si alguien desea definir polinomios más precisos, aquí tenemos los prototipos para ellos:

Pn[p] = C1 * ( (1 – p)/0.5 ) ^ K1 + C2 * ( (1 – p)/0.5 ) ^ K2 … + … + CN * ( (1 – p)/0.5 ) *KN
Pm[p] = C1 * ( p/0.5 ) ^ K1 + C2 * ( p/0.5 ) ^ K2 … + … + CN * ( p/0.5 ) ^ KN
С1 + С2 + … + … СN = 1 – coeficientes de peso del grado correspondiente
KN – grado del término correspondiente

Si miramos de cerca el polinomio general, podremos entender que el polinomio elegido es una versión más simple del general, con un solo término. Todos los principios aquí declarados se pueden verificar comprobando la fracción “n,m”, que será al mismo tiempo la confirmación indirecta adicional de lo anteriormente mencionado.

Para verificar estas suposiciones, crearemos el siguiente programa:

Comprobación de las fórmulas

Como podemos ver en los resultados del programa, todo funciona como necesitamos, y eso es suficiente. Para asegurarnos de ello, solo necesitamos comparar dos números; si estos coinciden, tanto el principio de anidación como la posibilidad de usar las fracciones “n,m” estarán confirmados.

Esquema general para obtener la mejor función de la familia limitada por el prototipo

Una vez comprobado el principio de anidación, deberemos decidir cómo se realizará la búsqueda de los coeficientes necesarios para el prototipo. Hemos elegido el tipo de búsqueda más simple y comprensible: la generación de números aleatorios en el rango requerido. El esquema de este método tendrá el aspecto siguiente:

Esquema del aproximador

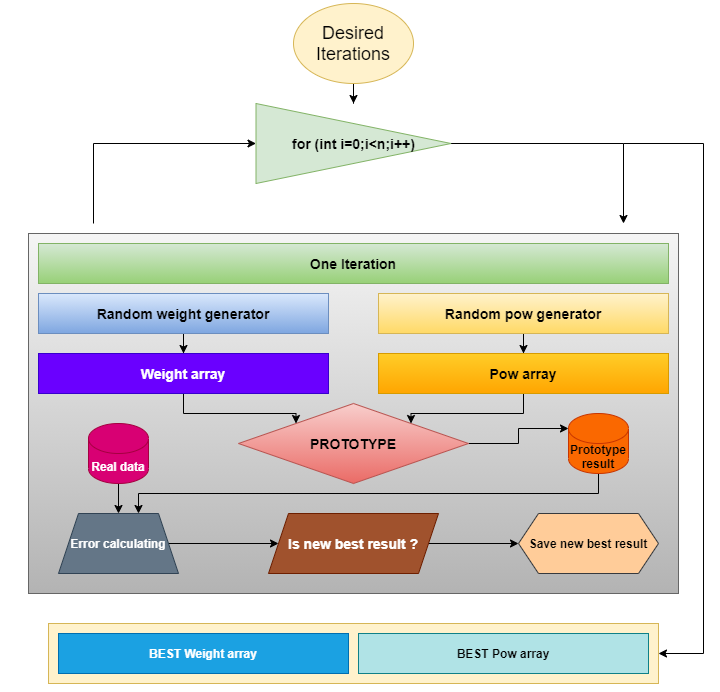
Lo más agradable es que este esquema resulta adecuado para cualquier prototipo de función cuyos coeficientes deban seleccionarse para hacer coincidir mejor los datos reales con el modelo matemático. Este esquema tendrá más validez, ya que hacia el final del artículo utilizaremos el mismo método para procesar otro prototipo.

Análisis profundo

Ahora, vamos a realizar un análisis más profundo de la estructura de esta fórmula y lo que describe. El resultado de la fórmula es el número promedio de saltos que atraviesa el precio antes de cruzar uno de los límites. En este caso, los saltos hacia arriba y hacia abajo se consideran iguales, pero en realidad esta igualdad solo resulta posible en el caso de un paseo aleatorio. Estas cosas no resultan suficientes para conseguir una descripción completa de un fractal asimétrico, por lo que necesitaremos definir en qué consiste realmente la magnitud dada. Parece intuitivamente claro que, en teoría, el número promedio de saltos, independientemente del tipo que tengan, dependerá tanto del número promedio de saltos al cruzar el límite superior como del número promedio de saltos al cruzar el límite inferior. Vamos a introducir estos valores primero para el caso en que se cruza el límite superior:

SP[U,ud] = S[U,u] * P[U] + S[U,d] * P[U] = (S[U,u] + S[U,d]) * P[U] = S[U] * P[U]
S[U] – número promedio de saltos (no importa su cantidad), siempre que la cadena de saltos haya alcanzado primero el límite superior
S[U,u] – número promedio de saltos hacia arriba, siempre que la cadena de saltos alcance primero el límite superior
S[U,d] – número promedio de saltos hacia abajo, siempre que la cadena de saltos alcance primero el límite inferior
P[U] – probabilidad de que el límite inferior se cruce primero
SP[U,ud] – número probabilístico promedio de saltos para cruzar el límite superior

Para cruzar el límite inferior, las fórmulas resultarán similares:

SP[D,ud] = S[D,u] * P[D] + S[D,d] * P[D] = (S[D,u] + S[D,d]) * P[D] = S[D] * P[D]
S[D] – número promedio de saltos (no importa su cantidad), siempre que la cadena de saltos haya alcanzado primero el límite inferior
S[D,u] – número promedio de saltos hacia arriba, siempre que la cadena de saltos alcance primero el límite inferior
S[D,d] – número promedio de saltos hacia abajo, siempre que la cadena de saltos alcance primero el límite inferior
P[D] – probabilidad de que el límite inferior se cruce primero
SP[D,ud] – número probabilístico promedio de saltos para cruzar el límite inferior

Y por supuesto está claro que:

S = SP[U,ud] + SP[D,ud]

Simplificando el concepto completo, podemos decir que el resultado de todas estas valoraciones es el hecho de que todas las magnitudes que podamos obtener al final y que nos interesen, dependerán de cinco magnitudes fundamentales:

S[U,u] = SP[U,u]/P[U] – número promedio de saltos hacia abajo, siempre que la cadena de saltos alcance primero el límite superior
S[U,d] = SP[U,d]/P[U] – número promedio de saltos hacia abajo, siempre que la cadena de saltos alcance primero el límite superior
S[D,u] = SP[D,u]/P[D] – número promedio de saltos hacia arriba, siempre que la cadena de saltos alcance primero el límite inferior
S[D,d] = SP[D,d]/P[D] – número promedio de saltos hacia abajo, siempre que la cadena de saltos alcance primero el límite inferior
P[U] – probabilidad de que el límite inferior se cruce primero

Buscaremos fórmulas para estas magnitudes basadas en los resultados de la operación fractal con diferentes parámetros de entrada. En el último artículo, seleccionamos las siguientes magnitudes como salida del fractal:

SP[U,u] – número probabilístico promedio de saltos hacia arriba, siempre que la cadena de saltos alcance primero el límite superior
SP[U,d] – número probabilístico promedio de saltos hacia abajo, siempre que la cadena de saltos alcance primero el límite superior
SP[D,u] – número probabilístico promedio de saltos hacia arriba, siempre que la cadena de saltos alcance primero el límite inferior
SP[D,d] – número probabilístico promedio de saltos hacia abajo, siempre que la cadena de saltos alcance primero el límite inferior
P[U] – probabilidad de que el límite inferior se cruce primero
P[D] – probabilidad de que el límite inferior se cruce primero
S = SP - número promedio de saltos de cualquier tipo

Vamos a agrupar por separado los elementos que se pueden expresar como magnitudes fundamentales:

SP[U]
S[U,ud] = S[U,u] + S[U,d]
S[D,ud] = S[D,u] + S[D,d]
P[D] = 1 – P[U]
S = SP[U,ud] + SP[D,ud]

Para tener la oportunidad de descubrir las matemáticas de los fractales, realizaremos un análisis bastante extenso; en resumen, todo se podrá reunir en un esquema bastante compacto que reflejará el proceso completo de búsqueda del modelo matemático obtenido:

Secuencia de búsqueda del modelo matemático

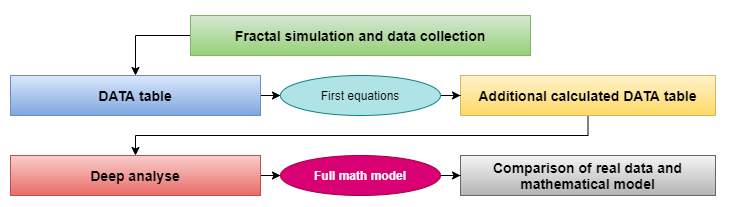
Recopilación de datos y conclusiones

Como resultado de un examen más detallado de los resultados del cálculo del fractal, hemos observado que las seis magnitudes inicialmente determinadas al construir el concepto de fractal universal están matemáticamente relacionadas. Inicialmente, realizamos pruebas en los límites simétricos e intentamos aislar cualquier dependencia entre estos valores, y conseguimos algo. Hemos hecho los cálculos para diez casos diferentes y ha resultado ser suficiente:

Índice de la prueba	Saltos en la mitad superior del corredor ( n )	Saltos en la mitad inferior del corredor ( m )	Probabilidad del salto inicial ( p )	Número probabilístico promedio de saltos superiores para el límite superior ( SP[U,u] )	Número probabilístico promedio de saltos inferiores para el límite superior ( SP[U,d] )	Número probabilístico promedio de saltos superiores para el límite inferior ( SP[D,u] )	Número probabilístico promedio de saltos inferiores para el límite inferior ( SP[D,d] )	Número probabilístico promedio de cualquier salto para el límite superior ( SP[U,ud] )	Número probabilístico promedio de cualquier salto para el límite inferior ( SP[D,ud] )
1	1	1	0.5	0.5	0	0.0	0.5	0.5	0.5
2	2	2	0.5	1.5	0.5	0.5	1.5	2.0	2.0
3	3	3	0.5	3.0	1.5	3.0	1.5	4.5	4.5
4	1	2	0.5	0.888888	0.2222222	0.111111	0.777777	1.11111111	0.8888888
5	2	3	0.5	2.2	1.0	0.8	2.0	3.2	2.8
6	1	2	0.6	1.038781	0.249307	0.066481	0.487534	1.288088	0.554016
7	2	3	0.6	2.811405	1.191072	0.338217	0.906713	4.0024777	1.244931
8	2	3	1.0	2.0	0.0	0.0	0.0	2.0	0.0
9	1	3	0.5	1.25	0.5	0.25	1	1.75	1.25
10	1	4	0.5	1.6	0.8	0.4	1.2	2.4	1.6

A continuación se muestra un recuadro con las magnitudes calculadas que no se muestran en el log del fractal. Los necesitaremos para valorar las dependencias entre magnitudes:

Índice de la prueba	Saltos en la mitad superior del corredor ( n )	Saltos en la mitad inferior del corredor ( m )	Probabilidad de cruzar el límite superior ( P(U) )	Probabilidad de cruzar el límite inferior ( P(D) )	Número promedio de saltos al cruzar el límite superior (S[U,ud]) = SP[U,ud]/P[U]	Número promedio de saltos al cruzar el límite inferior (S[D,ud]) = SP[D,ud]/P[D]	Número promedio de saltos superiores para el límite superior ( S[U,u] ) = SP[U,u]/P[U]	Número promedio de saltos inferiores para el límite superior ( S[U,d] ) = SP[U,d]/P[U]	Número promedio de saltos superiores para el límite inferior ( S[D,u] ) = SP[D,u]/(P[D])	Número promedio de saltos inferiores para el límite inferior ( S[D,d] ) = SP[D,d]/(P[D])	Número promedio de saltos ( S )
1	1	1	0.5	0.5	1.0	1.0	1.0	0.0	0.0	1.0	1
2	2	2	0.5	0.5	4.0	4.0	3.0	1	1	3	4
3	3	3	0.5	0.5	9.0	9.0	6	3	3	6	9
4	1	2	0.66666	0.3333333	1.6666666	2.6666666	1.3333333	0.33333333	0.33333333	2.33333333	2
5	2	3	0.6	0.4	5.3333333	7	3.6666666	1.66666666	2	5	6
6	1	2	0.789473	0.210526	1.631579	2.631579	1.315790	0.315789	0.315789	2.315789	1.842104
7	2	3	0.810166	0.189498	4.940318	6.569626	3.470159	1.470157	1.784805	4.784	5.2474087
8	2	3	1.0	0.0	2.0	0.0	2.0	0.0	0.0	0.0	2.0
9	1	3	0.75	0.25	2.3333333	5	1.6666666	0.6666666	1	4	3
10	1	4	0.8	0.2	3.0	8.0	2	1	2	6	4

Tras analizar cuidadosamente este recuadro, podemos encontrar las dos primeras ecuaciones que necesitamos para calcular las cuatro incógnitas a partir de las cuales se componen todas las demás magnitudes. Podemos obtener estas fórmulas mirando las columnas “S[U,u], S[U,d], S[D,u], S[D,d]”. Resulta muy interesante que los números allí obtenidos tengan la misma parte fraccionaria por pares en las columnas “S[U,u], S[U,d]” y en “ S[D,u], S[D,d]”. Entre otras cosas, podemos ver que “S[U,u] > S[U,d]” y “S[D,d] > S[D,u]”. Si restamos estas magnitudes por pares y las comparamos con "m, n", resultará que esta diferencia es exactamente igual al número correspondiente de saltos hasta el límite superior o inferior:

S[U,u] – S[U,d] = n
S[D,d] – S[D,u] = m

De esta forma, obtendremos dos ecuaciones muy importantes que nos ayudarán a definir las magnitudes fundamentales. Obviamente, las dos ecuaciones no bastarán para ello, pero podremos obtener dos ecuaciones más que nos permitirán determinar las mismas magnitudes, solo que partiendo de una lógica ligeramente distinta. Partiendo del hecho de que si realizamos experimentos con un fractal durante un tiempo infinitamente largo, entonces nos preguntaremos sobre la relación entre la frecuencia de aparición de los saltos hacia arriba y hacia abajo, no resultará difícil adivinar que estas frecuencias son proporcionales a las probabilidades correspondientes.

Estos ratios se pueden obtener si suponemos que:

Lim[N0 -- > +infinity] (N0[U]/N0) = p
Lim[N0 -- > +infinity] (N0[D]/N0) = 1-p
Lim[N0 -- > +infinity] (N0[U]/N) = S[UD,u]
Lim[N0 -- > +infinity] (N0[D]/N) = S[UD,d]
Lim[N0 -- > +infinity] (N0/N) = S
N0 – número de experimentos elementales realizados con los saltos iniciales (forman una experiencia compleja)
N – número de experimentos complejos que se componen a partir de experimentos simples

Si introducimos el multiplicador "N0/N0 = 1" en "3" y "4" y organizamos correctamente las fracciones en el interior, tendremos que:

Lim[N0 -- > +infinity] (N0[U]/N) = Lim[N0 -- > +infinity] (N0[U]/N0 * N0/N) = Lim[N0 -- > +infinity] (N0[U]/N0) * Lim[N0 -- > +infinity] (N0/N) = p*S = S[UD,u]
Lim[N0 -- > +infinity] (N0[D]/N) = Lim[N0 -- > +infinity] (N0[D]/N0 * N0/N) = Lim[N0 -- > +infinity] (N0[D]/N0) * Lim[N0 -- > +infinity] (N0/N) = (p-1)*S = S[UD,d]

El límite del producto se puede representar como el producto de los límites, si cada uno de estos límites es un número finito y no alcanza ni más ni menos infinito. En este caso, queda claro que ambos límites son precisamente de esa naturaleza. Así se muestran estas fórmulas. Como resultado, obtendremos las fórmulas correspondientes:

S[UD,u] = S*p
S[UD,d] = S*(1-p)

Será mejor expresar estos valores en términos fundamentales; entonces obtendremos las dos ecuaciones restantes para determinar todo lo que necesitamos:

S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)

Como resultado, encontraremos que hay cinco incógnitas en las cuatro ecuaciones. La quinta incógnita supone una de las probabilidades que conforman un grupo completo (las probabilidades de alcanzar uno de los límites). Para poder encontrar las cinco incógnitas, deberemos obtener una quinta ecuación, porque un sistema de ecuaciones solo puede tener una solución única si el número de ecuaciones es igual al número de incógnitas. La quinta ecuación se puede obtener intuitivamente si sabemos que representa la diferencia entre los saltos superiores e inferiores. De forma ideal, este sería el límite:

Lim[Nt[U] -- > +infinity] ((N0[U] - N0[D])/(Nt[U] - Nt[D]) = 1
Nt[U] = – número ideal de saltos básicos hacia arriba, calculado usando la probabilidad del salto básico hacia arriba
Nt[D] – número ideal de saltos básicos hacia abajo, calculado usando la probabilidad del salto básico hacia abajo
N0[U] – número real de saltos básicos
N0[D] – número real de saltos básicos hacia abajo

De forma similar, podemos encontrar un límite similar usando las probabilidades de cruzar los límites:

Lim[Nb[U] -- > +infinity] ((N0[U] - N0[D])/(Nb[U] - Nb[D]) = 1
Nb[U] – número ideal de saltos básicos hacia arriba, calculado usando la probabilidad de cruzar el límite superior
Nb[D] – número ideal de saltos básicos hacia abajo, calculado usando la probabilidad de cruzar el borde inferior
N0[U] – número real de saltos básicos
N0[D] – número real de saltos básicos hacia abajo

Partiendo de estos dos límites, podemos crear uno más complejo, por ejemplo, su suma, su diferencia o su producto o cociente. Vamos a elegir el cociente, así reduciremos la siguiente expresión, que nos salvará por completo del límite “N0[U] - N0[D]”. Como resultado, dividiendo ambos límites y transformando la ecuación, obtendremos lo siguiente:

P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S

Esta será nuestra quinta ecuación, partiendo de la cual podremos encontrar inmediatamente las probabilidades de cruzar los límites. Como resultado, conseguiremos un sistema de cinco ecuaciones. Este será su aspecto:

S[U,u] – S[U,d] = n
S[D,d] – S[D,u] = m
S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)
P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S = 2*p*S - S

Por cierto, un hecho interesante es que el sistema inicial de ecuaciones de cuatro incógnitas al final simplemente conduce a la misma ecuación. Podemos resolver este sistema de la forma clásica, eliminando sucesivamente las variables:

--> S[U,u] = n + S[U,d] – eliminamos “S[U,u]”
--> S[D,d] = m + S[D,u] – eliminamos “S[D,d]”
(n + S[U,d]) * P[U] + S[D,u] * ( 1 – P[U] ) = S*p – sustituimos todos los “3” en la ecuación
S[U,d] * P[U] + (m + S[D,u]) * ( 1 – P[U] ) = S*(1-p) – sustituimos todos los “4” en la ecuación

Después de realizar estas transformaciones, solo nos queda restar la ecuación “3” de “4”, y obtendremos la misma ecuación que hemos obtenido intuitivamente, confirmando así tanto el sistema de ecuaciones que obtuvimos inicialmente como la corrección de nuestros ideas. Pero, desafortunadamente, este sistema está tan organizado que no podemos obtener las cuatro magnitudes restantes. Inicialmente, asumimos que este sistema nos daría aun así todo lo que necesitamos, pero no. Para entender qué nos falta, hemos tenido que analizar con cierto detalle ese recuadro con los datos de los fractales e identificar de forma consistente la fórmula para una de estas cuatro magnitudes. Resulta muy positivo que, tras encontrar una fórmula para una de estas magnitudes, podamos usar el sistema resultante para encontrar todas las demás. No obstante, el sistema es útil.

Algoritmo para calcular el modelo matemático completo

En primer lugar, vamos a definir las ecuaciones inversas y su secuencia de uso para, conociendo “S[U,u]”, encontrar las demás magnitudes. Elegimos este valor porque hemos podido encontrar fórmulas para calcular dicha magnitud. Si la usamos, podemos encontrar inmediatamente el valor "S[U,d]" utilizando la primera ecuación:

S[U,d] = S[U,u] – n

Luego, podemos sustituir ambas magnitudes en las ecuaciones “3”, “4” y encontrar las magnitudes restantes “S[D,u]”, S[D.d]. Podemos calcular las magnitudes "S[D,u]" directamente, partiendo de la tercera ecuación:

S[D,u] = ( S*p – S[U,u] * P[U] ) / ( 1 – P[U] )

Solo nos queda obtener la fórmula para la última incógnita. Para ello, sustituimos la expresión obtenida para “S[U,d]” en la cuarta ecuación:

S[D,d] = ( S*(1-p) - S[U,d] * P[U]) / ( 1 – P[U] ) = ( S*(1-p) - ( S[U,u] – n ) * P[U] ) / ( 1 – P[U] )

Lo único que nos falta es el valor “P[U]”, que podemos obtener fácilmente resolviendo la quinta ecuación. Manos a la obra:

P[U] * n – (1 - P[U]) * m = 2*p*S – S
--> P[U] * (n + m) = 2 * p * S – S + m
--> P[U] = ( 2 * p * S – S + m ) / (n + m)

Los valores conocidos en este caso serán los siguientes números:

n - número de saltos superiores hasta el límite superior
m - número de saltos inferiores hasta el límite inferior
p - probabilidad del salto hacia arriba inicial
S[U,u] – número promedio de saltos superiores, siempre que se cruce el límite superior
P[U] - probabilidad de cruzar el límite superior

El valor “4” se calcula como ya lo hemos definido:

S[U,u] = Ss[m,n,p] = (n ^ Pn[p] ) * ( m ^ Pm[p] )
Pn[p] = 1 , if p >= 0.5
Pn[p] = ( (1 – p)/0.5 ) ^ K
Pm[p] = 1 , if p <= 0.5
Pm[p] = ( p/0.5 ) ^ K
K - grado que regula la planitud de la función

Calcularemos el coeficiente de planitud en un programa aparte un poco más tarde. Queda por determinar la magnitud calculada más importante. Como resultado del análisis de la magnitud del recuadro "S[U,u]" para los límites simétricos, hemos identificado las fórmulas incluso para dos magnitudes:

S[U,u] = Summ[ i = 0, n] ( i ) ; if n == m
S[U,d] = Summ[ i = 0, n] ( i-1 ) ; if n == m

El problema es que estas fórmulas solo funcionan para "p = 0.5" y los límites simétricos. Debemos expandir el concepto de estas fórmulas para los casos en que se dan límites asimétricos; luego podremos extenderlo a los casos en que tenemos distintos valores de “p”. Antes de abordar dichas generalizaciones, tenemos que considerar que los resultados de la prueba en el recuadro son aplicables solo a los casos “m> n”. En el caso de que “m <n”. Las fórmulas funcionarán ya para los valores “S[D,d], S[D,u]”. En este caso, deberemos crear un análogo especular del algoritmo para encontrar las demás magnitudes desconocidas.

De la misma forma, definiremos las ecuaciones inversas y su secuencia de uso, teniendo solo en cuenta que ya estamos usando “S[D,d]”. De la misma forma que en el algoritmo anterior, encontraremos el valor “S[D,u]” usando la segunda ecuación:

S[D,u] = S[D,d] – m

Luego, podemos sustituir ambas magnitudes en las ecuaciones “3”, “4” y encontrar las magnitudes restantes “S[U,u]”, S[U.d]. El valor "S[U,d]" se puede calcular directamente, partiendo de la cuarta ecuación:

S[U,d] = ( S*(1-p) - S[D,d] * ( 1 – P[U] ) ) / P[U]

Solo nos queda obtener la fórmula para la última incógnita. Para ello, sustituiremos la expresión obtenida para “S[U,d]” en la tercera ecuación:

S[U,u] = ( S*p – ( S[D,d] – m ) * ( 1 – P[U] ) ) / P[U]

Como resultado, hemos obtenido todos los datos necesarios para extrapolar las fórmulas “S[U,u], S[D,d]” a los casos “n != m”. Como resultado del análisis de los datos del recuadro, hemos obtenido los datos siguientes:

m > n, p = 0,5
S[U,u] = Summ[ i = 0 … n] ( i ) + (m-1)/3

Y, por supuesto, para el caso inverso:

m < n, p = 0,5
S[D,d] = Summ[ i = 0 … m] ( i ) + (n-1)/3

Para el caso estándar de los límites simétricos, naturalmente, todo esto resultará más simple:

m = n, p = 0,5
S[U,u] = Summ[ i = 0 … n] ( i )
S[D,d] = Summ[ i = 0 … m] ( i )

Prototipos para obtener la última ecuación

Ahora, procederemos a definir un prototipo de función modificada que describirá “S[U,u], S[D,d]” para todos los valores posibles de “p”. Para construir el prototipo de trabajo básico, necesitaremos tres puntos en el eje p y algunas suposiciones sobre la estructura general. A nuestro juicio, será suficiente considerar dos tipos de función genérica:

Sp[U,u] = S[U,u] ^ K(p)
Sp[D,d] = S[D,d] ^ K(q)
q = 1-p

El primer tipo puede ser tanto un prototipo de trabajo real como una especie de marcador que indique que una estructura es diferente y que se requiere una lógica de pensamiento distinta. Así lo hemos hecho, y resulta que la función de potencia es casi infaliblemente capaz de reunir todos los datos. Obviamente, podríamos crear prototipos más complejos y próximos a la verdad, pero esto resultaría redundante aquí. Lo más importante es comprender la lógica del pensamiento, y si alguien quiere pulir el modelo hasta la perfección, lo podrá hacer de forma muy simple usando nuestros datos como base. Vamos a crear un programa de prueba para este propósito:

Funciones encontradas basadas en prototipos

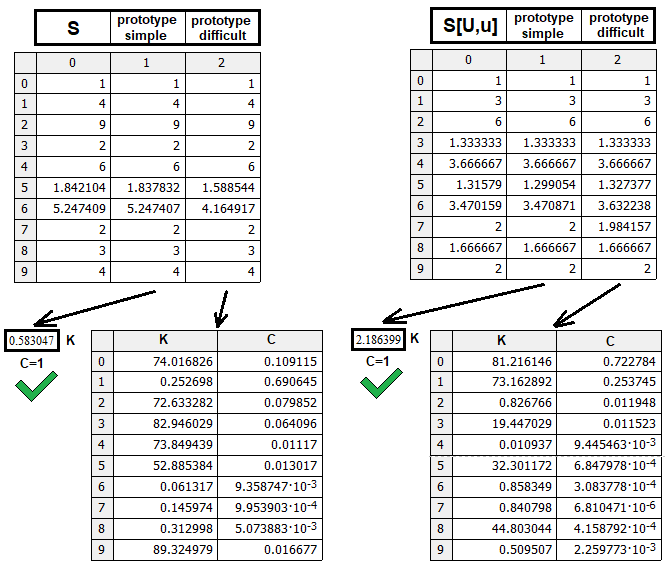
Aquí hay una comprobación para ambos prototipos “S(n,m,p), S[U,u](n,m,p) ” a la vez. No es necesario comprobar el prototipo “S[D,d](n,m,p)”, ya que esta función tiene un carácter especular respecto a “S[U,u](n,m,p)”, en el sentido de que ”S[D,d](n,m,p) = S[U,u](m,n,p-1)”. Esta figura compara la calidad de los prototipos encontrados según su eficiencia. Para encontrarlos, cada prototipo se ha probado con el mismo número de combinaciones aleatorias de coeficientes de peso y potencia en la fórmula, y, obviamente, los prototipos más simples con el mismo número de ciclos de búsqueda han dado un resultado más "bonito". No obstante, si queremos, podemos realizar cálculos que consuman mucho tiempo y ver de qué son capaces los prototipos más complejos.

Después de realizar la verificación, deberemos determinar la estructura interna de la función anidada “K(p)”, “K(q)”. En primer lugar, su estructura interna deberá asegurar la coincidencia obligatoria en los puntos “p=0, p=0.5, p=1”, q=0, q=0.5, q=1”. Conocemos los valores de la función en estos puntos, lo cual nos permitirá seleccionar más fácilmente el prototipo deseado:

p = 0.5 ; Sp[U,u] = S[U,u] --> K(0.5) = 1 ,
p = 1.0 ; Sp[U,u] = n = S[U,u]^(Log[S[U,u]-->n]) --> K(1.0) = Log[S[U,u]-->n]
p = 0.0 ; Sp[U,u] = 0 = S[U,u]^(-infinity) --> K(0.0) = -infinity
q = 0.5 ; Sp[D,d] = S[D,d] --> K(0.5) = 1 ,
q = 1.0 ; Sp[D,d] = n = S[D,d]^(Log[S[U,u]-->m]) --> K(1.0) = Log[S[D,d]-->m]
q = 0.0 ; Sp[D,d] = 0 = S[D,d]^(-infinity) --> K(0.0) = -infinity

Las expresiones primera y cuarta indican que el grado debe ser igual a uno en el punto del paseo aleatorio. La segunda y quinta expresiones indican que el grado debe ser tal que al elevarlo obtengamos “n” o “m”, lo cual podemos ver en el recuadro de resultados que tuvimos arriba. Y finalmente, el tercero y sexto indican que el grado debe tender a menos infinito para proporcionar cero. Este hecho implica además que los valores "p" y "q" deben estar en el denominador del prototipo, porque normalmente la división por cero solo produce tales valores límite del tipo infinito. Ya tenemos experiencia en la construcción de un prototipo de potencia para una función; podemos tomar este como base y reelaborarlo. Después de analizar profundamente el problema, hemos llegado a este prototipo:

K(p) = 1 + D * Summ(N) (Kn[0] * | (( p – 0.5 )/(0.5*p)) | ^ A[0] + Kn[1] * | (( p – 0.5 )/(0.5*p)) | ^ A[1] + …. + Kn[N] * | (( p – 0.5 )/(0.5*p)) | ^ A[N])
Kn[0] + Kn[1] + …. Kn[N] = Log[S[U,u]-->n] – 1
D = (( p – 0.5 )/(0.5*p)) / | (( p – 0.5 )/(0.5*p)) |
K(q) = 1 + C * Summ(N) (Km[0] * (( q – 0.5 )/(0.5*q)) ^ B[0] + Km[1] * (( q – 0.5 )/(0.5*q)) ^ B[1] + …. + Km[N] * (( q – 0.5 )/(0.5*q)) ^ B[N])
Km[0] + Km[1] + …. Km[N] = Log[S[D,d]-->m] – 1
C = (( q – 0.5 )/(0.5*q)) / | (( q – 0.5 )/(0.5*q)) |
Kn, Km son los pesos de los términos correspondientes
A, B son la sensibilidad de los términos

La función parece complicada, pero se construye sobre la base de una lógica sencilla. En “p=0.5, q=0.5”, todo lo que se encuentra bajo el signo de la suma se convierte en cero, y solo queda uno, proporcionando así las condiciones “1”, “4”. Si “p=1, q=1”, las fracciones correspondientes dentro de la suma se convertirán en la unidad, que se elevará a una potencia: “|(( p – 0.5 )/(0.5*p)) |”. Debemos señalar que estos términos se encuentran bajo el signo del módulo para excluir los valores complejos de la función al elevarse a una potencia; en lugar de ello, se considera el signo como factor adicional. La potencia deja de actuar en estos términos y la suma total se convierte en los números “ Log[S[U,u]-->n] – 1, Log[S[D,D]-->m] - 1”. Sumando este número con la unidad, obtendremos los valores requeridos de la función: “Log[S[U,u]-->n], Log[S[D,d]-->m]”.

Los polinomios de interpolación se construyen según una lógica similar; un ejemplo de esta sería el polinomio de Lagrange, ampliamente conocido y extendido. Nuestro polinomio se ha pensado para una tarea específica y es aplicable solo aquí: su ventaja es la máxima adaptabilidad a la tarea. Para encontrar la función necesaria de una familia dada de curvas, solo necesitaremos tomar dos matrices de números.

Implementación y prueba del modelo matemático

Gracias a las expresiones obtenidas, resulta muy sencillo implementar la funcionalidad para calcular cualquier fractal. Solo necesitaremos una estructura que será un contenedor con todos los datos que retornará la función principal. El resto de las funciones serán auxiliares. Para nuestro uso, solo necesitamos la última función:

struct MathModel1//structure for the first mathematical model
   {
   double S;//the average number of any steps
   double pU;//the probability that the price will first reach the upper border
   double pD;//the probability that the price will first reach the lower border
   double SUu;//the average number of steps up if the price first reaches the upper border
   double SUd;//the average number of steps down if the price first reaches the upper border
   double SDu;//the average number of steps up if the price first reaches the lower border
   double SDd;//the average number of steps down if the price first reaches the lower border
   
   double SPUu;//the average probable number of steps up if the price first reaches the upper border
   double SPUd;//the average probable number of steps down if the price first reaches the upper border
   double SPDu;//the average probable number of steps up if the price first reaches the lower border
   double SPDd;//the average probable number of steps down if the price first reaches the lower border
   
   double SPUud;//the average probable number of steps in any direction if the price first reaches the upper border
   double SPDud;//the average probable number of steps in any direction if the price first reaches the lower border
   
   double SUDu;//the average number of steps up when reaching any of the borders
   double SUDd;//the average number of steps down when reaching any of the borders
   };

double Ss(int n, int m,double p, double K)//prototype of the function of the average number of steps in any direction when reaching any border
   {
   if (p>=0.5) return n*MathPow(m,MathPow((1-p)/0.5,K));
   else return MathPow(n,MathPow(p/0.5,K))*m;
   }

double Log(double a, double b)//logarithm function for any base
   {
   if (MathLog(a) != 0) return MathLog(b)/MathLog(a);
   else return 0.0;
   }

double SUu(int n,int m)//average number of steps up to the upper border if p=0.5
   {
   double rez=0.0;
   if (m>n)
      { 
      for (int i=0;i<=n;i++) rez+=double(i);
      rez+=(m-1)/3.0;
      }
   if (m==n) for (int i=0;i<=n;i++) rez+=double(i);
   return rez;
   }
   
double SDd(int n,int m)//average number of steps down to the lower border if p=0.5
   {
   double rez=0.0;
   if (n>m)
      { 
      for (int i=0;i<=m;i++) rez+=double(i);
      rez+=(n-1)/3.0;
      }   
   if (m==n) for (int i=0;i<=m;i++) rez+=double(i);
   return rez;
   }   

double KpnEasy(int n,int m, double p,double A)//power prototype for steps up m>=n
   {
   double D;
   if ( p-0.5 != 0 ) D=(p-0.5)/MathAbs(p-0.5);
   else D=1.0;
   return 1.0 + D*(Log(SUu(n,m),n) - 1)*MathPow(((p-0.5)/(0.5*p)),A);
   }

double KpmEasy(int n,int m,double p,double A)//power prototype for steps down m<n
   {
   double D;
   if ( 0.5-p != 0 ) D=(0.5-p)/MathAbs(0.5-p);
   else D=1.0;
   return 1.0 + D*(Log(SDd(n,m),m) - 1)*MathPow(((0.5-p)/(0.5*(1.0-p))),A);
   }
   
double SUuS(int n,int m,double p, double A)//full prototype for average steps up m>=n
   {
   return MathPow(SUu(n,m),KpnEasy(n,m,p,A));
   }
   
double SDdS(int n,int m,double p, double A)//full prototype for average steps down  n>m
   {
   return MathPow(SDd(n,m),KpmEasy(n,m,p,A));
   }      
   
MathModel1 CalculateMathModel(int n, int m, double p,double K=0.582897,double A=2.189246)//calculating the entire mathematical model
   {
   MathModel1 Mt;
   if ( m >= n )
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SUu=SUuS(n,m,p,A);
      Mt.SUd=Mt.SUu-n;
      if (1.0-Mt.pU != 0.0) Mt.SDu=(Mt.S*p-Mt.SUu*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDu=0.0;
      if (1.0-Mt.pU != 0.0) Mt.SDd=(Mt.S*(1.0-p)-Mt.SUd*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDd=0.0;
      }
   else
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SDd=SDdS(n,m,p,A);
      Mt.SDu=Mt.SDd-m;
      if (Mt.pU != 0.0) Mt.SUd=(Mt.S*(1.0-p)-Mt.SDd*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUd=0.0;
      if (Mt.pU != 0.0) Mt.SUu=(Mt.S*p-Mt.SDu*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUu=0.0;      
      }
   
   Mt.SPUu=Mt.SUu*Mt.pU;
   Mt.SPUd=Mt.SUd*Mt.pU;
   Mt.SPDu=Mt.SDu*Mt.pD;
   Mt.SPDd=Mt.SDd*Mt.pD;
   
   Mt.SPUud=Mt.SPUu+Mt.SPUd;
   Mt.SPDud=Mt.SPDu+Mt.SPDd;
   
   Mt.SUDu=Mt.SPUu+Mt.SPDu;
   Mt.SUDd=Mt.SPUd+Mt.SPDd;
   
   return Mt;
   }

Para comprobar este modelo matemático, hemos implementado un análogo de este código en MathCad15; si hemos compuesto el modelo matemático correctamente, los resultados del recuadro coincidirán con el resultado que retornará el modelo matemático. Cualquier lector podrá familiarizarse con el listado de este programa, que se adjunta al artículo. No adjuntamos este listado porque ocuparía demasiado espacio en el artículo, pero el lector definitivamente necesitará verlo. Vamos a comparar las matrices y a asegurarnos de que el modelo matemático sea viable:

Comprobando la precisión del modelo matemático

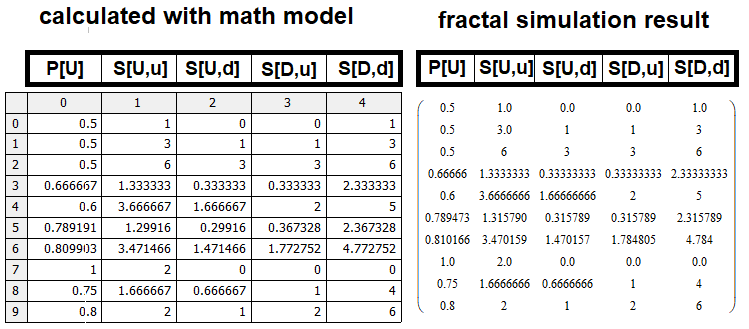
Está claro que en algunos lugares existen pequeñas "rugosidades", pero estas se deben únicamente a la efectividad de los prototipos que hemos encontrado para los valores "S, S[U,u], S[D,d]". Por otra parte, el factor adicional de las diferencias podrían ser los errores de simulación, que resultan mayores cuanto más grandes son los valores de "n, m" que tratamos de simular, ya que nos vemos obligados a limitar la profundidad de la simulación a causa de la falta de potencia de cálculo de las computadoras modernas.

Conclusión

El desarrollo de este modelo matemático ha requerido mucho tiempo, porque hemos tenido que pensar toda la parte matemática desde cero, pero estamos satisfechos con el resultado. En los próximos artículos, intentaremos desarrollar varios modelos matemáticos más universales para que, combinando estos, podamos calcular cualquier configuración comercial según sus principales características. Además, este modelo matemático resultará adecuado no solo para describir los procesos de fijación de precios, sino también para describir las señales comerciales y simplificar las estrategias complejas, reduciéndolas a otras más simples. Y esto nos llevará algún tiempo.

Enlaces

Combinatoria y teoría de la probabilidad en el trading (Parte I): Fundamentos

Combinatoria y teoría de la probabilidad en el trading (Parte I): Fractal universal

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/9570

Archivos adjuntos |

Descargar ZIP

Materials.zip (312.85 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores

Análisis de spread Bid/Ask en MetaTrader 5

Un indicador para informar de los niveles de spread Bid/Ask de sus brókeres. Ahora podremos usar los datos de ticks de MT5 para analizar cuál ha sido realmente el promedio histórico real del spread Bid/Ask reciente. No deberíamos necesitar mirar el spread actual, porque está disponible si mostramos las líneas de precio Bid/Ask.

Gráficos en la biblioteca DoEasy (Parte 82): Refactorización de los objetos de la biblioteca y colección de objetos gráficos

En el presente artículo, mejoraremos todos los objetos de la biblioteca: para ello, asignaremos a cada objeto su tipo único y continuaremos desarrollando la clase de colección de objetos gráficos de la biblioteca.

Explorando opciones para crear velas multicolores

En este artículo, abordaremos las distintas posibilidades de crear indicadores personalizados con velas, señalando sus correspondientes ventajas y desventajas.

Combinatoria y teoría de la probabilidad en el trading (Parte II): Fractal universal

En el presente artículo, continuaremos estudiando los fractales, prestando especial atención a la generalización de todo el material. En concreto, intentaremos hacer el material más compacto y comprensible, para poder usarlo de forma práctica en el trading.