Комбинаторика и теория вероятностей для трейдинга (Часть V): Анализ кривых

Содержание

• Введение
• Полезные формулы для упрощения данных
• Основы полученного метода преобразования
• Определение критериев сводимости
• Определение критериев для сравнения с исходной системой
• Оценка возможного коридора для вычисления необходимых величин
• Определение вероятности и среднего времени до пересечения верхней и нижней границы коридора
• Оценка эффективности простого преобразования
• Финальная корректировка и симуляция
• Выводы
• Заключение
• Ссылки

Введение

Продолжаю собирать основу для сборки многоступенчатых и масштабируемых торговых систем. В рамках данной статьи хочу показать, как можно использовать наработки предыдущих статей, чтобы иметь возможность приблизиться к более широким возможностям для описания процесса торговли. Это поможет оценивать стратегию с тех сторон, с которых не могут это сделать иные методы анализа. В данной статье я исследовал возможности сведения сложных выборок с множественными состояниями к простейшим выборкам с двойными состояниями. Данный анализ был произведен в стиле исследования.

Полезные формулы для упрощения данных

Представьте, что у вас есть стратегия, в которой имеется множество сделок, которые идут друг за другом, не перекрывая друг друга, то есть новый ордер открывается строго после того, как закрылся предыдущий. Если вдруг встает вопрос о вероятностях выигрыша или проигрыша, а также о вычислении среднего времени, за которое будет достигнут выигрыш или проигрыш данной стратегии то мы автоматически сталкиваемся с тем, что ордера могут иметь очень большое число состояний (закрываются с разными результатами).

Для того чтобы можно было применять к таким стратегиям формулы фракталов, необходимо сначала свести эти стратегии, к случаям, которые могут быть рассмотрены в рамках фракталов. Для того чтобы осуществить это, нам всего-то нужно представить нашу стратегию в виде ордера с равноудаленными стопами, у которого присутствует вероятность верхнего шага и нижнего шага, в точности как в нашем фрактале, тогда можно будет применять формулы фрактала. Кроме того, у шага вверх и у шага вниз может быть разное среднее время существования.

Для того чтобы свести любую стратегию к одной из стратегий, которые могут быть описаны в рамках фрактальных формул, которые были получены мною в предыдущей статье, в первую очередь необходимо определить какие величины должны быть известны, для того чтобы можно было применить формулы фракталов. Тут все довольно просто:

• P[1] – вероятность срабатывания верхнего шага
• T[1] – среднее время формирования шага вверх
• T[2] – среднее время формирования шага вниз

Первое что может быть полезно для понимания такого алгоритма, это предельные величины при стремлении количества шагов в бесконечность:

1. (P[1] * T[1] + (1 -P[1])*T[2]) * n = T(n)
2. (P[1] * Pr - (1 -P[1])*Pr) * n = P(n)

Для того чтобы более глубоко понять выражения выше, необходимо написать два вот таких предела:

• Lim(n --> +infinity)[P/P0(n)] = 1
• Lim(n --> +infinity)[T/T0(n)] = 1

Пределы говорят о том, что, если проводить одинаковые опыты в размере “n” штук, или торговлю, кому, как угодно, то мы получим как всегда разное количество суммарного времени, которое заняли все элементарные опыты, входящие в один общий, так и всегда разное положение конечного баланса нашей торговли. С другой стороны, интуитивно понятно, что при бесконечном количестве опытов, реальная величина будет стремиться к предельной.  Данный факт можно доказать, используя генераторы случайных чисел.

• n – эмулируемое количество шагов
• 1-P[1] – вероятность срабатывания нижнего шага
• T0(n) – реальное количество времени потраченное на “n” шагов
• P0(n) – реальное смещение баланса или цены за “n” шагов
• T(n) - предельное время потраченное на “n” шагов
• P(n) – предельное смещение за “n” шагов

В итоге видно, что результатом данной логики явились два уравнения, неизвестных в них много больше, чем их количество, это не мудрено, так как это лишь начало. Но эти уравнения описывают лишь производную систему (ту которую нам нужно получить). Для исходной системы уравнения будут похожи:

1. (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) * m = T(m)
2. (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * m  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * m = P(m)

• P*[1] + P[*2] + … + P*[N2] = 1 – вероятности образуют полную группу

Ну и точно такие же пределы, которые показывают те же самые величины:

• Lim(m --> +infinity)[P/P0(m)] = 1
• Lim(m --> +infinity)[T/T0(m)] = 1

Переменные, которые здесь используются описаны ниже:

• m – эмулируемое количество шагов
• T0(m) – реальное количество времени потраченное на “m” шагов
• P0(m) – реальное смещение баланса или цены за “m” шагов
• T(m) - реальное время потраченное на “m” шагов
• P(m) – реальное смещение за “m” шагов
• T = Lim(m --> +infinity) [ T(m) ] – предельное время
• N1 – количество исходов сделок с положительной прибылью, а так же их счетчик
• N2 – N1 + 1 – количество исходов сделок с отрицательной прибылью (N2 – их счетчик)

Понятно, что нам нужно на основе исходной системы получить новую, более простую, составленную из более сложной. Разница только в том, что все параметры исходной системы нам известны, а второй нет. Известным величинам даны постфиксы в виде “*”.

Если взять и приравнять вторые и первые уравнения из обеих систем, то можно исключить переменные “P” и “T”:

• (P[1] * T[1] + (1 -P[1])*T[2]) * n = (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) * m
• (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * m  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * m

В итоге мы потеряли два уравнения, но вместе с тем исключили две неизвестные, которые нам были абсолютно не нужны. В итоге в результате данных преобразований мы получили одно уравнение, неизвестными в котором являются следующие величины:

• P[1] – вероятность срабатывания верхнего шага (стопа)
• T[1] – среднее время существования верхнего шага
• T[2] – среднее время существования нижнего шага

Видно, что оба уравнения имеют похожую структуру вида:

1. A1*n = A2*m
2. B1*n = B2*m

Данная структура говорит о том, что одну из переменных “n” или “m” можно исключить, потеряв одно уравнение, для этого нужно выразить одну из величин, например из первого уравнения:

• m = ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )* n

После чего можно подставить это выражение во второе уравнение и посмотреть, что получится:

• (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) ) * n  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) ) * n

После данной подстановки видно, что обе части уравнения умножены на “n”, разделив их на данную величину можно исключить ее и получить уравнение, зависящее только от нужных нам величин:

• (P[1] * Pr - (1 -P[1])*Pr) = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )

Величину ‘Pr” мы считаем свободной, так как количество возможных систем, к которым можно все свести равно бесконечности. Мы можем задать абсолютно любой размер шага, главное, чтобы шаги вверх и вниз были равны по модулю. Остальные величины будут определены в результате решения системы уравнений. Пока что система имеет всего одно уравнение, но нам не хватает еще двух уравнений, которые можно получить, воспользовавшись полученными уравнениями из прошлого раздела.

Система должна в первую очередь иметь идентичную вероятность пересечения верхней и нижней границы коридора, а во-вторых, должна иметь идентичное среднее время до пересечения одной из границ. Два данных требования и дадут нам два недостающих уравнения. Начнем с того, как определить среднее время пересечения одной из границ. Среднее время пересечения одной из границ определяется средним количеством шагов вверх и вниз. Принимая во внимание результаты предыдущей статьи, можно написать:

• T[U,D] = (S[U,u] * T[1] + S[U,d] * T[2]) * P[U] + (S[D,u] * T[1] + S[D,d] * T[2]) * ( 1 – P[U] )

Данное уравнение говорит о том, что среднее время до пересечения одной из границ зависит от среднего количества шагов при условии пересечения одной из границ, а также от вероятности пересечения этих границ. Данный критерий обеспечит еще одно возможное уравнение для того, чтобы составить систему уравнений, которая позволит нам привести сложную торговую систему к более простой. Но это уравнение можно еще подробить на два:

• T[U] = S[U,u] * T[1] + S[U,d] * T[2]
• T[D] = S[D,u] * T[1] + S[D,d] * T[2]

Данные уравнения еще пригодятся нам ниже. Все эти величины вычисляются исходя из математической модели, полученной в предыдущей статье:

• S[U,u], S[U,d], S[D,u], S[D,d], P[U] = f(n,m,p) – все эти величины являются функциями от “n,m,p”
• n = B[U]/ Pr – в свою очередь “n” можно выразить через расстояние до верхней границы и шаг “Pr”
• m = B[D]/ Pr – в свою очередь “m” можно выразить через расстояние до верхней границы и шаг “Pr”
• Pr – выбранный шаг
• B[U] – расстояние до верхней границы
• B[D] – расстояние до нижней границы

Основы полученного метода преобразования

В качестве примера можно взять случайную стратегию и свести ее к требуемому эквиваленту. Я создал один из таких вариантов преобразования сложной многомерной системы в более простую, двумерную. Я постараюсь поэтапно описать весь процесс этого сведения. Перед тем как описывать все эти вещи, я проделал все это программно и проверил работоспособность метода. Программа будет приложена к статье. В своей программе я использовал немного иные, но такие же эффективные формулы для сравнения. В основе лежит мат модель, которая была получена в предыдущей статье. На ее основе мы можем получить следующие величины:

• P[U], S[U,u], S[U,d], S[D,u], S[D,d]

Из средних шагов можно получить среднее время до пересечения верхней или нижней границы. Сейчас не понято зачем все это нужно, но сейчас все станет понятно. Для того чтобы свести стратегию со множеством состояний, необходимо сначала сгенерировать эти стратегии. Я создал генератор стратегий на случайных числах, который поможет мне в этом. Для наглядности я выбрал пять рандомно сгенерированных кривых. Так они выглядят:

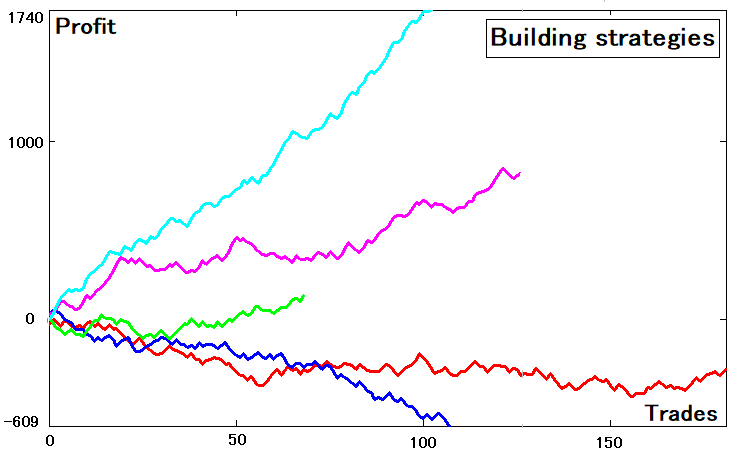
Видно, что стратегии имеют различные математические ожидания, количество сделок и их параметры. Видно, что среди данных кривых есть и убыточные, но это не должно нас волновать так как убыточная кривая – это, тоже кривая, просто ее параметры нам не нравятся. Ведь если нам что-то не нравится, вовсе не обязательно, что этого нет.

Теперь к сути. Видно, что на рисунке графики балансов, зависящие от номера трейда, точно так же, как это было бы видно в тестере стратегий торгового терминала. Исходя из этого каждой кривой соответствует некий массив, содержащий балансы:

• B[i] , i = 0…N
• N – количество трейдов

Данный массив можно получить из массива с параметрами ордеров. В нашем случае я буду предполагать, что контейнер с данными ордеров содержит лишь величину прибыли или убытка данного ордера, а также его длительность:

• Pr[i], T[i]

Буду считать, что остальные параметры нам недоступны. Я считаю это правильным, потому что, например, если мы захотим проанализировать какой-либо бектест или сигнал, то вряд ли эти данные для нас будут доступны, так как только в редких случаях эти данные кто-то сохраняет. Скорее люди будут ориентироваться по таким показателям как фактор восстановления, максимальная просадка, и похожим показателям, где сосредоточена лишь та информация, которая им нужна. Единственными данными торговли, которые сохраняются везде, являются:

1. Прибыль
2. Время открытия ордера
3. Время закрытия ордера

Конечно, от этого пострадает точность, но это неизбежно. Теперь можно написать, как получить массив с балансами из массива с прибылью:

• B[i] = B[i-1] + Pr[i]  if  i > 0
• B[i] = 0  else

Но для того, чтобы иметь возможность анализировать полученные стратегии в связке с временем, точно так же нужно составить аналогичный массив со временем:

• TL[i] = TL[i-1] + T[i]  if  i > 0
• TL[i] = 0  else

После того как определены абсциссы и ординаты всех таких кривых, их можно изобразить графически и увидеть, что есть отличия, так как мы уже имеем функции зависимости не от номера трейда, а от времени:

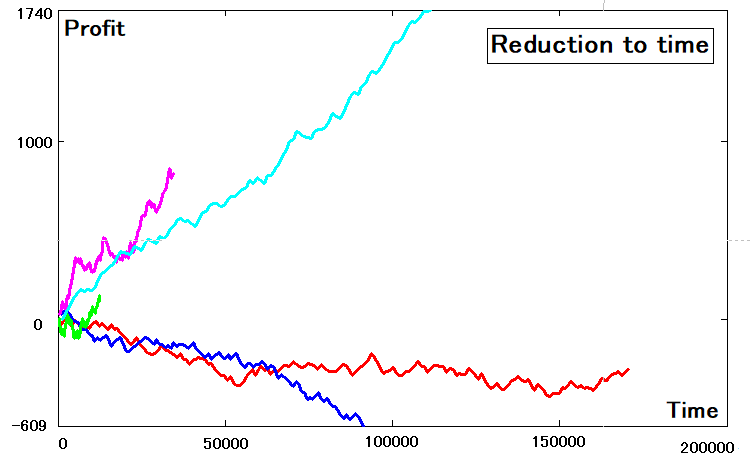
Определение критериев сводимости

Вот теперь с этими данными можно работать. Теперь можно определить критерии, по которым будем искать соответствия среди кривых с двумя состояниями профита. С точки зрения представления относительно времени, для сведения достаточно будет трех величин:

1. P[U] – вероятность пересечения верхней границы
2. T[U] – среднее время достижения верхней границы
3. T[D] – среднее время достижения нижней границы

Вторая и третья величина может быть посчитана так:

• T[U] = S[U,u] * T[u] + S[U,d] * T[d]
• T[D] = S[D,u] * T[u] + S[D,d] * T[d]

Что касается P[U], эта величина уже в готовом виде выдается математической моделью, которая была получена в предыдущей статье. И думаю, что нет смысла напоминать, что “P[D] = 1 – P[U]”. Получается, что из пяти величин, которые выдает математическая модель, можно сформировать необходимые нам три величины, которые описаны выше и даже не остается ничего лишнего. Что до этих двух уравнений, они были получены выше, просто тут я поменял обозначения для времени, думаю, так более читаемо.

Эти величины вычисляемые, и чтобы их подгонять к чему-то, нужно как-то получить их реальную величину из тех данных что у нас есть. После чего нужно подобрать такие параметры искомой эквивалентной кривой с двумя состояниями, чтобы все три вычисляемых параметра были максимально похожи на реальные показатели, так и получим три наших критерия. Сначала введем обозначения для известных величин:

• P*[U] – реальная вероятность пересечения границ выбранного коридора
• T*[U] – реальное среднее время до пересечения верхней границы коридора
• T*[D] – реальное среднее время до пересечения нижней границы коридора

Отклонение реальных и вычисляемых величин можно измерять либо в относительных величинах, либо в процентах. Если в процентах, то критерии будут такими:

• KPU = ( | P[U] – P*[U] | / ( P[U] + P*[U] ) ) * 100 %
• KTU = ( | T[U] – T*[U] | / ( T[U] + T*[U] ) ) * 100 %
• KTD = ( | T[D] – T*[D] | / ( T[D] + T*[D] ) ) * 100 %

Определение критериев для сравнения с исходной системой

Лучшей системой будет та, которая имеет минимум всех этих показателей. Но для того, чтобы получить возможность получать вычисляемые величины, необходимо сначала определить размер коридора, по которому мы будем определять реальные вероятности и реальное время до пересечения границ. Это можно изобразить визуально:

На рисунке пример определения такого коридора, для прибыльной стратегии. Пурпурные треугольники символизируют очередную точку проверки возможных движений вниз и вверх. Между двумя черными точками находится наше искомое минимальное движение. Если мы возьмем за основу максимальное движение, которое было за доступный период, то вероятность P[U] будет единицей. Ясно ,что это максимально некорректный выбор. Напротив, нам нужно минимальное движение, которое гарантирует пересечения как нижнего, так и верхнего коридора.

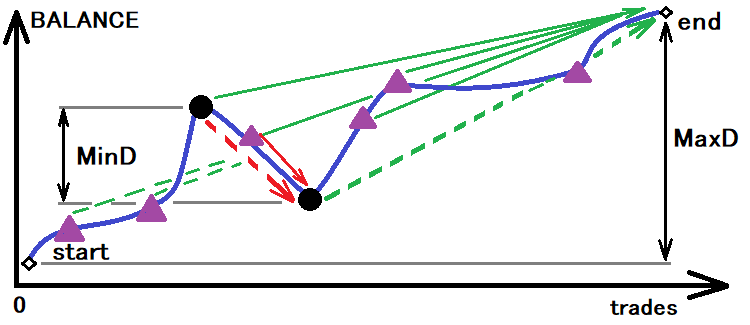
Оценка возможного коридора для вычисления необходимых величин

Но даже этого недостаточно. Все дело в том, что если брать за основу именно эту величину, то мы получим всего одно касание нижней границы, что тоже не даст большой точности. Лично я брал величину коридора в три раза меньше, чем данный минимум. При достаточной выборке касаний о границы, в таком случае будет достаточно. Ну вот с размером коридора определились, теперь коридор можно и подробить. Если считать, что сам коридор и есть шаг, то это значит, что:

• n, m = 1
• p = P[U]
• Pr * n = Pr * m  = 1/3 * MinD – половина ширины коридора
• Pr = ( 1/3 * MinD  ) / n = ( 1/3 * MinD  ) / m  – модуль шага
• T[U,u] = T[U]
• T[D,d] = T[D]
• T[U,d] = 0
• T[D,u] = 0

Этот вариант тоже можно использовать, в случае если у нас очень большая торговая выборка. Плюсом такого подхода будет являться отсутствие необходимости в применении математической модели дробления коридора, ведь в таком случае весь наш коридор и является одним шагом. Но в своих вычислениях я взял пример с применением мат модели, для разнообразия. Если использовать этот подход, то для подбора его параметров необходимо выделить следующие диапазоны его параметров:

• p = p1 … p2
• N = m = nm1 …. nm2

Я взял для примера вот такие диапазоны:

• p1 = 0.4, p2 = 0.6, nm1 = 1, nm2 = 3

Можно, конечно, брать и более широкие диапазоны, но не обязательно сразу и количество шагов, и вероятность. Можно один из интервалов расширить, а другой оставить без изменения. Например, увеличить “nm2”, тогда метод сможет охватить больший диапазон различных стратегий, а если математическая модель не может справиться с очередным вариантом, то можно перейти на метод без использования математической модели.

Определение вероятности и среднего времени до пересечения верхней и нижней границы коридора

После успешного подбора всех вышеописанных величин мы получим только вероятность “p” для шага вверх, но от нее уже можно будет отталкиваться, чтобы подобрать среднее время пересечения границ. Можно наглядно показать, как это осуществляется, немного преобразовав иллюстрацию выше:

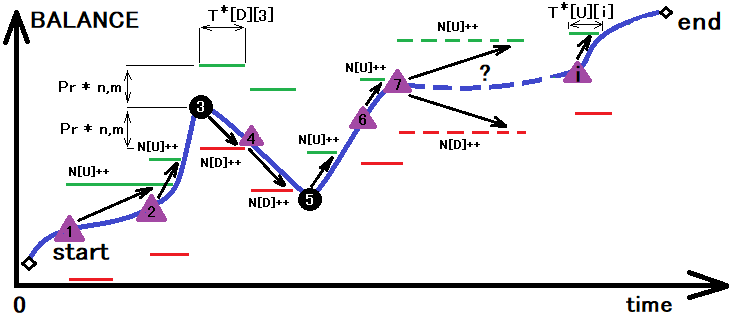
На рисунке изображен процесс суммирования пересечений верхних и нижних границ коридором, размер которого определен в результате предыдущего преобразования. Параллельно с суммированием этих пересечений производится вычисление времени, затраченного на пересечение. За одну эту операцию можно определить все величины со звездочкой, которые нам понадобятся:

• N[U] – количество пересечений верхней границы коридора
• N[D] – количество пересечений нижней границы коридора
• T[U][i] – массив с временем до пересечения верхней границы
• T[D][i] – массив с временем до пересечения нижней границы

Осталось только используя эти данные посчитать вероятность пересечения верхней границы и среднее время до пересечения верхней и нижней границы:

• P*[U] = N[U]/ ( N[U] + N[D] )
• T*[U] = Summ( 0…i ) [ T[U][i]  ] / N[U]
• T*[D] = Summ( 0…i ) [ T[D][i]  ] / N[D]

Раз найдены все величины, к которым предпочтительно должен сходиться наш двумерный эквивалент, то нужно определить с чего начнем поиск. Для этого нужно определить какая из этих величин носит наибольший приоритет по точности. Я выбрал вероятность пересечения верхней границы в качестве примера. Такой подход дает уменьшение требуемой вычислительной мощности на анализ. Если бы мы производили подбор сразу трех величин в трех интервалах, то мы получили бы три степени свободы системы, что на порядок увеличило бы время вычислений, тем более, что с возрастанием количества данных это могло дать время расчета несовместимое с реальностью. Вместо этого я в своей логике сделал сначала подбор вероятности шага вверх, а уже потом производил подбор среднего времени шагов вверх и вниз.

Хочу напомнить, чтобы никто не путался, в коридоре много шагов и время до пересечения границ это не время шагов. Точно так же с вероятностью, вероятность шага в определенном направлении – это, не вероятность пересечения границы коридора. Исключением является лишь ситуация “n=m=1”, которую я описал в самом начале.

В результате подбора мы получим следующие характеристики шага:

1. p – вероятность шага вверх
2. T[u] – средняя длительность шага вверх
3. T[d] – средняя длительность шага вниз
4. Pr – модуль шага в величинах прибыли

Оценка эффективности простого преобразования

Предположим, подобраны все параметры шагов, тогда как понять, насколько вообще была эффективна такая операция преобразования? Для оценки эффективности можно прочертить прямые к которым сходятся стратегии. Их наклон можно определить так:

• K = EndProfit / EndTime – коэффициент наклона прямой
• P0 = K * t – уравнение прямой

Вот так это будет выглядеть:

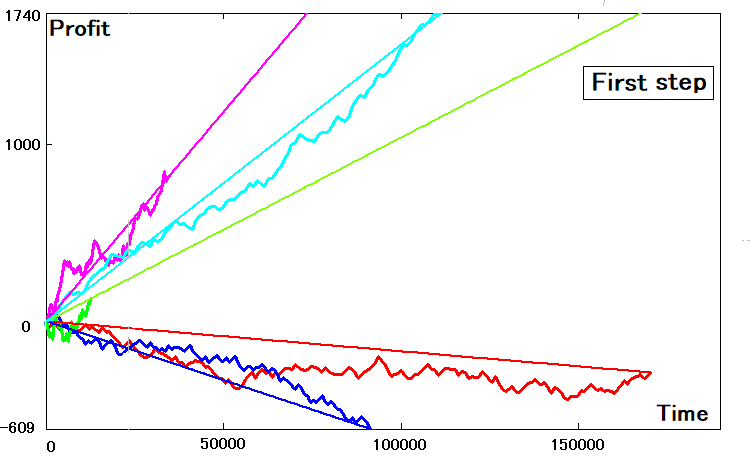
Если параметры двумерных кривых подобраны идеально, то их аналогичные прямые будут точно с таким же наклоном и касаться кривых баланса в конечных точках. Думаю, интуитивно понятно, что скорее всего такого совпадения не будет абсолютно всегда. Чтобы найти коэффициент наклона для подобранного двумерного эквивалента, мы можем использовать данные, подобранные для шага:

• MP = p * Pr – (1-p) * Pr – математическое ожидание смещения вверх для любого шага
• MT = p * T[u] + (1-p) * T[d] - математическое ожидание затраченного времени на формирование любого шага
• K = MP / MT – тот же коэффициент наклона прямой.

Я проделал это с помощью все той же программки и практически всегда получал что-то похожее на это:

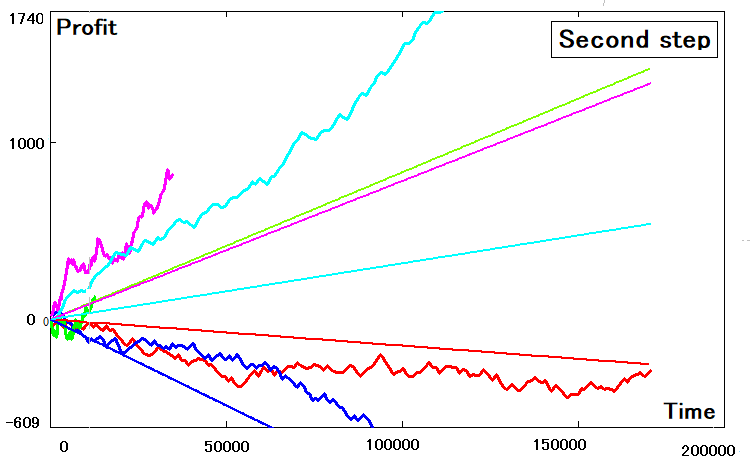
Видно, что далеко не все стратегии смогли корректно преобразоваться в двумерный эквивалент. Те, что не смогли преобразоваться, имеют достаточно ярко выраженные отклонения. Эти отклонения связаны со следующими причинами:

1. Погрешность вычисления величин со звездочкой
2. Несовершенство двумерной модели (менее гибкая модель)
3. Конечность возможного числа попыток поиска (также это одно и то же что ограниченные вычислительные мощности)

Принимая во внимание все эти факты, можно произвести определенные корректировки среднего времени шага, таким образом чтобы по крайней мере коэффициенты наклона исходной и производной модели выровнялись. Конечно, такие преобразования будут в ущерб отклонениям сводимых критериев, но иным способом нельзя будет добиться этого. Все-таки я считаю самым важным критерием именно коэффициент наклона прямой, потому что при стремлении к бесконечности количества трейдов исходная и производная стратегия должны слиться в одну линию. Если этого не происходит, то смысла в подобном преобразовании не много. А возможно, все дело не в методе преобразования, а в скрытых возможностях, которые еще нужно осмыслить.

Финальная корректировка и симуляция

Для того чтобы произвести подобное преобразование можно использовать пропорцию. Так как перед тем, как построить эти кривые у нас были массивы “TL[i]”, “B[i]”, которые эквивалентны времени прошедшему от начала кривой и до рассматриваемого ордера или сегмента, мы можем взять последние элементы этого массива и написать следующее:

• K = B[n] / TL[n]
• N – индекс последнего элемента массива балансов (конечный баланс)

В свою очередь, для прямых, полученных в предыдущем шаге, тоже можно посчитать такой коэффициент — он уже считался выше:

• K1 = MP / MT

Но понятно, что эти коэффициенты не равны, и мы должны скорректировать этот коэффициент. Сделать это можно так:

• K = MP / ( KT * MT )
• KT – корректировочный коэффициент

Теперь нужно внести этот коэффициент внутрь математического ожидания так, чтобы математическое ожидание не поменяло свой смысл, это можно сделать так:

• MTK = MT * KT = p * (T[u]* KT) + (1-p) * (T[d]* KT)

Видно, что в скобках образовались новые скорректированные величины времени, и можно их посчитать так:

1. Tn[u] = T[u]* KT
2. Tn[d] = T[d]* KT

Это и будет нашим скорректированным временем шага вверх и шага вниз. Сам корректировочный коэффициент можно будет посчитать, приравняв выражения для вычисления коэффициентов:

• B[n] / TL[n] = MP / ( KT * MT )

Разрешив уравнение относительно “KT”, получим выражение для вычисления данной величины:

• KT = ( MP / MT ) / ( B[n] / TL[n] ) = ( MP * TL[n] ) / ( MT * B[n] )

Все что остается, это скорректировать среднее время шага вверх и вниз. После этого можно считать процесс преобразования завершенным. В итоге мы получаем всего лишь набор из четырех величин, которые полностью описывают нашу стратегию, вместо огромных массивов описывающих более двух состояний:

1. p – вероятность шага вверх
2. Pr – модуль шага
3. T[u] – среднее время формирования шага вверх
4. T[d] – среднее время формирования шага вниз

Этих четырех параметров достаточно чтобы воссоздать саму стратегию с помощью симуляции. Главное, что теперь нам доступна программная симуляция стратегии вне привязки к рынку и времени. На примере наших пяти стратегий симуляция выглядела так:

Прямые линии тут взяты с первого шага. Эти линии проводились от нуля и до конца кривой реальной торговли. Видно, что симуляция довольно точно идет и рядом с линиями, что подтверждает правильность преобразований. Исключением является только синяя линия, я думаю, что это просто недоработки моего алгоритма. Уверен, эти мелочи можно исправить, потратив немного времени.

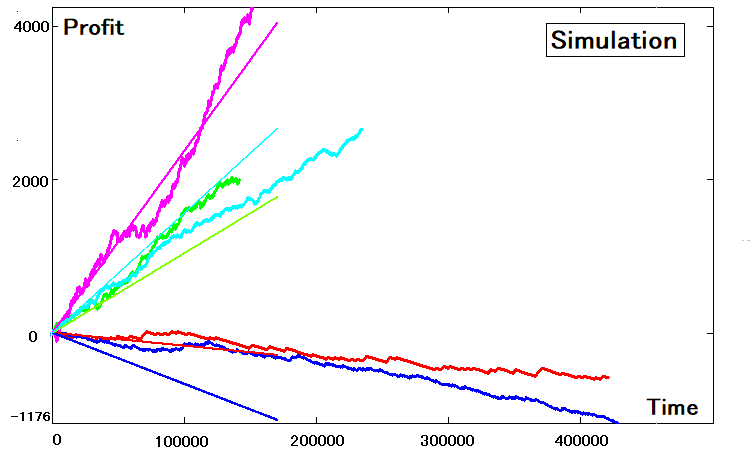
Выводы

В процессе исследования этой модели получены интересные мысли. Изначально, исследуя двумерные схемы и схемы с множеством состояний, мне хотелось просто получить более простое описание для сложных систем. В итоге по результатам исследования получены гораздо более ценные и простые выводы. Детали всего этого тяжело описать в статье, потому что слишком много технических нюансов и мелочей. Если вкратце, что дало это исследование:

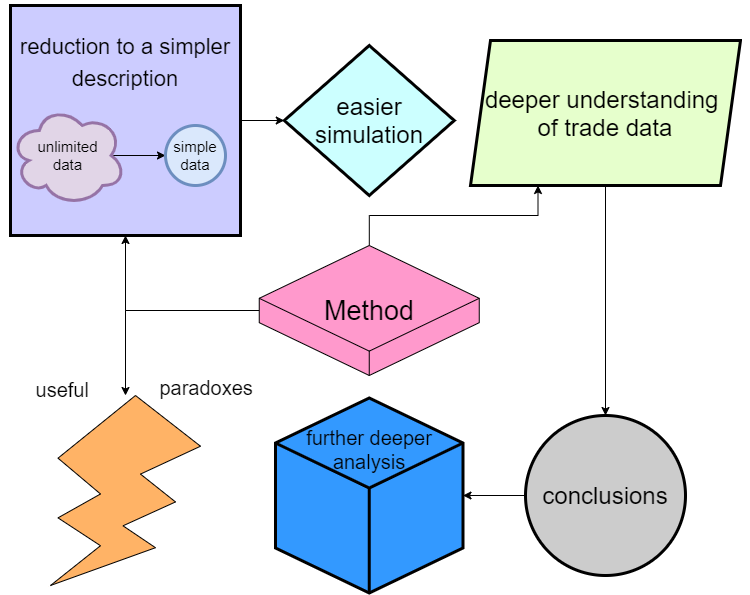
Можно перечислить все плюсы в список:

• Многие системы с множеством состояний можно сводить к двум состояниям (а значит возможен и процесс n в m состояний)
• Процесс преобразования можно использовать как механизм сжатия торговых данных
• Преобразованные данные можно вернуть обратно с помощью симуляции, что одновременно упрощает симуляцию (так как нужно симулировать всего два состояния)
• Более глубокое понимание вероятностных процессов внутри ценообразования позволяет сделать индивидуальные полезные заключения
• На основе полученной информации можно переходить к более глубокому анализу процесса торговли
• Уже в этом исследовании получены некоторые полезные фичи для торговли, пока я заношу их в разряд парадоксов

В итоге, конечно, основной мыслью цикла этих статей является построение простой и полезной математики, которая напрямую позволит создавать сверхстабильные и мультивалютные системы, основанные на теории вероятностей. Пока эта информация не слишком монолитна, но монолит построить можно только на хорошем фундаменте, этим я и занимаюсь.

Отдельно стоит сказать о парадоксах, которые выявлены в процессе исследования. Вот те расхождения, которые были получены в первой ступени преобразования, которые выражались в различном угле наклона эквивалентной прямой, наводят на мысли о том, что их можно использовать для преобразования случайной торговли в неслучайную, либо обеспечивать различные усилители торговых сигналов.

Иными словами, можно получить из некоторых нулевых стратегий, стратегии с положительным профит-фактором, с помощью как раз этих трюков с преобразованием множественных состояний в двойные эквиваленты, которые можно уже будет обрабатывать дальше и другими методами и усиливая их качество. Пока эти мысли слишком разрознены чтобы их собирать воедино, но дело до этого обязательно дойдет. Считаю это главным итогом исследования, ведь это потом пригодится, когда будем собирать советник.

Заключение

В этой статье я старался уйти от детального описания и старался не углубляться в детали. Конечно, не обошлось и без математики, но учитывая опыт предыдущих статей, вижу, что более общая информация гораздо полезнее деталей. Те, кто хочет более подробно разобраться в тонкостях метода, к статье приложена программа, в которой я проводил исследования. Я не стал описывать все алгоритмы, которые я там использовал, поскольку там очень много хоть и важной, но скучной математики, и в основном это работа с массивами данных и матрицами. Все равно те, кто будет что-то похожее делать, будут придерживаться своей логики, но в качестве отправной точки, можно что-то подчерпнуть оттуда.

Если разбираться не хочется, можно просто поиграться с разными стратегиями, поглядеть как они будут сведены, ведь эти программки я разрабатывал специально для статьи, собственно, как и раньше. Если говорить о том, что же будет дальше, я, думаю, постепенно будем переходить к конкретике и будем начинать писать крутой самоадаптирующийся алгоритм, который, как я надеюсь, сможет превзойти нейросети и в качестве, и в стабильности. Наработки есть. Но сначала нужно полностью достроить фундамент.

Ссылки

• Комбинаторика и теория вероятностей для трейдинга (Часть I): Основы
  
• Комбинаторика и теория вероятностей для трейдинга (Часть II): Универсальный фрактал
  
• Комбинаторика и теория вероятностей для трейдинга (Часть III): Первая математическая модель
• Комбинаторика и теория вероятностей для трейдинга (Часть IV): Логика Бернулли