Combinatória e teoria da probabilidade para negociação (Parte V): análise de curva

Sumário

• Introdução
• Fórmulas úteis para simplificar os dados
• Noções básicas do método de conversão resultante
• Definição de critérios de redutibilidade
• Determinação de critérios para comparação com o sistema original
• Avaliação de um possível corredor para calcular os valores necessários
• Determinação de probabilidade e de tempo médio antes do cruzamento dos limites superior e inferior do corredor
• Estimativa da eficiência de uma conversão simples
• Ajuste final e simulação
• Conclusões
• Conclusão
• Links

Introdução

Continuo a coletar a base para a montagem de sistemas de negociação multiestágio e escaláveis. Dentro da estrutura deste artigo, quero mostrar como você pode usar os desenvolvimentos dos artigos anteriores para se aproximar de possibilidades mais amplas para descrever o processo de negociação. Isso ajudará a avaliar outros aspetos da estratégia que outros métodos de análise não podem abordar. Neste artigo, explorei as possibilidades de reduzir amostras multiestado complexas a amostras simples de estado duplo. Essa análise foi feita como uma pesquisa.

Fórmulas úteis para simplificar os dados

Imagine que você tem uma estratégia em que existem muitas transações que se sucedem sem se sobreporem, ou seja, uma nova ordem é aberta estritamente após o fechamento da anterior. Se de repente surgir a questão sobre as probabilidades de ganhar ou perder, bem como calcular o tempo médio antes de essa estratégia alcançar o ganho ou a perda, automaticamente nos deparamos com que as ordens podem ter um número muito grande de estados (são fechadas com resultados diferentes).

Para poder aplicar fórmulas fractais a tais estratégias, primeiro é necessário reduzir essas estratégias a casos que podem ser considerados no âmbito dos fractais. Para fazer isso, basta representar nossa estratégia como uma ordem com stops equidistantes, que tem a probabilidade de uma etapa para cima e uma para baixo, assim como em nosso fractal - as fórmulas fractais podem ser aplicadas. Além disso, uma etapa para cima uma para baixo podem ter diferentes tempos de vida médios.

Para concentrar qualquer estratégia em uma das estratégias que podem ser descritas no âmbito das fórmulas fractais que obtive no artigo anterior, é necessário primeiro determinar quais valores devem ser conhecidos para poder aplicar as fórmulas dos fractais. Aqui tudo é bem simples:

• P[1] – probabilidade de acionar a etapa superior
• T[1] – tempo médio de geração da etapa para cima
• T[2] – tempo médio de formação da etapa para baixo

A primeira coisa que pode ser útil para entender tal algoritmo são os valores limite quando o número de etapas tende ao infinito:

1. (P[1] * T[1] + (1 -P[1])*T[2]) * n = T(n)
2. (P[1] * Pr - (1 -P[1])*Pr) * n = P(n)

Para entender mais profundamente as expressões acima, é necessário escrever dois desses limites:

• Lim(n --> +infinity)[P/P0(n)] = 1
• Lim(n --> +infinity)[T/T0(n)] = 1

Os limites dizem que se realizarmos os mesmos experimentos com o tamanho de "n" peças, ou negócios, o que for do agrado de cada um, teremos sempre uma quantidade diferente de tempo total de todos os experimentos elementares que compõem o total, e sempre uma posição diferente do equilíbrio final de nossa negociação. Por outro lado, é intuitivamente claro que com um número infinito de experimentos, o valor real tenderá ao limite. Este fato pode ser comprovado usando geradores de números aleatórios.

• n – número emulado de etapas
• 1-P[1] – probabilidade de acionamento da etapa inferior
• T0(n) – quantidade real de tempo gasto em “n” etapas
• P0(n) – saldo real ou mudança de preço para “n” etapas
• T(n) - limite de tempo gasto em “n” etapas
• P(n) - deslocamento limite em "n" etapas

Como resultado, fica claro que o resultado dessa lógica foram duas equações, isso é apenas o começo. Mas essas equações descrevem apenas o sistema derivado (aquele que precisamos obter). Para o sistema original, as equações serão semelhantes:

1. (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) * m = T(m)
2. (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * m  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * m = P(m)

• P*[1] + P[*2] + … + P*[N2] = 1 – probabilidades formam um grupo completo

E exatamente esses mesmos limites são os que mostram os mesmos valores:

• Lim(m --> +infinity)[P/P0(m)] = 1
• Lim(m --> +infinity)[T/T0(m)] = 1

As variáveis que são usadas aqui são descritas abaixo:

• m – número emulado de etapas
• T0(m) – quantidade real de tempo gasto em “m” etapas
• P0(m) – saldo real ou mudança de preço para “m” etapas
• T(m) – tempo real gasto em “m” etapas
• P(m) – deslocamento real após “m” etapas
• T = Lim(m --> +infinity) [T(m)] – limite de tempo
• N1 – o número de resultados de negócios com lucro positivo, bem como seu contador
• N2 - N1 + 1 – o número de resultados de negócios com lucro negativo (N2 - seu contador)

É claro que com base no sistema original precisamos obter um novo, mais simples, composto por um mais complexo. A única diferença é que todos os parâmetros do sistema original são conhecidos por nós, mas o segundo não é. Os valores conhecidos recebem pós-fixos assim “*”.

Se tomarmos e igualarmos a segunda e a primeira equações de ambos os sistemas, podemos eliminar as variáveis “P” e “T”:

• (P[1] * T[1] + (1 -P[1])*T[2]) * n = (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) * m
• (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * m  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * m

Como resultado, perdemos duas equações, mas ao mesmo tempo eliminamos duas incógnitas que absolutamente não precisávamos. Como resultado dessas conversões, obtivemos uma equação, onde o seguintes valores são desconhecidos:

• P[1] – probabilidade de acionar a etapa superior (stop)
• T[1] – tempo médio de existência da etapa superior
• T[2] – tempo médio de existência da etapa inferior

Pode-se ver que ambas as equações têm uma estrutura semelhante:

1. A1*n = A2*m
2. B1*n = B2*m

Essa estrutura diz que uma das variáveis “n” ou “m” pode ser eliminada, perdendo uma equação, para isso você precisa expressar um dos valores, por exemplo, a partir da primeira equação:

• m = ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )* n

Depois, você pode substituir essa expressão na segunda equação e ver o que acontece:

• (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) ) * n  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) ) * n

Após essa substituição, pode-se ver que ambas as partes da equação são multiplicadas por “n”; ao dividi-las por um determinado valor, podemos eliminá-la e obter uma equação que depende apenas dos valores que precisamos:

• (P[1] * Pr - (1 -P[1])*Pr) = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )  -  (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )

Consideramos o valor 'Pr' livre, pois o número de sistemas possíveis aos quais tudo pode ser reduzido é igual ao infinito. Podemos definir absolutamente qualquer tamanho de etapa, o principal é que as etapas para cima e para baixo devem ser iguais em valor absoluto. As quantidades restantes serão determinadas como resultado da resolução do sistema de equações. Até agora, o sistema tem apenas uma equação, mas faltam mais duas, que podem ser obtidas usando as obtidas na seção anterior.

O sistema deve, em primeiro lugar, ter uma probabilidade idêntica de cruzar os limites superior e inferior do corredor e, em segundo lugar, deve ter um tempo médio idêntico antes do cruzamento de um dos limites. Esses dois requisitos nos darão as duas equações que faltam. Vamos começar com como determinar o tempo médio para cruzar um dos limites. O tempo médio para cruzar um dos limites é determinado pelo número médio de etapas para cima e para baixo. Tendo em conta os resultados do artigo anterior, podemos escrever:

• T[U,D] = (S[U,u] * T[1] + S[U,d] * T[2]) * P[U] + (S[D,u] * T[1] + S[D,d] * T[2]) * ( 1 – P[U] )

Esta equação diz que o tempo médio antes do cruzamento de um dos limites depende do número médio de etapas, desde que um dos limites seja cruzado, bem como da probabilidade de cruzar esses limites. Este critério fornecerá outra equação para fazer um sistema de equações que nos permitirá reduzir um sistema de negociação complexo a um mais simples. Mas esta equação pode ser subdividida em duas:

• T[U] = S[U,u] * T[1] + S[U,d] * T[2]
• T[D] = S[D,u] * T[1] + S[D,d] * T[2]

Essas equações serão úteis para nós a seguir. Todos esses alores são calculados com base no modelo matemático obtido no artigo anterior:

• S[U,u], S[U,d], S[D,u], S[D,d], P[U] = f(n,m,p) – todas esses valores são funções de “n,m,p”
• n = B[U]/ Pr – por sua vez, "n" pode ser expresso em termos da distância até o limite superior e da etapa “Pr”
• m = B[D]/ Pr – por sua vez, "m" pode ser expresso em termos da distância até o limite superior e da etapa “Pr”
• Pr – etapa escolhida
• B[U] – distância até a borda superior
• B[D] – distância até a borda inferior

Noções básicas do método de conversão resultante

Como exemplo, podemos pegar uma estratégia aleatória e reduzi-la ao equivalente necessário. Criei uma dessas variantes para conversão de um sistema multidimensional complexo em um sistema bidimensional mais simples. Vou tentar descrever passo a passo todo o processo. Antes de descrever todas essas coisas, programei tudo e verifiquei o desempenho do método. O programa será anexado ao artigo. No meu programa, usei fórmulas de comparação ligeiramente diferentes, mas igualmente eficazes. Ele se baseia no modelo matemático que foi derivado do artigo anterior. Com base nele, podemos obter os seguintes valores:

• P[U], S[U,u], S[U,d], S[D,u], S[D,d]

A partir das etapas médias, você pode obter o tempo médio antes de cruzar o limite superior ou inferior. Agora não está claro por que tudo isso é necessário, mas já tudo ficará claro. Para reduzir uma estratégia multiestado, você deve primeiro gerar essas estratégias. Eu criei um gerador de estratégia de números aleatórios para me ajudar com isso. Eu escolhi cinco curvas geradas aleatoriamente para maior clareza. Veja como fica isso:

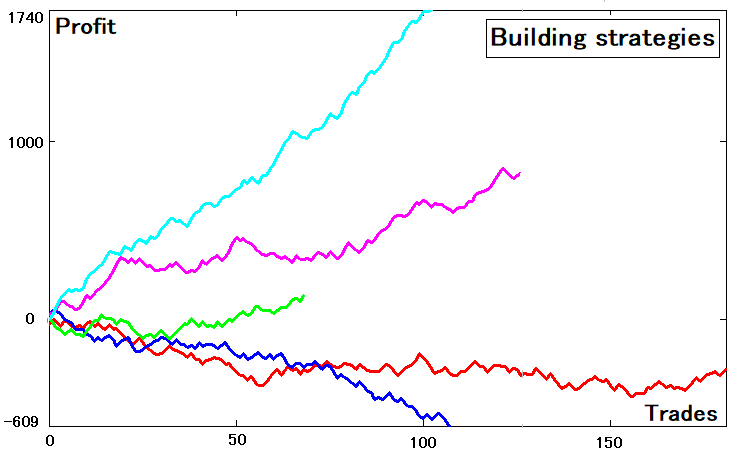
Pode-se observar que as estratégias possuem diferentes valores esperados, número de negócios e parâmetros. Pode-se ver que entre essas curvas existem as não lucrativas, mas isso não deve nos preocupar, pois a curva não lucrativa também é uma curva, apenas que não gostamos de seus parâmetros. Afinal, se não gostamos de algo, não é necessário que não exista.

Agora ao ponto. Pode-se ver que na figura, os gráficos de saldo que dependem do número do negócio são exatamente os mesmos que seriam vistos no testador de estratégia do terminal de negociação. Com base nisso, cada curva corresponde a um array contendo saldos:

• B[i] , i = 0…N
• N – número de negócios

Este array pode ser obtido do array com parâmetros de ordens. No nosso caso, assumirei que o contêiner de dados da ordem contém apenas o lucro ou prejuízo, bem como duração:

• Pr[i], T[i]

Vou assumir que os parâmetros restantes não estão disponíveis. Acho que isso está certo, porque, por exemplo, se quisermos analisar algum backtest ou sinal, é improvável que esses dados estejam disponíveis para nós, pois apenas em casos raros alguém salva esses dados. Em vez disso, as pessoas serão guiadas por indicadores como o fator de recuperação, rebaixamento máximo e indicadores semelhantes, onde apenas as informações de que precisam estão concentradas. Os únicos dados de negociação armazenados sempre são:

1. Lucro
2. Hora de abertura da ordem
3. Hora de fechamento da ordem

Claro, a precisão sofrerá com isso, mas isso é inevitável. Agora você pode escrever como obter um array com saldos a partir de um array com lucro:

• B[i] = B[i-1] + Pr[i]  if  i > 0
• B[i] = 0  else

Mas para poder analisar as estratégias resultantes em relação ao tempo, da mesma forma, você precisa criar um array semelhante com o tempo:

• TL[i] = TL[i-1] + T[i]  if  i > 0
• TL[i] = 0  else

Depois de determinadas as abcissas e ordenadas de todas essas curvas, elas podem ser plotadas e você pode ver que existem diferenças, pois já temos funções de dependência não do número do negócio, mas, sim, do tempo:

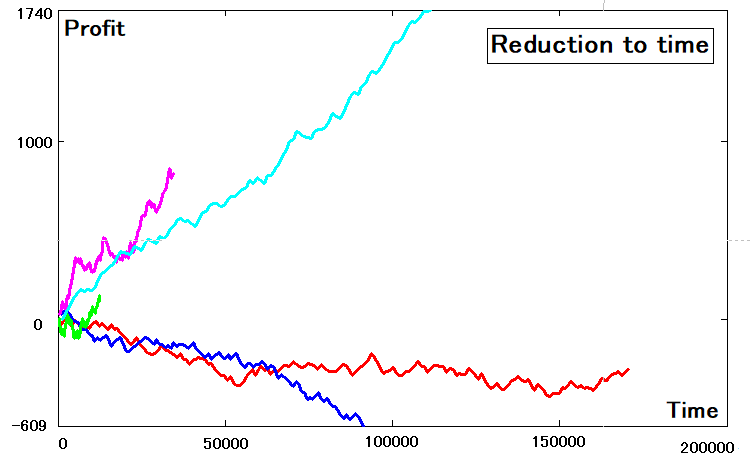
Definição de critérios de redutibilidade

Agora você pode trabalhar com esses dados. Agora podemos definir os critérios com os quais procuraremos correspondências entre as curvas com dois estados de lucro. Do ponto de vista da representação em relação ao tempo, três quantidades serão suficientes:

1. P[U] - probabilidade de cruzar o limite superior
2. T[U] – tempo médio antes de atingir o limite superior
3. T[D] – tempo médio antes de atingir o limite inferior

O segundo e terceiro valores podem ser calculados da seguinte forma:

• T[U] = S[U,u] * T[u] + S[U,d] * T[d]
• T[D] = S[D,u] * T[u] + S[D,d] * T[d]

Quanto a P[U], esse valor já é dado de forma acabada pelo modelo matemático que foi obtido no artigo anterior. E acho que não adianta lembrar que "P[D] = 1 - P[U]". Na verdade, com os cinco valores que o modelo matemático produz, podemos geras os três valores de que precisamos, que estão descritos acima. Quanto a essas duas equações, elas foram obtidas acima, só aqui mudei a notação para o tempo, acho que fica mais legível.

Esses valores são calculados e, para encaixá-los em algo, você precisa de alguma forma obter seu valor real a partir dos dados que temos. Depois disso, você precisa selecionar esses parâmetros da curva equivalente desejada com dois estados para que todos os três parâmetros calculados sejam o mais semelhantes possível aos indicadores reais, e obteremos nossos três critérios. Primeiro, introduzimos a notação para os valores conhecidos:

• P*[U] – probabilidade real de cruzamento dos limites do corredor selecionado
• T*[U] – tempo médio real antes do cruzamento do limite superior do corredor
• T*[D] – tempo médio real antes do cruzamento do limite inferior do corredor

O desvio dos valores reais e calculados pode ser medido em termos relativos ou como porcentagem. Se for percentual, os critérios serão os seguintes:

• KPU = ( | P[U] – P*[U] | / ( P[U] + P*[U] ) ) * 100 %
• KTU = ( | T[U] – T*[U] | / ( T[U] + T*[U] ) ) * 100 %
• KTD = ( | T[D] – T*[D] | / ( T[D] + T*[D] ) ) * 100 %

Determinação de critérios para comparação com o sistema original

O melhor sistema será aquele que tiver o mínimo de todos esses indicadores. Mas para poder obter valores calculados, primeiro é necessário determinar o tamanho do corredor com o qual determinaremos as probabilidades reais e o tempo real antes de cruzar os limites. Isso pode ser visualizado:

A figura mostra um exemplo de determinação de tal corredor para uma estratégia lucrativa. Os triângulos roxos simbolizam outro ponto de verificação para possíveis movimentos para cima e para baixo. Entre os dois pontos pretos está o nosso movimento mínimo desejado. Se tomarmos como base o movimento máximo que houve no período disponível, então a probabilidade P[U] será um. É claro que esta é a escolha mais incorreta. Pelo contrário, precisamos de um movimento mínimo que garanta o cruzamento dos corredores inferior e superior.

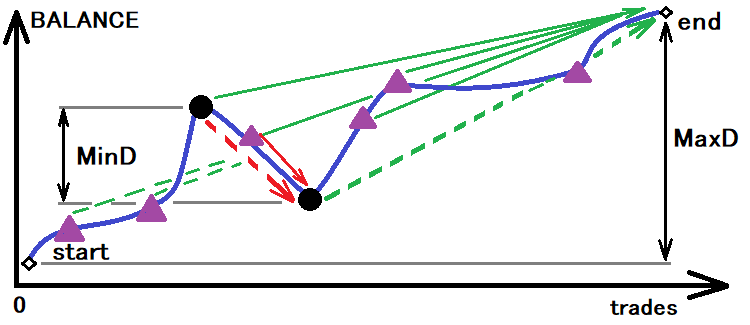
Avaliação de um possível corredor para calcular os valores necessários

Mas mesmo isso não é suficiente. Na verdade, se tomarmos esse valor como base, obteremos apenas um toque do limite inferior, o que também não dará grande precisão. Pessoalmente, tomei o valor do corredor três vezes menor que o mínimo dado. Com uma amostra suficiente de toques no limite, neste caso será suficiente. Bem, já decidimos o tamanho do corredor, agora o corredor pode ser detalhado. Se assumirmos que o corredor em si é uma etapa, isso significa que:

• n, m = 1
• p = P[U]
• Pr * n = Pr * m  = 1/3 * MinD – metade da largura do corredor
• Pr = ( 1/3 * MinD  ) / n = ( 1/3 * MinD  ) / m  – módulo da etapa
• T[U,u] = T[U]
• T[D,d] = T[D]
• T[U,d] = 0
• T[D,u] = 0

Esta variação também pode ser usada se tivermos uma amostra de negociação muito grande. A vantagem será a ausência da necessidade de utilizar um modelo matemático para dividir o corredor, pois neste caso todo o nosso corredor é uma etapa. Mas em meus cálculos, peguei um exemplo usando um modelo matemático, para variar. Se essa abordagem for usada, para selecionar seus parâmetros, será necessário selecionar os seguintes intervalos:

• p = p1 … p2
• N = m = nm1 …. nm2

Por exemplo, peguei os seguintes intervalos:

• p1 = 0.4, p2 = 0.6, nm1 = 1, nm2 = 3

Você pode, é claro, obter faixas mais amplas, mas não necessariamente o número de etapas e a probabilidade de uma só vez. Você pode expandir um dos intervalos e deixar o outro inalterado. Por exemplo, aumentar “nm2”, e fazer com que o método possa cobrir uma gama maior de estratégias diferentes e, se o modelo matemático não puder lidar com a próxima variação, você poderá alternar para o método sem usar o modelo matemático.

Determinação de probabilidade e de tempo médio antes do cruzamento dos limites superior e inferior do corredor

Após selecionar com sucesso todos os valores acima, obteremos apenas a probabilidade “p” para uma etapa, mas já será possível partir dela para selecionar o tempo médio de cruzamento de limite. Podemos ver como isso é feito, convertendo ligeiramente a ilustração acima:

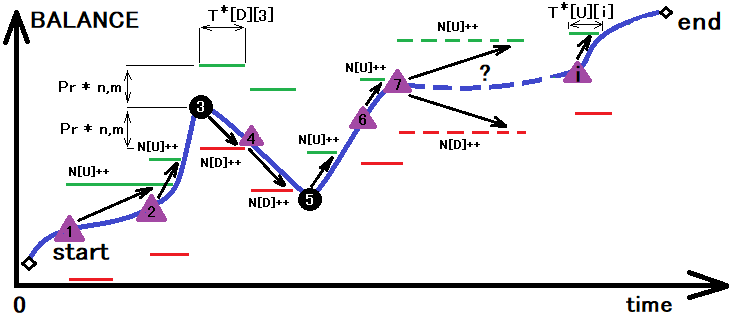
A figura mostra o processo de soma das interseções dos limites superior e inferior do corredor, cujo tamanho é determinado como resultado da conversão anterior. Em paralelo com a soma dessas interseções, é calculado o tempo gasto na interseção. Em uma operação, podemos determinar todas as quantidades, de que precisamos, com um asterisco:

• N[U] – número de cruzamentos do limite superior do corredor
• N[D] – número de cruzamentos do limite inferior do corredor
• T[U][i] – array com o tempo antes do cruzamento do limite superior
• T[S][i] – array com o tempo antes do cruzamento do limite inferior

Resta apenas usar esses dados para calcular a probabilidade de cruzamento do limite superior e o tempo médio antes do cruzamento dos limites superior e inferior:

• P*[U] = N[U]/ ( N[U] + N[D] )
• T*[U] = Summ( 0…i ) [ T[U][i]  ] / N[U]
• T*[D] = Summ( 0…i ) [ T[D][i]  ] / N[D]

Como encontramos todos os valores para os quais nosso equivalente bivariado deve convergir, precisamos determinar onde começar nossa busca. Para fazer isso, você precisa determinar qual desses valores tem a maior prioridade em termos de precisão. Eu escolhi a probabilidade de cruzar o limite superior como exemplo. Essa abordagem reduz o poder computacional necessário para análise. Se selecionássemos três valores de uma só vez em três intervalos, obteríamos três graus de liberdade do sistema, o que aumentaria o tempo de cálculo, especialmente porque com um aumento na quantidade de dados isso poderia dar um tempo de cálculo incompatível com a realidade. Em vez disso, na minha lógica, primeiro selecionei a probabilidade de uma etapa para cima e só então selecionei o tempo médio de etapas para cima e para baixo.

Quero lembrar, para que ninguém fique confuso, que há muitas etapas no corredor e o tempo antes do cruzamento dos limites não é o tempo das etapas. Da mesma forma com a probabilidade, a probabilidade de uma etapa em uma determinada direção não é a probabilidade de cruzar o limite do corredor. A única exceção é “n=m=1”, que descrevi no início.

Como resultado da seleção, obtemos as seguintes características de etapa:

1. p – probabilidade de etapa para cima
2. T[u] – duração média de etapa para cima
3. T[d] – duração média de etapa para baixo
4. Pr – módulo de etapa em valores de lucro

Estimativa da eficiência de uma conversão simples

Suponha que todos os parâmetros das etapas sejam selecionados, então como entender a eficácia dessa operação de conversão? Para avaliar a eficácia, você pode traçar linhas retas para as quais as estratégias convergem. Sua inclinação pode ser definida da seguinte forma:

• K = EndProfit / EndTime – coeficiente de inclinação da linha reta
• P0 = K * t – equação de linha reta

Ficará assim:

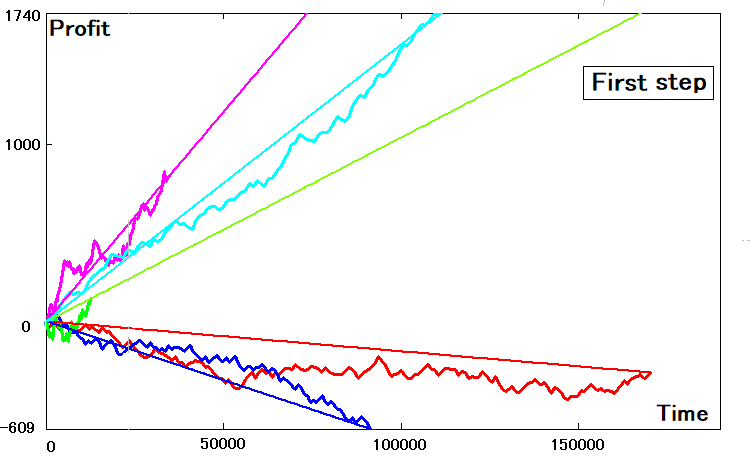
Se os parâmetros das curvas bidimensionais forem escolhidos idealmente, suas linhas retas análogas terão exatamente a mesma inclinação e tocarão as curvas de equilíbrio nos pontos finais. Acho que é intuitivamente claro que muito provavelmente essa coincidência nem sempre será absoluta. Para encontrar o fator de inclinação para o equivalente 2D ajustado, podemos usar os dados ajustados para a etapa:

• MP = p * Pr – (1-p) * Pr – expectativa matemática do deslocamento para cima para qualquer etapa
• MT = p * T[u] + (1-p) * T[d] – expectativa matemática do tempo gasto na formação de qualquer etapa
• K = MP / MT - o mesmo coeficiente de inclinação da linha reta.

Eu fiz isso usando o mesmo programa e quase sempre obtive algo semelhante a isso:

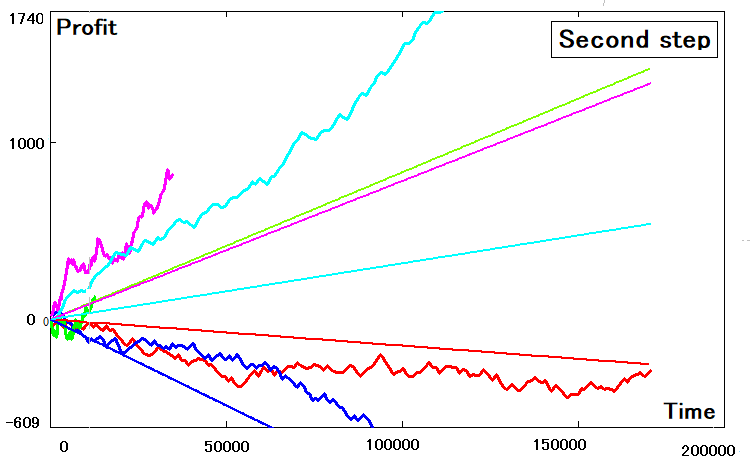
Pode-se observar que nem todas as estratégias foram capazes de se transformar corretamente em um equivalente bidimensional. As que não puderam ser transformadas apresentam desvios bastante pronunciados. Esses desvios se devem aos seguintes motivos:

1. Erro ao calcular valores com asterisco
2. Imperfeição do modelo bidimensional (modelo menos flexível)
3. Finitude do número possível de tentativas de pesquisa (isso também é o mesmo que poder de computação limitado)

Com todos esses fatos, é possível fazer alguns ajustes no tempo médio da etapa, de modo que pelo menos os coeficientes de inclinação dos modelos original e derivado sejam iguais. É claro que tais conversões serão em detrimento dos desvios dos critérios reduzidos, mas isso não pode ser alcançado de outra forma. Ainda assim, considero o coeficiente de inclinação da linha reta o critério mais importante, pois quando o número de negócios tende ao infinito, as estratégias original e derivada devem se fundir em uma única linha. Se isso não acontecer, então não há muito sentido em tal conversão. E talvez o ponto principal não esteja no método de conversão, mas nas possibilidades ocultas que ainda precisam ser compreendidas.

Ajuste final e simulação

Para fazer essa conversão, você pode usar uma proporção. Como antes de construir essas curvas tínhamos os arrays “TL[i]”, “B[i]”, que equivalem ao tempo decorrido desde o início da curva até a ordem ou segmento em questão, podemos pegar os últimos elementos e escrever o seguinte:

• K = B[n] / TL[n]
• N – índice do último elemento do array de saldos (saldo final)

Por sua vez, para as retas obtidas na etapa anterior, tal coeficiente também pode ser calculado - já foi considerado acima:

• K1 = MP / MT

Mas é claro que esses coeficientes não são iguais, e devemos fazer correções. Você pode fazer assim:

• K = MP / ( KT * MT )
• KT – fator de correção

Agora você precisa trazer esse coeficiente dentro da expectativa matemática para que esta não mude seu significado, isso pode ser feito assim:

• MTK = MT * KT = p * (T[u]* KT) + (1-p) * (T[d]* KT)

Pode-se ver que novos valores de tempo corrigidos foram formados entre parênteses, e podem ser calculados da seguinte forma:

1. Tn[u] = T[u]* KT
2. Tn[d] = T[d]* KT

Este será nosso tempo corrigido da etapa para cima e para baixo. O próprio fator de correção pode ser calculado igualando as expressões para estimar os coeficientes:

• B[n] / TL[n] = MP / ( KT * MT )

Uma vez resolvida a equação em relação a “KT”, obtemos uma expressão para calcular este valor:

• KT = ( MP / MT ) / ( B[n] / TL[n] ) = ( MP * TL[n] ) / ( MT * B[n] )

Tudo o que resta é ajustar o tempo médio da etapa para cima e para baixo. Depois disso, o processo de conversão pode ser considerado concluído. Como resultado, obtemos apenas um conjunto de quatro valores que descrevem completamente nossa estratégia, em vez de enormes arrays que descrevem mais de dois estados:

1. p – probabilidade de etapa para cima
2. Pr – módulo da etapa
3. T[u] – tempo médio de geração da etapa para cima
4. T[d] – tempo médio de formação da etapa para baixo

Esses quatro parâmetros são suficientes para recriar a própria estratégia usando simulação. O principal é que agora a simulação de software da estratégia está disponível para nós, independentemente do mercado e do tempo. Usando nossas cinco estratégias como exemplo, a simulação ficou assim:

As linhas retas aqui são tiradas da primeira etapa. Essas linhas foram desenhadas de zero até o final da curva de negociação real. Pode-se observar que a simulação é bastante precisa perto das linhas, o que confirma a correção das conversões. A única exceção é a linha azul, acho que são apenas falhas no meu algoritmo. Tenho certeza que essas pequenas coisas podem ser consertadas com um pouco de tempo.

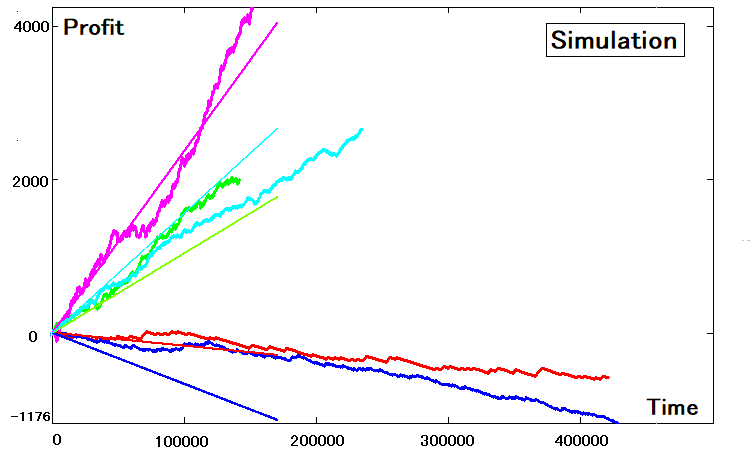
Conclusões

Durante o estudo deste modelo, surgiram pensamentos interessantes. Inicialmente, ao explorar circuitos 2D e multiestado, eu só queria obter uma descrição mais simples para sistemas complexos. Como resultado, conclusões muito mais valiosas e simples foram obtidas a partir dos resultados do estudo. Os detalhes de tudo isso são difíceis de descrever no artigo, porque há muitas nuances técnicas. Em poucas palavras, o que este estudo fez:

Podemos listar todos os prós na lista:

• Muitos sistemas com muitos estados podem ser reduzidos a dois estados (o que significa que o processo n em m estados também é possível)
• O processo de conversão pode ser usado como um mecanismo de compressão de dados de negociação
• Os dados convertidos podem ser realimentados através da simulação, o que simplifica as coisas (porque apenas dois estados precisam ser simulados)
• Compreender mais profundamente os processos probabilísticos dentro da precificação permite tirar conclusões úteis individuais.
• Com base nas informações recebidas, você pode proceder a uma análise mais profunda do processo de negociação
• Já neste estudo, foram obtidos alguns recursos úteis para negociação, enquanto os coloco na categoria de paradoxos

Como resultado, é claro, a ideia principal da série desses artigos é a construção de matemática simples, que permitirá diretamente a criação de sistemas ultraestáveis e multimoeda baseados na teoria das probabilidades. Até agora, essa informação não é muito monolítica, mas um monólito só pode ser construído sobre uma boa base, e é isso que estou fazendo.

Separadamente, vale mencionar os paradoxos que apareceram no decorrer do estudo. Aqui estão as discrepâncias obtidas no primeiro estágio da conversão, que foram expressas em um ângulo de inclinação diferente da linha reta equivalente, sugerem que elas podem ser usadas para converter negociações aleatórias em negociações não aleatórias ou fornecer amplificadores de sinais de negociação.

Em outras palavras, com algumas estratégias zero é possível obter estratégias com fator de lucro positivo, usando apenas esses truques da conversão de múltiplos estados em equivalentes duplos, que já podem ser processados posteriormente por outros métodos e aprimorando sua qualidade. Até agora, esses pensamentos estão muito dispersos para serem reunidos, mas as coisas definitivamente acontecerão. Considero este o principal resultado do estudo, ele será útil mais tarde quando montarmos o Expert Advisor.

Conclusão

Neste artigo, tentei fugir de uma descrição detalhada e não entrar em detalhes. Naturalmente, a matemática também está envolvida, mas dada a experiência de artigos anteriores, vejo que informações mais gerais são muito mais úteis do que detalhes. Aqueles que desejam entender os meandros do método com mais detalhes, o programa em que fiz a pesquisa está anexado ao artigo. Eu não descrevi todos os algoritmos que usei, porque há muita matemática embora importante, mas chata, e basicamente é trabalhar com arrays de dados. Mesmo assim, aqueles que farão algo semelhante manterão sua lógica, mas como ponto de partida, você pode desenhar algo a partir daí.

Se você não quer saber, você pode simplesmente brincar com diferentes estratégias para ver como elas são montadas, porque eu desenvolvi estes programas especificamente para o artigo, como eu fiz antes. Se falarmos sobre o que acontecerá a seguir, acho que gradualmente passaremos para os detalhes e começaremos a escrever um algoritmo de autoadaptação legal, que, espero, será capaz de superar as redes neurais tanto em qualidade quanto em estabilidade. Existem conquistas. Mas primeiro você precisa completar completamente a fundação.

Links

• Combinatória e teoria da probabilidade para negociação (Parte I): fundamentos
  
• Combinatória e teoria da probabilidade para negociação (Parte II): fractal universal
  
• Combinatória e teoria da probabilidade para negociação (Parte III): primeiro modelo matemático
• Combinatória e teoria da probabilidade para negociação (Parte IV): lógica de Bernoulli