Combinatoria e probabilità per il trading (Parte V): Analisi della curva

Contenuto

• Introduzione
• Moduli utili per semplificare i dati
• Fondamenti del metodo di trasformazione risultante
• Definizione dei criteri di riducibilità
• Definizione dei criteri di confronto con il sistema di origine
• Valutazione di un possibile corridoio per il calcolo dei valori richiesti
• Definire la probabilità e il tempo medio di attraversamento del confine superiore del corridoio.
• Stima dell'efficienza di una semplice trasformazione
• Regolazione finale e simulazione
• Riepilogo
• Conclusioni
• Riferimenti

Introduzione

Continuo a preparare le basi per la costruzione di sistemi di trading multi fase e scalabili. Nell'ambito di questo articolo, voglio mostrare come sia possibile utilizzare gli sviluppi degli articoli precedenti per avvicinarsi alle più ampie possibilità di descrizione del processo di trading. Questo aiuterà a valutare la strategia da quei lati che non sono coperti da altri metodi di analisi. In questo articolo ho esplorato le possibilità di trasformare complessi campioni con più stati, in campioni semplici a doppio stato. L'analisi è stata condotta con uno stile di ricerca.

Moduli utili per semplificare i dati

Supponiamo di avere una strategia con molte operazioni che si susseguono una dopo l'altra, senza sovrapporsi, cioè un nuovo ordine viene aperto rigorosamente dopo la chiusura del precedente. Se dobbiamo valutare la probabilità di vincita o perdita e misurare il tempo medio necessario per ottenere il profitto o la perdita, vedremo che gli ordini possono avere un numero molto elevato di stati differenti (vengono chiusi con risultati diversi).

Per poter applicare le formule frattali a tali strategie, dobbiamo prima convertirle in casi che possono essere considerati nel contesto dei frattali. Per implementare ciò, dobbiamo rappresentare la nostra strategia come un ordine con livelli di stop equidistanti, che ha la probabilità di una salita e una discesa, proprio come nel nostro frattale. Quindi, possiamo applicare le formule frattali. Inoltre, la salita e la discesa possono avere una durata differente.

Per ridurre qualsiasi strategia a una dei tipi che possono essere descritte nel quadro delle formule frattali, che abbiamo trovato nell'articolo precedente, dobbiamo prima determinare quali valori devono essere noti per poter applicare le formule frattali. Qui tutto è piuttosto semplice:

• P[1] - la probabilità della salita
• T[1] - tempo medio di formazione della salita
• T[2] - tempo medio di formazione della discesa

In primo luogo, dobbiamo considerare i valori limite quando il numero di passi tende all'infinito:

1. (P[1] * T[1] + (1 -P[1])*T[2]) * n = T(n)
2. (P[1] * Pr - (1 -P[1])*Pr) * n = P(n)

Per comprendere meglio le espressioni precedenti, è necessario scrivere due limiti:

• Lim(n --> +infinity)[P/P0(n)] = 1
• Lim(n --> +infinity)[T/T0(n)] = 1

I limiti dicono che se conduciamo gli stessi esperimenti nella quantità "n", o trade, otterremo sempre un tempo totale diverso che tutti gli esperimenti elementari inclusi nell'esperimento generale principale hanno richiesto. Inoltre, otterremo sempre posizioni differenti del saldo di trading finale. D'altra parte, è intuitivamente chiaro che con un numero infinito di esperimenti, il valore reale tenderà al limite.  Possiamo dimostrare questo fatto utilizzando generatori di numeri casuali.

• n - numero di passi emulati
• 1-P[1] - probabilità della discesa
• T0(n) - quantità reale di tempo impiegato per "n" passi
• P0(n) - spostamento reale del saldo o del prezzo per "n" passi
• T(n) - la quantità di tempo limite impiegato per "n" passi
• P(n) - lo spostamento limite per "n" passi

Questa logica si traduce in due equazioni che tuttavia ha troppe incognite. Non c'è da stupirsi, perché questo è solo l'inizio. Ma queste equazioni descrivono solo il sistema derivato (quello che dobbiamo ottenere). Le equazioni per il sistema originario sono simili:

1. (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) * m = T(m)
2. (P*[1] * Pr*[1] + P*[2]*Pr*[2] + ... + P*[N1]*Pr*[N1]) * m - (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + ... + P*[N2]*Pr*[N2]) * m = P(m)

• P*[1] + P[*2] + ... + P*[N2] = 1 - le probabilità formano un gruppo completo

Anche i limiti sono gli stessi e mostrano gli stessi valori:

• Lim(m --> +infinity)[P/P0(m)] = 1
• Lim(m --> +infinity)[T/T0(m)] = 1

Le variabili utilizzate qui, sono descritte di seguito:

• m - numero di passi emulati
• T0(m) - quantità reale di tempo impiegato per "m" passi
• P0(m) - spostamento reale del saldo o del prezzo per "m" passi
• T(m) - tempo reale impiegato per "m" passi
• P(m) - spostamento reale per "m" passi
• T = Lim(m --> +infinity) [ T(m) ] - tempo limite
• N1 - il numero di esiti dei trade con profitto positivo e il loro contatore
• N2 - N1 + 1 - numero di esiti dei trade con profitto negativo (N2 è il loro contatore)

Sulla base del sistema di partenza, dobbiamo crearne uno nuovo, più semplice, composto da uno più complesso. L'unica differenza è che conosciamo tutti i parametri del sistema originale. I valori noti sono indicati con i suffissi asterisco * .

Se equipariamo la seconda e la prima equazione di entrambi i sistemi, possiamo eliminare le variabili P e T:

• (P[1] * T[1] + (1 -P[1])*T[2]) * n = (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) * m
• (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + ... + P*[N1]*Pr*[N1]) * m - (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + ... + P*[N2]*Pr*[N2]) * m

Come risultato, abbiamo perso due equazioni, ma allo stesso tempo abbiamo eliminato due incognite che non erano necessarie. Come risultato di queste trasformazioni, abbiamo un'equazione, in cui le seguenti quantità sono sconosciute:

• P[1] - la probabilità della salita (stop)
• T[1] - la durata media della salita
• T[2] - la durata media della discesa

Queste due equazioni hanno una struttura simile:

1. A1*n = A2*m
2. B1*n = B2*m

La struttura indica che una delle variabili, "n" o "m", può essere esclusa per eliminare una delle equazioni. A tal fine, è necessario esprimere uno dei valori, ad esempio quello della prima equazione:

• m = ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + ... + P*[N])*T*[N] )* n

Quindi, sostituiamo l'espressione alla seconda equazione e vediamo il risultato:

• (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + ... + P*[N1]*Pr*[N1]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + ... + P*[N])*T*[N] ) ) * n - (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + ... + P*[N2]*Pr*[N2]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + ... + P*[N])*T*[N] ) ) * n

Ora, entrambe le parti dell'equazione vengono moltiplicate per "n". Quindi, dividendoli per "n", otterremo un'equazione che dipende solo dai valori richiesti:

• (P[1] * Pr - (1 -P[1])*Pr) = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + ... + P*[N1]*Pr*[N1]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + ... + P*[N])*T*[N] ) ) - (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + ... + P*[N2]*Pr*[N2]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + ... + P*[N])*T*[N] ) )

Il valore "Pr" è considerato libero, poiché il numero di sistemi a cui tutti possono essere ridotti è infinito. Possiamo impostare qualsiasi dimensione del passo, purché i passi verso l'alto (salita) e verso il basso (discesa) siano uguali in valore assoluto. Gli altri valori saranno determinati risolvendo un sistema di equazioni. Finora il sistema ha una sola equazione. Sono necessarie altre due equazioni, che possono essere ricavate utilizzando le equazioni ottenute nella sezione precedente.

Innanzitutto, il sistema deve avere una probabilità identica di attraversamento del corridoio superiore e di quello inferiore. Inoltre, dovrebbe avere un tempo medio identico per attraversare uno dei limiti. Questi due requisiti ci daranno le due equazioni mancanti. Iniziamo con il determinare il tempo medio di attraversamento del corridoio. Il tempo medio di attraversamento di uno dei limiti è determinato dal numero medio di passi verso l'alto e verso il basso. Tenendo conto dei risultati dell'articolo precedente, possiamo scrivere quanto segue:

• T[U,D] = (S[U,u] * T[1] + S[U,d] * T[2]) * P[U] + (S[D,u] * T[1] + S[D,d] * T[2]) * ( 1 - P[U] )

Questa equazione indica che il tempo medio di attraversamento di uno dei limiti dipende dal numero medio di passi in cui uno dei limiti viene attraversato, oltre che dalla probabilità di attraversamento. Questo criterio fornirà un'altra possibile equazione con cui creare un sistema di equazioni che ci permetterà di trasformare un sistema di trading complesso in uno più semplice. Questa equazione può essere suddivisa in altre due equazioni:

• T[U] = S[U,u] * T[1] + S[U,d] * T[2]
• T[D] = S[D,u] * T[1] + S[D,d] * T[2]

Queste equazioni ci serviranno in seguito. Tutti questi valori sono calcolati sulla base del modello matematico ottenuto nell'articolo precedente:

• S[U,u], S[U,d], S[D,u], S[D,d], P[U] = f(n,m,p) - tutti questi valori sono funzioni di "n,m,p".
• n = B[U]/ Pr - a sua volta, "n" può essere espresso in termini di distanza dal limite superiore e dal passo "Pr".
• m = B[D]/ Pr - a sua volta, "m" può essere espresso in termini di distanza dal limite inferiore e dal passo "Pr".
• Pr - passo selezionato
• B[U] - distanza dal limite superiore
• B[D] - distanza dal limite inferiore

Fondamenti del metodo di trasformazione risultante

Ad esempio, possiamo prendere una strategia casuale e convertirla nell'equivalente richiesto. Ho creato una delle varianti per trasformare un sistema multidimensionale complesso in uno più semplice e bidimensionale. Cercherò di fornire una descrizione passo passo di questo processo. Prima di procedere alla descrizione, ho implementato l'idea e testato le prestazioni del metodo. Il programma è allegato all'articolo. Nel mio programma ho utilizzato formule leggermente diverse ma ugualmente efficaci. Si basa sul modello matematico ottenuto nell'articolo precedente. Utilizzandolo, possiamo ottenere i seguenti valori:

• P[U], S[U,u], S[U,d], S[D,u], S[D,d]

Dai passi medi, possiamo ricavare il tempo medio prima che il confine superiore o inferiore venga attraversato. Lo scopo potrebbe non essere del tutto chiaro per ora. Dovrebbe diventare più chiaro con ulteriori spiegazioni. Per trasformare una strategia a più stati in una più semplice, dobbiamo prima generare le strategie pertinenti. Ho creato un generatore di strategie basato su numeri casuali. Per comodità, ho preso cinque strategie generate a caso. Sono le seguenti:

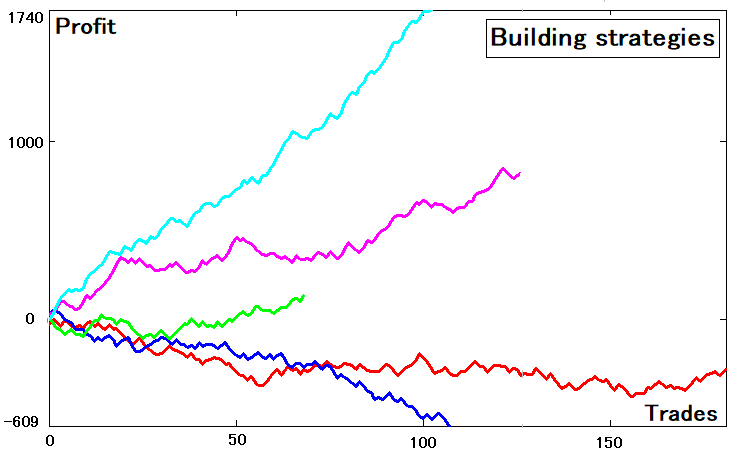
Queste strategie hanno diverse metriche di Expected Payoff, differenti numeri di operazioni e parametri. Alcune curve si perdono, ma va bene così, perché si tratta pur sempre di una curva, anche se i suoi parametri potrebbero non essere del tutto buoni.

Veniamo al punto. La figura mostra i grafici del saldo che dipendono dal numero di operazioni, simili ai grafici dello Strategy Tester. In base ad essa, esiste una certa serie di equilibri per ogni curva:

• B[i] , i = 0...N
• N - numero di trade

Questo array può essere ottenuto dall’array con i parametri dell’ordine. Presumo che il contenitore con i dati dell'ordine contenga solo il valore del profitto o della perdita dell'ordine e la sua durata:

• Pr[i], T[i]

Supponiamo che altri parametri non siano disponibili. Credo che questo sia corretto, perché quando vogliamo analizzare qualsiasi backtest o segnale, di solito questi dati non sono disponibili, poiché normalmente nessuno li salva. Più frequentemente, gli utenti controllano il fattore di recupero, il drawdown massimo e altre metriche simili. Gli unici dati di trading che vengono sempre salvati sono:

1. Profitto
2. Orario di apertura dell'ordine
3. Orario di chiusura dell'ordine

Naturalmente, l'indisponibilità di alcuni dati influisce sull'accuratezza, ma non c'è nulla da fare. Vediamo ora come ottenere un array con i saldi da un array con i profitti:

• B[i] = B[i-1] + Pr[i] if i > 0
• B[i] = 0 else

Per consentire l'analisi delle strategie ottenute rispetto al tempo, è necessario creare un array temporale simile:

• TL[i] = TL[i-1] + T[i] if i > 0
• TL[i] = 0 else

Dopo aver determinato le ascisse e le ordinate di tutte queste curve, possiamo tracciarle. Vedrete le differenze, poiché si tratta di funzioni che non dipendono dal numero di trade, ma dal tempo:

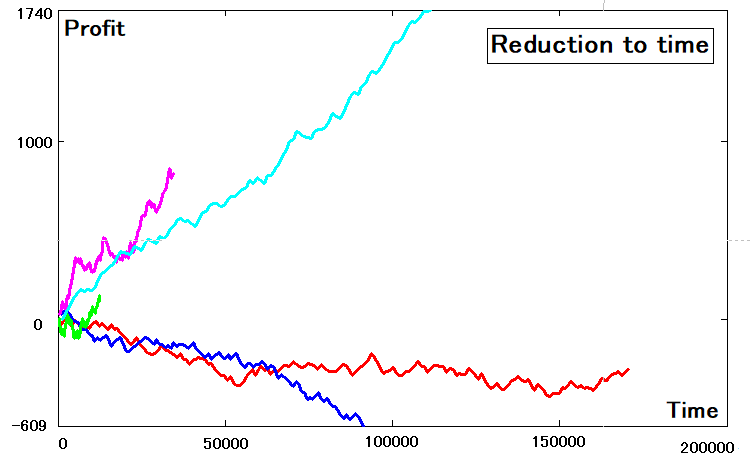
Definizione dei criteri di riducibilità

Possiamo lavorare ulteriormente con i dati ottenuti. Ora possiamo determinare i criteri in base ai quali verificheremo se le curve corrispondono a due stati di profitto. Dal punto di vista della rappresentazione relativa al tempo, tre grandezze saranno sufficienti:

1. P[U] - la probabilità di superare il limite superiore
2. T[U] - il tempo medio di raggiungimento del limite superiore
3. T[D] - il tempo medio del raggiungimento del limite inferiore

Il secondo e il terzo valore possono essere calcolati come segue:

• T[U] = S[U,u] * T[u] + S[U,d] * T[d]
• T[D] = S[D,u] * T[u] + S[D,d] * T[d]

Per quanto riguarda P[U], questo valore è fornito dal modello matematico ottenuto nell'articolo precedente e, come ricorderete, "P[D] = 1 - P[U]". Pertanto, sulla base dei cinque valori forniti dal modello matematico, possiamo ricavare i tre valori necessari descritti sopra. Per quanto riguarda queste due equazioni, le abbiamo ottenute in precedenza, ma qui ho cambiato la notazione per il tempo per comodità.

Questi valori sono calcolabili. Per ridurli a qualcosa, dobbiamo in qualche modo ottenere il loro valore reale in base a ciò che abbiamo. Quindi, dobbiamo trovare detti parametri della curva equivalente a due stati desiderata, tali che tutti e tre i parametri siano molto simili ai valori reali. È così che si ottengono i criteri. Per prima cosa, introduciamo la notazione per i valori noti:

• P*[U] - la probabilità reale di attraversare i limiti del corridoio selezionato
• T*[U] - il tempo medio reale prima che il limite superiore venga superato
• T*[D] - il tempo medio reale prima che il limite inferiore venga superato

La deviazione tra i valori reali e quelli calcolati può essere misurato in termini relativi o in percentuale. Se misurati in percentuale, i criteri saranno i seguenti:

• KPU = ( | P[U] - P*[U] | / ( P[U] + P*[U] ) ) * 100 %
• KTU = ( | T[U] - T*[U] | / ( T[U] + T*[U] ) ) * 100 %
• KTD = ( | T[D] - T*[D] | / ( T[D] + T*[D] ) ) * 100 %

Definizione dei criteri di confronto con il sistema di origine

Il sistema migliore è quello che presenta un minimo di tutti questi valori. Ora, per poter ottenere i valori calcolati, dobbiamo prima determinare la dimensione del corridoio, in base alla quale determineremo la probabilità reale e il tempo reale fino al breakout. Questa idea può essere visualizzata come segue:

La figura mostra un esempio di determinazione di tale corridoio per una strategia profittevole. I triangoli viola simboleggiano un altro punto di controllo per eventuali movimenti al rialzo e al ribasso. Il movimento minimo desiderato è compreso tra i punti neri. Se prendiamo come base il movimento massimo avvenuto nel periodo disponibile, allora la probabilità P[U] sarà pari a uno. Ovviamente, questa è la scelta più sbagliata. Perché abbiamo bisogno del valore minimo che garantisca l'attraversamento di entrambi i limiti inferiore e superiore.

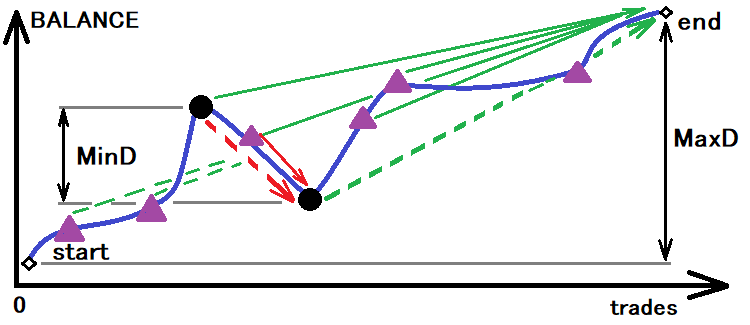
Valutazione di un possibile corridoio per il calcolo dei valori richiesti

Tuttavia, anche questo non è sufficiente. Se utilizziamo questo valore come base, avremo solo un tocco del limite inferiore, che non è nemmeno accurato. Personalmente, ho utilizzato il valore del corridoio tre volte inferiore del minimo indicato. Con un campione sufficiente di tocchi vincolati, questo valore sarà sufficiente. Ora che abbiamo determinato le dimensioni del corridoio, possiamo dividerlo. Se assumiamo che il corridoio stesso sia un passo, allora:

• n, m = 1
• p = P[U]
• Pr * n = Pr * m = 1/3 * MinD - metà della larghezza del corridoio
• Pr = ( 1/3 * MinD ) / n = ( 1/3 * MinD ) / m - passo modulo
• T[U,u] = T[U]
• T[D,d] = T[D]
• T[U,d] = 0
• T[D,u] = 0

Questa variante può essere utilizzata anche nel caso in cui si abbia un campione di trading molto ampio. Il vantaggio di questo approccio è che non è necessario utilizzare un modello matematico per suddividere il corridoio, perché in questo caso l'intero corridoio è un passo. Ma nei miei calcoli ho usato un modello matematico come esempio. Quando si utilizza questo approccio, è necessario individuare i seguenti intervalli di parametri per la selezione:

• p = p1 ... p2
• N = m = nm1 .... nm2

Nel mio esempio, ho utilizzato i seguenti intervalli:

• p1 = 0.4, p2 = 0.6, nm1 = 1, nm2 = 3

Naturalmente è possibile utilizzare intervalli più ampi. Facoltativamente, uno degli intervalli può essere ampliato, mentre l'altro può essere utilizzato così com'è. Ad esempio, se aumentiamo "nm2", il metodo può coprire una gamma più ampia di varie strategie. Se il modello matematico non è in grado di gestire la variante successiva, possiamo passare a quella senza modello matematico.

Definire la probabilità e il tempo medio di attraversamento del confine superiore del corridoio.

Dopo aver trovato con successo tutti i valori di cui sopra, otterremo solo la probabilità "p" per un passo avanti. Possiamo quindi utilizzare questo valore come base per trovare il tempo medio di attraversamento del confine. Questo può essere visualizzato con una leggera trasformazione dell'immagine precedente:

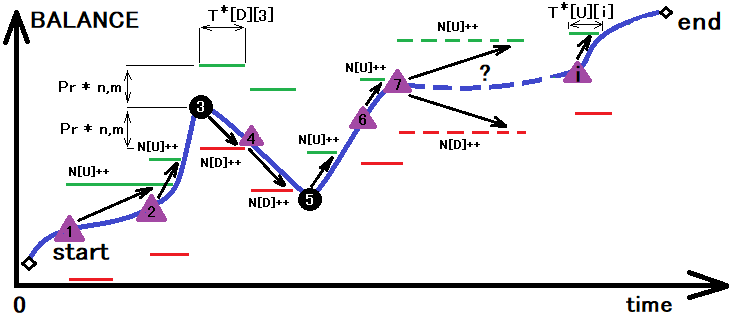
La figura mostra il processo di somma degli attraversamenti superiori e inferiori per il corridoio la cui dimensione è stata determinata come risultato della trasformazione precedente. Con la somma di questi attraversamenti, si calcola il tempo necessario per l'intersezione. Con un'unica operazione, possiamo determinare tutte le quantità con asterisco di cui abbiamo bisogno:

• N[U] - il numero di intersezioni del bordo superiore del corridoio
• N[D] - il numero di intersezioni del bordo inferiore del corridoio
• T[U][i] - array con il tempo che manca al superamento del bordo superiore
• T[D][i] - array con il tempo che manca al superamento del bordo inferiore

Utilizzando questi dati, calcoliamo la probabilità di attraversamento del bordo superiore e il tempo medio di attraversamento dei bordi superiore e inferiore:

• P*[U] = N[U]/ ( N[U] + N[D] )
• T*[U] = Summ( 0...i ) [ T[U][i] ] / N[U]
• T*[D] = Summ( 0...i ) [ T[D][i] ] / N[D]

Abbiamo trovato tutti i valori a cui ridurre il nostro equivalente bidimensionale. Ora dobbiamo definire da dove iniziare la ricerca. A tal fine, è necessario determinare quale di questi valori ha la massima priorità in termini di accuratezza. Ho scelto come esempio la probabilità di attraversare il confine superiore. Questo approccio riduce i requisiti computazionali dell'analisi. Se scegliamo di selezionare tre valori in tre intervalli, otterremmo tre gradi di libertà, il che aumenterebbe il tempo di calcolo. A volte i tempi di calcolo sono irreali. Invece, ho iniziato con la probabilità di salire e poi ho proceduto con il tempo medio di salita e discesa.

Voglio ricordarvi che ci sono molti passaggi nel corridoio e che il tempo di attraversamento non è il tempo dei passaggi. Inoltre, la probabilità di un passo in una certa direzione non è la probabilità di attraversamento del limite. L'unica eccezione è la situazione n=m=1 descritta all'inizio.

Di conseguenza, si ottengono le seguenti caratteristiche del passo:

1. p - probabilità di una salita
2. T[u] - durata media di una salita
3. T[d] - durata media di una discesa
4. Pr - modulo passo in valori di profitto

Stima dell'efficienza di una semplice trasformazione

Supponiamo di aver trovato tutti i parametri dei passi. Come valutare l'efficienza generale di questa operazione di trasformazione? Per valutare l'efficienza, possiamo tracciare delle linee rette a cui si riducono le strategie. La pendenza delle linee può essere definita come segue:

• K = EndProfit / EndTime - coefficiente di pendenza della retta
• P0 = K * t - equazione della retta

Ecco come apparirà:

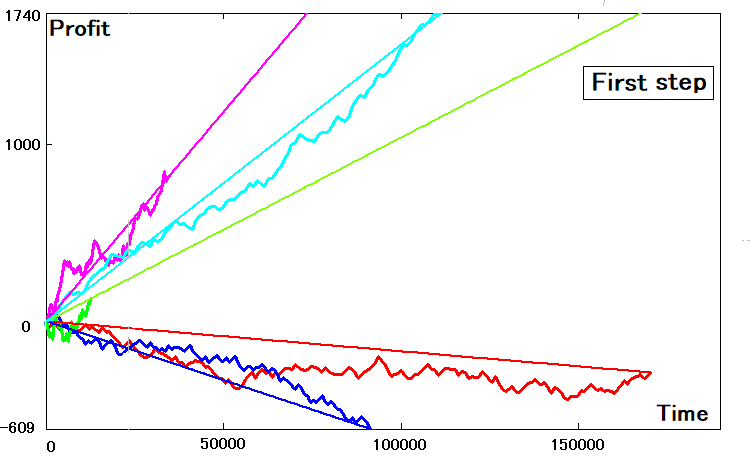
Se i parametri delle curve bidimensionali sono ideali, le loro analoghe rette avranno esattamente la stessa pendenza e toccheranno le curve di equilibrio nei punti finali. Credo sia chiaro che una simile coincidenza non potrà mai verificarsi. Per trovare il coefficiente di pendenza per questo equivalente, possiamo utilizzare i dati trovati per il passo:

• MP = p * Pr - (1-p) * Pr - aspettativa matematica di uno spostamento verso l'alto per qualsiasi passo
• MT = p * T[u] + (1-p) * T[d] - aspettativa matematica del tempo impiegato per la formazione di un qualsiasi passo
• K = MP / MT - coefficiente di pendenza della linea.

Ho usato lo stesso programma per il calcolo e ogni volta ho ottenuto un'immagine simile:

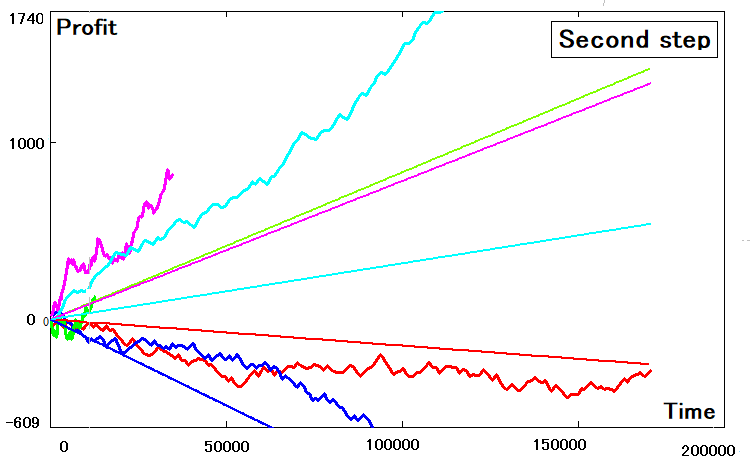
Non tutte le strategie potevano essere trasformate correttamente in un equivalente bidimensionale. Alcune di esse presentano evidenti deviazioni. Le deviazioni sono legate ai seguenti motivi:

1. Errore nel calcolo dei valori con asterisco
2. Imperfezione del modello bidimensionale (modello meno flessibile)
3. Finitezza del numero possibile di tentativi di ricerca (e della limitata potenza di calcolo)

Tenendo conto di tutti questi fatti, possiamo regolare il passo di tempo medio, in modo che almeno i coefficienti di pendenza dei modelli originali e derivati siano uguali. Naturalmente, tali trasformazioni influirebbero sulle deviazioni dei criteri che stiamo riducendo, ma non c'è altra soluzione. Credo che il criterio principale sia il coefficiente di pendenza della linea, perché se il numero di trade tende all'infinito, la strategia originale e quella derivata dovrebbero fondersi in un'unica linea. Se questo non avviene, non ha molto senso una trasformazione di questo tipo. Forse, tutto questo non è legato al metodo di trasformazione, ma alle possibilità nascoste che ora non sono del tutto chiare.

Regolazione finale e simulazione

Per effettuare tale trasformazione, possiamo utilizzare una proporzione. Prima di creare le curve, avevamo gli array TL[i], B[i], che equivalgono al tempo trascorso dall'inizio della curva all'ordine o segmento analizzato; possiamo prendere gli ultimi elementi dell'array e scrivere quanto segue:

• K = B[n] / TL[n]
• N - l'indice dell'ultimo elemento dell'array dei saldi (saldo finale)

Anche per le rette ottenute al passo precedente possiamo calcolare tale coefficiente. Era già stato calcolato in precedenza:

• K1 = MP / MT

Questi coefficienti non sono uguali, quindi è necessaria una correzione. Si può procedere come segue:

• K = MP / ( KT * MT )
• KT — coefficiente di correzione

Ora dobbiamo aggiungere questo coefficiente all'interno dell'aspettativa matematica, in modo che l'aspettativa matematica non cambi il suo significato. Si può procedere in questo modo:

• MTK = MT * KT = p * (T[u]* KT) + (1-p) * (T[d]* KT)

Come si può notare, i nuovi valori temporali corretti sono ora inclusi tra parentesi. Possono essere calcolati come segue:

1. Tn[u] = T[u]* KT
2. Tn[d] = T[d]* KT

Questo è il nostro tempo corretto di una salita e di una discesa. Per calcolare il coefficiente di correzione, equipariamo le espressioni di calcolo dei coefficienti:

• B[n] / TL[n] = MP / ( KT * MT )

Risolta l'equazione relativa a KT, si ottiene un'espressione per calcolare questo valore:

• KT = ( MP / MT ) / ( B[n] / TL[n] ) = ( MP * TL[n] ) / ( MT * B[n] )

È sufficiente regolare il tempo medio di una salita e di una discesa. A questo punto, il processo di conversione può considerarsi completato. Come risultato, otteniamo un insieme di quattro valori che descrivono completamente la nostra strategia — invece di enormi array che descrivono più di due stati:

1. p - probabilità di una salita
2. Pr - modulo passo
3. T[u] - tempo medio di formazione della salita
4. T[d] - tempo medio di formazione della discesa

Questi quattro parametri sono sufficienti per ricreare la strategia tramite simulazione. Ora questo software è a nostra disposizione, indipendentemente dal mercato e dal momento. La simulazione per le nostre cinque strategie è la seguente:

In questo caso utilizziamo le linee rette del primo passo. Queste linee sono tracciate da zero alla fine della curva di trade reale. Come si può vedere, la simulazione è molto vicina alle linee, il che conferma la correttezza delle trasformazioni. L'unica eccezione è la linea blu. Credo che il mio algoritmo presenti alcuni piccoli difetti, che possono essere risolti in poco tempo.

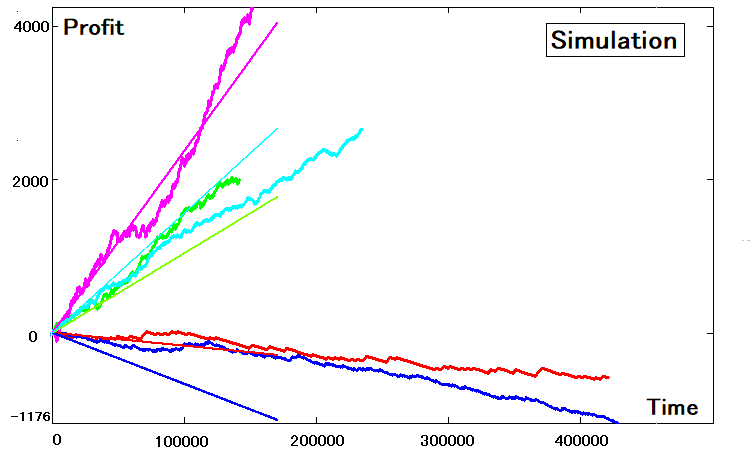
Riepilogo

Il processo di studio del modello ha generato idee interessanti. Originariamente, studiando gli schemi bidimensionali e gli schemi multi stato, volevo ottenere solo una descrizione semplificata per i sistemi complessi. Grazie a questa analisi, abbiamo ottenuto conclusioni molto più valide e semplici. I dettagli sono difficili da descrivere nell'articolo, poiché implicano troppe sfumature tecniche. In poche parole, questo studio ha prodotto:

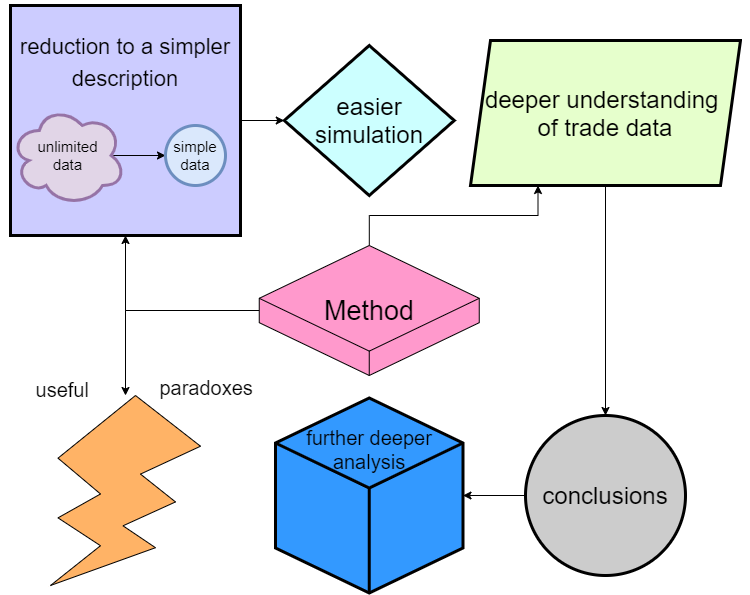
Tutti i vantaggi possono essere presentati in un elenco:

• Molti sistemi multi stato possono essere convertiti in sistemi a due stati (e quindi anche il processo da n a m stati è possibile)
• Il processo di conversione può essere utilizzato come meccanismo di compressione dei dati di trading.
• I dati convertiti possono essere reimmessi nella simulazione, il che semplifica anche la simulazione (perché devono essere simulati solo due stati).
• Una comprensione più approfondita dei processi probabilistici all'interno dei prezzi consente di trarre conclusioni utili a livello individuale.
• Sulla base delle informazioni ricevute, possiamo procedere a un'analisi più approfondita del processo di trading.
• Abbiamo ottenuto alcune caratteristiche utili per il trading — per ora le classifico come paradossi

Naturalmente, l'idea principale della serie è la costruzione di una matematica semplice e utile che permetta direttamente la creazione di sistemi ultra-stabili e multi-valuta basati sulla teoria della probabilità. Finora, le informazioni ottenute costituiscono una buona base per la costruzione di una soluzione monolitica.

Inoltre, vorrei menzionare i paradossi che abbiamo rivelato nel corso dello studio. Nella prima fase di trasformazione, abbiamo ottenuto discrepanze che si esprimevano in una diversa pendenza della retta equivalente. Penso che queste discrepanze possano essere utilizzate per convertire il trading casuale in trading non casuale, o per fornire vari amplificatori di segnale di trading.

In altre parole, potrebbero essere utili per convertire alcune strategie a zero in strategie con PF positivo se si applicano le trasformazioni per convertire i sistemi multi stato in sistemi a due stati, che possono essere ulteriormente gestiti con altri metodi volti a migliorarne la qualità. Per ora questi pensieri sono troppo vaghi e sparsi, ma alla fine si trasformeranno in idee. Considero questo il risultato principale dello studio, che utilizzeremo in seguito quando creeremo un Expert Advisor.

Conclusioni

In questo articolo ho cercato di non scendere troppo nei dettagli. Naturalmente, questo argomento coinvolge la matematica. Tuttavia, data l'esperienza degli articoli precedenti, vedo che le informazioni generalizzate sono più utili dei dettagli. Se volete studiare tutti i dettagli del metodo, utilizzate il programma allegato qui sotto — ho condotto una ricerca con questo programma. Non ho descritto tutti gli algoritmi utilizzati, perché implicano un sacco di matematica noiosa, fondamentalmente legata ad array di dati e matrici. Penso che se qualcuno desidera creare qualcosa di simile, si atterrà alla propria logica, ma potrà usare il programma presentato come punto di partenza.

Se non si vuole approfondire l'analisi, suggerisco di testare diverse strategie per vedere come verranno convertite. Per quanto riguarda le idee future, penso che passeremo gradualmente alla creazione di un solido algoritmo di auto-adattamento che sarà in grado di superare le reti neurali sia in termini di qualità che di stabilità. Ho già qualche idea. Ma prima dobbiamo completare le fondamenta.

Riferimenti

• Combinatoria e teoria della probabilità per il trading (Parte I): Le basi
  
• Combinatoria e teoria della probabilità per il trading (Parte II): Frattale universale
  
• Combinatoria e teoria della probabilità per il trading (Parte III): Il primo modello matematico
• Combinatoria e probabilità per il trading (Parte IV): Logica di Bernoulli