Combinatoires et probabilités pour le trading (Partie V) : Analyse des courbes

Sommaire

• Introduction
• Formules utiles pour simplifier les données
• Principes de la méthode de transformation résultante
• Définition des critères de réductibilité
• Définition des critères de comparaison avec le système source
• Évaluation d'un éventuel canal pour le calcul des valeurs requises
• Définition de la probabilité et du temps moyen jusqu'au franchissement de la limite supérieure du canal
• Estimation de l'efficacité d'une transformation simple
• Ajustement final et simulation
• Résumé
• Conclusion
• Références

Introduction

Je continue à préparer les bases de la construction de systèmes de trading multi-étapes et évolutifs. Dans le cadre de cet article, je souhaite montrer comment vous pouvez utiliser les développements des articles précédents pour vous rapprocher des possibilités plus larges de description du processus de trading. Cela permettra d'évaluer la stratégie sous des angles qui ne sont pas couverts par d'autres méthodes d'analyse. Dans cet article, j'ai exploré les possibilités de transformer des échantillons complexes à plusieurs états en échantillons simples à deux états. Cette analyse a été réalisée dans un style de recherche.

Formules utiles pour simplifier les données

Supposons qu'il existe une stratégie comportant de nombreuses transactions qui se succèdent sans se chevaucher. C'est-à-dire qu'un nouvel ordre est ouvert strictement après la clôture de l'ordre précédent. S'il s'agit d'évaluer la probabilité de gagner ou de perdre et de mesurer le temps moyen nécessaire pour réaliser une profit ou une perte, nous verrons que les ordres peuvent avoir un très grand nombre d'états différents (ils sont fermés avec des résultats différents).

Afin de pouvoir appliquer les formules fractales à ces stratégies, nous devons d'abord convertir ces stratégies en cas pouvant être considérés dans le cadre des fractales. Pour cela, nous devons représenter notre stratégie sous la forme d'un ordre avec des niveaux d'arrêt équidistants, qui a la probabilité d'un pas vers le haut et d'un pas vers le bas, tout comme dans notre fractale. Nous pouvons ensuite appliquer les formules fractales. De même, un pas vers le haut et un pas vers le bas peuvent avoir des durées de vie différentes.

Afin de réduire toute stratégie à l'un des types pouvant être décrits dans le cadre des formules fractales, que nous avons trouvées dans l'article précédent, nous devons d'abord déterminer quelles valeurs doivent être connues pour pouvoir appliquer les formules fractales. Tout est assez simple ici :

• P[1] - la probabilité du pas vers le haut
• T[1] - le temps moyen de formation du pas vers le haut
• T[2] - le temps moyen de formation du pas vers le bas

Nous devons tout d’abord considérer les valeurs limites lorsque le nombre de pas tend vers l'infini :

1. (P[1] * T[1] + (1 - P[1]) * T[2]) * n = T(n)
2. (P[1] * Pr - (1 - P[1]) * Pr) * n = P(n)

Afin de mieux comprendre les expressions ci-dessus, il est nécessaire d'écrire 2 limites :

• Lim(n --> +infini)[P / P0(n)] = 1
• Lim(n --> +infini)[T / T0(n)] = 1

Les limites indiquent que si nous menons les mêmes expériences dans le nombre "n", ou positions, nous obtiendrons toujours un temps total différent pour toutes les expériences élémentaires incluses dans l'expérience générale principale. Nous obtiendrons également toujours des positions différentes sur la balance de trading finale. D'autre part, il est intuitivement clair qu'avec un nombre infini d'expériences, la valeur réelle tendra vers la limite.  Nous pouvons prouver ce fait en utilisant des générateurs de nombres aléatoires.

• n - le nombre de pas émulés
• 1 - P[1] - la probabilité du pas vers le bas
• T0(n) - le temps réel passé sur "n" pas
• P0(n) - le déplacement réel de la balance ou du prix pour "n" pas
• T(n) - le temps limite passé sur "n" pas
• P(n) - le décalage de la limite pour "n" pas

Cette logique aboutit à 2 équations qui comportent cependant trop d'inconnues. Ce n'est pas surprenant, car ce n'est que le début. Mais ces équations ne décrivent que le système dérivé (celui que nous devons obtenir). Les équations pour le système source sont similaires :

1. (P*[1] * T[1] + P*[2])*T*[2] + ... + P*[N])*T*[N] ) * m = T(m)
2. (P*[1] * Pr*[1] + P*[2]*Pr*[2] + ... + P*[N1]*Pr*[N1]) * m - (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + ... + P*[N2]*Pr*[N2]) * m = P(m)

• P*[1] + P[*2] + ... + P*[N2] = 1 - les probabilités forment un groupe complet

Les limites sont également les mêmes et affichent les mêmes valeurs :

• Lim(m --> +infini)[P / P0(m)] = 1
• Lim(m --> +infini)[T / T0(m)] = 1

Les variables utilisées ici sont décrites ci-dessous :

• m - le nombre de pas émulés
• T0(m) - le temps réel passé sur "m" pas
• P0(m) - le déplacement réel de la balance ou du prix pour "m" pas
• T(m) - le temps réel passé sur "m" pas
• P(m) - le décalage réel pour "m" pas
• T = Lim(m --> +infini) [ T(m) ] - le temps limite
• N1 - le nombre de positions avec un profit positif et leur contrepartie
• N2 - N1 + 1 - le nombre de positions avec un bénéfice négatif (N2 est leur contrepartie)

Sur la base du système source, nous devons en créer un nouveau, plus simple, composé d'un système plus complexe. La seule différence est que nous connaissons tous les paramètres du système original. Les valeurs connues sont indiquées par des astérisques * postfixes.

Si nous mettons en équation la deuxième et la première équation des deux systèmes, nous pouvons éliminer les variables P et T :

• (P[1] * T[1] + (1 -P[1])*T[2]) * n = (P*[1] * T[1] + P*[2])*T*[2] + ... + P*[N])*T*[N] ) * m
• (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + ... + P*[N1]*Pr*[N1]) * m - (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + ... + P*[N2]*Pr*[N2]) * m

Nous avons ainsi perdu 2 équations, mais en même temps nous avons éliminé 2 inconnues qui n'étaient pas nécessaires. À la suite de ces transformations, nous avons une équation, dans laquelle les quantités suivantes sont inconnues :

• P[1] - la probabilité du pas vers le haut (arrêt)
• T[1] - la durée de vie moyenne du pas vers le haut
• T[2] - la durée de vie moyenne du pas vers le bas

Ces deux équations ont une structure similaire :

1. A1*n = A2*m
2. B1*n = B2*m

La structure indique que l'une des variables, "n" ou "m", peut être exclue pour éliminer l'une des équations. Pour cela, nous devons exprimer l'une des valeurs, par exemple celle de la première équation :

• m = ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + ... + P*[N])*T*[N] )* n

Nous substituons ensuite l'expression à la deuxième équation et nous obtenons le résultat suivant :

• (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + ... + P*[N1]*Pr*[N1]) * ((P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + ... + P*[N])*T*[N]) ) ) * n - (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + ... + P*[N2]*Pr*[N2]) * ((P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + ... + P*[N])*T*[N] ) ) * n

Les deux parties de l'équation sont maintenant multipliées par "n". En les divisant par "n", on obtient ainsi une équation qui ne dépend que des valeurs requises :

• (P[1] * Pr - (1 -P[1])*Pr) = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + ... + P*[N1]*Pr*[N1]) * ((P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + ... + P*[N])*T*[N]) ) ) - (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + ... + P*[N2]*Pr*[N2]) * ((P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + ... + P*[N])*T*[N] ) )

La valeur "Pr" est considérée comme libre, car le nombre de systèmes auxquels tous peuvent être ramenés est infini. Nous pouvons définir absolument n'importe quelle taille de pas, étant donné que les pas vers le haut et les pas vers le bas sont égaux en valeurs absolues. Les autres valeurs seront déterminées par la résolution d'un système d'équations. Jusqu'à présent, le système ne comporte qu'une seule équation. Nous avons besoin de 2 équations supplémentaires, qui peuvent être obtenues en utilisant les équations obtenues dans la section précédente.

Le système doit tout d’abord avoir une probabilité identique de franchissement de la limite supérieure et de la limite inférieure du canal. De plus, le temps moyen de franchissement de l'une des limites doit être identique. Ces deux exigences nous permettront d'obtenir les deux équations manquantes. Commençons par déterminer le temps moyen jusqu'au franchissement de la limite du canal. Le temps moyen jusqu'à ce que l'une des limites soit franchie est déterminé par le nombre moyen de pas vers le haut et vers le bas. En tenant compte des résultats de l'article précédent, nous pouvons écrire ce qui suit :

• T[U,D] = (S[U,u] * T[1] + S[U,d] * T[2]) * P[U] + (S[D,u] * T[1] + S[D,d] * T[2]) * ( 1 - P[U] )

Cette équation indique que le temps moyen pour franchir l'une des limites dépend du nombre moyen de pas lors du franchissement de l'une des limites, ainsi que de la probabilité de franchissement. Ce critère fournira une autre équation possible avec laquelle nous pourrons créer un système d'équations qui nous permettra de transformer un système de trading complexe en un système plus simple. Cette équation peut être divisée en 2 autres équations :

• T[U] = S[U, u] * T[1] + S[U, d] * T[2]
• T[D] = S[D, u] * T[1] + S[D, d] * T[2]

Nous aurons besoin de ces équations plus tard. Toutes ces valeurs sont calculées sur la base du modèle mathématique obtenu dans l'article précédent :

• S[U, u], S[U, d], S[D, u], S[D, d], P[U] = f(n, m, p) - toutes ces valeurs sont des fonctions de "n, m, p".
• n = B[U]/ Pr - à son tour, "n" peut être exprimé en termes de distance à la limite supérieure et au pas "Pr"
• m = B[D]/ Pr - à son tour, "m" peut être exprimé en termes de distance à la limite supérieure et au pas "Pr"
• Pr - l’étape sélectionnée
• B[U] - la distance à la limite supérieure
• B[D] - la distance à la limite inférieure

Principes de la méthode de transformation résultante

À titre d'exemple, nous pouvons prendre une stratégie aléatoire et la convertir en l'équivalent requis. J'ai créé l'une des variantes de transformation d'un système multidimensionnel complexe en un système bidimensionnel plus simple. Je vais essayer de décrire ce processus étape par étape. Avant de procéder à la description, j'ai mis en œuvre l'idée et testé les performances de la méthode. Le programme est joint à l'article. Dans mon programme, j'ai utilisé des formules légèrement différentes mais tout aussi efficaces. Il est basé sur le modèle mathématique obtenu dans l'article précédent. En l'utilisant, nous pouvons obtenir les valeurs suivantes :

• P[U], S[U, u], S[U, d], S[D, u], S[D, d]

À partir des pas moyens, nous pouvons obtenir le temps moyen avant que la limite supérieure ou la limite inférieure ne soit franchie. L'objectif n'est peut-être pas encore tout à fait clair. Mas les explications devraient vous aider. Pour transformer une stratégie multi-états en une stratégie plus simple, nous devons d'abord générer les stratégies correspondantes. J'ai créé un générateur de stratégies basé sur des nombres aléatoires. Par commodité, j'ai pris 5 stratégies générées de manière aléatoire. Les voici :

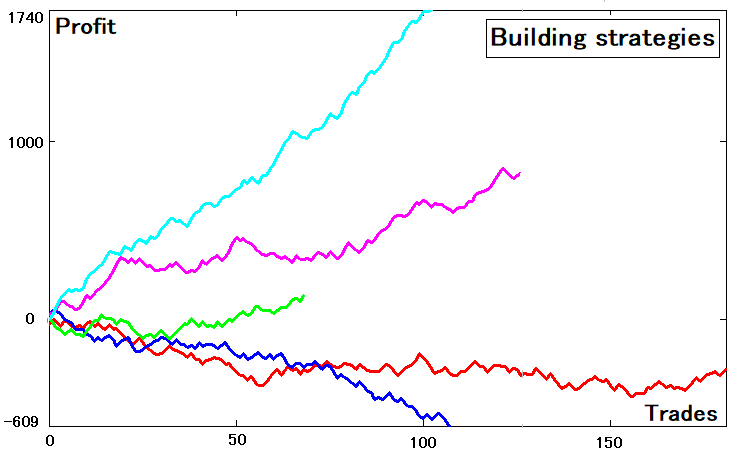
Ces stratégies ont des métriques de Gains Escomptés (Expected Payoff) différentes, un nombre d'opérations et des paramètres différents. Certaines courbes sont perdantes, mais ce n'est pas grave, car il s'agit toujours d'une courbe, même si ses paramètres ne sont pas tout à fait bons.

Venons-en maintenant au fait. La figure montre les courbes de solde qui dépendent du nombre de transactions, comme les graphiques du testeur de stratégie. Selon lui, il existe un certain nombre de soldes pour chaque courbe :

• B[i] , i = 0...N
• N - le nombre de transactions

Ce tableau peut être obtenu à partir du tableau des paramètres des ordres. Je suppose que le conteneur contenant les données de l'ordre ne contient que la valeur du profit ou de la perte de l'ordre, ainsi que sa durée de vie :

• Pr[i], T[i]

Supposons que d'autres paramètres ne soient pas disponibles. Je pense que c'est correct, car lorsque nous voulons analyser un backtest ou un signal, ces données ne sont généralement pas disponibles (car normalement personne ne les enregistre). Le plus souvent, les utilisateurs vérifient le facteur de récupération, la réduction maximale et d'autres paramètres similaires. Les seules données de trading qui sont toujours sauvegardées sont les suivantes :

1. Le profit
2. L’heure d'ouverture de l’ordre
3. L’heure de clôture de l’ordre

Bien sûr, l'indisponibilité de certaines données affectera la précision, mais il n'y a rien à faire. Voyons maintenant comment obtenir un tableau de soldes à partir d'un tableau de gains :

• B[i] = B[i-1] + Pr[i] si i > 0
• B[i] = 0 sinon

Afin de permettre l'analyse des stratégies obtenues en fonction du temps, nous devons créer un tableau temporel similaire :

• TL[i] = TL[i-1] + T[i] si i > 0
• TL[i] = 0 sinon

Après avoir déterminé les abscisses et les ordonnées de toutes ces courbes, nous pouvons les tracer. Vous verrez les différences, puisqu'il s'agit de fonctions qui dépendent non pas du nombre d'ordres, mais du temps :

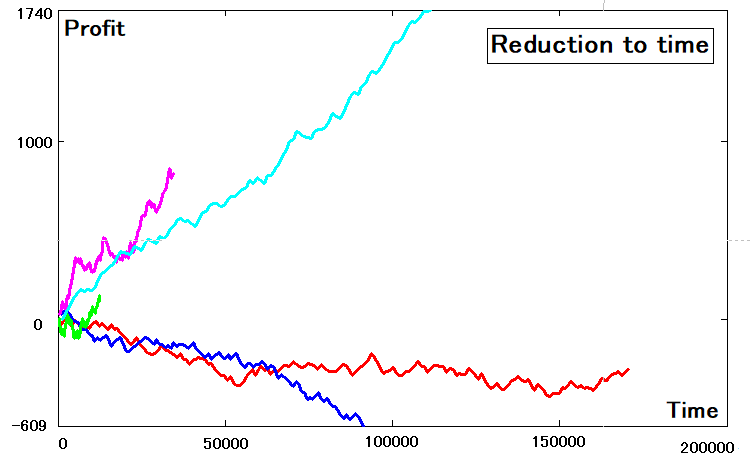
Définition des critères de réductibilité

Nous pouvons continuer à travailler avec les données obtenues. Nous pouvons maintenant déterminer les critères selon lesquels nous vérifierons si les courbes correspondent à deux états de profit. Du point de vue de la représentation par rapport au temps, 3 valeurs suffisent :

1. P[U] - la probabilité de franchir la limite supérieure
2. T[U] - le temps moyen jusqu'à ce que la limite supérieure soit atteinte
3. T[D] - le temps moyen jusqu'à ce que la limite inférieure soit atteinte

Les deuxième et troisième valeurs peuvent être calculées comme suit :

• T[U] = S[U, u] * T[u] + S[U, d] * T[d]
• T[D] = S[D, u] * T[u] + S[D, d] * T[d]

Quant à P[U], cette valeur est fournie par le modèle mathématique que nous avons obtenu dans l'article précédent. Et comme vous vous en souvenez : "P[D] = 1 - P[U]". Ainsi, sur la base des 5 valeurs fournies par le modèle mathématique, nous pouvons obtenir les 3 valeurs requises décrites ci-dessus. Quant à ces deux équations, nous les avons obtenues précédemment. Mais ici j'ai changé la notation pour le temps pour des raisons de commodité.

Ces valeurs sont calculables. Pour les réduire à quelque chose, nous devons d'une manière ou d'une autre obtenir leur valeur réelle sur la base de ce que nous possédons. Ensuite, nous devons trouver les paramètres de la courbe à 2 états équivalente souhaitée, de sorte que les trois paramètres soient très proches des valeurs réelles. C'est ainsi que nous obtenons les critères. Tout d'abord, introduisons la notation des valeurs connues :

• P*[U] - la probabilité réelle de franchir les limites du canal sélectionné
• T*[U] - le temps moyen réel jusqu'à ce que la limite supérieure soit franchie
• T*[D] - le temps moyen réel jusqu'à ce que la limite inférieure soit franchie

L'écart entre les valeurs réelles et les valeurs calculées peut être mesuré en termes relatifs ou en pourcentage. S'ils sont mesurés en pourcentage, les critères seront les suivants :

• KPU = ( | P[U] - P*[U] | / ( P[U] + P*[U] ) ) * 100 %
• KTU = ( | T[U] - T*[U] | / ( T[U] + T*[U] ) ) * 100 %
• KTD = ( | T[D] - T*[D] | / ( T[D] + T*[D] ) ) * 100 %

Définition des critères de comparaison avec le système source

Le meilleur système est celui qui présente le minimum de toutes ces valeurs. Pour pouvoir obtenir les valeurs calculées, nous devons maintenant d'abord déterminer la taille du canal, en fonction duquel nous déterminerons la probabilité réelle et le temps réel jusqu'à la cassure. Cette idée peut être visualisée comme cela :

La figure montre un exemple de détermination du canal pour une stratégie rentable. Les triangles violets symbolisent un autre point de contrôle pour d'éventuels mouvements à la hausse ou à la baisse. Le mouvement minimum souhaité se situe entre les points noirs. Si nous prenons comme base le mouvement maximal qui s'est produit au cours de la période disponible, la probabilité P[U] sera égale à 1. C'est évidemment le choix le plus incorrect. Car nous avons besoin de la valeur minimale qui garantit le franchissement des limites inférieure et supérieure.

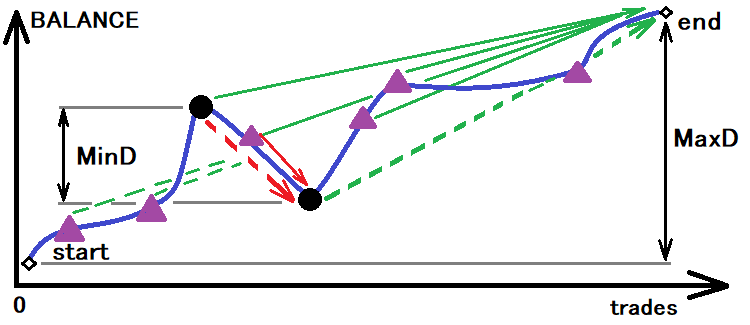
Évaluation d'un éventuel canal pour le calcul des valeurs requises

Mais cela ne suffit pas. Si nous utilisons cette valeur comme base, nous n'aurons qu'une seule touche de la limite inférieure, ce qui n'est pas non plus exact. Personnellement, j'ai utilisé la valeur du canal 3 fois moins que le minimum indiqué. Avec un échantillon suffisant de touches liées, cette valeur sera suffisante. Maintenant que nous avons déterminé la taille du canal, nous pouvons le diviser. Si nous supposons que le canal lui-même est une étape, alors :

• n, m = 1
• p = P[U]
• Pr * n = Pr * m = 1/3 * MinD - la moitié de la largeur du couloir
• Pr = ( 1/3 * MinD ) / n = ( 1/3 * MinD ) / m - le module du pas
• T[U, u] = T[U]
• T[D, d] = T[D]
• T[U, d] = 0
• T[D, u] = 0

Cette variante peut également être utilisée si vous disposez d'un très grand échantillon de transactions. L'avantage de cette approche est que nous n'avons pas besoin d'utiliser un modèle mathématique pour diviser le canal, car dans ce cas, notre canal entier est une étape. Mais dans mes calculs, j'ai utilisé un modèle mathématique comme exemple. Lorsque l'on utilise cette approche, il est nécessaire de trouver les plages de paramètres suivantes pour la sélection :

• p = p1 ... p2
• N = m = nm1 .... nm2

Dans mon exemple, j'ai utilisé les intervalles suivants :

• p1 = 0,4, p2 = 0,6, nm1 = 1, nm2 = 3

Bien entendu, vous pouvez utiliser des intervalles plus larges. Accessoirement, l'une des plages peut être élargie, alors l'autre est utilisée telle quelle. Par exemple, si nous augmentons "nm2", la méthode peut couvrir un éventail plus large de stratégies différentes. Si le modèle mathématique ne peut pas gérer la variante suivante, nous pouvons passer à la variante sans modèle mathématique.

Définition de la probabilité et du temps moyen jusqu'au franchissement de la limite supérieure du canal

Après avoir trouvé avec succès toutes les valeurs ci-dessus, nous n'obtiendrons que la probabilité "p" pour un pas en avant. Nous pouvons ensuite utiliser cette valeur comme base pour déterminer le temps moyen de passage de la limite. Ceci peut être visualisé par une légère transformation de l'image ci-dessus :

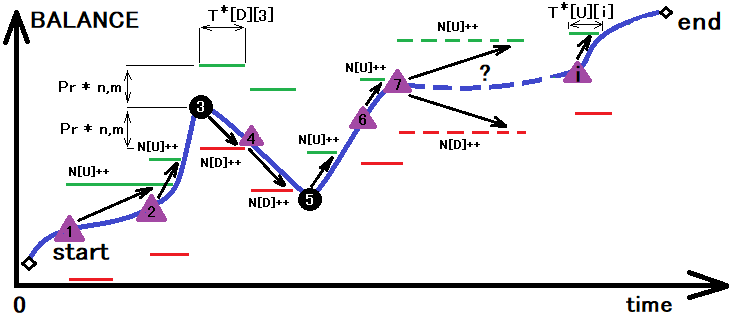
La figure montre le processus d'addition des passages supérieurs et inférieurs pour le canal dont la taille a été déterminée à la suite de la transformation précédente. La somme de ces croisements permet de calculer le temps nécessaire à l'intersection. En une seule opération, nous pouvons déterminer toutes les quantités avec astérisque dont nous avons besoin :

• N[U] - le nombre d'intersections du bord supérieur du canal
• N[D] - le nombre d'intersections du bord inférieur du canal
• T[U][i] - le tableau contenant le temps écoulé jusqu'à ce que la limite supérieure soit franchie
• T[D][i] - le tableau contenant le temps écoulé jusqu'à ce que la limite inférieure soit franchie

À l'aide de ces données, calculons la probabilité de franchissement de la limite supérieure et le temps moyen pour franchir les limites supérieure et inférieure :

• P*[U] = N[U] / ( N[U] + N[D] )
• T*[U] = Somme( 0...i ) [ T[U][i] ] / N[U]
• T*[D] = Somme( 0...i ) [ T[D][i] ] / N[D]

Nous avons trouvé toutes les valeurs auxquelles notre équivalent bidimensionnel doit être réduit. Il faut maintenant définir où commencer la recherche. Pour cela, nous devons déterminer laquelle de ces valeurs est la plus prioritaire en termes de précision. J'ai choisi comme exemple la probabilité de franchir la frontière supérieure. Cette approche réduit les besoins de calcul pour l'analyse. Si nous choisissons de sélectionner 3 valeurs dans 3 intervalles, nous aurons 3 degrés de liberté, ce qui augmentera le temps de calcul. Parfois, le temps de calcul est irréel. Au lieu de cela, j'ai commencé par la probabilité d'une hausse, puis à la durée moyenne des hausses et des baisses.

Je tiens à vous rappeler qu'il y a de nombreuses étapes dans le canal et que le temps du croisement n'est pas le temps des pas. De même, la probabilité d'un pas dans une certaine direction n'est pas la probabilité d'un franchissement d’une limite. La seule exception est la situation n=m=1 décrite au début.

En conséquence, nous obtenons les caractéristiques de pas suivantes :

1. p - la probabilité d'une hausse
2. T[u] - durée moyenne d'une hausse
3. T[d] - durée moyenne d'une baisse
4. Pr - module du pas dans les profits

Estimation de l'efficacité d'une transformation simple

Supposons que nous ayons trouvé tous les paramètres des étapes. Comment évaluer l'efficacité générale d'une telle opération de transformation ? Pour évaluer l'efficacité, nous pouvons tracer des lignes droites auxquelles les stratégies sont réduites. La pente des lignes peut être définie comme suit :

• K = EndProfit / EndTime - le coefficient de pente de la ligne
• P0 = K * t - l’équation linéaire

Voici à quoi cela ressemblera :

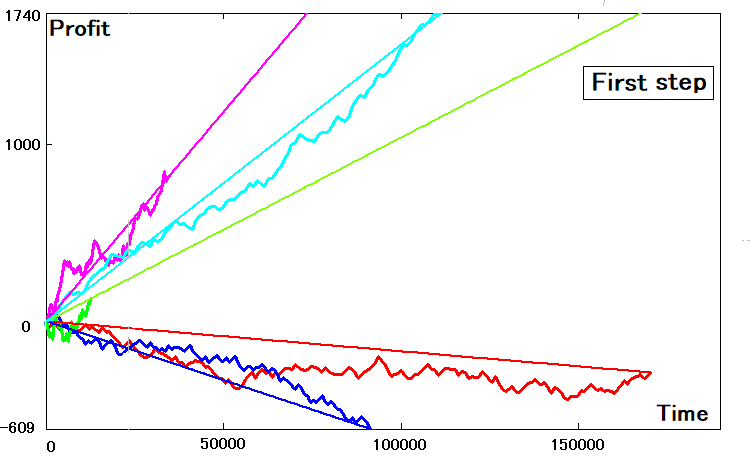
Si les paramètres des courbes bidimensionnelles sont idéaux, leurs droites similaires auront exactement la même pente et toucheront les courbes d'équilibre aux points extrêmes. Je pense qu'il est clair qu'une telle coïncidence ne peut en aucun cas se produire. Pour trouver le coefficient de pente de cet équivalent, on peut utiliser les données trouvées pour l'étape :

• MP = p * Pr - (1-p) * Pr - l’espérance mathématique d'une hausse pour n'importe quelle étape
• MT = p * T[u] + (1-p) * T[d] - l’espérance mathématique du temps consacré à la formation de n'importe quelle étape
• K = MP / MT - le coefficient de pente de la ligne.

J'ai utilisé le même programme pour les calculs et j'ai obtenu à chaque fois une image similaire :

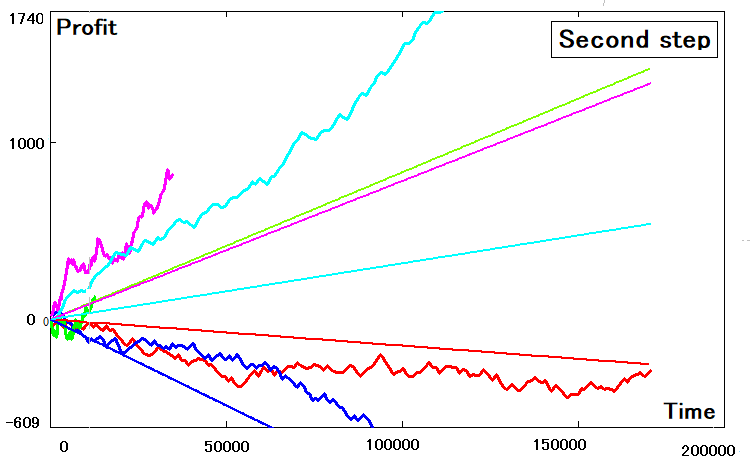
Toutes les stratégies n'ont pas pu être correctement transformées en un équivalent bidimensionnel. Certaines d'entre elles présentent des écarts évidents. Les écarts sont liés aux raisons suivantes :

1. Erreur de calcul des valeurs avec astérisque
2. Imperfection du modèle bidimensionnel (modèle moins flexible)
3. Finitude du nombre possible de tentatives de recherche (et puissance de calcul limitée)

En tenant compte de tous ces faits, nous pouvons ajuster le temps de pas moyen, de sorte qu'au moins les coefficients de pente du modèle original et du modèle dérivé soient égaux. De telles transformations affecteraient bien sûr les écarts des critères que nous réduisons, mais il n'y a pas d'autre solution. Je pense que le critère principal est le coefficient de pente de la ligne, car si le nombre de transactions tend vers l'infini, la stratégie originale et la stratégie dérivée devraient se fondre en une seule ligne. Si ce n'est pas le cas, cette transformation n'a pas beaucoup de sens. Peut-être que tout cela n'est pas lié à la méthode de transformation, mais aux possibilités cachées qui ne sont pas encore tout à fait claires.

Ajustement final et simulation

Pour effectuer une telle transformation, nous pouvons utiliser une proportion. Avant de créer les courbes, nous disposions des tableaux TL[i] et B[i], qui sont équivalents au temps écoulé depuis le début de la courbe jusqu'à l'ordre ou le segment analysé. Nous pouvons prendre les derniers éléments du tableau et écrire ce qui suit :

• K = B[n] / TL[n]
• N - l'indice du dernier élément du tableau des soldes (solde final)

Pour les droites obtenues à l'étape précédente, nous pouvons également calculer un tel coefficient. Il a déjà été calculé précédemment :

• K1 = MP / MT

Ces coefficients n'étant pas égaux, une correction est nécessaire. Cela peut se faire de la manière suivante :

• K = MP / ( KT * MT )
• KT - le coefficient de correction

Nous devons maintenant ajouter ce coefficient à l'intérieur de l'espérance mathématique afin que celle-ci ne change pas de sens. Cela peut se faire de la manière suivante :

• MTK = MT * KT = p * (T[u]* KT) + (1-p) * (T[d]* KT)

Comme vous pouvez le constater, les nouvelles valeurs horaires corrigées sont désormais incluses entre parenthèses. Elles peuvent être calculées comme suit :

1. Tn[u] = T[u] * KT
2. Tn[d] = T[d] * KT

C'est notre temps corrigé d'une hausse et d’une baisse. Pour calculer le coefficient de correction, nous mettons en équation les expressions de calcul des coefficients :

• B[n] / TL[n] = MP / ( KT * MT )

Après avoir résolu l'équation relative à KT, on obtient une expression permettant de calculer cette valeur :

• KT = ( MP / MT ) / ( B[n] / TL[n] ) = ( MP * TL[n] ) / ( MT * B[n] )

Il suffit d'ajuster le temps moyen d'une hausse et d'une baisse. Après cela, le processus de conversion peut être considéré comme achevé. Nous obtenons ainsi un ensemble de 4 valeurs qui décrivent complètement notre stratégie, au lieu d'énormes tableaux qui décrivent plus de 2 états :

1. p - la probabilité d'une hausse
2. Pr - le pas
3. T[u] - le temps moyen de formation d’une hausse
4. T[d] - le temps moyen de formation d’une baisse

Ces 4 paramètres suffisent à recréer la stratégie par simulation. Aujourd'hui, ce logiciel est à notre disposition, quels que soient le marché et le moment. La simulation pour nos 5 stratégies est la suivante :

Nous utilisons ici les lignes droites de la première étape. Ces lignes sont tracées de 0 jusqu’à l'extrémité de la courbe du trading réel. Comme vous pouvez le constater, la simulation est très proche des lignes, ce qui confirme la justesse des transformations. La seule exception est la ligne bleue. Je suppose qu'il y a quelques failles mineures dans mon algorithme, qui peuvent être corrigées avec un peu de temps.

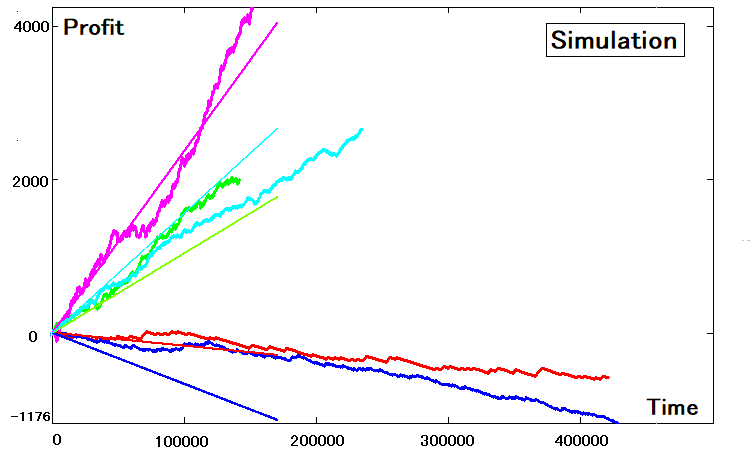
Résumé

Le processus d'étude du modèle a généré des idées intéressantes. À l'origine, lorsque j'étudiais les schémas bidimensionnels et les schémas multi-états, je ne cherchais qu'à obtenir une description simplifiée des systèmes complexes. Cette analyse nous a permis d'obtenir des conclusions beaucoup plus valables et simples. Les détails sont difficiles à décrire dans l'article, car ils impliquent trop de nuances techniques. En résumé, cette étude a donné les résultats suivants :

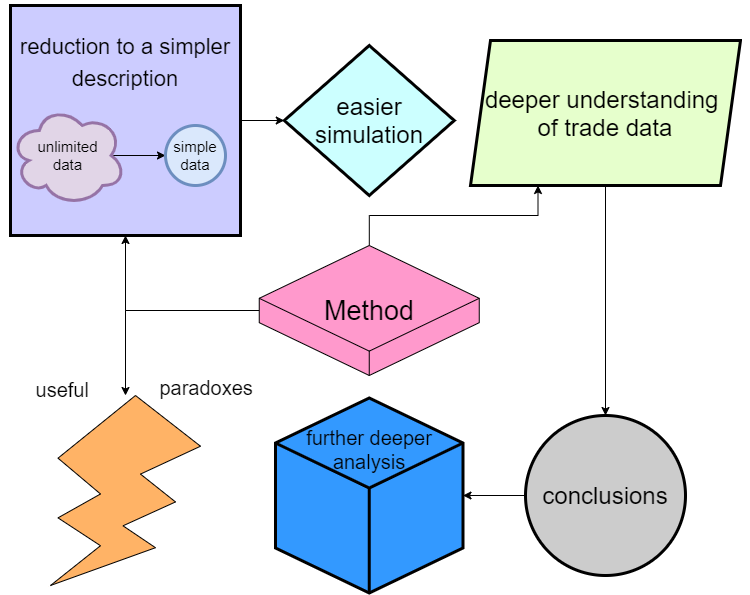
Tous les avantages peuvent être présentés dans une liste :

• De nombreux systèmes à plusieurs états peuvent être convertis en systèmes à 2 états (et le passage de n à m états est donc également possible).
• Le processus de conversion peut être utilisé comme mécanisme de compression des données de trading
• Les données converties peuvent être réinjectées dans la simulation, ce qui simplifie également la simulation (car seuls 2 états doivent être simulés).
• Une compréhension plus approfondie des processus probabilistes dans la fixation des prix permet de tirer des conclusions individuelles utiles.
• Sur la base des informations reçues, nous pouvons procéder à une analyse plus approfondie du processus de trading.
• Nous avons obtenu certaines caractéristiques utiles pour le trading - pour l'instant, je les classe dans la catégorie des paradoxes.

Bien sûr, l'idée principale de la série est la construction de mathématiques simples et utiles qui permettront directement la création de systèmes ultra-stables et multi-monnaies basés sur la théorie des probabilités. Jusqu'à présent, les informations obtenues constituent une bonne base pour l'élaboration d'une solution monolithique.

Je voudrais également mentionner les paradoxes que nous avons révélés au cours de l'étude. Lors de la première étape de transformation, nous avons obtenu des divergences qui se sont traduites par une pente différente de la ligne droite équivalente. Je pense que ces écarts peuvent être utilisés pour convertir des opérations aléatoires en opérations non aléatoires, ou pour fournir divers amplificateurs de signaux d'opérations.

En d'autres termes, elles peuvent être utiles pour convertir certaines stratégies nulles en stratégies à PF positif si nous appliquons des transformations pour convertir des systèmes à plusieurs états en systèmes à deux états, qui peuvent ensuite être traités à l'aide d'autres méthodes visant à améliorer leur qualité. Pour l'instant, ces pensées sont trop vagues et dispersées, mais elles finiront par se transformer en idées. Je considère qu'il s'agit là du principal résultat de l'étude, que nous utiliserons plus tard lors de la création d'un Expert Advisor.

Conclusion

Dans cet article, j'ai essayé de ne pas aller trop loin dans les détails. Bien entendu, ce sujet fait appel aux mathématiques. Mais au vu de l'expérience des articles précédents, je constate que les informations générales sont plus utiles que les détails. Si vous souhaitez étudier tous les détails de la méthode, veuillez utiliser le programme attaché ci-dessous. J'ai effectué des recherches dans le cadre de ce programme. Je n'ai pas décrit tous les algorithmes utilisés, car ils impliquent beaucoup de mathématiques ennuyeuses, essentiellement liées aux tableaux de données et aux matrices. Je pense que si quelqu'un souhaite créer quelque chose de similaire, il s'en tiendra à sa propre logique, mais pourra utiliser le programme présenté comme point de départ.

Si vous ne souhaitez pas approfondir l'analyse, je vous suggère de tester différentes stratégies pour voir comment elles seront converties. En ce qui concerne les idées futures, je pense que nous évoluerons progressivement vers la création d'un algorithme auto-adaptatif solide qui sera capable de surpasser les réseaux neuronaux à la fois en qualité et en stabilité. J'ai déjà quelques idées. Mais il faut d'abord compléter les fondations.

Références

• Combinatoire et théorie des probabilités pour le trading (Partie I) : L'essentiel
  
• Combinatoire et théorie des probabilités pour le trading (Partie II) : Fractale universelle
  
• Combinatoire et théorie des probabilités pour le trading (Partie III) : Le premier modèle mathématique
• Combinatoire et probabilité pour le trading (Partie IV) : Logique de Bernoulli