取引のための組合せ論と確率論(第V部): 曲線分析
目次
はじめに
多段階でスケーラブルな取引システムを構築するための基盤を引き続き準備します。本稿の枠組みの中で、以前の記事の発展をどのように使用して、取引プロセスを説明するためのより広い可能性に近づくことができるかを示したいと思います。これは、他の分析方法では対象外となっている側面からストラテジーを評価するのに役立ちます。本稿では、複雑な複数の状態を持つサンプルを単純な2つの状態を持つサンプルに変換する可能性について探究しました。この分析は研究式に行われました。
データを簡素化するための便利なフォーム
重複することなく次々に進行する多くの取引を持つストラテジーがあると仮定します。つまり、前の注文が閉じられた後にのみ新しい注文が開かれます。勝ち負けの確率を評価し、利益または損失を達成するために必要な平均時間を測定する必要がある場合、注文には非常に多くの異なる状態が存在する可能性があります(異なる結果で閉じられます)。
このようなストラテジーにフラクタル公式を適用できるようにするには、まず、これらのストラテジーをフラクタルの枠組内で検討できるケースに変換する必要があります。これを実装するには、フラクタルの場合と同様に、ステップアップとステップダウンの確率を持つ等距離のストップレベルを持つ注文としてストラテジーを表す必要があります。そうすれば、フラクタル式を適用できます。また、ステップアップとステップダウンで異なる存続期間を許容します。
ストラテジーを前回の記事で見つけたフラクタル式の枠組で説明できるタイプのいずれかに単純化するには、まず、フラクタル式を適用できるようにするためにどの値を知る必要があるかを判断する必要があります。ここではすべてが非常に単純です。
- P[1] –ステップアップの確率
- T[1] – アップステップの平均形成時間
- T[2] – ダウンステップの平均形成時間
まず、ステップ数が無限大になる傾向がある場合の極限値を考慮する必要があります。
- (P[1] * T[1] + (1 -P[1])*T[2]) * n = T(n)
- (P[1] * Pr - (1 -P[1])*Pr) * n = P(n)
上記の式をよりよく理解するには、次の2つの極限を記述する必要があります。
- Lim(n --> +infinity)[P/P0(n)] = 1
- Lim(n --> +infinity)[T/T0(n)] = 1
極限は、「n」の量で同じ実験を行う場合、つまり取引すると、主要な一般的な実験に含まれるすべての基本実験にかかった合計時間が常に異なることを示しています。また、最終的な取引残高のポジションは常に異なります。一方、実験の数が無限であると、実際の値が極限に達する傾向があることは直感的に明らかです。この事実は乱数ジェネレータを使用して証明できます。
- n - エミュレートされたステップ数
- 1-P[1] –ステップダウンの確率
- T0(n) –「n」ステップに費やされた実際の時間
- P0(n) –「n」ステップでの残高または価格の実際のシフト
- T(n) -「n」ステップに費やされた時間の極限値
- P(n) –「n」ステップでのシフトの極限値
この論理により、2つの方程式が生成されますが、未知数が多すぎます。まだ始めたばかりなので、これは驚くべきことではありません。ただし、これらの方程式は、派生システム(取得する必要のあるシステム)のみを記述します。ソースシステムの方程式は似ています。
- (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) * m = T(m)
- (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * m - (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * m = P(m)
- P*[1] + P[*2] + … + P*[N2] = 1 – 確率は完全なグループを形成する
極限も同じで、同じ値を示します。
- Lim(m --> +infinity)[P/P0(m)] = 1
- Lim(m --> +infinity)[T/T0(m)] = 1
ここで使用される変数については、以下で説明します。
- m –エミュレートされたステップ数
- T0(m) –「m」ステップに費やされた実際の時間
- P0(m) –「m」ステップの残高または価格の実際のシフト
- T(m) –「m」ステップに費やされた実際の時間
- P(m) –「m」ステップの実際のシフト
- T = Lim(m --> +infinity) [ T(m) ] – 時間の極限値
- N1 – 正の利益を伴う取引結果の数とそのカウンタ
- N2 – N1 + 1 – 負の利益を伴う取引結果の数(N2はそれらのカウンター)
ソースシステムに基づいて、より複雑なシステムで構成された、新しくより単純なシステムを作成する必要があります。唯一の違いは、元のシステムではすべてのパラメータがわかっているということです。既知の値は、アスタリスク*接尾辞で示されています。
両方のシステムの2番目と1番目の方程式を等しくすると、変数PとTを削除できます。
- (P[1] * T[1] + (1 -P[1])*T[2]) * n = (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) * m
- (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * m - (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * m
その結果、2つの方程式をなくしましたが、同時に、不要な2つの未知数が削除されました。これらの変換の結果として1つの方程式が得られますが、次が不明になります。
- P[1] –ステップアップ(停止)の確率
- T[1] - ステップアップの平均存続期間
- T[2] – ステップダウンの平均存続期間
これらの2つの方程式は類似した構造を持っています。
- A1*n = A2*m
- B1*n = B2*m
よって、変数の1つである「n」または「m」を除外して方程式の1つを削除できます。たとえば最初の式から値の1つを表現します。
- m = ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )* n
2番目の方程式に代入してて、結果を確認します。
- (P[1] * Pr - (1 -P[1])*Pr) * n = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) ) * n - (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) ) * n
方程式の両方の部分は「n」で乗算されていますが、「n」で徐算すると、必要な値のみに依存する方程式が得られます。
- (P[1] * Pr - (1 -P[1])*Pr) = (P*[1] * Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) ) - (P*[N2] * Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2]) * ( (P[1] * T[1] + (1 -P[1])*T[2]) / (P*[1] * T[1] + P*[2])*T*[2] + … + P*[N])*T*[N] ) )
すべてを単純化することができるシステムの数は無限であるため、値「Pr」はフリーと見なされます。ステップアップとステップダウンの絶対値が等しい場合、絶対的に任意のステップサイズを設定できます。他の値は、連立方程式を解くことによって決定されます。これまでのところ、システムには1つの方程式しかありません。さらに2つの方程式が必要です。これは、前のセクションで取得した方程式を使用して取得できます。
まず第一に、システムのコリドーの上限と下限の交差の確率が同じでなければなりません。また、境界の1つを越えるまでの平均時間も同じである必要があります。これらの2つの要件により、2つの欠落している方程式が得られます。コリドーの境界を越えるまでの平均時間を決定することから始めましょう。境界の1つを超えるまでの平均時間は、上下の平均ステップ数によって決まります。前回の記事の結果を考慮して、次のように書くことができます。
- T[U,D] = (S[U,u] * T[1] + S[U,d] * T[2]) * P[U] + (S[D,u] * T[1] + S[D,d] * T[2]) * ( 1 – P[U] )
この式は、境界の1つを越えるまでの平均時間は、境界の1つを越えるときの平均ステップ数と、交差する確率に依存することを示しています。この条件によって別の可能な方程式をたてて連立方程式を作成できるため、複雑な取引システムをより単純なものに変換することが可能になります。この方程式は、他の2つの方程式に分割できます。
- T[U] = S[U,u] * T[1] + S[U,d] * T[2]
- T[D] = S[D,u] * T[1] + S[D,d] * T[2]
これらの方程式は後で必要になります。これらの値はすべて、前の記事で取得した数学モデルに基づいて計算されています。
- S[U,u], S[U,d], S[D,u], S[D,d], P[U] = f(n,m,p) – これらの値はすべて「n、m、p」の関数です
- n = B[U]/ Pr - 次に、「n」は、上限までの距離とステップ「Pr」で表すことができます
- m = B[D]/ Pr – 次に、「m」は、上限までの距離とステップ「Pr」で表すことができます
- Pr – 選択したステップ
- B[U] – 上限までの距離
- B[D] –下限までの距離
結果として得られる変換方法の基本
例として、ランダムなストラテジーを必要な同等のものに変換することができます。複雑な多次元システムをより単純な2次元システムに変換するバリエーションの1つを作成したので、このプロセスを段階的に説明しようと思います。説明に進む前に、アイデアを実装し、メソッドのパフォーマンスをテストしました。プログラムは記事に添付されています。私のプログラムでは、わずかに異なるが同等に効果的な式を使用しました。これは、前の記事で得られた数学的モデルに基づいており、使用すると次の値を取得できます。
- P[U], S[U,u], S[U,d], S[D,u], S[D,d]
平均ステップから、上限または下限を越えるまでの平均時間を取得できます。目的は今のところはっきりしていないかもしれませんが、さらに説明すればより明確になるはずです。複数状態ストラテジーをより単純なストラテジーに変換するには、最初に関連するストラテジーを生成する必要があります。乱数ベースのストラテジージェネレーターを作成して、便宜上、ランダムに生成された5つのストラテジーを採用しました。それらは以下のとおりです。
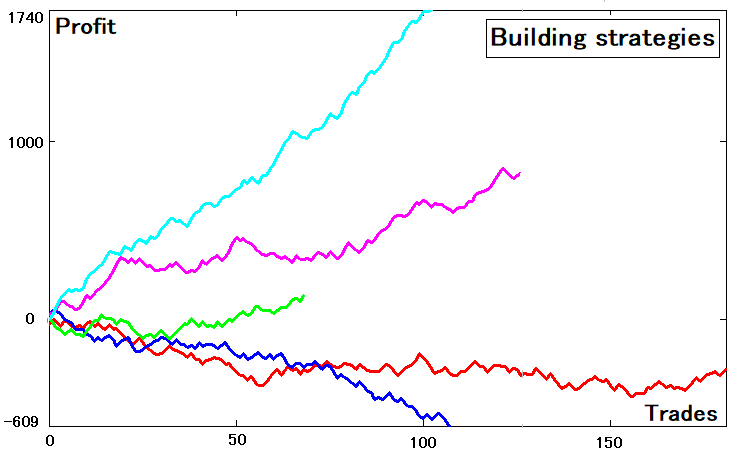
これらのストラテジーには、さまざまな期待ペイオフメトリックと取引数、パラメータがあります。いくつかの曲線は負けていますが、これは問題ありません。パラメータがあまり良くないかもしれませんが、それでも曲線であるからです。
ここで要点を説明します。この図は、ストラテジーテスターのグラフと同様、取引番号に依存する残高グラフを示しています。それによると、各曲線には特定の残高の配列があります。
- B[i] , i = 0…N
- N – 取引数
この配列は、注文パラメータを持つ配列から取得できます。注文データを含むコンテナには注文の利益または損失の値とその存続期間のみが含まれていると仮定します。
- Pr[i], T[i]
他のパラメータは利用できないと仮定しましょう。これは正しいと思います。バックテストやシグナルを分析する場合、通常は誰もこのデータを保存しないため、このデータは通常利用できません。多くの場合、ユーザは回復係数、最大ドローダウン、および同様のメトリックを確認するので、常に保存される唯一の取引データは次のとおりです。
- 利益
- 注文開始時間
- 注文終了時間
もちろん、一部のデータが利用できないことは精度に影響しますが、それとは何の関係もありません。次に、利益の配列から残高の配列を取得する方法を見てみましょう。
- B[i] = B[i-1] + Pr[i](i > 0の場合)
- B[i] = 0(その他の場合)
得られたストラテジーを時間に対して分析できるようにするには、同様の時間配列を作成する必要があります。
- TL[i] = TL[i-1] + T[i](i > 0の場合)
- TL[i] = 0(その他の場合)
そのようなすべての曲線の横座標と縦座標を決定したら、プロットすることができます。これらは取引番号ではなく時間に依存する関数であるため、違いがわかります。
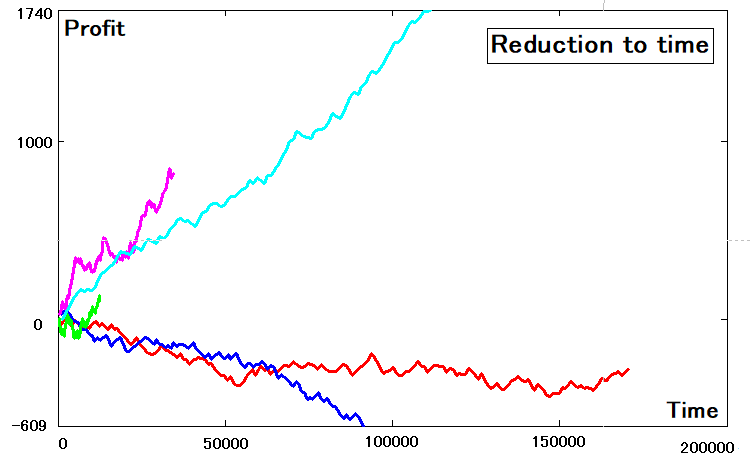
還元性基準の定義
得られたデータをさらに処理することができます。これで、曲線が2つの利益状態に一致するかどうかを確認するための基準を決定できます。時間に対する表現の観点からは、次の3つで十分です。
- P[U] –上限を越える確率
- T[U] – 上限に達するまでの平均時間
- T[D] – 下限に達するまでの平均時間
2番目と3番目の値は、次のように計算できます。
- T[U] = S[U,u] * T[u] + S[U,d] * T[d]
- T[D] = S[D,u] * T[u] + S[D,d] * T[d]
P[U]に関しては、この値は前の記事で取得した数学モデルによって提供されます。また、覚えているように、P[D] = 1 – P[U]です。したがって、数学モデルによって提供される5つの値に基づいて、上記の必要な3つの値を求めることができます。これらの2つの式については、以前に取得しましたが、ここでは便宜上、時間の表記を変更しました。
これらの値は計算可能です。それらを何かに単純化するためには、ここにあるものに基づいてそれらの真の価値を何とか得る必要があります。次に、3つのパラメータすべてが実際の値に非常に類似する、目的の同等の2状態曲線のパラメータを見つける必要があります。これが条件を取得する方法です。まず、既知の値の表記法を紹介しましょう。
- P*[U] – 選択したコリドーの境界を越える実際の確率
- T*[U] – 上限を超えるまでの実際の平均時間
- T*[D] – 下限を超えるまでの実際の平均時間
実際の値と計算された値の偏差は、相対的な用語またはパーセンテージで測定できます。パーセンテージで測定した場合、基準は次のようになります。
- KPU = ( | P[U] – P*[U] | / ( P[U] + P*[U] ) ) * 100 %
- KTU = ( | T[U] – T*[U] | / ( T[U] + T*[U] ) ) * 100 %
- KTD = ( | T[D] – T*[D] | / ( T[D] + T*[D] ) ) * 100 %
ソースシステムと比較するための基準の定義
最適なシステムは、これらすべての値が最小のシステムです。ここで、計算値を取得できるようにするには、最初にコリドーのサイズを決定する必要があります。これに従って、実際の確率とブレークアウトまでのリアルタイムを決定します。このアイデアは次のように視覚化できます。
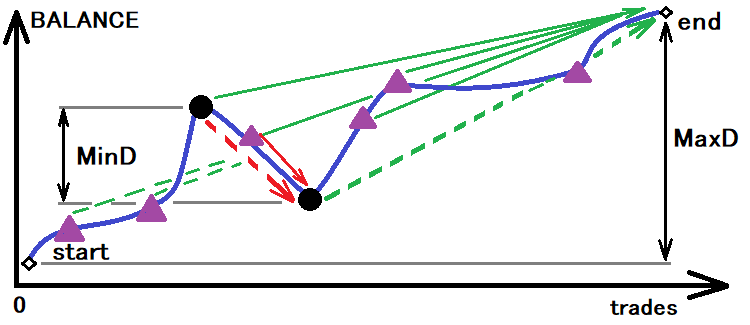
必要な値を計算するための可能なコリドーの評価
ただし、これでも十分ではありません。この値を基準として使用すると、下限が1回だけ表示されますが、これも正確ではありません。個人的には、コリドーの値を与えられた最小値の3分の1に使用しました。境界に達する十分なサンプルがあれば、この値で十分です。コリドーのサイズを決定したので、このコリドーを分割できます。コリドー自体がステップであると仮定すると、次のようになります。
- n, m = 1
- p = P[U]
- Pr * n = Pr * m = 1/3 * MinD – コリドー幅の半分
- Pr = ( 1/3 * MinD ) / n = ( 1/3 * MinD ) / m – ステップ モジュール
- T[U,u] = T[U]
- T[D,d] = T[D]
- T[U,d] = 0
- T[D,u] = 0
このバリアントは、非常に大きな取引サンプルがある場合にも使用できます。このアプローチの利点は、コリドーを分割するために数学モデルを使用する必要がないことです。この場合、コリドー全体が1つのステップであるためです。ただし、ここでの計算では、例として数学モデルを使用しました。このアプローチを使用する場合、選択するパラメータの次の範囲を見つける必要があります。
- p = p1 … p2
- N = m = nm1 …. nm2
この例では、次の範囲を使用しました。
- p1 = 0.4, p2 = 0.6, nm1 = 1, nm2 = 3
もちろん、より広い範囲を使用できます。オプションで、範囲の1つを広げ、もう1つをそのまま使用することができます。たとえば、「nm2」を増やすと、このメソッドはさまざまなストラテジーのより広い範囲をカバーできます。数学モデルが次のバリアントを処理できない場合は、数学モデルのないものに切り替えることができます。
コリドーの上部境界を越えるまでの確率と平均時間の定義
上記のすべての値を正常に見つけた後、ステップアップの確率「p」のみを取得します。次に、この値を、平均境界通過時間を見つけるための基礎として使用できます。これは、上の画像を少し変形することで視覚化できます。
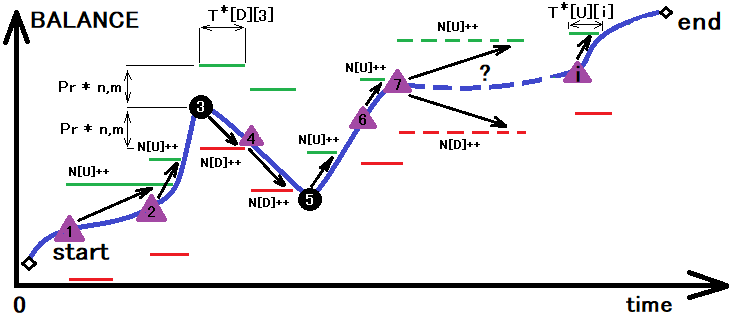
この図は、前回の変換の結果としてサイズが決定されたコリドーの上下の交差を合計するプロセスを示しています。これらの交差の合計とともに、交差に必要な時間を計算します。1つの操作で、必要なアスタリスクを使用してすべての数量を決定できます。
- N[U] – コリドーの上限の交差の数
- N[D] – コリドーの下限の交差の数
- T[U][i] – 上限を越えるまでの時間の配列
- T[D][i] – 下限を越えるまでの時間の配列
このデータを使用して、上限を越える確率と、上限と下限を越える平均時間を計算してみましょう。
- P*[U] = N[U]/ ( N[U] + N[D] )
- T*[U] = Summ( 0…i ) [ T[U][i] ] / N[U]
- T*[D] = Summ( 0…i ) [ T[D][i] ] / N[D]
2次元の同等物を減らす必要があるすべての値が見つかりました。次に、検索を開始する場所を定義する必要があります。これを行うには、これらの値のどれが精度の観点から最も優先度が高いかを判断する必要があります。例として、上限を越える確率を選択しました。このアプローチにより、分析の計算要件が軽減されます。3つの間隔で3つの値を選択すると、3つの自由度が得られ、計算時間が長くなります。時には計算時間が非現実的になります。代わりに、ステップアップの確率から始めて、ステップアップとステップダウンの平均時間に進みます。
コリドーにはステップがたくさんあり、項さする時間はステップの時間ではありません。また、特定の方向へのステップの確率は、境界を越える確率ではありません。唯一の例外は、冒頭で説明したn=m=1の状況です。
その結果、次のステップ特性が得られます。
- p –ステップアップの確率
- T [u] –ステップアップの平均期間
- T[d] – ステップダウンの平均期間
- Pr – 利益値のステップ係数
単純な変換の効率の見積もり
ステップのすべてのパラメータが見つかったとします。このような変換操作の一般的な効率を評価するにはどうすればいいでしょうか。効率を評価するためには、ストラテジーが縮小された直線を描くことができます。線の勾配は次のように定義できます。
- K = EndProfit / EndTime – 線の勾配係数
- P0 = K * t – 線の方程式
次のように見えます。
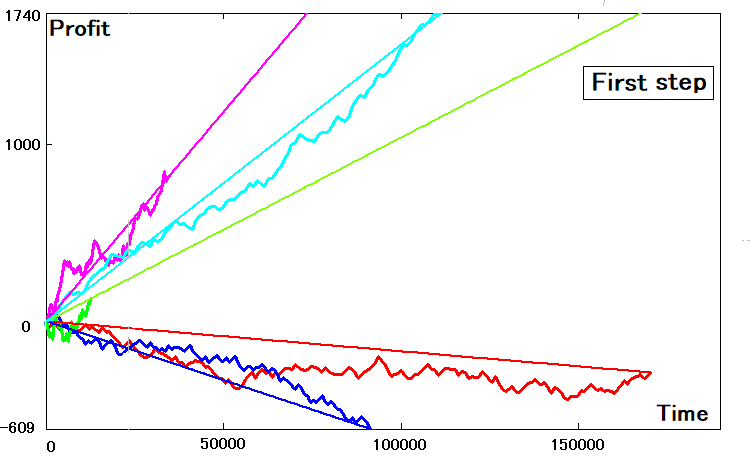
2次元曲線のパラメータが理想的である場合、それらの類似した直線はまったく同じ勾配を持ち、終点で残高曲線に接触します。そのような偶然の一致のほとんどは決して起こり得ないことは明らかだと思います。この同等物の勾配係数を見つけるために、ステップで見つかったデータを使用できます。
- MP = p * Pr – (1-p) * Pr – 任意のステップの上方シフトの数学的な期待値
- MT = p * T[u] + (1-p) * T[d] - 任意のステップの形成に費やされる時間の数学的な期待値
- K = MP / MT – 線の勾配係数
計算に同じプログラムを使用すると、毎回同じような結果が得られました。
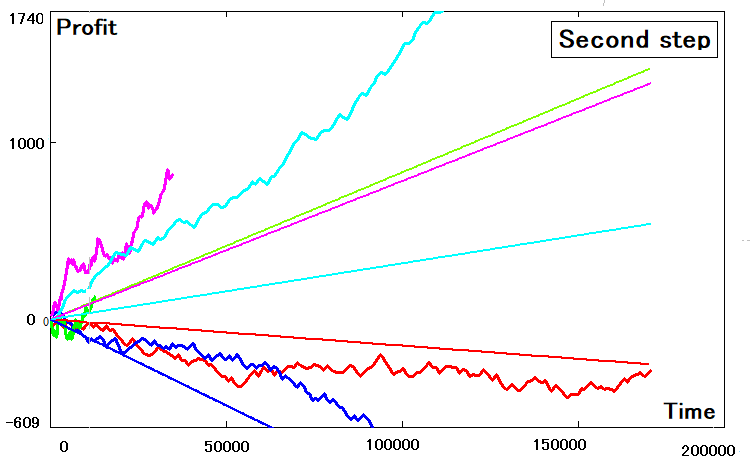
すべてのストラテジーを2次元の同等のものに正しく変換できるわけではありません。いくつかは明らかに逸脱します。逸脱は、次の理由に関連しています。
- アスタリスク付きの値の計算中にエラーが発生た
- 2次元モデルの不完全性(柔軟性の低いモデル)
- 可能な検索試行回数の有限性(および限られた計算能力)
これらすべての事実を考慮して、平均ステップ時間を調整して、少なくとも元のモデルと派生モデルの勾配係数が等しくなるようにすることができます。もちろん、そのような変換は、削減する基準の偏差に影響を与えますが、他の解決策はありません。取引数が無限になりがちな場合、元のストラテジーと派生したストラテジーを1つの線に結合する必要があるため、主な基準は線の勾配係数だと思います。これが起こらなければ、そのような変換にはあまり意味がありません。おそらく、これはすべて、変換の方法ではなく、現在は明確ではない隠れた可能性に関連しています。
最終調整とシミュレーション
このような変換を行うために、比率を使用できます。曲線を作成する前には配列TL[i]とB[i]がありました。これは、曲線の開始から分析された注文または線分になるまでの時間に相当します。配列の最後の要素を取得して、次を記述できます。
- K = B[n] / TL[n]
- N – 残高配列の最後の要素のインデックス(最終残高)
前のステップで得られた直線については、そのような係数を計算することもできます。それはすでに以前に計算されました。
- K1 = MP / MT
これらの係数は等しくないため、修正が必要です。これは次のように実行できます。
- K = MP / ( KT * MT )
- KT – 補正係数
次に、数学的な期待値がその意味を変えないように、この係数を数学的な期待値の中に追加する必要があります。これは次のように実行できます。
- MTK = MT * KT = p * (T[u]* KT) + (1-p) * (T[d]* KT)
ご覧のとおり、新しい修正された時間値が角かっこで囲まれています。それらは次のように計算できます。
- Tn[u] = T[u]* KT
- Tn[d] = T[d]* KT
これは、ステップアップとステップダウンの修正された時間です。補正係数を計算するために、係数計算式を等式化します。
- B[n] / TL[n] = MP / ( KT * MT )
KTに関連する方程式を解くと、この値を計算するための式が得られます。
- KT = ( MP / MT ) / ( B[n] / TL[n] ) = ( MP * TL[n] ) / ( MT * B[n] )
ステップアップとステップダウンの平均時間を調整するだけで、その後は変換プロセスは完了したと見なすことができます。その結果、3つ以上の状態を表す巨大な配列ではなく、ストラテジーを完全に表す4つの値のセットを取得します。
- p –ステップアップの確率
- Pr – ステップモジュール
- T[u] – 平均アップステップ形成時間
- T[d] – 平均ダウンステップ形成時間
シミュレーションによってストラテジーを再現するのにはこれらの4つのパラメータで十分です。現在、このソフトウェアは、市場や時間に関係なく利用できます。5つのストラテジーのシミュレーションは次のとおりです。
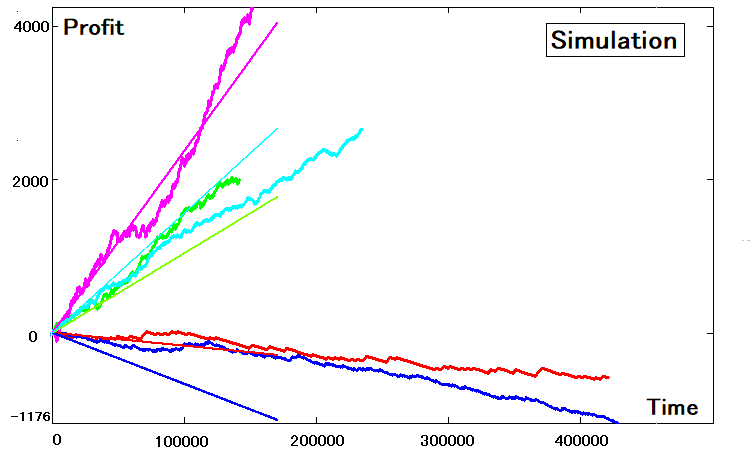
概要
モデル学習プロセスで興味深いアイデアを生み出しました。もともとは、2次元スキームと多次元スキームを研究するにあたって複雑なシステムの簡単な説明を取得したかっただけでしたが、分析の結果、はるかに価値のある単純な結論を受け取りました。技術的なニュアンスが多すぎるため、詳細を記事で説明するのは困難ですが、一言で言えば、この研究は次の結果をもたらしました。
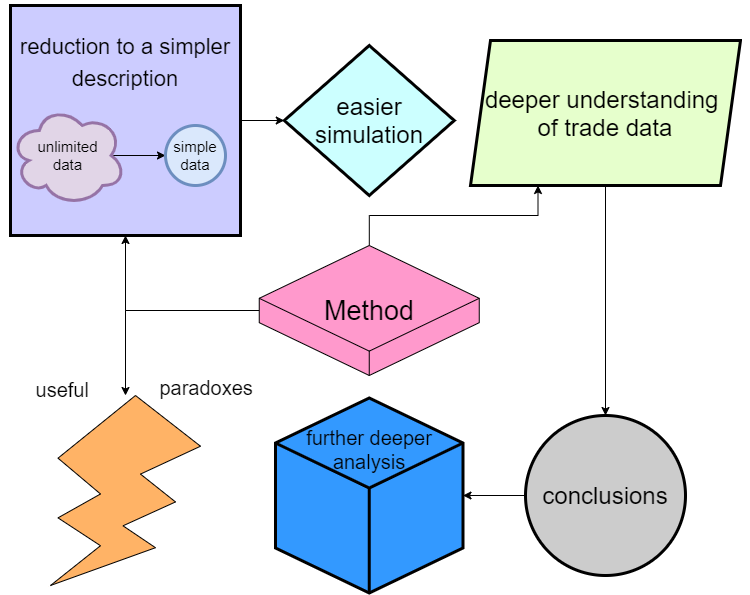
すべての利点を一覧表示できます。
- 多くの複数状態システムは2つの状態に変換できます(したがって、nからmの状態のプロセスも可能です)
- 変換プロセスは、取引データの圧縮メカニズムとして使用できます
- 変換されたデータはシミュレーションを通じてフィードバックできるため、シミュレーションも簡素化されます(2つの状態のみをシミュレーションする必要があるため)
- 価格設定内の確率的プロセスをより深く理解することで、個々の有用な結論が得られます
- 受け取った情報に基づいて、取引プロセスのより深い分析に進むことができます
- 取引に役立つ機能をいくつか入手しました。今のところ私はそれらをパラドックスとして分類しています
もちろん、この連載の主なアイデアは、確率論に基づいた極めて安定した多通貨システムの作成を直接可能にするための、シンプルで有用な数学の構築です。これまでのところ、得られた情報は、モノリスソリューションを構築するための優れた基盤として機能します。
また、調査の過程で明らかになったパラドックスについても触れておきたいと思います。最初の変換段階では、同等の直線の異なる勾配で表される不一致がありました。これらの不一致は、ランダム取引を非ランダム取引に変換したり、さまざまな取引シグナルのアンプを提供したりするために使用できると思います。
言い換えると、複数状態システムから2つの状態のシステムへの変換を適用すると、いくつかのゼロストラテジーを正のPFのストラテジーに変換するのに役立つ可能性があります。これは、品質の向上を目的とした他の方法を使用してさらに処理できます。今のところこれらの考えは曖昧すぎてまとまっていませんが、最終的にはアイデアに変えられます。これが調査の主な結果で、後でエキスパートアドバイザーを作成するときに使用します。
終わりに
本稿では、あまり深く掘り下げないようにしました。もちろん、このトピックには数学が関係してきますが、以前の記事での経験から、一般化された情報の方が詳細よりも役立つことがわかっています。メソッドの詳細をすべて調査したい場合は、以下に添付されているプログラムを使用してください。私はこのプログラムで調査を行いました。基本的にデータ配列と行列に関連する多くの退屈な数学が暗示されるため、使用されているすべてのアルゴリズムについては説明しませんでした。似たものを作る人は、自分自身の論理に固執するだろうと思いますが、提示されたプログラムを出発点として使うかもしれません。
より深く分析したくない場合は、さまざまなストラテジーをテストして、それらがどのように変換されるかを確認することをお勧めします。今後のアイデアとしては、品質と安定性の両面でニューラルネットワークを超える健全な自己適応アルゴリズムの作成に徐々に移行していくと思います。 すでにいくつかのアイデアがありますが、まず、基礎を完成させる必要があります。
参照資料
- 取引のための組合せ論と確率論(第I部):基本
- 取引のための組合せ論と確率論(第II部): ユニバーサルフラクタル
- 取引のための組合せ論と確率論(第III部): 初めての数学モデル
- 取引のための組合せ論と確率論(第IV部): ベルヌーイの定理
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/10071
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 MQL5でのAutoItの使用
MQL5でのAutoItの使用
 MQL5の行列とベクトル
MQL5の行列とベクトル
 固定プライスアクションストップロスまたは固定RSI(スマートストップロス)
固定プライスアクションストップロスまたは固定RSI(スマートストップロス)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索