Ticaret için kombinatorik ve olasılık teorisi (Bölüm V): Eğri analizi

İçindekiler

• Giriş
• Verileri basitleştirmek için faydalı formlar
• Ortaya çıkan dönüşüm yönteminin temelleri
• İndirgenebilirlik kriterlerinin tanımlanması
• Kaynak sistemle karşılaştırma için kriterlerin tanımlanması
• Gerekli değerlerin hesaplanması için olası bir koridorun değerlendirilmesi
• Koridorun üst sınırının geçilme olasılığının ve buna kadar olan ortalama sürenin tanımlanması
• Basit bir dönüşümün verimliliğinin değerlendirilmesi
• Son ayarlama ve simülasyon
• Özet
• Sonuç
• Referanslar

Giriş

Çok aşamalı ve ölçeklenebilir ticaret sistemleri oluşturmak için temel hazırlamaya devam ediyorum. Bu makale çerçevesinde, ticaret sürecini tanımlamaya yönelik daha geniş olasılıklara yaklaşmak için önceki makalelerdeki gelişmeleri nasıl kullanabileceğinizi göstermek istiyorum. Bu, bir stratejinin diğer analiz yöntemlerinin kapsamadığı yönlerden değerlendirilmesine yardımcı olacaktır. Bu makalede, karmaşık, çok durumlu sistemleri basit iki durumlu sistemlere dönüştürme olanaklarını araştırdım. Bu analizi bir araştırma tarzında gerçekleştirdim.

Verileri basitleştirmek için faydalı formlar

Üst üste binmeden birbiri ardına giden birçok ticaret işlemi içeren bir strateji olduğunu varsayalım, yani yeni bir emir kesinlikle bir öncekinin kapanmasından sonra açılmaktadır. Kazanma veya kaybetme olasılığını değerlendirmemiz ve kâr veya zarara ulaşmak için gereken ortalama süreyi ölçmemiz gerekirse, emirlerin çok sayıda farklı duruma sahip olabileceğini göreceğiz (farklı sonuçlarla kapanırlar).

Fraktal formüllerini bu tür stratejilere uygulayabilmek için öncelikle bu stratejileri fraktallar çerçevesinde değerlendirilebilecek durumlara dönüştürmemiz gerekmektedir. Bunu uygulamak için, stratejimizi, tıpkı fraktalımızda olduğu gibi, bir yukarı adım ve bir aşağı adım olasılığı olan eşit uzaklıkta durma seviyelerine sahip bir emir olarak temsil etmemiz gerekir. Daha sonra fraktal formüllerini uygulayabiliriz. Ayrıca, bir yukarı adım ve bir aşağı adım farklı ömürlere sahip olabilir.

Herhangi bir stratejiyi, bir önceki makalede bulduğumuz fraktal formülleri çerçevesinde tanımlanabilecek türlerden birine indirgemek için, öncelikle fraktal formüllerini uygulayabilmek adına hangi değerlerin bilinmesi gerektiğini belirlememiz gerekir. Burada her şey oldukça basit:

• P[1] - yukarı adım olasılığı
• T[1] - ortalama yukarı adım oluşum süresi
• T[2] - ortalama aşağı adım oluşum süresi

İlk olarak, adım sayısı sonsuza yöneldiğindeki limit değerlerini dikkate almamız gerekir:

1. (P[1]*T[1] + (1-P[1])*T[2])*n = T(n)
2. (P[1]*Pr - (1-P[1])*Pr)*n = P(n)

Yukarıdaki ifadeleri daha iyi anlayabilmek için şu iki limiti yazmalıyız:

• Lim(n --> +sonsuz)[P/P0(n)] = 1
• Lim(n --> +sonsuz)[T/T0(n)] = 1

Limitler, aynı deneyleri "n" miktarında veya işlem miktarında yaparsak, ana genel deneye dahil olan tüm temel deneylerin aldığı toplam sürenin her zaman farklı olacağını söylemektedir. Ayrıca, nihai ticaret bakiyesinde her zaman farklı konumlar elde edeceğiz. Öte yandan, sonsuz sayıda deney yapıldığında gerçek değerin limite doğru eğilim göstereceği sezgisel olarak açıktır. Bu gerçeği rastgele sayı üreteçleri kullanarak kanıtlayabiliriz.

• n - taklit edilen adım sayısı
• 1-P[1] – aşağı adım olasılığı
• T0(n) - "n" adım için harcanan gerçek zaman miktarı
• P0(n) - "n" adım için bakiye veya fiyatın gerçek kayması
• T(n) - "n" adım için harcanan limit zaman miktarı
• P(n) - "n" adım için limit kayması

Bu mantık, çok fazla bilinmeyenli iki denklemle sonuçlanır. Bu şaşırtıcı değil çünkü bu sadece bir başlangıç. Ancak bu denklemler yalnızca türetilmiş sistemi (elde etmemiz gereken) tanımlar. Kaynak sistem için denklemler benzerdir:

1. (P*[1]*T*[1] + P*[2]*T*[2] + … + P*[N]*T*[N])*m = T(m)
2. (P*[1]*Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1])*m - (P*[N1]*Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2])*m = P(m)

• P*[1]+P[*2]+…+P*[N2] = 1 - olasılıklar bir tam grup oluşturur

Limitler de aynıdır ve aynı değerleri gösterirler:

• Lim(m --> +sonsuz)[P/P0(m)] = 1
• Lim(m --> +sonsuz)[T/T0(m)] = 1

Burada kullanılan değişkenler aşağıda açıklanmıştır:

• m - taklit edilen adım sayısı
• T0(m) - "m" adım için harcanan gerçek zaman miktarı
• P0(m) - "m" adım için bakiye veya fiyatın gerçek kayması
• T(m) - "m" adım için harcanan limit zaman miktarı
• P(m) - "m" adım için limit kayması
• T = Lim(m --> +sonsuz)[T(m)] - limit zamanı
• N1 - pozitif kârlı ticaret sonuçlarının sayısı ve bunların sayacı
• N2 - N1+1 - negatif kârlı ticaret sonuçlarının sayısı (N2 bunların sayacıdır)

Kaynak sistemi temel alarak, daha karmaşık bir sistemden oluşan yeni ve daha basit bir sistem oluşturmamız gerekiyor. Tek fark, orijinal sistemin tüm parametrelerini biliyor olmamızdır. Bilinen değerler yıldız işareti (*) son ekiyle gösterilmektedir.

Her iki sistemdeki ikinci ve birinci denklemleri eşitlersek, P ve T değişkenlerini ortadan kaldırabiliriz:

• (P[1]*T[1] + (1-P[1])*T[2])*n = (P*[1]*T*[1] + P*[2]*T*[2] + … + P*[N]*T*[N])*m
• (P[1]*Pr - (1-P[1])*Pr)*n = (P*[1]*Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1])*m - (P*[N1]*Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2])*m

Sonuç olarak, iki denklemi kaybettik, ancak aynı zamanda gerekli olmayan iki bilinmeyeni de ortadan kaldırdık. Bu dönüşümlerin sonucunda, aşağıdaki niceliklerin bilinmediği bir denkleme sahip oluyoruz:

• P[1] - yukarı adım olasılığı (durma)
• T[1] - ortalama yukarı adım ömrü
• T[2] - ortalama aşağı adım ömrü

Bu iki denklem benzer bir yapıya sahiptir:

1. A1*n = A2*m
2. B1*n = B2*m

Yapı, denklemlerden birini ortadan kaldırmak için "n" veya "m" değişkenlerinden birinin hariç tutulabileceğini göstermektedir. Bunun için, örneğin ilk denklemdeki değerlerden birini ifade etmemiz gerekir:

• m = ((P[1]*T[1] + (1-P[1])*T[2])/(P*[1]*T*[1] + P*[2]*T*[2] + … + P*[N]*T*[N]))*n

Ardından, ifadeyi ikinci denklemde yerine koyalım ve sonucu görelim:

• (P[1]*Pr - (1-P[1])*Pr)*n = (P*[1]*Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1])*((P[1]*T[1] + (1-P[1])*T[2])/(P*[1]*T*[1] + P*[2]*T*[2] + … + P*[N]*T*[N]))*n - (P*[N1]*Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2])*((P[1]*T[1] + (1-P[1])*T[2])/(P*[1]*T*[1] + P*[2]*T*[2] + … + P*[N]*T*[N]))*n

Şimdi, denklemin her iki kısmı da "n" ile çarpılır. Böylece, bunları "n"e bölerek, yalnızca gerekli değerlere bağlı bir denklem elde edeceğiz:

• (P[1]*Pr - (1-P[1])*Pr) = (P*[1]*Pr*[1] + P*[2]*Pr*[2] + … + P*[N1]*Pr*[N1])*((P[1]*T[1] + (1-P[1])*T[2])/(P*[1]*T*[1] + P*[2]*T*[2] + … + P*[N]*T*[N])) - (P*[N1]*Pr*[N1] + P*[N1+1]*Pr*[N1+1] + … + P*[N2]*Pr*[N2])*((P[1]*T[1] + (1-P[1])*T[2])/(P*[1]*T*[1] + P*[2]*T*[2] + … + P*[N]*T*[N]))

"Pr" değeri, her şeyin indirgenebileceği sistem sayısı sonsuz olduğu için serbest olarak kabul edilecektir. Yukarı ve aşağı adımların mutlak değer olarak eşit olması koşuluyla, herhangi bir adım boyutu ayarlayabiliriz. Diğer değerler bir denklem sistemi çözülerek belirlenecektir. Şimdiye kadar sistemin sadece bir denklemi vardı. Önceki bölümde elde edilen denklemler kullanılarak elde edilebilecek iki denkleme daha ihtiyacımız var.

Öncelikle, sistemin üst ve alt koridor sınırlarının geçiş olasılığı aynı olmalıdır. Ayrıca, sınırlardan birini geçmek için ortalama sürenin de aynı olması gerekir. Bu iki gereklilik bize iki eksik denklem verecektir. Koridor sınırının geçilmesine kadar geçen ortalama süreyi belirlemekle başlayalım. Sınırlardan biri geçilene kadar geçen ortalama süre, yukarı ve aşağı atılan ortalama adım sayısına göre belirlenir. Bir önceki makalenin sonuçlarını dikkate alarak şunu yazabiliriz:

• T[U, D] = (S[U, u]*T[1] + S[U, d]*T[2])*P[U] + (S[D, u]*T[1] + S[D, d]*T[2])*(1-P[U])

Bu denklem, sınırlardan birinin geçilmesine kadar geçen ortalama sürenin, sınırlardan birinin geçildiği ortalama adım sayısına ve geçilme olasılığına bağlı olduğunu göstermektedir. Bu kriter, karmaşık bir ticaret sistemini daha basit bir sisteme dönüştürmemizi sağlayacak bir denklem sistemi oluşturabileceğimiz başka bir olası denklem sağlayacaktır. Bu denklem iki başka denkleme bölünebilir:

• T[U] = S[U, u]*T[1] + S[U, d]*T[2]
• T[D] = S[D, u]*T[1] + S[D, d]*T[2]

Bu denklemlere daha sonra ihtiyacımız olacaktır. Tüm bu değerler bir önceki makalede elde edilen matematiksel model temel alınarak hesaplanmıştır:

• S[U, u], S[U, d], S[D, u], S[D, d], P[U] = f(n, m, p) - tüm bu değerler "n, m, p" fonksiyonlarıdır
• n = B[U]/Pr - "n", üst sınıra olan uzaklık ve "Pr" adımı cinsinden ifade edilebilir
• m = B[D]/Pr - "m", alt sınıra olan uzaklık ve "Pr" adımı cinsinden ifade edilebilir
• Pr - seçilen adım
• B[U] - üst sınıra olan uzaklık
• B[D] - alt sınıra olan uzaklık

Ortaya çıkan dönüşüm yönteminin temelleri

Örnek olarak, rastgele bir strateji alabilir ve bunu gerekli eşdeğere dönüştürebiliriz. Çok boyutlu karmaşık bir sistemi daha basit, iki boyutlu bir sisteme dönüştürmenin yollarından birini oluşturdum. Bu süreci adım adım anlatmaya çalışacağım. Açıklamaya geçmeden önce, fikri uyguladım ve yöntemin performansını test ettim. Program makalenin ekinde yer almaktadır. Programımda biraz farklı ama aynı derecede etkili formüller kullandım. Bir önceki makalede elde edilen matematiksel modele dayanmaktadır. Onu kullanarak aşağıdaki değerleri elde edebiliriz:

• P[U], S[U, u], S[U, d], S[D, u], S[D, d]

Ortalama adımlardan, üst veya alt sınır geçilene kadar olan ortalama süreyi elde edebiliriz. Amaç şimdilik tam olarak net olmayabilir. Daha fazla açıklama ile daha net hale gelecektir. Çok durumlu bir stratejiyi daha basit bir stratejiye dönüştürmek için öncelikle ilgili stratejileri oluşturmalıyız. Rastgele sayı tabanlı bir strateji üreteci oluşturdum. Kolaylık olması açısından, rastgele oluşturulmuş beş strateji kullandım. Bunlar aşağıdaki gibidir:

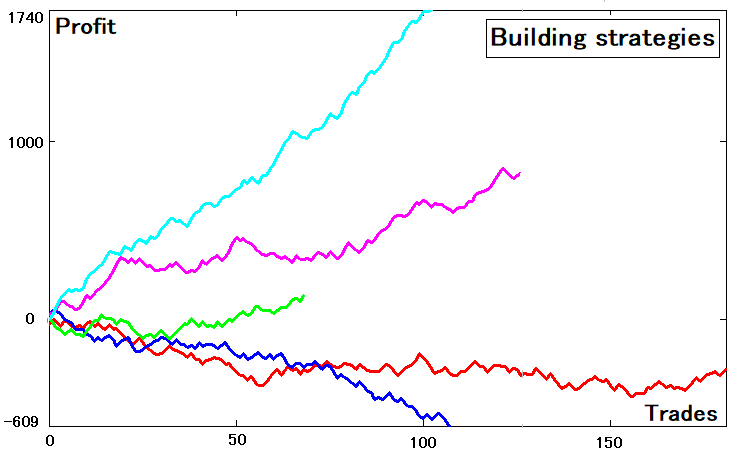
Bu stratejilerin farklı beklenen getiri ölçümleri, farklı işlem sayıları ve parametreleri vardır. Bazı eğriler kayıp oluşturmaktadır, ancak parametreleri çok iyi olmasa da hala bir eğri olduğu için bu bir sorun değildir.

Şimdi konuya gelelim. Şekilde, strateji sınayıcı grafiklerine benzer şekilde, işlem numarasına bağlı bakiye grafikleri gösterilmektedir. Buna göre, her bir eğri için belirli bir bakiye dizisi vardır:

• B[i], i = 0…N
• N - işlem sayısı

Bu dizi, emir parametrelerine sahip diziden elde edilebilir. Emir verilerinin bulunduğu dizinin yalnızca emir kâr veya zarar değerini ve ömrünü içerdiğini varsayıyorum:

• Pr[i], T[i]

Diğer parametrelerin mevcut olmadığını varsayalım. Bunun doğru olduğunu düşünüyorum, çünkü herhangi bir geriye dönük test veya sinyali analiz etmek istediğimizde, bu veriler genellikle bizim için mevcut değildir, çünkü normalde kimse bu verileri kaydetmez. Kullanıcılar daha sık olarak düzelme faktörünü, maksimum düşüşü ve benzer ölçümleri kontrol eder. Her zaman kaydedilen işlem verileri:

1. Kâr
2. Emir açılış zamanı
3. Emir kapanış zamanı

Elbette, bazı verilerin mevcut olmaması doğruluğu etkileyecektir, ancak bu konuda yapılacak bir şey yok. Şimdi, kârları içeren bir diziden bakiyeleri içeren bir dizinin nasıl elde edileceğini görelim:

• B[i] = B[i-1]+Pr[i] if i > 0
• B[i] = 0 else

Elde edilen stratejilerin zamana karşı analiz edilebilmesi için benzer bir zaman dizisi oluşturmamız gerekmektedir:

• TL[i] = TL[i-1]+T[i] if i > 0
• TL[i] = 0 else

Tüm bu eğrilerin apsis ve ordinatlarını belirledikten sonra, onları çizebiliriz. Farklılıkları göreceksiniz, çünkü bunlar işlem numarasına değil, zamana bağlı fonksiyonlardır:

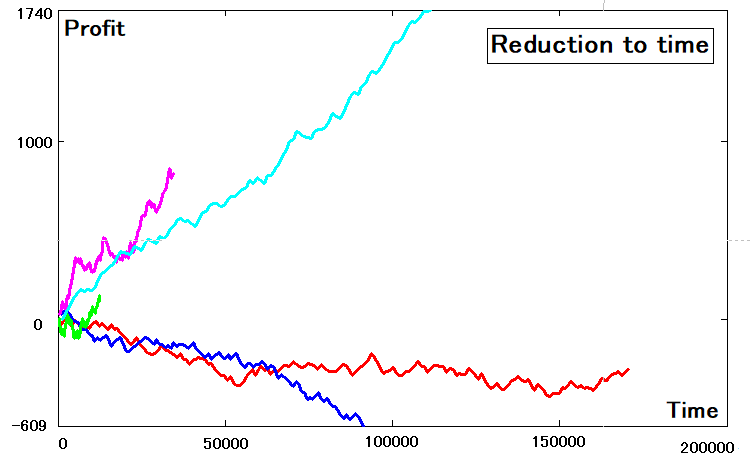
İndirgenebilirlik kriterlerinin tanımlanması

Elde edilen verilerle daha fazla çalışabiliriz. Şimdi, eğrilerin iki kâr durumuyla eşleşip eşleşmediğini kontrol edeceğimiz kriterleri belirleyebiliriz. Zamana göre temsil açısından bakıldığında, üç nicelik yeterli olacaktır:

1. P[U] - üst sınırı geçme olasılığı
2. T[U] - üst sınıra ulaşılana kadar geçen ortalama süre
3. T[D] - alt sınıra ulaşılana kadar geçen ortalama süre

İkinci ve üçüncü değerler aşağıdaki gibi hesaplanabilir:

• T[U] = S[U, u]*T[u] + S[U, d]*T[d]
• T[D] = S[D, u]*T[u] + S[D, d]*T[d]

P[U]'ya gelince, bu değer bir önceki makalede elde ettiğimiz matematiksel model tarafından sağlanmaktadır ve hatırlayacağınız gibi, "P[D] = 1-P[U]"dur. Böylece, matematiksel model tarafından sağlanan beş değere dayanarak, yukarıda açıklanan gerekli üç değeri elde edebiliriz. Bu iki denklem ise daha önce elde edilmişti, ancak burada kolaylık olması için zaman gösterimini değiştirdim.

Bu değerler hesaplanabilir. Onları bir şeye indirgemek için, sahip olduklarımıza dayanarak gerçek değerlerini bir şekilde elde etmemiz gerekir. Daha sonra, istenen eşdeğer iki durumlu eğrinin öyle parametrelerini bulmamız gerekir ki üç parametre de gerçek değerlere çok yakın olsun. Kriterleri bu şekilde elde ediyoruz. İlk olarak, bilinen değerler için notasyonu tanıtalım:

• P*[U] - seçilen koridorun sınırlarını geçmenin gerçek olasılığı
• T*[U] - üst sınır geçilene kadar geçen gerçek ortalama süre
• T*[D] - alt sınır geçilene kadar geçen gerçek ortalama süre

Gerçek ve hesaplanan değerler arasındaki sapma göreceli olarak ya da yüzde olarak ölçülebilir. Yüzde olarak ölçüldüğünde, kriterler aşağıdaki gibi olacaktır:

• KPU = ((|P[U]-P*[U]|)/(P[U]+P*[U]))*%100
• KTU = ((|T[U]-T*[U]|)/(T[U]+T*[U]))*%100
• KTD = ((|T[D]-T*[D]|)/(T[D]+T*[D]))*%100

Kaynak sistemle karşılaştırma için kriterlerin tanımlanması

En iyi sistem, tüm bu değerlerin en azına sahip olan sistemdir. Şimdi, hesaplanan değerleri elde edebilmek için öncelikle koridorun büyüklüğünü belirlememiz gerekir, buna göre gerçek olasılığı ve kırılmaya kadar gerçek zamanı belirleyeceğiz. Bu fikir aşağıdaki şekilde görselleştirilebilir:

Şekilde, kârlı bir strateji için böyle bir koridorun belirlenmesine ilişkin bir örnek gösterilmektedir. Mor üçgenler olası yukarı ve aşağı hareketler için başka bir kontrol noktasını sembolize eder. İstenen minimum hareket siyah noktalar arasındadır. Mevcut dönemde gerçekleşen maksimum hareketi temel alırsak, P[U] olasılığı 1 olacaktır. Açıktır ki, bu en yanlış seçimdir. Çünkü hem alt hem de üst sınırın geçişini garanti eden minimum değere ihtiyacımız vardır.

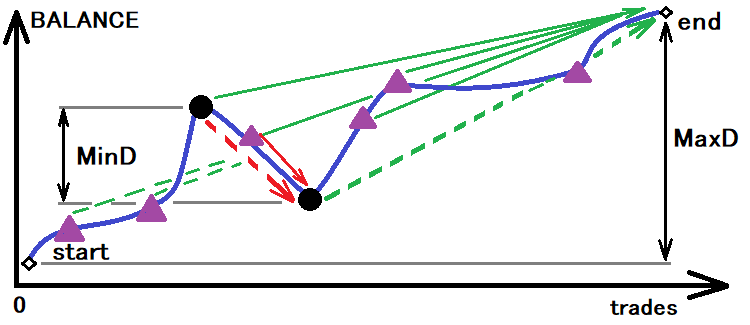
Gerekli değerlerin hesaplanması için olası bir koridorun değerlendirilmesi

Ancak bu bile yeterli değildir. Bu değeri temel olarak kullanırsak, alt sınıra yalnızca bir kez dokunmuş oluruz ki bu da doğru değildir. Şahsen, koridorun değerini sunulan minimum değerden üç kat daha az kullandım. Yeterli sayıda sınır dokunuşu örneklemi ile bu değer yeterli olacaktır. Artık koridor boyutunu belirlediğimize göre, bu koridoru bölebiliriz. Koridorun kendisinin bir adım olduğunu varsayarsak, o zaman:

• n, m = 1
• p = P[U]
• Pr*n = Pr*m = 1/3*MinD - koridor genişliğinin yarısı
• Pr = (1/3*MinD)/n = (1/3*MinD)/m - adım modülü
• T[U, u] = T[U]
• T[D, d] = T[D]
• T[U, d] = 0
• T[D, u] = 0

Bu, çok büyük bir ticaret örnekleminiz olması durumunda da kullanılabilir. Bu yaklaşımın avantajı, koridoru bölmek için matematiksel bir model kullanmamıza gerek olmamasıdır, çünkü bu durumda tüm koridorumuz bir adımdır. Ancak hesaplamalarımda örnek olarak matematiksel bir model kullandım. Bu yaklaşımı kullanırken, seçim için aşağıdaki parametre aralıklarını bulmak gerekir:

• p = p1…p2
• N = m = nm1...nm2

Örneğimde aşağıdaki aralıkları kullandım:

• p1 = 0.4, p2 = 0.6, nm1 = 1, nm2 = 3

Elbette daha geniş aralıklar kullanabilirsiniz. İsteğe bağlı olarak, aralıklardan biri genişletilebilirken diğeri olduğu gibi kullanılabilir. Örneğin, "nm2"yi artırırsak, yöntem daha geniş bir yelpazedeki çeşitli stratejileri kapsayabilir. Matematiksel model üstesinden gelemezse, matematiksel modele sahip olmayan yönteme geçebiliriz.

Koridorun üst sınırının geçilme olasılığının ve buna kadar olan ortalama sürenin tanımlanması

Yukarıdaki tüm değerleri başarıyla bulduktan sonra, yalnızca ‘yukarı adım’ için "p" olasılığını elde edeceğiz. Daha sonra bu değeri ortalama sınır geçiş süresini bulmak için temel olarak kullanabiliriz. Bu, yukarıdaki görselin hafif bir dönüşümü ile görselleştirilebilir:

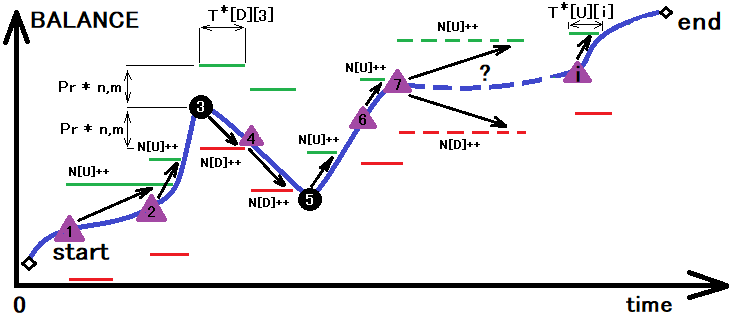
Şekil, bir önceki dönüşüm sonucunda boyutu belirlenen koridor için alt ve üst geçişlerin toplanması sürecini göstermektedir. Bu geçişlerin toplamı ile birlikte, kesişme için gereken süreyi hesaplarız. Tek bir işlemle, ihtiyacımız olan yıldız işaretli tüm büyüklükleri belirleyebiliriz:

• N[U] - koridorun üst sınırının kesişme noktalarının sayısı
• N[D] - koridorun alt sınırının kesişme noktalarının sayısı
• T[U][i] - üst sınır geçilene kadar geçen süreyi içeren dizi
• T[D][i] - alt sınır geçilene kadar geçen süreyi içeren dizi

Bu verileri kullanarak, üst sınırı geçme olasılığını ve üst ve alt sınırları geçmek için ortalama süreyi hesaplayalım:

• P*[U] = N[U]/(N[U]+N[D])
• T*[U] = Summ(0…i)[T[U][i]]/N[U]
• T*[D] = Summ(0…i)[T[D][i]]/N[D]

İki boyutlu eşdeğerimizin indirgenmesi gereken tüm değerleri bulduk. Şimdi, aramaya nereden başlayacağımızı tanımlamamız gerekiyor. Bunu yapmak için, bu değerlerden hangisinin doğruluk açısından en yüksek önceliğe sahip olduğunu belirlememiz gerekir. Örnek olarak üst sınırı geçme olasılığını seçtim. Bu yaklaşım, analiz için hesaplama gereksinimlerini azaltır. Üç aralıkta üç değer seçmeyi seçersek, üç serbestlik derecesi elde ederiz ve bu da hesaplama süresini artırır. Bazen hesaplama süresi gerçek dışı olabiliyordu. Bunun yerine, yukarı adım olasılığı ile başladım ve ardından yukarı ve aşağı adımların ortalama süresine geçtim.

Koridorda birçok adım olduğunu ve geçiş zamanının adımların zamanı olmadığını hatırlatmak isterim. Ayrıca, belirli bir yönde adım atma olasılığı, sınırı geçme olasılığı değildir. Bunun tek istisnası başlangıçta açıklanan n = m = 1 durumudur.

Sonuç olarak, aşağıdaki adım özelliklerini elde ederiz:

1. p - yukarı adım olasılığı
2. T[u] - yukarı adımın ortalama süresi
3. T[d] - aşağı adımın ortalama süresi
4. Pr - kar değerlerinde adım modülü

Basit bir dönüşümün verimliliğinin değerlendirilmesi

Adımların tüm parametrelerini bulduğumuzu varsayalım. Böyle bir dönüşüm işleminin genel verimliliği nasıl değerlendirilir? Verimliliği değerlendirmek için stratejilerin indirgendiği düz çizgiler çizebiliriz. Doğruların eğimi aşağıdaki gibi tanımlanabilir:

• K = EndProfit/EndTime - çizgi eğim katsayısı
• P0 = K*t - çizgi denklemi

Şu şekilde görünecektir:

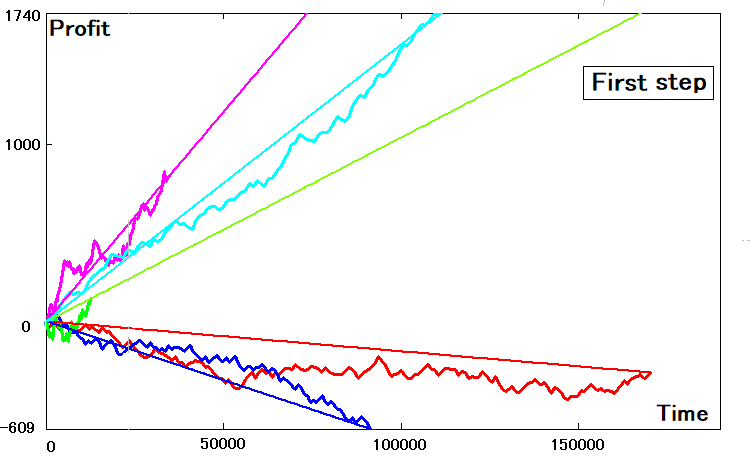
İki boyutlu eğrilerin parametreleri idealse, benzer düz çizgileri tam olarak aynı eğime sahip olacak ve uç noktalarda bakiye eğrilerine dokunacaktır. Bence böyle bir tesadüfün asla gerçekleşemeyeceği çok açıktır. Bu eşdeğerin eğim katsayısını bulmak için, adım için bulunan verileri kullanabiliriz:

• MP = p*Pr - (1-p)*Pr – herhangi bir adım için yukarı doğru bir kaymanın matematiksel beklentisi
• MT = p*T[u] + (1-p)*T[d] - herhangi bir adımın oluşumu için harcanan zamanın matematiksel beklentisi
• K = MP/MT - çizgi eğim katsayısı

Hesaplama için aynı programı kullandım ve her seferinde benzer bir görüntü elde ettim:

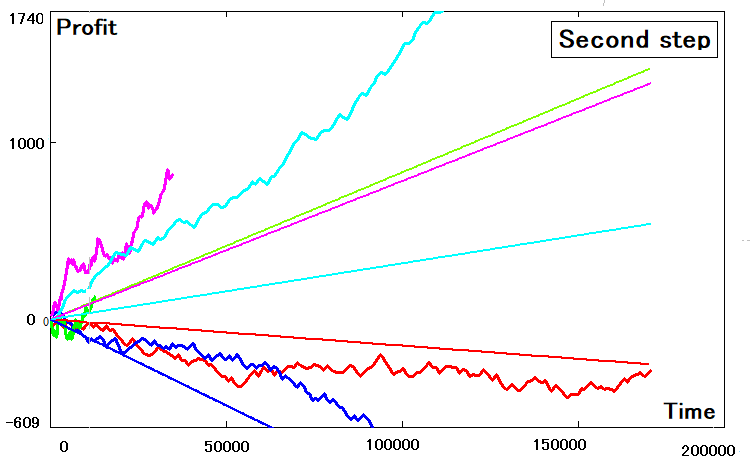
Tüm stratejiler doğru bir şekilde iki boyutlu bir eşdeğere dönüştürülemedi. Bazılarında belirgin sapmalar var. Sapmalar aşağıdaki nedenlerle bağlantılıdır:

1. Yıldız işaretli değerlerin hesaplanmasında hata
2. İki boyutlu modelin kusurlu olması (daha az esnek model)
3. Olası arama girişimi sayısının sonluluğu (ve sınırlı hesaplama gücü)

Tüm bu gerçekleri göz önünde bulundurarak, ortalama adım süresini ayarlayabiliriz, böylece en azından orijinal ve türetilmiş modellerin eğim katsayıları eşit olur. Elbette bu tür dönüşümler indirgediğimiz kriterlerin sapmalarını etkileyecektir, ancak başka bir çözüm yoktur. Bence ana kriter çizgi eğim katsayısıdır, çünkü işlem sayısı sonsuza giderse, orijinal ve türetilmiş stratejiler tek bir çizgide birleşmelidir. Eğer bu gerçekleşmezse, o zaman böyle bir dönüşümün pek bir anlamı kalmaz. Belki de tüm bunlar dönüşüm yöntemiyle değil, şu anda tam olarak açık olmayan gizli olasılıklarla bağlantılıdır.

Son ayarlama ve simülasyon

Böyle bir dönüşümü yapmak için bir orantı kullanabiliriz. Eğrileri oluşturmadan önce, eğrinin başlangıcından analiz edilen emre veya segmente kadar geçen süreye eşdeğer olan TL[i], B[i] dizilerine sahiptik, dizinin son elemanlarını alabilir ve aşağıdakileri yazabiliriz:

• K = B[n]/TL[n]
• N - bakiyeler dizisinin son elemanının indeksi (son bakiye)

Bir önceki adımda elde edilen düz çizgiler için de böyle bir katsayı hesaplayabiliriz. Zaten daha önce hesaplanmıştı:

• K1 = MP/MT

Bu katsayılar eşit değildir, bu nedenle bir düzeltme yapılması gerekir. Bu aşağıdaki şekilde yapılabilir:

• K = MP/(KT*MT)
• KT - düzeltme katsayısı

Şimdi matematiksel beklentinin anlamını değiştirmemesi için bu katsayıyı matematiksel beklentinin içine eklememiz gerekiyor. Bu şu şekilde yapılabilir:

• MTK = MT*KT = p*(T[u]*KT) + (1-p)*(T[d]*KT)

Gördüğünüz gibi, yeni düzeltilmiş zaman değerleri artık parantez içinde yer almaktadır. Bunlar aşağıdaki şekilde hesaplanabilir:

1. Tn[u] = T[u]*KT
2. Tn[d] = T[d]*KT

Bu, yukarı adım ve aşağı adım için düzeltilmiş zamanlardır. Düzeltme katsayısını hesaplamak için katsayı hesaplama ifadelerini eşitleriz:

• B[n]/TL[n] = MP/(KT*MT)

Denklemi KT'ye göre çözdüğümüzde, bu değeri hesaplamak için bir ifade elde ederiz:

• KT= (MP/MT)/(B[n]/TL[n]) = (MP*TL[n])/(MT*B[n])

Tek yapmamız gereken, yukarı ve aşağı adımın ortalama süresini ayarlamaktır. Bundan sonra, dönüştürme işlemi tamamlanmış sayılabilir. Sonuç olarak, ikiden fazla durumu tanımlayan büyük diziler yerine stratejimizi tamamen tanımlayan dört değerden oluşan bir küme elde ederiz:

1. p - yukarı adım olasılığı
2. Pr - adım modülü
3. T[u] - ortalama yukarı adım oluşum süresi
4. T[d] - ortalama aşağı adım oluşum süresi

Bu dört parametre, stratejiyi simülasyon yoluyla yeniden oluşturmak için yeterlidir. Artık bu yazılım, piyasadan ve zamandan bağımsız olarak bizim için kullanılabilir. Beş stratejimiz için simülasyon aşağıdaki gibidir:

Burada ilk adımdaki düz çizgileri kullanıyoruz. Bu çizgiler sıfırdan gerçek ticaret eğrisinin sonuna kadar çizilmiştir. Gördüğünüz gibi simülasyon çizgilere çok yakın, bu da dönüşümlerin doğruluğunu teyit ediyor. Bunun tek istisnası mavi çizgidir. Sanırım algoritmamda biraz zamanla düzeltilebilecek bazı küçük kusurlar var.

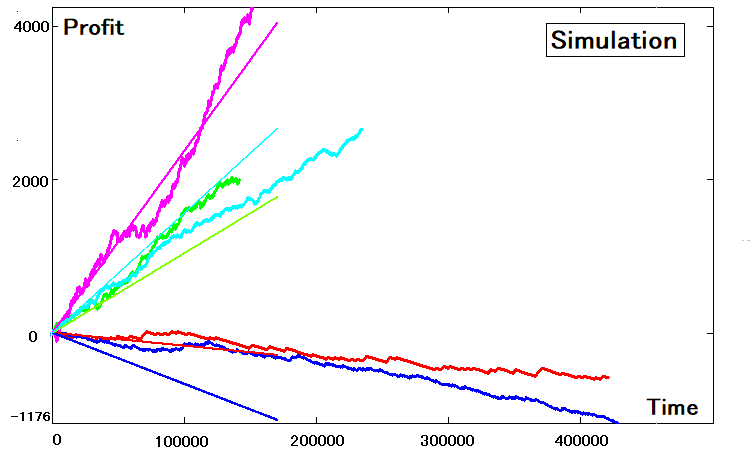
Özet

Model çalışma süreci ilginç fikirler üretti. Başlangıçta, iki boyutlu şemalar ve çok durumlu şemalar üzerinde çalışırken, yalnızca karmaşık sistemler için basitleştirilmiş bir açıklama elde etmek istedim. Bu analiz sonucunda çok daha değerli ve basit sonuçlara ulaştık. Çok fazla teknik nüans içerdiği için detayları makalede anlatmak zor. Özetle, bu çalışma şu sonuçları vermiştir:

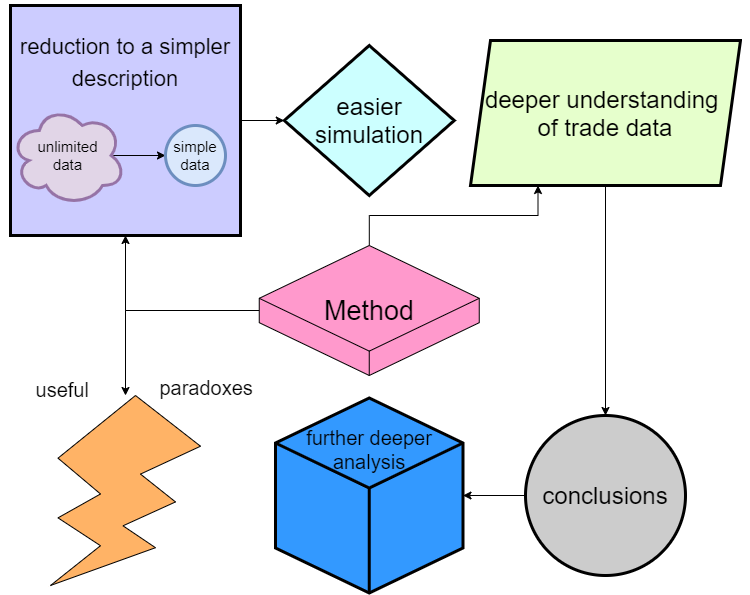
Tüm avantajlar bir liste halinde sunulabilir:

• Birçok çok durumlu sistem iki durumlu sistemlere dönüştürülebilir (ve bu nedenle n'den m durumuna geçiş süreci de mümkündür)
• Dönüştürme işlemi bir ticaret verisi sıkıştırma mekanizması olarak kullanılabilir
• Dönüştürülen veriler simülasyon aracılığıyla geri beslenebilir, bu da simülasyonu basitleştirir (çünkü sadece iki durumun simüle edilmesi gerekir)
• Fiyatlandırmadaki olasılıksal süreçlerin daha derinlemesine anlaşılması, bireysel olarak faydalı sonuçlara ulaşılmasını sağlar
• Elde edilen bilgilere dayanarak, ticaret sürecinin daha derin bir analizine geçebiliriz
• Ticaret için bazı faydalı özellikler elde ettik - şimdilik bunları paradokslar olarak kategorize ediyorum

Elbette serinin ana fikri, olasılık teorisine dayalı ultra istikrarlı ve çok dövizli sistemlerin oluşturulmasına doğrudan olanak sağlayacak basit ve kullanışlı matematiğin inşasıdır. Şimdiye kadar elde edilen bilgiler, yekpare bir çözüm oluşturmak için iyi bir temel oluşturmaktadır.

Ayrıca, çalışma sırasında ortaya çıkardığımız paradokslardan da bahsetmek istiyorum. İlk dönüşüm aşamasında, eşdeğer düz çizginin farklı bir eğimiyle ifade edilen tutarsızlıklar elde ettik. Bu tutarsızlıkların rastgele ticareti rastgele olmayan ticarete dönüştürmek ya da çeşitli ticaret sinyali yükselticileri sağlamak için kullanılabileceğini düşünüyorum.

Başka bir deyişle, çok durumlu sistemleri iki durumlu sistemlere dönüştürmek için dönüşümler uygularsak, bazı sıfır stratejileri pozitif PF'li stratejilere dönüştürmede yararlı olabilirler, bu da kalitelerini artırmayı amaçlayan diğer yöntemler kullanılarak yapılabilir. Şu ana kadar bu düşünceler çok belirsiz ve dağınık, ancak eninde sonunda fikirlere dönüştürülecektir. Bunu, daha sonra bir Uzman Danışman oluştururken kullanacağımız çalışmanın ana sonucu olarak görüyorum.

Sonuç

Bu makalede çok fazla detaya girmemeye çalıştım. Tabii ki bu konu matematik içeriyor. Ancak daha önceki makalelerden edindiğim tecrübeler ışığında, genel bilgilerin detaylardan daha faydalı olduğunu düşünüyorum. Yöntemin tüm ayrıntılarını incelemek istiyorsanız, lütfen aşağıda ekli programı kullanın - bu programda araştırma yaptım. Kullanılan tüm algoritmaları açıklamadım, çünkü bunlar temelde veri dizileri ve matrisleriyle ilgili çok sıkıcı matematik içeriyor. Benzer bir şey yaratmak isteyenlerin kendi mantıklarına bağlı kalacaklarını, ancak sunulan programı bir başlangıç noktası olarak kullanabileceklerini düşünüyorum.

Daha derinlemesine analiz etmek istemiyorsanız, nasıl dönüştürüleceklerini görmek için farklı stratejileri test etmenizi öneririm. Gelecekteki fikirlere gelince, bence yavaş yavaş hem kalite hem de istikrar açısından sinir ağlarını aşabilecek sağlam bir kendini uyarlayan algoritma yaratmaya geçeceğiz. Zaten bazı fikirlerim var. Ama önce temeli tamamlamamız gerekiyor.

Referanslar

• Ticaret için kombinatorik ve olasılık teorisi (Bölüm I): Temel bilgiler
  
• Ticaret için kombinatorik ve olasılık teorisi (Bölüm II): Evrensel fraktal
  
• Ticaret için kombinatorik ve olasılık teorisi (Bölüm III): İlk matematiksel model
• Ticaret için kombinatorik ve olasılık teorisi (Bölüm IV): Bernoulli mantığı