Self-adapting algorithm (Part III): Abandoning optimization

Introduction

Before reading this article, I recommend that you study the second article in the series "Developing a self-adapting algorithm (Part II): Improving efficiency". The methodology applied in the current article differs significantly from everything discussed earlier, but it will be useful to read the previous articles to understand the topic.

Analyzing drawbacks

Like in the previous article, I will start by analyzing the drawbacks of the previous successful version. The following shortcomings were detected during the analysis:

• Position open/close signals are generated based on the candle analysis. The candles are not stable in size. Some of them are large and some are small. It is not uncommon for positions to open based on an excess of bearish or bullish candles. After that, the numbers of bearish and bullish candles become equal, while the profit on open positions is still negative. So, should we close the positions or wait for profit? In the former case, the whole point of trading is reduced to nothing and the algorithm starts to receive losses. In the latter case, we will sooner or later face a significant drawdown.
• The price moves regardless of the type of candles. The market may be dominated by bearish candles, while the price moves up due to bullish candles being larger than bearish ones. This is especially unpleasant if you have open positions.
• The task of predicting the future size of candles still remains unsolved.
• Sometimes, after opening positions, an excess of one type of candles is not reduced for a long time, so the price may continue moving against open positions. This leads to significant drawdowns. Most importantly, it is not clear when the price will reverse and whether it will reverse at all.
• Positions are opened by time. Sometimes, the price stands still for a long time, while positions continue to open as new candles arrive. Such moments are especially dangerous during holidays, such as Christmas, when trading activity is low and the algorithm simply opens positions because of time.
• Algorithm settings should be optimized for each trading instrument individually. The only reason for setting these parameters is that they worked better on history. The algorithm passes backtests for 21 years but not for all instruments. Adjusting parameters to history is not the best solution.
• It is not obvious why it works better and more stable for some trading instruments and much worse for others.
• It is also unknown when the behavior of the trading instrument changes so that the algorithm suffers a loss. In fact, it is not known when the risky situation occurs. I can calculate the probability of such a moment, but it will be a very rough result.
• There is no theory explaining how the instrument will change in the future and why, therefore, it is necessary to use obviously sub-optimal parameters, so that there is a margin for fluctuations in the statistical parameters of the price series. This greatly reduces profitability.

I consider all of the above disadvantages significant. We can continue the modification of the algorithm improving the characteristics one after another but it is better to take all the best from it and start the development almost from scratch. I will start from revising the theoretical base.

The algorithm should be completely self-adapting, therefore it will be developed for the currency and exchange markets. It should work with any instrument. This is important because there should be a clear understanding of how one market is different from another. If there is such an understanding, then it makes sense to turn it into an algorithm. This time, I switched to the MetaTrader 5 platform because it has a more functional strategy tester and is available for working not only with FOREX instruments, but also with exchange ones.

During the development, you constantly need to answer the question: why a certain parameter has a certain value. In the ideal case, the reason for setting any value in the parameters should be justified.

Converting a candle chart into a block one

In the new version, I decided not to use candles because of their unstable parameters. More precisely, only M1 candles are to be used because moving on to handling ticks leads to a significant increase in resource consumption. Ideally, it is better to handle ticks.

I will analyze blocks of N points. The blocks are similar to renko but they are based on a slightly different algorithm. I have already mentioned block charts and their advantages in analysis in the article "What is a trend and is the market structure based on trend or flat".

Figure 1. Block chart

Figure 1 shows a block chart. The general view of the block chart is shown in the bottom part of the figure, while the upper image demonstrates how blocks look on the price chart. BLocks are built into the past and future from a fixed time. In the figure, the fixed time is shown as a yellow vertical line. This is a zero point, from which blocks are built into the past and future. The construction algorithm is mirrored. The fact that the blocks are built into the past and the future will be important in further development.

Blocks are needed because their main parameters are stable, controllable and, most importantly, profit/loss depends mainly on price movement in points.

Market model

The basic pattern is to be similar to the one I used in the previous algorithms: the local deviation of the number of bearish blocks from the number of bullish ones and the subsequent return to some equilibrium. The pattern is statistical, so we need to start by analyzing the statistical characteristics of block charts. To do this, I have developed a special indicator Max_distribution described in the article "What is a trend and is the market structure based on trend or flat".

The indicator measures statistical parameters of the price series divided into blocks. It is able to display data for several block sizes simultaneously. For example, we want to know what statistical characteristics the charts with a block size from 10 to 1000 points have. Set the minimum block size in the indicator settings and obtain blocks of all other sizes via the multiplication factor.

The main indicator operation mode is measuring the number of blocks the price moves vertically in N steps.

Figure 2. Changing the number of blocks vertically in 24 steps

Figure 2 shows an example. The number of blocks passed by the price in N steps is measured. The required number of samples (for example, 100) is collected and the average value is defined. Such an analysis is conducted for blocks of different size.

Figure 3. Average amplitude for different block sizes

Figure 3 shows an example of the vertical average amplitude distribution in blocks in 24 steps. Each histogram column is the average amplitude value for its block size. The number of samples is 1000. The measurements for the smallest blocks are to the left, while the ones for the largest blocks are to the right. For a block size of 0.00015, the price moves 5.9 blocks vertically in 24 steps and 1000 samples. For a block size of 0.00967, the price moves 4.2 blocks vertically in 24 steps and 1000 samples.

The red line indicates the reference value, which would occur if the price series were a random walk. For 24 steps, this is the value of 3.868 blocks vertically. The reference value is calculated by the combinatorial method and can be clearly represented by the table in Figure 4.

Figure 4. Calculating the reference value for 24 steps

Figure 4 shows the calculation of the reference vertical value of blocks the price moves on average in 24 steps in case of the random walk. In the last column, this value is converted to a power. The average amplitude of the random walk tends to 24^0.4526. The reference value can be re-calculated for each number of steps. The table is attached to the article in .xlsx format.

I conducted research on various trading instruments: about 35 currency pairs, over 100 stocks, 10 cryptocurrencies and about 10 commodities. There are no serious deviations. Generally, the picture is approximately similar for all instruments. Average amplitude ranges from 7 on fast growing cryptocurrencies to 3.8 on currency pairs. Some low-liquid stocks may even dip below 3.8.

The average amplitude was obtained in 24 steps or for some other number of steps, but what does this mean? Let's represent the chart in the form of a sinewave converted to a block form, as in Figure 5.

Figure 5. Sinewave in block form

Let the block size be such that there are 24 steps in half the period of the sinewave. Then the period will be 48 steps. If we measure the average amplitude in 25 samples of 24 steps, we obtain the average amplitude of 10.33 blocks in 24 steps. With an increase in the number of samples, the average amplitude tends to 12 or to the number of steps divided by 2. The price series is not a sinewave, but the sinewave is convenient for trading. Now if we get the value exceeding 12 when measuring the average amplitude, the block size is not big enough, and 24 blocks do not fit in half the period. But a value less than 12 will indicate two reasons: the blocks are too large or the trend movement on the price series is not as linear as on the sinewave. I am currently not considering the trend slope. I will do this later.

According to the readings of the developed Max_distribution indicator, we can roughly estimate how similar the price series is to a sinewave. To achieve this, let's see how the indicator histogram for a sinewave looks.

Figure 6. Dependence of the average amplitude on the block size for a sinewave

In Figure 6, we can see that in case of small blocks, the price moves 24 blocks vertically in 24 steps. But with an increase in the block size, the price moves smaller number of blocks in 24 steps. When the block size becomes comparable to the amplitude of fluctuations, the number of blocks vertically drops to zero. In Figure 3, the maximum value was 5.9 and tended to the reference one, 3.868. Thus, the price series can be represented as a "noisy" sinewave always having a certain trend component on some scales. In other words, the market should always have a scale currently showing a flat (the reversal probability is higher than the trend continuation one) and a scale currently showing a trend (the continuation probability is higher than the reversal one).

The reasons behind adopting this definition of trend and flat are explained in one of my previous articles "What is a trend and is the market structure based on trend or flat".

Using Max_distribution indicator, I have measured the average vertical number of blocks for different trading instruments not only for 24 but also for other numbers of steps. The example is shown in Figure 7.

Figure 7. Dependence of the average amplitude on the number of steps in the sample

White columns in Figure 7 display the measured movement amplitude for the number of steps from 10 to 120 with the step of 2 and 1000 samples for each measurement. Red lines indicate the reference value for the given number of steps. As we can see, no significant deviations from the main trend are observed with an increase in the number of steps. The overall shape of the measured value curve is similar to that of the reference one. The measurements were for GBPUSD, but I did research for other instruments as well. There are a lot of trading instruments whose histogram values exceed the reference one, but the general trend persists and can be described by a non-linear equation.

It is known that there can be no stable simple regularities in the market. This means that the current trend scales are constantly changing. At the same time, the flat scales also become trendy.

I will use the average amplitude for 24 steps from Figure 7. It is 3.86. I assume that the movement is to consist of a trend and flat parts similar to the sinewave. In this case, it is possible to calculate the trend part for the average amplitude. To achieve this, 3.86*2=7.72 vertical blocks for 24 steps are to be rounded up to 8 because the blocks can be of integer values only. If we get to the trend area, then the price moves 8 blocks vertically in 24 steps. Of course, the price can move 24 blocks vertically in 24 steps but this is of no importance. I will explain the reason later.

It turns out that the price moves 8 blocks vertically within 24 steps in the trend area. This means that there will be a movement with 16 blocks in one direction and 8 blocks in another. It is also known that the trend part should be followed by the flat one, so that the average amplitude remains stable (it is quite stable on a large number of samples). But the market is not a sinewave. As we can see on Figure 7, the number of vertical blocks is increased with an increase in the number of steps. Therefore, I will assume that the deviation from the average that occurs at fewer steps returns to the average at more steps.

The chart on Figure 7 allows us to define how much the price should pass on average in 26, 28, 30, 32 and 34 steps:

26 steps = 3.98; 28 steps = 4.11; 30 steps = 4.2; 32 steps = 4.36.

In 24 steps, the price already moves 8 blocks vertically, but in 28 steps, it should pass 4.1 blocks vertically on average, or 4 blocks if rounded down to the integer value. This means, a rollback from the previous movement of 4 blocks is possible in the next 4 steps. The market is not so predictable and it is unlikely that events will develop according to this scenario. The same chart on Figure 7 allows us to define that the price passes 8 blocks vertically in 116 steps on average.

Figure 8. Possible scenarios

Figure 8 shows two possible scenarios. These are two extreme options. They are unlikely and meant for visualization. Most probably, the events are to follow one of the intermediate scenarios. The most important thing now is that we know how much the price should pass within each number of steps on average. As we can see, the sharper the rollback, the deeper it is and vice versa.

In the long run, the amplitude tends to its average value. For 24 steps, this is 3.8 vertical blocks, while for 116 steps, this is 8 vertical blocks.

This is the structure of the model, which allows calculating the rollback characteristic specifically for each trading instrument based on the trend movement parameters and further price behavior. The sharper the trend movement and the faster the rollback, the deeper it becomes. The flatter the trend and the larger the rollback, the shallower the depth. Now all this can be expressed in numbers, using the statistical parameters of the instrument as a basis.

Figure 9. The trend movement and the rollback depth

Figure 9 shows how this looks on a real chart. We can see the sharp movement and the sharp rollback to the left. The rollback depth turns out to be more than 60%. To the right, there is a smoother movement and a longer rollback resulting in the 30% rollback. This happens because the price goes through a larger number of steps in the figure to the right, and its amplitude increases during the formation of the movement.

The reasons for this behavior can be explained not only by the fact that the price series has an average amplitude it adheres to, but also by the fact that sharp movements are caused by a sharp inflow/outflow of the capital into an asset by amounts that significantly exceed the current liquidity. After a position for a large amount is opened, it should be closed. It does not matter who owned the amount of funds — one participant or several. If we immediately close the position for the entire amount, the price returns to the original level, i.e. the rollback is 100%. But if the position is closed gradually with consideration to the incoming liquidity, then a larger amount causes a smaller movement. The faster a trader exits the position, the stronger the rollback from the movement created by his/her capital.

It is important that the pattern is confirmed by the fundamental features of pricing. 

The whole theory is not described in this section, but it is enough to start developing the algorithm. The rest will be described along the way.

Tracking the trend

Like in the previous algorithms, the robot is to trade a counter-trend movement and a position is made of a series of orders. The algorithm is to generate the series opening signal and its task is to define the entry point as accurately as possible. Ideally, the more often the signal is generated at the beginning of the series, the more profit can be obtained per unit of time. This means that the signal should be frequent and of high quality.

The robot will analyze the number of bearish and bullish blocks. If it finds a significant deviation in the number of bullish blocks from the normal value, then it generates a signal for a series of Sell positions. The same goes for bearish blocks. Their deviation leads to generating the Buy series signal.

Now I am going to develop the basic algorithm which is to be modified later on, therefore its modules should be flexible. The series start signal is to be based on the threshold bearish/bullish blocks excess percentage. The number of blocks for analysis is to be set in the range from the minimum value to the maximum one, as in the previous algorithms. However, this is done for other purposes here.

The threshold percentage for starting and completing the series

Since the block range is used for analysis (for example, 24-34), it would be incorrect to use a fixed threshold percentage for each number of blocks. The probability of the combination made of 24 blocks with the 75% excess of prevailing blocks is not equal to the probability of such a combination occurring for 34 blocks. The probability of the combinations is the same, meaning that the applied threshold percentage should be dynamic and depend on the probability of such a combination.

In the settings, the threshold percentage is to be set by the probability of falling into the range. Then it should be recalculated for the necessary number of blocks. The probability of falling into the range is calculated using the rules of combinatorics. I have created a table allowing to convert the probability into a threshold percentage for each number of blocks. 

Figure 10. Probability table

Figure 10 displays the table for recalculating the probability of falling into the opening percentage range. The table assumes that 100% of movements fall in the range of 0-16 vertical blocks for 16 steps. The probability of falling into the range of 2.1% (for the table in Figure 10) means that only 2.1% of all movements pass 10-16 blocks vertically in 16 steps. In the settings, set the probability of falling into the range, for example 2.2, while the algorithm searches for the nearest value less or equal to 2.2 using the table and takes the percentage corresponding to this value. Currently, it is 81.25%. Thus, each number of blocks has its own threshold percentage. The table is attached to the article in .xlsx format.

In the previous versions, positions were closed when the overall profit on open positions became less than the threshold one. This is not the best solution as it causes multiple issues. Since I work with blocks of a fixed size in this version, positions can be closed when the excess percentage falls down to the necessary value. If positions are opened on a fixed number of blocks, the number of blocks in the sample is increased during operation. 

The closure threshold percentage is also calculated via the probability of falling within the range. But the probability of falling into the range has an inverse scale. This has little significance though. The table features a separate column for calculating the closure percentage. Suppose that I want to close positions when the value becomes greater than or equal to 75. Then the nearest value greater than 75 is found. For 16 blocks, this is 78.9, which corresponds to the threshold closure percentage = 62.5%. 

During the operation, the number of blocks in the sample increases since new blocks are closed. Therefore, as long as positions are open, the closure percentage is recalculated for a larger number of blocks on each new block.

Take profit for all positions in the series is set to the expected closure point. This is how the algorithm of controlling the rollback depending on the current market state is implemented. The more blocks in the sample have been formed after the start of the series (trend movement), the less the resulting rollback.

The current implementation of the threshold percentages is not perfect. It was developed at the very start of the algorithm development. Later, I am going to revise the method. All opening/closure percentages are to be adjusted based on measuring the average amplitude for the current number of blocks. In the current version, I did not take into account that the price series parameters are asymmetrical for a rising and falling market. This may be of no importance in FOREX, but this is important for the stock market. I am going to consider this in the future versions of the algorithm.

The methodology of the threshold percentage has been developed, so now we are able to answer the question about the necessary threshold percentage without optimization. The following equation has been developed for this:

; 

• Nb - number of blocks for analysis;
• aa - average amplitude according to the indicator readings for a given number of blocks;
• Ka - average amplitude multiplication ratio. For a sinewave, the ratio is 2. However, the value should be made customizable for the market so that we can increase it a bit;
• Kc - average amplitude multiplication ratio for calculating the closure percentage;
• %open - threshold series start percentage.

We can perform the procedure for a single number of blocks only, while the rest is recalculated using the probability table.

The closure percentage can also be calculated in advance based on the indicator readings.

;

The equation for calculating the closure percentage looks the same. Only a different multiplication factor Kc is used. It should be made equal to 1 with the ability to customize it.

Based on the analysis of the average amplitude equal to 3.8, you can set the threshold percentage of opening for 24 blocks equal to 66.67%. Other values are recalculated using the probability table.

Tracking the trend

As I mentioned before, the market has no stable patterns and stable fluctuation amplitude. Analyzing a trend degree on a certain number of blocks having a fixed size is a questionable solution. The analysis window should be dynamic and adjusted in real time. Let the number of blocks be set by the range of 24-28. 

Why did I select such an analysis window? These values are selected based on the average amplitude = 3.8. They depend on the threshold open/close percentage. With this number of blocks after a signal, we obtain 4 profit blocks at the start of the series. The more blocks in the analysis window, the more accurate the algorithm. There is no fundamental difference how many profit blocks to get: 4 or 10, provided that the block size is proportionally changed. However, since positions are opened at each new block, their number increases with an increase in the operation accuracy. This will negatively impact the results. 

Next, we need to define the minimum block size that makes sense to analyze. The blocks are built according to the formed M1 candles. The minimum discretization rate is 1 minute. The blocks cannot be made too small since they will eventually be constructed inside a candle rendering such an analysis meaningless. Therefore, the minimum block size will be determined based on the size of the candles. To achieve this, we may use ATR for a large period, like 1440 minutes (day) or more, and multiply its value by the ratio. The ratio of 2-5 should be acceptable, although it depends on the trading instrument features.

If the candle size is very uneven, then it is better to use a larger ratio. The second criterion is commissions and spread. The profit received for 4 blocks should be significantly higher than the commissions we will pay. The smaller the block size, the more often there will be the series start signals and the more profit we can earn. Here we need to strike a balance. Eventually, the minimum block size depends on the candle size and commissions. There are clear criteria for choosing the minimum block size.

The described method of selecting the block size is good enough both in theory and in practice. However, I already have an improved mechanism based on the improved market model. Explaining the new mechanism requires a separate article, so I will restrict myself to the method described above here.

If the robot analyzes a certain number of blocks having a fixed size, it will not be profitable because the market parameters always change, market trends and rollbacks are of different size, so we need an adaptive mechanism.

The robot analyzes blocks having the minimum size. When it finds a small trend area with the excess percentage exceeding the threshold one, it should define the maximum scale for the presence of a trend. To do this, a larger area should be scanned. Since the number of blocks for analysis is fixed, we need to increase the block size and see what happens on the larger block size. I have named the minimum block size TF1 similar to the timeframe. This is a synthetic block timeframe. Larger blocks will be obtained using the multiplication ratio, KTF. For example, it will be equal to 1.1.

1. Series start signal

It is necessary to introduce the concept of a basic timeframe (block timeframes are meant here and below when talking about timeframes). The basic timeframe is the one, on which the series start signal was detected.

The algorithm should create several additional block timeframes and check for a series start signal on higher timeframes. 

In case of KTF=1.1, it is enough to look at the next 5 timeframes. So the largest timeframe block will be 1.6 times larger than the smallest timeframe block. If one of the higher timeframes features a signal start series, the algorithm switches to that timeframe and makes it basic. After finding the basic timeframe, we need to create 5 larger timeframes again and repeat scanning. This allows us to find the maximum timeframe with an excess above the threshold.

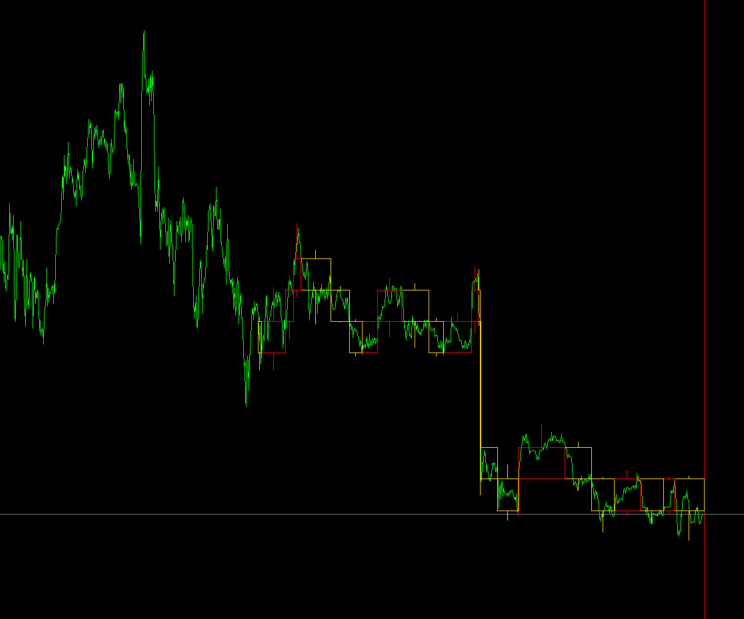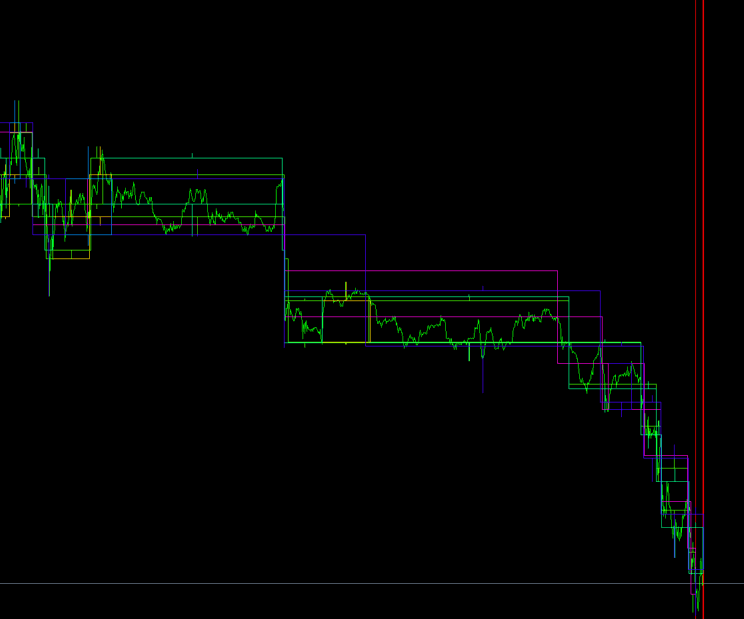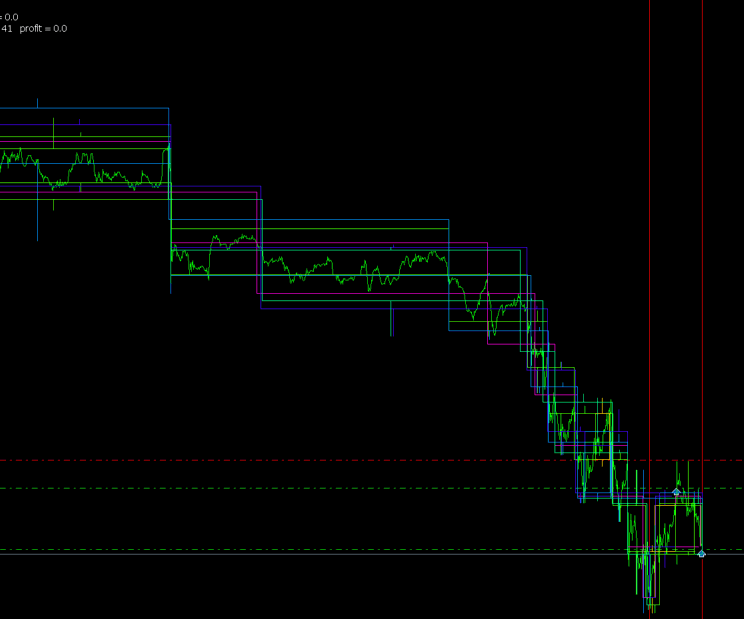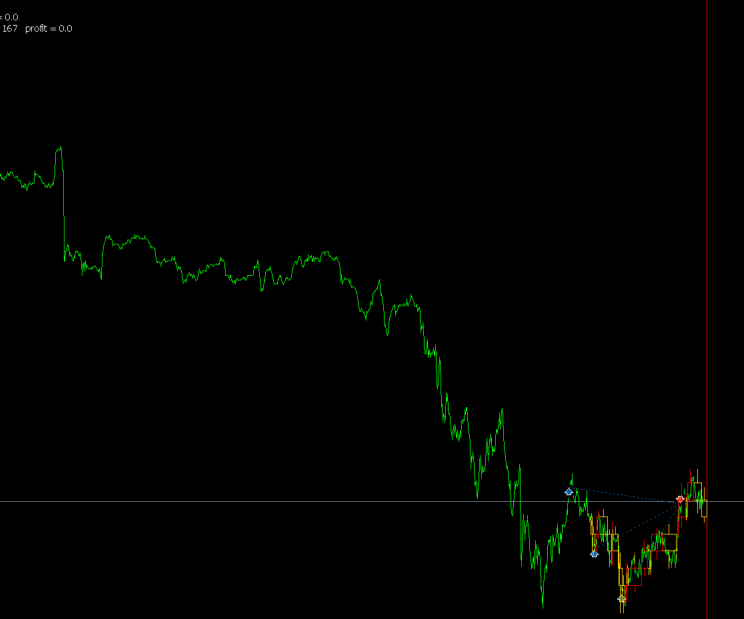
Animation 1

At this stage, the task is to find the maximum timeframe, on which there is a signal for the beginning of the series, and make it basic. Animation 1 shows how this works. We can see that the algorithm scans small blocks. As soon as the signal is found, it increases the block size and selects the basic timeframe with the maximum block size. It calculates the rollback for closing positions for the largest trend it could determine.

At this point, it becomes important to use the block number range instead of a fixed value. In the example, the signal is searched for the range of 24-28 blocks. A sample with a large number of blocks is considered a priority. If the signal is detected on both 24 and 28 blocks, 28 blocks become the basic sample. It is also the case with additional timeframes: the signal is searched for in the range of 24-28 blocks. A timeframe with a large block size is considered a priority. Within this timeframe, the priority is given to the sample with a large number of blocks.

Such a mechanism is needed because there is some inaccuracy in the construction of blocks. A timeframe with a large block size does not always cover a larger data range.

Figure 11. Blocks construction inaccuracy

Figure 11 demonstrates that 10 larger blocks may cover less data than 10 smaller blocks. The range of the number of analyzed blocks of 24-28 is used to minimize this effect. The robot may move to a larger basic timeframe and increase the number of blocks in the sample. After that, it will be easier for it to move to an even larger timeframe with fewer blocks in the sample.

So, why KTF = 1.1? The lower the multiplication factor, the more accurate the algorithm, but the more timeframes we need to view simultaneously. In order for the block size to increase 1.6 times relative to the basic timeframe, we need to view only 5 timeframes. If KTF = 1.05, we already have to look at 10 timeframes posing an additional computational load. But the smaller the multiplication ratio, the more accurate it becomes.

2. Delay in opening positions

The series start signal has been found but if we open positions now, the result will be dubious due to weak self-adaptation. The price may continue moving in the same direction and is likely to do so. We need to make sure that the maximum scale is found and the trend is over. To achieve this, the series start signal should be absent on the next timeframe and the algorithm should not be able to increase the basic timeframe. The series start signal on the higher timeframe is absent now but higher timeframe blocks cover a larger data range and move to the past relative to the trend start.

After defining the basic timeframe, we need to give time to the price to generate a signal on the higher timeframe. The price should move a sufficient distance so that we able to move to a larger timeframe. We can open a position only if enough time has passed for the formation of a signal on the higher timeframe, but the signal has not been formed. First, I solved the issue as described in (a). Then I significantly revised the mechanism, and it greatly improved the results. I will describe it in point (b).

a) Delay along the trend section

As a rule, higher timeframe blocks go deeper into history than basic timeframe ones. This means we should wait till 24-28 higher timeframe blocks fit into the same historical range as 24-28 blocks of the basic timeframe. The check should be performed on any candle.

Figure 12. Delay in opening positions to move to a higher timeframe

Figure 12 shows that we needed to wait for 2 minutes for the larger blocks to fit into the time range occupied by lesser blocks. If the series start signal is detected on one of the higher timeframes (we can see several of them) during a delay, the basic timeframe is increased and the delay is repeated. If the algorithm is unable to move on to the higher timeframe after the delay, the maximum trend scale has been found and it is time to open a position.

The method works, but it is far from perfect. It was implemented in the early algorithm version whose tests I am going to show. Therefore, I have described its work. The improved delay algorithm described in (b) has been developed during modification.

b) Delay based on the instrument statistical parameters

The method objective is similar to the one pursued in (a). The higher timeframe blocks should cover the same trend section as the basic timeframe ones.

In this method, I will use statistical parameters of the trading instrument to define the delay completion moment. During the delay, it is important for the algorithm to define that the trend is over, or move on to a higher timeframe, or open a position. Therefore, the best solution is to use the higher timeframe blocks to calculate the delay time. Since the main statistical characteristics of a trading instrument have already been taken into account in the %open threshold percentage, I will use it to define the delay duration.

First, define the number of blocks the price passes vertically when receiving the series start signal (Vb). Then use the basic and the next timeframe block sizes to define the number of higher timeframe blocks that should pass vertically to form all Vb blocks of the higher timeframe (Nd). After that, knowing that the price usually does not move strictly vertically and knowing the nature of the movement, we need to calculate the number of delay blocks of the higher timeframe (Nbd).

;

• Vb — number of predominant blocks for the series start;
• mnb  — minimum number of blocks from the analysis range. If the range is 24-28, then it is 24 blocks;
• Nd  — delay number;
• Bsd  — higher timeframe block size;
• BSB  — basic timeframe block size;
• kfd  — multiplication factor for adjusting the number of delay blocks;
• addkfd  — addition factor for adjusting the number of delay blocks.

Example: let mbn=24; %open=75; BSB=0.00064; Bsd= 0.0007. Then Vb=18. This means 18 blocks out of 24 should be of the same direction. Calculate the number of points the price moves within 18 blocks on the basic timeframe. 18*BSB = 0.01152. Calculate how much the price should pass within 18 blocks of the higher timeframe. 18*Bsd = 0.0126. Define how much points are missing to form all higher timeframe blocks. 0.0126-0.01152=0.00108. Divide the obtained value by the higher timeframe block size. Nd=0.00108/0.0007=1.54. It turns out 1.54 blocks are missing to move on to the higher timeframe.

The obtained value is valid if the price moves strictly vertically, which is not the case. Out of 24 blocks, only 18 ones are in one direction and 6 are in another. Therefore, 1.5 blocks should be recalculated into the right number of blocks for the trading instrument. This is how we obtain Nbd = 3. So, in reality, given the characteristics of the trend movement of this trading instrument, we need to wait for the formation of three higher timeframe blocks.

However, simply waiting for the necessary number of delay blocks (3 blocks in the example) to pass is not the most efficient solution. It makes sense to wait only if the price moves in the direction of the detected trend and the transition to a higher timeframe is possible. We need to multiply the minimum number of Nd blocks by the Bsd block size and single out the necessary number of points from the basic timeframe block closure price towards the trend. This is to be the reference point the price should reach to enable moving on to the higher timeframe. Now, after closing each new higher timeframe block, we need to check whether the remaining blocks are enough for the price to reach the reference point. 

For example: Nbd = 3 blocks, the trend is bearish. The reference point is located 1.54 blocks below the price of the basic timeframe block closure. The higher timeframe falling block was formed followed by the growing block. One delay block remains. There is no point in waiting further. If yet another delay block is formed, it will not be able to cross the reference point. There is no point in continuing the delay. The transition to a higher timeframe will not take place, we can open a position. 

All this is shown in animation 2.

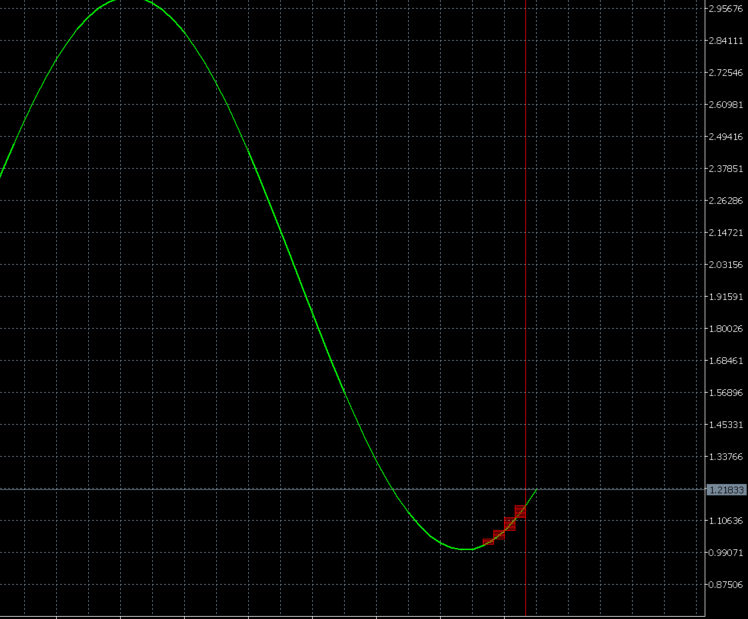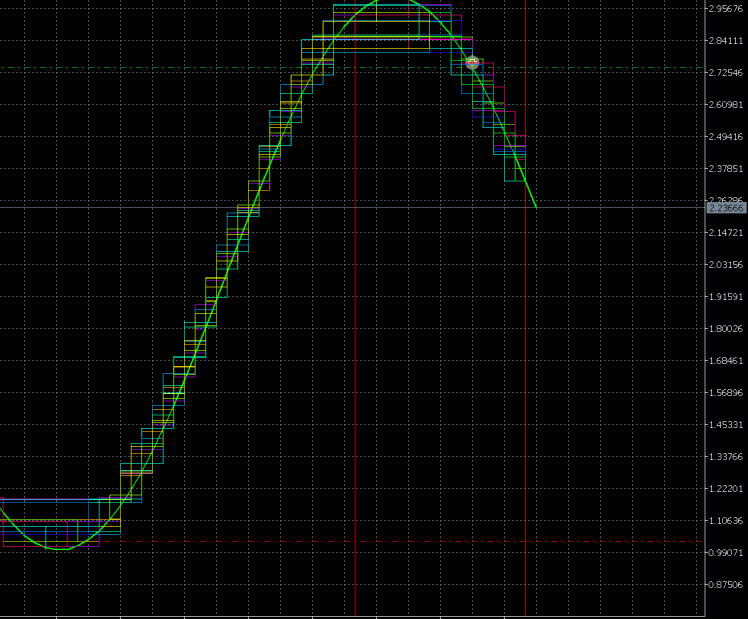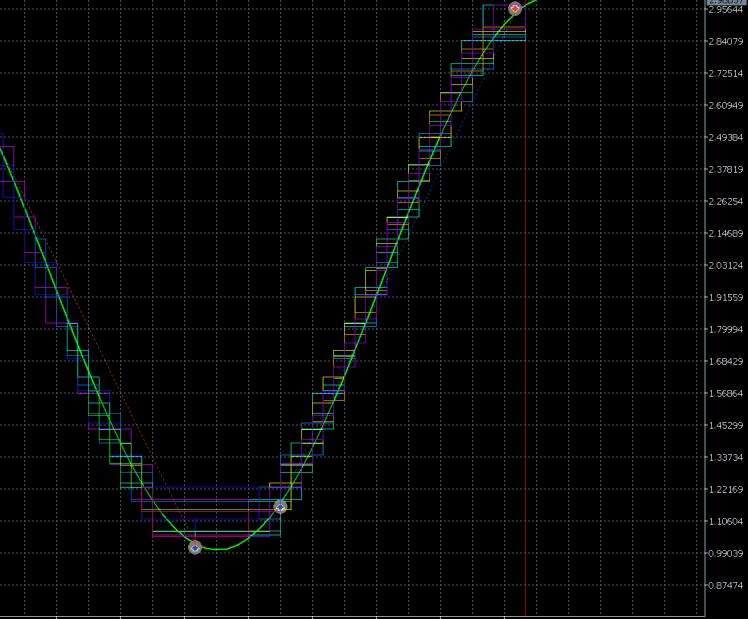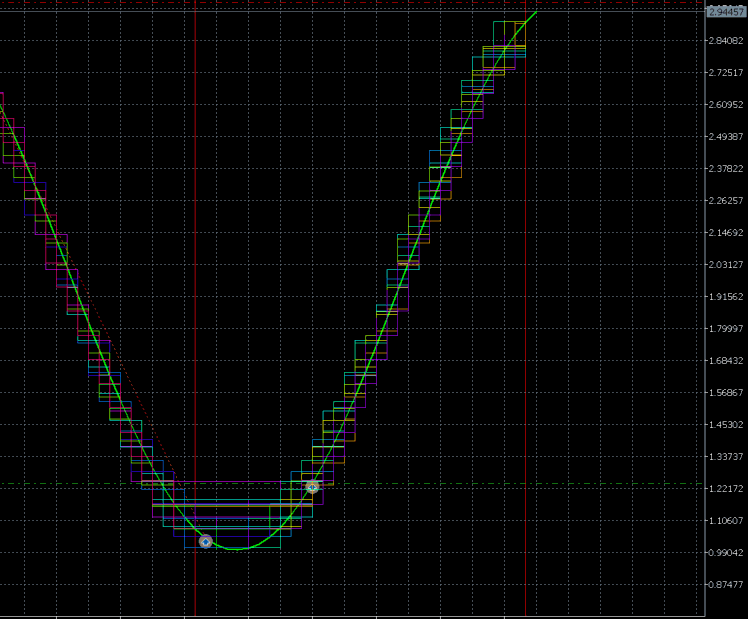
Animation 2

I took a sinewave as an example. The current version is unable to define the statistical characteristics of a trading instrument. So I set the opening and closing percentages manually. This ability will be implemented in the coming versions. The algorithm is to define the trading instrument on its own. It defines the block size and position opening moment.

We can see that the test starts from small blocks. Next, the algorithm increases the size of blocks, while tracking the trend. A position is opened after defining the maximum trend size. The rollback from the trend is calculated afterwards. For a sinewave, the rollback is 100%, therefore the closing point is calculated and take profit is set. I selected the sinewave for visualization and simplifying the understanding of the operation process. The algorithm uses almost the entire amplitude of the sinewave to make a profit, except for a small section of the second block at the beginning of a new trend section.

3. Tracking the series

After opening the first position in the series, the algorithm continues looking for the opportunity to move on to the higher timeframe in order to adjust its work and move on to higher timeframes in case of the trend continuation. Naturally, there will be cases when some positions are opened on a lesser timeframe, while some are opened on a higher one. The rollback size is always calculated from the largest trend the robot finds.

The resulting algorithm ignores two extreme market conditions. If the market is in flat and there is no trend on any scale (which is not typical of the trading instrument), the robot never starts the series. But if the market is in a stable trend, like during sharp market rises or falls, the algorithm is not able to open a position since it contantly increases the timeframe till the trend is over. In this case, the criteria for the trend completion is adjusted in proportion to the scale of the trend itself and the change in the statistical characteristics of the trading instrument.

Conclusion

The main objective is develop the algorithm able to handle any data fed to it. If the input data does not fit its robustness criteria, it will not trade. In other words, the task is not to develop a profitable algorithm for a specific market and try to predict the price direction. Insetad, the task is to make the algorithm profitable under certain conditions and the price series statistical characteristics. It should only trade when these conditions are met. If we know the conditions, at which the algorithm trades with profit, there is no need to trade when these conditions are not met. After creating such an algorithm, it should be equipped with knowledge about the nuances of the market price formation to improve the algorithm efficiency.

The described functionality is still not enough for a stable automatic operation, but a basic theoretical model and a basis for the algorithm operation have already been developed. The amount of completed work is considerable. It is difficult to fir everything into one article. Therefore, I will describe the rest of the functions and tests in the coming articles. 

The parameters of the developed functions have been moved to the settings so that they can be adjusted. The reasons for setting a certain value in the algorithm operation settings have a very specific explanation or even equations used to calculate them. There will be many settings in the final algorithm. They are needed to configure the algorithm itself, since it is to be quite complex, and its individual modules should effectively interact with each other. The settings in this algorithm are not intended to adjust the performance parameters to the history. They are meant for optimizing the operation and interaction of the modules.

The codes of the indicators that build blocks in the chart and indicator windows are attached to the article. These are the same indicators differing in visualization. The requirements specification for these indicators and the full requirements specification for the previous algorithm version are attached below.

Previous articles on this topic

Developing a self-adapting algorithm (Part I): Finding a basic pattern
Developing a self-adapting algorithm (Part II): Improving efficiency