
Matrix Utils, Extending the Matrices and Vector Standard Library Functionality
“You'll never reach perfection because there's always room for improvement.
Yet get along the way to perfection, you'll learn to get better.”
Introduction
In python a Utils class is a general purposed utility class with functions and lines of code which we can reuse without creating an instance of a class.
The Standard library for matrices provides us with some very important features and methods that we can use to Initialize, transform, manipulate matrices, and much more but like any other libraries ever built it can be extended to perform extra stuff that might be necessary/needed in some of the applications.
The functions and methods introduced below are in no particular order;
Contents:
- Reading Matrix from a CSV file
- Read Encoded values from CSV file
- Writing Matrix to a CSV file
- Transforming Matrix to vector
- Transforming vector to Matrix
- Transforming Array to vector
- Vector to Array
- Removing a single column from the matrix
- Removing multiple columns from a matrix
- Removing a row from the matrix
- Remove a single value from a vector
- Split matrix into train and testing matrices
- X and Y matrix split
- Create a design matrix
- One Hot encoding Matrix
- Obtaining the classes from a vector
- Creating a vector of Random values
- Appending one vector to the other
- Copying one vector to the other
Reading Matrix from a CSV file
This is a very important function as it allows us to load databases from a CSV file and store them in a matrix effortlessly. No need to emphasize the importance of this function because in the course of coding for trading systems we often need to load CSV files containing trading signals or trading history that we want our program to be able to access.
The first step in the function(You guessed it right?) is reading a CSV file, The first row of the CSV file is assumed to have strings only so even if there are values in the first row they will not be included in the matrix since the matrix can't contain string values, the values in the first row will be stored in the csv_header Array instead.while(!FileIsEnding(handle)) { string data = FileReadString(handle); //--- if(rows ==0) { ArrayResize(csv_header,column+1); csv_header[column] = data; } if(rows>0) //Avoid the first column which contains the column's header mat_[rows-1,column] = (double(data)); column++; //---
This array helps to keep track of the column names from the CSV file we just read.
Full code:
matrix CMatrixutils::ReadCsv(string file_name,string delimiter=",") { matrix mat_ = {}; int rows_total=0; int handle = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,delimiter); ResetLastError(); if(handle == INVALID_HANDLE) { printf("Invalid %s handle Error %d ",file_name,GetLastError()); Print(GetLastError()==0?" TIP | File Might be in use Somewhere else or in another Directory":""); } else { int column = 0, rows=0; while(!FileIsEnding(handle)) { string data = FileReadString(handle); //--- if(rows ==0) { ArrayResize(csv_header,column+1); csv_header[column] = data; } if(rows>0) //Avoid the first column which contains the column's header mat_[rows-1,column] = (double(data)); column++; //--- if(FileIsLineEnding(handle)) { rows++; mat_.Resize(rows,column); column = 0; } } rows_total = rows; FileClose(handle); } mat_.Resize(rows_total-1,mat_.Cols()); return(mat_); }
Usage:
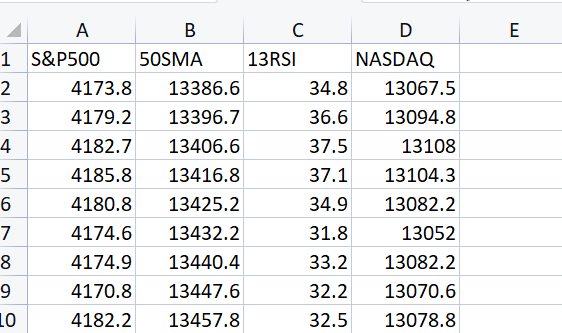
Here is the CSV file we want to load into a matrixLoading the CSV file to a matrix;
Print("---> Reading a CSV file to Matrix\n"); Matrix = matrix_utils.ReadCsv("NASDAQ_DATA.csv"); ArrayPrint(matrix_utils.csv_header); Print(Matrix);Output:
CS 0 06:48:21.228 matrix test (EURUSD,H1) "S&P500" "50SMA" "13RSI" "NASDAQ" CS 0 06:48:21.228 matrix test (EURUSD,H1) [[4173.8,13386.6,34.8,13067.5] CS 0 06:48:21.228 matrix test (EURUSD,H1) [4179.2,13396.7,36.6,13094.8] CS 0 06:48:21.228 matrix test (EURUSD,H1) [4182.7,13406.6,37.5,13108] CS 0 06:48:21.228 matrix test (EURUSD,H1) [4185.8,13416.8,37.1,13104.3] CS 0 06:48:21.228 matrix test (EURUSD,H1) [4180.8,13425.2,34.9,13082.2] CS 0 06:48:21.228 matrix test (EURUSD,H1) [4174.6,13432.2,31.8,13052] CS 0 06:48:21.228 matrix test (EURUSD,H1) [4174.9,13440.4,33.2,13082.2] CS 0 06:48:21.228 matrix test (EURUSD,H1) [4170.8,13447.6,32.2,13070.6] CS 0 06:48:21.228 matrix test (EURUSD,H1) [4182.2,13457.8,32.5,13078.8]
The reason I decided to build this function is that I couldn't find a way to read a CSV file from the Standard Library, I expected this to be the way forward to load the values from a file to a CSV Matrix.FromFile()
but was disappointed, If someone knows the way to do it from the docs, let me know in the discussion section of this Article.
Read Encoded Values from CSV File
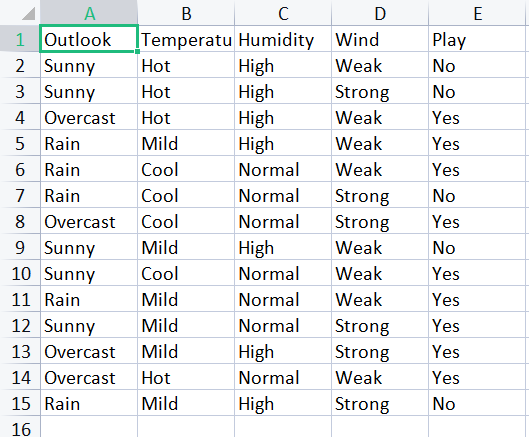
Often times you may need to read a CSV file that contains string values, these kinds of CSV files that contain strings are often encountered when one is looking to make classification algorithms, take a look at the most popular weather dataset;
To be able to encode this csv file we are going to read all of its data into a single array of string values, because matrices can't carry string values, Inside the ReadCsvEncode() function, The very first thing we have to do is to read know the columns present in given CSV file, Secondly we loop those columns where as in each iteration a csv is opened and a a single column is read entirely and the values of that column gets stored into the array of all values named toArr[].
//--- Obtaining the columns matrix Matrix={}; //--- Loading the entire Matrix to an Array int csv_columns=0, rows_total=0; int handle = CSVOpen(file_name,delimiter); if (handle != INVALID_HANDLE) { while (!FileIsEnding(handle)) { string data = FileReadString(handle); csv_columns++; //--- if (FileIsLineEnding(handle)) break; } } FileClose(handle); ArrayResize(csv_header,csv_columns); //--- string toArr[]; int counter=0; for (int i=0; i<csv_columns; i++) { if ((handle = CSVOpen(file_name,delimiter)) != INVALID_HANDLE) { int column = 0, rows=0; while (!FileIsEnding(handle)) { string data = FileReadString(handle); column++; //--- if (column==i+1) { if (rows>=1) //Avoid the first column which contains the column's header { counter++; ArrayResize(toArr,counter); //array size for all the columns toArr[counter-1]=data; } else csv_header[column-1] = data; } //--- if (FileIsLineEnding(handle)) { rows++; column = 0; } } rows_total += rows-1; } FileClose(handle); } //---
Once that is done the toArr[] looks like this when printed;
CS 0 06:00:15.952 matrix test (US500,D1) [ 0] "Sunny" "Sunny" "Overcast" "Rain" "Rain" "Rain" "Overcast" "Sunny" "Sunny" "Rain" "Sunny" "Overcast" CS 0 06:00:15.952 matrix test (US500,D1) [12] "Overcast" "Rain" "Hot" "Hot" "Hot" "Mild" "Cool" "Cool" "Cool" "Mild" "Cool" "Mild" CS 0 06:00:15.952 matrix test (US500,D1) [24] "Mild" "Mild" "Hot" "Mild" "High" "High" "High" "High" "Normal" "Normal" "Normal" "High" CS 0 06:00:15.952 matrix test (US500,D1) [36] "Normal" "Normal" "Normal" "High" "Normal" "High" "Weak" "Strong" "Weak" "Weak" "Weak" "Strong" CS 0 06:00:15.952 matrix test (US500,D1) [48] "Strong" "Weak" "Weak" "Weak" "Strong" "Strong" "Weak" "Strong" "No" "No" "Yes" "Yes" CS 0 06:00:15.952 matrix test (US500,D1) [60] "Yes" "No" "Yes" "No" "Yes" "Yes" "Yes" "Yes" "Yes" "No"
If you pay attention to this Array you will notice that the values from a CSV file are in the order that was obtained from the CSV file, from index 0 to 13 there is the first column, from index 14 to 27 there lies the second column, etc. and so on. Now from there it's easy to extract the values and encode them to finally store them to a matrix.
ulong mat_cols = 0,mat_rows = 0; if (ArraySize(toArr) % csv_columns !=0) printf("This CSV file named %s has unequal number of columns = %d and rows %d Its size = %d",file_name,csv_columns,ArraySize(toArr) / csv_columns,ArraySize(toArr)); else //preparing the number of columns and rows that out matrix needs { mat_cols = (ulong)csv_columns; mat_rows = (ulong)ArraySize(toArr)/mat_cols; } //--- Encoding the CSV Matrix.Resize(mat_rows,mat_cols); //--- string Arr[]; //temporary array to carry the values of a single column int start =0; vector v = {}; for (ulong j=0; j<mat_cols; j++) { ArrayCopy(Arr,toArr,0,start,(int)mat_rows); v = LabelEncoder(Arr); Matrix.Col(v, j); start += (int)mat_rows; } return (Matrix);
The LabelEncoder funtion() does just like it's name goes, it puts the same label to features that are similar in the column array, here is what on it's inside.
vector CMatrixutils::LabelEncoder(string &Arr[]) { string classes[]; vector Encoded((ulong)ArraySize(Arr)); Classes(Arr,classes); for (ulong A=0; A<classes.Size(); A++) for (ulong i=0; i<Encoded.Size(); i++) { if (classes[A] == Arr[i]) Encoded[i] = (int)A; } return Encoded; }
This function is an easy one, It loops the classes given against the entire array so that it can find similar features and put labels to them, the majority of the work is done inside the function Classes() highlighted in black.
void CMatrixutils::Classes(const string &Array[],string &classes_arr[]) { string temp_arr[]; ArrayResize(classes_arr,1); ArrayCopy(temp_arr,Array); classes_arr[0] = Array[0]; for(int i=0, count =1; i<ArraySize(Array); i++) //counting the different neighbors { for(int j=0; j<ArraySize(Array); j++) { if(Array[i] == temp_arr[j] && temp_arr[j] != "nan") { bool count_ready = false; for(int n=0; n<ArraySize(classes_arr); n++) if(Array[i] == classes_arr[n]) count_ready = true; if(!count_ready) { count++; ArrayResize(classes_arr,count); classes_arr[count-1] = Array[i]; temp_arr[j] = "nan"; //modify so that it can no more be counted } else break; //Print("t vectors vector ",v); } else continue; } } }
This function obtains the classes present in the given array and passes them to the referenced array classes_arr[]. This function has a variant for finding classes in a vector instead. More details about this function are found here.
vector CMatrixutils::Classes(vector &v)
Below is how to use this function;
Matrix = matrix_utils.ReadCsvEncode("weather dataset.csv"); ArrayPrint(matrix_utils.csv_header); Print(Matrix);
Output:
CS 0 06:35:10.798 matrix test (US500,D1) "Outlook" "Temperature" "Humidity" "Wind" "Play" CS 0 06:35:10.798 matrix test (US500,D1) [[0,0,0,0,0] CS 0 06:35:10.798 matrix test (US500,D1) [0,0,0,1,0] CS 0 06:35:10.798 matrix test (US500,D1) [1,0,0,0,1] CS 0 06:35:10.798 matrix test (US500,D1) [2,1,0,0,1] CS 0 06:35:10.798 matrix test (US500,D1) [2,2,1,0,1] CS 0 06:35:10.798 matrix test (US500,D1) [2,2,1,1,0] CS 0 06:35:10.798 matrix test (US500,D1) [1,2,1,1,1] CS 0 06:35:10.798 matrix test (US500,D1) [0,1,0,0,0] CS 0 06:35:10.798 matrix test (US500,D1) [0,2,1,0,1] CS 0 06:35:10.798 matrix test (US500,D1) [2,1,1,0,1] CS 0 06:35:10.798 matrix test (US500,D1) [0,1,1,1,1] CS 0 06:35:10.798 matrix test (US500,D1) [1,1,0,1,1] CS 0 06:35:10.798 matrix test (US500,D1) [1,0,1,0,1] CS 0 06:35:10.798 matrix test (US500,D1) [2,1,0,1,0]]
Writing a Matrix to a CSV file
This is another important function that can help write the Matrix to a CSV file without the need to hardcode things every time a new column is added to the matrix. To be able to write in a flexible way to a CSV file has been a struggle for a lot of folks in the forum > Post1, Post2, Post3. Here is how to do it using matrices;row = Matrix.Row(i); for(ulong j=0, cols =1; j<row.Size(); j++, cols++) { concstring += (string)NormalizeDouble(row[j],digits) + (cols == Matrix.Cols() ? "" : ","); }
This in the end will look just like a CSV file written with different columns manually. Since the matrix can't carry string values, I had to use an array of strings to let us write the header to this csv file.
Let's attempt to write this Matrix that was taken from a CSV file back to a new CSV file.
string csv_name = "matrix CSV.csv"; Print("\n---> Writing a Matrix to a CSV File > ",csv_name); string header[4] = {"S&P500","SMA","RSI","NASDAQ"}; matrix_utils.WriteCsv(csv_name,Matrix,header);
Below is the newly written CSV file;
Cool.
Transforming Matrix To Vector
Someone may ask themselves why transform a matrix to a vector? This comes in handy in many areas as you might not need a matrix all the time so what this function does is convert the Matrix to a vector, for example when you read the matrix from a CSV file when wanting to make a linear regression model the independent variable will be an nx1 or 1xn matrix, When trying to use the loss function such as the MSE you can't use the matrix to evaluate the model instead you will use the vector of this independent variable and the vector of the predicted values by the model.
Below is the code for it;vector CMatrixutils::MatrixToVector(const matrix &mat) { vector v = {}; if (!v.Assign(mat)) Print("Failed to turn the matrix to a vector"); return(v); }
Usage:
matrix mat = { {1,2,3}, {4,5,6}, {7,8,9} }; Print("\nMatrix to play with\n",mat,"\n"); //--- Print("---> Matrix to Vector"); vector vec = matrix_utils.MatrixToVector(mat); Print(vec);
Output:
2022.12.20 05:39:00.286 matrix test (US500,D1) ---> Matrix to Vector 2022.12.20 05:39:00.286 matrix test (US500,D1) [1,2,3,4,5,6,7,8,9]
Transforming vector to Matrix
This is the exact opposite of the function we just saw above, yet this is more important than you can imagine. Most of the time in machine learning models you need to perform multiplication operations between different matrices, Since the independent variables, are often stored in a vector you might need to transform them to an nx1 matrix to do the operations, these two opposite functions are important as they make our code for fewer variables by tweaking the existing ones.matrix CMatrixutils::VectorToMatrix(const vector &v) { matrix mat = {}; if (!mat.Assign(v)) Print("Failed to turn the vector to a 1xn matrix"); return(mat); }
Usage:
Print("\n---> Vector ",vec," to Matrix"); mat = matrix_utils.VectorToMatrix(vec); Print(mat);
Output:
2022.12.20 05:50:05.680 matrix test (US500,D1) ---> Vector [1,2,3,4,5,6,7,8,9] to Matrix 2022.12.20 05:50:05.680 matrix test (US500,D1) [[1,2,3,4,5,6,7,8,9]]
Transforming Array to vector
Who needs a lot of arrays inside machine learning programs? Arrays are very useful but they are very sensitive to the size. Adjusting them very often and playing with them might help the terminal to throw your programs out of chart with those arrays out of range sort of errors, even though vectors do the same thing but they are a bit more flexible than arrays, not to mention they are object-oriented you can return a vector from a function but not an array unless you want those code compilation errors and warnings.
vector CMatrixutils::ArrayToVector(const double &Arr[]) { vector v((ulong)ArraySize(Arr)); for(ulong i=0; i<v.Size(); i++) v[i] = Arr[i]; return (v); }
Usage:
Print("---> Array to vector"); double Arr[3] = {1,2,3}; vec = matrix_utils.ArrayToVector(Arr); Print(vec);
Output:
CS 0 05:51:58.853 matrix test (US500,D1) ---> Array to vector CS 0 05:51:58.853 matrix test (US500,D1) [1,2,3]
Vector to Array
We still can't forsake arrays at all as there might be times when the vector needs to be converted into an array that needs to be plugged in a function argument that takes arrays, or we might need to do some Array Sorting, Set as series, slicing, and, so much more manipulations that we couldn't do with vectors. bool CMatrixutils::VectorToArray(const vector &v,double &arr[]) { ArrayResize(arr,(int)v.Size()); if(ArraySize(arr) == 0) return(false); for(ulong i=0; i<v.Size(); i++) arr[i] = v[i]; return(true); }
Usage:
Print("---> Vector to Array"); double new_array[]; matrix_utils.VectorToArray(vec,new_array); ArrayPrint(new_array);
Output:
CS 0 06:19:14.647 matrix test (US500,D1) ---> Vector to Array CS 0 06:19:14.647 matrix test (US500,D1) 1.0 2.0 3.0
Matrix Remove Column
Just because we have loaded the CSV column to a matrix, it doesn't mean we need all the columns from it, In creating supervised machine learning model we need to drop some irrelevant columns and not to mention we may need to drop the response variable from the matrix full of independent variables.
Here is the code to do it:
void CMatrixutils::MatrixRemoveCol(matrix &mat, ulong col) { matrix new_matrix(mat.Rows(),mat.Cols()-1); //Remove the one Column for (ulong i=0, new_col=0; i<mat.Cols(); i++) { if (i == col) continue; else { new_matrix.Col(mat.Col(i),new_col); new_col++; } } mat.Copy(new_matrix); }
There is nothing magical inside the function, we create the new matrix sized with the same number of rows as the original matrix but with one column less.
matrix new_matrix(mat.Rows(),mat.Cols()-1); //Remove the one columnIn the new matrix, we ignore the column that is no longer needed from our new matrix, everything else will be stored, and that's it.
At the end of the function, we copy this new matrix to an old one.
mat.Copy(new_matrix);
Let's drop the column at the index of 1(Second column) from the matrix we just read from the CSV file
Print("Col 1 ","Removed from Matrix"); matrix_utils.MatrixRemoveCol(Matrix,1); Print("New Matrix\n",Matrix);
Output:
CS 0 07:23:59.612 matrix test (EURUSD,H1) Column of index 1 removed new Matrix CS 0 07:23:59.612 matrix test (EURUSD,H1) [[4173.8,34.8,13067.5] CS 0 07:23:59.612 matrix test (EURUSD,H1) [4179.2,36.6,13094.8] CS 0 07:23:59.612 matrix test (EURUSD,H1) [4182.7,37.5,13108] CS 0 07:23:59.612 matrix test (EURUSD,H1) [4185.8,37.1,13104.3] CS 0 07:23:59.612 matrix test (EURUSD,H1) [4180.8,34.9,13082.2] CS 0 07:23:59.612 matrix test (EURUSD,H1) [4174.6,31.8,13052] CS 0 07:23:59.612 matrix test (EURUSD,H1) [4174.9,33.2,13082.2] CS 0 07:23:59.612 matrix test (EURUSD,H1) [4170.8,32.2,13070.6] CS 0 07:23:59.612 matrix test (EURUSD,H1) [4182.2,32.5,13078.8]
Removing multiple columns from the Matrix
That was the case when trying to remove a single column but there are larger matrices that contain a lot of columns that we want to drop all at once, to achieve this we need to perform something tricky to avoid removing the needed columns and to also avoid trying to access values that are out of range, basically to safely remove the columns.
The new matrix columns' numbers/size needs to be equal to the total number of columns subtracted from the columns that we want to remove, The number of rows for each column is kept constant(same as the old matrix).
The first thing that we have to do is to loop through all the selected columns that we want to remove versus all the available columns in the old matrix, if the columns are supposed to be removed we will set all the values in that columns to zero. This is a wise operation to perform to end up with a clean operation.vector zeros(mat.Rows()); zeros.Fill(0); for(ulong i=0; i<size; i++) for(ulong j=0; j<mat.Cols(); j++) { if(cols[i] == j) mat.Col(zeros,j); }The last thing we have to do is to loop through the matrix again twice and check for all the columns filled with zero values and to remove those columns one by one.
vector column_vector; for(ulong A=0; A<mat.Cols(); A++) for(ulong i=0; i<mat.Cols(); i++) { column_vector = mat.Col(i); if(column_vector.Sum()==0) MatrixRemoveCol(mat,i); }
Notice the twice loops? they are very important because this matrix gets adjusted its size after each column is removed so it is very important to loop back again to check if we skipped any column.
Below is the full code for the function;void CMatrixutils::MatrixRemoveMultCols(matrix &mat,int &cols[]) { ulong size = (int)ArraySize(cols); if(size > mat.Cols()) { Print(__FUNCTION__," Columns to remove can't be more than the available columns"); return; } vector zeros(mat.Rows()); zeros.Fill(0); for(ulong i=0; i<size; i++) for(ulong j=0; j<mat.Cols(); j++) { if(cols[i] == j) mat.Col(zeros,j); } //--- vector column_vector; for(ulong A=0; A<mat.Cols(); A++) for(ulong i=0; i<mat.Cols(); i++) { column_vector = mat.Col(i); if(column_vector.Sum()==0) MatrixRemoveCol(mat,i); } }
Let's see this function in action, Let's try to remove the column at index 0 and at index 2;
Print("\nRemoving multiple columns"); int cols[2] = {0,2}; matrix_utils.MatrixRemoveMultCols(Matrix,cols); Print("Columns at 0,2 index removed New Matrix\n",Matrix);
Output:
CS 0 07:32:10.923 matrix test (EURUSD,H1) Columns at 0,2 index removed New Matrix CS 0 07:32:10.923 matrix test (EURUSD,H1) [[13386.6,13067.5] CS 0 07:32:10.923 matrix test (EURUSD,H1) [13396.7,13094.8] CS 0 07:32:10.923 matrix test (EURUSD,H1) [13406.6,13108] CS 0 07:32:10.923 matrix test (EURUSD,H1) [13416.8,13104.3] CS 0 07:32:10.923 matrix test (EURUSD,H1) [13425.2,13082.2] CS 0 07:32:10.923 matrix test (EURUSD,H1) [13432.2,13052] CS 0 07:32:10.923 matrix test (EURUSD,H1) [13440.4,13082.2] CS 0 07:32:10.923 matrix test (EURUSD,H1) [13447.6,13070.6] CS 0 07:32:10.923 matrix test (EURUSD,H1) [13457.8,13078.8]
Removing a row from the matrix
There might also be a need to remove a single row from the dataset because it is irrelevant or because one wants to reduce the number of columns just to see what works. This is not as important as removing the column from the matrix so we only have this function to remove a single row, we won't see the one for multiple rows, you can code for yourself if you want it.
The same idea was applied when attempting to remove the row from the matrix, We simply ignore the unwanted row in the new matrix that we are making.
void CMatrixutils::MatrixRemoveRow(matrix &mat, ulong row) { matrix new_matrix(mat.Rows()-1,mat.Cols()); //Remove the one Row for(ulong i=0, new_rows=0; i<mat.Rows(); i++) { if(i == row) continue; else { new_matrix.Row(mat.Row(i),new_rows); new_rows++; } } mat.Copy(new_matrix); }
Usage:
Print("Removing row 1 from matrix"); matrix_utils.MatrixRemoveRow(Matrix,1); printf("Row %d Removed New Matrix[%d][%d]",0,Matrix.Rows(),Matrix.Cols()); Print(Matrix);
Output:
CS 0 06:36:36.773 matrix test (US500,D1) Removing row 1 from matrix CS 0 06:36:36.773 matrix test (US500,D1) Row 1 Removed New Matrix[743][4] CS 0 06:36:36.773 matrix test (US500,D1) [[4173.8,13386.6,34.8,13067.5] CS 0 06:36:36.773 matrix test (US500,D1) [4182.7,13406.6,37.5,13108] CS 0 06:36:36.773 matrix test (US500,D1) [4185.8,13416.8,37.1,13104.3] CS 0 06:36:36.773 matrix test (US500,D1) [4180.8,13425.2,34.9,13082.2] CS 0 06:36:36.773 matrix test (US500,D1) [4174.6,13432.2,31.8,13052] CS 0 06:36:36.773 matrix test (US500,D1) [4174.9,13440.4,33.2,13082.2] CS 0 06:36:36.773 matrix test (US500,D1) [4170.8,13447.6,32.2,13070.6]
Vector remove index
This is a short one, This function helps remove a single item at a specific index from a vector. It is able to achieve such a result by just ignoring the number located at the given index from the vector, the rest of values gets stored into the new vector which is finally copied to the primary/referenced vector from the function argument.
void CMatrixutils::VectorRemoveIndex(vector &v, ulong index) { vector new_v(v.Size()-1); for(ulong i=0, count = 0; i<v.Size(); i++) if(i != index) { new_v[count] = v[i]; count++; } v.Copy(new_v); }
Below is how to use it:
vector v= {0,1,2,3,4}; Print("Vector remove index 3"); matrix_utils.VectorRemoveIndex(v,3); Print(v);
Output:
2022.12.20 06:40:30.928 matrix test (US500,D1) Vector remove index 3 2022.12.20 06:40:30.928 matrix test (US500,D1) [0,1,2,4]
Split matrix into train and testing matrices
I can't stress how important this function is when making a supervised machine learning model. We often need the dataset split into training and testing datasets so that we can train the dataset on some dataset and test it on the other dataset that the model has never seen before.
By default this function splits 70% of the dataset into the training sample and the rest 30% into the testing sample, There is no random state. Data is selected in the chronological order of the matrix, the first 70% of the data gets stored in the training matrix while the rest 30% gets stored into the testing matrix.
Print("---> Train / Test Split"); matrix TrainMatrix, TestMatrix; matrix_utils.TrainTestSplitMatrices(Matrix,TrainMatrix,TestMatrix); Print("\nTrain Matrix(",TrainMatrix.Rows(),",",TrainMatrix.Cols(),")\n",TrainMatrix); Print("\nTestMatrix(",TestMatrix.Rows(),",",TestMatrix.Cols(),")\n",TestMatrix);
Output:
CS 0 07:38:46.011 matrix test (EURUSD,H1) Train Matrix(521,4) CS 0 07:38:46.011 matrix test (EURUSD,H1) [[4173.8,13386.6,34.8,13067.5] CS 0 07:38:46.011 matrix test (EURUSD,H1) [4179.2,13396.7,36.6,13094.8] CS 0 07:38:46.011 matrix test (EURUSD,H1) [4182.7,13406.6,37.5,13108] CS 0 07:38:46.011 matrix test (EURUSD,H1) [4185.8,13416.8,37.1,13104.3] CS 0 07:38:46.011 matrix test (EURUSD,H1) [4180.8,13425.2,34.9,13082.2] .... .... CS 0 07:38:46.012 matrix test (EURUSD,H1) TestMatrix(223,4) CS 0 07:38:46.012 matrix test (EURUSD,H1) [[4578.1,14797.9,65.90000000000001,15021.1] CS 0 07:38:46.012 matrix test (EURUSD,H1) [4574.9,14789.2,63.9,15006.2] CS 0 07:38:46.012 matrix test (EURUSD,H1) [4573.6,14781.4,63,14999] CS 0 07:38:46.012 matrix test (EURUSD,H1) [4571.4,14773.9,62.1,14992.6] CS 0 07:38:46.012 matrix test (EURUSD,H1) [4572.8,14766.3,65.2,15007.1]
X and Y split matrices
When attempting to make supervised learning models after we just loaded the dataset into a matrix, the next thing we need is to extract the target variables from the matrix and store them independently the same as we want the independent variables to be stored in their matrix of values, This is the function to do that:if(y_index == -1) value = matrix_.Cols()-1; //Last column in the matrix
Usage:
Print("---> X and Y split matrices"); matrix x; vector y; matrix_utils.XandYSplitMatrices(Matrix,x,y); Print("independent vars\n",x); Print("Target variables\n",y);
Output:
CS 0 05:05:03.467 matrix test (US500,D1) ---> X and Y split matrices CS 0 05:05:03.467 matrix test (US500,D1) independent vars CS 0 05:05:03.468 matrix test (US500,D1) [[4173.8,13386.6,34.8] CS 0 05:05:03.468 matrix test (US500,D1) [4179.2,13396.7,36.6] CS 0 05:05:03.468 matrix test (US500,D1) [4182.7,13406.6,37.5] CS 0 05:05:03.468 matrix test (US500,D1) [4185.8,13416.8,37.1] CS 0 05:05:03.468 matrix test (US500,D1) [4180.8,13425.2,34.9] CS 0 05:05:03.468 matrix test (US500,D1) [4174.6,13432.2,31.8] CS 0 05:05:03.468 matrix test (US500,D1) [4174.9,13440.4,33.2] CS 0 05:05:03.468 matrix test (US500,D1) [4170.8,13447.6,32.2] CS 0 05:05:03.468 matrix test (US500,D1) [4182.2,13457.8,32.5] .... .... 2022.12.20 05:05:03.470 matrix test (US500,D1) Target variables 2022.12.20 05:05:03.470 matrix test (US500,D1) [13067.5,13094.8,13108,13104.3,13082.2,13052,13082.2,13070.6,13078.8,...]
Inside the X and Y split function, the selected column as y variables gets stored in the Y matrix while the rest of the remaining columns gets stored in the X Matrix.
void CMatrixutils::XandYSplitMatrices(const matrix &matrix_,matrix &xmatrix,vector &y_vector,int y_index=-1) { ulong value = y_index; if(y_index == -1) value = matrix_.Cols()-1; //Last column in the matrix //--- y_vector = matrix_.Col(value); xmatrix.Copy(matrix_); MatrixRemoveCol(xmatrix, value); //Remove the y column }
Making a Design Matrix
The design matrix is essential to the Least squares algorithm, It is just the x matrix(matrix of independent vatiables) with the first column filled with the values of one. This design matrix helps us obtain the coefficients for the linear regression model. Inside the function DesignMatrix() the vector filled with values of one gets created, it is then inserted to the first column of the matrix, while the rest of the columns are set to follow the order;Full code:
matrix CMatrixutils::DesignMatrix(matrix &x_matrix) { matrix out_matrix(x_matrix.Rows(),x_matrix.Cols()+1); vector ones(x_matrix.Rows()); ones.Fill(1); out_matrix.Col(ones,0); vector new_vector; for(ulong i=1; i<out_matrix.Cols(); i++) { new_vector = x_matrix.Col(i-1); out_matrix.Col(new_vector,i); } return (out_matrix); }
Usage:
Print("---> Design Matrix\n"); matrix design = matrix_utils.DesignMatrix(x); Print(design);
Output:
CS 0 05:28:51.786 matrix test (US500,D1) ---> Design Matrix CS 0 05:28:51.786 matrix test (US500,D1) CS 0 05:28:51.786 matrix test (US500,D1) [[1,4173.8,13386.6,34.8] CS 0 05:28:51.786 matrix test (US500,D1) [1,4179.2,13396.7,36.6] CS 0 05:28:51.786 matrix test (US500,D1) [1,4182.7,13406.6,37.5] CS 0 05:28:51.786 matrix test (US500,D1) [1,4185.8,13416.8,37.1] CS 0 05:28:51.786 matrix test (US500,D1) [1,4180.8,13425.2,34.9] CS 0 05:28:51.786 matrix test (US500,D1) [1,4174.6,13432.2,31.8] CS 0 05:28:51.786 matrix test (US500,D1) [1,4174.9,13440.4,33.2] CS 0 05:28:51.786 matrix test (US500,D1) [1,4170.8,13447.6,32.2] CS 0 05:28:51.786 matrix test (US500,D1) [1,4182.2,13457.8,32.5]
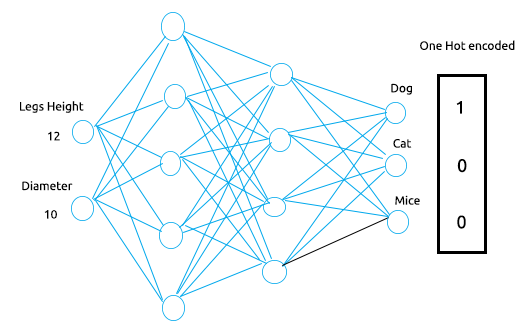
One Hot Encoding Matrix
Let's do someone hot encoding. This is a very important function that you will need when trying to make classification neural networks. This function proves to be of much importance as it makes it clear for the MLP to relate the outputs from the neuron in the last layer to the actual values.
In one hot encoded matrix, the vector for each row consists the zero values except for one value which is for the correct value that we want to hit which will have the value of 1.
To understand this well let's see the below example:
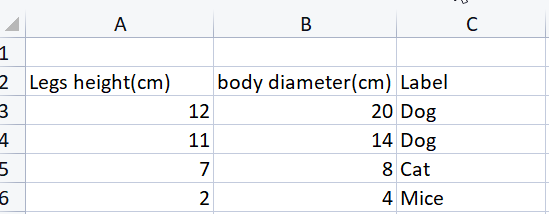
suppose this is the dataset that we want to train the neural network, to be able to classify between the three classes, Dog, Cat, and Mice based on their legs' height and their body diameter.
The Multilayer perceptron will have 2 input nodes/neurons one for the Legs Height and the other for the body diameter on the input layer, meanwhile the output layer will have 3 nodes representing the 3 outcomes Dog, Cat, and mice.
Now say that we feed this MLP with the value of 12 and 20 for height and diameter respectively, we expect the neural network to classify this to be a dog right? what the One hot encoding does is that it put the value of one in the node that has the correct value for the given training dataset in this case at the node for a dog the value of 1 will be put and the rest will carry the values of zero.
Since the rest of the values have zero's we can calculate the cost function by substituting the values of one hot encoded vector to each of the probabilities that the model gave us, this error will then be propagated back to the network in their respective previous nodes of a prior layer.
Ok, now let us see One hot Encoding in action.
This is our matrix in MetaEditor;
matrix dataset = { {12,28, 1}, {11,14, 1}, {7,8, 2}, {2,4, 3} };
This is the same dataset as the one you saw from a CSV except that the target are labelled in integers since we can't have strings in a matrix, by the way when and where can you use strings in calculations?
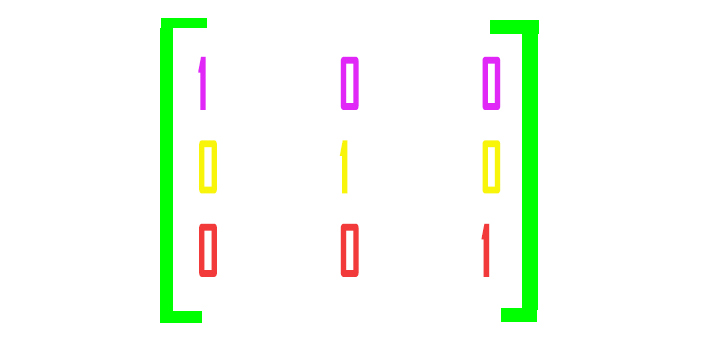
matrix dataset = { {12,28, 1}, {11,14, 1}, {7,8, 2}, {2,4, 3} }; vector y_vector = dataset.Col(2); //obtain the column to encode uint classes = 3; //number of classes in the column Print("One Hot encoded matrix \n",matrix_utils.OneHotEncoding(y_vector,classes));
Below is the output:
CS 0 08:54:04.744 matrix test (EURUSD,H1) One Hot encoded matrix CS 0 08:54:04.744 matrix test (EURUSD,H1) [[1,0,0] CS 0 08:54:04.744 matrix test (EURUSD,H1) [1,0,0] CS 0 08:54:04.744 matrix test (EURUSD,H1) [0,1,0] CS 0 08:54:04.744 matrix test (EURUSD,H1) [0,0,1]]
Obtaining the Classes from a vector
This function returns the vector containing the classes available in the given vector, for example; A vector with [1,2,3] has 3 different classes, A vector of [1,0,1,0] has two different classes. The role of the function is to return the available distinct classes.
vector v = {1,0,0,0,1,0,1,0}; Print("classes ",matrix_utils.Classes(v));
Output:
2022.12.27 06:41:54.758 matrix test (US500,D1) classes [1,0]
Creating a vector of Random values.
There are several times when we need to generate a vector full of random variables, This function can help. The most common use of this function is generating weights and bias vector for NN. You can also use it to make a randomized dataset samples.
vector Random(int min, int max, int size); vector Random(double min, double max, int size);
Usage:
v = matrix_utils.Random(1.0,2.0,10); Print("v ",v);
Output:
2022.12.27 06:50:03.055 matrix test (US500,D1) v [1.717642750328074,1.276955473494675,1.346263008514664,1.32959990234077,1.006469924008911,1.992980742820521,1.788445692312387,1.218909268471328,1.732139042329173,1.512405774101993]
Appending One Vector to Another.
This is something like string concatenation, but we concatenate vectors instead. I've found myself wanting to use this function in many cases. Below is what it's made up of,
vector CMatrixutils::Append(vector &v1, vector &v2) { vector v_out = v1; v_out.Resize(v1.Size()+v2.Size()); for (ulong i=v2.Size(),i2=0; i<v_out.Size(); i++, i2++) v_out[i] = v2[i2]; return (v_out); }
Usage:
vector v1 = {1,2,3}, v2 = {4,5,6}; Print("Vector 1 & 2 ",matrix_utils.Append(v1,v2));
Output:
2022.12.27 06:59:25.252 matrix test (US500,D1) Vector 1 & 2 [1,2,3,4,5,6]
Copying one Vector to Another
Last but not least, let's copy a vector to another vector by manipulating the vector just like Arraycopy, We often times do not need to copy the entire vector to another, we often need a chunk of it, the Copy method provided by the standard library falls flat in situation like this.
bool CMatrixutils::Copy(const vector &src,vector &dst,ulong src_start,ulong total=WHOLE_ARRAY) { if (total == WHOLE_ARRAY) total = src.Size()-src_start; if ( total <= 0 || src.Size() == 0) { printf("Can't copy a vector | Size %d total %d src_start %d ",src.Size(),total,src_start); return (false); } dst.Resize(total); dst.Fill(0); for (ulong i=src_start, index =0; i<total+src_start; i++) { dst[index] = src[i]; index++; } return (true); }
Usage:
vector all = {1,2,3,4,5,6}; matrix_utils.Copy(all,v,3); Print("copied vector ",v);
Output:
2022.12.27 07:15:41.420 matrix test (US500,D1) copied vector [4,5,6]
Final Thoughts
There is a lot we can do and much more functions we can add to the utils file but the functions and methods introduced in this article are the ones that I think you will find that you need them often if you've been using matrices for a while and when attempting to create complex trading systems such as the one inspired by machine learning.
Track the development for this Utility Matrix class on my GitHub repo > https://github.com/MegaJoctan/MALE5
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use


thanks for the article, its really inspiring.
btw, what i found to be hard to deal with is the training NN based ea on Metatreader.
the use of matrices and vectors do save me a lot of efforts, but still training lots of variables on metatreader optimizer is hard to do. i've tried to write the weights & biases to CSV file to be loaded by training agent on metatrader optimizer, yet its just stopped at step less than 100. over than that, its look like the agent is just breaking the csv file. its no longer contain the weights & biases value as it suppose to be.
do you might have any idea to train such numbers of variables.?
thanks for the article, its really inspiring.
btw, what i found to be hard to deal with is the training NN based ea on Metatreader.
the use of matrices and vectors do save me a lot of efforts, but still training lots of variables on metatreader optimizer is hard to do. i've tried to write the weights & biases to CSV file to be loaded by training agent on metatrader optimizer, yet its just stopped at step less than 100. over than that, its look like the agent is just breaking the csv file. its no longer contain the weights & biases value as it suppose to be.
do you might have any idea to train such numbers of variables.?
Its hard to tell without seeing the code and everything involved. I do not train the NN on the strategy tester I prefer to train trading parameters there. All my NN are self trained
thanks for the article, its really inspiring.
btw, what i found to be hard to deal with is the training NN based ea on Metatreader.
the use of matrices and vectors do save me a lot of efforts, but still training lots of variables on metatreader optimizer is hard to do. i've tried to write the weights & biases to CSV file to be loaded by training agent on metatrader optimizer, yet its just stopped at step less than 100. over than that, its look like the agent is just breaking the csv file. its no longer contain the weights & biases value as it suppose to be.
do you might have any idea to train such numbers of variables.?
If you are using the fast genetic algorithm of the tester you must be careful as it has different "motivations" depending on the way you set the reward up .
Like mr Msigwa said ,its preferable to train your nets with back propagation . You can train more weights and the network's only reward is increasing "accuracy"