Verwendung des Kalman-Filters für die Prognose der Preisrichtung
3 192
0
Einführung
Die Charts der Währungs- und Aktienkurse enthalten immer Kursschwankungen, die sich in Häufigkeit und Amplitude unterscheiden. Unsere Aufgabe ist es, aus diesen kurzen und langen Bewegungen die wichtigsten Trends zu bestimmen. Einige Händler zeichnen Trendlinien auf dem Chart, andere verwenden Indikatoren. In beiden Fällen ist es unser Ziel, die tatsächliche Preisbewegung vom Hintergrundrauschen zu trennen, der durch den Einfluss kleinerer Faktoren verursacht wird, die sich kurzfristig auf den Preis auswirken. In diesem Artikel schlage ich vor, den Kalman-Filter zu verwenden, um die Hauptbewegung vom Rauschen des Marktes zu trennen.
Die Idee, digitale Filter im Handel zu verwenden, ist nicht neu. Beispielsweise habe ich bereits die Verwendung von Tiefpassfiltern beschrieben. Aber der Perfektion sind keine Grenzen gesetzt, also lassen Sie uns noch eine weitere Strategie überlegen und die Ergebnisse vergleichen.
1. Kalman Filterprinzip
Also, was ist der Kalman-Filter und warum ist er für uns interessant? Hier ist die Definition des Filters aus Wikipedia:
Der Kalman-Filter ist ein Algorithmus, der im Laufe der Zeit getätigte Messungen verwendet, die statistisches Rauschen und andere Ungenauigkeiten enthalten.
Das bedeutet, dass der Filter ursprünglich für die Arbeit mit verrauschten Daten konzipiert wurde. Außerdem ist er in der Lage, mit unvollständigen Daten zu arbeiten. Ein weiterer Vorteil ist, dass er für dynamische Systeme konzipiert und eingesetzt wird, zu denen auch unsere Preischarts gehören.
Der Filter-Algorithmus arbeitet in zwei Schritten:
- Extrapolation (Vorhersage)
- Aktualisierung (Korrektur)
1.1. Extrapolation, Prediction of System Values
Die erste Phase des Filteralgorithmus nutzt ein zugrundeliegendes Modell des zu analysierenden Prozesses. Basierend auf diesem Modell wird eine einstufige Vorwärtsprognose erstellt.
(1.1)
Wobei:
- xk ist der extrapolierte Wert eines dynamischen Systems im k-ten Schritt,
- Fk ist das Zustandsübergangsmodell, das die Abhängigkeit des aktuellen Systemzustandes vom vorherigen zeigt,
- x^k-1 ist der vorherige Zustand des Systems (Filterwert im vorherigen Schritt),
- Bk ist das Eingangsmodell, das den Einfluss auf das System zeigt,
- uk ist der Steuerungsvektor auf das System.
Ein Steuerungseffekt kann, zum Beispiel, eine Pressemitteilung sein. In der Praxis ist der Effekt jedoch unbekannt und wird weggelassen, während sein Einfluss sich auf das Rauschen bezieht.
Dann wird der Kovarianzfehler des Systems vorhergesagt:
(1.2)
Wobei:
- Pk ist die extrapolierte Kovarianzmatrix des dynamischen Zustandsvektors des Systems,
- Fk ist das Zustandsübergangsmodell, das die Abhängigkeit des aktuellen Systemzustandes vom vorherigen zeigt,
- P^k-1 ist die Kovarianzmatrix des Zustandsvektors des vorherigen Schritts,
- Qk ist Kovarianzmatrix des Rauschens des Prozesses.
1.2. Aktualisierung der Systemwerte
Der zweite Schritt des Filteralgorithmus beginnt mit der Messung des aktuellen Systemzustandes zk. Der tatsächlich gemessene Wert des Systemzustandes wird unter Berücksichtigung des wahren Systemzustandes und des Messfehlers angegeben. In unserem Fall ist der Messfehler die Auswirkung des Rauschens auf das dynamische System.
Bis jetzt haben wir zwei verschiedene Werte, die den Zustand eines einzigen, dynamischen Prozesses repräsentieren. Dazu gehören der extrapolierte Wert des im ersten Schritt berechneten dynamischen Systems und der tatsächliche Messwert. Jeder dieser Werte charakterisiert mit einer gewissen Wahrscheinlichkeit den wahren Zustand unseres Prozesses, der sich also irgendwo zwischen diesen beiden Werten befindet. Unser Ziel ist es also, das Vertrauen, d.h. das Ausmaß, in dem diesem oder jenem Wert vertraut wird, zu bestimmen. Zu diesem Zweck werden die Iterationen der zweiten Phase des Kalman-Filters durchgeführt.
Anhand der verfügbaren Daten ermitteln wir die Abweichung des tatsächlichen Systemzustandes vom extrapolierten Wert.
(2.1)
Wobei:
- yk ist die Abweichung vom aktuellen Systemzustand im k-ten Schritt nach der Extrapolation,
- zk ist der aktuelle Systemzustand im k-ten Schritt,
- Hk ist die Messwertematrix, die die Abhängigkeit des aktuellen Systemzustandes von den berechneten Daten anzeigt (oftmals wird sie Eins),
- xk ist der extrapolierte Wert des dynamischen Systems im k-ten Schritt.
Im nächsten Schritt wird eine Kovarianzmatrix der Fehler berechnet:
(2.2)
Wobei:
- Sk ist die Kovarianzmatrix des Fehlervektors im k-ten Schritt,
- Hk ist die Messwertematrix, die die Abhängigkeit des aktuellen Systemzustandes von den berechneten Daten anzeigt,
- Pk ist die extrapolierte Kovarianzmatrix des dynamischen Zustandsvektors des Systems,
- Rk ist die Kovarianzmatrix des gemessenen Rauschens.
Dann wird die optimale Zuwachs ermittelt. Der Zuwachs spiegelt das Vertrauen in die berechneten und die empirischen Werte wider.
(2.3)
Wobei:
- Kk ist die Matrix mit den Werten des Kalman-Zuwachses,
- Pk ist die extrapolierte Kovarianzmatrix des dynamischen Zustandsvektors des Systems,
- Hk ist die Messwertematrix, die die Abhängigkeit des aktuellen Systemzustandes von den berechneten Daten anzeigt,
- Sk ist die Kovarianzmatrix des Fehlervektors im k-ten Schritt.
Jetzt verwenden wir den Kalman-Zuwachs, um den Systemzustand und die Kovarianzmatrix des geschätzten Zustandsvektors zu aktualisieren.
(2.4)
Wobei:
- x^k and x^k-1 sind die aktualisierten Werte im k-ten und (k-1)-ten Schritt,
- Kk ist die Matrix mit den Werten des Kalman-Zuwachses,
- yk ist die Abweichung vom aktuellen Systemzustand im k-ten Schritt nach der Extrapolation.
(2.5)
Wobei:
- Pk ist die aktualisierte Kovarianzmatrix des dynamischen Zustandsvektors des Systems,
- I ist die Identitätsmatrix,
- Kk ist die Matrix mit den Werten des Kalman-Zuwachses,
- Hk ist die Messwertematrix, die die Abhängigkeit des aktuellen Systemzustandes von den berechneten Daten anzeigt,
- Pk ist die extrapolierte Kovarianzmatrix des dynamischen Zustandsvektors des Systems.
All dies lässt sich wie folgt zusammenfassen
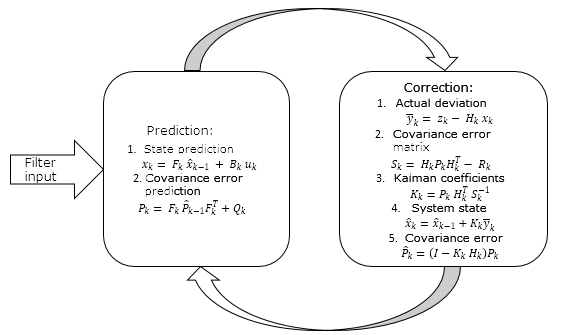
2. Die praktische Umsetzung des Kalman-Filters
Oben haben wir die Idee ausgebreitet, wie der Kalman-Filter arbeitet. Kommen wir jetzt zur praktischen Umsetzung. Die obige Matrixdarstellung von Filterformeln ermöglicht den Übernahme von Daten aus mehreren Quellen. Ich schlage vor, für den Filter die Schlusskurse der Bars zu verwenden und die Matrixdarstellung in eine diskrete zu vereinfachen.
2.1. Initialisierung der Eingabedaten
Vor dem Schreiben des Codes, definieren wir die Eingabedaten.
Wie bereits erwähnt, ist die Basis des Kalman-Filters ein dynamisches Prozessmodell, mit dem der nächste Prozesszustand vorhergesagt wird. Ursprünglich war der Filter für den Einsatz in linearen Systemen vorgesehen, bei denen der aktuelle Zustand einfach durch Anwenden eines Koeffizienten auf den vorherigen Zustand definiert werden kann. Unser Fall ist etwas schwieriger: Unser dynamisches System ist nichtlinear, und das Verhältnis variiert Schritt für Schritt. Darüber hinaus haben wir keine Ahnung von der Beziehung zwischen benachbarten Systemzuständen. Die Aufgabe mag unlösbar erscheinen. Hier ist eine trickreiche Lösung: Wir werden autoregressive Modelle verwenden, die in den Artikeln[1],[2],[3] beschrieben sind.
Beginnen wir. Zuerst deklarieren wir, die Klasse CKalman und die benötigten Variablen in dieser Klasse
class CKalman { private: //--- uint ci_HistoryBars; //Bars for analysis uint ci_Shift; //Shift of autoregression calculation string cs_Symbol; //Symbol ENUM_TIMEFRAMES ce_Timeframe; //Timeframe double cda_AR[]; //Autoregression coefficients int ci_IP; //Number of autoregression coefficients datetime cdt_LastCalculated; //Time of LastCalculation; bool cb_AR_Flag; //Flag of autoregression calculation //--- Values of Kalman's filter double cd_X; // X double cda_F[]; // F array double cd_P; // P double cd_Q; // Q double cd_y; // y double cd_S; // S double cd_R; // R double cd_K; // K public: CKalman(uint bars=6240, uint shift=0, string symbol=NULL, ENUM_TIMEFRAMES period=PERIOD_H1); ~CKalman(); void Clear_AR_Flag(void) { cb_AR_Flag=false; } };
Wir weisen den Variablen in der Initialisierungsfunktion der Klasse Anfangswerte zu.
CKalman::CKalman(uint bars, uint shift, string symbol, ENUM_TIMEFRAMES period) { ci_HistoryBars = bars; cs_Symbol = (symbol==NULL ? _Symbol : symbol); ce_Timeframe = period; cb_AR_Flag = false; ci_Shift = shift; cd_P = 1; cd_K = 0.9; }
Ich verwende einen Algorithmus aus dem Artikel [1], um das autoregressive Modell zu erstellen. Zwei 'private' Funktionen müssen zu diesem Zweck der Klasse hinzugefügt werden.
bool Autoregression(void); bool LevinsonRecursion(const double &R[],double &A[],double &K[]);
Die Funktion LevinsonRecursion wird dafür verwendet. Die Funktion Autoregression wurde geringfügig geändert, betrachten wir diese Funktion daher genauer. Am Anfang der Funktion prüfen wir die Verfügbarkeit der für die Analyse benötigten, historischen Daten. Wenn es nicht genügend historische Daten gibt, wird 'false' zurückgegeben.
bool CKalman::Autoregression(void) { //--- Prüfen auf unzureichende Dasten if(Bars(cs_Symbol,ce_Timeframe)<(int)ci_HistoryBars) return false;
Nun laden wir die benötigten historischen Daten und füllen damit das Array der aktuellen Koeffizienten des Zustandsübergangsmodell.
//--- double cda_QuotesCenter[]; //Data to calculate //--- make all prices available double close[]; int NumTS=CopyClose(cs_Symbol,ce_Timeframe,ci_Shift+1,ci_HistoryBars+1,close)-1; if(NumTS<=0) return false; ArraySetAsSeries(close,true); if(ArraySize(cda_QuotesCenter)!=NumTS) { if(ArrayResize(cda_QuotesCenter,NumTS)<NumTS) return false; } for(int i=0;i<NumTS;i++) cda_QuotesCenter[i]=close[i]/close[i+1]; // Calculate coefficients
Nach diesen Vorarbeiten ermitteln wir die Anzahl der Koeffizienten des autoregressiven Modells und berechnen deren Werte.
ci_IP=(int)MathRound(50*MathLog10(NumTS)); if(ci_IP>NumTS*0.7) ci_IP=(int)MathRound(NumTS*0.7); // Autoregressive model order double cor[],tdat[]; if(ci_IP<=0 || ArrayResize(cor,ci_IP)<ci_IP || ArrayResize(cda_AR,ci_IP)<ci_IP || ArrayResize(tdat,ci_IP)<ci_IP) return false; double a=0; for(int i=0;i<NumTS;i++) a+=cda_QuotesCenter[i]*cda_QuotesCenter[i]; for(int i=1;i<=ci_IP;i++) { double c=0; for(int k=i;k<NumTS;k++) c+=cda_QuotesCenter[k]*cda_QuotesCenter[k-i]; cor[i-1]=c/a; // Autocorrelation } if(!LevinsonRecursion(cor,cda_AR,tdat)) // Levinson-Durbin recursion return false;
Die Summe der erhaltenen, autoregressiven Koeffizienten wird auf '1' reduziert und das Flag der durchgeführten Berechnung auf 'true'.
double sum=0; for(int i=0;i<ci_IP;i++) { sum+=cda_AR[i]; } if(sum==0) return false; double k=1/sum; for(int i=0;i<ci_IP;i++) cda_AR[i]*=k;cb_AR_Flag=true;
Als nächstes initialisieren wir die Variablen, die für den Filter notwendig sind. Als Kovarianz des Rauschens nehmen wir die mittlere quadratische Abweichung der Werte für den analysierten Zeitraum.
cd_R=MathStandardDeviation(close);
Um den Wert der Kovarianz des Rauschens zu bestimmen, berechnen wir zunächst das Array der Werte des autoregressiven Modells und berechnen die quadratische Standardabweichung der Modellwerte.
double auto_reg[]; ArrayResize(auto_reg,NumTS-ci_IP); for(int i=(NumTS-ci_IP)-2;i>=0;i--) { auto_reg[i]=0; for(int c=0;c<ci_IP;c++) { auto_reg[i]+=cda_AR[c]*cda_QuotesCenter[i+c]; } } cd_Q=MathStandardDeviation(auto_reg);
Dann kopieren wir die aktuellen Koeffizienten des Zustandsübergangs in das Array cda_F kopiert, um sie später bei der Berechnung neuer Koeffizienten zu verwenden.
ArrayFree(cda_F); if(ArrayResize(cda_F,(ci_IP+1))<=0) return false; ArrayCopy(cda_F,cda_QuotesCenter,0,NumTS-ci_IP,ci_IP+1);
Für den Anfangswert unseres Systems, nehmen Sie das arithmetische Mittel der letzten 10 Werte.
cd_X=MathMean(close,0,10);
2.2. Vorhersage der Preisbewegung
Nachdem wir alle Ausgangsdaten für den Filter erhalten haben, können wir mit der praktischen Umsetzung beginnen. Die erste Stufe des Kalman-Filters ist, wie oben erwähnt, die Extrapolation des Systemzustands um einen Schritt nach vorne. Erstellen wir die 'public' Funktion Forecast, in der die Funktionen 1.1. implementiert werden und 1.2.
double Forecast(void);
Zu Beginn der Funktion prüfen wir, ob das Regressionsmodell bereits berechnet ist. Rufen Sie ggf. die Funktion seiner Berechnung auf. Wenn ein Fehler bei der Modellkonvertierung auftritt, wird EMPTY_VALUE zurückgegeben.
double CKalman::Forecast() { if(!cb_AR_Flag) { ArrayFree(cda_AR); if(Autoregression()) { return EMPTY_VALUE; } }
Danach berechnen wir dann den Abhängigkeitskoeffizienten des aktuellen Zustands des Systems aus dem vorherigen und speichern ihn in der Zelle '0' des Arrays cda_F, dessen Werte vorher um eine Zelle verschoben wurden.
Shift(cda_F); cda_F[0]=0; for(int i=0;i<ci_IP;i++) cda_F[0]+=cda_F[i+1]*cda_AR[i];
Dann berechnen wir erneut den Systemzustand und die Fehlerwahrscheinlichkeit.
cd_X=cd_X*cda_F[0]; cd_P=MathPow(cda_F[0],2)*cd_P+cd_Q;
Zuletzt gibt die Funktion den vorhergesagten Systemzustand zurück. In unserem Fall ist es der prognostizierte Schlusskurs der neuen Bar.
return cd_X;
}
2.3. Korrektur des Systemzustands
In der nächsten Stufe korrigieren wir, nach dem Erhalt des tatsächlichen Schlusskurses der Bar, den Systemzustand. Wir erstellen dazu eine 'public' Funktion namens Correction. In seinen Parametern übertragen wir den tatsächlichen Wert des Systemzustands, d.h. Schlusskurs des letzten Balkens.
double Correction(double z);
Diese Funktion implementiert den theoretischen Abschnitt 1.2. dieses Artikels. Der vollständige Code befindet sich im Anhang. Am Ende ihrer Operation gibt die Funktion den korrigierten Zustandswert des Systems zurück.
3. Demonstration des Kalman-Filters in der Praxis
Testen wir jetzt, wie die Klasse für den Kalman-Filter in der Praxis arbeitet. Erstellen Sie dazu auf der Grundlage der Klasse einen Indikator. Öffnet sich eine neue Kerze, ruft der Indikator die Korrekturfunktion des Systemzustandes auf und dann die Vorhersagefunktion, um den Schlusskurs der aktuellen Bars vorherzusagen. Die Funktionsaufrufe der Klasse erfolgen in anderer Reihenfolge, weil wir die Korrekturfunktion des Status' für die vorherige (geschlossene) Bar und die Schlusskursvorhersage für die aktuelle (gerade geöffneten Bar) aufrufen, dessen Schlusskurs uns ja noch unbekannt ist.
Der Indikator wird 2 Puffer haben. Die erste zeigt die prognostizierten Werte des Systemzustands an, die zweite die korrigierten. Ich habe absichtlich zwei Puffer erstellt, so dass der Indikator nicht neu gezeichnet wurde und man so das Ausmaß der Systemkorrektur in der zweiten Stufe der Filteroperation sehen kann. Der Indikatorcode ist einfach, er ist dem Anhang beigefügt. Hier werden nur seine Ergebnisse gezeigt.
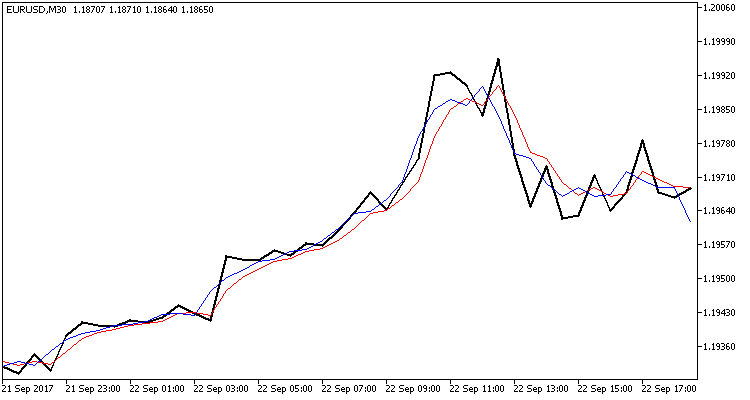
Das vorgestellte Diagramm zeigt drei gestrichelte Linien:
- Schwarz ist die Linie der aktuellen Schlusskurse
- Rot die Linie der prognostizierten Werte
- Blau ist die Linie des durch den Kalman-Filter aktualisierten Systemzustandes
Wie Sie sehen können, liegen beide Linien nahe bei den tatsächlichen Schlusskursen und mit guter Wahrscheinlichkeit, Umkehrpunkte zeigen zu können. Ich möchte noch einmal darauf aufmerksam machen, dass der Indikator nicht neu gezeichnet wird und die rote Linie zum Zeitpunkt des Eröffnens der Bar aufgebaut wird, wenn der Schlusskurs noch nicht bekannt ist.
Dies Chart zeigt die Konsistenz des verwendeten Filters und die Möglichkeit, damit ein Handelssystem aufzubauen.
4. Erstellen eines Moduls mit Handelssignalen für den MQL5 Wizard
Wir sehen auf dem obigen Chart, dass die rote Linie mit der Vorhersage des Systemstatus glatter ist als die schwarze Linie, die den tatsächliche Preis zeigt. Die blaue Linie, die den korrigierte Systemzustand zeigt, befindet sich immer dazwischen. Mit anderen Worten, ist die blaue Linie über der roten, zeigt das einen Aufwärtstrend. Umgekehrt, ist die blaue Linie unten der roten ist das ein Indiz für einen Abwärtstrend. Der Schnittpunkt der blauen und roten Linien signalisiert eine Trendwende.
Um diese Strategie zu testen Strategie, erstellen wir ein Modul mit Handelssignalen für den MQL5 Wizard. Das Erstellen eines Moduls mit Handelssignalen wird in mehreren Artikeln beschrieben: [1], [4], [5]. Ich werde kurz die Punkte beschreiben, die unsere Strategie betreffen.
Zuerst erstellen wir die Klasse CSignalKalman, die von CExpertSignal abgeleitet wird. Da unsere Strategie auf der Verwendung des Kalman-Filters basiert, müssen wir in unserer Klasse eine Instanz der oben erstellten CKalman-Klasse deklarieren. Da wir im Modul eine Instanz der Klasse CKalman deklarieren, initialisieren wir sie auch im Modul. Dafür müssen wir die Anfangsparameter dem Modul übergeben. Im Code sieht die Lösung für diese Probleme folgendermaßen aus:
//+---------------------------------------------------------------------------+ // wizard description start //+---------------------------------------------------------------------------+ //| Description of the class | //| Title=Signals of Kalman's filter design by DNG | //| Type=SignalAdvanced | //| Name=Signals of Kalman's filter design by DNG | //| ShortName=Kalman_Filter | //| Class=CSignalKalman | //| Page=https://www.mql5.com/ru/articles/3886 | //| Parameter=TimeFrame,ENUM_TIMEFRAMES,PERIOD_H1,Timeframe | //| Parameter=HistoryBars,uint,3000,Bars in history to analysis | //| Parameter=ShiftPeriod,uint,0,Period for shift | //+---------------------------------------------------------------------------+ // wizard description end //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class CSignalKalman: public CExpertSignal { private: ENUM_TIMEFRAMES ce_Timeframe; //Timeframe uint ci_HistoryBars; //Bars in history to analysis uint ci_ShiftPeriod; //Period for shift CKalman *Kalman; //Class of Kalman's filter //--- datetime cdt_LastCalcIndicators; double cd_forecast; // Forecast value double cd_corretion; // Corrected value //--- bool CalculateIndicators(void); public: CSignalKalman(); ~CSignalKalman(); //--- void TimeFrame(ENUM_TIMEFRAMES value); void HistoryBars(uint value); void ShiftPeriod(uint value); //--- method of verification of settings virtual bool ValidationSettings(void); //--- method of creating the indicator and timeseries virtual bool InitIndicators(CIndicators *indicators); //--- methods of checking if the market models are formed virtual int LongCondition(void); virtual int ShortCondition(void); };
In der Initialisierungsfunktion der Klasse werden den Variablen Standardwerte zugewiesen und die Klasse des Kalman-Filters initialisiert.
CSignalKalman::CSignalKalman(void): ci_HistoryBars(3000), ci_ShiftPeriod(0), cdt_LastCalcIndicators(0) { ce_Timeframe=m_period; if(CheckPointer(m_symbol)!=POINTER_INVALID) Kalman=new CKalman(ci_HistoryBars,ci_ShiftPeriod,m_symbol.Name(),ce_Timeframe); }
Wir berechnen die Systemzustände durch den Filter in der 'private' Funktion CalculateIndicators. Zu Beginn der Funktion überprüfen wir, ob die Filterwerte der aktuellen Bar berechnet wurden. Falls die Werte bereits neu berechnet wurden, verlassen wir die Funktion.
bool CSignalKalman::CalculateIndicators(void) { //--- Check time of last calculation datetime current=(datetime)SeriesInfoInteger(m_symbol.Name(),ce_Timeframe,SERIES_LASTBAR_DATE); if(current==cdt_LastCalcIndicators) return true; // Exit if data already calculated on this bar
Dann überprüfen wir den letzten Zustand des Systems. Wenn er nicht definiert ist, wird das Flag für die Berechnung des autoregressiven Modells in der Klasse CKalman zurückgesetzt, so dass das Modell neu berechnet wird, wenn später auf die Klasse zugegriffen wird.
if(cd_corretion==QNaN) { if(CheckPointer(Kalman)==POINTER_INVALID) { Kalman=new CKalman(ci_HistoryBars,ci_ShiftPeriod,m_symbol.Name(),ce_Timeframe); if(CheckPointer(Kalman)==POINTER_INVALID) { return false; } } else Kalman.Clear_AR_Flag(); }
Im nächsten Schritt prüfen wir, wie viele Bars nach dem letzten Funktionsaufruf generiert wurden. Wenn das Intervall zu groß ist, wird auch das Flag des für die Berechnung des autoregressive Modells zurückgesetzt.
int shift=StartIndex(); int bars=Bars(m_symbol.Name(),ce_Timeframe,current,cdt_LastCalcIndicators); if(bars>(int)fmax(ci_ShiftPeriod,1)) { bars=(int)fmax(ci_ShiftPeriod,1); Kalman.Clear_AR_Flag(); }
Dann werden für alle unberechneten Bars die Werte des Systemzustandes ermittelt.
double close[]; if(m_close.GetData(shift,bars+1,close)<=0) { return false; } for(uint i=bars;i>0;i--) { cd_forecast=Kalman.Forecast(); cd_corretion=Kalman.Correction(close[i]); }
Nach der Neuberechnung wird der Zustand des Systems neu berechnet und der Zeitpunkt des letzten Funktionsaufrufs gespeichert. War der Vorgang erfolgreich, gibt die Funktion 'true' zurück.
if(cd_forecast==EMPTY_VALUE || cd_forecast==0 || cd_corretion==EMPTY_VALUE || cd_corretion==0) return false; cdt_LastCalcIndicators=current; //--- return true; }
Die Entscheidungsfunktionen (LongCondition und ShortCondition) haben eine vollständig identische Struktur, aber mit einer Umkehrung bei der Eröffnung der Transaktion. Sehen wir uns den Code der Funktionen am Beispiel von ShortCondition an.
Führen Sie zunächst die Funktion aus, um die Werte des Filters neu zu berechnen. Wenn die Werte nicht berechnet werden konnten, wird die Funktion beendet und 0 zurückgegeben.
int CSignalKalman::ShortCondition(void) { if(!CalculateIndicators()) return 0;
Wurden die Filterwerte erfolgreich neu berechnet, werden die prognostizierten Werte mit den korrigierten vergleichen. Sind die prognostizierten Wert größer als die korrigierten, gibt die Funktion einen Gewichtungswert zurück. Ansonsten wird 0 zurückgegeben.
int result=0; //--- if(cd_corretion<cd_forecast) result=80; return result; }
Das Modul ist nach dem Umkehr-Prinzip aufgebaut, so dass keine Funktion für das Schließen von Positionen benötigt wird.
Der Code aller Funktionen befindet sich in den Dateien, die an den Artikel angehängt sind.
5. Testen des Expert Advisors
Eine detaillierte Beschreibung der Erstellung des Expert Advisor auf Basis des Signals-Moduls finden Sie im Artikel[1], daher überspringen wir diesen Schritt. Beachten Sie, dass der EA zu Testzwecken nur auf einem oben beschriebenen Handelsmodul mit konstanter Lotgröße und ohne Trailing-Stops basiert.
Der Expert Advisor wurde anhand der historischen Daten von EURUSD für August 2017 mit dem Zeitrahmen Н getestet. Für die Berechnung des autoregressiven Modells wurden historische Daten von 3000 Bars, d.h. fast 6 Monate, verwendet. Der EA wurde ohne Stop-Loss und Take-Profit getestet, um den deutlichen Einfluss des Kalman-Filters auf den Handel zu sehen.
Die Testergebnisse zeigen 49,33% gewinnbringenden Positionen. Die Werte für die höchsten und die durchschnittlichen profitablen Positionen übersteigen die entsprechenden Werte der Verlustpositionen. Im Allgemeinen zeigte der EA-Test einen Gewinn für den ausgewählten Zeitraum, und einen Profit-Faktor von 1,56. Screenshots zum Testen finden sich weiter unten.
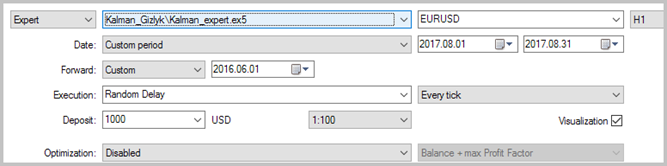
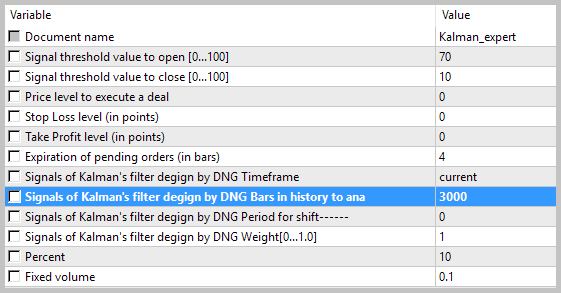
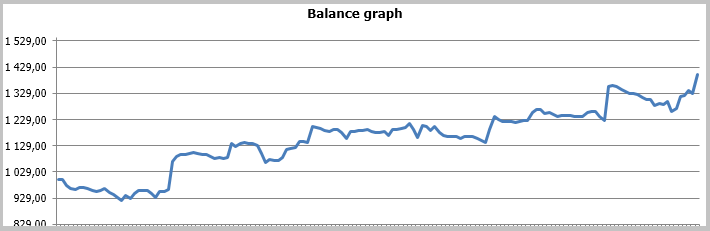
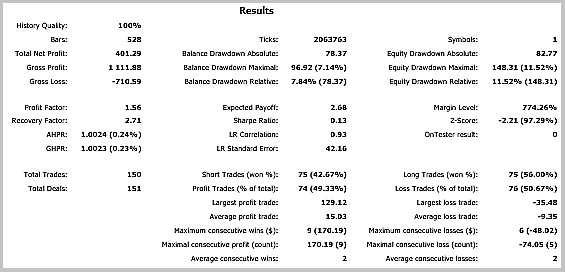
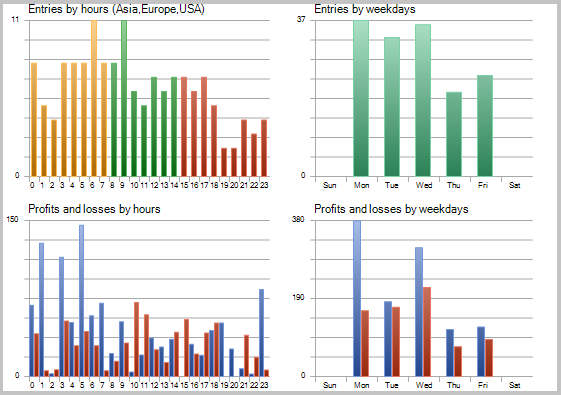
Eine detaillierte Analyse der Positionen auf dem Chart zeigen nachfolgend zwei Schwachstellen dieser Taktik:
- Ein Serie von Verlustpositionen in einer Seitwärtsbewegung
- Spätes Schließen offener Positionen
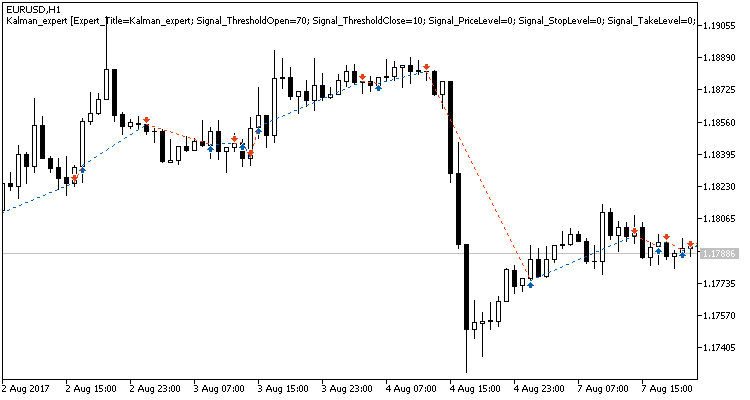
Die gleichen Probleme zeigten sich auch beim Testen von Expert Advisor mit einer adaptiven Trendfolgestrategien. Optionen zur Lösung dieser Probleme wurden in dem erwähnten Artikel vorgeschlagen. Im Gegensatz zur bisherigen Strategie zeigte die auf Kalman-Filtern basierende EA jedoch ein positives Ergebnis. Meiner Meinung nach kann die in diesem Artikel vorgeschlagene und beschriebene Strategie erfolgreich sein, wenn sie mit einem zusätzlichen Filter zur Bestimmung von Seitwärtsbewegungen ergänzt wird. Die Ergebnisse könnten durch die Verwendung eines Zeitfilters verbessert werden. Eine weitere Möglichkeit, die Ergebnisse zu verbessern, ist das Hinzufügen von Signalen, um Positionen zu schließen und so zu verhindern, dass bei starken Rückschlägen der Kurse Gewinne verloren gehen.
Schlussfolgerung
Wir haben das Prinzip des Kalman-Filters analysiert und auf seiner Basis einen Indikator und einen Expert Advisor erstellt. Tests haben gezeigt, dass dies eine vielversprechende Strategie ist, und haben dazu beigetragen, eine Reihe von Engpässen aufzudecken, die es zu beheben gilt.
Bitte beachten Sie, dass der Artikel nur allgemeine Informationen und ein Beispiel für die Erstellung eines Expert Advisors enthält, der in keiner Weise ein "Heiliger Gral" für den Einsatz im realen Handel ist.
Ich wünsche allen eine seriöse Herangehensweise an den Handel und gewinnbringende Geschäfte!
URL Links
- Wir betrachten die adaptive Trendfolgemethode in der Praxis
- Analyse der wesentlichen Merkmale von Zeitreihen
- AR Extrapolation der Kurse - Indikator für den MetaTrader 5
- Der MQL5 Assistent: Wie man ein Modul an Handelssignalen erzeugt
- In 6 Schritten zum eigenen automatischen Handelssystem!
- MQL5 Wizard: Neue Version
Die Programm dieses Artikels:
| # |
Name |
Typ |
Beschreibung |
|---|---|---|---|
| 1 | Kalman.mqh | Klassenbibliothek | Klasse des Kalman-Filters |
| 2 | SignalKalman.mqh | Klassenbibliothek | Ein Modul für Handelssignale auf Basis des Kalman-Filters |
| 3 | Kalman_indy.mq5 | Indikator | Der Indikator Kalman-Filter |
| 4 | Kalman_expert.mq5 | EA | Ein Expert Advisor auf Basis einer Strategie, die den Kalman-Filter verwendet |
| 5 | Kalman_test.zip | Archive | Das Archiv enthält die Ergebnisse der Tests des EAs, nachdem der EA im Strategietester gelaufen ist. |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/3886
Die Eröffnung durch Indikatoren bestimmen lassen
R-Quadrat als Gütemaß der Saldenkurve einer Strategie
Das Erstellen einer neuen Handelsstrategie und sich die Positionseröffnungen durch Indikatoren bestimmen lassen
Testen der Muster, die beim Handel mit Körben von Währungspaaren auftreten. Teil II
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.