
R-Quadrat als Gütemaß der Saldenkurve einer Strategie
Inhaltsverzeichnis
- Einführung
- Kritik an der üblichen Statistik für die Bewertung des Handelssystems
- Das Verhalten der gängigen Statistik von Tests eines Handelssystems
- Anforderungen an das Prüfkriterium für Handelssysteme
- Lineare Regression
- Korrelation
- Das Bestimmtheitsmaß R²
- Der Satz des Arcsinus und sein Beitrag zur Schätzung der Linearen Regression
- Aufzeichnen der Equity-Werte einer Strategie
- Berechnung des Bestimmtheitsmaßes R² mittels AlgLib
- Die praktische Verwendung von R²
- Vorteile und Einschränkungen
- Schlussfolgerung
Einführung
Jede Handelsstrategie bedarf einer objektiven Bewertung ihrer Effektivität. Dazu werden eine Vielzahl von statistischen Parametern verwendet. Viele von ihnen sind einfach zu berechnen und erlauben eine intuitive Bewertung. Andere sind schwieriger in der Konstruktion und Interpretation von Werten. Trotz all dieser Vielfalt gibt es nur sehr wenige aussagekräftige Messgrößen für die Schätzung eines nicht trivialen, aber gleichzeitig offensichtlichen Wertes - der Glätte der Saldenkurve eines Handelssystems. Dieser Artikel schlägt eine Lösung für dieses Problem vor. Es wird das nicht-triviale Bestimmtheitsmaß R² verwendet, das die attraktivste, möglichst glatte, steigende Saldenkurve erkennt, die jeder Händler anstrebt.
Natürlich bietet der MetaTrader 5 Terminal bereits einen ausgearbeiteten, zusammenfassenden Bericht, der die wichtigsten statistischen Werte eines Handelssystems zeigt. Die dargestellten Parameter sind jedoch nicht immer ausreichend. Glücklicherweise bietet MetaTrader 5 die Möglichkeit, benutzerdefinierte Schätzparameter zu schreiben, was genau das ist, was wir tun werden. Wir werden nicht nur das Bestimmtheitsmaß R² berechnen, sondern auch dessen Werte einschätzen, sie mit anderen Optimierungskriterien vergleichen und Regelmäßigkeiten ableiten, gefolgt von grundlegenden, statistischen Schätzungen.
Kritik an der üblichen Statistik für die Bewertung des Handelssystems
Jedes Mal, wenn ein Handelsbericht erstellt wird oder Ergebnisse der Backtests von Handelssystemen untersucht werden, werden uns mehrere "magische Zahlen" präsentiert, die analysiert werden können, um Rückschlüsse auf die Qualität des Handelssystems zu ziehen. Zum Beispiel sieht so ein typischer Testbericht im MetaTrader 5 Terminal aus:
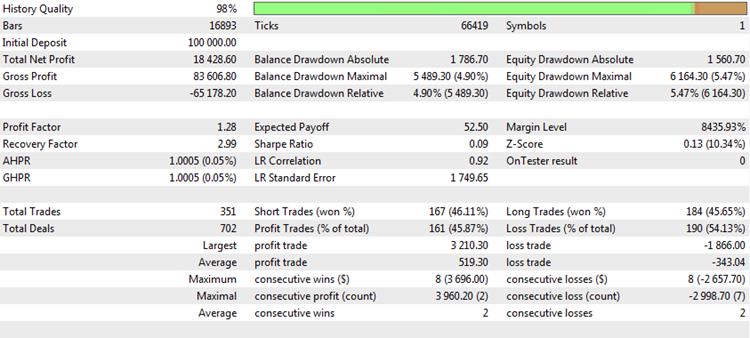
Abb. 1. Ergebnis eines Backtests einer Handelsstrategie
Er enthält eine Reihe von interessanten statistischen Werte und Messgrößen. Analysieren wir die beliebtesten und betrachten objektiv ihre Stärken und Schwächen.
Der Reingewinn (Im Bild oben "Total Net Profit"). Die Messgröße zeigt den Gesamtbetrag des Geldes, das während der Test- oder Handelsperiode verdient oder verloren wurde. Dies ist einer der wichtigsten Erfolgsparameter. Das primäre Ziel eines jeden Händlers ist es, den Gewinn zu maximieren. Es gibt verschiedene Möglichkeiten, dies zu tun, aber das Endergebnis bleibt gleich, der Reingewinn. Der Reingewinn hängt nicht immer von der Anzahl der Positionen ab und ist praktisch unabhängig von anderen Parametern, obwohl das Gegenteil nicht der Fall ist. Es ist also invariant in Bezug auf andere Messgrößen und kann daher unabhängig von diesen verwendet werden. Allerdings hat dieser Wert auch gravierende Nachteile.
Erstens ist der Reingewinn direkt davon abhängig, wie stark das Kapital genutzt wird. Wenn das steigende Kapital verwendet wird, wächst der Gewinn nichtlinear. Häufig kommt es zu einem exponentiellen, explosiven Wachstum der Kontostandes. In diesem Fall erreichen die Zahlen, die am Ende des Tests als Reingewinn verbucht werden, oft astronomische Werte, die nichts mit der Realität zu tun haben. Wenn eine konstante Lotgröße gehandelt wird, sind die Einzahlungsschritte linearer, aber auch in diesem Fall hängt der Gewinn vom gewählten Volumen ab. Wenn z.B. die Prüfung mit dem in der obigen Tabelle gezeigten Ergebnis unter Verwendung einer festen Lotgröße mit dem Volumen von 0,1 Kontakten durchgeführt wurde, dann kann ein erzielter Gewinn von 15.757 $ als bemerkenswertes Ergebnis betrachtet werden. Wenn aber das Handelsvolumen 1,0 Lot betrug, dann ist das Testergebnis mehr als bescheiden. Aus diesem Grund ziehen es die erfahrenen Tester vor, eine Lotgröße, die auf 0,1 oder 0,01 festgelegt ist, auf den Forex-Markt zu setzen. In diesem Fall ist die kleinste Änderung des Saldos gleich einem point des Handelsinstrumentes, was die Analyse dieses Merkmals objektiver macht.
Zweitens, das Endergebnis hängt von der Länge der getesteten Periode oder der Dauer der Handelsgeschichte ab. Beispielsweise könnte der in der obigen Tabelle angegebene Reingewinn in einem Jahr oder in fünf Jahren erzielt worden sein. Und in jedem Fall bedeutet die gleiche Zahl eine völlig andere Effektivität einer Strategie.
Und drittens wird der Bruttogewinn zum allerletzten Zeitpunkt fixiert. Allerdings kann es in diesem Moment zu einem starken Gewinneinbruch kommen, der vielleicht vor einer Woche noch nicht stattgefunden hat. Mit anderen Worten, dieser Parameter ist stark abhängig von den Start- und Endpunkten, die für den Test oder die Erstellung des Berichts ausgewählt wurden.
Profit-Faktor. Dies ist wohl die beliebteste Kennziffer der professionellen Händler. Während Neulinge nur den Gesamtgewinn sehen wollen, ist es für Profis unerlässlich, den Umsatz der investierten Gelder zu kennen. Wenn der Verlust eines Geschäfts als eine Art Investition betrachtet wird, dann zeigt Profit-Faktor die Marginalität des Handels. Wenn z.B. nur zwei Positionen gehandelt wurden, der erste verlor $1000 und der zweite gewann $2000, dann ist der Profit-Faktor dieser Strategie $2000/1000 = 2.0. Das ist eine sehr gute Zahl. Darüber hinaus ist Profit-Faktor von der Zeitspanne des Tests noch vom Basisvolumen abhängig. Deshalb mögen es Profis so sehr. Aber er hat auch Nachteile.
Einer davon ist, dass die Werte des Profit-Faktors stark von der Anzahl der Positionen abhängig sind. Wenn es nur wenige Geschäfte gibt, ist es durchaus möglich, einen Profit-Faktor von 2,0 oder sogar 3,0 zu erhalten. Andererseits, wenn es zahlreiche Positionen gibt, dann wäre es ein großer Erfolg, einen Profit-Faktor von 1,5 zu erhalten.
Erwartetes Ergebnis (Expected Payoff). Es handelt sich um ein sehr wichtiges Merkmal, das das Durchschnittsergebnis angibt. Wenn die Strategie profitabel ist, ist das erwartete Ergebnis positiv; verlierende Strategien haben einen negativen Wert. Wenn das erwartete Ergebnis mit den Kosten aus Spread oder Kommission vergleichbar ist, kann eine solche Strategie real kaum Geld verdienen. Normalerweise sollte die Erwartete Auszahlung im Strategy Tester unter idealen Ausführungsbedingungen positiv und die Saldenkurve eine glatte aufsteigende Linie. Im Live-Trading kann sich das Durchschnittsergebnis jedoch aufgrund möglicher so genannter Requotes oder Slippages, die das Ergebnis der Strategie negativ beeinflussen und reale Verluste verursachen können, etwas schlechter als das theoretisch berechnete Ergebnis entwickeln.
Aber es gibt auch Nachteile. Die wichtigste ist die Anzahl der Positionen. Es kein Problem, einen großen Wert für das erwartete Ergebnis mit nur ein paar Positionen zu erzielen. Auf der anderen Seite, bei einer großen Anzahl von Positionen tendiert des erwartete Ergebnis zu Null. Da es sich um eine lineare Messgröße handelt, kann sie nicht in Strategien mit aktiven Geldmanagement verwendet werden. Aber professionelle Händler schätzen es sehr und verwenden es in linearen Systemen mit einem konstanten Lotvolumen, indem sie es mit der Anzahl der Positionen vergleichen.
Anzahl der Positionen. Dies ist ein wichtiger Parameter, der die meisten anderen Merkmale explizit oder indirekt betrifft. Angenommen, ein Handelssystem gewinnt in 70% der Fälle. Gleichzeitig sind die absoluten Werte von Gewinn und Verlust gleichwertig, ohne andere mögliche Ergebnisse der Positionen in der Handelsstrategie. Ein solches System scheint hervorragend zu sein, aber was passiert, ist, dass die Effizienz nur auf der Grundlage der letzten beiden Positionen bewertet wird? In 70% der Fälle wird einer von ihnen profitabel sein, aber die Wahrscheinlichkeit, dass beide Geschäfte profitabel sind, beträgt nur 49%. Das heißt, das Gesamtergebnis der beiden Positionen wird in mehr als der Hälfte der Fälle gleich Null sein. Folglich wird die Statistik in der Hälfte der Fälle zeigen, dass die Strategie nicht in der Lage ist, Geld zu verdienen. Der Profit-Faktor ist immer gleich Eins, des erwartete Ergebnis und der Gewinn sind gleich Null, und die anderen Parameter zeigen ebenfalls einen Wert von Null an.
Deshalb muss die Anzahl der Positionen ausreichend groß sein. Aber was ist mit ausreichend gemeint? Es ist allgemein anerkannt, dass jede Stichprobe mindestens 37 Messungen haben muss. Dies ist eine magische Zahl in der Statistik, sie markiert die untere Grenze der Repräsentativität eines Parameters. Natürlich reicht diese Menge an Positionen nicht aus, um ein Handelssystem zu bewerten. Mindestens 100-150 Position müssen existieren, damit das Ergebnis zuverlässig ist. Darüber hinaus ist dies auch für viele professionelle Händler noch nicht ausreichend. Sie entwerfen Systeme, die mindestens 500-1000 Positionen machen, um später mit diesen Ergebnissen die Möglichkeit zu prüfen, ob das System für den Live-Handel geeignet ist.
Das Verhalten der üblichen statistischen Parameter beim Testen von Handelssystemen
Die wichtigsten Parameter in der Statistik der Handelssysteme wurden diskutiert. Schauen wir uns an, was sie können. Gleichzeitig werden wir ihre Nachteile hervorheben, um zu sehen, wie der Vorschlag einer R²-Statistik helfen kann, sie zu überwinden. Dazu verwenden wir den gebrauchsfertigen CImpulse 2.0 EA, der im Artikel "Universeller Expert Advisor: CUnIndicator und das Arbeiten mit Pending Orders" beschrieben ist. Es wurde wegen seiner Einfachheit und Optimierbarkeit ausgewählt, im Gegensatz zu anderen Experten aus dem Standardpaket des MetaTrader 5, das für die Zwecke dieses Artikels äußerst wichtig ist. Zusätzlich wird eine bestimmte Code-Infrastruktur benötigt, die bereits für die CStrategy Trade Engine geschrieben wurde, so dass es nicht nötig ist, die gleiche Aufgabe zweimal zu erledigen. Alle Quellcodes für das Bestimmtheitsmaß sind so geschrieben, dass sie auch außerhalb von CStrategy problemlos verwendet werden können - zum Beispiel in Bibliotheken Dritter oder Experten.
Der Reingewinn (Im Bild oben "Total Net Profit"). Wie bereits erwähnt, ist der Nettogewinn (oder Gesamtgewinn) das Endergebnis dessen, was der Händler erreichen will. Je größer der Gewinn, desto besser. Die Bewertung einer Strategie anhand des Endgewinns ist jedoch nicht immer ein Garant für den Erfolg. Betrachten wir die Ergebnisse der Strategie von CImpulse 2.0 für EURUSD im Testzeitraum von 2015.01.15 bis 2017.10.10.10:
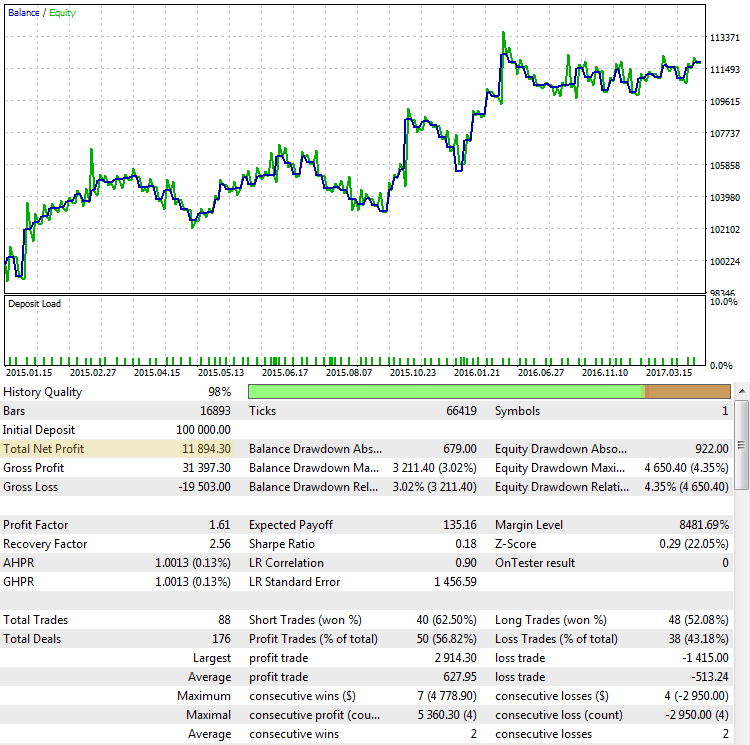
Abb. 2. Die Strategie CImpulse, EURUSD, 1H, 2015.01.15 - 2017.10.01, PeriodMA: 120, StopPercent: 0.67
Die Strategie zeigt ein stetiges Wachstum des Gesamtgewinns in diesem Testintervall. Er ist positiv und beläuft sich auf 11.894 USD für den Handel mit einem Kontrakt. Das ist ein gutes Ergebnis. Aber schauen wir, wie ein anderes Szenario aussieht, bei dem der Endgewinn nahe dem des ersten Beispiels liegt:
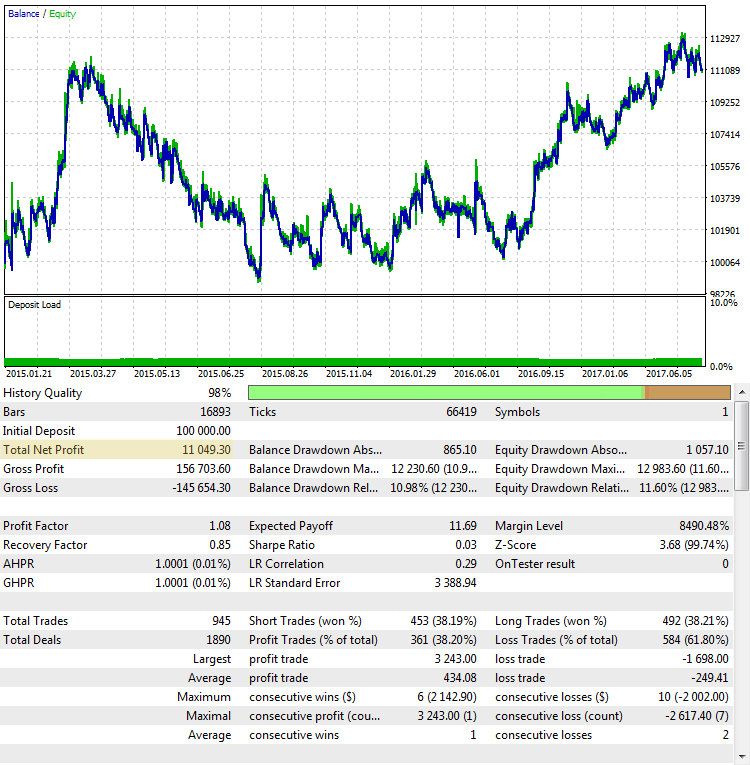
Abb. 3. Die Strategie CImpulse, EURUSD, 1H, 2015.01.15 - 2017.10.01, PeriodMA: 110, StopPercent: 0.24
Trotz der Tatsache, dass der Gewinn in beiden Fällen fast gleich ist, sehen sie wie völlig unterschiedliche Handelssysteme aus. Der endgültige Gewinn im zweiten Fall scheint ebenfalls zufällig zu sein. Wäre der Test Mitte 2015 zu Ende gegangen, wäre der Gewinn nahe Null gewesen.
Hier ist ein weiterer erfolgloser Lauf der Strategie, auch mit einem Endergebnis nahe dem des ersten Beispiels:
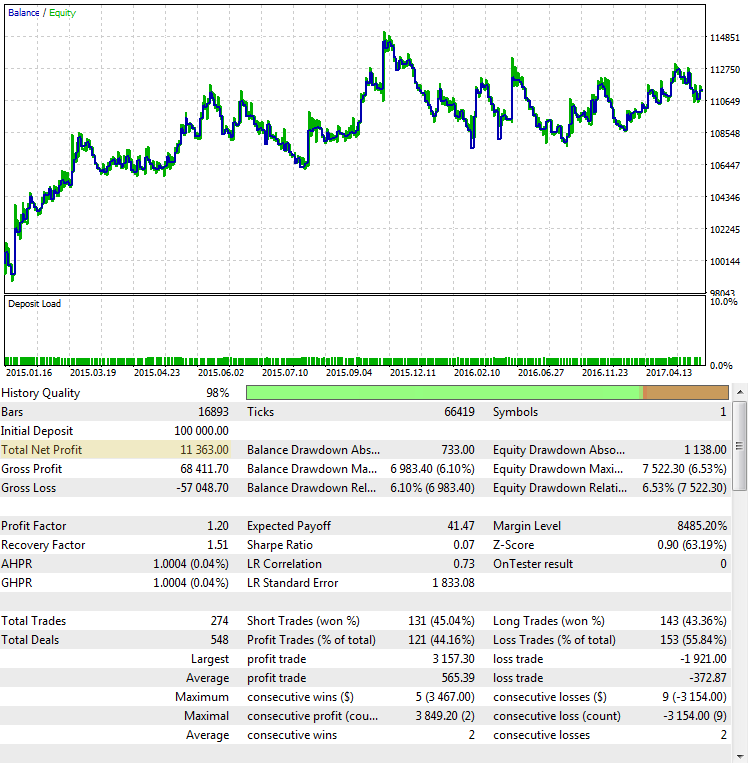
Abb. 4. Die Strategie CImpulse, EURUSD, 1H, 2015.01.15 - 2017.10.01, PeriodMA: 45, StopPercent: 0.44
Aus der Grafik geht hervor, dass der Gewinn überwiegend im ersten Halbjahr 2015 erzielt wurde. Es folgt eine längere Stagnationsphase. Eine solche Strategie ist für den Live-Handel nicht praktikabel.
Profit-Faktor. Der Profit-Faktor ist viel weniger abhängig vom Endergebnis. Sein Wert hängt von jeder Position ab und zeigt das Verhältnis aller gewonnenen Gelder zu allen verlorenen Geldern. Es ist zu erkennen, dass in Abb. 2 der Profit-Faktor recht hoch ist, in Abb. 4 ist er niedriger und in Abb. 3 liegt er fast an der Grenze zwischen profitablen und unrentablen Systemen. Dennoch ist Profit-Faktor kein universelles Merkmal, auch er lässt sich täuschen. Schauen wir uns andere Beispiele an, bei denen der Profit-Faktor nicht so eindeutig sind:
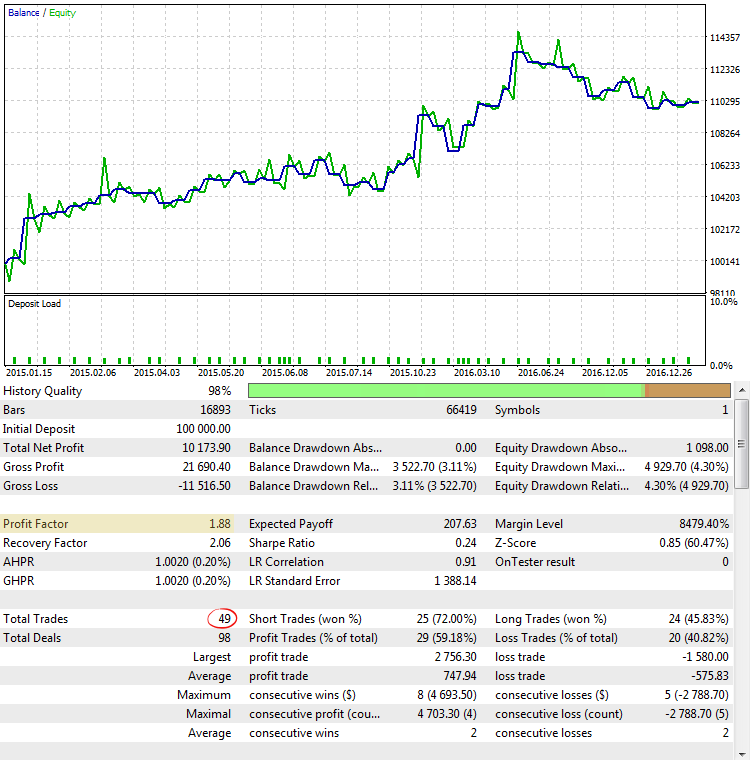
Abb. 5. Die Strategie CImpulse, EURUSD, 1H, 2015.01.15 - 2017.10.01, PeriodMA: 60, StopPercent: 0.82
Abb. 5 zeigt das Ergebnis eines Strategie-Testlaufs mit einem der größten Werte des Profit-Faktors. Die Saldenkurve sieht vielversprechend aus, aber die erhaltene Statistik ist irreführend, da der Profit-Faktor aufgrund der sehr geringen Anzahl von Positionen überhöht ist.
Überprüfen wir diese Aussage auf zweierlei Weise. Der erste Weg: Herausfinden der Abhängigkeit des Profit-Faktors von der Anzahl der Positionen. Dies geschieht durch die Optimierung der Strategie von CImpulse im Strategietester unter Verwendung einer Vielzahl von Parametern:

Abb. 6. Optimierung von CImpulse mit einer Vielzahl von Parameterwerten
Speichern der Ergebnisse der Optimierung:
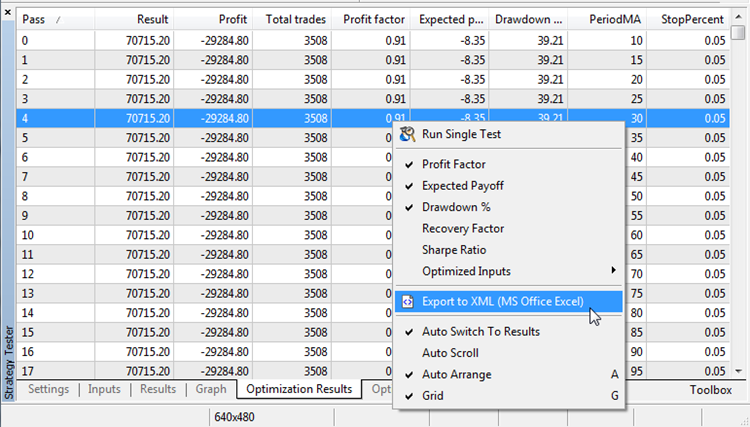
Abb. 7. Exportieren der Ergebnisse der Optimierung
Jetzt können wir ein Abhängigkeitsdiagramm der Werte des Profit-Faktors von der Anzahl der Positionen erstellen. In Excel z.B. geht das ganz einfach, indem man die entsprechenden Spalten auswählt und auf den Knopf für ein Punktdiagramm im Reiter der Diagramme drückt.
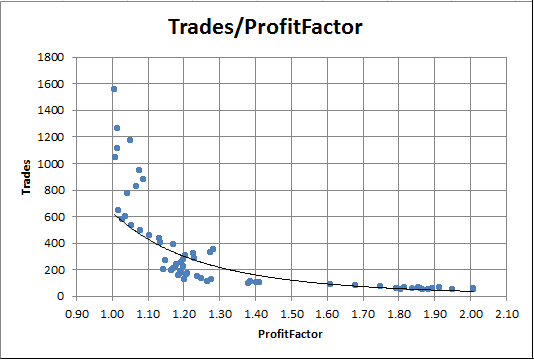
Abb. 8. Abhängigkeit des Profit-Faktors von der Anzahl der Positionen
Die Grafik zeigt deutlich, dass die Durchläufe mit hohem Profit-Faktor immer sehr wenige Positionen haben. Umgekehrt ist der Profit-Faktor bei einer großen Anzahl von Positionen praktisch gleich Eins.
Der zweite Weg, um festzustellen, dass die Werte des Profit-Faktors von der Anzahl der Positionen abhängen und nicht von der Qualität der Strategie, basiert auf einem Out-Of-Sample-Test (OOS). Dies ist übrigens eine der zuverlässigsten Methoden, um die Robustheit der erhaltenen Ergebnisse zu bestimmen. Robustheit ist ein Maß für die Stabilität einer statistischen Methode in Schätzungen. OOS eignet sich nicht nur zum Testen des Profit-Faktors, sondern auch für andere Indikationen. Für unsere Zwecke werden die gleichen Parameter gewählt, aber ein anderes Zeitintervall - von 2012.01.01 bis 2015.01.01.01:
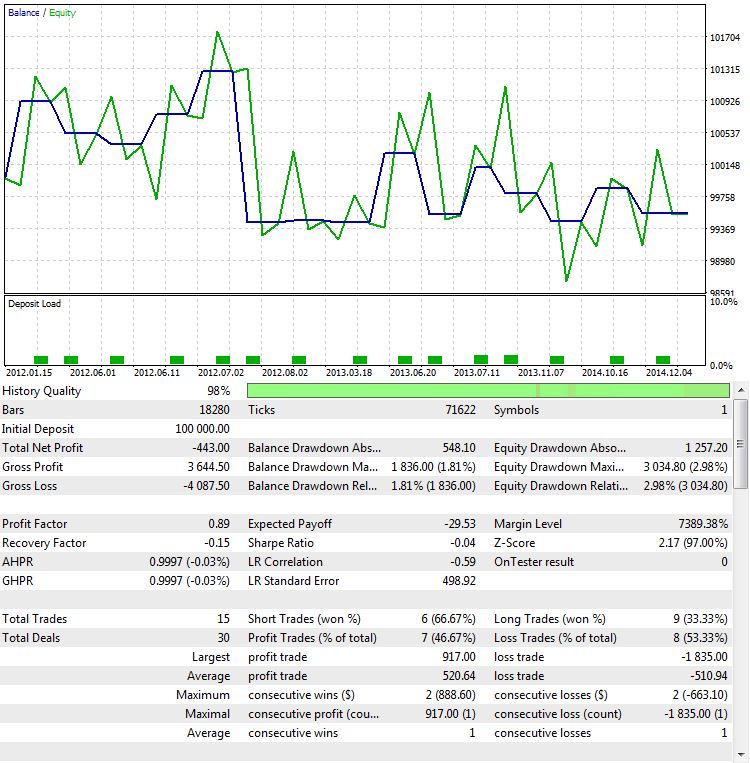
Abb. 9. Die Prüfung der Strategie Out-Of-Sample
Wie man sieht, ist das Verhalten vollkommen anders. Es erzeugt Verlust statt Gewinn. Dies ist ein logisches Ergebnis, da das erhaltene Ergebnis bei einer so geringen Anzahl von Positionen fast immer zufällig ist. Das bedeutet, dass ein zufälliger Gewinn in einem Zeitintervall durch einen Verlust in einem anderen Zeitintervall ausgeglichen wird, was in Abb. 9 gut veranschaulicht wird.
Erwartetes Ergebnis (Expected Payoff). Wir werden uns nicht lange mit diesem Parameter beschäftigen, denn seine Fehler ähneln denen des Profit-Faktors. Hier ist das Abhängigkeitsdiagramm des Erwarteten Ergebnisses von der Anzahl der Positionen:
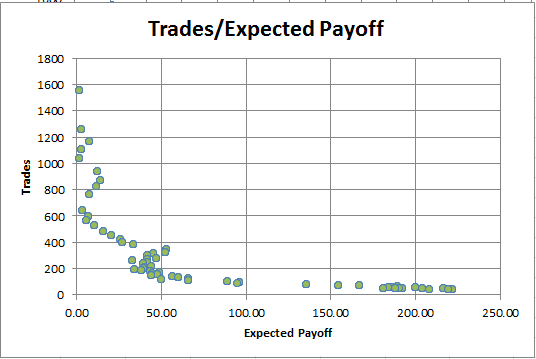
Abb. 10. Die Abhängigkeit dee Erwarteten Ergebnisses von der Anzahl der Positionen
Es zeigt sich, dass je mehr Geschäfte getätigt werden, desto kleiner wird das Erwartete Ergebnis. Diese Abhängigkeit wird sowohl bei profitablen als auch bei unrentablen Strategien immer beobachtet. Daher kann das Erwartete Ergebnis nicht das einzige Kriterium für die Optimalität einer Handelsstrategie sein.
Anforderungen an das Prüfkriterium für Handelssysteme
Nach Prüfung der Hauptkriterien der statistischen Bewertung eines Handelssystems muss gefolgert werden, dass die Anwendbarkeit jedes Kriteriums begrenzt ist. Für jedes von ihnen gibt es Beispiele, deren Messgröße gute Ergebnis suggerieren, die Strategie selbst jedoch nicht.
Es gibt keine idealen Kriterien, um die Robustheit eines Handelssystems zu bestimmen. Aber es ist möglich, Eigenschaften zu formulieren, über die ein starkes, statistisches Kriterium verfügen muss.
- Anforderungen an das Prüfkriterium für ein Handelssystem. Viele Parameter einer Handelsstrategie hängen davon ab, wie lange die Testphase dauert. Zum Beispiel, je größer die getestete Periode für eine profitable Strategie ist, desto größer ist der Endgewinn. Es hängt von der Dauer und dem Erholungsfaktor (recovery factor) ab. Er errechnet sich aus dem Verhältnis des Gesamtgewinns zum maximale Rückschlag (maximum drawdown). Da der Gewinn periodenabhängig ist, wächst der Erholungsfaktor mit der Zunahme der Testperiode mit. Eine Invarianz (Unabhängigkeit) in Bezug auf den Zeitraum ist notwendig, um die Effektivität verschiedener Strategien für verschiedene Testzeiträume zu vergleichen;
- Unabhängigkeit vom Zeitpunkt des Testendes. Wenn zum Beispiel eine Strategie "über Wasser bleibt", indem sie lediglich versucht, virtuelle Verluste offener Positionen auszusitzen, kann der Zeitpunkt des Testendes einen entscheidenden Einfluss auf den letzten Kontostand haben. Wenn der Test im Augenblick eines "Verlust-Aussitzens" beendet wird, wird der nicht realisierte Verlust (Equity) zum realisierten Saldo und ein signifikanter Verlust wird auf das Konto geschrieben. Eine statistische Auswertung sollte vor solchen Betrügereien schützen und einen objektiven Blick auf das Funktionieren des Handelssystems bieten.
- Einfache Interpretation. Alle Parameter des Handelssystems sind quantitativ, d.h. jede Statistik wird durch eine bestimmte Zahl charakterisiert. Diese Zahl muss intuitiv sein. Je einfacher die Interpretation des ermittelten Wertes, desto verständlicher ist der Parameter. Es ist auch wünschenswert, dass der Parameter innerhalb bestimmter Grenzen liegt, da die Analyse großer und potentiell unendlicher Zahlen oft kompliziert ist.
- Gültige Ergebnisse auch bei einer kleinen Anzahl von Positionen. Dies ist wohl die schwierigste Anforderung unter den Merkmalen einer guten Messgröße. Alle statistischen Methoden sind abhängig von der Anzahl der Messungen. Je mehr von ihnen, desto stabiler sind die erhaltenen statistischen Werte. Natürlich ist es unmöglich, dieses Problem in einer kleinen Stichprobe vollständig zu lösen. Es ist jedoch möglich, die Auswirkungen von zu wenig Daten abzumildern. Zu diesem Zweck entwickeln wir zwei Arten der Funktion für die Bewertung von R²: Eine Implementierung wird dieses Kriterium auf der Grundlage der Anzahl der verfügbaren Deals aufbauen. Der andere berechnet das Kriterium anhand des variablen Gewinns der Strategie (Equity).
Bevor wir direkt zur Beschreibung des Bestimmtheitsmaßes R² übergehen, untersuchen wir seine Bestandteile im Detail. Dies wird helfen, den Zweck dieses Parameters und die Prinzipien, auf denen er basiert, zu verstehen.
Lineare Regression
Die Lineare Regression ist die lineare Abhängigkeit einer Variablen y von einer anderen unabhängigen Variablen x, ausgedrückt durch die Formel y = ax+b. In dieser Formel ist а der Multiplikator, b der Bias-Koeffizient. In Wirklichkeit kann es mehrere unabhängige Variablen geben, und ein solches Modell wird als multiples lineares Regressionsmodell bezeichnet. Wir werden jedoch nur den einfachsten Fall betrachten.
Die lineare Abhängigkeit kann in Form eines einfachen Graphen visualisiert werden. Nehmen wir den Tages-Chart EURUSD von 2017.06.21 bis 2017.09.21. Dieses Segment ist nicht zufällig ausgewählt: In diesem Zeitraum war bei diesem Währungspaar ein moderater Aufwärtstrend zu beobachten. So sieht es in MetaTrader aus:
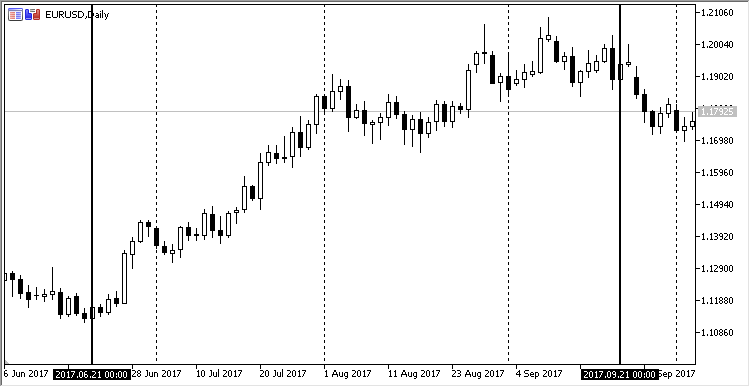
Abb. 11. Die Entwicklung des EURUSD vom 21.06.2017 bis 21.08.2017 im täglichen Zeitrahmen
Speichern wir diese Kursdaten und verwenden sie, um ein Diagramm, z.B. in Excel, zu erstellen.
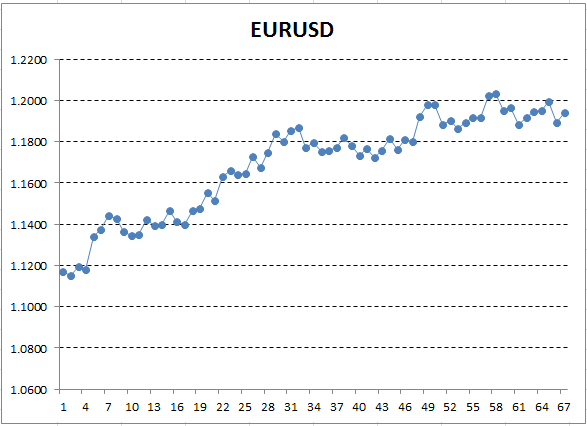
Abb. 12. Die Kurse des EURUSD (Schlusskurse) als Exceldiagramm
Hier entspricht die Y-Achse dem Preis, und X ist die Ordnungszahl der Messung (die Zeiten wurden durch Ordnungszahlen ersetzt). Auf dem resultierenden Diagramm ist der aufsteigende Trend mit bloßem Auge sichtbar, aber wir benötigen eine quantitative Interpretation dieses Trends. Am einfachsten ist es, eine Gerade zu zeichnen, die dem untersuchten Trend am genauesten entspricht. Es wird als Lineare Regression bezeichnet. Zum Beispiel kann die Linie so gezeichnet werden:
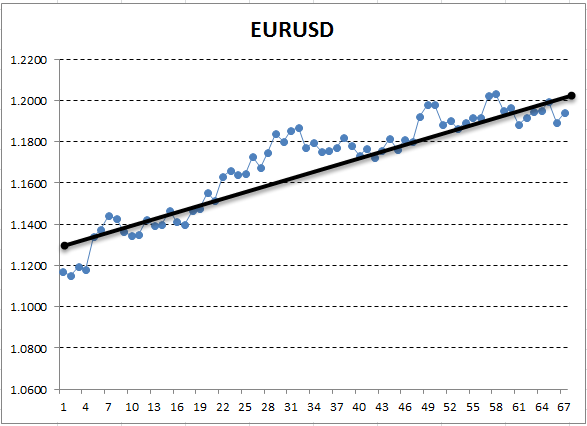
Abb. 13. Die Lineare Regression eines Aufwärtstrends, manuell gezeichnet
Wenn das Diagramm ziemlich glatt ist, ist es möglich, eine solche Linie zu zeichnen, dass die Punkte des Diagramms um den Mindestabstand davon abweichen. Umgekehrt ist es bei einem Graphen mit großer Amplitude nicht möglich, eine Linie auszuwählen, die die Änderungen genau beschreibt. Dies liegt daran, dass die Lineare Regression nur zwei Koeffizienten hat. Tatsächlich haben uns die Geometriestunden gelehrt, dass zwei Punkte ausreichen, um eine Linie zu zeichnen. Aus diesem Grund ist es nicht einfach, eine gerade Linie in einen "gekrümmten" Graphen einzufügen. Dies ist eine wertvolle Eigenschaft, die auch in Zukunft nützlich sein wird.
Aber wie kann man herausfinden, wie man eine gerade Linie richtig zeichnet? Mit mathematischen Methoden können die Linearen Regressionskoeffizienten optimal berechnet werden, so dass alle verfügbaren Punkte die Mindestsumme der Abstände zu dieser Linie haben. Dies wird in der folgenden Tabelle erläutert. Angenommen, es gibt 5 beliebige Punkte und zwei Linien, die durch sie verlaufen. Von den beiden Linien ist es notwendig, diejenige mit der geringsten Summe der Abstände zu den Punkten zu wählen:
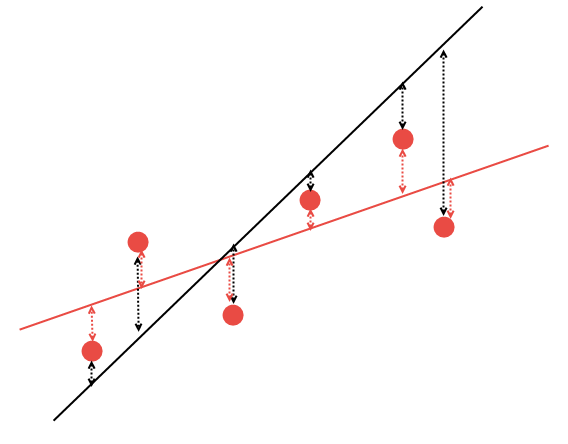
Abb. 14. Die Auswahl der geeigneten Linearen Regression
Es ist klar, dass von den beiden Linearen Regressionsgeraden die rote Linie die gegebenen Daten besser beschreibt: Die Punkte #2 und #6 liegen deutlich näher an der roten Linie als an der schwarzen. Die restlichen Punkte sind ungefähr gleich weit entfernt, sowohl von der schwarzen als auch von der roten Linie. Mathematisch ist es möglich, die Koordinaten der Linie zu berechnen, die diese Regelmäßigkeit am besten beschreiben würde. Berechnen wir diese Koeffizienten aber nicht manuell, sondern verwenden stattdessen die fertige mathematische Bibliothek AlgLib.
Korrelation
Nach der Berechnung der Linearen Regression ist es notwendig, die Korrelation zwischen dieser Linie und den Daten, für die sie berechnet wird, zu ermitteln. Korrelation ist die statistische Beziehung von zwei oder mehr Zufallsvariablen. In diesem Fall bedeutet die Zufälligkeit der Variablen, dass die Messungen dieser Variablen nicht voneinander abhängig sind. Die Korrelation wird von -1,0 bis +1,0 gemessen. Ein Wert nahe Null zeigt an, dass die untersuchten Variablen keine Wechselbeziehungen haben. Der Wert von +1.0 bedeutet eine direkte Abhängigkeit, -1.0 zeigt eine inverse Abhängigkeit. Die Korrelation wird durch verschiedene Formeln berechnet. Hier wird Pearsons Korrelationskoeffizient verwendet:
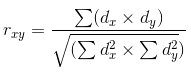
dx und dy in der Formel entsprechen den für die Zufallsvariablen x und y berechneten Varianzen. Die Varianz ist ein Maß für die Variation einer Variablen. Im Allgemeinen kann man es als die Summe der Quadrate der Abstände zwischen den Daten und der Linearen Regression beschreiben.
Der Korrelationskoeffizient der Daten mit einer Linearen Regression zeigt, wie gut die Gerade diese Daten beschreibt. Wenn die Datenpunkte in großer Entfernung von der Linie liegen, ist die Varianz hoch und die Korrelation niedrig und umgekehrt. Die Korrelation ist sehr einfach zu interpretieren: Null bedeutet, dass es keine Wechselbeziehung zwischen Regression und Daten gibt; ein Wert nahe bei Eins zeigt eine starke direkte Abhängigkeit.
Berichte in MetaTrader haben speziellen statistische Messgröße. Sie wird LR-Korrelation genannt und zeigt die Korrelation zwischen der Saldenkurve und der Linearen Regression, die für diese Kurve gefunden wurde. Wenn die Saldenkurve glatt ist, ist die Annäherung an eine gerade Linie gut. In diesem Fall liegt der LR-Korrelationskoeffizient nahe bei 1,0 oder mindestens über 0,5. Ist die Saldenkurve instabil, und wechseln sich Anstiege mit Abstürzen ab, dann tendiert der Korrelationskoeffizient zu Null.
Die LR-Korrelation ist ein interessanter Parameter. In der Statistik ist es jedoch nicht üblich, die Daten und die beschreibende Regression direkt über den Korrelationskoeffizienten zu vergleichen. Der Grund dafür wird im nächsten Abschnitt erläutert.
Das Bestimmtheitsmaß R²
Die Berechnungsmethode für den Bestimmtheitsmaß R² ähnelt der Berechnungsmethode für die LR-Korrelation. Der Endwert wird aber zusätzlich quadriert. Es kann Werte von 0,0 bis +1,0 annehmen. Diese Zahl zeigt den Anteil der erklärten Werte an der Gesamtstichprobe. Die Lineare Regression dient als Erklärungsmodell. Streng genommen muss das Erklärungsmodell keine Lineare Regression sein, sondern es können auch andere verwendet werden. Die Werte von R² erfordern jedoch keine weitere Verarbeitung für eine Lineare Regression. Bei komplexeren Modellen ist die Approximation in der Regel besser und die Werte von R² müssen zusätzlich durch spezielle "Strafen" reduziert werden, um eine adäquate Schätzung zu ermöglichen.
Schauen wir uns genauer an, was das Erklärungsmodell hervorbringt. Dazu führen wir ein kleines Experiment durch: Wir verwenden die spezialisierte Programmiersprache R-Project und generieren einen Random Walk, für den der erforderliche Koeffizient berechnet wird. Random Walk ist ein Prozess mit Eigenschaften, die denen der realen Finanzinstrumenten sehr ähnlich sind. Um einen Random Walk zu erhalten, genügt es, mehrere Zufallszahlen, die nach dem normalverteilt sind, nacheinander zu addieren.
Der Quellcode in R mit einer detaillierten Beschreibung dessen, was getan wird:
x <- rnorm(1000) # Erstellen von 1000 normalverteilte Zufallszahlen # Ihre Varianz ist Eins und der Erwartungswert Null rwalk <- cumsum(x) # Durch die kumulierte Summe dieser Zahlen erhalten wir eine Grafik des klassischen Random Walk plot(rwalk, type="l", col="darkgreen") # Darstellen der Daten in Form eines linearen Grafik rws <- lm(rwalk~c(1:1000)) # Zeichnen des linearen Modells y=a*x+b, mit x der Anzahl der Messungen und y dem Wert des Vektors des Random Walks title("Line Regression of Random Walk") abline(rws) # Anzeigen der resultierenden Linearen Regression auf dem Chart
Die Funktion rnorm gibt jedes Mal andere Daten zurück. Wenn wir also dieses Experiment wiederholen möchten, wird das Diagramm anders aussehen.
Das Ergebnis des obigen Codes:
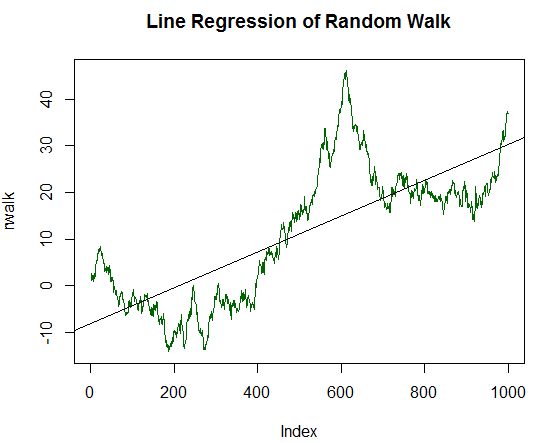
Abb. 15. Der Random Walk und dessen Linearen Regression
Das daraus resultierende Diagramm ähnelt dem eines beliebigen Finanzinstruments. Seine Lineare Regression wurde berechnet und als schwarze Linie des Diagramms ausgegeben. Auf den ersten Blick ist die Beschreibung der Dynamik eines Random Walk eher mittelmäßig. Aber wir brauchen eine quantitative Abschätzung der Qualität der Linearen Regression. Dazu wird die Funktion 'summary' verwendet, die ein zusammenfassende Statistik über das Regressionsmodell ausgibt:
summary(rws) Call: lm(formula = rwalk ~ c(1:1000)) Residuals: Min 1Q Median 3Q Max -16.082 -6.888 -1.593 4.174 30.787 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -8.187185 0.585102 -13.99 <2e-16 *** c(1:1000) 0.038404 0.001013 37.92 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 9.244 on 998 degrees of freedom Multiple R-squared: 0.5903, Adjusted R-squared: 0.5899 F-statistic: 1438 on 1 and 998 DF, p-value: < 2.2e-16
Hier ist eine Zahl am interessantesten - R². Diese Messgröße beträgt 0,5903. Folglich beschreibt die Lineare Regression 59,03% aller Werte, während die restlichen 41% ungeklärt bleiben.
Dies ist ein sehr sensibler Indikator, der gut auf eine glatte, flache Datenlinie reagiert. Um dies zu veranschaulichen, setzen wir das Experiment fort: Einführung einer stabilen Wachstumskomponente in die Zufallsdaten. Ändern wir dazu den Mittelwert oder den Erwartungswert um 1/20 der Abweichung der ursprünglich erzeugten Daten:
x_trend1 <- x+(sd(x)/20.0) # Ermitteln der Standardabweichung der Werte von x, dividieren durch 20.0 und summiere das Ergebnis zu jeden Wert von x # Jeder der so geänderten Werte von x werden dem neuen Vektor x_trend1 zugewiesen rwalk_t1 <- cumsum(x_trend1) # Durch die kumulierte Summe dieser Zahlen erhalten wir eine Grafik des Random Walk plot(rwalk_t1, type="l", col="darkgreen") # Anzeigen der Daten als lineare Grafik title("Line Regression of Random Walk #2") rws_t1 <- lm(rwalk_t1~c(1:1000))# Zeichnen des linearen Modells y=a*x+b, mit x, der Anzahl der Messungen, und y, dem Wert des Vektors des Random Walks abline(rws_t1) # Anzeige der resultierenden Linearen Regression auf dem Chart
Das Ergebnis ist einer geraden Linie viel ähnlicher:
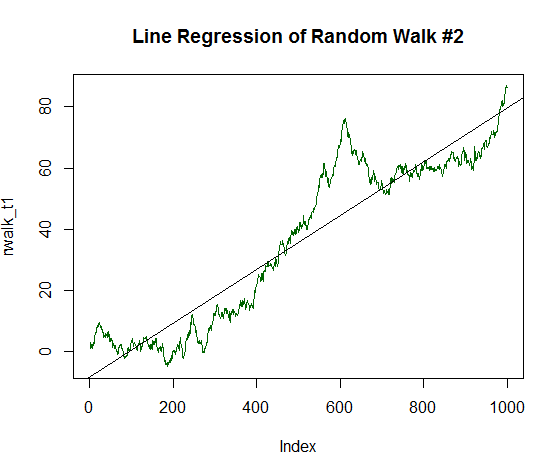
Abb. 16. Der Random Walk mit einem positiven Erwartungswert, der gleich 1/20 seiner Varianz beträgt
Dessen Statistik ergibt Folgendes:
summary(rws_t1) Call: lm(formula = rwalk_t1 ~ c(1:1000)) Residuals: Min 1Q Median 3Q Max -16.082 -6.888 -1.593 4.174 30.787 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -8.187185 0.585102 -13.99 <2e-16 *** c(1:1000) 0.087854 0.001013 86.75 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 9.244 on 998 degrees of freedom Multiple R-squared: 0.8829, Adjusted R-squared: 0.8828 F-statistic: 7526 on 1 and 998 DF, p-value: < 2.2e-16
Es ist klar, dass R² deutlich höher ist und einen Wert von 0,8829 hat. Aber befassen wir uns nicht weiter damit, sondern verdoppeln wir die Bestimmungskomponente des Diagramms, bis zu 1/10 der Standardabweichung der Ausgangsdaten. Der Code dafür ist ähnlich wie der vorherige Code, jedoch mit der Division durch 10.0 und nicht durch 20.0. Das neue Diagramm gleicht nun fast vollständig einer geraden Linie:
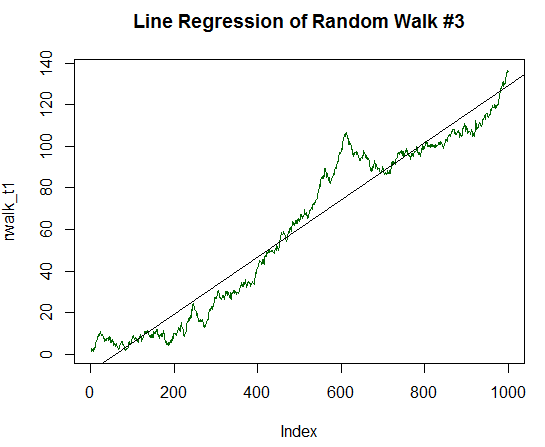
Abb. 17. Der Random Walk mit einem positiven Erwartungswert, der gleich 1/10 seiner Varianz beträgt
Berechnung der Statistik:
Call: lm(formula = rwalk_t1 ~ c(1:1000)) Residuals: Min 1Q Median 3Q Max -16.082 -6.888 -1.593 4.174 30.787 4 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -8.187185 0.585102 -13.99 <2e-16 *** c(1:1000) 0.137303 0.001013 135.59 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 9.244 on 998 degrees of freedom Multiple R-squared: 0.9485, Adjusted R-squared: 0.9485 F-statistic: 1.838e+04 on 1 and 998 DF, p-value: < 2.2e-16
R² wurde noch höher und betrug 0,9485. Diese Grafik ist sehr ähnlich der Balance-Dynamik der gewünschten profitablen Handelsstrategie. Ignorieren wir aber auch das. Erhöhen wir den Erwartungswert auf bis zu 1/5 der Standardabweichung:
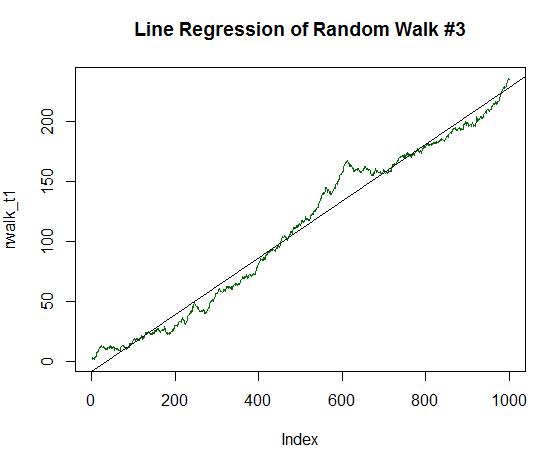
Abb. 18. Der Random Walk mit einem positiven Erwartungswert, der gleich 1/5 seiner Varianz beträgt
Berechnung der Statistik:
Call: lm(formula = rwalk_t1 ~ c(1:1000)) Residuals: Min 1Q Median 3Q Max -16.082 -6.888 -1.593 4.174 30.787 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -8.187185 0.585102 -13.99 <2e-16 *** c(1:1000) 0.236202 0.001013 233.25 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 9.244 on 998 degrees of freedom Multiple R-squared: 0.982, Adjusted R-squared: 0.982 F-statistic: 5.44e+04 on 1 and 998 DF, p-value: < 2.2e-16
Es ist klar, dass R² jetzt fast gleich Eins ist. Die Grafik zeigt deutlich, dass die Zufallsdaten in Form der grünen Linie fast vollständig auf der glatten Geraden liegen.
Der Satz des Arcsinus und sein Beitrag zur Schätzung der Linearen Regression
Es gibt einen mathematischen Beweis dafür, dass sich ein Zufallsprozess immer weiter von seinem Ausgangspunkt entfernt. Das nennt man den ersten und den zweiten Satz des Arcsinus. Sie werden nicht im Detail besprochen, nur die logische Konsequenz dieser Theoreme wird definiert.
Auf ihrer Grundlage sind Trends in zufälligen Prozessen eher unvermeidlich als unwahrscheinlich. Mit anderen Worten, es gibt mehr zufällige Trends in solchen Prozessen als zufällige Schwankungen in der Nähe des Ausgangspunktes. Dies ist eine sehr wichtige Eigenschaft, die einen wesentlichen Beitrag zur Auswertung statistischer Kennzahlen leistet. Dies zeigt sich besonders deutlich beim Linearen Regressionskoeffizienten (LR-Korrelation). Trends lassen sich besser durch eine Lineare Regression beschreiben, die flach ist. Dies ist darauf zurückzuführen, dass Trends mehr Bewegungen in eine Richtung enthalten, was zu einer glatten Linie führt.
Wenn es mehr Trends in zufälligen Prozessen als Seitwärtsbewegungen gibt, dann wird die LR-Korrelation auch ihre Werte im Allgemeinen überschätzen. Um diesen nicht-trivialen Effekt zu sehen, erzeugen wir 10000 unabhängige Random Walks mit einer Varianz von 1,0 und einem Erwartungswert von Null. Berechnen wir die LR-Korrelation für jedes dieser Diagramme und stellen dann eine Verteilung dieser Werte grafisch dar. Für diese Zwecke schreiben wir ein einfaches Testskript in R:
sample_r2 <- function(samples = 100, nois = 1000) { lags <- c(1:nois) r2 <- 0 # R^2 rating lr <- 0 # Line Correlation rating for(i in 1:samples) { white_nois <- rnorm(nois) walk <- cumsum(white_nois) model <- lm(walk~lags) summary_model <- summary(model) r2[i] <- summary_model$r.squared*sign(walk[nois]) lr[i] <- (summary_model$r.squared^0.5)*sign(walk[nois]) } m <- cbind(r2, lr) }
Das Skript berechnet die LR-Korrelation und R². Der Unterschied zwischen ihnen wird sich später zeigen. Das Skript wurde um eine kleine Ergänzung erweitert. Der resultierende Korrelationskoeffizient wird mit dem Endzeichen des synthetischen Graphen multipliziert. Wenn das Endergebnis kleiner als Null ist, ist die Korrelation negativ, andernfalls positiv. Dies geschieht, um negative Ergebnisse einfach und schnell von positiven zu trennen, ohne auf andere statistische Werte zurückgreifen zu müssen. So funktioniert die LR-Korrelation in MetaTrader 5, das gleiche Prinzip wird auch für R² verwendet.
Also zeichnen wir die Verteilung der LR-Korrelation für 10000 unabhängige Stichproben, von denen jede aus 1000 Messungen besteht:
ms <- sample_r2(10000, nois=1000) hist(ms[,2], breaks = 30, col="darkgreen", density = 30, main = "Distribution of LR-Correlation")
Das Ergebnis zeigt deutlich :Die Richtigkeit der Definition:
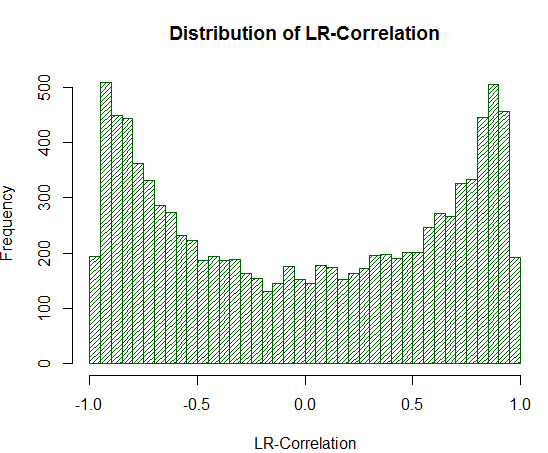
Abb. 19. Die Verteilung der LR-Korrelation für 10000 Random Walks
Wie aus dem Experiment hervorgeht, werden die Werte der LR-Korrelation im Bereich von +/- 0,75 - 0,95 deutlich überschätzt. Das bedeutet, dass die LR-Korrelation oft fälschlicherweise eine hohe positive Schätzung abgibt, wo sie es nicht sollte.
Betrachten wir nun, wie sich R² bei derselben Stichprobe verhält:
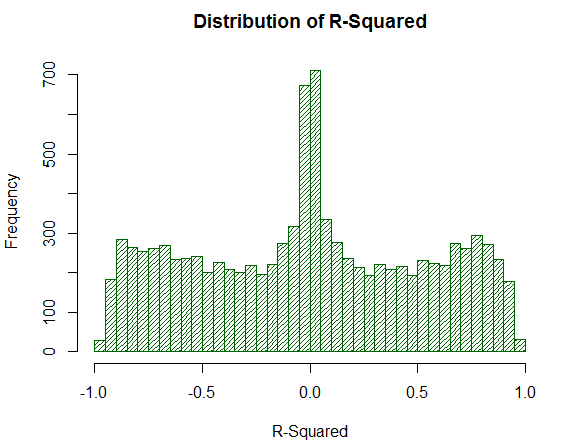
Abb. 20. Verteilung für R² von 10000 Random Walks
Der Wert von R² ist nicht zu hoch, obwohl dessen Verteilung einheitlich sind. Es ist erstaunlich, wie eine einfache mathematische Handlung (Quadrieren) die unerwünschten Spitzeneffekte der Verteilung vollständig negiert. Aus diesem Grund kann die LR-Korrelation nicht direkt analysiert werden - eine zusätzliche mathematische Transformation ist notwendig. Zu beachten ist auch, dass R² einen signifikanten Teil der analysierten virtuellen Salden von Strategien auf einen Punkt nahe Null verschiebt, während die LR-Korrelation ihnen stabile Durchschnittsschätzungen liefert. Das ist eine positive Eigenschaft.
Aufzeichnen der Equity-Werte einer Strategie
Nachdem wir die Theorie besprochen haben, kann R² im Terminal des Metatraders implementiert werden. Natürlich könnten wir den einfachen Weg gehen und ihn mit den Positionen aus der Historie berechnen. Es wird jedoch eine weitere Verbesserung eingeführt. Wie bereits erwähnt, muss jeder statistische Parameter gegenüber einer kleinen Anzahl von Positionen resistent sein. Leider kann R² seinen Wert unangemessen erhöhen, wenn es nur wenige Positionen, wie jede andere Statistik auch. Um dies zu vermeiden, wird auf Basis der Werte des Equity berechnet — den nicht realisierten Gewinnen. Die Idee dahinter ist, dass, wenn der EA nur 20 Positionen pro Jahr erzeugt, es sehr schwierig ist, seine Effizienz einzuschätzen. Das Ergebnis ist höchstwahrscheinlich zufällig. Aber wenn der Saldo dieses EAs mit einer bestimmten Periodizität (z.B. einmal pro Stunde) gemessen wird, gibt es eine Menge Messwerte für die Darstellung der Statistik. In diesem Fall werden es mehr als 6000 sein.
Darüber hinaus wirkt eine solche Messung Systemen entgegen, die ihre nicht realisierten Verluste aussitzen. Diese Drawdowns sind in der Equity vorhanden, nicht aber im Saldo. Eine auf der Grundlage der Salden berechnete Statistik warnt nicht vor auftretenden Problemen. Eine Kennzahl, die unter Berücksichtigung des nicht realisierter Gewinn/Verluste berechnet wird, spiegelt jedoch die objektive Situation auf dem Konto wider.
Das Equity einer Strategie wird auf unkonventionelle Weise gesammelt. Dies liegt daran, dass die Erhebung dieser Werte zwei Hauptpunkte erfordert, die berücksichtigt werden müssen:
- Häufigkeit der Erhebung der Werte
- Ermittlung von Ereignissen, deren Empfang eine Überprüfung des Equitys erfordert.
Ein Expert Advisor arbeitet z.B. nur per Timer im H1-Zeitfenster. Es wird im Modus "Nur Eröffnungspreise" getestet. Daher können die Daten für diesen EA nicht mehr als einmal pro Stunde gesammelt werden, und die Überprüfung dieser Daten kann nur dann durchgeführt werden, wenn das OnTimer-Ereignis ausgelöst wird. Die effektivste Lösung ist, einfach die Leistungsfähigkeit der CStrategy-Engine zu nutzen. Tatsache ist, dass CStrategy alle Ereignisse in einer einzigen Ereignisbehandlung sammelt und den erforderlichen Zeitrahmen automatisch überwacht. Die Lösung von optima besteht also darin, eine spezielle Agentenstrategie zu schreiben, die alle erforderlichen statistischen Werte berechnet. Es wird vom CManagerList Strategy Manager erstellt. Die Klasse wird nur ihren Agenten in die Liste der Strategien aufnehmen, die die Änderungen am Konto überwachen.
Der Quellcode dieses Agenten lautet wie folgt:
//+------------------------------------------------------------------+ //| UsingTrailing.mqh | //| Copyright 2017, Vasiliy Sokolov. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2017, Vasiliy Sokolov." #property link "https://www.mql5.com" #include "TimeSeries.mqh" #include "Strategy.mqh" //+------------------------------------------------------------------+ //| Integriert sich als Experte in das Portfolio von Strategien | //| zeichnet Equity auf | //+------------------------------------------------------------------+ class CEquityListener : public CStrategy { private: //-- Aufzeichnungsfrequenz CTimeSeries m_equity_list; double m_prev_equity; public: CEquityListener(void); virtual void OnEvent(const MarketEvent& event); void GetEquityArray(double &array[]); }; //+------------------------------------------------------------------+ //| Festlegen einer Standardfrequenz | //+------------------------------------------------------------------+ CEquityListener::CEquityListener(void) : m_prev_equity(EMPTY_VALUE) { } //+------------------------------------------------------------------+ //| Aufzeichnen aller möglichen Equity-Werte | //| events | //+------------------------------------------------------------------+ void CEquityListener::OnEvent(const MarketEvent &event) { if(!IsTrackEvents(event)) return; double equity = AccountInfoDouble(ACCOUNT_EQUITY); if(equity != m_prev_equity) { m_equity_list.Add(TimeCurrent(), equity); m_prev_equity = equity; } } //+------------------------------------------------------------------+ //| Rückgabe des der Equity-Werte als Array vom Typ double | //+------------------------------------------------------------------+ void CEquityListener::GetEquityArray(double &array[]) { m_equity_list.ToDoubleArray(0, array); }
Der Agent selbst besteht aus zwei Methoden: Einer neu definierten Methode OnEvent und einer Methode zur Rückgabe der Equity-Werte. Hier liegt das Hauptinteresse auf der Klasse CTimeSeries, die erstmals in CStrategy erscheint. Es handelt sich um eine einfache Tabelle, bei der die Daten im Format: Datum, Wert, Spaltennummer hinzugefügt werden. Alle gespeicherten Werte werden nach der Zeit sortiert. Der Zugriff auf das gewünschte Datum erfolgt über die binäre Suche, was die Arbeit mit der Sammlung erheblich beschleunigt. Die Methode OnEvent prüft, ob das aktuelle Ereignis das Öffnen eines neuen Balkens ist, und wenn ja, speichert sie einfach den neuen Equity-Wert.
R² reagiert auf eine Situation, in der es lange Zeit keine Deals mehr gibt. Zu diesem Zeitpunkt werden die unveränderten Equity-Werte aufgezeichnet. Die Equity-Grafik bildet eine sogenannte "Leiter". Um dies zu verhindern, vergleicht die Methode den Wert mit dem vorherigen Wert. Stimmen die Werte überein, wird der Datensatz übersprungen. Somit kommen nur die Veränderungen des Equity in die Liste.
Integrieren wir jetzt diese Klasse in die CStrategy-Engine. Die Integration erfolgt von oben, auf der Ebene von CStrategyList. Dieses Modul ist für die Berechnung von benutzerdefinierten, statistischen Werte geeignet. Es kann mehrere dieser benutzerdefinierten, statistischen Werte geben. Daher wird eine Enumeration aller möglichen Statistikarten eingeführt:
//+------------------------------------------------------------------+ //| Bestimmt den Typ des benutzerdefinierten Kriteriums, | //| berechnet nach der Optimierung. | //+------------------------------------------------------------------+ enum ENUM_CUSTOM_TYPE { CUSTOM_NONE, // Benutzerdefinierte Kriterium wird nicht berechnet CUSTOM_R2_BALANCE, // R² auf Basis der Salden CUSTOM_R2_EQUITY, // R² auf Basis des Equity };
Die obige Aufzählung zeigt, dass das benutzerdefinierte Optimierungskriterium drei Typen hat: R² auf Basis der Ergebnisse der Positionen, R² auf Basis der Equity-Werte und keine Berechnung der statistischen Werte.
Fügen wir die Möglichkeit hinzu, die Art der benutzerdefinierten Berechnung zu konfigurieren. Versorgen wir dazu die Klasse CStrategyList mit zusätzlichen Methoden SetCustomOptimaze*:
//+------------------------------------------------------------------+ //| Setzt R² als Kriterium der Optimierung. Der Koeffizient ist | //| berechnet für geschlossenen Positionen. | //+------------------------------------------------------------------+ void CStrategyList::SetCustomOptimizeR2Balance(ENUM_CORR_TYPE corr_type) { m_custom_type = CUSTOM_R2_BALANCE; m_corr_type = corr_type; } //+------------------------------------------------------------------+ //| Setzt R² als Kriterium der Optimierung. Der Koeffizient ist | //| berechnet auf Basis der aufgezeichneten Equity-Werte. | //+------------------------------------------------------------------+ void CStrategyList::SetCustomOptimizeR2Equity(ENUM_CORR_TYPE corr_type) { m_custom_type = CUSTOM_R2_EQUITY; m_corr_type = corr_type; }
Jede dieser Methoden setzt den Wert ihrer internen Variablen von ENUM_CUSTOM_TYPE auf m_custom_type und den zweiten Parameter, gleich der Korrelationsart ENUM_CORR_TYPE:
//+------------------------------------------------------------------+ //| Korrelation Typ | //+------------------------------------------------------------------+ enum ENUM_CORR_TYPE { CORR_PEARSON, // Pearsons Korrelation CORR_SPEARMAN // Spearmans Rangkorrelation };
Dieser zusätzliche Parameter muss gesondert behandelt werden. Tatsache ist, dass R² nichts anderes ist als die Korrelation zwischen dem Graphen und seinem linearen Modell. Die Korrelationsart selbst kann sich jedoch unterscheiden. Verwenden wir die mathematische Bibliothek AlgLib. Sie unterstützt zwei Methoden zur Berechnung der Korrelation: Pearsons und Spearmans. Pearsons Formel ist klassisch und gut geeignet für homogene, normal verteilte Daten. Spearmans Rangkorrelation ist widerstandsfähiger gegen Preisspitzen, die häufig auf dem Markt beobachtet werden. Daher wird unsere Berechnung es ermöglichen, mit jeder Variante der Berechnung von R² zu arbeiten.
Nachdem alle Daten vorbereitet sind, fahren wir mit der Berechnung von R² fort. Sie wird in gesonderte Funktionen verschoben:
//+------------------------------------------------------------------+ //| Rückgabe von R² auf Basis der Kontosalden | //+------------------------------------------------------------------+ double CustomR2Balance(ENUM_CORR_TYPE corr_type = CORR_PEARSON); //+------------------------------------------------------------------+ //| Rückgabe von R² auf Basis des Equity | //| Die Equity-Werte werden im Array 'equity' übergeben | //+------------------------------------------------------------------+ double CustomR2Equity(double& equity[], ENUM_CORR_TYPE corr_type = CORR_PEARSON);
Sie befinden sich in einer separaten Datei namens RSquare.mqh. Die Berechnung ist in Form von Funktionen angeordnet, so dass der Anwender diesen Berechnungsmodus einfach und schnell in sein Projekt einbinden kann. In diesem Fall ist es nicht notwendig, CStrategy zu verwenden. Um z.B. R² in Ihrem Experten zu berechnen, definieren wir einfach die Systemfunktion OnTester neu:
double OnTester() { return CustomR2Balance(); }
Wenn es jedoch notwendig ist, die Strategie Equity zu berechnen, müssen Benutzer, die CStrategy nicht einsetzen, dies selbst tun.
Das letzte, was in CStrategyList getan werden muss, ist die Definition der Methode OnTester:
//+------------------------------------------------------------------+ //| Ergänzen der Überwachung des Equity | //+------------------------------------------------------------------+ double CStrategyList::OnTester(void) { switch(m_custom_type) { case CUSTOM_NONE: return 0.0; case CUSTOM_R2_BALANCE: return CustomR2Balance(m_corr_type); case CUSTOM_R2_EQUITY: { double equity[]; m_equity_exp.GetEquityArray(equity); return CustomR2Equity(equity, m_corr_type); } } return 0.0; }
Betrachten wir nun die Implementierung der Funktionen CustomR2Equity und CustomR2Balance.
Berechnung des Bestimmtheitsmaßes R² mittels AlgLib
Der Bestimmtheitsmaß R² wird implementiert und Verwendung von AlgLib — einer plattformübergreifenden Bibliothek für numerische Analysen. Es hilft bei der Berechnung verschiedener, statistischer Kriterien, von einfachen bis hin zu den fortgeschrittensten.
Hier sind die Schritte zur Berechnung des Koeffizienten.
- Holen wir uns die Equity-Werte und wandeln sie in die Matrix M[x, y] um, wobei x die Zahl der Messungen und y der Wert des Equity ist.
- Berechnen wir für die erhaltene Matrix die Koeffizienten a und b der Linearen Regressionsgleichung.
- Generieren wir die Linearen Regressionswerte für jedes X und fügen Sie sie in das Array ein.
- Ermitteln wir den Korrelationskoeffizienten der Linearen Regression und die Equity-Werte anhand einer der beiden Korrelationsformeln.
- Berechnen von R² und dessen Vorzeichens.
- Rückgabe des normalisierten Wertes von R² an die aufrufende Funktion.
Diese Schritte werden von der Funktion CustomR2Equity durchgeführt. Der Quellcode ist wie folgt:
//+------------------------------------------------------------------+ //| Rückgabe von R² auf Basis des Equity | //| Die Equity-Werte werden im Array 'equity' übergeben | //+------------------------------------------------------------------+ double CustomR2Equity(double& equity[], ENUM_CORR_TYPE corr_type = CORR_PEARSON) { int total = ArraySize(equity); if(total == 0) return 0.0; //-- Der Matrix zuweisen: Y - Equity-Wert, X - Ordnungszahl des Wertes CMatrixDouble xy(total, 2); for(int i = 0; i < total; i++) { xy[i].Set(0, i); xy[i].Set(1, equity[i]); } //-- Ermitteln der Koeffizienten a und b für das lineare Modell y = a*x + b; int retcode = 0; double a, b; CLinReg::LRLine(xy, total, retcode, a, b); //-- Erzeugen der Werte der Linearen Regression für jedes X; double estimate[]; ArrayResize(estimate, total); for(int x = 0; x < total; x++) estimate[x] = x*a+b; //-- Ermitteln des Koeffizienten der Korrelation der Werte mit der Linearen Regression double corr = 0.0; if(corr_type == CORR_PEARSON) corr = CAlglib::PearsonCorr2(equity, estimate); else corr = CAlglib::SpearmanCorr2(equity, estimate); //-- Finde R² und dessen Vorzeichen double r2 = MathPow(corr, 2.0); int sign = 1; if(equity[0] > equity[total-1]) sign = -1; r2 *= sign; //-- Rückgabe von der normalisierten Schätzung von R², auf Hundertstel genau return NormalizeDouble(r2,2); }
Dieser Code bezieht sich auf drei statistische Methoden: CAlgLib::LRLine, CAlglib::PearsonCorr2 und CAlglib::SpearmanCorr2. Die wichtigste ist CAlgLib::LRLine, die direkt die Linearen Regressionskoeffizienten berechnet.
Beschreiben wir nun die zweite Funktion zur Berechnung von R²: CustomR2Balance. Wie der Name schon sagt, berechnet diese Funktion den Wert auf der Grundlage der geschlossenen Positionen. All seine Arbeit besteht darin, ein Array vom Typ double zu bilden, das die Salden enthält, indem es über alle geschlossenen Positionen iteriert.
//+------------------------------------------------------------------+ //| Rückgabe von R² auf Basis der Kontosalden | //+------------------------------------------------------------------+ double CustomR2Balance(ENUM_CORR_TYPE corr_type = CORR_PEARSON) { HistorySelect(0, TimeCurrent()); double deals_equity[]; double sum_profit = 0.0; int current = 0; int total = HistoryDealsTotal(); for(int i = 0; i < total; i++) { ulong ticket = HistoryDealGetTicket(i); double profit = HistoryDealGetDouble(ticket, DEAL_PROFIT); if(profit == 0.0) continue; if(ArraySize(deals_equity) <= current) ArrayResize(deals_equity, current+16); sum_profit += profit; deals_equity[current] = sum_profit; current++; } ArrayResize(deals_equity, current); return CustomR2Equity(deals_equity, corr_type); }
Sobald das Array gebildet ist, wird es an die zuvor erwähnte CustomR2Equity-Funktion übergeben. Tatsächlich ist die CustomR2Equity-Funktion universell einsetzbar. Sie berechnet den Wert von R² für alle Daten, die im Array equity[] enthalten sind, unabhängig davon, ob es sich um die Salden- oder die Equity-Version handelt.
Der letzte Schritt ist eine kleine Änderung im Code des CImpulse EA, nämlich die Übersteuerung des OnTester-Systemereignisses:
//+------------------------------------------------------------------+ //| Tester Ereignis | //+------------------------------------------------------------------+ double OnTester() { Manager.SetCustomOptimizeR2Balance(CORR_PEARSON); return Manager.OnTester(); }
Diese Funktion setzt den Typ des benutzerdefinierten Parameters und gibt dann seinen Wert zurück.
Jetzt können wir den berechneten Koeffizienten in Aktion sehen. Sobald der Backtest mit der Strategie von CImpulse gestartet ist, erscheint der Parameter im Report:
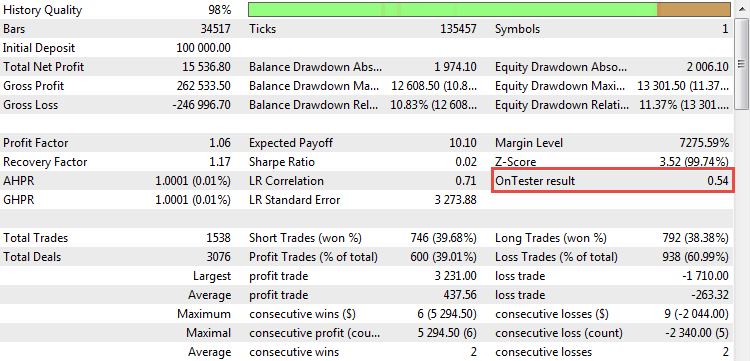
Abb. 21. Der Wert von R² als nutzerdefiniertes Optimierungskriterium
Praktische Anwendung des Parameters R²
Jetzt, da R² als benutzerdefiniertes Optimierungskriterium eingebaut ist, ist es an der Zeit, es in der Praxis auszuprobieren. Dies geschieht durch die Optimierung von CImpulse im Zeitrahmen М15 des EURUSD-Währungspaares. Speichern wir das erhaltene Ergebnis der Optimierung in einer Excel-Datei und vergleichen wir sie dann anhand der erhaltenen statistischen Werte mehrere Läufe, die nach verschiedenen Kriterien ausgewählt wurden.
Die vollständige Liste der Optimierungsparameter findet sich weiter unten:
- Symbol: EURUSD
- Zeitrahmen: H1
- Zeitraum: 2015.01.03 - 2017.10.10
Der Bereich der Parameter des EAs ist in der Tabelle aufgeführt:
| Parameter | Start | Step | Stop Sign | Number of steps |
|---|---|---|---|---|
| PeriodMA | 15 | 5 | 200 | 38 |
| StopPercent | 0.1 | 0.05 | 1.0 | 19 |
Nach der Optimierung erhalten wir eine Punktewolke der Optimierungen aus den 722 Varianten:
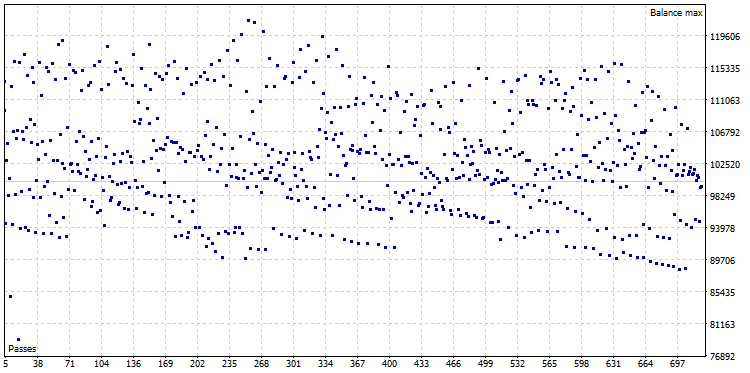
Abb. 22. Die Punktwolke der Optimierung von CImpulse, Symbol - EURUSD, Zeitrahmen - H1
Wählen wir den Testlauf mit dem maximalen Profit und zeigen die Saldenkurve:
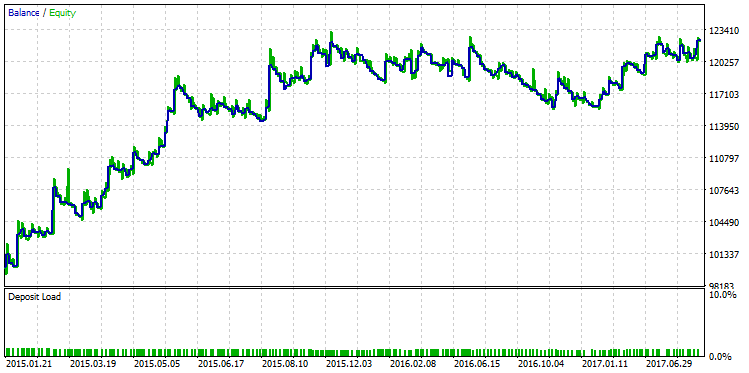
Abb. 23. Saldenkurve der Strategie, ausgewählt nach dem Kriterium des maximalen Gewinns
Suchen wir nun den besten Lauf entsprechend dem Parameter R². Vergleichen wir dazu die Optimierungsläufe in der XML-Datei. Wenn Microsoft Excel auf dem Computer installiert ist, wird die Datei automatisch darin geöffnet. Die Arbeiten umfassen Sortierung und Filterung. Wählen wir uns den Tabellentitel und drücken dann den gleichnamigen Button (Home -> Sortieren & Filtern -> Filtern). Damit ist es möglich, die Darstellung der Spalten individuell anzupassen. Sortieren wir die Läufe nach dem benutzerdefinierten Optimierungskriterium:
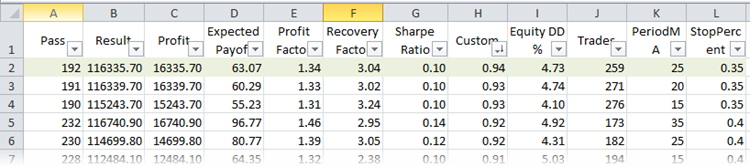
Abb. 24. Optimierungsläufe in Microsoft Excel, sortiert nach R²
Die erste Zeile in der Tabelle hat den besten Wert von R² der gesamten Stichprobe. In der obigen Abbildung ist sie grün markiert. Dieser Satz von Parametern im Strategie-Tester gibt einen Saldenkurve, das wie folgt aussieht:
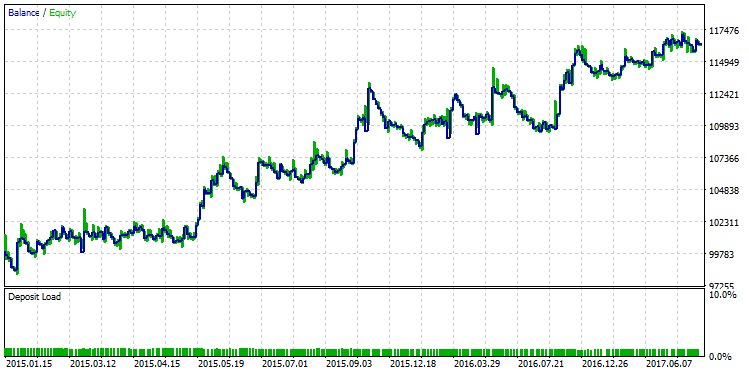
Abb. 25. Saldenkurve einer Strategie, die nach dem Kriterium des maximalen R² ausgewählt wurde.
Der qualitative Unterschied zwischen diesen beiden Saldenkurven ist mit bloßem Auge sichtbar. Während im Dezember 2015 der Testlauf mit dem maximalen Gewinn "einbrach", setzte die andere Variante mit dem maximalen R² ihr stetiges Wachstum fort.
Oftmals hängt R² von der Anzahl der Positionen ab und kann bei kleinen Stichprobe zu hohe Werte aufweisen. Insofern korreliert R² mit dem Profit-Faktor. Bei bestimmten Strategietypen gehen ein hoher Wert des Profit-Faktors und ein hoher Wert von R^2 Hand in Hand. Dies ist jedoch nicht immer der Fall. Zur Veranschaulichung wählen wir ein Gegenbeispiel aus der Stichprobe, das den Unterschied zwischen R² und Profit-Faktor verdeutlicht. Die folgende Abbildung zeigt einen Testlauf mit einem der höchsten Profit-Faktor-Werte von 2,98:
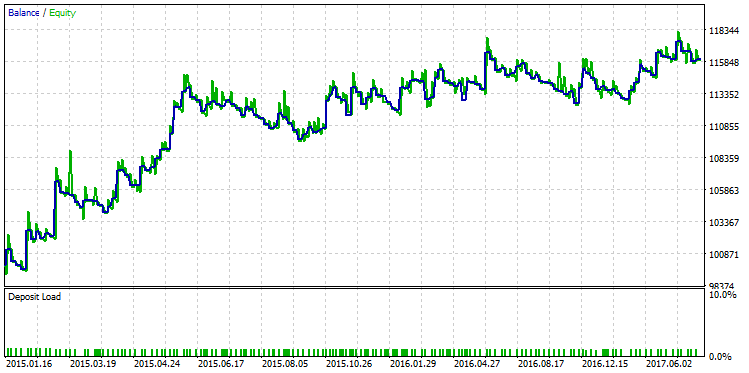
Abb. 26. Testlauf der Strategie mit einem Profit-Faktor von 2.98
Die Grafik zeigt, dass, obwohl die Strategie ein stetiges Wachstum aufweist, die Qualität der Saldenkurve der Strategie immer noch niedriger ist als diejenige mit dem maximalen R².
Vorteile und Einschränkungen
Jede statistische Kennzahl hat ihre Vor- und Nachteile. R² bildet da keine Ausnahme. Die folgende Tabelle zeigt die Fehler und Lösungen, die sie mildern können:
| Nachteile | Die Lösung |
|---|---|
| Abhängig von der Zahl der Positionen. Überhöhte Wert durch eine kleine Zahl von Positionen. | Berechnen von R² auf Basis des Equity löst teilweise das Problem. |
| Korreliert mit den bestehenden Messgrößen der Strategieeffektivität, insbesondere mit dem Profit-Faktor und dem Reingewinn der Strategie. | Die Korrelation liegt nicht bei 100%. Abhängig von den Merkmalen der Strategie kann es vorkommen, dass R² mit keiner anderen Messgröße korreliert oder schwach korreliert. |
| Die Berechnung erfordert komplexe, mathematische Berechnungen. | Der Algorithmus wird mit Hilfe der Bibliothek AlgLib implementiert, an die die gesamte Komplexität delegiert wird. |
| Ausschließlich für die Schätzung von linearen Prozessen oder Systemen, die mit einem festen Los handeln. | Nicht anwendbar auf Handelssysteme, die ein Kapitalisierungssystem verwenden (Money Management). |
Beschreiben wir das Problem der Anwendung von R² auf nichtlineare Systeme (z.B. eine Handelsstrategie mit einem dynamischen Lot) genauer.
Das Hauptziel eines jeden Händlers ist die Maximierung des Gewinns. Eine notwendige Voraussetzung dafür ist der Einsatz verschiedener Kapitalisierungssysteme. Das Kapitalisierungssystem ist die Umwandlung eines linearen Prozesses in einen nichtlinearen Prozess (z.B. in einen exponentiellen Prozess). Aber eine solche Transformation macht die meisten statistischen Parameter bedeutungslos. So ist z.B. der Parameter "Endgewinn" für kapitalisierte Systeme bedeutungslos, da schon eine leichte Verschiebung der Zeitintervallprüfung oder die Änderung eines Strategieparameters um ein Hundertstel Prozent das Endergebnis um das Zehn- oder Hundertfache verändern kann.
Auch andere Parameter der Strategie verlieren an Bedeutung, wie z.B. Profit-Faktor, Erwartetes Ergebnis, maximaler Gewinn/Verlust, etc. In diesem Sinne bildet auch R² keine Ausnahme. Erstellt für die lineare Schätzung der Gleichgewichtskurvenglätte, wird sie bei der Bewertung nichtlinearer Prozesse machtlos. Daher sollte jede Strategie in linearer Form getestet werden, und erst danach sollte der gewählten Option ein Kapitalisierungssystem hinzugefügt werden. Besser ist es, nichtlineare Systeme mit speziellen statistischen Kenngrößen (z.B. GHPR) auszuwerten oder den Ertrag in Jahresprozenten zu berechnen.
Schlussfolgerung
- Die statistischen Standardparameter für die Bewertung von Handelssystemen haben bekannte Nachteile, die es zu berücksichtigen gilt.
- Unter den Standardmessgrößen in MetaTrader 5 kann nur die LR-Korrelation die Glätte der Saldenkurve einer Strategie abzuschätzen. Allerdings sind seine Werte oft überhöht.
- R² ist eine der wenigen Messgrößen, die die Glätte sowohl der Saldenkurve als auch die der Equitykurve einer Strategie berechnen kann. Gleichzeitig ist R² frei von den Nachteilen der LR-Korrelation.
- Die mathematische Bibliothek AlgLib wird bei der Berechnung von R² verwendet. Die Berechnung selbst hat viele Modifikationen und wird im entsprechenden Beispiel ausführlich beschrieben.
- Das benutzerdefinierte Optimierungskriterium kann in einen Expert Advisor integriert werden, so dass alle Experten diese Messgröße automatisch und ohne ihre Beteiligung berechnen können. Eine Anleitung dazu findet sich im Beispiel der Integration von R² in die CStrategy Trading Engine.
- Eine ähnliche Integrationsmethode kann verwendet werden, um zusätzliche Daten zu berechnen, die für die Berechnung von benutzerdefinierten, statistischen Werte benötigt werden. Für R² sind dies die Daten der nicht realisierten Gewinne der Strategie (Equity). Die Aufzeichnung der nicht realisierten Gewinne erfolgt durch die CStrategy Trading Engine.
- Das Bestimmtheitsmaß ermöglicht die Auswahl von Strategien mit einem Wachstum des Saldos/Eigenkapitals. In diesem Fall kann es vorkommen, dass der Auswahlprozess, der auf anderen Parametern basiert, solche Varianten verpasst.
- R² hat, wie jede andere statistische Kennzahl, seine Nachteile, die bei der Arbeit mit diesem Wert berücksichtigt werden müssen.
So ist es sicher zu sagen, dass der Bestimmtheitsmaß R² eine wichtige Ergänzung zum bestehenden Satz der Messgrößen des MetaTrader 5 ist. Sie erlaubt es, die Glätte der Saldenkurve einer Strategie abzuschätzen, die für sich genommen ein nicht-trivialer Indikator ist. R² ist einfach zu verwenden: Seine Werte sind an den Bereich von -1,0 bis +1,0 gebunden und signalisieren einen negativen Trend der Strategie (Werte nahe -1,0), keinen Trend (Werte nahe 0,0) oder einen positiven Trend (Werte nahe +1,0). Dank all dieser Eigenschaften, Zuverlässigkeit und Einfachheit kann R² für den Einsatz beim Aufbau eines profitablen Handelssystems empfohlen werden.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/2358
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Verwendung des Kalman-Filters für die Prognose der Preisrichtung
Verwendung des Kalman-Filters für die Prognose der Preisrichtung
 Testen der Muster, die beim Handel mit Körben von Währungspaaren auftreten. Teil II
Testen der Muster, die beim Handel mit Körben von Währungspaaren auftreten. Teil II
 Die Eröffnung durch Indikatoren bestimmen lassen
Die Eröffnung durch Indikatoren bestimmen lassen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Es gibt hier eine Menge Informationen, die die Gründe und den Code erklären, und ich weiß das zu schätzen. Hier ist die Tl;dr-Version für diejenigen von uns, für die das meiste davon ging über unsere Köpfe:
1. Fügen Sie die Includes hinzu
2. Und den OnTester:
Das ist es, es auf der Grundlage der Balance zu implementieren.
Wenn Ihr EA CStrategy verwendet (wie die Assistenten EAs tun), dann fügen Sie die gleichen umfasst, und Sie können auf das Eigenkapital wie diese wechseln:
Was ich noch nicht herausgefunden habe, und ich hoffe, dass mir jemand dabei helfen kann, ist, wie man den Equity Listener in einem eigenen EA implementiert, der nicht auf CStrategy basiert. Alles, was der Artikel sagt, ist:
Und ich bin völlig ratlos, wie ich das anstellen soll.Die Fehler wurden behoben. Das Archiv ist beigefügt.
Danke, habe den Artikel aktualisiert.
Es sollte sehr ähnlich sein... ein Vergleich steht auf meiner langen, unorganisierten ToDo-Liste!
Normalisieren Sie das Volumen: Nehmen Sie den Gewinn und teilen Sie ihn durch die Losgröße.
Oder teilen Sie balance[0] durch balance[1], um die Rendite zu erhalten, und berechnen Sie r^2 für die Renditekurve