Usando el filtro de Kalman en la predicción del precio

MetaTrader 5 — Sistemas comerciales | 17 noviembre 2017, 14:23

4 666

Introducción

En el gráfico de cotizaciones de las monedas o acciones, siempre vemos las fluctuaciones de precios que se diferencian por su frecuencia y la amplitud. Nuestro objetivo consiste en determinar las tendencias principales tras estos movimientos cortos y largos. Para eso, algunos trazan las líneas de tendencia en el gráfico, otros utilizan los indicadores. En ambos casos, nuestro objetivo es filtrar el movimiento verdadero del precio separándolo del ruido provocado por la influencia de algunos factores insignificantes que afectan el precio a corto plazo. En este artículo, yo propongo separar los ruidos parásitos usando el filtro de Kalman (KF).

La idea de usar los filtros digitales no es nueva en el trading. Yo también ya he contado sobre el uso de los filtros de frecuencia baja. Pero, como se dice, la perfección no tiene límites. Y en busca de las mejores estrategias, vamos a considerar una variante más, y comparar los resultados.

1. Principio del trabajo del filtro de Kalman

Pues, ¿qué es el filtro de Kalman y por qué merece la pena fijarnos en él? La Wikipedia da la siguiente definición.

El filtro de Kalman es un filtro recursivo eficaz que estima el vector del estado de un sistema dinámico, usando una serie de las dimensiones incompletas y ruidosas.

Es decir, esta herramienta fue desarrollada desde el principio para trabajar con los datos ruidosos. También es capaz de trabajar con datos incompletos. Y, finalmente, otra ventaja más que posee, es que ha sido diseñado y se usa para los sistemas dinámicos, a los que pertenece nuestro gráfico de precios.

El trabajo del filtro está dividido en dos fases:

Extrapolación (predicción)
Corrección

1.1. Extrapolación es la predicción de los valores del sistema

La base de la primera etapa del trabajo del filtro es algún modelo del proceso analizado. De acuerdo con este modelo, se construye la predicción del estado del sistema a un paso adelante.

(1.1)

Donde:

xk — valor extrapolado del sistema dinámico en el paso k,
Fk — matriz del modelo de la dependencia del estado actual del sistema de su estado anterior,
x^k-1 — estado anterior del sistema (valor del filtro en el paso anterior),
Bk — matriz de la influencia del impacto de control en el sistema,
uk — impacto de control en el sistema.

Bajo el impacto de control se puede considerar, por ejemplo, el factor de noticias. Pero en la práctica, el impacto de control generalmente se desconoce y se omite, y su impacto se refiere a los ruidos.

Luego, se predice el error de la covarianza del sistema:

(1.2)

Donde:

Pk — matriz extrapolada de covarianza del vector del estado de nuestro sistema dinámico,
Fk — matriz del modelo de la dependencia del estado actual del sistema de su estado anterior,
P^k-1 — matriz de covarianza del vector del estado corregida en el paso anterior,
Qk — matriz de covarianza del ruido del proceso.

1.2. Corrección de los valores del sistema

La segunda etapa del trabajo del filtro del proceso se empieza con la medición del estado real del sistema zk. Aquí, el valor medido del estado del sistema prácticamente se indica tomando en cuenta el estado real del sistema y el error de mediciones. En nuestro caso, bajo el error de mediciones se entienden los impactos de ruidos en el sistema dinámico.

Hasta este momento, en nuestra disposición tenemos dos valores diferentes que representan el estado de un proceso dinámico. Se trata del valor extrapolado del sistema dinámico que hemos calculado en la primera etapa, y prácticamente del valor medido. Cada uno de estos valores, con un determinado grado de probabilidad, caracteriza el estado real de nuestro proceso que se encuentra en algún punto entre estos dos. Por tanto, nuestro objetivo consiste en determinar el grado de confianza hacia uno u otro valor. Precisamente para eso se realizan las iteraciones del segundo etapa del filtro de Kalman.

Basándose en los datos existentes, determinamos la desviación del estado real del sistema del valor extrapolado.

(2.1)

Aquí:

yk — desviación del estado real del sistema en el paso k del extrapolado,
zk — estado real del sistema en el paso k,
Hk — matriz de las mediciones que refleja la dependencia del estado real del sistema de los datos calculado (en la práctica, a menudo adquiere el valor de uno),
xk — valor extrapolado del sistema dinámico en el paso k.

En el siguiente paso se calcula la matriz de covarianza para el vector del error:

(2.2)

Aquí:

Sk — matriz de covarianza para el vector del error en el paso k,
Hk — matriz de las mediciones que refleja la dependencia del estado real del sistema de los datos calculado,
Pk — matriz extrapolada de covarianza del vector del estado de nuestro sistema dinámico,
Rk — matriz de covarianza del ruido de mediciones.

Luego, se determina el valor óptimo de así llamados coeficientes de reforzamiento, que prácticamente reflejan un grado de confianza al valor calculado y al valor empírico.

(2.3)

Aquí:

Kk — matriz de los coeficientes de reforzamiento de Kalman,
Pk — matriz extrapolada de covarianza del vector del estado de nuestro sistema dinámico,
Hk — matriz de las mediciones que refleja la dependencia del estado real del sistema de los datos calculado,
Sk — matriz de covarianza para el vector del error en el paso k,

Ahora, basándose en los coeficientes de Kalman, corregimos el valor del estado de nuestro sistema y la matriz de covarianza de la estimación del vector del estado.

(2.4)

Donde:

x^k y x^k-1 — valores corregidos en el paso k y k-1,
Kk — matriz de los coeficientes de reforzamiento de Kalman,
yk — desviación del estado real del sistema en el paso k del extrapolado.

(2.5)

Donde:

P^k — matriz corregida de covarianza del vector del estado de nuestro sistema dinámico,
I — matriz de la identidad,
Kk — matriz de los coeficientes de reforzamiento de Kalman,
Hk — matriz de las mediciones que refleja la dependencia del estado real del sistema de los datos calculado,
Pk — matriz extrapolada de covarianza del vector del estado de nuestro sistema dinámico.

Podemos esquematizar todo lo que hemos dicho arriba.

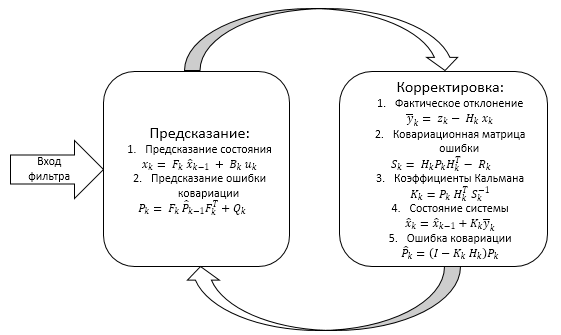
2. Implementación práctica del filtro de Kalman

Bien, hemos hecho una idea de cómo trabaja el filtro de Kalman. Vamos a realizar su implementación práctica. La representación de matriz de las fórmulas del filtro descrita antes supone que nosotros obtenemos los datos de varias fuentes. Pero yo propongo construir el filtro a base de los precios de cierre de las barras, y simplificar así la representación de matriz hasta la representación discreta.

2.1. Inicialización de datos iniciales

Antes de empezar a escribir el código, vamos a aclarar el tema de los datos fuente.

Como ya ha sido dicho antes, el filtro de Kalman se basa en el modelo de un proceso dinámico, y según este modelo se predice el siguiente estado de este proceso. Inicialmente, este filtro fue propuesto para trabajar con sistemas lineales en los cuales el estado actual del sistema se establece fácilmente a través del coeficiente respecto al estado anterior. Nosotros lo tenemos más difícil: en nuestro caso, no se trata de un sistema lineal, sino de un sistema dinámico donde el coeficiente se cambia paso a paso. Es más, no tenemos ni menor idea de la dependencia entre dos estados lindantes del sistema. Podría parecer que el problema no tiene solución. Pero vamos a recurrir a la astucia usando los modelos autoregresivos descritos en los artículos [1],[2],[3].

Pues bien, empezamos. Primero, declaramos la clase CKalman, y dentro de ella, las variables necesarias.

class CKalman
  {
private:
//---
   uint              ci_HistoryBars;               //Bars for analysis
   uint              ci_Shift;                     //Shift of autoregression calculation
   string            cs_Symbol;                    //Symbol
   ENUM_TIMEFRAMES   ce_Timeframe;                 //Timeframe
   double            cda_AR[];                     //Autoregression coefficients
   int               ci_IP;                        //Number of autoregression coefficients
   datetime          cdt_LastCalculated;           //Time of LastCalculation;
   
   bool              cb_AR_Flag;                   //Flag of autoregression calculation
//--- Values of Kalman's filter
   double            cd_X;                         // X
   double            cda_F[];                      // F array
   double            cd_P;                         // P
   double            cd_Q;                         // Q
   double            cd_y;                         // y
   double            cd_S;                         // S
   double            cd_R;                         // R
   double            cd_K;                         // K
   
public:
                     CKalman(uint bars=6240, uint shift=0, string symbol=NULL, ENUM_TIMEFRAMES period=PERIOD_H1);
                    ~CKalman();
   void              Clear_AR_Flag(void)  {  cb_AR_Flag=false; }
  };

Declaramos los valores iniciales a las variables dentro de la función de la inicialización de la clase.

CKalman::CKalman(uint bars, uint shift, string symbol, ENUM_TIMEFRAMES period)
  {
   ci_HistoryBars =  bars;
   cs_Symbol      =  (symbol==NULL ? _Symbol : symbol);
   ce_Timeframe   =  period;
   cb_AR_Flag     =  false;
   ci_Shift       =  shift;
   cd_P           =  1;
   cd_K           =  0.9;
  }

Para construir el modelo autoregresivo, he usado el algoritmo del artículo [1]. Para eso, añadimos dos funciones private a la clase.

   bool              Autoregression(void);
   bool              LevinsonRecursion(const double &R[],double &A[],double &K[]);

La función LevinsonRecursion ha sido traspasada sin alteraciones. En cuanto a la función Autoregression, la he modificado un poco, por eso vamos a estudiarla más detalladamente. Al principio de la función, comprobamos la presencia del historial necesario para el análisis, y si no es suficiente, se devuelve false.

bool CKalman::Autoregression(void)
  {
   //--- check for insufficient data
   if(Bars(cs_Symbol,ce_Timeframe)<(int)ci_HistoryBars)
      return false;

Cargamos el historial necesario en el array, y llenamos el array de los coeficientes reales de la dependencia del estado actual del sistema del estado anterior.

//---
   double   cda_QuotesCenter[];                          //Data to calculate

//--- make all prices available
   double close[];
   int NumTS=CopyClose(cs_Symbol,ce_Timeframe,ci_Shift+1,ci_HistoryBars+1,close)-1;
   if(NumTS<=0)
      return false;
   ArraySetAsSeries(close,true);
   if(ArraySize(cda_QuotesCenter)!=NumTS)
     {
      if(ArrayResize(cda_QuotesCenter,NumTS)<NumTS)
         return false;
     }
   for(int i=0;i<NumTS;i++)
      cda_QuotesCenter[i]=close[i]/close[i+1];           // Calculate coefficients

Después de realizar los trabajos preparativos, determinamos el número de los coeficientes del modelo autoregresivo y calculamos sus valores.

   ci_IP=(int)MathRound(50*MathLog10(NumTS));
   if(ci_IP>NumTS*0.7)
      ci_IP=(int)MathRound(NumTS*0.7);                         // Autoregressive model order
  
   double cor[],tdat[];
   if(ci_IP<=0 || ArrayResize(cor,ci_IP)<ci_IP || ArrayResize(cda_AR,ci_IP)<ci_IP || ArrayResize(tdat,ci_IP)<ci_IP)
      return false;
   double a=0;
   for(int i=0;i<NumTS;i++)
      a+=cda_QuotesCenter[i]*cda_QuotesCenter[i];    
   for(int i=1;i<=ci_IP;i++)
     {  
      double c=0;
      for(int k=i;k<NumTS;k++)
         c+=cda_QuotesCenter[k]*cda_QuotesCenter[k-i];
      cor[i-1]=c/a;                                            // Autocorrelation
     } 
  
   if(!LevinsonRecursion(cor,cda_AR,tdat))                     // Levinson-Durbin recursion
      return false;

Convertimos la suma de los coeficientes de autoregresión obtenidos a "1" y establecemos el conmutador del cálculo realizado en el estado true.

   double sum=0;
   for(int i=0;i<ci_IP;i++)
     {
      sum+=cda_AR[i];
     }
   if(sum==0)
      return false;
  
   double k=1/sum;
   for(int i=0;i<ci_IP;i++)
      cda_AR[i]*=k;

   cb_AR_Flag=true;

Luego, inicializamos las variables necesarias para el filtro. Como covarianza del ruido de las mediaciones, vamos a coger la desviación media cuadrática de los valores close para el período analizado.

   cd_R=MathStandardDeviation(close);

Para determinar el valor de la covarianza del ruido del proceso, primero calcularemos el array de los valores del modelo autoregresivo y cogeremos la desviación media cuadrática de los valores del modelo.

   double auto_reg[];
   ArrayResize(auto_reg,NumTS-ci_IP);
   for(int i=(NumTS-ci_IP)-2;i>=0;i--)
     {
      auto_reg[i]=0;
      for(int c=0;c<ci_IP;c++)
        {
         auto_reg[i]+=cda_AR[c]*cda_QuotesCenter[i+c];
        }
     }
   cd_Q=MathStandardDeviation(auto_reg);

Prácticamente, copiamos los coeficientes de la dependencia del estado actual del sistema respecto al estado anterior al array cda_F para usarlos luego en los cálculos de nuevos coeficientes.

   ArrayFree(cda_F);
   if(ArrayResize(cda_F,(ci_IP+1))<=0)
      return false;
   ArrayCopy(cda_F,cda_QuotesCenter,0,NumTS-ci_IP,ci_IP+1);

Para el valor inicial de nuestro sistema cogemos la media aritmética de 10 últimos valores.

   cd_X=MathMean(close,0,10);

2.2. Predicción del movimiento del precio

Después de obtener todos los datos iniciales para trabajar con el filtro, se puede empezar con su implementación práctica. La primera etapa del trabajo del filtro de Kalman, como ya se ha mencionado antes, es la extrapolación del estado del sistema a un paso adelante. Creamos la función public Forecast, en la que serán implementadas las funciones 1.1. y 1.2.

double            Forecast(void);

Al principio de la función, comprobamos si está calculado ya el modelo regresivo. Si es necesario, llamamos la función para el cálculo. Si el recálculo del modelo falla, se devuelve EMPTY_VALUE,

double CKalman::Forecast()
  {
   if(!cb_AR_Flag)
     {
      ArrayFree(cda_AR);
      if(Autoregression())
        {
         return EMPTY_VALUE;
        }
     }

Luego, calculamos el coeficiente de la dependencia del estado actual del estado anterior y lo guardamos en la celda "0" del array cda_F, moviendo previamente sus valores a una celda.

   Shift(cda_F);
   cda_F[0]=0;
   for(int i=0;i<ci_IP;i++)
      cda_F[0]+=cda_F[i+1]*cda_AR[i];

Después de eso, recalculamos el estado del sistema y la probabilidad del error.

   cd_X=cd_X*cda_F[0];
   cd_P=MathPow(cda_F[0],2)*cd_P+cd_Q;

Al final de la función, devuelve el estado pronosticado del sistema. En nuestro caso, es el precio pronosticado del cierre de nueva barra.

   return cd_X;
  }

2.3. Corrección del estado del sistema

En la siguiente etapa, después de obtener el valor real del cierre de la barra, hagamos la corrección del sistema. Para eso, creamos la función Correction tipo public. En sus parámetros, vamos a pasar el valor obtenido prácticamente del estado del sistema, es decir, el precio del cierre de la última barra.

double            Correction(double z);

En esta función, tenemos implementado el apartado teórico 1.2. del presente artículo. Su código completo se puede encontrar en el anexo. Cuando la función termina su trabajo, devuelve el valor corregido del estado del sistema.

3. Demostración del trabajo del filtro de Kalman en la práctica

Vamos a testear el trabajo de la clase del filtro de Kalman en la práctica. Para eso, creamos un pequeño indicador en base de la clase. Va a llamar a la función de la corrección del sistema cuando se abre una vela nueva, y luego llamará a la función de la predicción para predecir el precio del cierre de la barra actual. No se asuste de la permutación de la llamada a las funciones de la clase, es que vamos a llamar a la función de la corrección del estado para la barra anterior (cerrada), y la predicción del precio del cierre para la barra actual (barra recién abierta), cuyo precio del cierre aun desconocemos.

En el indicador habrá 2 búferes. Los valores pronosticados del estado del sistema van a introducirse en el primero, y los valores corregidos, en el segundo. He hecho dos búferes con premeditación par que el indicador no se redibuje y se pueda ver los volúmenes de la corrección del sistema en la segunda etapa del trabajo del filtro. El código del indicador no es complejo, se adjunta al artículo. Aquí, muestro los resultados de su trabajo.

Filtro de Kalman en el gráfico

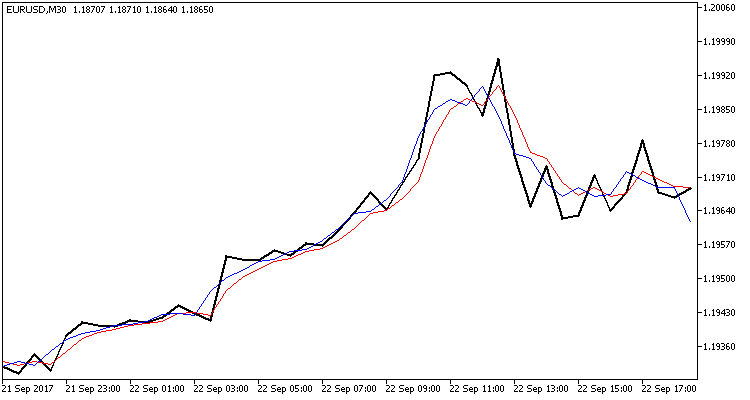
En este gráfico puede ver tres líneas quebradas:

Línea negra — precio real del cierre de las barras;
Línea roja — precio pronosticado del cierre;
Línea azul — estado del sistema corregido por el filtro de Kalman.

Como vemos, ambas líneas están cerca de los precios reales del cierre, y muestran los momentos de la reversión con buen grado de probabilidad. Me gustaría mencionar otra vez que el indicador no se redibuja y la línea roja se construye en el momento de la apertura de la barra, cuando el precio del cierre todavía se desconoce.

El gráfico completo muestra la viabilidad del trabajo del filtro en cuestión y la posibilidad de la construcción del sistema comercial con su uso.

4. Creamos el módulo de las señales comerciales para el generador de los Asesores Expertos en MQL5

Observando el gráfico de arriba, se puede notar que la línea roja de la predicción del estado del sistema es más suavizada en comparación con la línea real del precio. Y la línea azul que corrige el estado del sistema siempre se encuentra entre otras dos. En otras palabras, si la línea azul está por encima de la roja, eso indica en la tendencia alcista. Y al revés, la línea azul por debajo de la roja indica en la tendencia bajista. Por tanto, la intersección de la línea azul y la roja es la señal sobre el cambio de la tendencia.

Para probar esta estrategia, creamos el módulo de las señales comerciales para el generador de los Asesores Expertos en MQL5. La técnica de la creación de los módulos de las señales comerciales fue descrita varias veces en los artículos de esta web: [1], [4], [5]. Ya ha llegado la hora para contar brevemente sobre los momentos que se refieren a nuestra estrategia.

Primero, creamos la clase del módulo CSignalKalman, que se hereda de CExpertSignal. Puesto que nuestra estrategia está construida en el uso del filtro de Kalman, tenemos que declarar en nuestra clase la instancia de la clase CKalman creada antes. Puesto que nosotros declaramos la instancia de la clase CKalman en el módulo, entonces vamos a iniciarlo en el módulo también. Para eso, en su lugar, necesitamos pasar los parámetros iniciales en el módulo. En el código, la solución de estas tareas es la siguiente:

//+---------------------------------------------------------------------------+
// wizard description start
//+---------------------------------------------------------------------------+
//| Description of the class                                                  |
//| Title=Signals of Kalman's filter degign by DNG                            |
//| Type=SignalAdvanced                                                       |
//| Name=Signals of Kalman's filter degign by DNG                             |
//| ShortName=Kalman_Filter                                                   |
//| Class=CSignalKalman                                                       |
//| Page=https://www.mql5.com/es/articles/3886                                |
//| Parameter=TimeFrame,ENUM_TIMEFRAMES,PERIOD_H1,Timeframe                   |
//| Parameter=HistoryBars,uint,3000,Bars in history to analysis               |
//| Parameter=ShiftPeriod,uint,0,Period for shift                             |
//+---------------------------------------------------------------------------+
// wizard description end
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalKalman: public CExpertSignal
  {
private:
   ENUM_TIMEFRAMES   ce_Timeframe;        //Timeframe
   uint              ci_HistoryBars;      //Bars in history to analysis
   uint              ci_ShiftPeriod;      //Period for shift
   CKalman          *Kalman;              //Class of Kalman's filter
   //---
   datetime          cdt_LastCalcIndicators;
   
   double            cd_forecast;         // Forecast value
   double            cd_corretion;        // Corrected value
   //---
   bool              CalculateIndicators(void);
       
public:
                     CSignalKalman();
                    ~CSignalKalman();
   //---
   void              TimeFrame(ENUM_TIMEFRAMES value);
   void              HistoryBars(uint value);
   void              ShiftPeriod(uint value);
   //--- method of verification of settings
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);
  };

En la función de la inicialización de la clase, asignamos el valor predefinido a las variables e inicializamos la clase del filtro de Kalman.

CSignalKalman::CSignalKalman(void):    ci_HistoryBars(3000),
                                       ci_ShiftPeriod(0),
                                       cdt_LastCalcIndicators(0)
  {
   ce_Timeframe=m_period;
   
   if(CheckPointer(m_symbol)!=POINTER_INVALID)
      Kalman=new CKalman(ci_HistoryBars,ci_ShiftPeriod,m_symbol.Name(),ce_Timeframe);
  }

El cálculo del estado del sistema usando el filtro se realiza en private de la función CalculateIndicators. Al principio de la función, comprobamos si se calculan los valores del filtro en la barra actual. Si los valores ya están recalculados, salimos de la función.

bool CSignalKalman::CalculateIndicators(void)
  {
   //--- Check time of last calculation
   datetime current=(datetime)SeriesInfoInteger(m_symbol.Name(),ce_Timeframe,SERIES_LASTBAR_DATE);
   if(current==cdt_LastCalcIndicators)
      return true;                  // Exit if data alredy calculated on this bar

Luego comprobamos el último estado del sistema. Si no está definido, reseteamos la bandera del cálculo del modelo autoregresivo en la clase CKalman, para tener recalculado el modelo cuando accedemos a la clase la próxima vez.

   if(cd_corretion==QNaN)
     {
      if(CheckPointer(Kalman)==POINTER_INVALID)
        {
         Kalman=new CKalman(ci_HistoryBars,ci_ShiftPeriod,m_symbol.Name(),ce_Timeframe);
         if(CheckPointer(Kalman)==POINTER_INVALID)
           {
            return false;
           }
        }
      else
         Kalman.Clear_AR_Flag();
     }

En el siguiente paso, comprobamos cuántas barras se han formado tras la última llamada a la función. Si el intervalo es muy grande, también reseteamos la bandera del cálculo del modelo autoregresivo.

   int shift=StartIndex();
   int bars=Bars(m_symbol.Name(),ce_Timeframe,current,cdt_LastCalcIndicators);
   if(bars>(int)fmax(ci_ShiftPeriod,1))
     {
      bars=(int)fmax(ci_ShiftPeriod,1);
      Kalman.Clear_AR_Flag();
     }

Luego, recalculamos los valores del estado del sistema para todas las barras no calculadas.

   double close[];
   if(m_close.GetData(shift,bars+1,close)<=0)
     {
      return false;
     }
  
   for(uint i=bars;i>0;i--)
     {
      cd_forecast=Kalman.Forecast();
      cd_corretion=Kalman.Correction(close[i]);
     }

Después de recalcular, comprobamos el estado del sistema y guardamos la hora de la última llamada a la función. Si la operación se finaliza con éxito, devuelve true.

   if(cd_forecast==EMPTY_VALUE || cd_forecast==0 || cd_corretion==EMPTY_VALUE || cd_corretion==0)
      return false;
  
   cdt_LastCalcIndicators=current;
  //---
   return true;
  }

Las funciones de la toma de decisiones (LongCondition y ShortCondition) tienen una estructura absolutamente idéntica, con una condición de espejo de la apertura de la transacción. Usaremos la función ShortCondition como ejemplo para demostrar el código de la función.

Primero, iniciamos la función del recálculo de los valores del filtro. Si el recálculo de los valores del filtro falla, salimos de la función y devolvemos 0.

int CSignalKalman::ShortCondition(void)
  {
   if(!CalculateIndicators())
      return 0;

Al hacer el recálculo de los valores del filtro con éxito, comparamos el tamaño pronosticado con el tamaño corregido. Si el tamaño pronosticado es más que tamaño corregido, la función devuelve el valor ponderado. De lo contrario, devuelve 0.

   int result=0;
   //--- 
   if(cd_corretion<cd_forecast)
      result=80;
   return result;
  }

El módulo está construido según el principio «reversivo», por eso no hemos escrito las funciones del cierre de las posiciones aquí.

Puede encontrar el código de todas las funciones en los archivos adjuntos al artículo.

5. Simulación del EA

La descripción detallada para crear el EA usando el módulo de las señales comerciales [1], omitimos este paso. Sólo mencionaré que para la prueba de la calidad de las señales, el EA ha sido creado en un solo módulo comercial creado antes, con el lote estático y sin usar el Trailing Stop.

La prueba del EA fue realizada en los datos históricos del agosto de 2017, en EURUSD con el timeframe Н1. Para calcular el modelo autoregresivo, se usaban los datos históricos en 3000 barras, lo que comprende casi 6 meses. La simulación se realizaba sin colocación de Stop Loss y Take Profit, lo que permitió ver la influencia sólo de las señales del filtro de Kalman en el trading.

Los resultados de la prueba mostraron 49,33% de las transacciones rentables. El beneficio de una transacción máxima y media rentable supera los valores correspondientes de las transacciones no rentables. En total, obtuvimos el beneficio para el período de testeo, el factor del benefició alcanzó 1,56. A continuación, tiene las capturas de pantalla de la simulación.

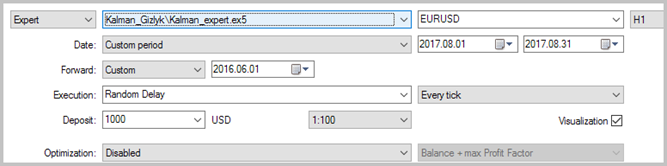
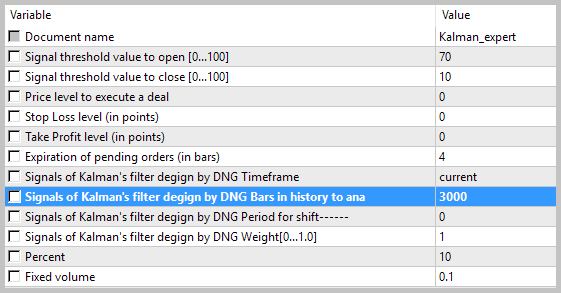
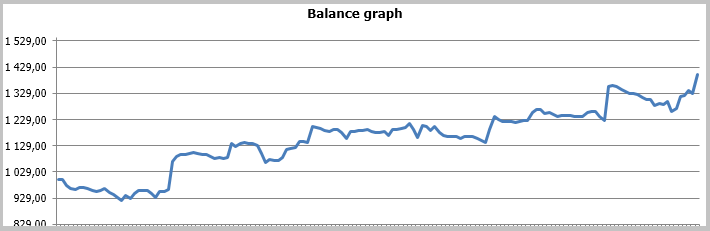
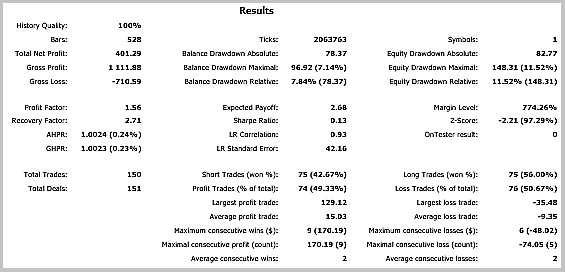
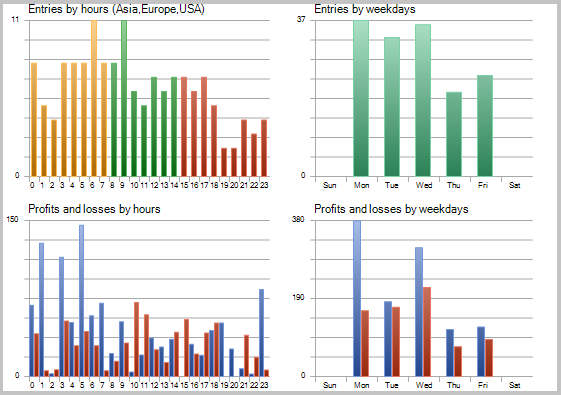
Si observamos con atención las transacciones en el gráfico de precios, atraen la atención 2 cuellos de botella de esta táctica:

series de transacciones falladas en los movimientos planos (flat);
la última salida de la posición abierta.

Resultados de la prueba en el gráfico de precios

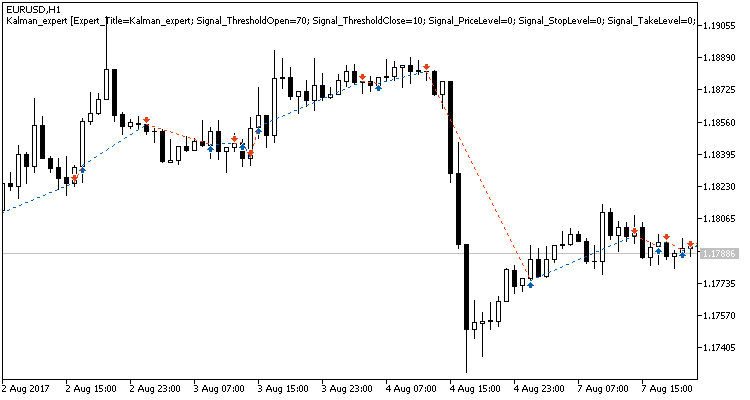
Las mismas zonas problemáticas fueron destacadas durante el testeo del Asesor Experto según la estrategia del seguimiento adaptativo del mercado, ahí mismo fueron propuestas las opciones para solucionar el problema. Pero, a diferencia de la estrategia anterior, el EA con el filtro de Kalman demostró el resultado positivo. Según mi opinión, la estrategia propuesta en este artículo tiene todas las posibilidades de tener éxito, si completamos las definiciones de los movimientos de flat con un filtro adicional. Probablemente, se podrá aumentar la rentabilidad de la estrategia si se usa sólo durante unas horas determinadas. Además, para aumentar la rentabilidad de la estrategia, es necesario mejorar las señales de la salida de la posición, lo que permitirá no perder el beneficio obtenido en caso de los giros bruscos del precio.

Conclusión

Hemos considerado el principio del trabajo del filtro de Kalman y hemos diseñado un indicador y un Asesor Experto a su base. La simulación ha demostrado las probabilidades de esta estrategia, pero también ha revelado una serie de problemas que requieren soluciones.

También me gustaría advertir que este artículo contiene sólo una información general y un ejemplo de la construcción del EA, que en ningún caso pretende a ser un «Grial» para el uso en el trading real.

¡Les deseo a todos una manera práctica de tratar el trading y las transacciones rentables!

Referencias

Programas usados en el artículo:

#	Nombre	Tipo	Descripción
1	Kalman.mqh	Librería de la clase	Clase del filtro de Kalman
2	SignalKalman.mqh	Librería de la clase	Módulo de señales comerciales según el filtro de Kalman
3	Kalman_indy.mq5	Indicador	Indicador del filtro de Kalman
4	Kalman_expert.mq5	Asesor Experto	EA según la estrategia con el uso del filtro de Kalman
5	Kalman_test.zip	Archivo	El archivo contiene los resultados del testeo del Asesor Experto en el Probador de Estrategias.

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/3886

Archivos adjuntos |

Descargar ZIP

Kalman_test.zip (95.5 KB)

MQL5.zip (290.55 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores

Neuroredes profundas (Parte IV). Creación, entrenamiento y simulación de un modelo de neurored

En el artículo se analizan las nuevas posibilidades del paquete darch (v.0.12.0). Se describen los resultados del entrenamiento de una red neuronal profunda con diferentes tipos de datos, estructura y secuencia de entrenamiento. También se analizan los resultados.

Nuevo enfoque a la interpretación de la divergencia clásica e inversa

En este artículo se considera el método clásico de la construcción de la divergencia y el modo de la interpretación distinto de él. Este nuevo método de la interpretación ha sido puesto como base de la estrategia comercial descrita en el presente artículo.

R cuadrado como evaluación de la calidad de la curva del balance de la estrategia

En este artículo se describe cómo construir el criterio personalizado de la optimización de R². Usando este criterio se puede evaluar la calidad de la curva del balance de la estrategia y eligir las estrategias más estables y crecientes regularmente. Se describen los principios de su construcción, así como los métodos estadísticos que se usan para evaluar las propiedades y la calidad de esta métrica.

Arbitraje triangular

Este artículo está dedicado a un método del trading popular, el arbitraje triangular. Este tema ha sido analizado lo más detallado posible, han sido considerados las ventajas y desventajas de la estrategia, ha sido desarrollado el código del Asesor Experto.