Использование фильтра Калмана в прогнозе направления цены

Введение

На графике курсов валют или акций мы всегда видим ценовые колебания, которые отличаются частотой и амплитудой. Наша задача — определить основные тенденции за этими короткими и длинными движениями. Кто-то для этого наносит на график трендовые линии, кто-то использует индикаторы. В обоих случаях наша цель — отфильтровать истинное ценовое движение от шума, вызванного влиянием незначительных факторов, кратковременно влияющих на цену. В этой статье я предлагаю отделять посторонние шумы с использованием фильтра Калмана.

Идея использования цифровых фильтров в трейдинге не нова. В том числе и я уже рассказывал об использовании фильтров низкой частоты. Но, как говорится, нет предела совершенству, и в поисках лучших стратегий рассмотрим еще один вариант и сравним результаты.

1. Принцип работы фильтра Калмана

Итак, что же такое фильтр Калмана и почему нам стоит обратить на него внимание? Википедия дает такое определение фильтра:

Фильтр Калмана — эффективный рекурсивный фильтр, оценивающий вектор состояния динамической системы, используя ряд неполных и зашумленных измерений.

Т.е. изначально этот инструмент был разработан для работы с зашумленными данными. Способен он работать и с неполными данными. И, наконец, еще одно его достоинство — в том, что он разработан и применяется для динамических систем, к которым относится и наш ценовой график.

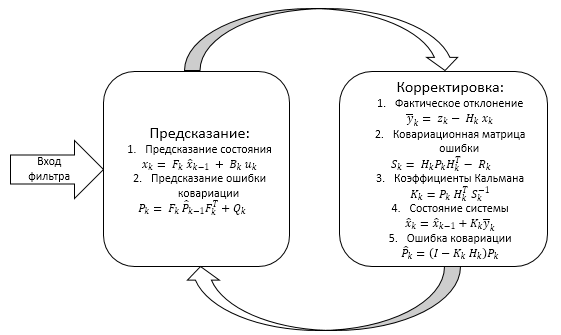
Работа фильтра разделена на два этапа:

1. Экстраполяция (предсказание)
2. Корректировка

1.1. Экстраполяция — предсказание значений системы

В основе первого этапа работы фильтра лежит некая модель анализируемого процесса. По ней строится предсказание состояния системы на один шаг вперед.

 (1.1)

Где:

• xk — экстраполированное значение динамической системы на k-том шаге,
• Fk — матрица модели зависимости текущего состояния системы от предыдущего,
• x^k-1 — предыдущее состояние системы (значение фильтра на предыдущем шаге),
• Bk — матрица влияния управляющего воздействия на систему,
• uk — управляющее воздействие на систему.

Под управляющим воздействием можно воспринимать, например, новостной фактор. Но на практике, как правило, управляющее воздействие неизвестно и упускается, а его воздействие относится к шумам.

Затем предсказывается ошибка ковариации системы:

 (1.2)

Где:

• Pk — экстраполированная ковариационная матрица вектора состояния нашей динамической системы,
• Fk — матрица модели зависимости текущего состояния системы от предыдущего,
• P^k-1 — скорректированная на предыдущем шаге ковариационная матрица вектора состояния,
  
• Qk — ковариационная матрица шума процесса.

1.2. Корректировка значений системы

Второй этап работы фильтра начинается с измерения фактического состояния системы zk. Здесь фактически измеренное значение состояние системы указывается с учетом действительного состояния системы и погрешности измерений. В нашем случае под погрешностью измерений имеются в виду воздействия шумов на динамическую систему.

К настоящему моменту в нашем распоряжении есть две разные величины, которые представляют состояние одного динамического процесса. Это экстраполированное значение динамической системы, которое мы рассчитали на первом этапе, и фактически измеренное значение. Каждая из этих величин с определенной долей вероятности характеризует истинное состояние нашего процесса, которое, таким образом, находится где-то между ними двумя. Следовательно, наша цель — определить, в какой степени мы доверяем тому или иному значению. Для этого и проводятся итерации второго этапа фильтра Калмана.

Исходя из имеющихся данных, определяем отклонение фактического состояния системы от экстраполированного значения.

 (2.1)

Здесь:

• yk — отклонение фактического состояния системы на k-том шаге от экстраполированного,
• zk — фактическое состояние системы на k-том шаге,
  
• Hk — матрица измерений, которая отображает зависимость фактического состояния системы от рассчитанных данных (на практике часто принимает единичное значение),
• xk — экстраполированное значение динамической системы на k-том шаге.

Следующим шагом рассчитывается ковариационная матрица для вектора ошибки:

 (2.2)

Здесь:

• Sk — ковариационная матрица вектора ошибки на k-том шаге,
• Hk — матрица измерений, которая отображает зависимость фактического состояния системы от рассчитанных данных,
  
• Pk — экстраполированная ковариационная матрица вектора состояния нашей динамической системы,
• Rk — ковариационная матрица шума измерений.

Затем определяется оптимальное значение так называемых коэффициентов усиления, которые и отображают степень доверия расчетной и эмпирической величинам.

  (2.3)

Здесь: 

• Kk — матрица коэффициентов усиления Калмана,
  
• Pk — экстраполированная ковариационная матрица вектора состояния нашей динамической системы,
  
• Hk — матрица измерений, которая отображает зависимость фактического состояния системы от рассчитанных данных,
• Sk — ковариационная матрица вектора ошибки на k-том шаге.

Теперь по уже полученным коэффициентам Калмана корректируем значение состояния нашей системы и ковариационную матрицу оценки вектора состояния.

 (2.4)

Где:

• x^k и x^k-1 — скорректированные значения на k-том и k-1 шаге,
• Kk — матрица коэффициентов усиления Калмана,
  
• yk — отклонение фактического состояния системы на k-том шаге от экстраполированного.

 (2.5)

Где:

• P^k — скорректированная ковариационная матрица вектора состояния нашей динамической системы,
  
• I — матрица идентичности,
• Kk — матрица коэффициентов усиления Калмана,
• Hk — матрица измерений, которая отображает зависимость фактического состояния системы от рассчитанных данных,
  
• Pk — экстраполированная ковариационная матрица вектора состояния нашей динамической системы.

Обобщить все вышесказанное можно нижеприведенной схемой

2. Практическая реализация фильтра Калмана

Итак, мы получили представление о том, как работает фильтр Калмана. Приступим к его практической реализации. Матричное представление формул фильтра, описанное выше, предусматривает, что данные мы получаем из нескольких источников.   Я же предлагаю построить фильтр по ценам закрытия баров и упростить таким образом матричное представление до дискретного.

2.1. Инициализация исходных данных

Прежде чем начать писать код, определимся с исходными данными.

Как уже говорилось выше, в основе фильтра Калмана — модель динамического процесса, по которой предсказывается следующее состояние этого процесса. Изначально этот фильтр был предложен для работы с линейными системами, в которых текущее состояние системы легко задается через коэффициент к предыдущему. Нам сложнее: мы имеем дело с не линейной динамической системой, где коэффициент изменяется пошагово. Более того, у нас нет ни малейшего представления о зависимости между двумя соседними состояниями системы. Задача, казалось бы, неразрешимая. Но давайте немного схитрим и воспользуемся авторегрессионными моделями, о которых уже рассказывалось в статьях [1],[2],[3].

Итак, начнем. Для начала объявим класс CKalman, а в нем — необходимые переменные

class CKalman
  {
private:
//---
   uint              ci_HistoryBars;               //Bars for analysis
   uint              ci_Shift;                     //Shift of autoregression calculation
   string            cs_Symbol;                    //Symbol
   ENUM_TIMEFRAMES   ce_Timeframe;                 //Timeframe
   double            cda_AR[];                     //Autoregression coefficients
   int               ci_IP;                        //Number of autoregression coefficients
   datetime          cdt_LastCalculated;           //Time of LastCalculation;
   
   bool              cb_AR_Flag;                   //Flag of autoregression calculation
//--- Values of Kalman's filter
   double            cd_X;                         // X
   double            cda_F[];                      // F array
   double            cd_P;                         // P
   double            cd_Q;                         // Q
   double            cd_y;                         // y
   double            cd_S;                         // S
   double            cd_R;                         // R
   double            cd_K;                         // K
   
public:
                     CKalman(uint bars=6240, uint shift=0, string symbol=NULL, ENUM_TIMEFRAMES period=PERIOD_H1);
                    ~CKalman();
   void              Clear_AR_Flag(void)  {  cb_AR_Flag=false; }
  };

В функции инициализации класса присвоим начальные значения переменным.

CKalman::CKalman(uint bars, uint shift, string symbol, ENUM_TIMEFRAMES period)
  {
   ci_HistoryBars =  bars;
   cs_Symbol      =  (symbol==NULL ? _Symbol : symbol);
   ce_Timeframe   =  period;
   cb_AR_Flag     =  false;
   ci_Shift       =  shift;
   cd_P           =  1;
   cd_K           =  0.9;
  }

Для построения авторегрессионной модели я воспользовался алгоритмом из статьи [1]. Для этого добавим в класс две private функции.

   bool              Autoregression(void);
   bool              LevinsonRecursion(const double &R[],double &A[],double &K[]);

Функция LevinsonRecursion перенесена без изменений, а функцию Autoregression я слегка модифицировал, поэтому давайте рассмотрим ее подробней. В начале функции мы проверяем наличие необходимой для анализа истории, и если ее недостаточно, возвращается false.

bool CKalman::Autoregression(void)
  {
   //--- check for insufficient data
   if(Bars(cs_Symbol,ce_Timeframe)<(int)ci_HistoryBars)
      return false;

Загружаем необходимую историю в массив и заполняем массив фактических коэффициентов зависимости текущего состояния системы от предыдущего.

//---
   double   cda_QuotesCenter[];                          //Data to calculate

//--- make all prices available
   double close[];
   int NumTS=CopyClose(cs_Symbol,ce_Timeframe,ci_Shift+1,ci_HistoryBars+1,close)-1;
   if(NumTS<=0)
      return false;
   ArraySetAsSeries(close,true);
   if(ArraySize(cda_QuotesCenter)!=NumTS)
     {
      if(ArrayResize(cda_QuotesCenter,NumTS)<NumTS)
         return false;
     }
   for(int i=0;i<NumTS;i++)
      cda_QuotesCenter[i]=close[i]/close[i+1];           // Calculate coefficients

После проведенных подготовительных работ определяем количество коэффициентов авторегрессионной модели и рассчитываем их значения.

   ci_IP=(int)MathRound(50*MathLog10(NumTS));
   if(ci_IP>NumTS*0.7)
      ci_IP=(int)MathRound(NumTS*0.7);                         // Autoregressive model order
  
   double cor[],tdat[];
   if(ci_IP<=0 || ArrayResize(cor,ci_IP)<ci_IP || ArrayResize(cda_AR,ci_IP)<ci_IP || ArrayResize(tdat,ci_IP)<ci_IP)
      return false;
   double a=0;
   for(int i=0;i<NumTS;i++)
      a+=cda_QuotesCenter[i]*cda_QuotesCenter[i];    
   for(int i=1;i<=ci_IP;i++)
     {  
      double c=0;
      for(int k=i;k<NumTS;k++)
         c+=cda_QuotesCenter[k]*cda_QuotesCenter[k-i];
      cor[i-1]=c/a;                                            // Autocorrelation
     } 
  
   if(!LevinsonRecursion(cor,cda_AR,tdat))                     // Levinson-Durbin recursion
      return false;

Сумму полученных коэффициентов авторегрессии приводим к "1" и устанавливаем флаг проведенного расчета в состояние true.

   double sum=0;
   for(int i=0;i<ci_IP;i++)
     {
      sum+=cda_AR[i];
     }
   if(sum==0)
      return false;
  
   double k=1/sum;
   for(int i=0;i<ci_IP;i++)
      cda_AR[i]*=k;

   cb_AR_Flag=true;

Далее инициализируем необходимые для фильтра переменные. В качестве ковариации шума измерений возьмем среднеквадратичное отклонений значений close за анализируемый период.

   cd_R=MathStandardDeviation(close);

Для определения значения ковариации шума процесса сначала рассчитаем массив значений авторегрессионной модели и возьмем среднеквадратичное отклонение значений модели.

   double auto_reg[];
   ArrayResize(auto_reg,NumTS-ci_IP);
   for(int i=(NumTS-ci_IP)-2;i>=0;i--)
     {
      auto_reg[i]=0;
      for(int c=0;c<ci_IP;c++)
        {
         auto_reg[i]+=cda_AR[c]*cda_QuotesCenter[i+c];
        }
     }
   cd_Q=MathStandardDeviation(auto_reg);

Фактические коэффициенты зависимости текущего состояния системы от предыдущего скопируем в массив cda_F, чтобы потом использовать их при расчете новых коэффициентов.

   ArrayFree(cda_F);
   if(ArrayResize(cda_F,(ci_IP+1))<=0)
      return false;
   ArrayCopy(cda_F,cda_QuotesCenter,0,NumTS-ci_IP,ci_IP+1);

Для начального значения нашей системы возьмем среднее арифметическое из 10 последних значений.

   cd_X=MathMean(close,0,10);

2.2. Предсказание движения цены

После того, как мы получили все исходные данные для работы фильтра, можно приступить к его практической реализации. Первый этап работы фильтра Калмана, как уже упоминалось выше, — экстраполяция состояния системы на один шаг вперед. Создадим public функцию Forecast, в которой будут реализованы функции 1.1. и 1.2.

double            Forecast(void);

В начале функции проверим, рассчитана ли уже регрессионная модель. В случае необходимости вызовем функцию ее расчета. При ошибке пересчета модели возвращается EMPTY_VALUE,

double CKalman::Forecast()
  {
   if(!cb_AR_Flag)
     {
      ArrayFree(cda_AR);
      if(Autoregression())
        {
         return EMPTY_VALUE;
        }
     }

Затем рассчитываем коэффициент зависимости текущего состояния системы от предыдущего и сохраняем его в "0" ячейку массива cda_F, значения которого предварительно сдвигаем на одну ячейку.

   Shift(cda_F);
   cda_F[0]=0;
   for(int i=0;i<ci_IP;i++)
      cda_F[0]+=cda_F[i+1]*cda_AR[i];

После этого пересчитываем состояние системы и вероятность ошибки.

   cd_X=cd_X*cda_F[0];
   cd_P=MathPow(cda_F[0],2)*cd_P+cd_Q;

В конце функция возвращает прогнозное состояние системы. В нашем случае это прогнозируемая цена закрытия нового бара.

   return cd_X;
  }

2.3. Корректировка состояния системы

На следующем этапе, после получения фактического значения закрытия бара, проведем корректировку состояния системы. Для этого создадим public функцию Correction. В ее параметрах будем передавать фактически полученное значение состояния системы, т.е. цену закрытия последнего бара.

double            Correction(double z);

В этой функции реализован теоретический раздел 1.2. этой статьи. С ее полным кодом можно ознакомиться во вложении. По окончанию своей работы функция возвращает скорректированное значение состояния системы.

3. Демонстрация работы фильтра Калмана на практике

Испытаем работу нашего класса по фильтру Калмана на практике. Для этого на базе класса создадим небольшой индикатор. На открытии новой свечи он будет вызывать функцию корректировки состояния системы, а затем — функцию предсказания для прогноза цены закрытия текущего бара. Не пугайтесь перестановки вызова функций класса, ведь мы будем вызывать функцию корректировки состояния для предыдущего (закрытого) бара и прогноз цены закрытия для текущего (только что открытого бара), цена закрытия которого нам неизвестна.

В индикаторе будут 2 буфера. В первый будут выводиться прогнозные значения состояния системы, во второй — скорректированные. Я намеренно создал два буфера, чтобы индикатор не перерисовывался и можно было увидеть масштабы корректировки системы на втором этапе работы фильтра. Код индикатора несложный, он приведен во вложении. Здесь же я приведу результаты его работы.

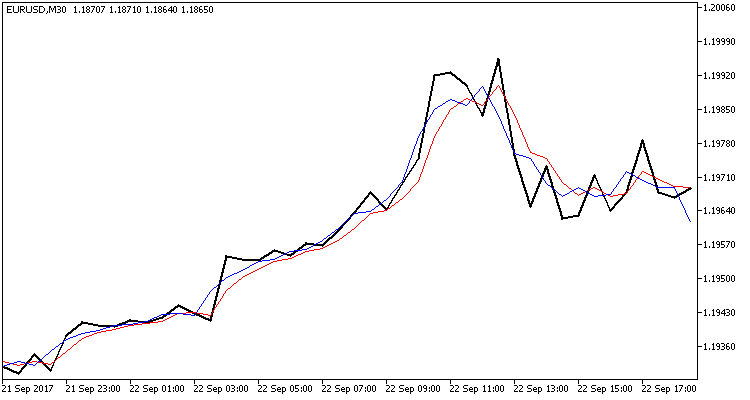
На представленном графике отображаются три ломаные линии:

• Черная — фактическая цена закрытия баров;
• Красная — прогнозная цена закрытия;
• Синяя — скорректированное фильтром Калмана состояние системы.

Как видим, обе линии находятся рядом с фактическими ценами закрытия и с хорошей долей вероятности показывают разворотные моменты. Хочу еще раз обратить внимание, что индикатор не перерисовывается и красная линия строится в момент открытия бара, когда еще не известна цена закрытия.

Подобный график показывает состоятельность работы используемого фильтра и возможность построения торговой системы с его использованием.

4. Создаем модуль торговых сигналов для генератора экспертов MQL5

Рассматривая график, представленный выше, можно заметить, что красная линия прогнозирования состояния системы более сглажена, по сравнению с черной линией фактической цены. При этом синяя линия скорректированного состояния системы всегда находится между двумя другими. Иными словами, если синяя линия выше красной, то это свидетельствует о бычьем тренде. И наоборот, синяя линия ниже красной говорит о медвежьем тренде. Следовательно, пересечение синей и красной линии — сигнал о смене тренда.

Для тестирования этой стратегии создадим модуль торговых сигналов для генератора экспертов MQL5. О методике создания модулей торговых сигналов уже не раз рассказывалось в статьях на этом сайте [1], [4], [5]. Я же вкратце расскажу о моментах, касающихся нашей стратегии.

Для начала создаем класс модуля CSignalKalman, который наследуется от CExpertSignal. Поскольку наша стратегия построена на использовании фильтра Калмана, то мы должны объявить в нашем классе экземпляр созданного выше класса CKalman. Поскольку мы объявляем экземпляр класса CKalman в модуле, то и инициализировать его будем в модуле. В свою очередь, для этого нам нужно передать в модуль исходные параметры. В коде решение этих задач выглядит так:

//+---------------------------------------------------------------------------+
// wizard description start
//+---------------------------------------------------------------------------+
//| Description of the class                                                  |
//| Title=Signals of Kalman's filter degign by DNG                            |
//| Type=SignalAdvanced                                                       |
//| Name=Signals of Kalman's filter degign by DNG                             |
//| ShortName=Kalman_Filter                                                   |
//| Class=CSignalKalman                                                       |
//| Page=https://www.mql5.com/ru/articles/3886                                |
//| Parameter=TimeFrame,ENUM_TIMEFRAMES,PERIOD_H1,Timeframe                   |
//| Parameter=HistoryBars,uint,3000,Bars in history to analysis               |
//| Parameter=ShiftPeriod,uint,0,Period for shift                             |
//+---------------------------------------------------------------------------+
// wizard description end
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalKalman: public CExpertSignal
  {
private:
   ENUM_TIMEFRAMES   ce_Timeframe;        //Timeframe
   uint              ci_HistoryBars;      //Bars in history to analysis
   uint              ci_ShiftPeriod;      //Period for shift
   CKalman          *Kalman;              //Class of Kalman's filter
   //---
   datetime          cdt_LastCalcIndicators;
   
   double            cd_forecast;         // Forecast value
   double            cd_corretion;        // Corrected value
   //---
   bool              CalculateIndicators(void);
       
public:
                     CSignalKalman();
                    ~CSignalKalman();
   //---
   void              TimeFrame(ENUM_TIMEFRAMES value);
   void              HistoryBars(uint value);
   void              ShiftPeriod(uint value);
   //--- method of verification of settings
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);
  };

В функции инициализации класса присвоим значения по умолчанию переменным и инициализируем класс фильтра Калмана.

CSignalKalman::CSignalKalman(void):    ci_HistoryBars(3000),
                                       ci_ShiftPeriod(0),
                                       cdt_LastCalcIndicators(0)
  {
   ce_Timeframe=m_period;
   
   if(CheckPointer(m_symbol)!=POINTER_INVALID)
      Kalman=new CKalman(ci_HistoryBars,ci_ShiftPeriod,m_symbol.Name(),ce_Timeframe);
  }

Вычислять состояния системы фильтром будем в private функции CalculateIndicators. В начале функции мы проверим, не рассчитывались ли значения фильтра на текущем баре. В случае, если значения уже пересчитаны, выходим из функции.

bool CSignalKalman::CalculateIndicators(void)
  {
   //--- Check time of last calculation
   datetime current=(datetime)SeriesInfoInteger(m_symbol.Name(),ce_Timeframe,SERIES_LASTBAR_DATE);
   if(current==cdt_LastCalcIndicators)
      return true;                  // Exit if data alredy calculated on this bar

Затем проверяем последнее состояние системы. Если оно не определено, сбрасываем флаг расчета авторегрессионной модели в классе CKalman, чтобы при последующем обращении к классу модель была пересчитана заново.

   if(cd_corretion==QNaN)
     {
      if(CheckPointer(Kalman)==POINTER_INVALID)
        {
         Kalman=new CKalman(ci_HistoryBars,ci_ShiftPeriod,m_symbol.Name(),ce_Timeframe);
         if(CheckPointer(Kalman)==POINTER_INVALID)
           {
            return false;
           }
        }
      else
         Kalman.Clear_AR_Flag();
     }

На следующем шаге проверяем, сколько баров сформировалось после последнего вызова функции. При слишком большом интервале также сбрасываем флаг расчета авторегрессионной модели.

   int shift=StartIndex();
   int bars=Bars(m_symbol.Name(),ce_Timeframe,current,cdt_LastCalcIndicators);
   if(bars>(int)fmax(ci_ShiftPeriod,1))
     {
      bars=(int)fmax(ci_ShiftPeriod,1);
      Kalman.Clear_AR_Flag();
     }

Затем пересчитываем значения состояния системы для всех непросчитанных баров.

   double close[];
   if(m_close.GetData(shift,bars+1,close)<=0)
     {
      return false;
     }
  
   for(uint i=bars;i>0;i--)
     {
      cd_forecast=Kalman.Forecast();
      cd_corretion=Kalman.Correction(close[i]);
     }

После пересчета проверяем состояние системы и сохраняем время последнего вызова функции. В случае успешного завершения операций функция возвращает true.

   if(cd_forecast==EMPTY_VALUE || cd_forecast==0 || cd_corretion==EMPTY_VALUE || cd_corretion==0)
      return false;
  
   cdt_LastCalcIndicators=current;
  //---
   return true;
  }

Функции принятия решений (LongCondition и ShortCondition) имеют полностью идентичную структуру с зеркальным условием открытия сделки. Код функций рассмотрим на примере функции ShortCondition.

Сначала запускаем функцию пересчета значений фильтра. В случае неудачи пересчета значений фильтра выходим из функции и возвращаем 0.

int CSignalKalman::ShortCondition(void)
  {
   if(!CalculateIndicators())
      return 0;

При удачном пересчете значений фильтра сравниваем предсказанную и скорректированную величины. Если предсказанная величина больше скорректированной, то функция возвращает весовое значение. В противном случае возвращается "0".

   int result=0;
   //--- 
   if(cd_corretion<cd_forecast)
      result=80;
   return result;
  }

Модуль построен по принципу "перевертыша", поэтому мы в нем не прописываем функции закрытия позиций.

С кодом всех функций можно ознакомиться в приложенных к статье файлах.

5. Тестирование советника

Подробное описание создания советника с использованием модуля торговых сигналов описано в статье [1], этот шаг пропустим. Отмечу только, что для тестирования качества сигналов советник был создан только на одном, выше созданном торговом модуле со статическим лотом и без использования трейлинг-стопа.

Тестирование советника проводилось на исторических данных за август 2017 года по EURUSD на таймфрейме Н1. Для расчета авторегрессионной модели использовались исторические данные на 3000 барах, что составляет почти 6 месяцев. Тестирование проводилось без установки стоп-лоссов и тейк-профитов, что позволило увидеть влияние только сигналов фильтра Калмана на торговлю.

Результаты тестирования показали 49.33% прибыльных сделок. При этом прибыль максимальной и средней прибыльной сделки превышает соответствующие показатели убыточных сделок. В целом это дало прибыль за тестируемый период, профит-фактор составил 1.56. Скриншоты тестирования приведены ниже.

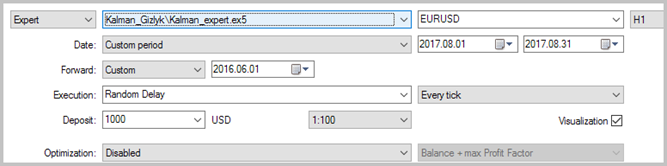
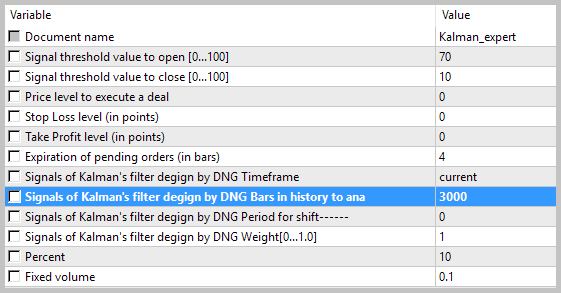
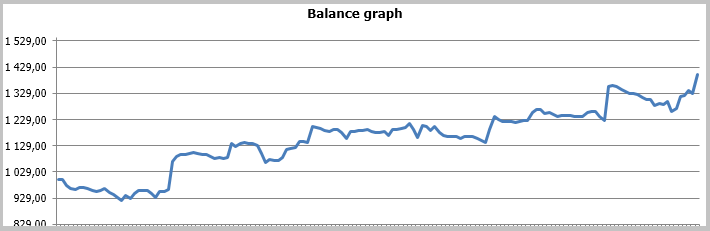
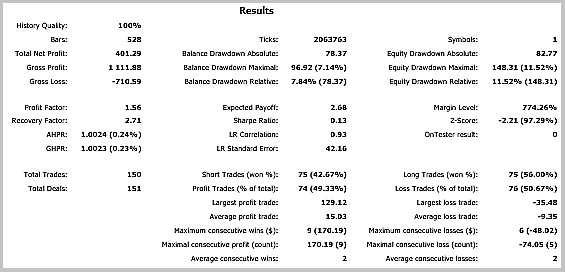
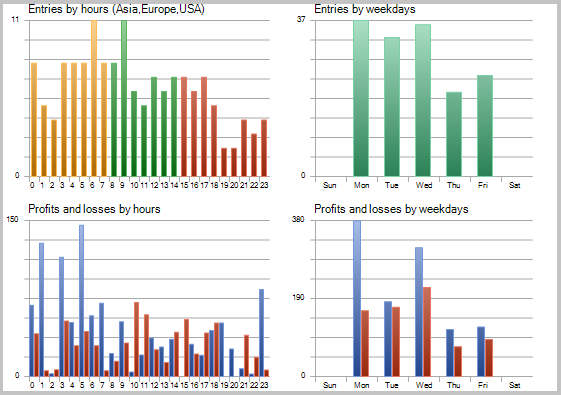
При детальном рассмотрении сделок на ценовом графике обращают на себя внимание 2 узких места этой тактики:

• серии неудачных сделок во флэтовых движениях;
• поздний выход из открытой позиции.

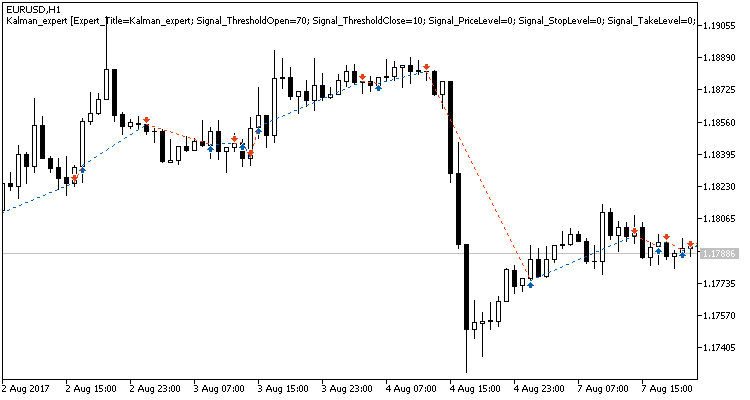
Эти же проблемные зоны были отмечены и при тестировании советника по стратегии адаптивного следования за рынком, там же были предложены варианты решения вопроса. Но, в отличие от предыдущей стратегии, советник с фильтром Калмана показал положительный результат. На мой взгляд, предложенная в этой статье стратегия имеет шансы стать успешной, если ее дополнить дополнительным фильтром определения флэтовых движений. Возможно, получится повысить прибыльность стратегии при использовании ее только в определенные часы. Также для повышения прибыльности стратегии следует проработать сигналы выхода из позиции, что позволит не терять полученную прибыль при резких обратных ценовых движениях. 

Заключение

Мы рассмотрели принцип работы фильтра Калмана и построили на его основе индикатор и советник. Тестирование показало перспективность этой стратегии, но параллельно и высветило ряд узких мест, требующих решения.

Также хочу обратить внимание, что в статье лишь приведена общая информация и пример построения советника, который ни в коем случае не является "граалем" для использования в реальной торговле.

Желаю всем серьезного подхода к торговле и прибыльных сделок!

Ссылки

1. Рассматриваем на практике адаптивный метод следования за рынком.
2. Анализ основных характеристик временных рядов.
3. Авторегрессивная модель (AR) экстраполяции цен - индикатор для MetaTrader 5
4. Мастер MQL5: Как написать свой модуль торговых сигналов
5. Создай торгового робота за 6 шагов!
6. Мастер MQL5: Новая версия

Программы, используемые в статье:

#	Имя	Тип	Описание
1	Kalman.mqh	Библиотека класса	Класс фильтра Калмана
2	SignalKalman.mqh	Библиотека класса	Модуль торговых сигналов по фильтру Калмана
3	Kalman_indy.mq5	Индикатор	Индикатор фильтра Калмана
4	Kalman_expert.mq5	Эксперт	Эксперт по стратегии с использованием фильтра Калмана
5	Kalman_test.zip	Архив	Архив содержит результаты тестирования советника в тестере стратегий.