
Analyse der wesentlichen Merkmale von Zeitreihen
Einleitung
Die Analyse von durch Kursreihen wiedergegebenen Vorgängen ist eine recht anspruchsvolle Aufgabe, die häufig einen nicht unerheblichen Zeit- und Arbeitsaufwand erfordert. Das hängt mit den Besonderheiten der untersuchten Abfolgen zusammen sowie damit, dass es ungeachtet der großen Anzahl von Veröffentlichungen mitunter schwierig ist, die für die jeweilige Aufgabe passende Programmierungslösung zu finden.
Selbst wenn man ein geeignetes Skript oder einen brauchbaren Indikator gefunden hat, bedeutet das keineswegs, dass der jeweilige Quellcode nicht doch noch an die konkrete Aufgabe angepasst werden muss.
Außerdem erfordern diese Programme auch zur Lösung einfachster Aufgaben häufig den Einsatz von Eingangsparametern, deren tieferer Sinn einzig den Entwicklern bekannt ist, sich Außenstehenden dagegen nicht immer ganz erschließt.
Selbstredend stellen diese Schwierigkeiten bei der Durchführung ernsthafter Untersuchungen kein unüberwindliches Hindernis dar, aber wenn lediglich eine Annahme überprüft oder einfach nur eine gewisse Neugierde befriedigt werden soll, bleibt eben genau diese Befriedigung versagt. Genau deshalb entstand die Idee der Programmierung eines universellen Hilfsmittels, das die einfache Durchführung einer provisorischen Analyse der Hauptmerkmale und -parameter einer Eingangssequenz ermöglicht.
Dieses Hilfsmittel muss äußerst einfach einzurichten sein und darf zur Vereinfachung seiner Handhabung keinerlei Eingangsparameter erfordern. Gleichzeitig müssen die berechneten Parameter und Merkmale den Charakter der untersuchten Sequenz hinreichend vollständig und anschaulich abbilden.
Die provisorische Berechnung der Merkmale kann einen Beitrag zur Bestimmung der Richtung der weiteren vertiefenden Analyse leisten oder die eine andere Annahme bereits in der Anfangsphase widerlegen und somit dem Verlust von Zeit für ihre weitere Betrachtung vorbeugen.
Bekanntermaßen schneiden universelle Programme, was ihre Eigenschaften betrifft, verglichen mit spezialisierten Lösungen häufig schlechter ab. Das eben ist der Preis der Universalität, die so gut wie nie ohne ein ganzes System von Kompromissen erreicht werden kann. Nichtsdestotrotz wird in dem hier vorliegenden Beitrag der Versuch unternommen, genau so ein universelles Hilfsmittel zu erstellen, das den Vorgang der provisorischen Analyse der Sequenzeigenschaften maximal vereinfacht.
Installation und Leistungsvermögen
Die gepackte Datei TSAnalysis.zip am Ende dieses Beitrags beinhaltet das Verzeichnis \TSAnalysis mit allen für die Arbeit benötigten Dateien. Nachdem Entpacken des Archivs muss dieses Verzeichnis samt seines gesamten Inhalts in das Verzeichnis \MQL5\Scripts kopiert werden. In dem kopierten Verzeichnis \TSAnalysis befindet sich das Prüfskript TSAexample.mq5, das nach der Zusammenstellung ausgeführt werden kann.
Dieses Skript, das die Klasse TSAnalysis nutzt, bereitet die Daten auf und ruft den voreingestellten Browser auf, um sie darzustellen. Dabei ist zu berücksichtigen, dass in der Programminstanz auf dem Ausgabegerät (Terminal) die Verwendung externer DLL zugelassen ein muss, damit die Klasse TSAnalysis ordnungsgemäß funktioniert. Zur Deinstallation muss lediglich das Verzeichnis \TSAnalysis gelöscht werden.
De gesamte zur Analyse der Sequenzen verwendete Quellcode ist in Form der Klasse TSAnalysis umgesetzt und findet sich komplett in der Datei TSAnalysis.mqh.
Bei der Verwendung dieser Klasse für die Analyse der Eingangssequenz werden folgende Angaben berechnet und abgebildet:
- Die Anzahl der Elemente der Abfolge;
- Höchst- und Tiefstwert der Sequenz (max, min);
- Der Median;
- Der Durchschnittswert (average);
- Die Streuung (variance);
- Die Standardabweichung (standard deviation);
- Die erwartungstreue Streuung (unbiased variance);
- Die erwartungstreue Standardabweichung (unbiased standard deviation);
- Die Schiefe (skewness);
- Die Wölbung (kurtosis);
- Die Überwölbung (excess kurtosis);
- Der Jarque-Bera-Test;
- Der p-Wert des Jarque-Bera-Tests;
- Der korrigierte Jarque-Bera-Test.
- Die p-Werte des korrigierten Jarque-Bera-Tests;
- Die Grenzen für die Werte außerhalb der Sequenz (Ausreißer);
- Die Histogrammdaten;
- Die Daten für das Diagramm der normalen Wahrscheinlichkeit;
- Die Daten für das Diagramm der Autokorrelationsfunktion (Korrelogramm);
- Die Werte des 95%-Zuverlässigkeitsintervalls der Autokorrelationsfunktion;
- Die Daten des Diagramms des anhand der Autokorrelationsfunktion erstellten Spektrums;
- Die Daten des Diagramms der partiellen Autokorrelationsfunktion;
- Die Daten des Diagramms der nach dem Prinzip der maximalen Entropie durchgeführten Berechnung des Spektrums.
In der untersuchten Klasse TSAnalysis kommt zur Veranschaulichung der erhaltenen Ergebnisse die virtuelle Methode „show“ zum Einsatz, die lediglich für die Art der Abbildung der bereits aufbereiteten Angaben zuständig ist.
Deshalb kann die Ausgabe der Ergebnisse durch die einfache Neufestlegung dieser Methode in den abgeleiteten Nachfahren der Klasse TSAnalysis in jeder verfügbaren Form organisiert werden und nicht nur mithilfe einer HTML-Datei wie in der Basisklasse, in der nach dem Anlegen der Datei mit den Daten für die Abbildung der Diagramme ein Internetbrowser aufgerufen wird.
Bevor wir zur Betrachtung der Klasse TSAnalysis beginnen, sei ein Ergebnis ihrer Verwendung an einer Versuchsdatenabfolge vorgestellt. Die Abbildung zeigt das Ergebnis der Ausführung des Skripts TSAexample.mq5.
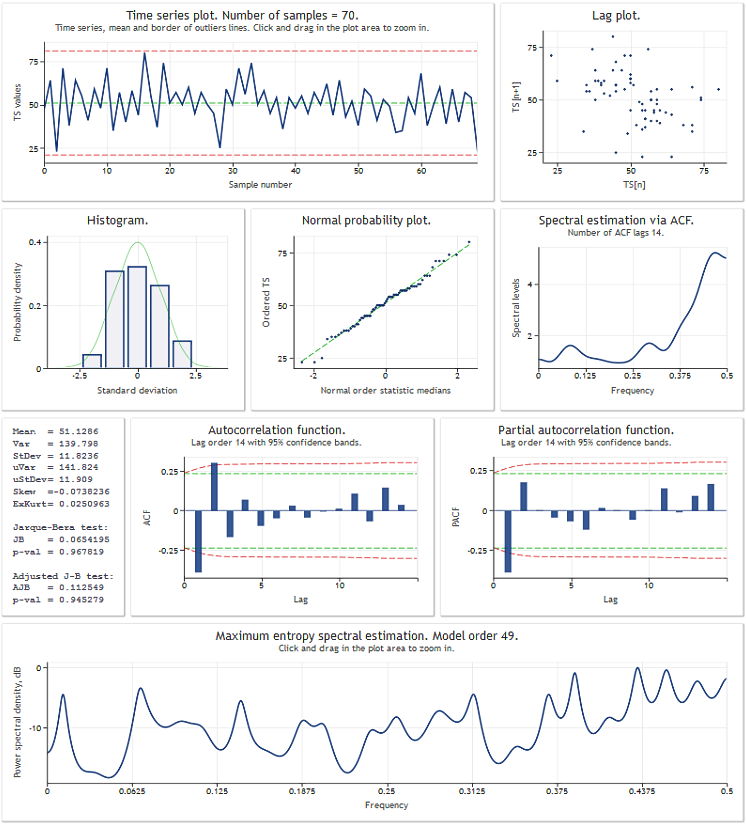
Abbildung 1. Ergebnis der Ausführung des Skripts TSAexample.mq5
Nachdem wir einen ersten Eindruck von dem Leistungsvermögen der Klasse TSAnalysis gewonnen haben, wollen wir sie im Folgenden etwas eingehender betrachten.
Die Klasse TSAnalysis
Die Klasse TSAnalysis (s. die Datei TSAnalysis.mqh) beinhaltet lediglich eine allgemein zugängliche (public) Methode, „Calc“, in der alle erforderlichen Berechnungen ausgeführt werden, anschließend erfolgt der Aufruf der virtuellen Methode „show“. Diese Methode sehen wir uns später kurz an. Jetzt befassen wir uns zunächst Schritt für Schritt mit dem Wesen der ausgeführten Berechnungen.
Die Verwendung der Klasse TSAnalysis werden der zu untersuchenden Eingangssequenz einige Beschränkungen auferlegt.
Zunächst einmal muss die Abfolge mindestens acht Elemente umfassen. Diese Beschränkung ist vermutlich kein allzu strenges Kriterium, da in der Praxis kaum die Notwendigkeit der Untersuchung derart kurzer Sequenzen entstehen dürfte.
Neben der Mindestlänge der Abfolge ist zu beachten, dass der Wert der Streuung der Eingangssequenz nicht nahe null liegen darf. Diese Vorgabe ist dadurch bedingt, dass der Streuungswert in den weiteren Berechnungen verwendet wird, und dass er, um ein stabiles Ergebnis zu erhalten, eine bestimmte Größe nicht unterschreiten darf.
Abfolgen mit einer Streuung, die eine sehr kleine Größe aufweist, sind nicht so häufig anzutreffen, weswegen auch diese Beschränkung aller Wahrscheinlichkeit nach kein ernstes Hindernis darstellen sollte. Und im Fall einer zu kurzen Abfolge sowie bei einem zu nah bei null liegenden Streuungswert wird die Ausführung der Berechnungen ausgesetzt und im Protokoll erscheint eine entsprechende Fehlermeldung.
Es gibt eine weitere implizite Beschränkung in Verbindung mit der zulässigen Höchstlänge der Eingangssequenz. Diese Beschränkung ist nicht ausdrücklich formuliert, sie hängt von der Leistungsfähigkeit des verwendeten Rechners sowie dem auf diesem bereitgestellten Speicherplatz ab und wird rein subjektiv nach der Ausführungszeit des Skripts und dem Tempo der Abbildung der Ergebnisse in dem jeweiligen Webbrowser wahrgenommen. Wir gehen davon aus, dass die Verarbeitung von einer Abfolge aus 2.000 bis 3.000 Elementen keine ernsthaften Probleme verursachen dürfte.
Als Grundlage für die Berechnung der statistischen Parameter einer Abfolge dient der unten aufgeführte Codeabschnitt der Methode „Calc“ (s. die Datei TSAnalysis.mqh).
Eine Darstellung des verwendeten Algorithmus findet sich unter der Verknüpfung: Algorithmen zur Streuungsberechnung.
. . . Mean=0; sum2=0; sum3=0; sum4=0; for(i=0;i<NumTS;i++) { n=i+1; delta=TS[i]-Mean; a=delta/n; Mean+=a; // Mean (average) sum4+=a*(a*a*delta*i*(n*(n-3.0)+3.0)+6.0*a*sum2-4.0*sum3); // sum of fourth degree b=TS[i]-Mean; sum3+=a*(b*delta*(n-2.0)-3.0*sum2); // sum of third degree sum2+=delta*b; // sum of second degree } . . .
Infolge der Ausführung dieses Codeabschnitts werden folgende Werte berechnet:
![]()
mit n = NumTS, die Anzahl der Elemente in der Abfolge (Sequenz).
Mithilfe der gewonnenen Werte erfolgt die Berechnung folgender Parameter:
Streuung und Standardabweichung:
![]()
Erwartungstreue Streuung und Standardabweichung:
![]()
Der Asymmetriekoeffizient (die Schiefe):
![]()
Der Wölbungskoeffizient (die Kurtosis). Der kleinste Wölbungskoeffizient ist gleich 1, bei einer Abfolge mit Normalverteilung beträgt er 3.
![]()
Die Überwölbung (excess kurtosis):
![]()
In diesem Fall ist der kleinste Wölbungskoeffizient ist gleich -2, während er bei einer Abfolge mit Normalverteilung 0 beträgt.
Üblicherweise wird für die erste provisorische Überprüfung auf das Vorliegen einer Normalverteilung der untersuchten Abfolge das Jarque-Bera-Kriterium eingesetzt, das anhand der bekannten Werte der Asymmetrie- und Überwölbungskoeffizienten leicht zu berechnen ist. Bei dem Jarque-Bera-Kriterium strebt die Größe der statistischen Signifikanz (des p-Werts) bei zunehmender Länge der Abfolge asymptotisch gegen die inverse Chi-Quadrat-Verteilungsfunktion mit zwei Freiheitsgraden.
Somit ergibt sich:
![]()
Bei kurzen Folgen weist der auf diese Weise gewonnene p-Wert zwangsläufig einen deutlich sichtbaren Fehler auf. Dessen ungeachtet kommt genau diese Art der Berechnung sehr häufig zum Einsatz. Es ist schwer zu sagen, womit das zusammenhängt, mag sein, dass die Einfachheit und Klarheit der verwendeten Ausdrücke anziehend wirken, oder es kann mit dem Umstand verbunden sein, dass es sich bei dem Jarque-Bera-Kriterium für sich genommen nicht um eine ideale Normalitätsprüfung handelt, weswegen die Durchführung noch genauerer Berechnungen zwecklos ist.
In unserem Fall erfolgt die Berechnung des Jarque-Bera-Kriteriums und des ihm entsprechenden p-Wertes in der Methode „Calc“ (s. die Datei TSAnalysis.mqh) in Übereinstimmung mit den oben aufgeführten Ausdrücken.
Darüber hinaus wird ein korrigierter Jarque-Bera-Test berechnet:
![]()
mit
![]()
Die korrigierte Fassung des Jarque-Bera-Tests verringert den Fehler bei dem mithilfe dieses Verfahrens ermittelten p-Wert bei kurzen Abfolgen zwar, ganz beseitigen lässt er sich jedoch nicht.
Es ist davon auszugehen, dass das Endergebnis der Analyse ein Diagramm der Eingangssequenz beinhaltet, das eine Linie wiedergibt, die dem Durchschnittswert entspricht, sowie die Linien, die die Grenzen festlegen, bei deren Überschreiten die Werte als ungültig und damit als außerhalb der gegebenen Abfolge liegend (kurz als: Ausreißer) betrachtet werden können.
Diese Grenzen werden in diesem Fall wie folgt berechnet:
![]()
![]()
Dieser Ausdruck stammt aus dem Buch „Statistik für Devisenhändler“ von S. V. Bulaschev unter Verweis auf das Buch „Berechnung der Fehlerhaftigkeit von Messergebnissen“ von P. V. Novickij und I. A. Zograf. Nach der Ermittlung der Grenzen ist keine weitere Bearbeitung der Eingangssequenz vorgesehen, die Anzeige dieser Grenzen hat lediglich informellen Charakter.
Weiterhin ist zu empfehlen, außer dem Diagramm der Eingangsfunktion auch ein Histogramm mit der empirischen Schätzung der Verteilung der Eingangssequenz anzuzeigen. Die Anzahl der Intervalle zum Anlegen des Histogramms wird wie folgt bestimmt (s. S. V. Bulaschev, Statistik für Devisenhändler):
![]()
Das Ergebnis wird auf die nächste ungerade ganze Zahl abgerundet. Ist der erhaltene Wert kleiner als fünf, wird die Zahl 5 verwendet.
Die Anzahl der Elemente in den Datenfeldern für die x- und y-Achsen des Histogramms entsprechen der gefundenen Anzahl der Intervalle plus zwei, da zu dem Histogramm links und rechts zwangsweise jeweils eine Spalte mit dem Wert null hinzugefügt wird.
Unten wird ein Codeausschnitt (s. die Datei TSAnalysis.mqh) vorgestellt, der die Daten für die Erstellung des Histogramms aufbereitet.
. . . n=(int)MathRound((Kurt+1.5)*MathPow(NumTS,0.4)/6.0); if((n&0x01)==0)n--; if(n<5)n=5; // Number of bins ArrayResize(XHist,n); ArrayResize(YHist,n); ArrayInitialize(YHist,0.0); a=MathAbs(TSort[0]-Mean); b=MathAbs(TSort[NumTS-1]-Mean); if(a<b)a=b; v=Mean-a; delta=2.0*a/n; for(i=0;i<n;i++)XHist[i]=(v+(i+0.5)*delta-Mean)/StDev; // Histogram. X-axis for(i=0;i<NumTS;i++) { k=(int)((TS[i]-v)/delta); if(k>(n-1))k=n-1; YHist[k]++; } for(i=0;i<n;i++)YHist[i]=YHist[i]/NumTS/delta*StDev; // Histogram. Y-axis . . .
In dem aufgeführten Code stehen:
- NumTS für die Anzahl der Elemente in der Abfolge,
- XHist[] und YHist[] für die Datenfelder mit den Daten für die x- bzw. die y-Achse sowie
- TSort[] für das Datenfeld mit der geordneten Eingangssequenz.
Bei diesem Berechnungsverfahren werden die Werte der x-Skala in Einheiten der Standardabweichung ausgedrückt, während die Werte der y-Skala der Wahrscheinlichkeitsdichte entsprechen.
Zum Anlegen eines Diagramms mit der Skala der Normalverteilung als Werte für die y-Achse wird die in aufsteigender Richtung angeordnete Eingangssequenz verwendet. Die Anzahl der Werte der y- bzw. der x-Achse wird als gleich angenommen. Für die Berechnung der Werte der x-Achse sind zunächst die Werte für den Median sowie für den Fall der gleichmäßigen Verteilung zu finden:
![]()
![]()
![]()
Des Weiteren werden aus ihnen mithilfe der Umkehrfunktion der Normalverteilung (s. die Methode ndtri) die Werte der x-Skala errechnet.
Zum Anlegen der Diagramme der Autokorrelationsfunktion (AKF) und der partiellen Autokorrelationsfunktion (PAKF) sowie zur Berechnung des Spektralwertes der Eingangssequenz gemäß dem Prinzip der maximalen Entropie müssen die Werte der Autokorrelationsfunktion gefunden werden.
Die Anzahl der Werte, die in den AKF- und PAKF-Diagrammen abgebildet werden sollten, legen wir wie folgt fest:
![]()
![]()
![]()
Die auf diese Weise ermittelte Anzahl an Werten wird zur Abbildung der Autokorrelationsfunktion in dem Diagramm vollkommen ausreichen, aber zur weiteren Berechnung des Spektrums der Autoregression wäre es wünschenswert, über eine erheblich größere Anzahl berechneter AKF-Werte zu verfügen, die in unserem Fall gleich der Ordnung des verwendeten Autoregressionsmodells sein müsste.
Die Ordnung des IP-Modells bestimmen wir anhand des ermittelten Wertes NLags:
![]()
![]()
Die Formalisierung der Bestimmung der optimalen Ordnung des Modells zur Berechnung des Spektrums ist recht schwierig. Bei einem Modell niedriger Ordnung erhält man übermäßig geglättete Ergebnisse, bei einer zu hohen Ordnung dagegen aller Wahrscheinlichkeit nach ein instabiles Spektrum mit einer großen Wertestreuung.
Außerdem beeinflusst auch die Art der Eingangssequenz die Ordnung des Modells, weshalb die anhand des oben vorgestellten Ausdrucks ermittelte Ordnung IP wird sich in einigen Fällen als überhöht erweisen, in anderen dagegen als zu gering. Leider ist es nicht gelungen, einen effektiveren Ansatz zur Ermittlung der benötigten Modellordnung zu finden.
Somit muss für die Eingangssequenz die der bei der Berechnung des Spektrums der Abfolge verwendeten Ordnung des IP-Modells entsprechende Anzahl der AKF-Werte bestimmt werden.
. . . ArrayResize(cor,IP); a=0; for(i=0;i<NumTS;i++)a+=TSCenter[i]*TSCenter[i]; for(i=1;i<=IP;i++) { c=0; for(k=i;k<NumTS;k++)c+=TSCenter[k]*TSCenter[k-i]; cor[i-1]=c/a; // Autocorrelation } . . .
Der hier vorliegende Ausschnitt aus dem Quellcode (s. die Datei TSAnalysis.mqh) veranschaulicht den Vorgang zur Berechnung der Autokorrelationsfunktion (AKF). Das Ergebnis der Berechnung wird in dem Datenfeld cor[] abgelegt. Wie wir sehen, wird zunächst der Wert des Nullkoeffizienten der Autokorrelation berechnet, und danach folgt im Arbeitsablauf die Berechnung und Normalisierung der übrigen Koeffizienten. Bei dieser Normalisierung ist der Nullkoeffizient stets gleich eins, weswegen er nicht in dem Datenfeld cor[] gespeichert werden muss.
Dieses Datenfeld (Array) enthält die IP entsprechende Anzahl an Koeffizienten, beginnend mit dem ersten. Bei der Berechnung der AKF verwenden wir das Datenfeld TSCenter[] mit der Eingangssequenz, von deren gesamten Elementen jeweils der Durchschnittswert subtrahiert wurde.
Zur Verkürzung der für die Berechnung der AKF benötigten Zeit können Methoden benutzt werden, die sich auf die Verwendung schneller Umwandlungsalgorithmen stützen, zum Beispiel FFT. In unserem Fall ist die für die Berechnung der AKF aufgewendete Zeit jedoch absolut annehmbar, weshalb keine Notwendigkeit besteht, den Programmcode zu verkomplizieren.
Unter Verwendung der gefundenen Werte für die Korrelationskoeffizienten ist die Erstellung eines AKF-Diagramms (Korrelogramms) recht einfach. Um in diesem Diagramm die Grenzen (confidence bands) des 95%-Zuverlässigkeitsintervalls abbilden zu können, werden ihre Werte gemäß den unten aufgeführten Ausdrücken (Formeln) berechnet.
Für das bei der Zufälligkeitsprüfung verwendete Intervall:
![]()
Für das bei der Bestimmung der Ordnung des ARIMA-Modells verwendete Intervall:
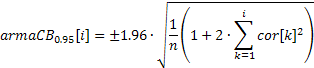
Im ersten Fall weist das Zuverlässigkeitsintervall einen konstanten Wert auf, wogegen es im zweiten um die Erhöhung der Zahl des Autokorrelationskoeffizienten vergrößert.
Manchmal kann das stark geglättete, lediglich die allgemeine Tendenz der Häufigkeitsverteilung wiedergebende Frequenzverhalten der Eingangssequenz in den Mittelpunkt des Interesses rücken. Zum Beispiel bei einem erheblichen Anstieg im Bereich der niedrigen oder hohen Häufigkeit oder bei vorherrschend mittleren Häufigkeiten usw.
Die Abbildung eines solchen Frequenzverhaltens erfolgt bevorzugt anhand eines linearen Maßstabs, um die vorherrschenden Häufigkeitsbereiche stärker hervorzuheben. Ein solcher Amplitudengang kann auf der Grundlage der zuvor ermittelten Autokorrelationskoeffizienten abgebildet werden. Zur Berechnung des Amplitudengangs verwenden wir die der Anzahl der in dem Diagramm abzubildenden AKF entsprechende Menge von Koeffizienten.
In Anbetracht dessen, dass diese Menge nicht groß ist, müssten als Ergebnis ausreichend glatte Werte für das Spektrum erhalten werden.
In diesem Fall kann das Frequenzverhalten der Abfolge auf folgende Weise anhand der Autokorrelationskoeffizienten wiedergegeben werden:
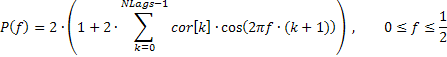
Der nachfolgend angeführte Codeausschnitt (s. die Datei TSAnalysis.mqh) dient der Berechnung des Amplitudengangs anhand des vorgestellten Ausdrucks:
. . . n=320; // Number of X-points ArrayResize(Spect,n); v=M_PI/n; for(i=0;i<n;i++) { a=i*v; b=0; for(k=0;k<NLags;k++)b+=((double)NLags-k)/(NLags+1.0)*ACF[k]*MathCos(a*(k+1)); Spect[i]=2.0*(1+2*b); // Spectrum Y-axis } . . .
Es sei darauf hingewiesen, dass die Werte der Autokorrelationskoeffizienten in dem vorgestellten Codeausschnitt zur zusätzlichen Glättung um eine Dreiecksfensterfunktion erweitert wurden.
Für eine umfassendere Analyse des Spektrums wurde als nächstes Glättungsverfahren das Prinzip der maximalen Entropie gewählt. Die Auswahl einer universellen Methode zur Berechnung des Spektrums ist recht schwierig. Die mit den klassischen parameterlosen Methoden der Spektralanalyse verbundenen Nachteile sind wohl bekannt.
Als Methoden dieser Art seien die der Periodogramme und der Korrelogramme genannt, sie können mithilfe der Algorithmen der schnellen Fourier-Transformation problemlos umgesetzt werden. Aber ungeachtet der großen Stabilität der Ergebnisse erfordern diese Methoden zu lange Eingangssequenzen, um eine ausreichend hohe Auflösung zu liefern. Im Gegensatz dazu können parametrische Methoden zur Spektralberechnung (z. B. Autoregressionsmethoden) auch für kurze Abfolgen eine deutlich bessere Auflösung gewährleisten.
Unglücklicherweise sind bei der Verwendung dieser Methoden nicht nur die Besonderheiten der jeweiligen Umsetzung zu berücksichtigen, sondern auch die Art der Eingangssequenz. Dabei ist es recht schwierig die geeignetste Ordnung des Autoregressionsmodells zu bestimmen, mit deren Erhöhung die Auflösung zunimmt, aber auch die Streuung der erhaltenen Ergebnisse. Bei Verwendung stark erhöhter Werte der Ordnung des Modells beginnen diese Methoden, instabile Ergebnisse zu liefern.
Vergleichende Charakteristiken unterschiedlicher Algorithmen zur Berechnung von Spektren bietet das Buch: Digitale Spektralanalyse und ihre Anwendung von S. L. Marple. Wie bereits erwähnt wurde hier das Prinzip der maximalen Entropie gewählt. Diese Methode liefert vermutlich die geringste Auflösung im Vergleich zu anderen Autoregressionsverfahren, dennoch ist die Wahl in der Hoffnung, stabilere Spektralberechnungen zu erhalten, gerade auf sie gefallen.
Sehen wir uns die Abfolge der Berechnungen zur Ermittlung des Autoregressionsspektrums einmal genauer an. Über die Auswahl der Ordnung des Modells wurde bereits gesprochen, weswegen wir davon ausgehen, dass diese bereits festgelegt wurde und gleich IP ist, sowie dass die IP Koeffizienten der Autokorrelation cor[] bereits berechnet wurden.
Zur Ermittlung der Autoregressionskoeffizienten anhand der bekannten Koeffizienten der Autokorrelation verwenden wir den in Form der Levinson-Rekursion umgesetzten rekursiven Algorithmus nach Levinson und Durbin.
//----------------------------------------------------------------------------------- // Calculate the Levinson-Durbin recursion for the autocorrelation sequence R[] // and return the autoregression coefficients A[] and partial autocorrelation // coefficients K[] //----------------------------------------------------------------------------------- void TSAnalysis::LevinsonRecursion(const double &R[],double &A[],double &K[]) { int p,i,m; double km,Em,Am1[],err; p=ArraySize(R); ArrayResize(Am1,p); ArrayInitialize(Am1,0); ArrayInitialize(A,0); ArrayInitialize(K,0); km=0; Em=1; for(m=0;m<p;m++) { err=0; for(i=0;i<m;i++)err+=Am1[i]*R[m-i-1]; km=(R[m]-err)/Em; K[m]=km; A[m]=km; for(i=0;i<m;i++)A[i]=(Am1[i]-km*Am1[m-i-1]); Em=(1-km*km)*Em; ArrayCopy(Am1,A); } return; }
Diese Methode weist drei Eingangsparameter auf. Bei allen dreien handelt es sich um Verknüpfungen zu Datenfeldern (Arrays). Wird diese Methode eingesetzt, müssen in dem ersten Datenfeld R[] die Eingangskoeffizienten der Autokorrelation abgelegt werden. Diese Werte bleiben im Verlauf der Berechnungen unverändert.
Die ermittelten Autokorrelationskoeffizienten kommen in das Datenfeld A[]. Außerdem werden in dem Datenfeld K[] die Werte der partiellen Autokorrelationsfunktion abgelegt, die den Koeffizienten der Abbildung des Autoregressionsmodells mit umgekehrtem Vorzeichen entsprechen. Die Ordnung des Modells wird nicht als Eingangsparameter übertragen, es wird angenommen, dass sie gleich der Anzahl der Elemente des Eingangsdatenfeldes R[] ist.
Deshalb ist es unumgänglich, dass die Umfänge der Ausgangsdatenfelder nicht geringer sind als der des Eingangsdatenfeldes, was innerhalb der Funktion nicht überprüft wird. Nach Abschluss der Berechnungen werden weder der Nullkoeffizient der Autoregression noch der Nullkoeffizient der partiellen Autokorrelationsfunktion in den Datenfeldern A[] bzw. K[] gespeichert.
Wir setzen voraus, dass sie stets gleich eins sind. Somit werden die Koeffizienten mit den Kennziffern von 1 bis IP (nicht zu verwechseln mit den mit null beginnenden Kennziffern der Datenfelder selbst) ebenso wie in der Eingangssequenz in den Ausgangsdatenfeldern abgelegt.
Die ermittelten Werte der partiellen Autokorrelationsfunktion werden im Weiteren lediglich zur Abbildung in dem entsprechenden Diagramm verwendet, der Autoregressionskoeffizienten dagegen wird zur Berechnung des mithilfe des folgenden Ausdrucks bestimmten Frequenzverhaltens verwendet:
![]()
Die Berechnung des Frequenzverhaltens erfolgt für 4.096 Werte der normalisierten Frequenz in einem Wertebereich von 0 bis 0,5. Bei der unmittelbaren Berechnung der Amplitudengangwerte anhand der oben vorgestellten Formel ist der Zeitaufwand zu groß, er kann jedoch erheblich verringert werden, wenn zur Ermittlung der Summe der komplexen Exponenten der Algorithmus der schnellen Fourier-Transformation genutzt wird.
In der Methode Calc kommt dazu statt der schnellen Fourier-Transformation die ebenfalls schnelle Hartley-Transformation (FHT) zur Anwendung.
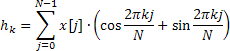
Bei der Hartley-Transformation werden keine komplexen Operationen verwendet, und Ein- wie Ausgangssequenz sind reell. Die umgekehrte Hartley-Transformation wird anhand derselben Formel berechnet, die lediglich eine zusätzliche Multiplikation mit dem Faktor 1/N erfordert.
Bei einer reellen Eingangssequenz besteht zwischen den Koeffizienten dieser Transformation und den Koeffizienten der Fourier-Transformation eine unmittelbare Verbindung.
![]()
Hinweise zu den Algorithmen der schnellen Hartley-Transformation liefern die Verknüpfungen in der Algorithmenbibliothek FXT algorithm library und in den Diskreten Transformationen nach Fourier und Hartley.
Bei der hier vorliegenden Umsetzung wurde die Funktion der schnellen Hartley-Transformation in der Form der Methode fht umgesetzt.
//----------------------------------------------------------------------------------- // Radix-2 decimation in frequency (DIF) fast Hartley transform (FHT). // Length is N = 2 ** ldn //----------------------------------------------------------------------------------- void TSAnalysis::fht(double &f[], ulong ldn) { const ulong n = ((ulong)1<<ldn); for (ulong ldm=ldn; ldm>=1; --ldm) { const ulong m = ((ulong)1<<ldm); const ulong mh = (m>>1); const ulong m4 = (mh>>1); const double phi0 = M_PI / (double)mh; for (ulong r=0; r<n; r+=m) { for (ulong j=0; j<mh; ++j) { ulong t1 = r+j; ulong t2 = t1+mh; double u = f[t1]; double v = f[t2]; f[t1] = u + v; f[t2] = u - v; } double ph = 0.0; for (ulong j=1; j<m4; ++j) { ulong k = mh-j; ph += phi0; double s=MathSin(ph); double c=MathCos(ph); ulong t1 = r+mh+j; ulong t2 = r+mh+k; double pj = f[t1]; double pk = f[t2]; f[t1] = pj * c + pk * s; f[t2] = pj * s - pk * c; } } } if(n>2) { ulong r = 0; for (ulong i=1; i<n; i++) { ulong k = n; do {k = k>>1; r = r^k;} while ((r & k)==0); if (r>i) {double tmp = f[i]; f[i] = f[r]; f[r] = tmp;} } } }
Bei Aufruf dieser Methode erfolgt die Übertragung der Verknüpfung zu dem Eingangsdatenfeld f[] sowie zu der vorzeichenlosen ganzen Zahl Idn, die die Länge der Transformation N = 2 ** ldn festlegt, auf deren Eingang. Der Umfang des Datenfeldes f[] darf nicht kleiner sein als die Länge der Transformation N. Es sollte nicht vergessen werden, dass innerhalb der Funktion keinerlei Überprüfungen in dieser Richtung ausgeführt werden. Ebenfalls zu bedenken ist, dass das Ergebnis der Transformation in demselben Datenfeld gespeichert wird, in dem auch die Eingangsdaten abgelegt wurden.
Die Eingangsdaten selbst werden nach erfolgter Transformation nicht gespeichert. In der betrachteten Methode Calc zur Ermittlung der 4.096 Amplitudengangwerte wird eine Transformation im Umfang von N=8.192 verwendet. Im Anschluss an die Berechnung des Quadrates der absoluten Beträge des Transformationsergebnisses und seine Vorzeichenumkehrung wird das erhaltene Resultat auf seinen Höchstwert normalisiert und auf ein logarithmisches Maß gebracht.
Im Übrigen weist die Methode Calc keine ernsthaften Besonderheiten auf, falls erforderlich kann ihre Umsetzung mithilfe der Datei TSAnalysis.mqh vertieft werden.
Alle ermittelten und für die Abbildung aufbereiteten Werte werden nach der Berechnung in Variablen gespeichert, die Elemente der Klasse TSAnalysis sind. Deshalb müssen sie bei Aufruf der virtuellen Methode show zur Anzeige der Ergebnisse nicht als Argumente übertragen werden.
Veranschaulichung
Bekanntermaßen wurde die Methode show als virtuell deklariert. Deshalb kann bei ihrer Transformation die erforderliche Methode zur Wiedergabe der Berechnungsergebnisse abweichend von der vorhergehenden umgesetzt werden. In der vorgeschlagenen Klasse TSAnalysis erfolgt die Veranschaulichung auf dem Wege der Erstellung einer Datei mit den Daten sowie durch den Aufruf eines Webbrowsers, um sie anzuzeigen.
Damit der Webbrowser diese Daten wiedergeben kann, kommt die in demselben Verzeichnis wie die übrigen Dateien für dieses Projekt abgelegte Datei TSA.htm zum Einsatz. Dieses Verfahren zur Abbildung grafischer Informationen wurde bereits in dem Beitrag Schaubilder und Diagramme in HTML ausführlich beschrieben.
In der Methode show der Klasse TSAnalysis erfolgt die Formatierung und Speicherung aller zur Wiedergabe bestimmten Berechnungsergebnisse in einer Variablen der Art „string“ (s. die Datei TSAnalysis.mqh). Eine auf diese Weise angelegte lange Zeile wird in einem Zug in der Datei TSDat.txt gespeichert. Die Erstellung dieser Datei und die Eingabe der Daten in sie erfolgt mithilfe MQL5-üblicher Instrumente, weshalb die Datei in dem Verzeichnis \MQL5\Files angelegt wird.
Im weiteren Verlauf wird diese Datei mithilfe des Aufrufs externer Systemfunktionen in das Verzeichnis des jeweiligen Vorhabens verschoben. Anschließend wird der jeweilige Webbrowser zur Anzeige der Datei TSA.htm gestartet, die wiederum Daten aus der Datei TSDat.txt verwendet. Da in der Methode show der Aufruf der Systemfunktionen ausgeführt wird, muss in der Anwendungsinstanz auf dem jeweiligen Ausgabegerät (Terminal) die Verwendung fremder DLL zur Arbeit mit der Klasse TSAnalysis zugelassen sein.
Beispiele
Die Datei TSAexample.mq5 in der gepackten Datei TSAnalysis.zip enthält ein Anwendungsbeispiel für die Klasse TSAnalysis.
//----------------------------------------------------------------------------------- // TSAexample.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "TSAnalysis.mqh" //----------------------------------------------------------------------------------- // Script program start function //----------------------------------------------------------------------------------- void OnStart() { double bd[]={47,64,23,71,38,64,55,41,59,48,71,35,57,40,58,44,80,55,37,74,51,57,50, 60,45,57,50,45,25,59,50,71,56,74,50,58,45,54,36,54,48,55,45,57,50,62,44,64,43,52, 38,59,55,41,53,49,34,35,54,45,68,38,50,60,39,59,40,57,54,23}; TSAnalysis *tsa=new TSAnalysis; tsa.Calc(bd); delete tsa; }
Wie zu sehen ist der Aufruf dieser Klasse recht einfach, wenn das Datenfeld mit der Eingangssequenz vorbereitet ist, kostet es keinerlei Mühe, es zur Analyse an die Methode Calc weiterzugeben. Dabei darf allerdings nicht vergessen werden, den Speicherplatz mithilfe des Aufrufs der Methode „delete“ freizugeben. Das Ergebnis der Ausführung dieses Skripts wurde bereits zu Beginn dieses Beitrages vorgestellt.
Zur Veranschaulichung der Effektivität der durchgeführten Spektralberechnungen sehen wir uns weitere Beispiele mit erzeugten Abfolgen an.
Für den Anfang verwenden wir eine aus zwei Sinuskurven bestehende Abfolge:
int i,n; double a,x[]; n=400; ArrayResize(x,n); a=2*M_PI; for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i);
Die Abbildung zeigt die Berechnung des Frequenzverhaltens dieser Abfolge.
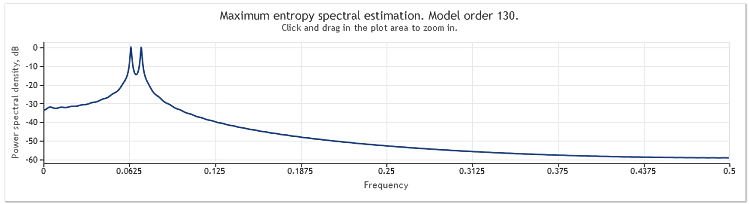
Abbildung 2. Berechnung des Spektrums Zwei Sinuskurven
Obwohl beide Sinuskurven gut zu erkennen sind, zeigt sich bei Vergrößerung des uns interessierenden Diagrammabschnitts, dass die Höhepunkte auf den Frequenzen 0,0637 bzw. 0,0712 liegen. Das heißt, sie weichen ein wenig von den tatsächlichen Werten ab. Besteht eine Abfolge aus lediglich einer Sinuskurve, ist eine solche Abweichung nicht zu beobachten. Wir schreiben diese Erscheinung den Besonderheiten der von uns gewählten Methode der Spektralanalyse zu.
Wir erhöhen den Schwierigkeitsgrad der Aufgabe weiter, indem wir unsere Abfolge um eine Zufallskomponente erweitern. Dazu verwenden wir den in Form der Klasse RNDXor128 umgesetzten Pseudozufallsfolgengenerator aus der gepackten Datei RNDXor128.zip am Ende dieses Beitrags.
Zum Anlegen eines Prüfsignals wurde folgender Codeausschnitt genutzt:
int i,n; double a,x[]; RNDXor128 *rnd=new RNDXor128; n=800; ArrayResize(x,n); a=2*M_PI; for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i)+rnd.Rand_Norm(); delete rnd;
In diesem Beispiel wurden zwei Sinuskurven um ein zufälliges Signal mit Normalverteilung und gleichmäßiger Streuung ergänzt.
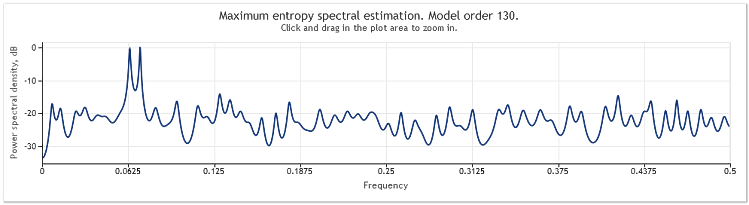
Abbildung 3. Berechnung des Spektrums. Zwei Sinuskurven plus Zufallssignal
Dabei bleiben die Sinuskurvenkomponenten gut erkennbar.
Nach der fünffachen Vergrößerung der Amplitude des zufälligen Bestandteils erscheinen die Sinuskurven ernsthaft verschleiert.
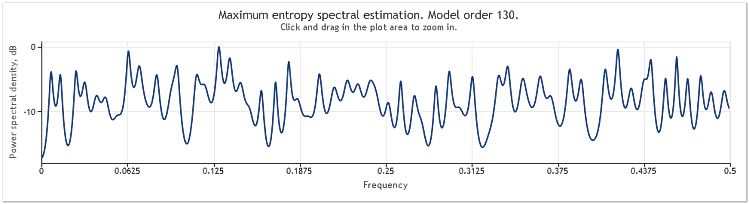
Abbildung 4. Berechnung des Spektrums. Zwei Sinuskurven plus Zufallssignal mit größerer Amplitude
Bei einer Erweiterung der Länge der Abfolge von 400 auf 800 Elemente werden die Sinuskurven wieder gut erkennbar.
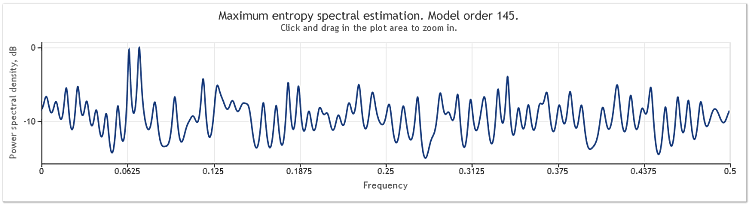
Abbildung 5. Zwei Sinuskurven plus Zufallssignal mit größerer Amplitude. N=800
Dabei ist die Ordnung des Autoregressionsmodells von 130 auf 145 angestiegen. Die Heraufsetzung der Länge der Abfolge hat zu einer Erhöhung der Ordnung des Modells geführt, im Ergebnis hat sich dadurch die Auflösungsleistung der Spektralberechnung verbessert, wodurch die Höhepunkte in dem Diagramm deutlicher hervortreten.
Die Berechnung des Spektrums für die Notierungen des Währungspaares (Kürzels) EURUSD, D1 im Verlauf zweier Jahre (2009 und 2010) sieht aus wie folgt:

Abbildung 6. EURUSD-Notierungen. 2009 - 2010. Zeitraum D1
Die Eingangssequenz enthielt 519 Werte und die Ordnung des Modells war, wie aus der Abbildung folgt, gleich 135.
Wie wir sehen, weist diese Spektralberechnung eine ganze Reihe deutlich ausgeprägter Höhepunkte auf. Um zu bestimmen, ob es sich bei diesen Höhepunkten tatsächlich um periodische Bestandteile der Kursnotierungen handelt, reichen diese Berechnungen allein allerdings nicht aus.
Das Auftreten von Höhepunkten im Frequenzverhalten kann durch das Vorliegen einer Zufallskomponente ausreichender Größe in den Notierungen oder die offenkundige Nichtstationarität der betrachteten Abfolge bedingt sein.
Deshalb ist es stets wünschenswert, vor der abschließenden Schlussfolgerung bezüglich des Vorhandenseins eines periodischen Bestandteils das gewonnene Ergebnis anhand der Daten eines anderen Abschnitts aus der Abfolge oder eines anderen Zeitraums zu bestätigen. Außerdem können bei der Untersuchung der Zyklizität statt der Abfolge selbst versuchsweise auch deren Abträge verwendet werden.
Fazit
Da sich die in diesem Beitrag vorgestellte Methode zur Spektralberechnung auf die Autokorrelationskoeffizienten stützt, fehlen bei ihrer Verwendung in der Eingangssequenz stets deren Durchschnittswerte. Häufig ist die Entfernung eines konstanten Bestandteils aus der Eingangssequenz schlicht unverzichtbar, beim Einsatz von Autoregressionsmethoden kann ihre Entfernung jedoch in einigen Fällen zu Verzerrungen der Spektralberechnung im Niederfrequenzbereich führen.
Ein Beispiel für derartige Verzerrungen bietet das Ende des Kapitels „Kurzzusammenfassung der Ergebnisse bezüglich der Spektralberechnung“ in dem Buch Digitale Spektralanalyse und ihre Anwendung von S. L. Marple. In unserem Fall lässt uns die gewählte Methode der Spektralanalyse keine Wahl, deshalb sei hier nur kurz daran erinnert, dass Spektralberechnungen stets nur für Abfolgen mit entferntem Durchschnittswert ausgeführt werden.
Literatur
- Wuertz, Diethelm, und Katzgraber, Helmut, (2009): Precise finite-sample quantiles of the Jarque-Bera adjusted Lagrange multiplier test, Eidgenössische Technische Hochschule, Zürich, 2009.
- Tanweer-ul-Islam, Asad Zaman, Normality Testing - A new Direction, IIE, Internationale Islamische Universität, Islamabad, Pakistan, 2008.
- Carlos M. Urzua, Portable and powerful tests for normality, Institut für Technologische und Höhere Studien Monterrey, Campus Ciudad de Mexico, 2007.
- Comparison of Common Tests for Normality
- S. V. Bulaschev. Statistics for Traders (Statistik für Devisenhändler) - Мoskau: Sputnik +, 2003. - 245 S.
- P. V. Novickij, I. A. Zograf. Berechnung der Fehlerhaftigkeit von Messergebnissen. Energoatomizdat, 1991.
- S. L. Marple Jr., Digital Spectral Analysis with Applications (Digitale Spektralanalyse und ihre Anwendung). Moskau: Mir, 1990.
- David J. Sheskin, Handbook of Parametric and Nonparametric Statistical Procedures, Chapman and Hall/CRC.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/292
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Zeitreihenvorhersage mittels exponentieller Glättung
Zeitreihenvorhersage mittels exponentieller Glättung
 Leistungsfähige adaptive Indikatoren - Theorie und Umsetzung in MQL5
Leistungsfähige adaptive Indikatoren - Theorie und Umsetzung in MQL5
 Analyse der statistischen Eigenschaften von Indikatoren
Analyse der statistischen Eigenschaften von Indikatoren
 Der MQL5-Assistent für Neueinsteiger
Der MQL5-Assistent für Neueinsteiger
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Der Artikel Analysing the main characteristics of time series wurde veröffentlicht:
Autor: Viktor
Viktor, guten Tag.
Leider ist es mir nicht möglich, die endgültigen Informationen zu erhalten. Die Merkmale, die in der ursprünglichen Form erscheinen, werden angezeigt: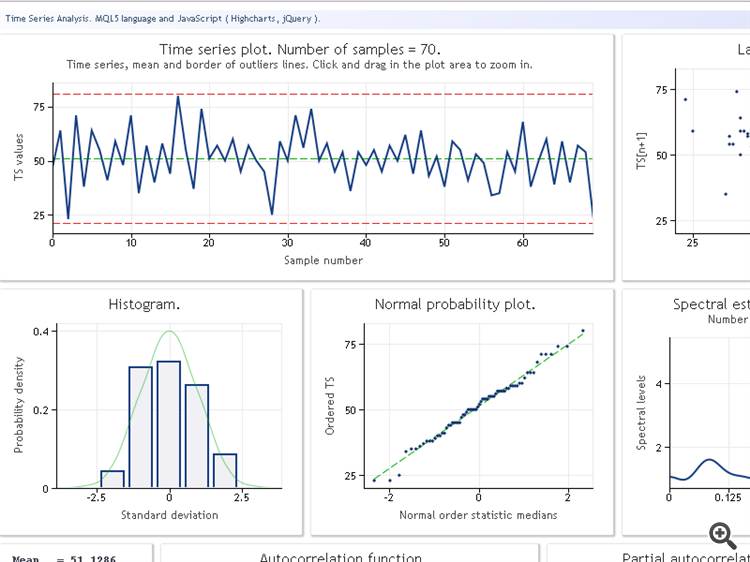
Sehen Sie sich den Text des Skripts TSAexample.mq5 an.
Darin wird das Array bd[] mit Werten der untersuchten Sequenz gefüllt und dann als Argument beim Aufruf der Calc-Methode der Klasse TSAnalysis verwendet.
Schreiben Sie Ihr eigenes Skript (oder Ihren eigenen Indikator), bilden Sie ein Array mit Ihrer Sequenz mit einer beliebigen verfügbaren Methode und übergeben Sie es als Argument an die Calc-Methode in Analogie zu dem im Artikel genannten Beispiel.
Es scheint mir, dass Sie dazu in der Lage sein sollten.
Sieger.
Was bedeutet das Akronym "IP"?
Sehen Sie sich den Text des Skripts TSAexample.mq5 an.
Darin wird das Array bd[] mit Werten der untersuchten Sequenz gefüllt und dann als Argument beim Aufruf der Calc-Methode der Klasse TSAnalysis verwendet.
Schreiben Sie Ihr eigenes Skript (oder Ihren eigenen Indikator), bilden Sie ein Array mit Ihrer Sequenz mit einer beliebigen verfügbaren Methode und übergeben Sie es als Argument an die Calc-Methode in Analogie zu dem im Artikel genannten Beispiel.
Es scheint mir, dass Sie dazu in der Lage sein sollten.
Sieger.
Alles funktioniert einwandfrei! Ein sehr praktisches Werkzeug! Ich danke Ihnen!