Tiefe Neuronale Netzwerke (Teil VI). Gruppen von Klassifikatoren von Neuronalen Netzen: Bagging
830
0
Inhalt
- Einführung
- Ensembles von Neuronalen Netzen
- Bagging
- Generierung der Quelldatensätze
- Sortieren nach der Wichtigkeit der Information
- Erstellen, Trainieren und Testen des Ensembles der Klassifikatoren
- Kombinieren der individuellen Ausgabe der Klassifikatoren (Durchschnitt/Abstimmung)
- Ensembles bereinigen mit den entsprechenden Methoden
- Optimieren der Hyperparameter der Ensemblemitglieder. Merkmale und Methoden
- Training und Testen des Ensembles mit den optimierten Hyperparameter
- Schlussfolgerung
- Anlagen
Einführung
Der vorherige Artikel dieser Serie diskutierte die Hyperparameter des DNN-Modells, trainierte und testetet sie. Die Qualität des resultierenden Modells war recht hoch.
Wir diskutierten auch die Möglichkeiten, wie die Qualität der Klassifizierung verbessert werden kann. Eine davon ist die Verwendung eines Ensembles von Neuronalen Netzen. Diese Variante der Verstärkung wird in diesem Artikel diskutiert.
1. Ensembles von Neuronalen Netzen
Studien zeigen, dass Ensembles von Klassifikatoren in der Regel genauer sind als einzelne Klassifikatoren. Ein solches Ensemble ist in Abbildung 1a dargestellt. Es verwendet mehrere Klassifikatoren, wobei jeder von ihnen eine Entscheidung über das als Eingabe gelieferte Objekt trifft. Diese Einzelentscheidungen werden dann in einem Kombinator (Combiner) zusammengefasst. Das Ensemble gibt eine Klassenbezeichnung für das Objekt aus.
Es ist intuitiv, dass das Ensemble der Klassifikatoren nicht genau definiert werden kann. Diese allgemeine Unsicherheit ist in Abbildung 1b-d dargestellt. Im Wesentlichen ist jedes Ensemble selbst ein Klassifikator (Abbildung 1b). Die Basisklassifikatoren, die sie enthalten, extrahieren komplexe Funktionen von (oft impliziten) Gesetzmäßigkeiten, und der Kombinator wird zu einem einfachen Klassifikator, der diese Funktionen aggregiert.
Andererseits hindert uns nichts daran, einen herkömmlichen Standard-Klassifikator für Neuronale Netze als Ensemble zu bezeichnen (Abbildung 1c). Neuronen auf der vorletzten Schicht können als separate Klassifikatoren betrachtet werden. Ihre Entscheidungen müssen im Kombinator, dessen Rolle die oberste Schicht spielt, "entschlüsselt" werden.
Und schließlich können die Funktionen als primitive Klassifikatoren und der Klassifikator als deren komplexer Kombinator betrachtet werden (Abbildung 1d).
Wir kombinieren einfache trainierbare Klassifikatoren, um eine genaue Entscheidung über die Klassifizierung zu erhalten. Aber ist das der richtige Weg?
In ihrem kritischen Übersichtsartikel "Multiple Classifier Combination: Lessons and Next steps", veröffentlicht 2002, schrieb Tin Kam Ho:
"Anstatt nach den besten Eigenschaften und dem besten Klassifikator zu suchen, suchen wir jetzt nach den besten Klassifikatoren und dann nach der besten Kombinationsmethode. Man kann sich vorstellen, dass wir sehr bald nach den besten Kombinationsmethoden und dann nach dem besten Weg suchen werden, sie alle zu nutzen. Wenn wir die Chance nicht nutzen, die grundlegenden Probleme, die sich aus dieser Herausforderung ergeben, zu überprüfen, werden wir zwangsläufig in eine solche unendliche Wiederholung getrieben, indem wir immer kompliziertere Kombinationsschemata und Theorien mitschleppen und das ursprüngliche Problem allmählich aus den Augen verlieren."
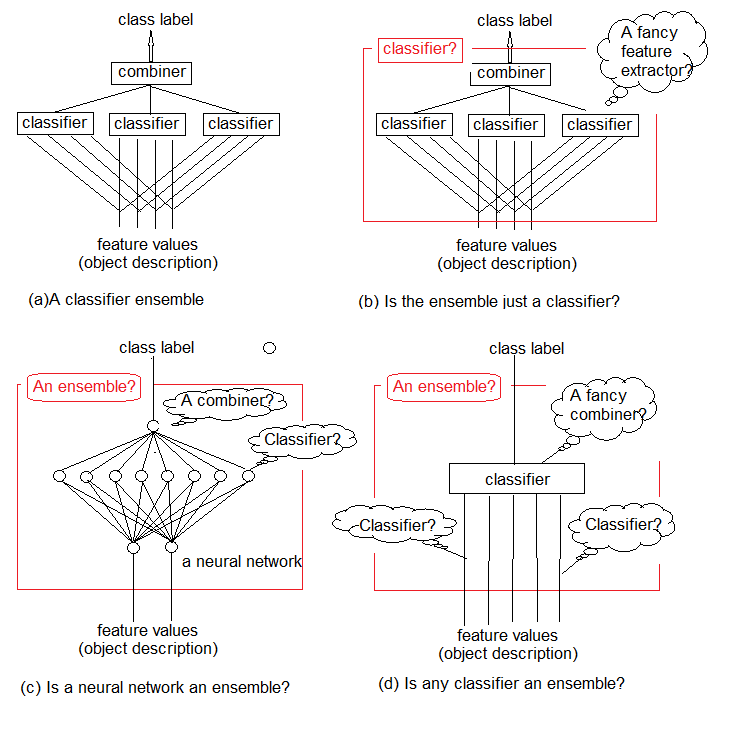
Abb. 1. Was ist ein Ensemble von Klassifikatoren?
Die Lektion ist, dass wir den optimalen Weg finden müssen, um bestehende Werkzeuge und Methoden zu nutzen, bevor wir neue komplexe Projekte erstellen.
Es ist bekannt, dass Klassifikatoren Neuronaler Netze "universelle Näherungswerte" sind. Dies bedeutet, dass jede Klassifikationsgrenze, unabhängig von ihrer Komplexität, durch ein endliches Neuronales Netz mit beliebiger Genauigkeit approximiert werden kann. Dieses Wissen gibt uns jedoch keine Möglichkeit, ein solches Netzwerk aufzubauen oder zu trainieren. Die Idee der Kombination von Klassifikatoren ist ein Versuch, das Problem zu lösen, indem man ein Netzwerk von verwalteten Bausteinen zusammenstellt.
Methoden zur Zusammenstellung eines Ensembles sind Meta-Algorithmen, die mehrere maschinelle Lernmethoden zu einem prädiktiven Modell zusammenfassen, um:
- Varianz reduzieren - Bagging;
- Bias reduzieren - Boosting;
- Vorhersagen verbessern - Stacking.
Diese Methoden lassen sich in zwei Gruppen einteilen:
- Parallele Methoden zur Konstruktion eines Ensembles, bei denen die Basismodelle parallel erzeugt werden (z.B. ein "random forest"). Die Idee ist, die Unabhängigkeit zwischen den Basismodellen zu nutzen und den Fehler durch Mittelung zu reduzieren. Daher ist die wichtigste Voraussetzung für Modelle - geringe gegenseitige Korrelation und hohe Vielfalt.
- Sequentielle Ensemble-Methoden, bei denen die Basismodelle sequentiell generiert werden (z.B. AdaBoost, XGBoost). Die Grundidee dabei ist die Nutzung der Abhängigkeit zwischen den Basismodellen. Hier kann die Gesamtqualität erhöht werden, indem man bisher falsch klassifizierten Beispielen höhere Gewichte zuordnet.
Die meisten Ensemble-Methoden verwenden einen einzigen Basis-Lernalgorithmus, um homogene Basismodelle zu erstellen. Dies führt zu homogenen Ensembles. Es gibt auch Methoden mit heterogenen Modellen (Modelle verschiedener Typen). Dadurch entstehen heterogene Ensembles. Damit die Ensembles genauer sind als die einzelnen Mitglieder, sollten die Basismodelle so vielfältig wie möglich sein. Mit anderen Worten, je mehr Informationen von den Basisklassifizierern kommen, desto höher ist die Genauigkeit des Ensembles.
Abbildung 2 zeigt 4 Ebenen der Erstellung eines Ensembles von Klassifikatoren. Zu jedem von ihnen stellen sich Fragen, die im Folgenden erörtert werden.
Abb. 2. Die vier Ebenen des Erstellens eines Ensembles von Klassifikatoren
Diskutieren wir das im Detail.
1. Kombinatoren
Einige Ensemble-Methoden definieren keinen Kombinator. Aber für die Methoden, die das tun, gibt es drei Arten von Kombinatoren.
- Nicht trainierbar. Ein Beispiel für eine solche Methode ist eine einfache "Mehrheitsentscheidung".
- Trainierbar. Diese Gruppe umfasst "gewichtete Mehrheitsentscheidungen" und "Naive Bayes" sowie den Ansatz der "Klassifikatorauswahl", bei dem die Entscheidung über ein bestimmtes Objekt von einem Klassifikator des Ensembles getroffen wird.
- Meta-Klassifikator. Die Ausgaben der Basisklassifikatoren werden als Eingänge für den zu trainierenden neuen Klassifikator betrachtet, der zu einem Kombinator wird. Diesen Ansatz nennt man "komplexe Verallgemeinerung", "Verallgemeinerung durch Training" oder einfach "Stacking". Der Aufbau eines Trainingsdatensatzes für einen Meta-Klassifikator ist eines der Hauptprobleme dieses Kombinators.
2. Aufbau eines Ensembles
Sollen die Basisklassifizierer parallel (unabhängig) oder sequentiell trainiert werden? Ein Beispiel für sequentielles Training ist AdaBoost, wobei der Trainingsdatensatz jedes hinzugefügten Klassifikators von dem zuvor erstellten Ensemble abhängt.
3. Vielfalt
Wie kann man Unterschiede im Ensemble erzeugen? Die folgenden Optionen werden vorgeschlagen.
- Variieren der Trainingsparameter. Verwenden Sie unterschiedliche Ansätze und Parameter beim Training der einzelnen Basisklassifikator. Beispielsweise ist es möglich, die Neuronengewichte in den verborgenen Schichten des Neuronalen Netzes jedes Basisklassifikators mit verschiedenen Zufallsvariablen zu initialisieren. Es ist auch möglich, die Hyperparameter zufällig zu setzen.
- Variieren der Stichproben - nehmen Sie ein individuelles Bootstrap-Stichproben aus dem Trainingsdatensatz für jedes Mitglied des Ensembles.
- Variieren der Prädiktoren - erstellen Sie einen benutzerdefinierten Satz von zufällig bestimmten Prädiktoren für jeden Basisklassifikator. Dies ist der sogenannte vertikale Split des Trainingsdatensatzes.
4. Ensemblegröße
Wie bestimmt man die Anzahl der Klassifikatoren in einem Ensemble? Wird das Ensemble durch gleichzeitiges Training der erforderlichen Anzahl von Klassifikatoren oder iterativ durch Hinzufügen/Entfernen von Klassifikatoren aufgebaut? Mögliche Optionen:
- Die Nummer wird im Voraus reserviert.
- Die Anzahl wird im Laufe der Ausbildung festgelegt.
- Klassifikatoren werden überproduziert und dann ausgewählt.
5. Vielseitigkeit (relativ zum Basisklassifikator)
Einige Ensemble-Ansätze können mit jedem Klassifikatormodell verwendet werden, während andere an einen bestimmten Klassifikatortyp gebunden sind. Ein Beispiel für ein "klassifikatorenspezifisches" Ensemble ist der Random Forest. Sein Basisklassifikator ist der Entscheidungsbaum. Es gibt also zwei Varianten von Ansätzen:
- Es kann nur ein bestimmtes Modell des Basisklassifikators verwendet werden;
- Es kann jedes Modell des Basisklassifikators verwendet werden.
Bei der Schulung und Optimierung der Parameter des Klassifikatorensembles sollte man zwischen der Optimierung der Lösung und der Optimierung der Abdeckung unterscheiden.
- Die Optimierung der Entscheidungsfindung bezieht sich auf die Auswahl eines Kombinators für ein festes Ensemble von Basisklassifikatoren (Ebene A in Abbildung 2).
- Die Optimierung der alternativen Abdeckung bezieht sich auf die Erstellung diverser Basisklassifikatoren mit einem festen Kombinator (Ebenen B, C und D in Abbildung 2).
Diese Einteilung des Ensemble-Designs reduziert die Komplexität des Problems, so dass sie sinnvoll erscheint.
Eine sehr detaillierte und tiefgehende Analyse der Ensemblemethoden findet sich in den Büchern Combining Pattern Classifiers, Methods and Algorithms, Second Edition. Ludmila Kuncheva und Ensemble Methods, Foundations and Algorithms. Eine empfehlenswerte Literatur!
2. Bagging
Der Name der Methode leitet sich ab von Bootstrap AGGregatING. Bagging-Ensembles werden wie folgt gebildet:
- Es wird eine Bootstrap-Probe aus dem Trainingsdatensatz extrahiert;
- Es wird jeder Klassifikator auf seine eigene Stichprobe trainiert;
- Es werden die einzelnen Ausgaben der einzelnen Klassifikatoren unter eine Klassenbezeichnung zusammengefasst. Haben einzelne Ausgaben die Form einer Klassenbezeichnung, so wird mit einfacher Mehrheit abgestimmt. Wenn die Ausgabe von Klassifikatoren eine kontinuierliche Variable ist, dann wird entweder eine Mittelwertbildung durchgeführt oder die Variable wird in eine Klassenbezeichnung umgewandelt, gefolgt von einer einfachen Mehrheitsentscheidung.
Kehren wir zu Abbildung 2 zurück und analysieren wir alle Ebenen der Erstellung eines Ensembles von Klassifikatoren für die Baggingmethode.
A: Aggregationsebene
Auf dieser Ebene werden die aus den Klassifikatoren gewonnenen Daten zusammengefasst und eine einzige Ausgabe aggregiert.
Wie kombinieren wir einzelne Ausgaben? Wir verwenden einen nicht trainierbaren Kombinator (Mittelung, einfache Stimmenmehrheit).
B: Ebene der Klassifikatoren
Auf der Ebene B findet die gesamte Arbeit mit Klassifikatoren statt. Hier stellen sich mehrere Fragen.
- Verwenden wir unterschiedliche oder gleiche Klassifikatoren? Die gleichen Klassifikatoren werden beim Bagging verwendet.
- Welcher Klassifikator wird als der Basisklassifikator ausgewählt? Wir verwenden ELM (Extreme Learning Machines).
Schauen wir uns das im Detail an. Die Auswahl des Klassifikators und seine Begründung ist ein wichtiger Teil der Arbeit. Listen wir die wichtigsten Anforderungen an die Basisklassifikator auf, um ein hochwertiges Ensemble zu schaffen.
Erstens muss der Klassifikator einfach sein: Tiefe Neuronale Netze werden nicht empfohlen.
Zweitens müssen die Klassifikatoren unterschiedlich sein: mit unterschiedlichen Initialisierungen, Lernparametern, Trainingsdatensatzs, etc.
Drittens ist die Geschwindigkeit des Klassifikators wichtig: Modelle sollten nicht stundenlang trainiert werden müssen.
Viertens sollten die Klassifikationsmodelle schwach sein und ein Vorhersageergebnis von etwas mehr als 50% liefern.
Und schließlich ist die Instabilität des Klassifikators wichtig, damit die Vorhersageergebnisse einen weiten Bereich haben.
Es gibt eine Option, die alle diese Anforderungen erfüllt. Es ist eine spezielle Art von Neuronalen Netzwerken - ELM (Extreme Learning Machines), die als alternative Lernalgorithmen anstelle von MLP vorgeschlagen wurden. Formal ist es ein vollständig verbundenes Neuronales Netzwerk mit einer versteckten Schicht. Aber ohne die iterative Bestimmung von Gewichten (Training) wird es außergewöhnlich schnell. Es wählt die Gewichte der Neuronen in der ausgeblendeten Schicht einmalig während der Initialisierung zufällig aus und bestimmt dann analytisch ihr Ausgangsgewicht entsprechend der gewählten Aktivierungsfunktion. Eine detaillierte Beschreibung des ELM-Algorithmus und eine Übersicht über seine vielen Varianten finden Sie im beigefügten Archiv.
- Wie viele Klassifikatoren sind notwendig? Beginnen wir mit 500 und reduzieren später das Ensemble.
- Ist das parallele oder sequentielle Training der verwendeten Klassifikatoren? Wir verwenden das parallele Training, das für alle Klassifikatoren gleichzeitig stattfindet.
- Welche Parameter der Basisklassifikatoren können verändert werden? Die Anzahl der versteckten Schichten, die Aktivierungsfunktion, die Stichprobengröße des Trainingsdatensatzes. Alle diese Parameter unterliegen der Optimierung.
C: Funktionsumfang für die identifizierte Regelmäßigkeiten
- Werden alle Prädiktoren oder nur einzelne Teilmengen für jeden Klassifikator verwendet? Alle Klassifikatoren verwenden eine Untermenge von Prädiktoren. Aber die Anzahl der Prädiktoren kann optimiert werden.
- Wie wählt man eine solche Untermenge? In diesem Fall werden spezielle Algorithmen verwendet.
D: Ebene der Eingangsdaten und deren Manipulationen
Auf dieser Ebene werden die Quelldaten dem Eingang des Neuronalen Netzes zum Training zugeführt.
Wie man die Eingangsdaten manipuliert, um eine hohe Diversität und individuelle Genauigkeit zu erreichen? Bootstrap-Samples werden für jeden Klassifikator einzeln verwendet. Die Größe des Bootstrap-Samples ist für alle Ensemblemitglieder gleich, wird aber optimiert.
Um Experimente mit ELM-Ensembles durchzuführen, gibt es zwei Pakete in R (elmNN, ELMR) und ein Paket in Python (hpelm). Testen wir zunächst die Möglichkeiten des elmNNN-Pakets, das das klassische ELM implementiert. Das Paket elmNN ist für die Erstellung, das Training und das Testen mit der ELM-Batch-Methode konzipiert. So stehen die Trainings- und Testmuster vor dem Training bereit und werden dem Modell einmalig zugeführt. Das Paket ist sehr einfach.
Das Experiment besteht aus den folgenden Phasen.
- Generierung der Quelldatensätze
- Sortieren nach der Wichtigkeit der Information
- Trainieren und testen des Ensembles der Klassifikatoren
- Kombinieren der individuellen Ausgabe der Klassifikatoren (Durchschnitt/Abstimmung)
- Ensembles bereinigen mit den entsprechenden Methoden
- Suche nach Metriken der Qualität des Ensembles der Klassifikatoren
- Bestimmen der optimalen Parameter der Ensemblemitglieder. Methoden
- Training und Testen des Ensembles mit den optimierten Parametern
Generierung der Quelldatensätze
Es wird die letzte Version von MRO 3.4.3 für die Experimente verwendet. Sie verfügt über mehrere neue für unser Ziel geeignete Pakte.
Starten wir RStudio, gehen dann zu GitHub/Part_I, um die Datei Cotir.RData mit Kursen des Terminals herunterzuladen, und holen zuletzt die Datei FunPrepareData.R mit Funktionen zu Datenaufbereitung von GitHub/Part_IV.
Bisher wurde festgestellt, dass ein Datensatz mit kalkulatorischen Ausreißern und normalisierten Daten bessere Ergebnisse im Training mit Pretraining ermöglicht. Wir werden es verwenden. Wir könnten auch die anderen zuvor betrachteten Vorverarbeitungsmöglichkeiten testen.
Bei der Einteilung in Teilmengen für pretrain/train/val/test nutzen wir die erste Möglichkeit, die Klassifizierungsqualität zu verbessern — die Anzahl der Proben für das Training zu erhöhen. Die Anzahl der Stichproben in der Untermenge 'pretrain' wird auf 4000 erhöht.
#----Prepare------------- library(anytime) library(rowr) library(elmNN) library(rBayesianOptimization) library(foreach) library(magrittr) library(clusterSim) #source(file = "FunPrepareData.R") #source(file = "FUN_Ensemble.R") #---prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) preproc <- PreNorm(DTcap, meth = meth) DTcap.n <- NormData(DTcap, preproc = preproc) }, env)
Durch Ändern des Parameters start in der Funktion SplitData() ist es möglich, Datensätze zu erhalten, die um den Betrag des Starts verschoben sind. Dies ermöglicht es, die Qualität in verschiedenen Teilen der Preisspanne in der Zukunft zu überprüfen und festzustellen, wie sie sich in der Geschichte verändert.
Erstellen von Datensätzen (pretrain/train/test/test1) für Pretraining, Feinabstimmung und dem Testen, erfasst in der Liste X. Umwandeln der Zielvariable von einem Datenrahmen in einen nominalen Typ (0.1).
#---Data X-------------
evalq({
list(
pretrain = list(
x = DTcap.n$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$pretrain$Class %>% as.numeric() %>% subtract(1)
),
train = list(
x = DTcap.n$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$train$Class %>% as.numeric() %>% subtract(1)
),
test = list(
x = DTcap.n$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$val$Class %>% as.numeric() %>% subtract(1)
),
test1 = list(
x = DTcap.n$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$test$Class %>% as.numeric() %>% subtract(1)
)
) -> X
}, env)
Sortieren nach der Wichtigkeit der Information
Testen der Funktion clusterSim::HINoV.Mod() (siehe Paket für weitere Details). Es ordnet die Variablen basierend auf Clustering mit unterschiedlichen Abständen und Methoden. Wir verwenden die Standardparameter. Es steht Ihnen frei, mit anderen Parametern zu experimentieren. Die Konstante numFeature <- 10 erlaubt es, die Anzahl der besten Prädiktoren bestF dem Modell zuzuführen.
Berechnungen werden mit den Datensatz X$pretrain durchgeführt
require(clusterSim)
evalq({
numFeature <- 10
HINoV.Mod(x = X$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> r
r$stopri[ ,1] %>% head(numFeature) -> bestF
}, env)
print(env$r$stopri)
[,1] [,2]
[1,] 5 0.9242887
[2,] 11 0.8775318
[3,] 9 0.8265240
[4,] 3 0.6093157
[5,] 6 0.6004115
[6,] 10 0.5730556
[7,] 1 0.5722479
[8,] 7 0.4730875
[9,] 4 0.3780357
[10,] 8 0.3181561
[11,] 2 0.2960231
[12,] 12 0.1009184
Die Reihung nach Rang der Prädiktor zeigt der Code oben Die ersten 10 sind unten aufgeführt, sie werden im Weiteren verwendet.
> colnames(env$X$pretrain$x)[env$bestF] [1] "v.fatl" "v.rbci" "v.ftlm" "rbci" "v.satl" "v.stlm" "ftlm" [8] "v.rftl" "pcci" "v.rstl"
Die Datensätze für die Experimente sind fertig.
Die Funktion Evaluate(), die die Metriken aus den Testergebnissen berechnet, wird aus dem vorherigen Artikel genommen. Der Wert von mean(F1) wird als Optimierungskriterium (Maximierung) verwendet. Wir laden diese Funktion in die Umgebung 'env'.
Erstellen, Trainieren und Testen des Ensembles
Trainieren Sie das Ensemble Neuronaler Netze (n <- 500 Einheiten) und kombinieren Sie diese in Ens. Jedes Neuronale Netzwerk wird mit einer eigenen Stichprobe trainiert. Die Stichprobe wird durch Extraktion von 7/10 Beispielen aus dem Trainingsdatensatz nach dem Zufallsprinzip mit Austausch erzeugt. Für das Modell müssen zwei Parameter eingestellt werden: nh' - die Anzahl der Neuronen in die verdeckten Schicht und 'act' - die Aktivierungsfunktion. Das Paket bietet die folgenden Optionen für Aktivierungsfunktionen:
- - sig: Sigmoid
- - sin: Sinus
- - radbas: Radiale Basis
- - hardlim: konstantes Limit
- - hardlims: symmetrische, konstantes Limit
- - satlins: Satlinien
- - tansig: Tangens-Sigmoid
- - tribas: Trianguläre Basis
- - poslin: positiv linear
- - purelin: linear
Wenn man bedenkt, dass es 10 Eingangsvariablen gibt, nehmen wir zunächst nh = 5. Die Aktivierungsfunktion wird als actfun = "sin" verstanden. Das Ensemble lernt schnell. Ich wählte die Parameter intuitiv, basierend auf meinen Erfahrungen mit Neuronalen Netzen. Sie können andere Optionen ausprobieren.
#---3-----Train---------------------------- evalq({ n <- 500 r <- 7 nh <- 5 Xtrain <- X$pretrain$x[ , bestF] Ytrain <- X$pretrain$y Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = "sin") } }, env)
Betrachten wir kurz die Berechnungen im Skript. Wir definieren die Konstanten n (die Anzahl der Neuronalen Netze im Ensemble) und r (die Größe der Bootstrap-Stichprobe, die für das Training des Neuronalen Netzes verwendet wird. Dieses Beispiel wird für jedes Neuronale Netzwerk im Ensemble unterschiedlich sein). nh ist die Anzahl der Neuronen in der versteckten Schicht. Dann definieren wir den Satz der Eingangsdaten Xtrain mit dem Hauptdatensatz X$pretrain und lassen nur bestimmte Prädiktoren bestF zu.
Dadurch entsteht ein Ensemble Ens[[500]] bestehend aus 500 einzelnen Neuronalen Netzwerk-Klassifikatoren. Wir testen es auf dem Testdatensatz Xtest aus dem Hauptdatensatz X$train mit den besten Prädiktoren bestF. Das generierte Ergebnis ist y.pr[1001, 500] - ein Datenrahmen von 500 kontinuierlichen, prädiktiven Variablen.
#---4-----predict------------------- evalq({ Xtest <- X$train$x[ , bestF] Ytest <- X$train$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> y.pr #[ ,n] }, env)
Kombinieren einzelner Ausgaben von Klassifikatoren. Methoden (Mittelwertbildung / Abstimmung)
Die Basisklassifikator eines Ensembles können folgende Ausgabearten haben:
- Klassenbenennung
- Klassifizierte Klassenbezeichnungen, wenn sie mit der Anzahl der Klassen >2 klassifiziert sind.
- Kontinuierliche numerische Vorhersage/Grad der Unterstützung.
Die Basisklassifikatoren haben als Ausgabe eine kontinuierliche numerische Variable (den Grad der Unterstützung). Die Unterstützungsgrade für diesen Eingang X können unterschiedlich interpretiert werden. Es kann die Zuverlässigkeit der vorgeschlagenen Labels oder die Bewertung möglicher Wahrscheinlichkeiten für Klassen sein. Für unseren Fall wird die Zuverlässigkeit der vorgeschlagenen Klassifikationbezeichnungen als Output dienen.
Die erste Variante der Kombination ist mittelnd: Sie liefert den Mittelwert der einzelnen Ausgaben. Dann wird es in Klassenbezeichnungen umgewandelt, während die Konvertierungsschwelle als 0.5 angenommen wird.
Die zweite Variante der Kombination ist eine einfache Mehrheitsabstimmung. Dazu wird jeder Ausgabe zunächst von einer kontinuierlichen Variable in Klassenbeschriftungen[-1, 1] konvertiert (die Konvertierungsschwelle beträgt 0,5). Dann werden alle Ausgaben summiert, und wenn das Ergebnis größer als 0 ist, wird Klasse 1 zugewiesen, ansonsten Klasse 0.
Wir bestimmen anhand der erhaltenen Klassenbezeichnungen die Metriken (Accuracy, Precision, Recall und F1).
Ensemble bereinigen. Methoden
Die Anzahl der Basisklassifikatoren war zunächst überflüssig, um später die besten von ihnen auszuwählen. Dazu werden die folgenden Methoden angewendet:
- Rang basierter Schnitt - Auswahl aus einem Ensemble, geordnet nach einer bestimmten Qualitätsnote:
- Fehlerreduzierung - Sortieren der Klassifikatoren nach dem Klassifizierungsfehler und Auswahl von mehreren der Besten (mit dem geringsten Fehler);
- Kappa-Schnitt - ordnen der Ensemblemitglieder nach der Kappa-Statistik und auswählen der gewünschten Anzahl mit den wenigsten Noten.
- Clustering-basiertes Bereinigen - Vorhersageergebnisse des Ensembles werden nach einer beliebigen Methode gebündelt, wonach mehrere Vertreter aus jedem Cluster ausgewählt werden. Clustering-Methoden:
- Partitionierung (z.B. SOM, k-mean);
- hierarchisch;
- dichtebasiert (z.B. dbscan);
- GMM-basiert.
- Optimierungsbasierte Bereinigung - evolutionäre oder genetische Algorithmen werden für die Auswahl der Besten verwendet.
Ensemble-Bereinigung ist die gleiche Auswahl an Prädiktoren. Daher können die gleichen Methoden wie bei der Auswahl der Prädiktoren angewendet werden (dies wurde in den vorherigen Artikeln der Serie behandelt).
Die Auswahl aus einem Ensemble, geordnet nach den Fehlern der Klassifikation (Bereinigung durch Reduzierung des Fehlers), wird für weitere Berechnungen verwendet.
Insgesamt werden die folgenden Methoden in den Experimenten eingesetzt:
- Kombinatoren-Methode - Mittelwertbildung und einfache Mehrheitsentscheidung;
- Metriken - Accuracy, Precision, Recall und F1;
- Bereinigen - Auswahl aus dem Ensemble, sortiert nach dem Klassifizierungsfehler basierend auf dem Mittelwert (F1).
Die Schwelle für die Umwandlung einzelner Ausgaben von kontinuierlichen Variablen in Klassenbezeichnungen beträgt 0,5. Seien Sie gewarnt: Dies ist nicht die beste, sondern die einfachste Option. Es kann später verbessert werden.
a) Ermittlung der besten Einzelklassifikatoren des Ensembles
Wir bestimmen den Mittelwert (F1) aller 500 Neuronalen Netze und wählen mehrere 'bestNNN' mit den besten Ergebnissen. Die Anzahl der besten Neuronalen Netze für Mehrheitsentscheidungen muss ungerade sein, also wird sie wie folgt definiert: (numEns*2 + 1).
#---5-----best---------------------- evalq({ numEns <- 3 foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN Score[bestNN] %>% round(3) }, env) [1] 0.720 0.718 0.718 0.715 0.713 0.713 0.712
Betrachten wir kurz die Berechnungen im Skript. In der foreach()-Schleife wandeln wir die kontinuierliche Vorhersage y.pr[ ,i] von jedem Neuronalen Netz ins Numerische [0,1] um, bestimmen den Mittelwert (F1) dieser Vorhersage und geben den Wert als Vektor Score[500] zurück. Dann sortieren wir die Daten des Vektors Score in absteigender Reihenfolge, bestimmen die Indizes von bestNN Neuronalen Netzen mit den besten (höchsten) Ergebnissen. Ausgabe der Metrik-Werte dieser besten Mitglieder des Score[bestNNN], gerundet auf 3 Nachkommastellen. Wie man sieht, sind die Einzelergebnisse nicht sehr hoch.
Hinweis: Jeder Trainings- und Testlauf führt zu einem anderen Ergebnis, da die Proben und die Startinitialisierung der Neuronalen Netze unterschiedlich sind!
So wurden die besten Einzelklassifikatoren des Ensembles ermittelt. Testen wir sie an den Stichproben X$test und X$test1 mit folgenden Kombinationsmethoden: Mittelwertbildung und einfache Mehrheitsentscheidung.
b) Mittelwertbildung
#---6----test averaging(test)-------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.75 0.723 0.739 0.731 1 0.75 0.774 0.760 0.767
Ein paar Worte zu den Berechnungen im Skript. Bestimmen wir die Größe des Ensembles n, Eingänge Xtest und Zielwert Ytest mit Hilfe des Hauptsets X$test. Berechnen wir dann in der foreach-Schleife (nur wenn der Index gleich den 'bestNNN' Indizes ist) die Vorhersagen dieser besten Neuronalen Netze, summieren sie und dividieren sie durch die Anzahl der besten Neuronalen Netze. Wir konvertieren die Ausgabe einer kontinuierlichen Variable in eine nominale Variable (0,1) und berechnet die Metriken. Wie wir sehen können, sind die Bewertungen der Klassifikationsqualität deutlich höher als die der einzelnen Klassifikatoren.
Führen wir den gleichen Test mit dem Datensatz X$test1 durch, das sich neben X$test befindet. Schätzen wir die Qualität.
#--6.1 ---test averaging(test1)--------- evalq({ n <- len(Ens) Xtest <- X$test1$x[ , bestF] Ytest <- X$test1$y foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.745 0.716 0.735 0.725 1 0.745 0.770 0.753 0.761
Die Qualität der Klassifizierung ist praktisch unverändert geblieben und bleibt recht hoch. Dieses Ergebnis zeigt, dass das Ensemble der Neuronalen Klassifikatoren eine hohe Qualität der Klassifizierung nach dem Training und Bereinigen über einen viel längeren Zeitraum (in unserem Beispiel 750 Takte) beibehält als die DNN, die im vorherigen Artikel erhalten wurde.
c) Einfache Mehrheitsentscheidung
Bestimmen wir die Metriken der Vorhersage, die von den besten Klassifikatoren des Ensembles, aber kombiniert durch einfache Abstimmung. Konvertieren wir zunächst die kontinuierlichen Vorhersagen der besten Klassifikatoren in Klassenbezeichnungen (-1/+1) und summieren dann alle Vorhersagebezeichnungen. Ist die Summe größer als 0, so wird Klasse 1 ausgegeben, ansonsten - Klasse 0. Wir testen zunächst alles mit dem Datensatz X$test:
#--7 --test--voting(test)-------------------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest) } %>% apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>% apply(1, function(x) sum(x)) -> vot ifelse(vot > 0, 1, 0) -> ClVot Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.745 0.716 0.735 0.725 1 0.745 0.770 0.753 0.761
Das Ergebnis ist praktisch das gleiche wie das der Mittelung. Tests mit dem Datensatz X$test1:
#--7.1 --test--voting(test1)-------------------- evalq({ n <- len(Ens) Xtest <- X$test1$x[ , bestF] Ytest <- X$test1$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest) } %>% apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>% apply(1, function(x) sum(x)) -> vot ifelse(vot > 0, 1, 0) -> ClVot Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.761 0.787 0.775 0.781 1 0.761 0.730 0.743 0.737
Unerwartet erwies sich das Ergebnis als besser als alle vorherigen, und das trotz der Tatsache, dass der Datensatz X$test1 hinter X$test liegt.
Dies bedeutet, dass die Klassifizierungsqualität des gleichen Ensembles mit den gleichen Daten, aber mit unterschiedlicher Kombinationsmethode sehr unterschiedlich sein kann.
Trotz der Tatsache, dass die Hyperparameter der einzelnen Klassifikatoren im Ensemble intuitiv gewählt wurden und offensichtlich nicht optimal sind, wurde eine hohe und stabile Qualität der Klassifikation erreicht, sowohl durch Mittelung als auch durch einfache Mehrheitsabstimmung.
Fassen wir alles zusammen. Schematisch lässt sich der gesamte Prozess der Erstellung und Erprobung eines Ensembles Neuronaler Netze in 4 Phasen unterteilen:
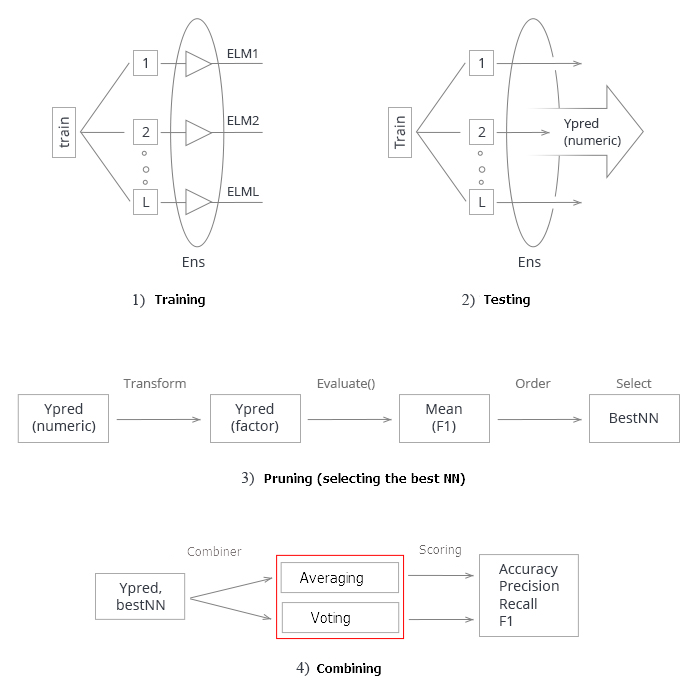
Abb. 3. Struktur des Trainings und des Testens des Ensembles von Neuronalen Netzen mit den Kombinator Mittelung/Abstimmung
1. Trainieren des Ensembles Wir trainieren L Neuronale Netze mit Stichproben (Bootstrap) aus dem Trainingsdatensatz. Wir erhalten das Ensemble trainierter Neuronaler Netze.
2. Wir testen das Ensemble Neuronaler Netze auf dem Testdatensatz. Wir erhalten kontinuierliche Vorhersagen einzelner Klassifikatoren.
3. Wir bereinigen das Ensemble, indem wir das beste n nach einem bestimmten Qualitätskriterium auswählen. In diesem Fall ist es mean(F1).
4. Mit Hilfe kontinuierlicher Vorhersagen der besten Einzelklassifikatoren können diese mit Hilfe von Mittelwertbildung oder einfacher Mehrheitsentscheidung kombiniert werden. Danach bestimmen wir die Metriken.
Die beiden letzten Schritte (Bereinigen und Kombinieren) haben mehrere Implementierungsmöglichkeiten. Gleichzeitig kann ein erfolgreiches Bereinigen des Ensembles (korrekte Identifizierung der Besten) die Leistung deutlich steigern. In diesem Fall wird die optimale Umwandlungsschwelle einer kontinuierlichen Vorhersage in eine nominale gefunden. Daher ist die Ermittlung der optimalen Parameter in diesen Phasen eine mühsame Aufgabe. Diese Schritte werden am besten automatisch und mit dem besten Ergebnis durchgeführt. Haben wir die Fähigkeit, dies zu tun und die Qualität des Ensembles zu verbessern? Es gibt mindestens zwei Möglichkeiten, dies zu tun, wir werden sie überprüfen.
- Optimieren der Hyperparameter einzelner Klassifikatoren des Ensembles (Bayes'scher Optimierer).
- DNN wird als Kombinator der einzelnen Ausgaben des Ensembles verwendet. Die Verallgemeinerung erfolgt durch Lernen.
Wir bestimmen die optimalen Parameter der einzelnen Klassifikatoren des Ensembles. Methoden
Einzelne Klassifikatoren in unserem Ensemble sind ELM-Neuronale Netze. Das Hauptmerkmal von ELM ist, dass ihre Eigenschaften und Qualität hauptsächlich von der zufälligen Initialisierung der Neuronengewichte der versteckten Schicht abhängen. Da andere Dinge gleich sind (Anzahl der Neuronen und Aktivierungsfunktionen), wird jeder Trainingslauf ein neues Neuronales Netzwerk erzeugen.
Diese Funktion von ELM eignet sich hervorragend für die Erstellung von Ensembles. Im Ensemble initialisieren wir nicht nur die Gewichte jedes Klassifikators mit Zufallswerten, sondern stellen jedem Klassifikator auch eine separate, zufällig generierte Trainingsprobe zur Verfügung.
Um jedoch die besten Hyperparameter eines Neuronalen Netzes auszuwählen, muss seine Qualität nur von den Änderungen eines bestimmten Hyperparameters abhängen und sonst nichts. Andernfalls macht die Suche keinen Sinn.
Ein Widerspruch entsteht: Auf der einen Seite brauchen wir ein Ensemble mit möglichst vielen Mitgliedern, auf der anderen Seite ein Ensemble mit verschiedenen, aber festen Mitgliedern.
Eine reproduzierbare, dauerhafte Vielfalt ist erforderlich.
Ist es möglich? Zeigen wir dies am Beispiel eines Ensemble-Trainings. Es wird das Paket "doRNG" (Reproduzierbare Zufallszahlengenerierung RNG) verwendet. Für die Reproduzierbarkeit der Ergebnisse ist es besser, Berechnungen in einem Thread durchzuführen.
Wir beginnen ein neues Experiment in einer sauberen globalen Umgebung. Wir laden die Kurse und die notwendigen Bibliotheken erneut, definieren und sortieren die Quelldaten erneut und wählen erneut die besten Prädiktoren numFeature. Wir führen alles in einem Skript aus.
#----Prepare------------- library(anytime) library(rowr) library(elmNN) library(rBayesianOptimization) library(foreach) library(magrittr) library(clusterSim) library(doRNG) #source(file = "FunPrepareData.R") #source(file = "FUN_Ensemble.R") #---prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) preproc <- PreNorm(DTcap, meth = meth) DTcap.n <- NormData(DTcap, preproc = preproc) #--1-Data X------------- list( pretrain = list( x = DTcap.n$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$pretrain$Class %>% as.numeric() %>% subtract(1) ), train = list( x = DTcap.n$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$train$Class %>% as.numeric() %>% subtract(1) ), test = list( x = DTcap.n$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$val$Class %>% as.numeric() %>% subtract(1) ), test1 = list( x = DTcap.n$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$test$Class %>% as.numeric() %>% subtract(1) ) ) -> X #---2--bestF----------------------------------- #require(clusterSim) numFeature <- 10 HINoV.Mod(x = X$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") %$% stopri[ ,1] -> orderX orderX %>% head(numFeature) -> bestF }, env)
Alle benötigten Anfangsdaten stehen jetzt bereit. Wir trainieren das Ensemble der Neuronalen Netze:
#---3-----Train---------------------------- evalq({ Xtrain <- X$pretrain$x[ , bestF] Ytrain <- X$pretrain$y setMKLthreads(1) n <- 500 r <- 7 nh <- 5 k <- 1 rng <- RNGseq(n, 12345) Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) k <- k + 1 idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = "sin") } setMKLthreads(2) }, env)
Was passiert während der Ausführung? Wir definieren die Ein- und Ausgabedaten für das Training (Xtrain, Ytrain) und setzen die MKL-Bibliothek in den Single-Thread-Modus. Wir initialisieren bestimmte Konstanten, indem wir eine Folge von Zufallszahlen rng erzeugen, die den Zufallszahlengenerator bei jeder neuen Iteration von foreach() initialisieren.
Wir dürfen nach Abschluss der Iterationen nicht vergessen, MKL wieder in den Multithread-Modus zu versetzen. Im Single-Threaded-Modus sind die Berechnungsergebnisse etwas schlechter.
So erhalten wir ein Ensemble mit verschiedenen Einzelklassifikatoren, die aber bei jeder Wiederholung des Trainings unverändert bleiben. Dies lässt sich leicht überprüfen, indem man die Berechnungen von 4 Etappen (Zug/Prädikat/Best/Test) mehrmals wiederholt. Berechnungsreihenfolge: train/predict/best/test_averaging/test_voting.
#---4-----predict------------------- evalq({ Xtest <- X$train$x[ , bestF] Ytest <- X$train$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> y.pr #[ ,n] }, env) #---5-----best---------------------- evalq({ numEns <- 3 foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN Score[bestNN] %>% round(3) }, env) # [1] 0.723 0.722 0.722 0.719 0.716 0.714 0.713 #---6----test averaging(test)-------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) }, env) # Accuracy Precision Recall F1 # 0 0.75 0.711 0.770 0.739 # 1 0.75 0.790 0.734 0.761 #--7 --test--voting(test)-------------------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest) } %>% apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>% apply(1, function(x) sum(x)) -> vot ifelse(vot > 0, 1, 0) -> ClVot Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>% round(3) }, env) # Accuracy Precision Recall F1 # 0 0.749 0.711 0.761 0.735 # 1 0.749 0.784 0.738 0.760
Egal wie oft diese Berechnungen wiederholt werden (natürlich mit den gleichen Parametern), das Ergebnis bleibt unverändert. Das ist genau das, was wir brauchen, um die Hyperparameter der Neuronalen Netze, aus denen das Ensemble besteht, zu optimieren.
Wir definieren zunächst die Liste der zu optimierenden Hyperparameter, finden so deren Wertebereiche und schreiben eine Fitnessfunktion, um das Optimierungskriterium (Maximierung) und die Vorhersage des Ensembles zurückzugeben. Die Qualität der einzelnen Klassifikatoren wird durch vier Parameter beeinflusst:
- Die Anzahl der Prädiktoren in den Eingabedaten;
- Die Größe der für das Training verwendeten Stichprobe;
- Die Anzahl der Neuronen in der ausgeblendeten Schicht;
- Die Aktivierungsfunktion.
Listen wir die Hyperparameter und ihre Wertebereiche auf:
evalq({
#type of activation function.
Fact <- c("sig", #: sigmoid
"sin", #: sine
"radbas", #: radial basis
"hardlim", #: hard-limit
"hardlims", #: symmetric hard-limit
"satlins", #: satlins
"tansig", #: tan-sigmoid
"tribas", #: triangular basis
"poslin", #: positive linear
"purelin") #: linear
bonds <- list(
numFeature = c(3L, 12L),
r = c(1L, 10L),
nh <- c(1L, 50L),
fact = c(1L, 10L)
)
}, env)
Betrachten wir den obigen Code etwas näher. Dort ist Fact ein Vektor möglicher Aktivierungsfunktionen. Die Liste bonds definiert die zu optimierenden Parameter und deren Wertebereiche.
- numFeature - die Anzahl der als Eingabe gespeisten Prädiktoren; minimal 3, maximal 12;
- r - Anteil des im Bootstrap verwendeten Trainingsdatensatzes. Vor der Berechnung wird sie durch 10 geteilt.
- nh - die Anzahl der Neuronen in der versteckten Schicht; Minimum 1, Maximum 50.
- fact - Index der Aktivierungsfunktion im Vektor Fact.
Bestimmen der Fitnessfunktion.
#---Fitnes -FUN----------- evalq({ Ytrain <- X$pretrain$y Ytest <- X$train$y Ytest1 <- X$test$y n <- 500 numEns <- 3 fitnes <- function(numFeature, r, nh, fact){ bestF <- orderX %>% head(numFeature) Xtrain <- X$pretrain$x[ , bestF] setMKLthreads(1) k <- 1 rng <- RNGseq(n, 12345) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } setMKLthreads(2) #---predict--- Xtest <- X$train$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- Xtest1 <- X$test$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
Hier sind einige Details über das Skript. Wir nehmen die Berechnung der Ziele (Ytrain, Ytest, Ytest1) aus der Fitnessfunktion, da diese bei der Parametersuche nicht verändert werden und initialisieren die Konstanten:
n - die Anzahl der Neuronalen Netze im Ensemble;
numEns - die Anzahl der besten Einzelklassifikatoren (numEns*2 + 1), deren Vorhersagen kombiniert werden sollen.
Die Funktion fitnes() hat 4 formale Parameter, die optimiert werden sollten. Später trainieren wir in der Funktion das Ensemble, berechnen predict und bestimmen bestNN der Besten, Schritt für Schritt. Am Ende kombinieren wir die Vorhersagen dieser besten mit Hilfe der Mittelwertbildung und berechnen die Metriken. Die Funktion gibt eine Liste zurück, die das Optimierungskriterium Score = mean(F1) und die Vorhersage enthält. Wir optimieren das Ensemble, das die Kombination durch Mittelwertbildung nutzt. Die Fitnessfunktion zur Optimierung der Hyperparameter des Ensembles mit einfacher Stimmenmehrheit ist bis auf den letzten Teil ähnlich. Sie können die Optimierung selbst durchführen.
Überprüfen wir Funktionsfähigkeit der Fitnessfunktion und deren Ausführungszeit:
#---------- evalq( system.time( res <- fitnes(numFeature = 10, r = 7, nh = 5, fact = 2) ) , env) user system elapsed 8.65 0.19 7.86
Es dauert ungefähr 9 Sekunden bis das Ergebnisse aller Berechnungen vorliegt.
> env$res$Score [1] 0.761
Jetzt können wir die Optimierung der Hyperparameter mit 10 zufälligen Anfangspunkten und 20 Iterationen beginnen. Wir suchen das beste Ergebnis.
#------ evalq( OPT_Res <- BayesianOptimization(fitnes, bounds = bonds, init_grid_dt = NULL, init_points = 10, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) Best Parameters Found: Round = 23 numFeature = 8.0000 r = 3.0000 nh = 3.0000 fact = 7.0000 Value = 0.7770
Wir sortieren die optimierte History nach den Werten und wählen die besten 10.
evalq({
OPT_Res %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init
best.init
}, env)
numFeature r nh fact Value
1 8 3 3 7 0.777
2 8 1 5 7 0.767
3 8 3 2 7 0.760
4 10 7 9 8 0.759
5 8 5 4 7 0.758
6 8 2 7 8 0.756
7 8 6 9 7 0.755
8 8 3 4 8 0.754
9 9 2 13 9 0.752
10 11 2 24 4 0.751
Interpretieren wir die erhaltenen Hyperparameter des besten Ergebnisses. Die Anzahl der Prädiktoren ist 8, die Stichprobengröße ist 0,3, die Anzahl der Neuronen in der versteckten Schicht ist 3, die Aktivierungsfunktion ist "radbas". Dies beweist einmal mehr, dass die Bayes'sche Optimierung ein breites Spektrum verschiedener Modelle bietet, die sich nicht intuitiv ableiten lassen. Es ist notwendig, die Optimierung mehrmals zu wiederholen und das beste Ergebnis auszuwählen.
So wurden die optimalen Hyperparameter des Trainings gefunden. Testen wir das Ensemble mit ihnen.
Training und Testen des Ensembles mit den optimierten Parametern
Testen wir das Ensemble, das mit den oben erhaltenen optimierten Parametern und dem Trainingsdatensatz erhalten haben. Bestimmen wir die besten Mitglieder des Ensembles, kombinieren ihre Ergebnisse durch Mittelwertbildung und sehen uns die endgültigen Metriken an. Das Skript ist unten aufgelistet.
Wenn wir das Ensemble Neuronaler Netze trainieren, erstellen wir es auf die gleiche Weise wie bei der Optimierung.
#--1-Train--optEns-predict--best--test-average------------------------ evalq({ Ytrain <- X$pretrain$y Ytest <- X$train$y Ytest1 <- X$test$y n <- 500 numEns <- 3 #--BestParams-------------------------- best.par <- OPT_Res$Best_Par %>% unname numFeature <- best.par[1] # 8L r <- best.par[2] # 3L nh <- best.par[3] # 3L fact <- best.par[4] # 7L bestF <- orderX %>% head(numFeature) Xtrain <- X$pretrain$x[ , bestF] setMKLthreads(1) k <- 1 rng <- RNGseq(n, 12345) #---train--- OptEns <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } setMKLthreads(2) #---predict--- Xtest <- X$train$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(OptEns[[i]], newdata = Xtest) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- Xtest1 <- X$test$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(OptEns[[i]], newdata = Xtest1)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) -> OptScore caret::confusionMatrix(Ytest1, ensPred) -> cm }, env)
Schauen wir uns die Ergebnis der 7 besten Neuronalen Netze des Ensembles an:
> env$Score[env$bestNN] [1] 0.7262701 0.7220685 0.7144137 0.7129644 0.7126606 0.7101981 0.7099502
Das Ergebnis nach der Mittelung der besten Neuronalen Netze:
> env$OptScore Accuracy Precision Recall F1 0 0.778 0.751 0.774 0.762 1 0.778 0.803 0.782 0.793 > env$cm Confusion Matrix und Statistik Reference Prediction 0 1 0 178 52 1 59 212 Accuracy : 0.7784 95% CI : (0.7395, 0.8141) No Information Rate : 0.5269 P-Value [Acc > NIR] : <2e-16 Kappa : 0.5549 Mcnemar's Test P-Value : 0.569 Sensitivity : 0.7511 Specificity : 0.8030 Pos Pred Value : 0.7739 Neg Pred Value : 0.7823 Prevalence : 0.4731 Detection Rate : 0.3553 Detection Prevalence : 0.4591 Balanced Accuracy : 0.7770 'Positive' Class : 0
Dieses Ergebnis ist deutlich besser als das jedes einzelnen Neuronalen Netzwerks im Ensemble und ist vergleichbar mit den Ergebnissen von DNN mit den optimalen Parametern, die im vorherigen Artikel dieser Serie erzielt wurden.
Schlussfolgerung
- Ensembles von Klassifikatoren von Neuronalen Netzen, die aus einfachen und schnellen ELM-Neuronalen Netzen bestehen, weisen eine Klassifizierungsqualität auf, die mit der von komplexeren Modellen (DNN) vergleichbar ist.
- Die Optimierung der Hyperparameter einzelner Klassifikatoren im Ensemble führt zu einer Steigerung der Klassifikationsqualität von bis zu Acc = 0,77 (95% CI = 0,73 - 0,81).
- Die Klassifizierungsqualität eines Ensembles mit Mittelwertbildung und eines Ensembles mit Mehrheitsentscheidung ist in etwa gleich.
- Nach dem Training behält das Ensemble seine Klassifizierungsqualität bis zu einer Tiefe von mehr als der Hälfte der Größe des Trainingsdatensatzes bei. In diesem Fall bleibt die Qualität für bis zu 750 Bars erhalten, was deutlich höher ist als der gleiche Wert bei DNN (250 Bars).
- Durch die Optimierung der Umwandlungsschwelle der kontinuierlichen prädiktiven Variable in eine nominale Variable (Kalibrierung, optimales CutOff, genetische Suche) kann die Klassifikationsqualität des Ensembles deutlich gesteigert werden.
- Die Klassifizierungsqualität des Ensembles kann auch durch den Einsatz eines trainierbaren Modells (Stacking) als Kombinator erhöht werden. Es kann ein Neuronales Netz oder ein Ensemble von Neuronalen Netzen sein. Im nächsten Teil des Artikels werden diese beiden Varianten der Stapelung getestet. Wir werden neue Funktionen der Bibliothek TensorFlow für den Aufbau eines Neuronalen Netzwerks testen.
Anlagen
GitHub/PartVI beinhaltet:
- FUN_Ensemble.R - Funktionen zur Durchführung aller in diesem Artikel beschriebenen Berechnungen.
- RUN_Ensemble.R - Skripte zum Erstellen, Trainieren und Testen des Ensembles.
- Optim_Ensemble.R - Skripte zur Optimierung der Hyperparameter der Neuronalen Netze im Ensemble.
- SessionInfo_RunEns.txt - Pakete zum Erstellen und Testen des Ensembles.
- SessionInfo_OptEns.txt - Pakete zur Optimierung der Hyperparameter des NN-Ensembles.
- ELM.zip - Archiv von Artikeln über ELM Neuronale Netze.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/4227
Panels verbessern: Transparenz hinzufügen, Hintergrundfarbe ändern und von CAppDialog/CWndClient übernehmen
Social Trading. Kann eine gutes Signal weiter verbessert werden?
Ein Expert Advisor mit GUI: Erstellen des Panels (Teil I)
Ein visueller Strategieentwickler Erstellen eines Handelsroboters ohne zu programmieren
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.