Tiefe neuronale Netzwerke (Teil III). Stichprobenauswahl und Verminderung der Dimensionen
873
0
Inhalt
- Einführung
- 1. Stichprobenauswahl
- 2. Verminderung der Dimensionen
- 2.1. Hauptkomponentenanalyse (Principal component analysis, PCA)
- 2.2. Unabhängigkeitsanalyse (Independent component analysis, ICA)
- 2.3. Probabilistische Hauptkomponentenanalyse (PPCA)
- 2.4. Autoencoder (nichtlineare PCA)
- 2.5. Inverse nichtlineare PCA (NLPCA)
- 3. Aufteilung der Daten in die Datensätze train/val/test
- Schlussfolgerung
- Anwendung
Einführung
Dies ist der dritte (und letzte) Artikel, der die Datenaufbereitung beschreibt - die wichtigste Phase der Arbeit mit neuronalen Netzen. Wir werden uns mit zwei sehr wichtigen Methoden der Datenaufbereitung befassen. Sie eliminieren Rauschen und vermindern die Dimension der Eingangsdaten. Die Beschreibung der Methoden wird mit ausführlichen Beispielen und Grafiken ergänzt.
1. Stichprobenauswahl
Das Rauschen in Stichproben beziehen sich auf die falsche Kennzeichnung von Trainingsstichproben. Dies ist eine sehr unerwünschte Eigenschaft der Daten. Um dies zu beseitigen, wird das Programmpaket NoiseFilterR verwendet, das klassische und moderne Rauschfilter einsetzt.
In letzter Zeit hat das Data Mining mit immer komplexeren Problemen zu kämpfen, die mit dem Charakter von Daten verbunden sind. Es ist nicht das Volumen der Daten, sondern ihre Unvollkommenheit und die unterschiedlichen Formen stellen die Forschern vor eine Vielzahl verschiedener Szenarien. Die vorbereitende Datenverarbeitung ist daher zu einem wichtigen Bestandteil des KDD-Prozesses (Knowledge Discovery from Databases) geworden. Gleichzeitig bietet die Entwicklung der Software für eine vorbereitende Datenverarbeitung ausreichende Arbeitsmittel.
Für die folgenden Algorithmen ist eine vorbereitende Datenverarbeitung erforderlich, um maximale Informationen aus einem Datensatz extrahieren zu können. Dies sind die energie- und zeitaufwendigsten Schritte im gesamten Prozess von KDD. Die vorbereitende Datenverarbeitung kann in Teilaufgaben unterteilt werden. Dies kann z. B. die Auswahl von Prädiktoren oder das Entfernen fehlender und verrauschter Daten sein. Die Auswahl der Prädiktoren zielt darauf ab, die wichtigsten Eigenschaften für das Training zu extrahieren, was eine Vereinfachung der Modelle und eine Verkürzung der Berechnungszeit ermöglicht. Die Verarbeitung fehlender Daten ist notwendig, um möglichst viele Daten zu speichern. Verrauschte Daten sind entweder falsche Daten oder Daten, die außerhalb der ihrer Verteilung liegen.
All diese Probleme können mit einer weit verbreiteten Software gelöst werden. Das Werkzeug KEEL (RKEEL) enthält z. B. eine Vielzahl von Algorithmen der vorbereitenden Datenverarbeitung, die alle oben genannten Verfahren abdecken. Es gibt auch andere populäre Lösungen wie WEKA (RWEKA) oder RapidMiner für die Auswahl von Prädiktoren. Es gibt auch eine Reihe von einzigartigen Programmpakete für das Data Mining wie R, KNIME oder Python
Die statistische Software "R, The Comprehensive R Archive Network" (CRAN) enthält eine Vielzahl von Paketen zur Lösung von Problemen der vorbereitenden Datenverarbeitung.
Echte Datensätze sind immer unvollkommen und verrauscht. Dieses Rauschen wirkt sich negativ auf das Training von Klassifikatoren aus, was wiederum die Vorhersagegenauigkeit verringert, die Modelle unnötig verkompliziert und die Berechnungszeit verlängert.
Die Literatur zur Klassifizierung unterscheidet zwei verschiedene Arten von Rauschen: Verrauscht als Eigenschaft der Daten und verrauschte Kategorisierung (oder Klassenrauschen). Das Erste betrifft die Unvollkommenheiten der Trainingsdaten, das Zweite führt zu Fehlern bei der Klassifizierung. Das Paket NoiseFiltersR konzentriert sich hauptsächlich auf das Rauschen bei der Klassifizierung - das schädlichste, da die Qualität der Klassen für die Ausbildung von Klassifikatoren sehr wichtig ist.
Zwei Hauptansätze zur Lösung des Problems des verrauschten Klassifizierung werden hier vorgestellt. Sie können sie in der jüngsten Arbeit von Benoit Frenay und Michel Verleysen im Detail studieren.
- Einerseits setzt er beim Algorithmus an, in dem er das Problem durch einen robusten Klassifizierungsalgorithmus löst, den das Rauschen nicht sehr beeinträchtigt. Jeder Algorithmus ist in diesem Fall eine spezifische, nicht universelle Lösung.
- Andererseits versucht er auf der Ebene der Daten (Filter), eine Strategie der Datenreinigung zu entwickeln, die vor dem Training des Klassifikators durchgeführt wird. Das Paket NoiseFiltersR nutzt den zweiten Ansatz. Dies liegt daran, dass eine vorbereitende Datenverarbeitung nur einmal möglich ist, und danach die Klassifikation beliebig oft verändert werden können.
Die folgenden Klassifikatoren sind resistent gegen Rauschen: С4.5, J48 und Jrip (WEKA).
Führen wir ein Experiment durch. Behandeln wir die folgenden Datensätze: DT (Rohdaten vor der Vorbereitung), DTn (nur normalisierter Rohdatensatz), DTTanh.n (ohne Ausreißer, tan-transformiert und normalisiert) und train mit der Funktion ORBoostFilter(), einem Filter zur Rauschunterdrückung. Sehen wir, wie sich die Verteilung nach einer solchen Behandlung verändert.
evalq({
#-----DT---------------------
out11 <- ORBoostFilter(Class~., data = DT$train, N = 10, useDecisionStump = TRUE)
DT$train_clean1 <- out11$cleanData
#----------DTTanh.n------------------------
out1 <- ORBoostFilter(Class~., data = DTTanh.n$train, N = 10, useDecisionStump = TRUE)
DTTanh.n$train_clean1 <- out1$cleanData
#-----------DTn--------------------------------
out12 <- ORBoostFilter(Class~., data = DTn$train, N = 10, useDecisionStump = TRUE)
DTn$train_clean1 <- out12$cleanData
},
env)
#---Ris1-----------------
require(funModeling)
evalq({
par(mfrow = c(1,3))
par(las = 1)
boxplot(DT$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
main = "DT$train_clean1")
boxplot(DTn$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
main = "DTn$train_clean1")
boxplot(DTTanh.n$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
main = "DTTanh.n$train_clean1")
par(mfrow = c(1,1))
}, env)
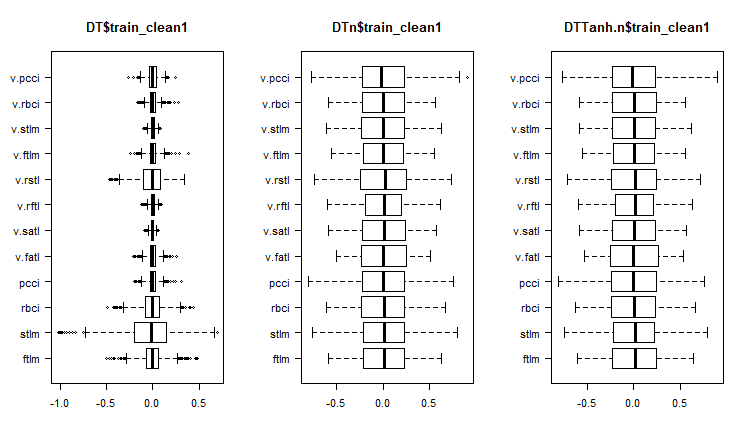
Abb. 1. Verteilung der Prädiktoren in den Datensätzen nach dem Entfernen der verrauschten Daten
Betrachten wir die Variation und die Kovarianz dieser Datensätze:
#----Ris2------------------ require(GGally) evalq(ggpairs(DT$train_clean1 %>% select(-Data), columns = c(1:6, 13), mapping = aes(color = Class), title = "DT$train_clean1/1"), env)
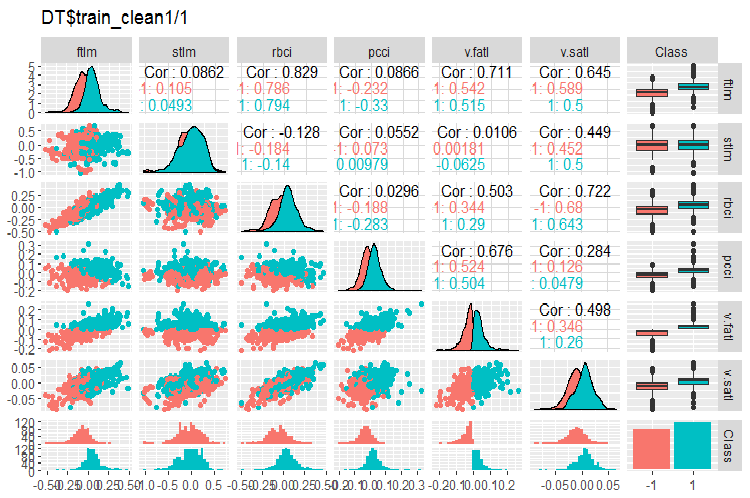
Abb. 2. Variation und Kovarianz im Datensatz DT$train_clean1/1 nach dem Entfernen der verrauschten Daten
#-----Ris3--- evalq(ggpairs(DT$train_clean1 %>% select(-Data), columns = 7:13, mapping = aes(color = Class), title = "DT$train_clean1/2"), env)
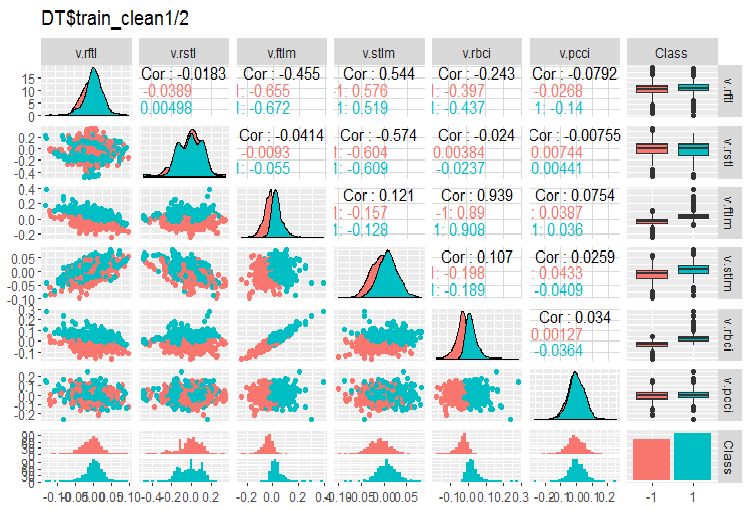
Abb. 3. Variation und Kovarianz im Datensatz DT$train_clean1/2 nach dem Entfernen der verrauschten Daten
Wie viele Daten wurden aus dem Datensatz DT$train entfernt?
> env$out11$remIdx %>% length()
[1] 658
Rund 30%. Es gibt jetzt zwei Möglichkeiten fortzufahren. Die Erste ist, verrauschte Daten aus dem Datensatz train zu entfernen und es dem Modell zum Training zu übergeben. Die Zweite ist, sie neu zu klassifizieren, und das Modell mit allen Daten von train zu trainieren, aber mit einer zusätzlichen Schicht für die Zielvariablen. Bei dieser Anzahl von verrauschten Daten sieht das zweite Szenario günstiger aus. Wir sollten es testen.
Was können wir auf den Diagrammen der variablen Verteilungen ohne Rauschen erkennen?
- Eine sehr ausgeprägte Aufteilung der Verteilung der Prädiktoren durch die Zielvariable. Es ist sehr wahrscheinlich, dass dies die Genauigkeit des von uns trainierten Modells deutlich erhöhen wird.
- Es wurden fast alle Ausreißer entfernt.
Wir werden die Datensätze DTn$train DTTanh.n$train mit dem Filter säubern. Und es überrascht, dass die verrauschten Variablen fast die gleichen sind wie im ersten Fall.
c(env$out1$remIdx %>% length(), env$out12$remIdx %>% length())
[1] 652 653
Bedeutet dies, dass eine Transformationen die verrauschten Daten nicht verbessert? Das verdient, getestet zu werden.
Werfen wir einen Blick auf die Variation und Kovarianz des Datensatzes DTTanh.n$train nach dem Entfernen der verrauschten Variablen.
#----Ris4----------------------- evalq(ggpairs(DTTanh.n$train_clean1, columns = 1:13, mapping = aes(color = Class), upper = "blank", title = "DTTanh.n$train_clean_all"), env)
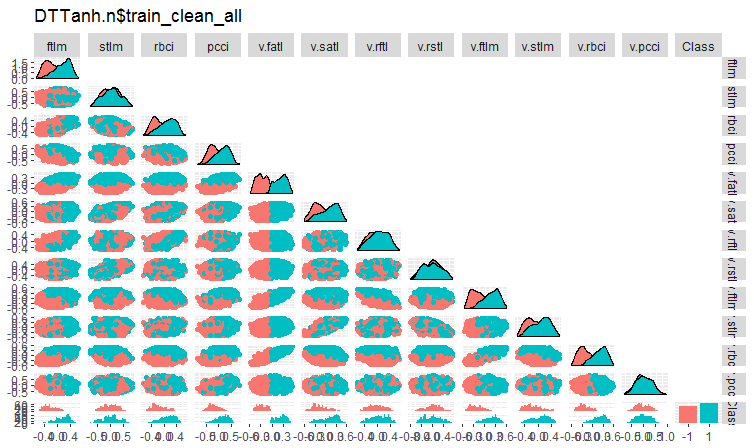
Abb. 4. Variation und Kovarianz im Datensatz DTTanh.n$train_clean Set nach dem Entfernen der verrauschten Daten.
Die Kovarianz aller Variablen mit der Variablen v.fatl ist sehr interessant. Wir können die Prädiktoren visuell identifizieren, die für die Zielvariable irrelevant sind. Es sind dies stlm, v.rftl, v.rstl, v.pcci. Wir werden diese Annahme mit anderen Methoden und anderen Datensätzen testen.
Dasselbe Diagramm für DTn$train_clean1:
#-------ris5---------- require(GGally) evalq(ggpairs(DTn$train_clean1 %>% select(-Data), columns = 1:13, mapping = aes(color = Class), upper = "blank", title = "DTn$train_clean1_all"), env)
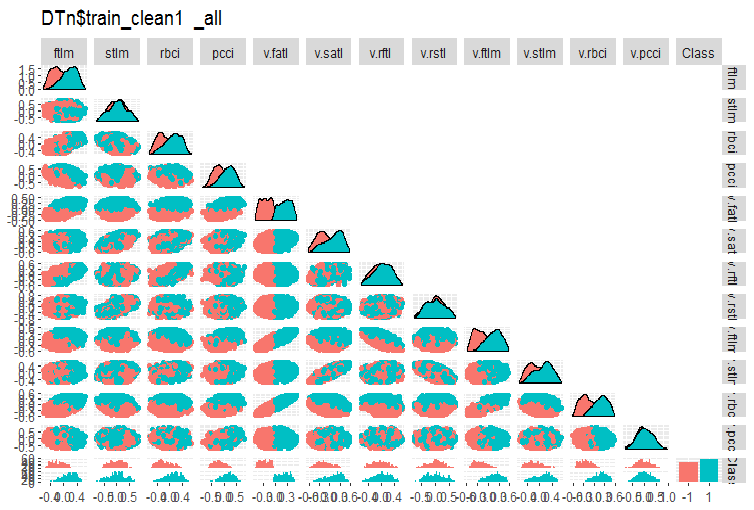
Abb. 5. Variation und Kovarianz im Datensatz DTn$train_clean nach dem Entfernen der verrauschten Daten.
Hier können wir sehen, dass die Variation der Prädiktoren stlm, v.rftl, v.rstl, v.pcci nicht durch die Niveaus der Zielvariablen getrennt ist. Die Entscheidung, was mit den verrauschten verrauschten Variable zu tun ist, liegt nach der Durchführung des experimentellen Trainings mit einem Modell beim Entwickler.
Schauen wir jetzt, wie sich die Bedeutung der Prädiktoren in diesen Datensätzen nach der Entfernung von verrauschten Daten verändert hat.
#--------Ris6--------------------------- require(smbinning) par(mfrow = c(1,3)) evalq({ df <- renamepr(DT$train_clean1) %>% targ.int sumivt.dt = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.dt, cex = 0.8) rm(df) }, env) evalq({ df <- renamepr(DTTanh.n$train_clean1) %>% targ.int sumivt.tanh.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.tanh.n, cex = 0.8) rm(df) }, env) evalq({ df <- renamepr(DTn$train_clean1) %>% targ.int sumivt.dtn = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.dtn, cex = 0.8) rm(df) }, env) par(mfrow = c(1, 1))
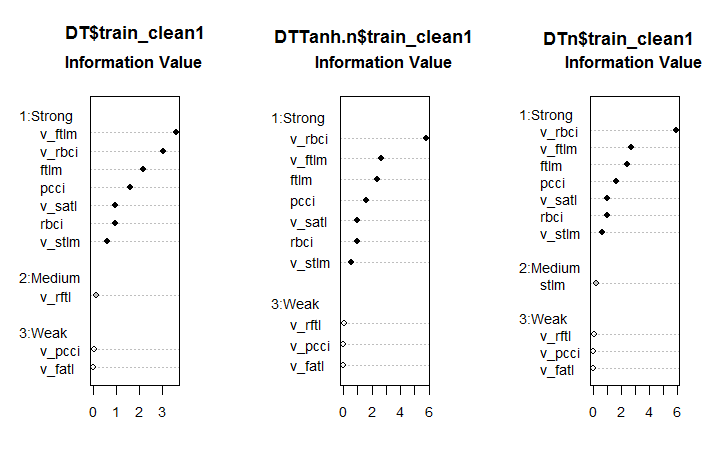
Abb. 6. Bedeutung der Prädiktoren in drei Gruppen
Das ist ein unerwartetes Ergebnis. Die Variable v.fatl Variable erwies sich als die Schwächste der Schwachen!
Die sieben starken Prädiktoren sind in allen Datensätzen dieselben. Ein Prädiktor mittlerer Stärke erscheint im ersten und im dritten Datensatz. Diese Berechnung identifizierte die Prädiktoren stlm, v.rftl, v.rstl, v.pcci als irrelevant, was mit der früheren Berechnung übereinstimmt. All diese Berechnungen müssen durch die Experimente mit einem realen Modell verifiziert werden.
Das Paket NoiseFilterR enthält mehr als ein Dutzend weitere Filter zur Identifizierung von verrauschten Daten. Fröhliches Experimentieren!
2. Verminderung der Dimensionen
Unter der Verminderung der Dimensionen versteht man die Transformation der Ausgangsdaten mit vielen Dimensionen in eine neue Darstellung mit weniger Dimensionen unter Beibehaltung der wichtigen Informationen. Idealerweise entsprechen die Dimensionen der transformierten Darstellung den internen Dimensionen der Daten. Die interne Dimensionen der Daten ist die minimale Anzahl von Variablen, die für die Darstellung aller möglichen Merkmale der Daten erforderlich ist. Diese Algorithmen werden traditionell zur Reduzierung der Dimensionen verwendet: Hauptkomponentenanalyse (Principal Component Analisys PCA), Unabhängigkeitsanalyse (Independent Component Analisys ICA), Einzelwertzergliederung (Singular Value Decomposition, SVD) etc.
Die Reduzierung der Dimensionen ermöglicht es, den so genannten Fluch der Dimensionen und andere unerwünschte Eigenschaften von Räumen mit sehr vielen Dimensionen zu mildern. Im Stadium der Beschreibung der Daten gibt es folgende Ziele.
- Die Reduktion der Rechenkosten der Datenverarbeitung
- Verminderung des Bedarfs von Trainingswiederholungen. Je weniger Eigenschaften, desto weniger Objekte werden für eine stabile Wiederherstellung der verdeckten Beziehung in den Daten benötigt und desto besser ist die Qualität der Wiederherstellung solcher Beziehungen.
- Komprimieren der Daten für eine effektivere Speicherung von Informationen. In diesem Fall muss neben der Transformation X → T auch die Möglichkeit bestehen, die inverse Transformation T → X durchzuführen
- Visualisierung der Daten. Die Projektion einer Stichprobe auf einen zwei- oder dreidimensionalen Raum ermöglicht es, diese Stichprobe grafisch darzustellen
- Extrahieren neuer Merkmale. Die während der Transformation X → T gewonnenen neuen Merkmale können bei der folgenden Implementierung von Erkennungslösungen (wie z. B. der Hauptkomponentenanalyse) einen signifikanten Einfluss haben
Bitte beachten Sie, dass alle nachfolgend kurz beschriebenen Methoden zur Verminderung der Dimensionen zur Klasse des nicht überwachten Trainings gehören. Dies bedeutet, dass nur die Merkmalsbeschreibung der Objekte X (Prädiktor) eine Rolle bei den Anfangsinformationen spielen.
2.1. Hauptkomponentenanalyse (PCA)
Die Hauptkomponentenanalyse (Principal component analysis, PCA) ist eine der einfachsten Methoden, um die Dimensionen der Daten zu vermindern. Die wichtigsten Ideen zu dieser Methode gehen zurück auf das 19. Jahrhundert. Das Prinzip dieser Methode besteht darin, eine Hyperebene einer gegebenen Dimension im Anfangsraum zu finden und den Datensatz auf diese Hyperebene zu projizieren. Es wird die Hyperebene mit dem kleinsten Fehler in den Projektionsabweichungen (Summe der quadrierten Abweichungen) gewählt.
Die Dimensionen des reduzierten Raumes d können vom Anwender vorgegeben werden. Dieser Wert kann leicht gewählt werden, wenn es ein Problem mit der der Datenvisualisierung (d = 2 oder d = 3) gibt, oder eine Stichprobe in einen vorgegebenen Speicherraum einzufügen. In anderen Fällen ist die Wahl von d aus früheren Annahmen nicht ersichtlich.
Es gibt eine einfache heuristische Methode zur Auswahl des Wertes d für die Methode der Hauptkomponenten. Eine der Besonderheiten der Methode der Hauptkomponenten ist, dass alle reduzierten Räume für d = 1, 2, . . . ineinander verschachtelt sind. Auf diese Weise können wir, nachdem alle Eigenvektoren und Eigenwerte der Kovarianzmatrix berechnet sind, einen reduzierten Raum für jeden beliebigen Wert von d erhalten. Um den Wert für d zu wählen, können die Eigenwerte absteigend auf dem Diagramm angezeigt und die Trennschwelle kann auf Werte nahe Null eingestellt werden. Eine andere Möglichkeit, einen Wert für d zu wählen, besteht darin, den Schwellwert so zu wählen, dass ein bestimmter Prozentsatz der Gesamtfläche unter der Kurve rechts von der Schwelle bleibt (z. B. 5% oder 1%).
Vereinfacht ausgedrückt kann PCA als vorbereitende Unterdrückung von Rauschprädiktoren betrachtet werden, wenn deren Anzahl signifikant ist (>50).
2.2. Unabhängigkeitsanalyse (ICA)
Im Gegensatz zur PCA ist die Unabhängigkeitsanalyse (Independent Component Analysis, ICA) ein neues Verfahren, das jedoch in verschiedenen Bereichen der Datenerhebung schnell an Popularität gewinnt.
Die Methode der unabhängigen Komponenten ist in der Signalverarbeitung weit verbreitet. Diese Technik wandelt die anfänglichen Daten linear in neue Komponenten um. Die neuen Komponenten werden statistisch voneinander so unabhängig sein wie möglich. Unabhängige Komponenten sind nicht notwendigerweise orthogonal, aber ihre statistische Unabhängigkeit ist eine strengere Bedingung als das Fehlen einer statistischen Korrelation in der PCA.
Die Methoden PCA und ICA sind im Paket caret durch die Funktion preProcess() implementiert. In dieser Funktion kann entweder die Anzahl der Hauptkomponenten oder ein kumulativer Prozentsatz von der PCA eingestellt werden. Diese Unabhängigkeitsanalyse umfasst zwei Schritte. Zunächst werden die erforderlichen Parameter aus dem Datensatz train berechnet. Anschließend werden die Datensätze und alle später eintreffenden neuen Daten mit Hilfe von predict() transformiert.
Tabelle 1. Comparative characteristics of PCA and ICA
| Methoden | Vorteile | Nachteile | Besonderheiten | Ergebnis, in den meisten Fällen | Berechnung neuer Hauptkomponenten |
|---|---|---|---|---|---|
| PCA | Einfachheit der Berechnungen |
| Keine eindeutige Lösung (Unsicherheit bei Rotationen). Jede neue Berechnung, die auf einem Trainingstest basiert, wird verschiedene Hauptkomponenten ergeben. |
| Tnew = Xnew * P |
| ICA | Einfachheit der Berechnungen |
| Mit einem großen Unterschied in den Dimensionen der Eingangsdaten und unabhängigen Komponenten, verwendet nacheinander PCA -> ICA. |
| Snew =scale( Xnew )* W * K |
Experimentieren wir. Laden Sie die Ergebnisse des Skripts aus dem ersten Teil des Artikels Part_1. Rda in Rstudio. Hier der Inhalt von env:
> ls(env) [1] "cap1" "cap2" "Close" "Data" "dataSet" [6] "dataSetCap" "dataSetClean" "dataSetOut" "High" "i" [11] "k" "k.cap" "k.out" "lof.x" "lof.x.cap" [16] "Low" "lower" "med" "Open" "out.ftlm" [21] "out.ftlm1" "pr" "pre.outl" "preProClean" "Rlof.x" [26] "Rlof.x.cap" "sk" "sk.cap" "sk.out" "test" [31] "test.out" "train" "train.out" "upper" "Volume" [36] "x" "x.cap" "x.out"Nehmen wir den Datensatz x.cap mit begrenzten Ausreißern und berechnen seine prinzipiellen und unabhängigen Komponenten mit der Funktion preProcess::caret. Wir geben explizit die Anzahl der Komponenten für PCA und ICA an. Wir werden aber die Normalisierung für ICA nicht näher erläutern.
require(caret)
evalq({
prePCA <- preProcess(x.cap,
pcaComp = 5,
method = Hmisc::Cs(center, scale, pca))
preICA <- preProcess(x.cap,
n.comp = 3,
method = "ica")
}, env)
Schauen wir uns die Parameter der Transformation an:> str(env$prePCA) List of 20 $ dim : int [1:2] 7906 11 $ bc : NULL $ yj : NULL $ et : NULL $ invHyperbolicSine: NULL $ mean : Named num [1:11] -0.001042 -0.003567 -0.000155 -0.000104 -0.000267 ... ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... $ std : Named num [1:11] 0.091 0.237 0.1023 0.0377 0.0356 ... ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... $ ranges : NULL $ rotation : num [1:11, 1:5] -0.428 -0.091 -0.437 -0.107 -0.32 ... ..- attr(*, "dimnames")=List of 2 .. ..$ : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... .. ..$ : chr [1:5] "PC1" "PC2" "PC3" "PC4" ... $ method :List of 4 ..$ center: chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ scale : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ pca : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ ignore: chr(0) $ thresh : num 0.95 $ pcaComp : num 5 $ numComp : num 5 $ ica : NULL $ wildcards :List of 2 ..$ PCA: chr(0) ..$ ICA: chr(0) $ k : num 5 $ knnSummary :function (x, ...) $ bagImp : NULL $ median : NULL $ data : NULL - attr(*, "class")= chr "preProcess"
Wir interessieren uns für drei Listen. Diese sind prePCA$mean, prePCA$std (Parameters der Normalisierung) und prePCA$rotation (Matrix der Rotation und der Last).
> str(env$preICA) List of 20 $ dim : int [1:2] 7906 11 $ bc : NULL $ yj : NULL $ et : NULL $ invHyperbolicSine: NULL $ mean : Named num [1:11] -0.001042 -0.003567 -0.000155 -0.000104 -0.000267 ... ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... $ std : Named num [1:11] 0.091 0.237 0.1023 0.0377 0.0356 ... ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... $ ranges : NULL $ rotation : NULL $ method :List of 4 ..$ ica : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ center: chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ scale : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ... ..$ ignore: chr(0) $ thresh : num 0.95 $ pcaComp : NULL $ numComp : NULL $ ica :List of 3 ..$ row.norm: logi FALSE ..$ K : num [1:11, 1:3] -0.214 -0.0455 -0.2185 -0.0534 -0.1604 ... ..$ W : num [1:3, 1:3] -0.587 0.77 -0.25 -0.734 -0.636 ... $ wildcards :List of 2 ..$ PCA: chr(0) ..$ ICA: chr(0) $ k : num 5 $ knnSummary :function (x, ...) $ bagImp : NULL $ median : NULL $ data : NULL - attr(*, "class")= chr "preProcess"Hier haben wir die gleichen $Mittelwert und $std und die zwei Matrizen $K und $W. Das Paket caret zur Berechnung von ICA verwendet das Paket fastICA mit folgendem Algorithmus:
- Nach der Zentrierung der Ausgangsmatrix (Normalisierung der Zeilen ist möglich) erhalten wir die Matrix X
- Dann wird die Matrix X in die Richtungen der Hauptkomponenten projiziert und wir erhalten PCA = X * K als Ergebnis
- Danach wird PCA mit der Entmischungsmatrix multipliziert und es ergeben sich die unabhängige Komponenten ICA = X * K * W
Wir berechnen PCA und ICA auf zwei Arten mit Hilfe der Funktion predore::caret und der Parameter, die wir durch die Funktion preProcess erhalten werden.
require(magrittr)
evalq({
pca <- predict(prePCA, x.cap)
ica <- predict(preICA, x.cap)
pca1 <- ((x.cap %>% scale(prePCA$mean, prePCA$std)) %*%
prePCA$rotation)
ica1 <- ((x.cap %>% scale(preICA$mean, preICA$std)) %*%
preICA$ica$K) %*% preICA$ica$W
colnames(ica1) <- colnames(ica1, do.NULL = FALSE, prefix = 'ICA')
},env)
evalq(all_equal(pca, pca1), env)
# [1] TRUE
evalq(all_equal(ica, ica1), env)
# [1] TRUE
Das Ergebnis ist identisch, was zu erwarten war.
Die Verwendung des Paketes pcaPP ist eine zuverlässigere Methode zur Berechnung von PCA. Diese Methode identifiziert die Hauptkomponenten genauer.
Das Paket fastICA enthält viele zusätzliche Funktionen und Parameter für eine flexiblere und vollständigere Berechnung der unabhängigen Komponenten. Ich würde fastICA empfehlen und nicht eine Funktion aus caret.
2.3 Probabilistische Hauptkomponentenanalyse (PPCA)
PCA hat eine probabilistische Modell, PPCA. Eine probabilistische Anpassung dieser Methode bietet eine Reihe von Vorteilen.
- Eine Gelegenheit, den EM-Algorithmus für die Suche nach einer Lösung zu nutzen. Der EM-Algorithmus ist ein effektiveres Berechnungsverfahren in der Situation, wenn d ≪ D
- Korrekte Verarbeitung fehlender Werte. Diese werden einfach in die Liste der verdeckten Variablen der probabilistischen Modelle aufgenommen. Dann wird der EM-Algorithmus auf dieses Modell angewendet.
- Eiue Möglichkeit des Übergangs zum Modell der Mischverteilungen, das die Anwendbarkeit des Verfahrens erweitert
- Eine Möglichkeit, den Bayes'schen Ansatz zur Lösung des Problems zur Modellauswahl zu nutzen. Insbesondere kann ein theoretisch gerechtfertigtes Schema zur Auswahl der Dimensionen des reduzierten Raumes d erstellt werden (siehe[24,25])
- Eine Möglichkeit der Generierung neuer Objekte aus dem probabilistischen Modell
- Um der Klassifizierung willen - eine Möglichkeit, Verteilungen von einzelnen Objektklassen für die weitere Verwendung in den Schemata der Klassifikation zu modellieren
- Der Wert der Wahrscheinlichkeitsfunktion ist ein universelles Kriterium, das es erlaubt, verschiedene probabilistische Modelle miteinander zu vergleichen. Ausreißer in einem Datensatz lassen sich anhand des Wahrscheinlichkeitswertes leicht identifizieren.
Ähnlich wie das klassische Modell der PCA ist das probabilistische Modell PCA invariant in Bezug auf die Wahl der Basis in der Hyperebene.
Im Gegensatz zum klassischen Modell der PCA, bei dem nur die Hyperebene wiederhergestellt wird, die die Daten am besten erklärt, stellt das probabilistische Modell das gesamte Modell der Datenvariabilität wieder her. Es beschreibt nämlich die Verteilung der Daten in alle Richtungen. Die Lösung umfasst also nicht nur die Richtungs-Basisvektoren der Hyperebene, die durch die Eigenvektoren der Kovarianzmatrix definiert sind, sondern auch die Längen dieser Basisvektoren.
Um PPCA und andere nichtlineare Methoden zur Gewinnung der wichtigsten Komponenten zu nutzen, kann das Paket pcaMethods verwendet werden.
Das Paket pcaMethods ist eine Sammlung verschiedener Realisierungen von PCA und Werkzeuge zur Kreuzvalidierung und Visualisierung von Ergebnissen. Die Methoden erlauben vor allem die Anwendung von PCA auf unvollständige Datensätze und können daher für die Auswertung fehlender Werte (NA) verwendet werden. Das Paket befindet sich im Repository Bioconductor und kann wie folgt installiert werden.
source("https://bioconductor.org/biocLite.R") biocLite("pcaMethods") library(pcaMethods)
Alle Methoden des Pakets geben die allgemeine Klasse pcaRes zurück, die das Ergebnis enthält. Dies gibt dem Anwender eine hohe Flexibilität. Die umklammernde Funktion pca() ermöglicht über ihren Namen den Zugriff auf alle benötigten Typen von PCA. Unten ist eine Liste der Algorithmen mit einer kurzen Beschreibung:
- svdPCA ist eine umklammernde Funktion der Standardfunktion prcomp.
- svdImpute ist die Implementation des Algorithmus zur Begrenzung von NA. Er toleriert große Zahlen von NA (>10%).
- Probabilistic PCA (ppca) PPCA toleriert Zahlen von NA zwischen 10% und 15%.
- Bayesian PCA (bpca) Ähnlich wie bei der probabilistischen PCA wird hier der EM-Ansatz mit dem Bayes'schen Modell zur Berechnung der Wahrscheinlichkeit der Wiederherstellung des Wertes verwendet. Dieser Algorithmus ist tolerant gegenüber einer relativ großen Anzahl fehlender Daten (> 10%). Bewertungen und Belastungen, die von dieser Methode zurückgegeben werden unterscheiden sich von denen von РСА. Dies hängt damit zusammen, dass BPCA speziell für die Bewertung fehlender Werte entwickelt wurde und auf dem Variation Bayes'schen Framework (VBF) mit automatischer Relevanzerkennung (ARD) basiert. Dieser Algorithmus erzwingt keine Orthogonalität zwischen den Belastungen. Die Autoren von BPCA haben nämlich herausgefunden, dass ein Einschließen des Orthogonalitätskriteriums die Vorhersagen verschlechtert.
- Inverse nonlinear PCA (NLPCA) eignet sich am besten für experimentellen Daten, bei denen die Beziehung zwischen Prädiktoren und der Zielvariablen nichtlinear ist. NLPCA basiert auf dem Training des Dekodierungsteils des assoziativen neuronalen Netzes (Autoencoder). Die Belastungen sind in der verdeckten Schicht des Netzes sichtbar. Fehlende Werte in den Trainingsdaten werden bei der Fehlerberechnung während der Rückpropagation einfach ignoriert. Auf diese Weise kann NLPCA für die Verarbeitung von fehlenden Werten auf die gleiche Weise verwendet werden, wie bei einem standardmäßigen PCA? Der einzige Unterschied besteht darin, dass die Belastungen P nun durch ein neuronales Netz repräsentiert werden. Diese Art der Verminderung der Dimensionen werden wir im Abschnitt "Autoencoder" näher untersuchen.
- Nipals PCA ist eine nichtlineare Auswertung durch iterative, partielle kleinste Quadrate. Dies ist ein Algorithmus aus dem Kern der Regression von PLS, der PCA mit fehlenden Werten durchführen kann, die außerhalb der jeweiligen internen Produkte liegen. Er toleriert eine kleine Anzahl (normalerweise nicht mehr als 5%) fehlender Daten.
- Local least squares (LLS) imputation ist die Algorithmus/Funktion llsImpute() zur Auswertung fehlender Werte basierend auf der linearen Kombination von k-nächsten Nachbarn unvollständiger Variablen. Der Abstand zwischen den Variablen ist definiert als der absolute Wert des Pearson, Spearman oder Kendall Korrelationskoeffizienten. Die optimale Linearkombination kann durch die Lösung eines lokalen Problems der kleinsten Quadrate gefunden werden.
In der aktuellen Implementierung werden zwei Möglichkeiten zur Auswertung fehlender Werte vorgestellt. Diese Methoden unterscheiden sich geringfügig. Der erste Weg ist die Begrenzung der Suche nach Nachbarn in der Teilmenge der vollständigen Variablen. Diese Methode ist vorzuziehen, wenn die Anzahl der undefinierten Variablen relativ gering ist. Die zweite Methode betrachtet alle Variablen als Kandidaten. Fehlende Werte werden hier zunächst durch den Durchschnitt der Spalten ersetzt. Diese Methode iteriert dann mit der aktuellen Auswertung als Input für die LLS-Regression, bis die Änderungen zwischen der neuen und der alten Auswertung einen bestimmten Schwellenwert (0,001) unterschreiten.
Leider erlauben mir das Thema dieses Artikels und sein Umfang nicht, über alle vorgeschlagenen Algorithmen dieses genialen Paketes zu schreiben. NLPCA werden wir erst später im Vergleich zum Autoencoder betrachten.
2.4. Autoencoder
Autoassoziative Netze sind seit der Entstehung von tiefen neuronalen Netzen weit verbreitet. In einem meiner vorherigen Artikel haben wir uns eingehend mit dem Aufbau und den Eigenschaften von Trainingsautoencodern (AE), gestapelten Autoencodern, eingeschränkten Boltzmann-Maschinen (RBM) und anderem beschäftigt.
Ein Autoencoder ist ein neuronales Netzwerk mit einer oder mehreren verdeckten Schichten und einer Anzahl von Neuronen in der Eingangsschicht, die der Anzahl der Neuronen in der Ausgangsschicht entspricht. Der Hauptzweck von AE ist es, die Eingangsdaten so genau wie möglich darzustellen. Für AE werden die gleichen Trainings-, Regularisierungs- und Neuronenaktivierungsmethoden verwendet, wie sie auch für standardmäßige, neuronales Netze verwendet werden. Ein Modell der AE kann mit Hilfe eines beliebigen Pakets für den Aufbau neuronaler Netze erstellt werden, was es erlaubt, eine Matrix von verdeckten Schichtgewichten zu extrahieren. Wir verwenden das Paket autoencoder. Das folgende Beispiel soll helfen, mögliche AE-Strukturen abzurufen:
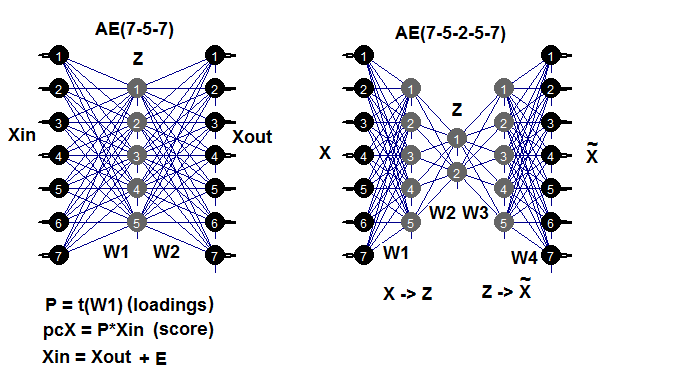
Abb. 7. Strukturelles Diagramm des autoencoders (drei und fünf Schichten)
Die Gewichtsmatrix W1 zwischen der ersten (Eingang) und der verdeckten Schicht ist die Belastung, die durch das Training erreicht wird. Nach der Projektion (Multiplikation) der Eingangsmatrix Xin auf die Belastung P erhalten wir eine reduzierte Matrix (im wesentlichen die Hauptkomponenten). Wir erhalten das gleiche Ergebnis mit predict(). Diese Funktion ermöglicht es, entweder die verdeckten Schichten (wenn hidden.output = TRUE) oder die Ausgabeschicht des Autoencoders (wenn hidden.output = FALSE) auszugeben.
Nach dem Training des AE können wir die Gewichtsmatrix W1 und den Wiederherstellungsfehler aus dem Modell extrahieren. Wenn wir den Testdatensatz mit einlesen, können wir auch den Testfehler aus dem Modell erhalten. Der Trainingsfehler hängt stark von den Parametern des AE ab und sehr stark vom Verhältnis n.hidden/n.in. Je größer dieses Verhältnis, desto größer der Wiederherstellungsfehler. Wenn wir eine signifikante Verminderung der Dimensionen erreichen wollen, können zwei AEs konsequenterweise miteinander verbunden werden. Wenn es zum Beispiel 12 Eingänge gibt, können wir ein Modell 12-7-12 trainieren, predere() von der verdeckten Ebene ausführen und es einem Autoencoder 7-3-7 eingeben. Die Ermäßigung beträgt 12 -> 3. Fröhliches Experimentieren!
Es sollte erwähnt werden, dass das Paket zwar die Fähigkeit beansprucht, eine mehrschichtige AE zu erstellen und zu trainieren, aber ich war nicht in der Lage, dies zu tun.
Führen wir ein Experiment durch. Sie verfügen bereits über Part_1. RData mit Berechnungsergebnissen des ersten Teils des Artikels. Unten ist eine Folge von Berechnungen:
- Erstellen der Datensätze train/val/test aus den Daten dataSet und Abrufen der Liste DT;
- Begrenzen der Ausreißer und Abrufen der Liste DTcap;
- Normalisieren unserer Datensätze mit den Methoden ("center", "scale", "spatialSign"). Sie können auch andere Methoden für die Transformation und Normalisierung als die gerade erwähnten verwenden;
- Trainieren des Modells von Autoencoder mit drei Neuronen in der verdeckten Schicht. Erkunden Sie andere Varianten. Mit zunehmender Anzahl verdeckter Neuronen verringert sich der Wiederherstellungsfehler;
- Mit Hilfe des trainierten Modells und predict() erhalten wir das Ergebnis der verdeckten Schicht. Dies ist im wesentlichen eine reduzierte Matrix (РСА). Ergänzen einer Zielvariablen;
- Zeichnen des Diagramms der Variation und der Kovariation der reduzierten Stichproben train/val/test/.
require(FCNN4R)
require(deepnet)
require(darch)
require(tidyverse)
require(magrittr)
#----Clean---------------------
require(caret)
require(pipeR)
evalq(
{
train = 1:2000
val = 2001:3000
test = 3001:4000
DT <- list()
dataSet %>%
preProcess(., method = c("zv", "nzv", "conditionalX")) %>%
predict(., dataSet) %>%
na.omit -> dataSetClean
list(train = dataSetClean[train, ],
val = dataSetClean[val, ],
test = dataSetClean[test, ]) -> DT
rm(dataSetClean, train, val, test)
},
env)
#------outlier-------------
require(foreach)
evalq({
DTcap <- list()
foreach(i = 1:3) %do% {
DT[[i]] %>%
select(-c(Data, Class)) %>%
as.data.frame() -> x
if (i == 1) {
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
prep.outlier(x[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
}
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = x[ ,i], impute = T, fill = T,
lower = lower, upper = upper,
med = med, cap1 = cap1, cap2 = cap2)
} %>% as.data.frame() -> x.cap
colnames(x.cap) <- colnames(x)
return(x.cap)
} -> DTcap
foreach(i = 1:3) %do% {
cbind(DTcap[[i]], Class = DT[[i]]$Class)
} -> DTcap
DTcap$train <- DTcap[[1]]
DTcap$val <- DTcap[[2]]
DTcap$test <- DTcap[[3]]
rm(lower, upper, med, cap1, cap2, x.cap, x)
}, env)
#------normalize-----------
evalq(
{
method <- c("center", "scale", "spatialSign") #, "expoTrans") #"YeoJohnson",
# "spatialSign"
preProcess(DTcap$train, method = method) -> preproc
list(train = predict(preproc, DTcap$train),
val = predict(preproc, DTcap$val),
test = predict(preproc, DTcap$test)
) -> DTcap.n
#foreach(i = 1:3) %do% {
# cbind(DTcap.n[[i]], Class = DT[[i]]$Class)
#} -> DTcap.n
},
env)
#----train-------
require(autoencoder)
evalq({
train <- DTcap.n$train %>% select(-Class) %>% as.matrix()
val <- DTcap.n$val %>% select(-Class) %>% as.matrix()
test <- DTcap.n$test %>% select(-Class) %>% as.matrix()
## Set up the autoencoder architecture:
nl = 3 ## number of layers (default is 3: input, hidden, output)
unit.type = "tanh" ## specify the network unit type, i.e., the unit's
## activation function ("logistic" or "tanh")
N.input = ncol(train) ## number of units (neurons) in the input layer (one unit per pixel)
N.hidden = 3 ## number of units in the hidden layer
lambda = 0.0002 ## weight decay parameter
beta = 0 ## weight of sparsity penalty term
rho = 0.01 ## desired sparsity parameter
epsilon <- 0.001 ## a small parameter for initialization of weights
## as small gaussian random numbers sampled from N(0,epsilon^2)
max.iterations = 3000 ## number of iterations in optimizer
## Train the autoencoder on training.matrix using BFGS
##optimization method
AE_13 <- autoencode(X.train = train, X.test = val,
nl = nl, N.hidden = N.hidden,
unit.type = unit.type,
lambda = lambda,
beta = beta,
rho = rho,
epsilon = epsilon,
optim.method = "BFGS", #"BFGS", "L-BFGS-B", "CG"
max.iterations = max.iterations,
rescale.flag = FALSE,
rescaling.offset = 0.001)}, env)
## Report mean squared error for training and test sets:
#cat("autoencode(): mean squared error for training set: ",
# round(env$AE_13$mean.error.training.set,3),"\n")
## Extract weights W and biases b from autoencoder.object:
#evalq(P <- AE_13$W, env)
#-----predict-----------
evalq({
#Train <- predict(AE_13, X.input = train, hidden.output = FALSE)
pcTrain <- predict(AE_13, X.input = train, hidden.output = TRUE)$X.output %>%
tbl_df %>% cbind(., Class = DTcap.n$train$Class)
#Val <- predict(AE_13, X.input = val, hidden.output = FALSE)
pcVal <- predict(AE_13, X.input = val, hidden.output = TRUE)$X.output %>%
tbl_df %>% cbind(., Class = DTcap.n$val$Class)
#Test <- predict(AE_13, X.input = test, hidden.output = FALSE)
pcTest <- predict(AE_13, X.input = test, hidden.output = TRUE)$X.output %>%
tbl_df %>% cbind(., Class = DTcap.n$test$Class)
}, env)
#-----graph---------------
require(GGally)
evalq({
ggpairs(pcTrain,columns = 1:ncol(pcTrain),
mapping = aes(color = Class),
title = "pcTrain")},
env)
evalq({
ggpairs(pcVal,columns = 1:ncol(pcVal),
mapping = aes(color = Class),
title = "pcVal")},
env)
evalq({
ggpairs(pcTest,columns = 1:ncol(pcTest),
mapping = aes(color = Class),
title = "pcTest")},
env)
Schauen wir und das Bild an
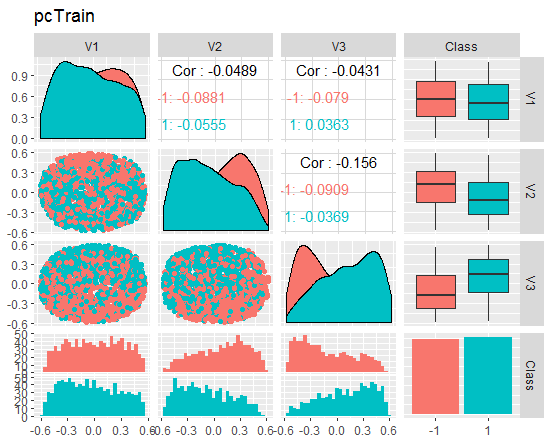
Abb. 8. Variation und Kovariation des reduzierten Datensatzes train
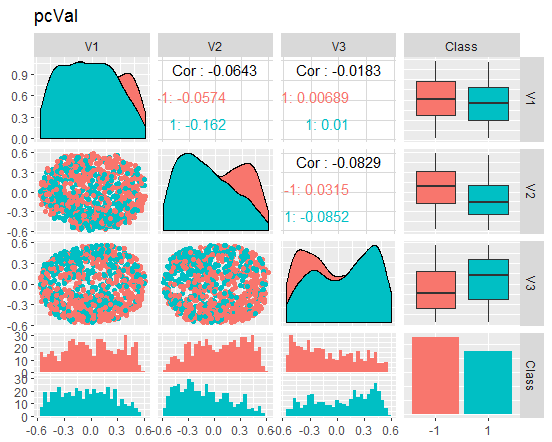
Abb. 9. Variation und Kovariation des reduzierten Datensatzes val
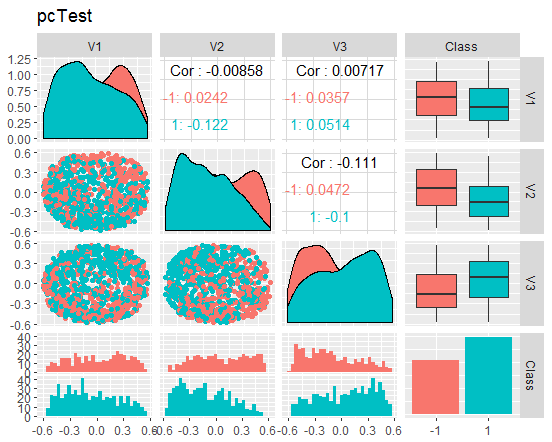
Abb. 10. Variation und Kovariation des reduzierten Datensatzes test
Was sagen uns diese Diagramme? Wir sehen, dass die Hauptkomponenten (V1, V2, V3) gut durch die Ebenen der Zielvariablen getrennt sind. Die Verteilungen in den Datensätzen train/val/test sind verzerrt. Wir sollten die verrauschte Stichproben entfernen und sehen, ob sich das Bild dadurch verbessert. Sie können es selbst machen.
Kleiner Exkurs: NLPCA
Um die Daten nach den Hauptkomponenten aufteilen zu können, ist es wichtig, Anwendungen für die reine Verminderung der Dimensionen und den Anwendungen zu unterscheiden, bei denen der Schwerpunkt hauptsächlich auf der Identifizierung und Erkennung von einzigartigen und sinnvollen Komponenten liegt, das üblicherweise als Merkmalsextraktion bezeichnet wird.
Anwendungen zur reinen Verminderung der Dimensionen mit dem Schwerpunkt Rauschunterdrückung und Datenkompression erfordern nur einen Subraum mit hoher Beschreibungskapazität. Die Möglichkeiten, einzelne Komponenten für diesen Teilraum zu separieren, sind nicht eingeschränkt und müssen daher nicht eindeutig sein. Die einzige Voraussetzung ist, dass der Subraum maximale Informationen über den mittleren quadratischen Fehler (MSE) liefert. Da einzelne Komponenten, die diesen Teilraum abdecken, vom Algorithmus ohne vorgegebene Reihenfolge oder differenzierte Gewichtung verarbeitet werden, spricht man von einer symmetrischen Trainingstyp. Dieser Trainingstyp beinhaltet eine nichtlineare PCA, die von einem standardmäßigen, assoziativen neuronalen Netz (Autoencoder) durchgeführt wird, er wird s-NLPCA genannt. Im vorherigen Teil des Artikels haben wir diese Variante bereits besprochen.
Die nichtlineare, hierarchische PKA (h-NLPCA) bietet nicht nur einen optimalen, nichtlinearen Subraum, der durch Komponenten abgedeckt wird, sondern begrenzt auch nichtlineare Komponenten durch eine gleiche, hierarchische Ordnung, ähnlich wie lineare Komponenten in der Standard-PKA. Die Hierarchie in diesem Zusammenhang wird durch zwei wichtige Eigenschaften erklärt - Skalierbarkeit und Stabilität. Skalierbarkeit bedeutet, dass die ersten n Komponenten die maximale Streuung erklären, die von einem n-dimensionalen Unterraum abgedeckt werden kann. Stabilität bedeutet, dass die i-te Komponente der n-Komponentenlösung identisch ist mit der i-ten Komponente der m-Komponentenlösung.
Ein hierarchische Reihenfolge erzeugt unkorrelierte Komponenten. Die Nichtlinearität bedeutet auch, dass h-NLPCA in der Lage ist, komplexe, nichtlineare Korrelationen zwischen Komponenten zu beseitigen. Dies hilft, nützliche und sinnvolle Komponenten herauszufiltern. Durch Skalieren der nichtlinearen, unkorrelierten Komponente zur Einheitsvarianz erhalten wir außerdem eine komplexe nichtlineare Aufhellung (sphärische Transformation). Dies ist eine sinnvolle Vorverarbeitung für solche Anwendungen wie Regression, Klassifikation oder einer blinde Teilung von Quellen. Da nichtlineares Aufhellen Nichtlinearitäten in den Daten beseitigt, können die nachfolgend angewandten Methoden linear sein. Dies ist besonders wichtig für ICA, das durch den Einsatz dieses nichtlinearen Aufhellens auf einen nichtlinearen Ansatz ausgeweitet werden kann.
Aber wie erreichen wir ein hierarchische Ordnung? Eine einfache Sortierung der symmetrisch, verarbeiteten Komponenten nach der Streuung ergibt nicht die gewünschte hierarchische Ordnung - weder linear noch nichtlinear. Eine Hierarchie kann durch zwei miteinander verbundene Methoden erreicht werden: entweder durch Begrenzung der Streuung im Komponentenraum oder durch Begrenzung des quadratischen Rekonstruktionsfehlers im Originalraum. Ähnlich wie bei der linearen PCA muss auch bei der i-ten Komponente die höchste i-te Streuung berücksichtigt werden.
In einem nichtlinearen Fall kann diese Einschränkung unwirksam oder uneinheitlich sein, ohne dass es zu zusätzlichen Einschränkungen kommt. Im Gegenteil, der Wiederherstellungsfehler kann viel besser kontrolliert werden, da er als ein absoluter Wert invariant ist, gegenüber jeder Skalierung in einer Transformation. Daher ist die hierarchische Begrenzung eines Fehlers eine effektivere Methode. In einem einfachen, linearen Fall können wir die hierarchische Anordnung der Komponenten durch den sequentiellen Ansatz erreichen, bei dem die Komponenten nacheinander auf die verbleibende Varianz des quadratischen Fehlers der vorhergehenden extrahiert werden. In einem nichtlinearen Fall funktioniert dies weder sequentiell noch gleichzeitig beim parallelen Training mehrerer Netzwerke. Die verbleibende Varianz kann unabhängig von der nichtlinearen Transformation nicht durch den quadratischen Fehler interpretiert werden. Die Lösung besteht darin, nur ein Netzwerk mit einer Hierarchie von Subnetzen zu verwenden. Dies ermöglicht es uns, eine Hierarchie direkt in der Fehlerfunktion zu formulieren.
2.5. Inverse nichtlineare PCA
In diesem Kapitel des Artikels wird ein nichtlineares PCA ein inverses Problem lösen. Während das ursprüngliche Problem die Vorhersage der Ausgabe aus dem gegebenen Eingang ist, ist das umgekehrte Problem die Bewertung des Eingangs, die am besten zu einem gesetzten Ergebnis passt. Da wir weder das Modell noch den Prozess der Datengenerierung kennen, werden wir mit einem so genannten blinden Reverse-Problem konfrontiert.
Eine einfache, lineare PCA kann sowohl bei der ursprünglichen als auch bei der inversen Problematik gleichermaßen gut verwendet werden, je nachdem, ob die benötigten Komponenten als Ausgaben vorhergesagt oder als Eingangsdaten durch einen entsprechenden Algorithmus ausgewertet werden. Autoassoziatives Netzwerk (AE) modelliert das direkte und das inverse Modell gleichzeitig.
Das direkte Modell wird durch den ersten Teil des AE durch die Extraktionsfunktion Fextr: X → Z definiert. Das inverse Modell wird durch den zweiten Teil von AE definiert, durch die Generierungsfunktion Fgen: Z → X. Das erste Modell ist besser geeignet für eine lineare PKA und funktioniert bei einer nichtlinearen PKA nicht so gut. Dies geschieht, weil dieses Modell wegen des Problems "one-to-many" sehr komplex und schwierig zu lösen sein kann. Zwei identische Datensätze X können unterschiedlichen Werten der Z-Komponenten entsprechen.
Der inverse, nichtlineare PCA erfordert nur den zweiten Teil des autoassoziativen Netzes (Abb. 11), was durch das Netz 3-7-12 veranschaulicht wird. Dieser Teil der Generation ist die umgekehrte Abbildung von Fgen, die Muster von großen Dimensionen X aus ihren Z-Darstellungen mit kleineren Dimensionen generiert oder rekonstruiert. Diese Werte der Z-Komponenten sind nun unbekannte Eingaben, die geschätzt werden können, indem die Teilfehler σ zurück an die Eingangsschicht Z übertragen werden.
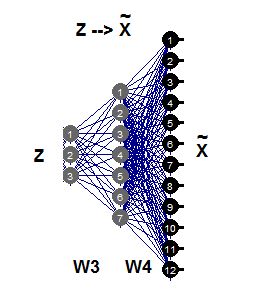
Abb. 11. Inverse nichtlineare РСА
Vergleichen wir die erhaltenen Ergebnisse mit AE und der Verwendung der Funktion nlpca::pcaMethods. Diese Funktion wurde früher in diesem Artikel erwähnt. Führen Sie die Berechnung der gleichen Daten mit der gleichen Anfangsreduzierungsbedingung 12->3 durch und vergleichen Sie die Ergebnisse.
Nehmen Sie dazu den Datensatz DTcap.n$train Set, entfernen Sie die Zielvariable Class und wandeln Sie sie in eine Matrix um. Zentrieren Sie den Datensatz. Stellen Sie die Struktur des neuronalen Netzes auf (3,8,12), den Rest der Parameter finden Sie im folgenden Skript. Nachdem dem Erhalt der Ergebnis wählen Sie die Hauptkomponenten (Punkte) aus, fügen Sie die Zielvariable zu ihnen hinzu und zeichnen Sie ein Diagramm.
Es sollte erwähnt werden, dass dieser Algorithmus sehr langsam ist und jeder neue Start ein neues Ergebnis liefert, das sich vom vorherigen unterscheidet.
require(pcaMethods)
evalq({
DTcap.n$train %>% tbl_df %>%
select(-Class) %>% as.matrix() %>%
prep(scale = "none", center = TRUE) -> train
resNLPCA <- pca(train,
method = "nlpca", weightDecay = 0.01,
unitsPerLayer = c(3, 8, 12),
center = TRUE, scale = "none",# c("none", "pareto", "vector", "uv")
nPcs = 3, completeObs = FALSE,
subset = NULL, cv = "none", # "none""q2"), ...)
maxSteps = 1100)
rm(train)},
env)
#--------
evalq(
pcTrain <- resNLPCA@scores %>% tbl_df %>%
cbind(., Class = DTcap.n$train$Class)
, env)
#------graph-------
require(GGally)
evalq({
ggpairs(pcTrain,columns = 1:ncol(pcTrain),
mapping = aes(color = Class),
title = "pcTrain -> NLPCA(3-8-12) wd = 0.01")},
env)
#----------
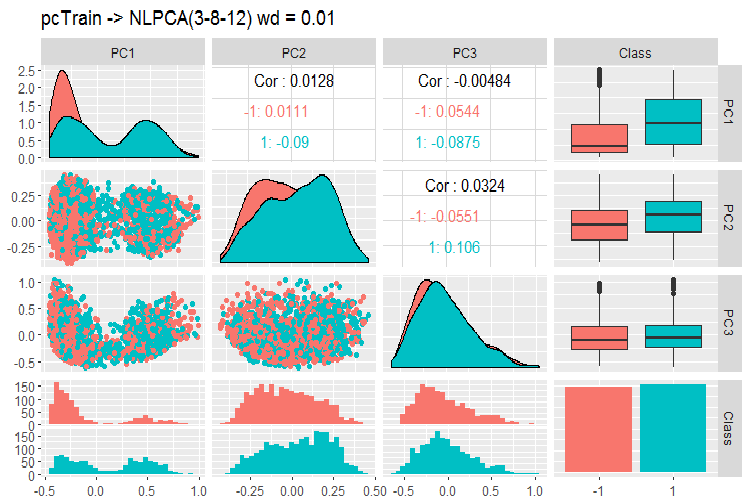
Abb. 12. Variation und Kovarianzen der Hauptkomponenten mit NLPCA
Was sehen wir auf diesem Bild? Die Hauptkomponenten sind durch die Niveaus der Zielvariablen gut getrennt und haben eine sehr geringe Korrelation. Die dritte Komponente scheint unnötig zu sein. Werfen wir einen Blick auf die allgemeinen Informationen dieses Modells.
> print(env$resNLPCA) nlpca calculated PCA Importance of component(s): PC1 PC2 PC3 R2 0.3769 0.2718 0.09731 Cumulative R2 0.3769 0.6487 0.74599 12 Variables 2000 Samples 0 NAs ( 0 %) 3 Calculated component(s) Data was mean centered before running PCA Data was NOT scaled before running PCA Scores structure: [1] 2000 3 Loadings structure: Inverse hierarchical neural network architecture 3 8 12 Functions in layers linr tanh linr hierarchic layer: 1 hierarchic coefficients: 1 1 1 0.01 scaling factor: 0.3260982
Hier gibt es ein Problem Das Ergebnis liefert keine Matrix der Gewichte für W3 und W4. In anderen Worten, wir haben keine Belastungen P, und wir können die wichtigsten Komponenten S (scores) für die Datensätze test und val nicht erhalten. Dieses Problem besteht in zwei andere gute Methoden der Verminderung der Dimensionen - tSNE, ICS. Wir könnten diese Probleme halbwegs leicht lösen, aber wir sollten besser keinen Weg mit ungewissem Ausgang beschreiten.
Das Paket enthält zwei weitere Methoden - probabilistische und Bayes'sche РСА. Sie sind schnell und liefern die Belastungen, über die leicht die Hauptkomponenten der Datensätze test und val erhalten werden können. Ich bringe ein Beispiel, nur für die PPCA.
#=======PPCA===================
evalq({
DTcap.n$train %>% tbl_df %>%
select(-Class) %>% as.matrix() -> train
DTcap.n$val %>% tbl_df %>%
select(-Class) %>% as.matrix() -> val
DTcap.n$test %>% tbl_df %>%
select(-Class) %>% as.matrix() -> test
resPPCA <- pca(train, method = "ppca",
center = TRUE, scale = "none",# c("none", "pareto", "vector", "uv")
nPcs = 3, completeObs = FALSE,
subset = NULL, cv = "none", # "none""q2"), ...)
maxIterations = 3000)
},
env)
#-----------
>print(env$resPPCA)
ppca calculated PCA
Importance of component(s):
PC1 PC2 PC3
R2 0.2873 0.2499 0.1881
Cumulative R2 0.2873 0.5372 0.7253
12 Variables
2000 Samples
0 NAs ( 0 %)
3 Calculated component(s)
Data was mean centered before running PCA
Data was NOT scaled before running PCA
Scores structure:
[1] 2000 3
Loadings structure:
[1] 12 3
Zeichnen des Diagramms der Belastungen und der Bewertungen der Komponenten 1 und 2:
slplot(env$resPPCA, pcs = c(1,2), lcex = 0.9, sub = "Probabilistic PCA")
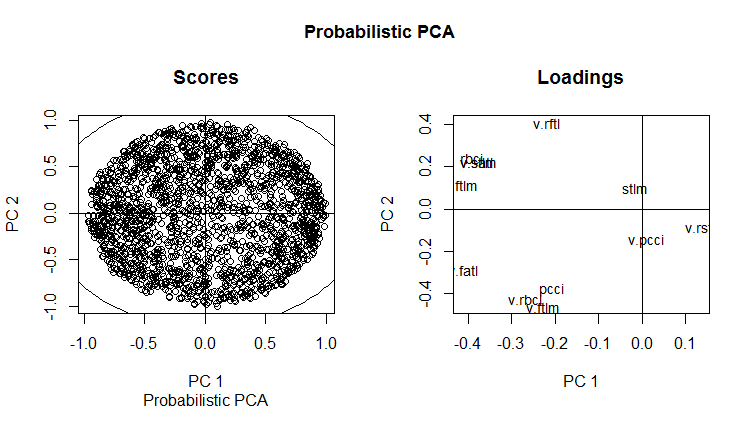
Abb. 13. РС1 und РС2 der probabilistischen РСА (Belastung und Bewertung)
Nachfolgend sind die Tabellen der Variation und der Kovarianz der Hauptkomponenten des PPCA der Datensätze train/val/test dargestellt. Sie finden das Skript auf GitHub.
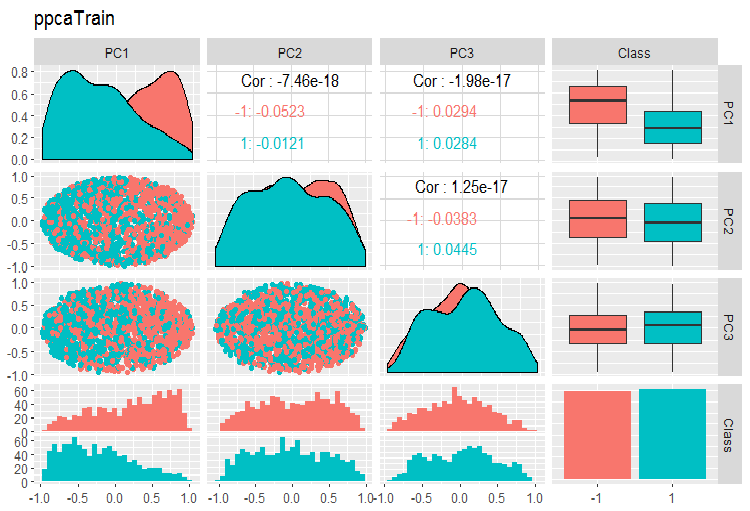
Abb. 14. Variation und Kovarianz der Hauptkomponenten des mit PPCA erhaltenen Datensatzes train
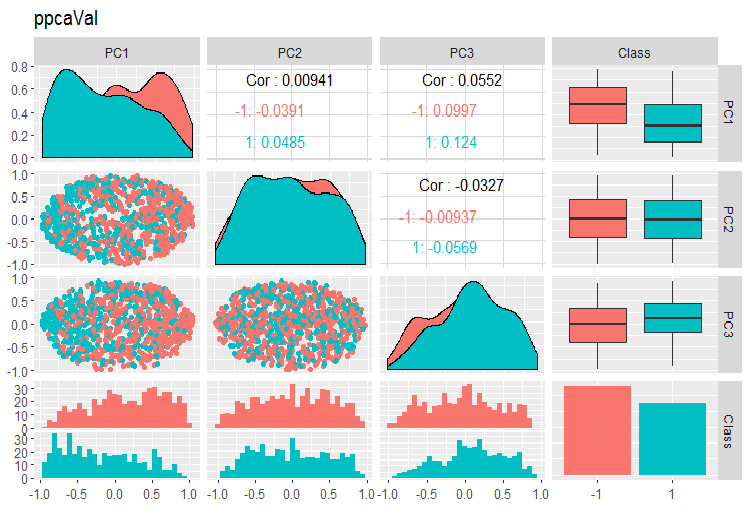
Abb. 15. Variation und Kovarianz der Hauptkomponenten des mit PPCA erhaltenen Datensatzes val
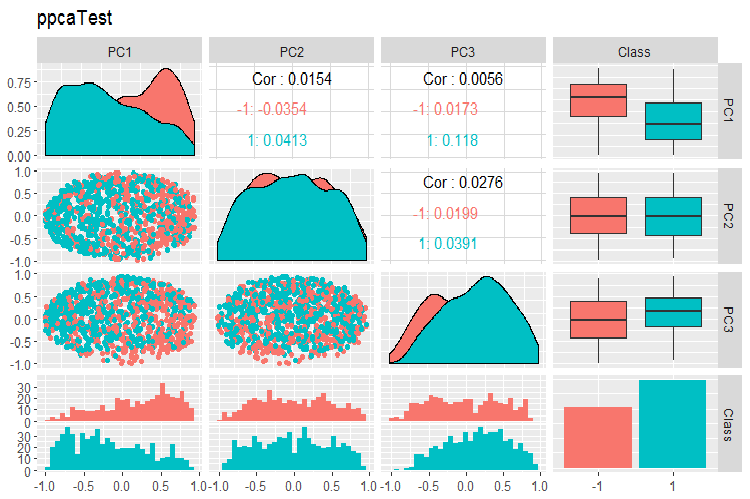
Abb. 16. Variation und Kovarianz der Hauptkomponenten des mit PPCA erhaltenen Datensatzes test
Die Trennung der Zielkomponenten der Hauptkomponenten, die wir mit PPCA erhalten haben, ist nicht besser als die gleiche Reduktion mit dem oben besprochenen Autoencoder. Die Vorteile von PPCA und BPCA sind ihre Geschwindigkeit und ihre Einfachheit. Die Qualität sollte mit einem bestimmten Klassifizierungmodell bewertet werden.
3.Aufteilen der Daten in die Datensätze train/valid/test sets
In diesem Teil bleibt alles so, wie es in den vorangegangenen Artikeln beschrieben wurde. Während des Trainings: train/valid/test, gleitendes Fenster, wachsendes Fenster, seltener - bootstrap. Während der Wahl des Modells: Kreuzvalidierung. Die Frage, ob eine ausreichende Größe dieser Datensätze ermittelt werden kann, ist noch offen.
Ich möchte eine interessante Aussage von Win Wector LLC über die Verwendung des Datensatzes train während der Vorverarbeitungstransformation erwähnen. Sie sagen, dass, wenn die Hauptkomponenten auf dem Trainingsdatensatz identifiziert wurden, das Modell auf die Hauptkomponenten trainiert werden sollte, die auf dem Validierungsdatensatz erhalten wurden. Das bedeutet, dass ein verwendeter Datensatz nicht zum Training eines Modells verwendet werden kann. Dies kann getestet werden, wenn das Netzwerk trainiert wird.
Schlussfolgerung
Wir haben fast alle Phasen der Datenaufbereitung für das Training tiefer neuronaler Netze berücksichtigt. Wie Sie sehen können, ist dies ein komplexer und zeitaufwändiger Schritt, der gute, theoretische Kenntnisse erfordert. Ohne Verständnis und Fähigkeiten, Daten für die folgenden Schritte aufzubereiten, sind alle weiteren Aktionen sinnlos.
Es ist unmöglich, ein gutes Ergebnis ohne eine visuelle Kontrolle aller Berechnungen im Stadium der Datenaufbereitung zu erreichen. Die ungeduldigen und faulen Menschen werden die Pakete "preprocomb" und "metaheur" mögen, die ihnen helfen, automatisch die am besten geeigneten vorbereitende Aufbereitung zu finden.
Anwendung
Die Skripte dieses Artikels finden Sie hier: GitHub/Part_III.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/3526
Tiefe neuronale Netzwerke (Teil IV). Erstellen, trainieren und testen eines Modells des neuronalen Netzes
Tiefe neuronale Netzwerke (Teil II). Ausarbeitung und Auswahl von Prädiktoren
Cross-Plattform Expert Advisor: Stopps
Grafisches Interface XI: Texteingabefelder und Kombinationsfelder in Tabellenzellen (build 15)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.