Tiefes Neuronales Netzwerk mit geschichtetem RBM. Selbsttraining, Selbstkontrolle

Dieser Artikel ist eine Fortsetzung des vorherigen Artikels über tiefe Neuronale Netzwerke und Prädikatorauswahl. Wir besprechen hier die Eigenschaften der Neuronalen Netzwerke in Form des "Stacked RMB" (geschichtete Restricted Boltzmann Maschine) und deren Umsetzung durch das Paket "darch". Die Möglichkeit der Verwendung eines "Hidden Markov Model" für die Verbesserung der Vorhersage eines Neuronalen Netzes wird auch besprochen werden. Schließlich werden wir alles in einem funktionierendem Expert Advisor implementieren.

Inhalt

• 1. Struktur des DBN
• 2. Vorbereitung und Auswahl der Daten
• 2.1. Eingabevariablen
• 2.2. Ausgabevariablen
• 2.3. Die ersten Quelldaten
• 2.3.1. Löschen stark korrelierter Variablen
• 2.4. Auswahl der wichtigsten Variablen
• 3. Experimenteller Teil.
• 3.1. Das Modell
• 3.1.1. Kurzbeschreibung des Paketes "darch"
• 3.1.2. Erstellen des DBN Modells. Parameter.
• 3.2. Die Bildung der Stichproben für Training und Test.
• 3.2.1. Klassenausgleich und Vorverarbeitung.
• 3.2.2. Kodierung der Zielvariablen
• 3.3. Trainieren des Modells
• 3.3.1. Vortraining
• 3.3.2. Feinabstimmung
• 3.4. Testen des Modells. Metriken.
• 3.4.1. Decodierung der Vorhersagen.
• 3.4.2. Ergebnisverbesserung der Vorhersage
• Kalibrierung
• Glätten mit einer Markov-Kette
• Abstimmung der vorhergesagten Signale der theoretischen Gleichgewichtskurve
• 3.4.3. Metriken
• 4. Struktur der Expert Advisors
• 4.1. Beschreibung der Arbeitsweise des Expert Advisors
• 4.2. Selbstkontrolle. Selbsttraining
• Installation und Programmstart
• Mittel und Wege der Verbesserung der Indikatoren.
• Schlussfolgerung

Einführung

Zur Vorbereitung der Daten des Experimentes verwenden wir die Variablen aus dem vorigen Artikel über die Auswertung und Auswahl der Vorhersagen. Wir bilden eine anfängliche Stichprobe, bereinigen sie und wählen die entscheidenden Variablen.

Betrachten wir die Möglichkeiten der Aufteilung der ersten Stichprobe in Trainings-, Test- und Validierungsdaten.

Unter Verwendung des Paketes "darch" erstellen wir ein Modell eine DBN Netzes und trainieren es mit unseren Daten. Nach den Tests des Modells erhalten wir Kennzahlen, mit denen wir die Qualität des Modells erkennen können. Wir berücksichtigen die vielen Einstellungsmöglichkeiten des Paketes für das Netzwerk.

Außerdem verwenden wir das "Hidden Markov Model", um die Vorhersagen des Neuronales Netzes zu verbessern.

Wir entwickeln einen Expert Advisor, dessen Modell regelmäßig on-the-fly ohne Unterbrechung des Handelns trainiert wird, basierend auf den Ergebnissen einer kontinuierlichen Überwachung. Das DBN Modell des Paketes "darch" wird durch den Expert Advisor verwendet. Wir berücksichtigen auch den Expert Advisor, der SAE DBN aus dem vorherigen Artikel verwendet.

Weiters zeigen wir Wege und Methoden, die Qualität der Indikatoren des Modells zu verbessern.

1. Die Struktur eines tiefen Neuronalen Netzes initialisiert durch ein "Stacked RBM" (DN_SRBM)

Wir erinnern uns, ein DN_SRBM besteht aus n RBMs, die der Anzahl der verborgenen Ebenen entspricht und im Grunde dem Neuronalen Netzwerk selbst. Das Training besteht aus zwei Stufen.

Die erste Stufe ist das Vortraining (PRE-TRAINING). Jedes RBM wird systematisch trainiert, ohne Überwachung der Eingabedaten (without target). Nach den ersten Wichtungen der verborgenen Ebenen werden die RBMs zu den entsprechenden, verborgenen Ebenen des Neuronales Netzwerkes weitergeleitet.

In der zweiten Stufe wird das Neuronale Netzwerk mit Überwachung trainiert. Detaillierte Informationen finden sich im vorherigen Artikel, sie werden daher nicht wiederholt. Zu erwähnen ist allein, dass wir jetzt, anders als das dort verwendete Paket "deepnet", das Paket "darch" verwenden, das mehr Möglichkeiten zur Gestaltung und Optimierung bietet. Weitere Details im Laufe der Erstellung des Modells. Fig. 1 zeigt die Struktur und den Trainingsprozess DN_SRBM

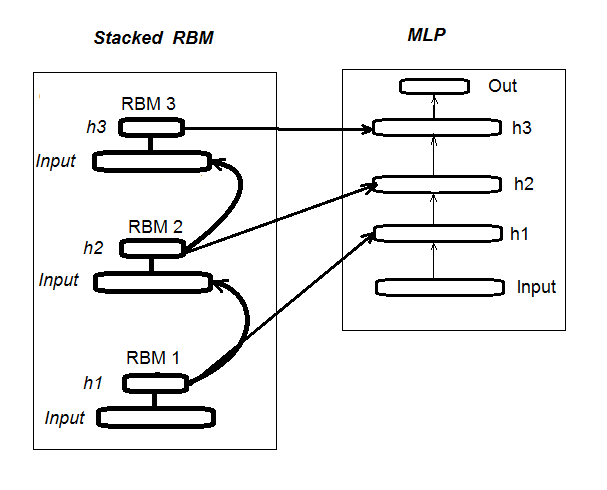
Fig. 1. Struktur des DN SRBM

2. Vorbereitung und Auswahl der Daten

2.1. Eingabevariablen (Signale und Kennziffern)

Im vorherigen Artikel haben wir ja bereits über die Evaluierung und Selektion der Kennziffern gesprochen, sodass dafür hier keine Notwendigkeit besteht. Erwähnt sei nur die Verwendung von 11 Indikatoren (alle Oszillatoren: ADX, Aroon, ATR, CCI, chaikinVolatility, CMO, MACD, RSI, stoch, SMI, Volatilität). Verschiedene Variablen einiger Indikator wurden ausgewählt. So dass wir 17 Eingabevariablen haben. Wir verwenden die Kurse der letzten 6000 Bars von EURUSD, М30 ab dem 14.02.16, und berechnen die Werte der Indikatoren mit der Funktion In().

#---2---------------------------------------------
In <- function(p = 16){
  require(TTR)
  require(dplyr)
  require(magrittr)
  adx <- ADX(price, n = p) %>% as.data.frame %>% 
    mutate(.,oscDX = DIp - DIn) %>% 
    transmute(.,DX, ADX, oscDX) %>% 
    as.matrix()
  ar <- aroon(price[ ,c('High', 'Low')], n = p) %>% 
    extract(,3)
  atr <- ATR(price, n = p, maType = "EMA") %>%
    extract(,1:2)
  cci <- CCI(price[ ,2:4], n = p)
  chv <- chaikinVolatility(price[ ,2:4], n = p)
  cmo <- CMO(price[ ,'Med'], n = p)
  macd <- MACD(price[ ,'Med'], 12, 26, 9) %>% 
    as.data.frame() %>% 
    mutate(., vsig = signal %>% 
             diff %>% c(NA,.) %>% multiply_by(10)) %>% 
    transmute(., sign = signal, vsig) %>% 
    as.matrix()
  rsi <- RSI(price[ ,'Med'], n = p)
  stoh <- stoch(price[ ,2:4], nFastK = p, 
                nFastD =3, nSlowD = 3, 
                maType = "EMA") %>%
                                as.data.frame() %>% 
                                mutate(., oscK = fastK - fastD) %>%
                                transmute(.,slowD, oscK) %>% 
                                as.matrix()
  smi <- SMI(price[ ,2:4],n = p, nFast = 2, 
             nSlow = 25, nSig = 9)
  kst <- KST(price[ ,4])%>% as.data.frame() %>% 
                                mutate(., oscKST = kst - signal) %>%
                                select(.,oscKST) %>% as.matrix()
  In <- cbind(adx, ar, atr, cci, chv, cmo, macd, 
              rsi, stoh, smi, kst)
  return(In)
}

Wir erhalten als Ausgabe eine Matrix der Eingabedaten.

2.2 Ausgabedaten (Zielvariable)

Als eine Zielvariable verwenden wir die Signale aus der Funktion ZZ(). Diese Funktion berechnet ZigZag und ein Signal:

#----3------------------------------------------------
ZZ <- function(pr = price, ch = ch , mode="m") {
  require(TTR)
  require(magrittr)
  if (ch > 1) ch <- ch/(10 ^ (Dig - 1))
  if (mode == "m") {pr <- pr[ ,'Med']}
  if (mode == "hl") {pr <- pr[ ,c("High", "Low")]}
  if (mode == "cl") {pr <- pr[ ,c("Close")]}
  zz <- ZigZag(pr, change = ch, percent = F, 
               retrace = F, lastExtreme = T)
  n <- 1:length(zz)
  dz <- zz %>% diff %>% c(., NA)
  sig <- sign(dz)
  for (i in n) { if (is.na(zz[i])) zz[i] = zz[i - 1]}
  return(cbind(zz, sig))
}

Die Parameter der Funktion:

pr = price – Matrix der OHLCMed-Kurse;

ch – der kleinste Abstand zwischen den Punkten (4 Signale) oder ein fester Wert (zum Beispiel ch = 0.0035);

mode – Kalkulationspreis ("m" - Medium, "hl" - High und Low), "cl" - Close), Medium ist der Standard.

Die Funktion liefert eineuelldaten bildet, die stark korrelierten Var Matrix mit zwei Variablen — tatsächlich den ZigZag und das Signal auf Basis des Winkels des ZigZags im Intervall [-1;1]. Wir verschieben das Signal um ein Bar nach links (Richtung Zukunft). Dies besondere Signal wird zum Training des Neuronalen Netzwerks verwendet.

Wir berechnen Signale für ZZ mit einem Punktabstand aus mindestens 37 Points (4 Signale).

> out <- ZZ(ch = 37, mode = "m")
Loading required package: TTR
Loading required package: magrittr
> table(out[ ,2])

  -1    1 
2828 3162

Wie wir sehen können, sind die Klassen etwas unausgeglichen. Für das Trainingsmodell müssen wir sie anpassen.

2.3. Die ersten Quelldaten

Schreiben wir also eine Funktion zur Anpassung der ersten Quelldaten, der Beseitigung von Unsicherheiten in den Daten und der Umwandlung der Zielvariablen in zwei Klassen "-1" und "+1". Diese Funktion vereint die zuvor geschriebenen Funktionen In() und ZZ(). Wir verwenden nur die letzten 500 Bars zur Auswertung der Qualität der Vorhersagen des Modells.

#-----4---------------------------------
form.data <- function(n = 16, z = 37, len = 500){
  require(magrittr)
  x <- In(p = n)
  out <- ZZ(ch = z, mode = "m")
  data <- cbind(x, y = out[ ,2]) %>% 
    as.data.frame %>% head(., (nrow(x)-len))%>%
        na.omit
  data$y <- as.factor(data$y)
  return(data)
}

2.3.1. Löschen stark korrelierter Variablen

Wir löschen Variable mit einem Korrelationskoeffizient von über 0,9 von unseren ersten Einstellungen. Wir schreiben eine Funktion, die die ersten Quelldaten bildet, die stark korrelierten Variablen entfernt und die Daten bereinigt zurückgibt.

Wir können vorab prüfen, welche Daten mit mehr als 0,9 korrelieren.

> data <- form.data(n = 16, z = 37) # Vorbereitung der Daten
> descCor <- cor(data[ ,-ncol(data)])# Entfernen der Zielvariablen
> summary(descCor[upper.tri(descCor)])
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
-0.1887  0.0532  0.2077  0.3040  0.5716  0.9588 
> highCor <- caret::findCorrelation(descCor, cutoff = 0.9)
> highCor
[1] 12  9 15
> colnames(data[ ,highCor])
[1] "rsi" "cmo" "SMI"

Also können wir die obigen Variablen entfernen. Löschen wir sie aus dem Daten.

> data.f <- data[ ,-highCor]
> colnames(data.f)
 [1] "DX"     "ADX"    "oscDX"  "ar"     "tr"    
 [6] "atr"    "cci"    "chv"    "sign"   "vsig"  
[11] "slowD"  "oscK"   "signal" "vol"    "Class" 

Wir schreiben alles in eine Funktion:

#---5-----------------------------------------------
cleaning <- function(n = 16, z = 37, cut = 0.9){
  data <- form.data(n, z)
  descCor <- cor(data[ ,-ncol(data)])
  highCor <- caret::findCorrelation(descCor, cutoff = cut)
  data.f <- data[ ,-highCor]
  return(data.f)
}
> data.f <- cleaning()

Nicht alle Autoren von Paketen und Forscher sind sich einig, dass Daten hoher Korrelation entfernt werden sollten. Vergleichen wir also hier beide Optionen. In unserem Fall wählen wir die Lösch-Option.

2.4. Auswahl der wichtigsten Variablen

Wichtige Variablen werden auf Basis von drei Kennzeichen ausgewählt: globale Bedeutung, lokaler Bedeutung (in Verbindung) und die partielle Bedeutung der Klasse. Wir nutzen die Möglichkeiten des Paketes "randomUniformForest", so wie sie im vorigen Artikel detailliert beschrieben wurden. Alle vorherigen und folgenden Aktionen werden in einer Funktion wegen der Kompaktheit konzentriert. Einmal ausgeführt, erhalten wir drei Gruppen als Ergebnis:

• mit den besten Variablen in Beitrag und Interaktion;
• mit den besten Variablen für die Klasse "-1";
• mit den besten Variablen für die Klasse "+1".

#-----6------------------------------------------------
prepareBest <- function(n, z, cut, method){
  require(randomUniformForest) 
  require(magrittr)
  data.f <<- cleaning(n = n, z = z, cut = cut)
  idx <- rminer::holdout(y = data.f$Class)
  prep <- caret::preProcess(x = data.f[idx$tr, -ncol(data.f)], method = method)
  x.train <- predict(prep, data.f[idx$tr, -ncol(data.f)])
  x.test <- predict(prep, data.f[idx$ts, -ncol(data.f)])
  y.train <- data.f[idx$tr, ncol(data.f)]
  y.test <- data.f[idx$ts, ncol(data.f)]
#---------
  ruf <- randomUniformForest( X = x.train, Y = y.train,
                              xtest = x.test, ytest = y.test,
                              mtry = 1, ntree = 300,
                              threads = 2, nodesize = 1
                       )
  imp.ruf <- importance(ruf, Xtest = x.test)
  best <- imp.ruf$localVariableImportance$classVariableImportance %>% 
                  head(., 10) %>% rownames()
#-----partImport
  best.sell <- partialImportance(X = x.test, 
                                imp.ruf, 
                                whichClass = "-1",
                                nLocalFeatures = 7) %>% 
                                row.names() %>% 
                                as.numeric() %>% 
                                colnames(x.test)[.]
  best.buy <- partialImportance(X = x.test,
                                   imp.ruf,
                                   whichClass = "1",
                                nLocalFeatures = 7) %>% 
                                row.names() %>% 
                                as.numeric() %>% 
                                colnames(x.test)[.]
  dt <- list(best = best, buy = best.buy, sell = best.sell)
  return(dt)
}

Erklären wir die Reihenfolge der Berechnung. Formale Parameter:

n – Parameter der Eingangsdaten

z – Parameter der Ausgangsdaten;

cut – Schwellenwert für die Korrelation von Variablen;

method – Methode der Vorverarbeitung der Eingangsdaten.

Reihenfolge der Berechnung:

• erstelle die erste Gruppe von Daten.f, die hoch korrelierte Variablen entfernt, und speichere sie es zur weiteren Verwendung;
• identifiziere die Indizes der Stichprobe des Trainings und der Tests von idx;
• bestimme die Parameter der Vorverarbeitung von prep;
• unterteile die erste Stichprobe in eine Trainings- und eine Testgruppe und normalisiere die Eingangsdaten;
• trainieren und testen des Modells RUF mit den erhaltenen Eingangsdaten;
• berechne die Wichtigkeit der imp.ruf Variablen;
• wähle die 10 wichtigsten Variablen für einen Beitrag und Interaktion — best;
• wähle die 7 wichtigsten Variablen für jede Klasse "-1" und "+1" — best.buy, best.sell;
• erstelle ein Liste mit den drei Gruppen der Kennzeichen — best, best.buy, best.sell.
  

Wir berechnen diese Gruppen und bewerten die Werte der globalen, lokalen und Teilbedeutung der ausgewählten Variablen.

> dt <- prepareBest(16, 37, 0.9, c("center", "scale","spatialSign"))
Loading required package: randomUniformForest
Labels -1 1 have been converted to 1 2 for ease of computation and will be used internally 
       as a replacement.

1 - Global Variable Importance (14 most important based on information gain) :
Note: most predictive features are ordered by 'score' and plotted. Most discriminant ones
should also be taken into account by looking 'class' and 'class.frequency'.

   variables score class class.frequency percent
1        cci  4406    -1            0.51  100.00
2     signal  4344    -1            0.51   98.59
3        ADX  4337    -1            0.51   98.43
4       sign  4327    -1            0.51   98.21
5      slowD  4326    -1            0.51   98.18
6        chv  4296    -1            0.52   97.51
7       oscK  4294    -1            0.52   97.46
8        vol  4282    -1            0.51   97.19
9         ar  4271    -1            0.52   96.95
10       atr  4237    -1            0.51   96.16
11     oscDX  4200    -1            0.52   95.34
12        DX  4174    -1            0.51   94.73
13      vsig  4170    -1            0.52   94.65
14        tr  4075    -1            0.50   92.49
   percent.importance
1                   7
2                   7
3                   7
4                   7
5                   7
6                   7
7                   7
8                   7
9                   7
10                  7
11                  7
12                  7
13                  7
14                  7


2 - Local Variable importance
Variables interactions (10 most important variables at first (columns) and second (rows) order) :
For each variable (at each order), its interaction with others is computed.

                cci  slowD    atr     tr     DX
atr          0.1804 0.1546 0.1523 0.1147 0.1127
cci          0.1779 0.1521 0.1498 0.1122 0.1102
slowD        0.1633 0.1375 0.1352 0.0976 0.0956
DX           0.1578 0.1319 0.1297 0.0921 0.0901
vsig         0.1467 0.1209 0.1186 0.0810 0.0790
oscDX        0.1452 0.1194 0.1171 0.0795 0.0775
tr           0.1427 0.1168 0.1146 0.0770 0.0750
oscK         0.1381 0.1123 0.1101 0.0725 0.0705
sign         0.1361 0.1103 0.1081 0.0704 0.0685
signal       0.1326 0.1068 0.1045 0.0669 0.0650
avg1rstOrder 0.1452 0.1194 0.1171 0.0795 0.0775
               vsig  oscDX   oscK signal     ar
atr          0.1111 0.1040 0.1015 0.0951 0.0897
cci          0.1085 0.1015 0.0990 0.0925 0.0872
slowD        0.0940 0.0869 0.0844 0.0780 0.0726
DX           0.0884 0.0814 0.0789 0.0724 0.0671
vsig         0.0774 0.0703 0.0678 0.0614 0.0560
oscDX        0.0759 0.0688 0.0663 0.0599 0.0545
tr           0.0733 0.0663 0.0638 0.0573 0.0520
oscK         0.0688 0.0618 0.0593 0.0528 0.0475
sign         0.0668 0.0598 0.0573 0.0508 0.0455
signal       0.0633 0.0563 0.0537 0.0473 0.0419
avg1rstOrder 0.0759 0.0688 0.0663 0.0599 0.0545
                chv    vol   sign    ADX avg2ndOrder
atr          0.0850 0.0850 0.0847 0.0802      0.1108
cci          0.0824 0.0824 0.0822 0.0777      0.1083
slowD        0.0679 0.0679 0.0676 0.0631      0.0937
DX           0.0623 0.0623 0.0620 0.0576      0.0881
vsig         0.0513 0.0513 0.0510 0.0465      0.0771
oscDX        0.0497 0.0497 0.0495 0.0450      0.0756
tr           0.0472 0.0472 0.0470 0.0425      0.0731
oscK         0.0427 0.0427 0.0424 0.0379      0.0685
sign         0.0407 0.0407 0.0404 0.0359      0.0665
signal       0.0372 0.0372 0.0369 0.0324      0.0630
avg1rstOrder 0.0497 0.0497 0.0495 0.0450      0.0000


Variable Importance based on interactions (10 most important) :
   cci    atr  slowD     DX     tr   vsig  oscDX 
0.1384 0.1284 0.1182 0.0796 0.0735 0.0727 0.0677 
  oscK signal   sign 
0.0599 0.0509 0.0464 

Variable importance over labels (10 most important variables conditionally to each label) :
       Class -1 Class 1
cci        0.17    0.23
slowD      0.20    0.09
atr        0.14    0.15
tr         0.04    0.12
oscK       0.08    0.03
vsig       0.06    0.08
oscDX      0.04    0.08
DX         0.07    0.08
signal     0.05    0.04
ar         0.04    0.02

Ergebnisse

1. Nach der globalen Bedeutung sind alle 14 Eingangsgrößen gleich.
2. Die besten 10 werden durch die Gesamtbeitrag (globale Wichtigkeit) und Interaktion (lokale Wichtigkeit) bestimmt.
3. Die sieben besten Variablen der Teilbedeutung jeder Klasse sind im Bild unten aufgezeigt.

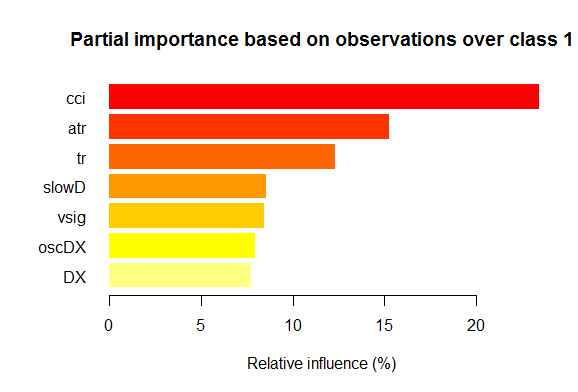
Fig. 2. Teilbedeutung der Variablen der Klasse "1"

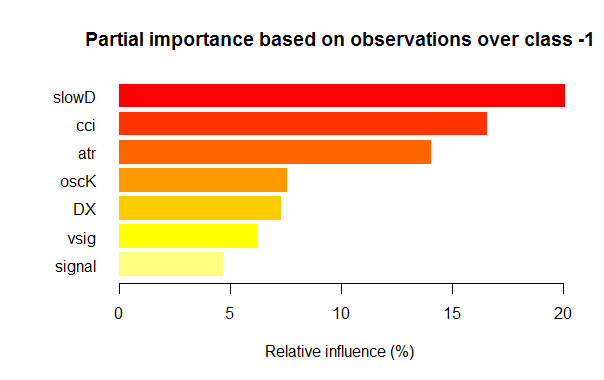
Fig. 3. Teilbedeutung der Variablen der Klasse "-1"

Wie wir sehen können, sind die wichtigsten Variablen für die verschiedenen Klassen unterschiedlich, sowohl in Struktur als auch in der Reihenfolge. Zum Beispiel ist für die Klasse "-1" slowD die wichtigste Variable, aber für die Klasse "+1" steht sie nur auf Platz 4.

Damit haben wir unsere Datensätze. Beginnen wir zu experimentieren.

3. Experimenteller Teil.

Für die Experimente verwenden wir die Sprache R — Revolution R Open, Version 3.2.2, angeboten von der Revolution Analytics Company, um genau zu sein. http://www.revolutionanalytics.com/revolution-r-open

Diese Version hat eine Reihe von Vorteilen gegenüber der regulären R 3.2.2:

• schnelle und qualitativ bessere Berechnungen durch eine parallele ("multi-threaded") Verarbeitung mit der Intel® Math Kernel Library ;
  
• verbesserte Wiederholbarkeit durch das R Toolkit. Eine kleine Erklärung: Die Sprache R wird durch Verbesserungen existierender und Entwicklung neuer Pakete ständig weiterentwickelt. Der Nachteil solcher Prozesse ist, dass frühere Ergebnisse nicht immer reproduzierbar sind. Das heißt, Ihr Programm, geschrieben vor ein paar Monaten, arbeitet plötzlich nach dem nächsten Update der Pakete nicht mehr. Viel Zeit geht damit verloren, die Fehler zu finden und zu entfernen, nach einem solchen Update. Zum Beispiel, der Expert Advisor, Teil des ersten Artikels über tiefe Neuronale Netze, hat bei seiner Erstellung gut funktioniert. Ein paar Monate später aber begannen die Nutzer sich über das Nichtfunktionieren zu beklagen. Die Analyse zeigte, dass die Aktualisierung des Paketes "svSocket" zum Ausfall des Expert Advisor geführt hat, aber ich konnte den Grund nicht feststellen. Der endgültige Expert Advisor wird dem Artikel beigefügt. Es war ein drängendes Problem und konnte durch Revolution Analytics leicht gelöst werden. Jetzt, wenn eine neue Version freigegeben wird, werden die Bedingungen aller Pakete im CRAN-Repository am Datum der Veröffentlichung durch eine Kopie auf deren Spiegelserver festgemacht. Nicht kann im CRAN-Repository nach diesem Datum die auf dem Spiegelserver von Revolution "eingefrorenen" Pakete ändern. Darüber hinaus macht diese Firma, beginnend ab Oktober 2014, tägliche "Snapshots" vom CRAN-Repository, um die relevanten Zustände Versionen der Pakete zu fixieren. Mit deren Paket "checkpoint" können wir alle für ein bestimmtes Datum relevanten Pakete herunterladen. Mit anderen Worten, wir haben jetzt ein Art Zeitmaschine.

Und noch eine Nachricht. Vor neun Monaten kaufte Microsoft Revolution Analytics und versprach die Entwicklung voranzutreiben und Revolution R Open (RRO) weiterhin kostenlos zur Verfügung zu stellen. Dem folgten eine Reihe von Nachrichten über Weiterentwicklungen von RRO und Revolution R Enterpise (ganz zu schweigen von der Integration von R in SQL Server, PowerBI, Azure und Cortana Analitics). Gerade wurde bekannt gegeben, dass das nächste RRO Update sich Microsoft R Open nennt, und Revolution R Enterprise — Microsoft R Server. Nicht viel früher teilte Microsoft mit, dass R auch im Visual Studio verfügbar sein wird. R Tools für Visual Studio (RTVS) folgt den Python Tools for Visual Studio model. Es ist eine freie Version von Visual Studio, die eine komplette IDE für R bietet, mit den Möglichkeiten Skripte interaktiv zu editieren und zu debuggen.

Als der Artikel fertig wurde, wurde Microsoft R Open (R 3.2.3) freigegeben, daher werden wir uns im weiteren auf die Version dieses Artikels beziehen.

3.1. Das Modell

3.1.1. Kurzbeschreibung des Paketes "darch"

Das Paket "darch" der Ver. 0.10.0-Paket bietet eine Breite Palette von Funktionen, die es nicht nur ermöglichen, das Modell zu erstellen und zu trainieren, sondern es auch Stein um Stein nach unseren Wünschen zu erstellen. Wie vorher angedeutet, besteht ein tiefes Neuronales Netz aus n RBMs (n = Schichten-1) und einem MLP Neuronales Netz mit einer Anzahl von Schichten. Das schichtweise Vortraining des RBM wird mit nicht formatierten Daten ohne Überwachung durchgeführt. Die Feinabstimmung des Neuronalen Netzwerkes wird mit Überwachung und formatierten Daten durchgeführt. Die Trennung dieser Lernphasen ermöglicht uns die Verwendung von unterschiedlichen Datenmengen (aber nicht Datenstrukturen!) oder um mehrere fein abgestimmte Modelle allein auf Basis des Vortrainings zu erhalten. Weiters, sind die Daten für das Vortraining und die Feinabstimmung dieselben, kann das Training in einem Durchgang statt in zweien durchgeführt werden. Oder das Vortraining kann gleich ganz übersprungen werden, und es wird nur das mehrschichtige Neuronale Netzwerk verwendet, oder andererseits kann nur das RBM ohne Neuronales Netzwerk verwendet werden. Gleichzeitig haben wir Zugriff auf alle internen Parameter. Das Paket ist für fortgeschrittene Anwender gedacht. Im Weiteren werden wir die unterteilten Prozesse analysieren: Vortraining und Feinabstimmung.

3.1.2. Erstellen des DBN Modells. Parameter.

Wir beschreiben den Prozess von Bildung, Training und Testen des DBN-Modells.

1. Erstellen des Objektes 'darch' mit einer tiefen Architektur unter Verwendung der erforderlichen Parameter

newDArch(layers, batchSize, ff=FALSE, logLevel=INFO, genWeightFunc=generateWeights),

wobei:

• layers: Array mit der Anzahl von Schichten und den Neuronen in jeder Schicht. Zum Beispiel: layers = c(5,10,10,2) – eine Eingangsschicht mit 5 (sichtbaren) Neuronen, zwei verdeckten Schichten mit jeweils 10 Neuronen und einer Ausgabeschicht mit zwei Ausgängen.
• BatchSize: Größe der Kleinstichprobe während des Trainings.
• ff: Angabe, ob das ff-Format für die Wichtungen, Abweichungen und dem Ausgang verwendet werden sollen. Das ff-Format komprimiert große Datenmengen für die Sicherung.
• LogLevel: Level für Log und Ausgabe dieser Funktion.
• GenWeightFunction: Funktion zur Erstellung der Matrix der RBM Wichtungen. Es ist möglich, die Aktivierungsfunktion des Nutzers zu verwenden.

Das erstellte darch-Objekt hat (Schichten - 1) RBMs, die zusammen in ein Netzwerk laufen, das für das Vortraining des Neuronalen Netzwerks verwendet wird. Zwei Attribute fineTuneFunction und executeFunction enthalten Funktionen zur Feinabstimmung (backpropagation standardmäßig) und zur Ausführung (runDarch standardmäßig). Das Training des Neuronalen Netzwerkes läuft über zwei Trainingsfunktionen: preTrainDArch() und fineTuneDArch(). Die erste Funktion trainiert das RBM Netz ohne Überwachung unter Verwendung der genannten "contrastive divergence". Die zweite Funktion verwendet die Attribute der Funktion fineTuneFunction zur Feinabstimmung des Neuronalen Netzwerkes. Nach einem Lauf des Neuronalen Netzwerkes können die Ausgaben jeder Schicht in den Attributen von executeOutputs oder nur in den Attributen der Ausgabeschicht gefunden werden.

2. Funktion des Vortrainings des darch-Objektes

preTrainDArch(darch, dataSet, numEpoch = 1, numCD = 1, ..., trainOutputLayer = F),

wobei:

• darch : Instanz der Klasse 'darch';
• dataSet: Datengruppe des Trainings;
• numEpoch: Anzahl der Trainingsläufe;
• numCD : Anzahl der Probenläufe. Normalerweise nur eine;
• ... : zusätzliche Parameter für die Übergabe an die Funktion trainRBM;
• trainOutputLayer: Signal, ob die Ausgabeschicht des RBM zu trainieren ist.

Diese Funktion führt die Trainingsfunktion trainRBM() für jedes RBM durch, in dem sie nach jedem Training die Wichtungen und Verschiebungen (biases) auf die relevante Schicht des Neuronalen Netzwerkes des darch-Objektes kopiert.

3. Die Funktion für die Feinabstimmung im darch-Objekt

fineTuneDArch(darch, dataSet, dataSetValid = NULL, numEpochs = 1, bootstrap = T, 
              isBin = FALSE, isClass = TRUE, stopErr = -Inf, stopClassErr = 101, 
              stopValidErr = -Inf, stopValidClassErr = 101, ...),

wobei:

• darch : Instanz der Klasse 'darch';
• dataSet : Datengruppe des Trainings (verwendbar für die Validierung) und Testens;
• dataSetValid : Datengruppe für die Validierung;
• numxEpoch : Anzahl der Trainingsläufe;
• bootstrap : logisch, wenn für der Erzeugung der Validierungsdaten ein "Bootstrap" verwendet werden soll;
• isBin : Soll die Ausgang als logische Werte interpretiert werden. Standard ist FALSE. Falls TRUE wird jeder Wert über 0,5 als 1, und darunter — als 0.
• isClass : Anzeige, ob das Netz auf Klassifizierung trainiert werden soll. Wenn TRUE wird eine Klassifizierung durch Statistik errechnet. Standard ist TRUE.
• stopErr : Stoppkriterium des Trainings des Neuronales Netzes bei Auftreten eines Fehlers während des Trainings. -Inf ist Standard;
• stopClassErr : Stoppkriterium des Trainings des Neuronales Netzes bei Auftreten eines Klassifikationsfehlers während des Trainings. 101 ist der Standard;
• stopValidErr : Stoppkriterium des Trainings des Neuronales Netzes bei Auftreten eines Fehlers in den Validierungsdaten. -Inf ist Standard;
• stopValidClassErr : Stoppkriterium des Trainings des Neuronales Netzes bei Auftreten eines Klassifikationsfehlers während der Validierung. 101 ist der Standard;
• ... : zusätzliche Parameter, die der Trainingsfunktion übergeben werden können.

Die Funktion trainiert das Netzwerk mit einer Funktion gespeichert in den Attributen fineTuneFunction des darch-Objektes. Die Eingabedaten (trainData, validData, testData) und die zugehörigen Klassen (targetData, validTargets, testTargets) können als Datengruppe oder als ff-Matrix übertragen werden. Die Daten und Klassen der Validierung und des Testens sind nicht obligatorisch. Gibt es sie, wird das Neuronale Netzwerk damit arbeiten und die Statistiken berechnen. Das Attribut isBin legt fest, ob die Ausgabedaten binäre zu interpretieren sind. Ist isBin = TRUE, wird jeder Wert über 0,5 als 1, und darunter — als 0 interpretiert. Wir können auch ein Stoppkriterium auf einer Fehlerbasis (stopErr, stopValidErr) oder Klassifikation (stopClassErr, stopValidClassErr) beim Training oder der Validierung definieren.

Alle Funktionsparameter haben Standardwerte. Aber natürlich kann man auch andere Werte setzen. So zum Beispiel:

Es gibt diese Funktionen zur Aktivierung eines Neurons — sigmoidUnitDerivative, linearUnitDerivative, softmaxUnitDerivative, tanSigmoidUnitDerivative. sigmoidUnitDerivative ist der Standard.

Die Funktionen für die Feinabstimmung des Neuronalen Netzwerkes — backpropagation ist der Standard, Resilient Propagation rpropagation ist auch in vier Varianten verfügbar ("Rprop+", "Rprop-", "iRprop+", "iRprop-") und minimizeClassifier (diese Funktion wird durch die Klassifizierer des darch-Netzwerks mittels konjugierter Gradienten trainiert). Für die letzten beiden Algorithmen und für diejenigen, die ein tiefes Wissen über das Thema haben, wird eine eigene Umsetzung der Feinabstimmung des Neuronalen Netzes mit einer Konfiguration mit ihrem verschiedenen Parametern angeboten. Zum Beispiel:

rpropagation(darch, trainData, targetData, method="iRprop+",
             decFact=0.5, incFact=1.2, weightDecay=0, initDelta=0.0125,
             minDelta=0.000001, maxDelta=50, ...),

wobei:

• darch – darch-Objekt des Trainings;
• trainData – Eingabedaten für das Training;
• targetData – erwartete Ausgabe des Trainings;
• method – Trainingsmethode. Standardmäßig "iRprop+". "Rprop+", "Rprop-", "iRprop-" sind möglich;
• decFact – Reduktionsfaktor des Trainings. Standardmäßig 0.5;
• incFact - Zuwachsfaktor des Trainings. Standardmäßig 1.2;
• weightDecay – Reduktionswichtung beim Training. Standardmäßig 0;
• initDelta – Initialisierungswert beim Update. Standardmäßig 0.0125;
• minDelta – Untergrenze der Schrittweite. Standardmäßig 0.000001;
• maxDelta – Obergrenze der Schrittweite. Standardmäßig 50.

Die Funktion gibt das darch-Objekt mit dem trainierten Neuronalen Netz zurück.

3.2. Die Bildung der Stichproben für Training und Test.

Wir haben bereits die erste Datengruppe gebildet. Jetzt müssen wir in die Gruppen für das Training, die Validierung und das Testen unterteilen. Das Verhältnis ist standardmäßig 2/3. Verschiedene Pakete mit vielen Funktionen können für diese Trennung verwendet werden. Ich verwende rminer::holdout(), es berechnet Indizes, um die Ausgangsdaten in Training- und Testgruppe zu unterteilen.

holdout(y, ratio = 2/3, internalsplit = FALSE, mode = "stratified", iter = 1,
        seed = NULL, window=10, increment=1),

wobei:

• y – gewünschte Zielvariable, ein numerischer Vektor oder Faktor, in diesem Fall wird eine geschichtete Trennung (das heißt, das Verhältnis zwischen den Klassen ist für alle gleich);
• ratio – Trennungsverhältnis (in Prozent — bestimmt die Größe der Trainingsdaten; oder die Gesamtzahl der Gruppen — bestimmt die Größe der Testdaten);
• internalsplit – Wenn TRUE, werden die Trainingsdaten noch einmal geteilt in Training und Validierung. Das gleiche Verhältnis gilt für die interne Trennung;
• mode – Modus der Probennahme. Mögliche Optionen:
• stratified – Zufallsschichtung (mit dem y Faktor, sonst standardmäßig eine Zufallsaufteilung);
• random – standardmäßige Zufallsaufteilung;
• order – statischer Modus, wenn die erste Gruppe für das Training und die verbleibenden — zum Testen (allgemein für Zeitreihen verwendet);
• rolling – rollendes Fenster auch bekannt als gleitendes Fenster (verbreitet in der Vorhersage von Aktien und Finanzmärkten), ähnliche wie order, nur, dass das Fenster sich auf seine Größe bezieht, iter — rollendes Iterieren und Inkrementieren — Anzahl der Stichproben über die das Fenster mit jeder Iteration sich vorwärts bewegt. Die Größe der Trainingsgruppe in jeder Iteration wird durch das Fenster bestimmt, während die Testgruppe entsprechend des Verhältnisses ist, außer bei der letzten Iteration (da könnte sie kleiner sein).
• incremental – Inkrementeller Modus des Wieder-Lernens, auch bekannt als ansteigendes Fenster, so wie order, nur bleibt die Fenstergröße gleich der Anfänglichen, iter — rollendes Iterieren und Inkrementieren — Anzahl der Beispiele, die bei jeder Iteration hinzugefügt werden. Bei jeder Iteration wird die Größe der Trainingsstichprobe erhöht (+increment), wobei die Größe der Teststichprobe äquivalent dem Verhältnis ist, außer bei der letzten, da könnte es kleiner sein.
• iter – Anzahl der Iterationen im inkrementellen Modus des Wieder-Lernens (nur, wenn Modus = "rolling" oder "incremental", iter wird normal in der Schleife gesetzt).
• seed – bei NULL wird "random seed" verwendet, andernfalls ist der Anfangswert ("seed") fix (wiederholte Berechnungen führen zum gleichen Ergebnis);
• window – Größe des Trainingsfenster (im Modus = "rolling") oder die Anfangsgröße des Trainingsfenster (wenn mode = "incremental");
• increment – Anzahl von Beispielen, die dem Trainingsfenster hinzugefügt werden bei jeder Iteration (wenn mode="incremental" oder mode="rolling").

3.2.1. Klassenausgleich und Vorverarbeitung.

Wir schreiben eine Funktion, die (falls nötig) die Anzahl der Klassen in der Stichprobe and den höheren Wert anpasst, die Stichprobe in eine Trainingsgruppe und eine Testgruppe aufteilt, die Vorverarbeitung (Normalisierung, wenn nötig) durchführt und eine Liste mit den relevanten Gruppen zurückgibt — train, test. Für einen Ausgleich verwenden wir die Funktion caret::upSample(), die Stichproben so verändert, dass die Verteilung in den Klassen gleich ist. Ich muss sagen, dass nicht alle Forscher es notwendig finden, die Klassen auszugleichen. Aber, wie bereits bekannt, ist die Praxis das Kriterium der Wahrheit, und die Ergebnisse meiner vielen Experimente zeigen, dass ausgeglichene Stichproben immer bessere Trainingsergebnisse zeigen. Obwohl, es soll niemanden nicht von weiteren Experimenten abhalten.

Für die Vorverarbeitung verwenden wir die Funktion caret::preProcess(). Die Parameter der Vorverarbeitung werden in der Variablen prepr gesichert. Da das im vorigen Artikel besprochen und angewandt wurde, wird es hier nicht weiter erläutert.

#---7----------------------------------------------------
prepareTrain <- function(x , y, 
                         rati, mod = "stratified", 
                         balance = F, 
                         norm, meth)
{
  require(magrittr)
  require(dplyr)
  t <- rminer::holdout(y = y, ratio = rati,
                       mode = mod)
  train <- cbind(x[t$tr, ], y = y[t$tr])
  if(balance){
    train <- caret::upSample(x = train[ ,best], 
                             y = train$y, 
                             list = F)%>% tbl_df
    train <- cbind(train[ ,best], select(train, y = Class))
  }
  test <- cbind(x[t$ts, ], y = y[t$ts])
  if (norm) {
    prepr <<- caret::preProcess(train[ ,best], method = meth)
    train = predict(prepr, train[ ,best])%>% cbind(., y = train$y)
    test =  predict(prepr, test[ ,best] %>% cbind(., y = test$y))
  }
  DT <- list(train = train,
             test = test)
  return(DT)
}

Ein Kommentar zur Vorverarbeitung: Die Eingabevariablen werden im Bereich (-1, 1) normiert.

3.2.2. Kodierung der Zielvariablen

Zur der Lösung der Klassifikationsaufgabe verwenden wir die Zielvariable, bestehend aus mehreren Ebenen (Klassen). Das Modell verwendet einen Vektor (Spalte), der aus aufeinander folgenden Zuständen des Ziels besteht. Zum Beispiel, y = с("1", "1", "2", "3", "1"). Um ein Neuronales Netzwerk zu trainieren, muss die Zielvariable in eine Matrix umgewandelt werde, die so viele Spalten hat, wie es Klassen gibt. In jeder Zeile dieser Matrix darf nur in einer Spalte eine 1 stehen. Diese Umwandlung zusammen mit der Verwendung der Aktivierungsfunktion softmax() der Ausgabeschicht erlaubt es, die Wahrscheinlichkeiten der Zustände der vorhergesagten Zielvariablen für jede Klasse zu erhalten. Die Funktion classvec2classmat() enthält den Quellcode. Das ist nicht die einzige oder beste Methode, die Zielvariable zu programmierenwir werden sie ihrer Einfachheit wegen verwenden.Die inverse Transformation (Decodierung) der vorhergesagten Werte der Zielvariablen erhalten wir durch eine andere Methode, die wir gleich besprechen werden.

3.3. Trainieren des Modells

3.3.1. Vortraining

Wie bereits erwähnt, erstellen wir zuerst ein tiefes Architektur-Objekt mit dem Namen DArch, die auch standardmäßig die erforderliche Anzahl von RBMs mit den Parametern des Vortraining beinhaltet, und das Neuronale Netzwerk, standardmäßig initialisiert mit zufälligen Gewichten und der Aktivierungsfunktion der Neuronen. Bei der Erstellung des Objektes können, wenn nötig, die Parameter des Vortrainings geändert werden. Danach wird das RBM-Netz ohne Überwachung vortrainiert durch das Übertragen der Trainingsstichprobe (ohne Zielvariable) an die Ausgabe. Nachdem das abgeschlossen ist, erhalten wir DАrch mit den Wichtungen und Bias des RBM-Trainings, die dem Neuronalen Netzwerk übergeben werden. Wir sollten im Voraus die Verteilung der verdeckten Neuronen in Schichten in Form eines Vektors (zum Beispiel) festlegen:

L<- c( 14, 50, 50, 2)

Die Anzahl der Neuronen in der Eingangsschicht ist gleich der Anzahl der Eingangsvariablen. Die beiden verborgene Schichten enthalten jeweils 50 Neuronen, die Ausgabeschicht zwei. Lassen Sie mich das erklären. Hat eine Zielvariable (Faktor) zwei Schichten (Klassen), ist das in der Tat für die Ausgabe ausreichend. Aber die Konvertierung des Vektors in eine Matrix mit zwei Spalten, jede für eine Klasse, erlaubt uns die Aktivierungsfunktion softmaxzu verwenden, die gut die Klassifizierungen der Ausgabeschicht bewältigen kann. Darüber hinaus gibt uns die Ausgabe in Form von Wahrscheinlichkeiten der Klassen zusätzliche Möglichkeiten für eine nachfolgende Analyse der Ergebnisse. Dieses Thema wird in Kürze behandelt.

Die Anzahl der Durchläufe wurde experimentell ermittelt, in der Regel im Bereich von 10 bis 50.

Die Anzahl der Probendurchläufe bleibt normalerweise konstant, aber dieser Parameter kann auch erhöht werden, wenn Sie experimentieren möchten. Es wird in einer eigenen Funktion festgelegt:

#----8--------------------------------------------------------------
pretrainDBN <- function(L, Bs, dS, nE, nCD, InM = 0.5, FinM = 0.9)
{
  require(darch)
# Erstelle das Objekt DArch
  dbn <- newDArch(layers = L, batchSize = Bs, logLevel = 5)
# setze InitialMomentum 
  setInitialMomentum(dbn) <- InM 
# setze FinalMomentum   
  setFinalMomentum(dbn) <- FinM
# setze die Schaltpunkte vom ersten zum letzten    
  setMomentumSwitch(dbn) <- round(0.8 * nE)
  dbn <- preTrainDArch(dbn, dataSet = dS, 
                  numEpoch = nE,
                  numCD = nCD, 
                  trainOutputLayer = T)
  return(dbn)
}

3.3.2. Feinabstimmung

Wie bereits besprochen, verfügt das Paket über diese Funktionen zur Feinabstimmung backpropagation(), rpropagation(), minimizeClassifier(), minimizeAutoencoder(). Die beiden letzten werden nicht berücksichtigt, da sie nicht ausreichend dokumentiert sind, und es keine Anwendungsbeispiele gibt. Diese Funktionen zeigten in meinen Experimenten keine gute Ergebnisse.

Ich möchte auch etwas über die Paket-Aktualisierungen sagen. Als ich anfing diesen Artikel zu schreiben, war die aktuelle Version 0.9, und als er fertig war, erschien Version 0.10 mit zahlreichen Änderungen. Alle Berechnungen mussten erneuert werden. Auf der Basis kurzer Tests kann ich sagen, die Arbeitsgeschwindigkeit hat sich deutlich erhöht, anders als die Qualität der Ergebnisse (aber das ist wohl mehr ein Fehler des Nutzer, denn des Paketes selbst).

Wir betrachten die beiden ersten Funktionen. Die Erste (backpropagation) wird standardmäßig durch das Objekt DАrch bestimmt und verwendet die Parameter des Trainings für das Neuronales Netzwerkes von hier. Die zweite Funktion (rpropagation) hat auch Standardparameter und vier Trainingsmethoden (siehe oben), mit dem Standard "iRprop+". Sie können sich natürlich beide Parameter und die Trainingsmethode ändern. Die Anwendung dieser Funktionen ist einfach: ändern Sie die Funktion der Feinabstimmung in FineTuneDarch()

setFineTuneFunction(dbn) <- rpropagation  

Zusätzlich zu den Einstellungen für die Feinabstimmung, müssen wir (wenn nötig) die Funktion der Aktivierung der Neuronen in jeder Schicht bestimmen. Wir wissen, dass sigmoidUnit standardmäßig für alle Schichten gesetzt ist. Es ist Teil der Pakete sigmoidUnitDerivative, linearUnitDerivative, tanSigmoidUnitDerivative, softmaxUnitDerivative. Die Feinabstimmung wird in einer eigenen Funktion bestimmt, die auch die Wahl der Funktion zur Feinabstimmung ermöglicht. Wir versammeln die möglichen Funktionen der Aktivierung in einer separaten Liste:

actFun <- list(sig = sigmoidUnitDerivative,
               tnh = tanSigmoidUnitDerivative,
               lin = linearUnitDerivative,
               soft = softmaxUnitDerivative)

Wir schreiben eine Funktion zur Feinabstimmung, die zwei Neuronale Netzwerke trainiert und erstellt: erstens — trainieren mit der Funktion backpropagation, zweitens — mittels rpropagation:

#-----9-----------------------------------------
fineMod <- function(variant=1, dbnin, dS, 
                    hd = 0.5, id = 0.2,
                    act = c(2,1), nE = 10)
{
  setDropoutOneMaskPerEpoch(dbnin) <- FALSE
  setDropoutHiddenLayers(dbnin) <- hd
  setDropoutInputLayer(dbnin) <- id
  layers <<- getLayers(dbnin)
  stopifnot(length(layers)==length(act))
  if(variant < 0 || variant >2) {variant = 1}
  for(i in 1:length(layers)){
    fun <- actFun %>% extract2(act[i])
    layers[[i]][[2]] <- fun
  }
  setLayers(dbnin) <- layers
  if(variant == 1 || variant == 2){ # backpropagation
    if(variant == 2){# rpropagation
      #setDropoutHiddenLayers(dbnin) <- 0.0
      setFineTuneFunction(dbnin) <- rpropagation
    }
    mod = fineTuneDArch(darch = dbnin, 
                        dataSet = dS, 
                        numEpochs = nE,
                        bootstrap = T)
    return(mod)
  }
}

Einige Klarstellungen über die formalen Parameter der Funktion.

• variant - Auswahl der Funktion zur Feinabstimmung (1- backpropagation, 2- rpropagation).
• dbnin - Ergebnis des Modells aus dem Vortraining.
• dS - Datensatz für die Feinabstimmung (dataSet).
• hd - Koeffizient der Probenahme (hiddenDropout) in den verdeckten Schichten des Neuronalen Netzwerks.
• id - Koeffizient der Probenahme (inputDropout) in der Eingangsschicht des Neuronalen Netzwerks.
• act - Vektor für die Auswahl der Aktivierung der Neuronen für jede Schicht des Neuronalen Netzwerks. Die Länge des Vektors ist um eine Einheit kürzer als die Anzahl der Schichten.
• nE - Anzahl der Trainingsläufe.

dataSet — eine neue Variable, die in dieser Version erschien. Ich verstehe nicht wirklich den Grund ihrer Erscheinung. Normalerweise hat die Sprache zwei Möglichkeiten die Variablen dem Modell zu übermitteln — mit dem Paar (x, y) oder mit einer Formel (y~., Daten). Die Erscheinung dieser Variablen verbessert nicht die Qualität, sondern verwirrt nur den Benutzer. Aber der Autor mag seine Gründe haben, mir sind sie unbekannt.

3.4. Testen des Modells. Metriken.

Getestet wird das trainierte Modell mit der Testgruppe. Es muss berücksichtigt werden, wir berechnen zwei Metriken: formale Richtigkeit und qualitatives K. Die relevanten Informationen werden weiter unten bereitgestellt. Zu diesem Zweck benötigen wir Daten zweier unterschiedlicher Stichproben, ich erkläre warum. Zum Berechnen der Genauigkeit benötigen wir Werte der Zielvariablen und des ZigZag, der, wie wir erinnern, meistens auf der letzten Bar keinen Wert hat. Daher, die Testgruppe zur Berechnung der Genauigkeit bestimmen wir mit der Funktion prepareTrain(), und den des qualitativen Indikators mit folgender Funktion

#---10-------------------------------------------
prepareTest <- function(n, z, norm, len = 501)
{
  x <- In(p = n ) %>% na.omit %>% extract( ,best) %>% 
    tail(., len)
  CO <- price[ ,"CO"] %>% tail(., len)
  if (norm) {
    x <- predict(prepr,x)
  }
  dt <- cbind(x = x, CO = CO) %>% as.data.frame()
  return(dt)
}

Die Modelle werden auf den letzten 500 Bars der "history" getestet.

Für die tatsächliche Prüfung verwenden wir testAcc() und testBal().

#---11-----
testAcc <- function(obj, typ = "bin"){
  x.ts <- DT$test[ ,best] %>% as.matrix()
  y.ts <- DT$test$y %>% as.integer() %>% subtract(1)
  out <- predict(obj, newdata = x.ts, type = typ) 
  if (soft){out <- max.col(out)-1} else {out %<>% as.vector()}               
  acc <- length(y.ts[y.ts == out])/length(y.ts) %>% 
    round(., digits = 4)
  return(list(Acc = acc, y.ts = y.ts, y = out))
}
#---12-----
testBal <- function(obj, typ = "bin") {
  require(fTrading)
  x <- DT.test[ ,best]
  CO <- DT.test$CO
  out <- predict(obj, newdata = x, type = typ) 
  if(soft){out <- max.col(out)-1} else {out %<>% as.vector()} 
  sig <- ifelse(out == 0, -1, 1)
  sig1 <- Hmisc::Lag(sig) %>% na.omit
  bal <- cumsum(sig1 * tail(CO, length(sig1)))
  K <- tail(bal, 1)/length(bal) * 10 ^ Dig
  Kmax <- max(bal)/which.max(bal) * 10 ^ Dig
  dd <- maxDrawDown(bal)
  return(list(sig = sig, bal = bal, K = K, 
              Kmax = Kmax, dd = dd))
}

Die erste Funktion retourniert Acc und die Werte der (real oder geschätzt) für eine mögliche, spätere Analyse. Die zweite Funktion liefert für den EA das vorhergesagte Signal sig, die erreichte balance auf Basis dieses Signals (bal), den Koeffizienten der Qualität (К), den Maximalwert dieses Koeffizienten in der Testgruppe (Kmax) und dem Maximum Drawdown (dd) in derselben Stichprobe.

Bei der Berechnung der balance darf nicht vergessen werden, dass das Signal sich auf eine zukünftige Bar bezieht, die sich noch nicht gebildet hat und deshalb aus der Berechnung wieder gelöscht werden muss. Wir erreichten das durch eine Verschieben des Vektors sig um eine Bar nach rechts.

3.4.1. Decodierung der Vorhersagen.

Die erhaltenen Ergebnisse können mit der Methode "WTA" dekodiert werden (Konvertierung der Matrix in einen Vektor). Die Klasse entspricht der Spaltennummer mit dem Maximalwert der Wahrscheinlichkeit und der Schwellenwert der Wahrscheinlichkeit kann auf einen Wert unter dem der Klasse, die nicht bestimmt ist.

out <- classmat2classvec(out, threshold = 0.5) 
oder
out <- max.col(out)-1

Wenn der Schwellenwert auf 0.5 gesetzt wird, und die größte Wahrscheinlichkeit in der Spalte ist unter diesem Schwellenwert, erhalten wir eine zusätzliche Klasse ("nicht definiert"). Das sollte bei der Berechnung der Metriken wir Accuracy berücksichtigt werden.

3.4.2. Ergebnisverbesserung der Vorhersage

Ist es möglich, die Vorhersage zu verbessern, nachdem sie empfangen wurde? Es gibt dafür drei Möglichkeiten.

• Kalibrierung

Die Kalibrierung ist die Berechnung des Möglichkeitsbereiches, der den realen Daten am ehesten entspricht. Dazu gibt es eine eigene Funktion im Paket CORElearn:

CORElearn::calibrate(correctClass, predictedProb, class1 = 1,  
                     method = c("isoReg", "binIsoReg", "binning", "mdlMerge"),  
                     weight=NULL, noBins=10, assumeProbabilities=FALSE)

wobei:

• correctClass — Vektor mit den korrekten Bezeichnungen der Klassen der Problem-Klassifikationen;
• predictedProb — Vektor mit der vorhergesagten Klasse 1 (Wahrscheinlichkeit) mit der gleichen Länge wie correctClass;
• method — eine der Folgenden ("isoReg", "binIsoReg", "binning", "mdlMerge"). Für weitere Informationen lesen Sie bitte die Paketbeschreibung;
• weight — Vektor (falls vorhanden), er sollte die gleiche Länge haben wie correctClass, und das Gewicht jeder Beobachtung darstellen, ansonsten sind die Standardgewichte aller Beobachtungen 1;
• noBins — Wert ist abhängig von method und bestimmt die gewünschte oder die anfängliche Anzahl von Kanälen;
• assumeProbabilities — logisch, wenn TRUE, dann wird der Wert von predictedProb im Bereich von [0, 1] erwartet, d. h. eine Wahrscheinlichkeit, andernfalls kann der Algorithmus für eine einfache "Isotonic Regression" verwendet werden.

Diese Methode wird angewendet für eine Zielvariable mit zwei Stufen festgelegt durch einen Vektor.

• Glättung der Vorhersageergebnisse durch Markovketten

Dies ist ein riesiges und komplexes Thema und verdient einen eigenen Artikel, daher werde ich nicht tief in die Theorie eindringen und nur das Wichtigste erklären.

Der Markovprozess  — ist ein stochastischer Prozess mit folgenden Eigenschaften: zu jedem Zeitpunkt t0 gilt, die Wahrscheinlichkeit eines zukünftigen Zustandes hängt ausschließlich vom augenblicklichen Zustand ab und auch nicht davon, wie dieser Zustand erreicht worden ist.

Klassifikation eines zufälligen Markovprozesses:

• diskrete Zustände und diskrete Zeitpunkte (Markovkette);
• kontinuierliche Zustände und diskrete Zeitpunkte (Markovsequenz);
• diskrete Zustände und kontinuierlicher Zeit (kontinuierliche Markovkette);
• kontinuierlicher Zustand und kontinuierliche Zeit.

Hier werden im Weiteren nur Markovprozesse mit diskreten Zuständen S1, S2, ..., Sn. betrachtet.

Markovkette  — zufälliger Markovprozess mit diskreten Zuständen und Zeitpunkten.
Die Zeitpunkte t1, t2, ... zu denen sich der Zustand S des System ändern kann, werden als ein Prozess aufeinander folgender Schritte betrachtet. Es wird nicht die Zeit t , sondern die Schrittnummer 1,2,...,k,... als Argument der Berechnungen verwendet.

Zufallsprozesse werden durch eine Reihe von Zuständen S(0), S(1), S(2), ..., S(k), ... beschrieben, wobei S(0) der Erstzustand ist (vor dem ersten Schritt); S(1) — der Zustand nach dem ersten Schritt; S(k)  — der Zustand des Systems nach der Schrittnummer k.

Die Wahrscheinlichkeiten der Zustände der Markovkette  sind Pi(k) die Wahrscheinlichkeit nach dem k-ten Schritt (und vor dem (k + 1)) das System S ist im Zustand Si(i = 1 , 2 , ..., n) .

Die Anfangsverteilung der Wahrscheinlichkeiten der Markovkette — Verteilung der Wahrscheinlichkeiten der Zustände des Anfangs der Prozesse.
Wahrscheinlichkeit des Übergangs (Übergangswahrscheinlichkeit) im k-ten Schritt vom Zustand Si zum Zustand Sj — Bedingte Wahrscheinlichkeit, dass das System S nach dem k-ten Schritt den Zustand Sj hat, unter der Bedingung, dass es davor im Zustand Si war (nach k—1 Schritt).

Uniforme Markovkette — Markovkette, deren Übergangswahrscheinlichkeit nicht von der Schrittnummer abhängen (von der Zeit), sondern nur zwischen welchen Zuständen der Übergang stattfindet..

Übergangswahrscheinlichkeit einer uniformen Markovkette Рij  bildet eine quadratische Matrix n х n. Die hat folgende Eigenschaften:

1. Jede Zeile beschreibt den gewählten Zustand des Systems und seiner Elemente — Wahrscheinlichkeiten aller möglichen Übergänge in einem Schrittes des gewählten (des i-ten) Zustands.
2. Elemente der Spalten — Wahrscheinlichkeiten aller möglichen Übergänge in einem Schritt des gesetzten (j) Zustands.
3. Die Summe der Wahrscheinlichkeiten jeder Zeile ist 1.
4. Auf der Hauptdiagonale — Wahrscheinlichkeit Рij, dass das System den Zustand Si nicht verlässt, sondern darin verbleibt.

Der Markovprozess kann beobachtbar oder verborgen (hidden) sein. Das Hidden Markov Model (HMM) besteht aus einem Paar diskreter stochastischer Prozesse {St} und {Xt}. Der beobachtbare Prozess {Xt} ist mit einem verborgenen (hidden) Markovprozesss {St} verbunden über eine so genannte bedingte Wahrscheinlichkeit.

Streng genommen ist der beobachtbare Markovprozess von Zuständen (Klassen) unserer Zielzeitreihe ist nicht uniform. Offensichtlich hängt die Wahrscheinlichkeit des Übergangs von einem Zustand zum anderen von der Zeitdauer in dem aktuellen Zustand ab. D. h. während der ersten Schritte ist die Wahrscheinlichkeit einer Zustandsänderungen gering und steigt mit der Zeit. Dieses Modelle ist das so genannten Hidden Semi-Markov Model (HSMM). Wir werden es aber nicht weiter analysieren.

Aber die Idee ist folgende: Basierend auf einer diskreten Reihe von idealen Signalen (Ziele) vom ZigZag finden wir die Parameter des HMM. Dann, nach der Vorhersage der Signale durch das Neuronale Netzwerk, glätten wir sie mit НММ.

Was bringt uns das? Normalerweise gibt es bei der Vorhersage durch Neuronale Netzwerke so genannte "Emissionen", Zustandsveränderung für 1-2 Bars. Wir wissen, dass die Zielvariable nicht von so kurzer Dauer ist. Durch das Modell der Zielvariable über die geschätzte Reihung, können wir höhere Übergangswahrscheinlichkeit erreichen.

Wir verwenden das Paket "mhsmm" zur Berechnung von "Hidden Markov" und "Semi-Markov". Wir verwenden die Funktion smooth.discrete(), die die diskreten Werte der Zeitreihen glättet.

obj <- smooth.discrete(y)

Standardmäßig erhalten wir die geglättete Folge der Zustände am Ende — als wahrscheinlichere Folge von Zuständen unter Verwendung des Viterbi Algorithmus (auch global dekodiert). Es gibt auch eine Möglichkeit, eine anderen Methode der — Glättung zu verwenden, die die individuell wahrscheinlichsten Zustände identifiziert (oder lokal dekodiert).

Eine Standardmethode wird zur Glättung der Zeitreihen angewendet

sm.y <- predict(obj, x = new.y)

• Abstimmung der vorhergesagten Signale der theoretischen Gleichgewichtskurve

Das Konzept ist wie folgt. Mit der Balancelinie können wir die Abweichung vom Mittelwert berechnen. Über diese Abweichungen berechnen wir die Korrektursignale. Ist die Abweichung negativ, deaktiviert sie die Leistung der vorhergesagten Signale oder kehrt sie um. Die Idee ist generell gut, aber es gibt einen Nachteil. Die Bar Null hat ein vorhergesagtes Signal, aber es gibt keinen Balancewert und damit ein Korrektursignal. Es gibt zwei Möglichkeiten, dies Problem zu lösen: durch Klassifizierung — das Korrektursignal auf Basis existierender Korrektursignale und Abweichungen vorhersagen; durch Regression — mit der vorhandenen Abweichungen der gebildeten Bar die Abweichung der neuen Bar schätzen und auf dieser Basis das Korrektursignal bestimmen. Es gibt eine einfachere Lösung, wir nehmen das Korrektursignal der neuen Bar einfach auf Basis der bereits gebildeten Bar.

Da die oben genannten Methoden bereits bekannt und getestet sind, versuchen wir, sie zu implementieren und die Möglichkeiten der Markovketten zu nutzen. Das Paket "markovchain" erschien vor kurzem mit einer Reihe von Funktionen, die es ermöglichen, mit den beobachteten diskreten Prozessen die Parameter des Hidden-Markov-Modell zu bestimmen und dann zukünftige Zustände über mehrere Bars in die Zukunft zu projizieren. Die Idee entstammt diesem Artikel.

3.4.3. Metriken

Zur Bewertung der Qualität der Vorhersage des Modells verwenden wir die ganze Bandbreite von Metriken (Genauigkeit, AUC, ROC und andere). Im vorigen Artikel habe ich erwähnt, dass in unserem Fall mit den formalen Metriken eine Qualität nicht definiert werden kann Das Ziel eines Expert Advisors ist ein maximalen Gewinn bei einem akzeptablen Drawdown. Zu diesem Zweck wurde der Qualitätsindikator K eingeführt, und er zeigt den durchschnittlichen Gewinn in Points je Bar in einem fixen Zeitraum von der Länge N. Er wird berechnet, indem der kumulative Return (sig, N) durch die Länge des Zeitraumes N dividiert wird. Die Genauigkeit wird nur als Richtwert berechnet werden.

Schließlich führen wir Berechnungen durch und die erhalten die Testergebnisse:

• Ausgabedaten. Wir haben bereits die Matrix der Preise, price[] , als Ergebnis der Funktion price.OHLC()  erhalten. Sie enthält die Durchschnittspreise und die Preise der Bars. Alle Ausgabedaten können über das "Icon" erhalten werden, das in der Anlage von Rstudio ist.

# Finde Konstanten  
n = 34; z = 37; cut = 0.9; soft = TRUE. 
# Finde Vorverarbeitungsmethode  
method = c("center", "scale","spatialSign")
# Bilde die Anfangsstichprobe
data.f <- form.data(n = n, z = z)
# finde die wichtigen Kennzeichen 
best <- prepareBest(n = n, z = z, cut = cut, norm = T, method) 
# Berechnung, sie dauert ungefähr 3 Minuten mit einem 2-Kernelprozessor. Sie können diese Stufe überspringen, wenn Sie mögen, 
# und verwende alle Kennzeichen in der Zukunft. Daher kommentieren Sie die vorherige Zeile und
# 'ent-kommentieren' Sie die beiden unteren.
# data.f <- form.data(n = n, z = z)
# best <- colnames(data.f) %>% head(., ncol(data.f) - 1)
# Vorbereitung der Daten für das Training des Neuronalen Netzwerkes
DT <- prepareTrain(x = data.f[ , best],
                   y = data.f$y,
                   balance = TRUE,
                   rati = 501, mod = "stratified",
                   norm = TRUE, meth = method) 

# Lade die benötigte Bibliothek
require(darch)
require(foreach)
# Identifiziere die verfügbaren Funktionen für die Aktivierung
actFun <- list(sig = sigmoidUnitDerivative,
               tnh = tanSigmoidUnitDerivative,
               lin = linearUnitDerivative,
               soft = softmaxUnitDerivative)
# Konvertiere die Zielvariable
if (soft) { y <- DT$train$y %>% classvec2classmat()} # into matrix
if (!soft) {y = DT$train$y %>% as.integer() %>% subtract(1)} # to vector with values [0, 1]
# Erstelle dataSet für das Training
dataSet <- createDataSet(
  data = DT$train[ ,best] %>% as.matrix(), 
  targets = y ,
  scale = F
)
# Identifiziere die Konstanten des Neuronalen Netzwerkes
# Anzahl der Neuronen der Eingangsschicht (ist gleich der Anzahl der Kennzeichen)
nIn <- ncol(dataSet@data)
# Anzahl der Neuronen in der Ausgabeschicht 
nOut <- ncol(dataSet@targets)
# Vektor mit einer Anzahl von Neuronen in jeder Schicht des Neuronalen Netzes
# Falls eine andere Struktur des Neuronalen Netzes verwendet wird, sollte dieser Vektor umgeschrieben werden
Layers = c(nIn, 2 * nIn , nOut)
# Andere Daten in Bezug zum Training
Bath = 50
nEp = 100
ncd = 1
# Vortraining des Neuronalen Netzes
preMod <- pretrainDBN(Layers, Bath, dataSet, nEp, ncd)
# Zusätzliche Parameter für die Feinabstimmung
Hid = 0.5; Ind = 0.2; nEp = 10
# Trainiere zwei Modelle, eines mit backpropagation, das andere mit rpropagation
# dies ist nur, um die Ergebnisse zu vergleichen
model <- foreach(i = 1:2, .packages = "darch") %do% {
  dbn <- preMod
  if (!soft) {act = c(2, 1)}
  if (soft) {act = c(2, 4)}
  fineMod(variant = i, dbnin = dbn, 
          hd = Hid, id = Ind,
          dS = dataSet, act = act, nE = nEp)
}
# Test, um Accuracy zu erhalten
resAcc <- foreach(i = 1:2, .packages = "darch") %do% {
  testAcc(model[[i]]) 
}
# Vorbereiten der Stichprobe, um den Qualitätskoeffizient zu testen
DT.test <- prepareTest(n = n, z = z, T)
# Test
resBal <- foreach(i = 1:2, .packages = "darch") %do% {
  testBal(model[[i]]) 
}

Sehen wir und die Ergebnis an:

> resAcc[[1]]$Acc
[1] 0.5728543
> resAcc[[2]]$Acc
[1] 0.5728543

Es ist gleich schlecht für beide Modelle.

Aber der Qualitätskoeffizient:

> resBal[[1]]$K
[1] 5.8
> resBal[[1]]$Kmax
[1] 20.33673
> resBal[[2]]$Kmax
[1] 20.33673
> resBal[[2]]$K
[1] 5.8

Er zeigt die gleiche, gute Leistung. Jedoch ist der große Drawdown irgendwie beunruhigend:

> resBal[[1]]$dd$maxdrawdown
[1] 0.02767

Versuchen wir, das durch ein Korrektursignal aus der nachfolgenden Berechnung zu korrigieren:

bal <- resBal[[1]]$bal
# Signal der letzten 500 Bars
sig <- resBal[[1]]$sig[1:500]
# Mittelwert aus der Balancelinie
ma <- pracma::movavg(bal,16, "t")
# Momentum des Mittelwertes 
roc <- TTR::momentum(ma, 3)%>% na.omit
# Abweichung der Balancelinie vom Durchschnitt
dbal <- (bal - ma) %>% tail(., length(roc))
# Summe der beiden Vektoren
dbr <- (roc + dbal) %>% as.matrix()
# Berechnen des Korrektursignals
sig.cor <- ifelse(dbr > 0, 1, -1) # sign(dbr) gives the same result
# Ergebnissignal
S <- sig.cor * tail(sig, length(sig.cor))
# Balance des Ergebnissignals
Bal <- cumsum(S * (price[ ,"CO"]%>% tail(.,length(S))))
# Qualitätskoeffizient des korrigierten Signals
Kk <- tail(Bal, 1)/length(Bal) * 10 ^ Dig
> Kk
[1] 28.30382

Die gezeigte Qualität des Ergebnisses des korrigierten Signals ist sehr gut. Mal sehen, wie die Linien dbal, roc und dbr, verwendet für die Berechnung des Korrektursignals, im Linienchart aussehen.

matplot(cbind(dbr, dbal, roc), t="l", col=c(1,2,4), lwd=c(2,1,1))
abline(h=0, col=2)
grid()

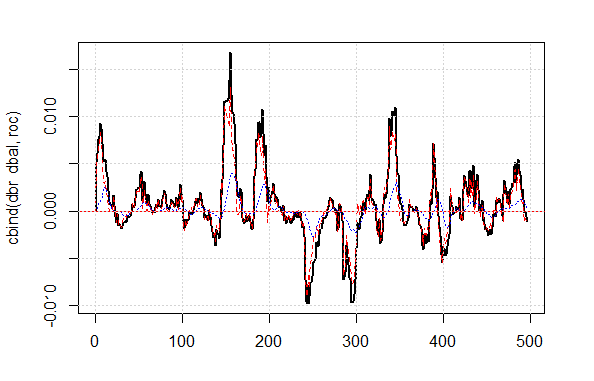
Fig.4 Abweichung der Balancelinie vom Durchschnitt

Balancelinie vor und nach der Signalkorrektur zeigt Fig. 5.

plot(c(NA,NA,NA,Bal), t="l")
lines(bal, col= 2)
lines(ma, col= 4)

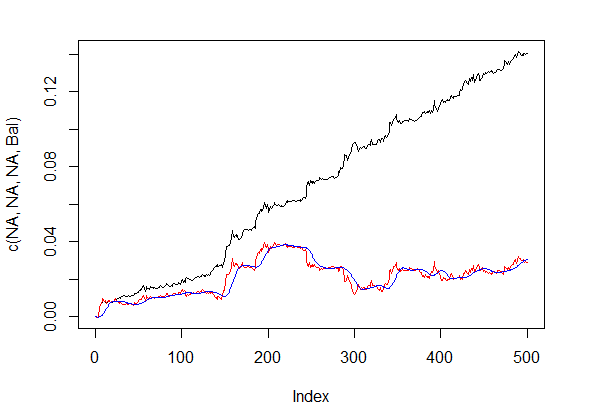
Fig.5 Balancelinie vor und nach der Signalkorrektur

Wir haben also den vom Neuronalen Netz vorhergesagten Wert des Signals für die Bar Null, aber nicht dessen Korrekturwert. Wir wollen das Hidden-Markov-Modell für die Vorhersage dieses Signals verwenden. Basierend auf den beobachteten Zuständen des Korrektursignals identifizieren wir die Parameter des Modells mit den Werten der letzten Zustände, um so die Zustände der nächsten, zukünftigen Bar vorherzusagen. Zuerst schreiben wir die Funktion correct(), die das Korrektursignal berechnet, um dann das resultierende Signal und qualitativen Indikatoren zu prognostizieren. Mit anderen Worten, wir konzentrieren, was wir oben ausgeführt haben, in einer Berechnung.

Ich möchte klarstellen: Das "Signal" in dem Artikel ist eine Folge ganzer Zahlen: -1 oder 1. Der "Zustand" ist eine Folge der ganzen Zahlen 1 und 2 entsprechend den Signalen. Für die gegenseitige Konvertierungen verwenden wir diese Funktionen:

#---13----------------------------------
        sig2stat <- function(x) {x %>% as.factor %>% as.numeric}
        stat2sig <- function(x) ifelse(x==1, -1, 1)
        #----14--correct-----------------------------------
        correct <- function(sig){
          sig <- Hmisc::Lag(sig) %>% na.omit
          bal <- cumsum(sig * (price[ ,6] %>% tail(.,length(sig))))
          ma <- pracma::movavg(bal, 16, "t")
          roc <- TTR::momentum(ma, 3)%>% na.omit
          dbal <- (bal - ma) %>% tail(., length(roc))
          dbr <- (roc + dbal) %>% as.matrix()
          sig.cor <- sign(dbr)
          S <- sig.cor * tail(sig, length(sig.cor))
          bal <- cumsum(S * (price[ ,6]%>% tail(.,length(S))))
          K <- tail(bal, 1)/length(bal) * 10 ^ Dig
          Kmax <- max(bal)/which.max(bal) * 10 ^ Dig
          dd <- fTrading::maxDrawDown(bal)
          corr <<- list(sig.c = sig.cor, sig.res = S, bal = bal, Kmax = Kmax, K = K, dd = dd)
          return(corr)
         }

Um den Signalvektor mit der Vorhersage für die nächste Bar zu erhalten, verwenden wir das Paket "markovchain" und die Funktion pred.sig().

#---15---markovchain----------------------------------
pred.sig <- function(sig, prev.bar = 10, nahead = 1){
          require(markovchain)
        # Transformiere das beobachtete Korrektursignal in Zustände  
          stat <- sig2stat(sig)
        # Berechne die Modellparameter
        # wenn das Modell noch nicht in der Umgebung existiert       
          if(!exists('MCbsp')){
             MCbsp <<- markovchainFit(data = stat, 
                                method = "bootstrap",
                                nboot = 10L,
                                name="Bootstrap MС")
         }
        # Setze die notwendigen Konstanten
          newData <- tail(stat, prev.bar)
          pr <- predict(object = MCbsp$estimate, 
                                newdata = newData,
                                n.ahead = nahead)
        # Übertrage das vorhergesagte Signal zum Eingangssignal
          sig.pr <- c(sig, stat2sig(pr))
          return(sig.pr = sig.pr)
}

Jetzt müssen wir nur noch das resultierende Signal für einen Expert Advisor bereitstellen:

sig <- resBal[[1]]$sig
sig.cor <- correct(sig)
sig.c <- sig.cor$sig.c
pr.sig.cor <- pred.sig(sig.c)
sig.pr <- pr.sig.cor$sig.pr
# Der resultierende Signalvektor für den Expert Advisor 
S <- sig.pr * tail(sig, length(sig.pr))

• Glättung des vorhergesagten Signals.

Wir schreiben eine Funktion, die das diskrete Signal mit dem Modell der Hidden-Markov-Kette glättet. Dazu verwenden wir das Paket "mhsmm".

#---16---smooth------------------------------------
smoooth <- function(sig){
# Glättung des vorhergesagten Signals
# bestimme die Parameter der Hidden-Markov-Kette
# Wenn noch kein Modell in dieser Umgebung existiert
    require(mhsmm)
    if(!exists('obj.sm')){
         obj.sm <<- sig2stat(sig)%>% smooth.discrete()
    }
# Glätten des Signals mit dem erhaltenen Modell
    sig.s <- predict(obj.sm, x = sig2stat(sig))%>% 
             extract2(1)%>% stat2sig()
# Berechne die Balance mit dem geglätteten Signal
     sig.s1 <- Hmisc::Lag(sig.s) %>% na.omit
     bal <- cumsum(sig.s1 * (price[ ,6]%>% tail(.,length(sig.s1))))
     K <- tail(bal, 1)/length(bal) * 10 ^ Dig
     Kmax <- max(bal)/which.max(bal) * 10 ^ Dig
     dd <- fTrading::maxDrawDown(bal)
     return(list(sig = sig.s, bal = bal, Kmax = Kmax, K = K, dd = dd))
}

Wir berechnen und vergleichen die Balance auf Basis der vorhergesagten und geglätteten Signale.

sig <- resBal[[1]]$sig
sig.sm <- smoooth(sig)
plot(sig.sm$bal, t="l")
lines(resBal[[1]]$bal, col=2)

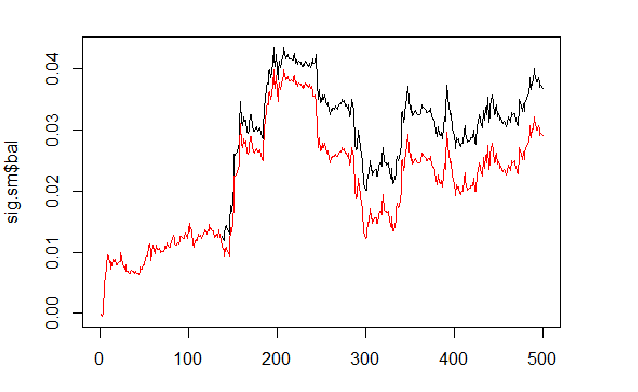
Fig.6 Balance auf Basis der vorhergesagten und geglätteten Signale

Wie wir sehen können, hat sich die Qualität etwas verbessert, aber der Drawdown ist geblieben. So würden wir die Methode in unserem Expert Advisor nicht verwenden.

sig.sm$dd
$maxdrawdown
[1] 0.02335
$from
[1] 208
$to
[1] 300

4. Struktur des Algorithmus des EAs

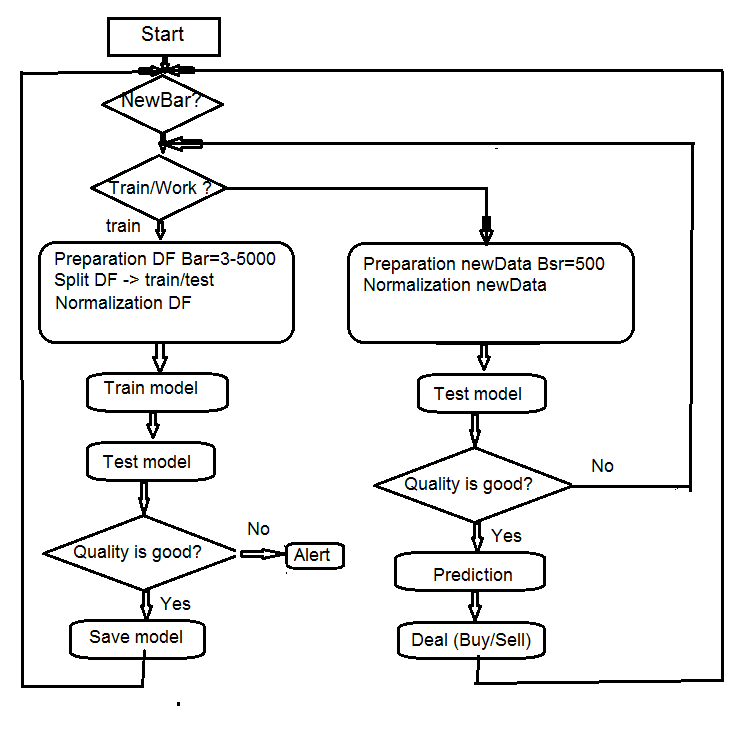
Fig.7 Struktur des Algorithmus des EAs

4.1. Beschreibung der Arbeitsweise des Expert Advisors

Da der Expert Advisor mit zwei Datenströmen (MMS und Rterm) arbeitet, beschreiben wir den Prozess Ihrer Interaktion. Wir erläutern einzeln die Arbeitsweise jedes Datenstroms.

4.1.1 MQL

Nachdem der Expert Advisor auf dem Chart gestartet wurde:

In der Funktion init()

• Überprüfen wir die Einstellungen des Terminals (DLL-Verfügbarkeit, die Berechtigung zum Handel);
• Setzen den Timer;
• Starten Rterm;
• Berechnen und übertragen der benötigten Konstanten für die Arbeit mit dem R-Process;
• Prüfung, ob Rterm arbeitet, wenn nicht - Alert();
• Beenden von init().
  

In der Funktion deinit()

• Beenden des Timers;
• Löschen der Grafikobjekte;
• Stopp Rterm.

In der Funktion onTimer()

• Prüfung, ob Rterm arbeitet;
• Wenn Rterm nicht belegt ist und es eine neue Bar gibt (LastTime != Time[0]):
• Festlegen der "Depth of History" abhängig davon, ob das der Erststart des Expert Advisors ist;
• Bilden von vier Vektoren der Kurse (Open, High, Low, Close) und ihre Übertragung an Rterm;
• Starten des Skriptes und gehen Sie, ohne auf die Ergebnisse zu warten;
• Setze get_sig = true;
• Setze LastTime= Time[0].
  
• Ansonsten, wenn Rterm läuft, nicht blockiert ist, und get_sig = true:
• Bestimmung der Länge des Vektors sig, den wir von Rterm erhalten müssten;
• Anpassung der Länge des erhaltenen Vektors an die Länge der Quelle. Bei einem Fehler beendet sich Rprocess;
• Erhalt der Reihe der Signale (Vektor);
• Festlegen, was auf Grund des letzten Signals geschehen soll (BUY, SELL, Nichts);
• Erhalten wir ein reales Signal, nicht ERR, setzen wir get_sig=false.
  
• Der Rest ist Standard:
• CheckForClose()
• CheckForOpen()

Unser Experte ist jetzt nur ein "Arbeiter", der die Aufträge ausführt, die vom "Denker" übertragen werden, er überwacht den Zustand der offenen Positionen und das Auftreten von Fehlern während ihrer Eröffnung und er leistet all die anderen Dinge eines standardmäßigen Expert Advisors.

4.1.2 Rterm

Dieses Skript besteht aus zwei Teilen. Der erste Teil wird beim Erststart ausgeführt, der zweite — im Weiteren.

• Wenn first:
• Die benötigten Bibliothek herunterladen (wenn nötig) und in der Umgebung von Rterm installieren;
• Bestimmen der benötigten Funktionen;
• Erstellen der Kursmatrix;
• Vorbereiten der Daten der Stichprobe für das Training und das Testen;
• Erstelle das Trainingsmodell;
• Testen des Modells;
• Berechnen der Signale für die Leistungsfähigkeit;
• Prüfe die Qualität der Vorhersage. Ist es größer oder gleich dem Minimum — fortfahren. Sonst — sende Warnung.
• Wenn !first:
• Vorbereiten der Daten der Stichprobe für das Testen und die Vorhersage;
• Testen des Modells mit neuen Daten;
• Berechnen der Signale für die Leistungsfähigkeit;
• Prüfe die Qualität der Vorhersage. Ist es größer oder gleich dem Minimum — fortfahren. Sonst — setzen wir first = TRUE, d.h. wir forcieren ein neues Training des Modells.

4.2. Selbstkontrolle und Selbsttraining

Die Qualitätskontrolle des vorhergesagten Signals durch den Koeffizienten K. Es gibt zwei Wege, die Grenzen der akzeptablen Qualität festzustellen. Erstens — einen kleinsten Wert des Koeffizienten in Relation zu seinem Maximum festlegen. Wenn К < Kmax * 0.8, dann sollten wir das Training wiederholen oder den Expert Advisor stoppen. Zweitens — ein Mindestwert von К, sodass dessen Erreichen dieselbe Aktion auslöst. Unser Expert Advisor verwendet die zweite Methode.

5. Installation und Programmstart

Dem Artikel sind zwei Expert Advisors beigefügt: e_DNSAE.mq4 und e_DNRBM.mq4. Beide verwenden dieselben Daten und praktisch die gleichen Funktionen. Der Unterschied liegt allein im verwendeten Modell des tiefen Netzwerkes. Der erste EA verwendet DN, initiiert SAE und das Paket "deepnet". Die Beschreibungen der Pakete finden sich im vorherigen Artikel über tiefe Neuronale Netzwerke. Der zweite EA verwendet DN, initiiert RBM und das Paket "darch".

Standardpfade der Dateien:

• *.mq4 im Ordner ~/MQL4/Expert
• *.mqh im Ordner ~/MQL4/Include
• *.dll im Ordner ~/MQL4/Libraries
• *.r im Ordner C:/RData

Das Setzen des Pfads für die Sprache R und die Skripte (in beiden mq4: #define und *.r: source() ).

Wird der Expert Advisor das erste Mal gestartet, lädt er die notwendigen Bibliotheken aus dem Internet und kopiert sie in die lokale Umgebung für Rterm. Sie können sie auch in Übereinstimmung mit der beigefügten Liste selbst installieren.

Als allgemeine Regel gilt, der R-Prozess "stoppt", weil ihm die notwendigen Bibliotheken fehlen, weil die Pfade in den Skripten falsch angegeben wurden und nur in letzter Instanz - wegen eines Syntaxfehler im Skript.

Die Screenshots der Sessions mit den Originaldaten sind separate beigefügt, Sie können sie mit Rstudio öffnen und überprüfen, ob alles funktioniert, aber auch die Experimente durchführen.

6. Mittel und Wege der Verbesserung der Indikatoren.

Es gibt ein paar Möglichkeiten, die Qualität der Indikatoren zu verbessern.

• Bewertung und Auswahl der Prädiktoren — nutze genetische Algorithmen zur Optimierung (GA).
• Bestimme die optimalen Parameter der Prädiktoren und der Zielvariablen — GA.
• Bestimme die optimalen Parameter des Neuronales Netzes — GA.

Diese Maßnahmen helfen, die Qualität der Indikatoren erheblich zu verbessern.

Schlussfolgerung

Experimente mit dem Paket "darch" zeigten folgenden Ergebnisse.

• Das tiefe Neuronale Netz, initiiert durch RBM, sind schlechter als SAE. Schlechte Nachrichten für uns.
• Das Netzwerk ist schnell trainiert.
• Das Paket hat ein großes Potenzial zur Verbesserung der Qualität der Vorhersage durch die Zugriffsmöglichkeiten auf fast alle internen Parameter des Modells.
• Das Paket ermöglicht die Verwendung entweder eines Neuronalen Netzes oder eines RBM mit einer sehr breiten Palette von Optionen in Bezug zu anderen Standardmethoden.
• Das Paket wird ständig weiterentwickelt und der Entwickler verspricht die Einführung zusätzlicher Eigenschaften in der nächsten Version.
• Wie vom Autor versprochen wurde von МТ4/МТ5 die Verwendung der Sprache R und der Zugriff auf ihre Pakete und Funktionen ermöglicht und das eröffnet die Möglichkeit, die neuesten Algorithmen ohne zusätzliche DLL zu verwenden.

Dateianhänge

1. R Session des Prozesses Sess_DNRBM_GBPUSD_30
2. Zip-Datei mit dem "e_DNRBM" Expert Advisor
3. Zip-Datei mit dem "e_DNSAE" Expert Advisor