Tiefe Neuronale Netzwerke (Teil VII). Ensembles von Neuronalen Netzen: Stacking
940
0
Inhalt
- Einführung
- 1. Vorbereiten der Eingabedaten für die trainierbaren Kombinatoren
- 2. Grundsättzliches Vergleichsmodell
- 3. Keras/TensorFlow Bibliotheken. Allgemeine Beschreibung und Installation
- 4. Der Kombinator der Ausgabe des Bagging-Ensembles — Neuronales Netz
- 5. Analyse der experimentellen Ergebnisse
- Schlussfolgerung
- Anlagen
Einführung
Modelle der Basisebene des Ensembles (einzelne Klassifikatoren) werden mit einem kompletten Set trainiert. Dann wird das Metamodell mit den Ensemble-Ausgaben trainiert, die während der Vorhersage basierend auf dem Testset erhalten wurden. In diesem Fall werden die Ausgänge der Basisklassifikatoren des Ensembles zu den Eingangsdaten des neuen trainierten Klassifikators, der selbst ein Kombinator ist. Dieser Ansatz wird "komplexe Kombination" oder "Verallgemeinerung durch Lernen" genannt, häufiger einfach "stacking".
Eines der Hauptprobleme dieses Kombinators ist der Aufbau eines Trainingssets für den Metaklassifikator.
Experimentieren wir mit dem Bau und der Erprobung von Ensembles mit Stacking. Diese werden ein Ensemble der neuronalen Netzwerk-Klassifikatoren von ELM mit den früher erhaltenen, optimalen Hyperparametern verwenden. Die Ausgänge des bereinigten Ensembles werden im ersten Experiment verwendet, alle Eingänge des Ensembles im zweiten Experiment. Als Kombinatoren werden beide Varianten über vollständig verbundene neuronale Netze verfügen, jedoch mit unterschiedlichen Strukturen. In zukünftigen Experimenten werden wir prüfen, wie sich Multimodalität und Multitasking auf die Qualität der Klassifizierung neuronaler Netze auswirken.
Zur Abschätzung der Vorhersagequalität in diesen Varianten werden Basisvergleichsmodelle verwendet.
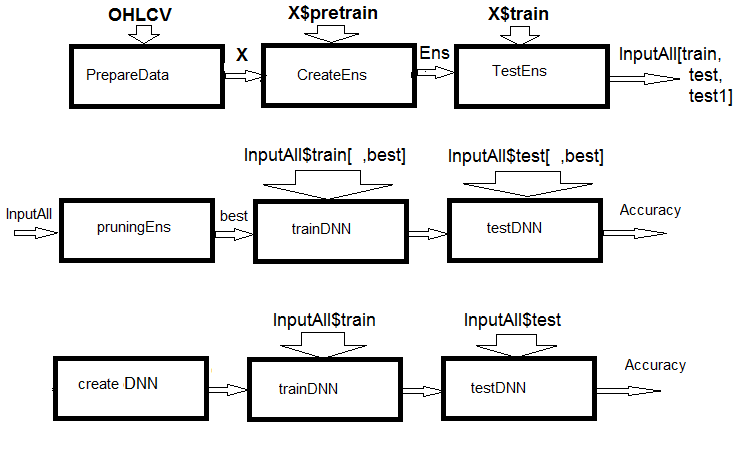
Abb. 1. Schema der Berechnungen
Wie man der Abbildung entnehmen kann, besteht das Experiment aus drei Teilen.
- Wir bereiten die Eingangsdaten für das Ensemble vor, trainieren das ELM-Ensemble und erhalten die Vorhersagen für train/test/test1 sets. Diese Sets dienen als Eingänge für InputAll des trainierbaren Kombinators.
- Bereinigen wir das Ensemble: Wir wählen die besten ELM-Vorhersagen nach der Wichtigkeit der Informationen. Wir testen die Basisvergleichsmodule, um Referenzmetriken zu erhalten, trainieren und testen die DNN mit diesen Daten, berechnen die Metriken der Modelle und vergleichen sie mit den Metriken des Basismodells.
- Wir erstellen ein multimodales und multitasking neuronales Netzwerk, trainieren es und testen es auf den InputAll-Sets. Wir Berechnen die Metriken der erhaltenen Modelle und vergleichen diese mit den Metriken des Basismodells.
1. Aufbereitung der Eingabedaten für den trainierbaren Kombinator
Für die Experimente wird die R-Version 3.4.4 verwendet. Sie enthält einige neue Pakete, die wir noch nicht verwendet haben.
Wir starten RStudio. Dann laden wir die Datei Cotir.RData mit den Kursen des Terminals von GitHub/Part_I und die Dateien Importar.R, Libary.R, FunPrepareData_VII.R, FUN_Stacking.R mit Datenaufbereitungsfunktionen von GitHub/Part_VII. Achtung: Die Reihenfolge, in der die Datei geladen werden, ist wichtig! Ich habe die Funktionen leicht modifiziert, um Berechnungen zu beschleunigen und die Lesbarkeit der Skripte zu verbessern. Auch eine Reihe von Prädiktoren ist für die Experimente erforderlich.
Wir verwenden die gleichen Kurse und teilen sie in die gleichen Muster wie in den vorherigen Artikeln dieser Serie. Schreiben wir ein Skript zur Vorbereitung der Ausgangsdaten. Die Berechnungsdetails werden nicht mehr berücksichtigt - sie wurden bereits beschrieben. Die Änderungen beziehen sich auf die Verwendung des Pakets dplyr und den Import der Pakete und Funktionen in die Arbeitsumgebung. dplyr ist ein sehr nützliches Paket, das die Datenmanipulation erleichtert. Es gibt aber manchmal Überraschungen beim Debuggen, die viele Stunden der Fehlersuche in Anspruch nehmen.
Lassen Sie mich das klarstellen. Beim Laden der Bibliothek dplyr erscheinen folgende Warnungen in der Konsole:
> library(dplyr) Attaching package: ‘dplyr’ The following objects are masked from ‘package:stats’: filter, lag The following objects are masked from ‘package:base’: intersect, setdiff, setequal, union
Ein Konflikt der Funktionsnamen ist offensichtlich. Um das Problem zu lösen, war es notwendig, das Paket, aus dem eine bestimmte Funktion aufgerufen wird, explizit anzugeben. Zum Beispiel dplyr::filter(), dplyr::lag. Das zweite Problem: Oft werden nur ein oder zwei Funktionen aus dem Paket benötigt, aber es ist notwendig, die gesamte Bibliothek zu laden. Und bestimmte Pakete (z.B. caret) sind umfangreich und rufen abhängige Paketen, die wir nicht benötigen. In diesem Sinne ist der Stil für den Import von Funktionen und Paketen in Python logischer. Zum Beispiel:
from theano import function, config, shared, tensor import numpy as np import time
In der ersten Zeile werden eine Reihe von Funktionen aus dem Paket theano importiert, in der zweiten Zeile wird das Paket numpy als np bezeichnet, und in der dritten - das Paket time geladen. Das Gleiche ist in R im Paket importar implementiert, das nur zwei Funktionen hat - import() und import_fun(). Das erste ermöglicht den Import von Paketen, das zweite dient dem Import von Funktionen. Das erste musste jedoch in import_pack() umbenannt werden, damit es nicht mit reticulate::import() kollidiert.
Zusätzlich wurden neue Variablen eingeführt, die für die Experimente notwendig sind. Wir erzeugen zwei Datensätze - data1 und data2 und ordnen ihre Prädiktoren nach der Wichtigkeit der Informationen.
Nachfolgend gibt es ein Skript zur Vorbereitung der ersten Daten für die Experimente. Es ist in der Datei Prepare.R verfügbar.
#--0--Library------------- # source(file = "importar.R") # source(file = "Library.R") # source(file = "FunPrepareData_VII.R") # source(file = "FUN_Stacking.R") #--1-prepare---- evalq({ # combine quotes OHLCV, Med, Typ, W into data frame # calculate the predictors and the target dt <- PrepareData(Data, Open, High, Low, Close, Volume) # split the initial data into pretrain/train/val/test DT <- SplitData(dt$feature, 4000, 1000, 500, 250, start = 1) # define the parameters of outliers pre.outl <- PreOutlier(DT$pretrain) # impute the outliers in all sets DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) # set the method for normalizing the predictors meth <- "spatialSign" #"expoTrans" "range" "spatialSign", # define the normalization parameters preproc <- PreNorm(DTcap$pretrain, meth = meth, rang = c(-0.95, 0.95)) # normalize the predictors in all sets DTcap.n <- NormData(DTcap, preproc = preproc) }, env)
Im Block 0 (Bibliothek) laden wir die notwendigen Bibliotheken und Funktionen. Vier Dateien mit den Skripten sollten in der angegebenen Reihenfolge geladen werden. In Block 1 (vorbereiten), erstellen wir die Prädiktoren und normalisieren diese, indem wir die Ausreißer entfernen. Die Normalisierungsmethode kann geändert werden.
Wie bilden nun zwei Datensätze - data1 und data2. Im ersten Satz werden digitale Filter und ihre Unterschiede erster Ordnung als Prädiktoren verwendet, und das Vorzeichen der Veränderung der Differenz erster Ordnung im Zickzack dient als Ziel. Im zweiten Satz werden die Prädiktoren die Differenzen erster Ordnung der Kurse von High/Low/Clos und die Differenzen der Kurse CO/HO/LO/HL sein, während die Differenz erster Ordnung des ZigZag das Ziel sein wird. Das Skript ist unten aufgeführt und ist in der Datei Prepare.R verfügbar.
#--2-Data X------------- evalq({ foreach(i = 1:length(DTcap)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, ftlm, stlm, rbci, pcci, fars, v.fatl, v.satl, v.rftl, v.rstl,v.ftlm, v.stlm, v.rbci, v.pcci, Class)} -> data1 X1 <- vector(mode = "list", 4) foreach(i = 1:length(X1)) %do% { data1[[i]] %>% dp$select(-c(Data, Class)) %>% as.data.frame() -> x data1[[i]]$Class %>% as.numeric() %>% subtract(1) -> y list(x = x, y = y)} -> X1 list(pretrain = X1[[1]] , train = X1[[2]] , test = X1[[3]] , test1 = X1[[4]] ) -> X1 }, env) #----------------- evalq({ foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, CO, HO, LO, HL, dC, dH, dL)} -> data2 X2 <- vector(mode = "list", 4) foreach(i = 1:length(X2)) %do% { data2[[i]] %>% dp$select(-Data) %>% as.data.frame() -> x DT[[i]]$dz -> y list(x = x, y = y)} -> X2 list(pretrain = X2[[1]] , train = X2[[2]] , test = X2[[3]] , test1 = X2[[4]] ) -> X2 }, env)
Ordnen wir die Prädiktoren in beiden Sätzen in absteigender Reihenfolge ihrer Informationsbedeutung an. Schauen wir uns an, wie sie geordnet sind. Das Skript ist unten aufgeführt und ist in der Datei Prepare.R verfügbar.
#---3--bestF----------------------------------- #require(clusterSim) evalq({ orderF(x = X1$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") %$% stopri[ ,1] -> orderX1 }, env) colnames(env$X1$pretrain$x)[env$orderX1] [1] "v.fatl" "v.rbci" "v.ftlm" "fars" "v.satl" "stlm" [7] "rbci" "ftlm" "v.stlm" "v.rftl" "pcci" "v.rstl" [13] "v.pcci evalq({ orderF(x = X2$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") %$% stopri[ ,1] -> orderX2 }, env) colnames(env$X2$pretrain$x)[env$orderX2] [1] "dC" "CO" "HO" "LO" "dH" "dL" "HL"
Von besonderem Interesse ist die Reihenfolge der Kursprädikatoren.
Um die Eingabedaten für die Kombinatoren aufzubereiten, ist es notwendig:
- Ein ELM-Ensemble zu erstellen und es mit dem X1$pretrain Trainingsset zu trainieren;
- Eine Vorhersage des Sets X1$train mit dem trainierten Ensemble zu machen. Dies ist das Trainingsset InputTrain.
- Eine Vorhersage des Sets X1$test mit dem trainierten Ensemble zu machen. Dies ist das Testset InputTest;
- eine Vorhersage des Sets X1$test1 mit dem trainierten Ensemble zu machen. Dies ist das Testset InputTest1.
Wir definieren die Variablen und Konstanten, schreiben die Funktionen createEns() und GetInputData() - es wird der Wert aller Ausgänge des Ensembles zurückgegeben. Die Werte der createEns() Funktionsparameter wurden bereits erreicht nach Optimierung des Ensembles. Sie könnten jetzt andere Werte haben. Das folgende Skript befindet sich in der Datei FUN_Stacking().
#----Library------------- import_fun(rminer, holdout, holdout) #source(file = "FunPrepareData_VII.R") #----Input------------- evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear n <- 500 #---createENS---------------------- createEns <- function(numFeature = 8L, r = 7L, nh = 5L, fact = 7L, order, X){ # determine the indices of the best predictors bestF <<- order %>% head(numFeature) # choose the best predictors for the training set Xtrain <- X$pretrain$x[ , bestF] #setMKLthreads(1) k <- 1 rng <- RNGseq(n, 12345) #---creste Ensemble--- Ens <<- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } return(Ens) } #---GetInputData -FUN----------- GetInputData <- function(Ens, X){ #---predict-InputTrain-- Xtest <- X$train$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> predEns #[ ,n] #---predict--InputTest---- Xtest1 <- X$test$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest1) } -> InputTest #[ ,n] #---predict--InputTest1---- Xtest2 <- X$test1$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest2) } -> InputTest1 #[ ,n] #---res------------------------- return(list(InputTrain = predEns, InputTest = InputTest, InputTest1 = InputTest1)) } }, env)
Wir erstellen ein Ensemble und berechnen die Eingaben der trainierbaren Kombinators:
#---4--createEns---------------- evalq({ Ytrain <- X1$pretrain$y Ytest <- X1$train$y Ytest1 <- X1$test$y Ytest2 <- X1$test1$y Ens <- vector(mode = "list", n) createEns(order = orderX1, X = X1) -> Ens GetInputData(Ens, X1) -> res }, env)
Ergebnisstruktur:
> env$res %>% str() List of 3 $ InputTrain: num [1:1001, 1:500] 0.811 0.882 0.924 0.817 0.782 ... $ InputTest : num [1:501, 1:500] 0.5 0.383 0.366 0.488 0.359 ... $ InputTest1: num [1:251, 1:500] 0.32 0.246 0.471 0.563 0.451 ...
2. Grundsättzliches Vergleichsmodell
Es entstehen zwei trainierbare Kombinatoren. Der eine ersetzt die Mittelwertbildung der Ausgänge der besten neuronalen Netze des Ensembles, der zweite die Bereinigung und die Mittelwertbildung. Daher werden für beide Optionen Noten für die Klassifizierungsqualität benötigt.
Ensemble neuronaler Netze
Für die erste Option wird das ELM-Ensemble mit den optimalen Parametern das Basis-Vergleichsmodell sein.
Da die zweite Option über 500 Eingänge verfügt, wird das Paket varbvs verwendet. Es bietet schnelle Algorithmen zur Auswahl der Bayes'schen Modelle zur Auswahl der Variablen und zur Berechnung der Bayes'schen Koeffizienten, wobei das Ergebnis mittels linearer oder logistischer Regression modelliert wird. Diese Algorithmen basieren auf den im Artikel "Scalable variational inference for Bayesian variable selection in regression, and its accuracy in genetic association studies" beschriebenen Variationsannäherungen. Diese Software wurde für die Arbeit mit großen Datensätzen mit mehr als einer Million Variablen und Tausenden von Stichproben verwendet.
Für die erste Option, schreiben wir die zusätzliche Funktionen getBest(), testAver(), testVot() und berechnen die Metriken. Die Funktionen sind in der Datei FUN_Stacking.R verfügbar.
evalq({
getBest <- function(Ens, x, y, nb){
n <- length(Ens)
foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
predict(Ens[[i]], newdata = x)} -> y.pr
foreach(i = 1:n, .combine = "c") %do% {
median(y.pr[ ,i])} ->> th
foreach(i = 1:n, .combine = "c") %do% {
ifelse(y.pr[ ,i] > th[i], 1, 0) -> Ypred
Evaluate(actual = y, predicted = Ypred)$Metrics$F1 %>%
mean()
} -> Score
Score %>% order(decreasing = TRUE) %>% head(2*nb + 1) -> best
y.pr[ ,best] %>%
apply(1, sum) %>%
divide_by(length(best)) %>%
median() -> med
return(list(Score = Score, bestNN = best, med = med))
}
testAver <- function(Ens, x, y, best, med){
n <- length(Ens)
foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:%
when(i %in% best) %do% {
predict(Ens[[i]], newdata = x)} %>%
apply(1, sum) %>% divide_by(length(best)) -> ensPred
ifelse(ensPred > med, 1, 0) -> clAver
Evaluate(actual = y, predicted = clAver)$Metrics[ ,2:5] %>%
round(3) -> Score
return(list(Score = Score, Ypred = ensPred, clAver = clAver))
}
testVot <- function(Ens, x, y, best){
n <- length(Ens)
foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:%
when(i %in% best) %do% {
predict(Ens[[i]], newdata = x)} %>%
apply(2, function(x) ifelse(x > th[i], 1, -1)) %>%
apply(1, function(x) sum(x)) -> vot
ifelse(vot > 0, 1, 0) -> ClVot
Evaluate(actual = y, predicted = ClVot)$Metrics[ ,2:5] %>%
round(3) -> Score
return(list(Score = Score, Ypred = ClVot))
}
}, env)
Diese Funktionen wurden bereits besprochen. Deshalb werden wir nicht weiter darauf eingehen. Ihre Ergebnisse sind jedoch erwähnenswert.
- Die Funktion getBest() liefert die Metriken (Score), die Indizes der besten einzelnen Klassifikatoren des Ensembles (bestNN), den Median der gemittelten Ausgabe des Ensembles (med), der beim Testen des Modells verwendet wird. Der Medianvektor th[500] aller Ausgänge des Ensembles wird in die Umgebung eingefügt.
- Die Funktion testAver() liefert die Metriken (Score), die gemittelte kontinuierliche Vorhersage des Ensembles (Ypred) und die nominale Vorhersage des Ensembles (clAver) zurück.
- Die Funktion testVot() gibt die Metriken (Score) und die nominale Vorhersage des Ensembles (Ypred) zurück.
Testen wir das erstellte Ensemble mit zwei Testsets mit Mittelwertbildung und Mehrheitsabstimmung und sehen uns dann die Metriken an.
#--2---test---- evalq({ Ytrain <- X1$pretrain$y Ytest <- X1$train$y Ytest1 <- X1$test$y Ytest2 <- X1$test1$y Ens <- vector(mode = "list", n) Ens <- createEns(order = orderX1, X = X1) #---3------ resBest <- getBest(Ens, x = X1$train$x[ , bestF], y = Ytest, nb = 3) #---4--averaging--- ScoreAver <- testAver(Ens, x = X1$test$x[ , bestF], y = Ytest1, best = resBest$bestNN, med = resBest$med) ScoreAver1 <- testAver(Ens, x = X1$test1$x[ , bestF], y = Ytest2, best = resBest$bestNN, med = resBest$med) #---5--voting---- ScoreVot <- testVot(Ens, x = X1$test$x[ , bestF], y = Ytest1, best = resBest$bestNN) ScoreVot1 <- testVot(Ens, x = X1$test1$x[ , bestF], y = Ytest2, best = resBest$bestNN) }, env) > env$ScoreAver$Score Accuracy Precision Recall F1 0 0.75 0.708 0.778 0.741 1 0.75 0.794 0.727 0.759 > env$ScoreAver1$Score Accuracy Precision Recall F1 0 0.753 0.750 0.826 0.786 1 0.753 0.758 0.664 0.708 > env$ScoreVot$Score Accuracy Precision Recall F1 0 0.752 0.702 0.800 0.748 1 0.752 0.808 0.712 0.757 > env$ScoreVot1$Score Accuracy Precision Recall F1 0 0.741 0.739 0.819 0.777 1 0.741 0.745 0.646 0.692
Gute Leistung bei beiden Testsets. Im Folgenden wird bei der Analyse der Ergebnisse der Klassifizierungsfehler in bias/variance/noise zerlegt und der Beitrag jeder Komponente zum Gesamtfehler geschätzt.
Für die zweite Option (500 Eingaben) ist das Skript zum Training des Modells unten aufgeführt. Sie befindet sich in der Datei varb.R.
library(varbvs) evalq({ vr <- varbvs(X = res$InputTrain, Z = NULL, y = Ytest, family = "binomial", optimize.eta = TRUE, logodds = seq(-6,-2, 0.25), nr = 250, initialize.params = TRUE, maxiter = 1e5, verbose = FALSE) summary(vr, cred.int = 0.95, nv = 7, nr = 1e5) %>% print() }, env) Summary of fitted Bayesian variable selection model: family: binomial num. hyperparameter settings: 17 samples: 1001 iid variable selection prior: yes variables: 500 fit prior var. of coefs (sa): yes covariates: 1 fit approx. factors (eta): yes maximum log-likelihood lower bound: -579.4602 Hyperparameters: estimate Pr>0.95 candidate values sa 8.09 [7.63,8.54] NA--NA logodds -2.26 [-2.75,-2.00] (-6.00)--(-2.00) Selected variables by probability cutoff: >0.10 >0.25 >0.50 >0.75 >0.90 >0.95 3 3 3 3 3 3 Top 7 variables by inclusion probability: index variable prob PVE coef* Pr(coef.>0.95) X18 18 X18 1.00000 NA 4.529 [+3.861,+5.195] X5 5 X5 1.00000 NA 1.955 [+1.543,+2.370] X255 255 X255 1.00000 NA 2.097 [+1.537,+2.660] X109 109 X109 0.00948 NA -1.033 [-2.008,-0.057] X404 404 X404 0.00467 NA -0.665 [-1.350,+0.024] X275 275 X275 0.00312 NA -0.726 [-1.735,+0.286] X343 343 X343 0.00299 NA -0.604 [-1.353,+0.149] *See help(varbvs) about interpreting coefficients in logistic regression.
Unter Verwendung der erhaltenen Modells berechnen wir die Vorhersage mit den beides Sets und die Metriken.
env$vr$pip %>% order() %>% tail(7) -> bestNN_vr evalq({ predict(vr, res$InputTest) -> pr.vr1 Evaluate(actual = Ytest1, predicted = pr.vr1)$Metrics[ ,2:5] %>% round(3) -> metr.test confus(table(Ytest1, pr.vr1)) -> cm1 predict(vr, res$InputTest1) -> pr.vr2 Evaluate(actual = Ytest2, predicted = pr.vr2)$Metrics[ ,2:5] %>% round(3) -> metr.test1 confus(table(Ytest2, pr.vr2)) -> cm2 }, env) > env$metr.test Accuracy Precision Recall F1 0 0.78 0.750 0.783 0.766 1 0.78 0.808 0.779 0.793 > env$metr.test1 Accuracy Precision Recall F1 0 0.729 0.765 0.732 0.748 1 0.729 0.689 0.726 0.707
Das Ergebnis ist ausgezeichnet, viel besser als die Metrik des Ensembles.
Alle Daten, die für die Fortsetzung der Experimente benötigt werden, stehen bereit.
Da die Bibliotheken keras / tensorflow in Zukunft verwendet werden sollen, werden sie im Folgenden kurz besprochen.
3. Keras/TensorFlow libraries. Allgemeine Beschreibung und Installation
Der stark wachsende Bereich der tiefen neuronalen Netze wurde durch eine Reihe von Open-Source-Bibliotheken ergänzt. Dazu gehören - TensorFlow(Google), CNTK(Microsoft), Apache MXNet und viele andere. Da alle diese und andere wichtige Softwareentwickler Mitglieder des R-Konsortiums sind, sind alle diese Bibliotheken mit APIs für R ausgestattet.
Alle oben genannten Bibliotheken sind "low-level". Sie sind für Anfänger schwer zu erlernen und zu verwenden. In diesem Sinne entwickelte das Team des Rstudios das Paket keras für R.
Keras ist eine High-Level-API für neuronale Netzwerke. Das Paket ist so konzipiert, dass es die Möglichkeit bietet, schnell Prototypen zu erstellen und die Leistung eines Modells experimentell zu testen. Hier sind die wichtigsten Merkmale von Keras:
- Ermöglichen eines gleichmäßige Arbeiten auf einer CPU oder GPU.
- Es git eine benutzerfreundliche API, die die Erstellung von Prototypen von tiefen Lernmodellen auf einfache Weise ermöglicht.
- Eingebaute Unterstützung für "convolutional networks" (für Computer Vision), "recurrent networks" (für Verarbeitungssequenzen) und beliebige Kombinationen davon.
- Unterstützt beliebige Netzwerkarchitekturen: Modelle mit mehreren Eingängen oder mehreren Ausgängen, Layer-Sharing, Model-Sharing, etc. Dies bedeutet, dass Keras im Wesentlichen geeignet ist, um ein beliebiges tiefes Lernmodell zu erstellen, von einem Speichernetzwerk bis zu einer Neuronalen Turing-Maschine.
- Es kann auf mehreren Backends arbeiten, darunter TensorFlow, CNTK oder Theano.
Keras ist ein API für Menschen, nicht für Maschinen. Das Paket reduziert die kognitive Belastung: Es bietet konsistente und einfache APIs, minimiert die Anzahl der Benutzeraktionen und gibt ein effektives Feedback über Benutzerfehler. All dies macht Keras einfach zu erlernen und zu bedienen. Aber das bedeutet keine Verringerung der Flexibilität: Da Keras die Low-Level-Sprachen des tiefen Lernens integriert (insbesondere TensorFlow), erlaubt es Ihnen, alles zu implementieren, was Sie in der Basissprache erstellen können.
Sie können ein Keras Modell mit Hilfe von mehreren tiefen Lernmodulen entwickeln. Jedes Keras-Modell, das nur eingebettete Layer verwendet, kann ohne Änderungen zwischen all diesen Backends übertragen werden: Sie können ein Modell mit einem Backend trainieren und in ein anderes Backend laden. Verfügbare Backends sind u.a:
- TensorFlow Backend (von Google)
- CNTK Backend (von Microsoft)
- Theano Backend
Man kann ein Modell von Keras auf verschiedenen Hardwareplattformen laufen lasen, nicht nur auf der CPU:
- NVIDIA GPUs
- Google TPUs, über das Backend TensorFlow und Google Cloud
- GPUs mit OpenCL, wie die von AMD, über das Keras Backend PlaidML
Installation des Backends von Keras und Tensorflow
Keras und TensorFlow können so konfiguriert werden, dass sie auf einer CPU oder GPU arbeiten. Die CPU-Version ist viel einfacher zu installieren und einzurichten, daher ist es die beste Wahl, um mit dem Paket zu beginnen. Hier sind die Handbücher für die CPU und GPU Versionen von der TensorFlow Website:
- TensorFlow nur mit CPU-Unterstützung. Wenn Ihr System über keinen NVIDIA® Grafikprozessor verfügt, müssen Sie diese Version installieren.
- TensorFlow mit GPU-Unterstützung. TensorFlow Programme laufen normalerweise deutlich schneller auf einer GPU als auf einer CPU. Wenn Ihr System über einen NVIDIA® Grafikprozessor verfügt, der alle Voraussetzungen erfüllt und Sie leistungskritische Anwendungen ausführen müssen, sollten Sie diese Version installieren.
Die einzige unterstützte Installationsmethode unter Windows ist "conda". Das bedeutet, dass Sie Anaconda 3.x (Python 3.5.x/3.6.x) für Windows vor der Installation von Keras installieren sollten. Ich habe Anaconda3(Python3.6) installiert.
Installieren Sie zunächst das Paket keras von CRAN:
install.packages("keras")
Das Interface Keras R verwendet standardmäßig TensorFlow. Um sowohl die Hauptbibliothek Keras als auch das TensorFlowBackend zu installieren, verwenden Sie die Funktion install_keras ():
# default installation library(keras) install_keras()
So werden die CPU-Versionen von Keras und TensorFlow installiert. Wenn Sie ein benutzerdefiniertes Setup benötigen - zum Beispiel mit einem NVIDIA Grafikprozessor, sehen Sie in der Dokumentation. Um TensorFlow einer bestimmten Version oder mit GPU-Unterstützung zu installieren, gehen Sie wie folgt vor:
# install with GPU version of TensorFlow # (NOTE: only do this if you have an NVIDIA GPU + CUDA!) install_keras(tensorflow = "gpu") # install a specific version of TensorFlow install_keras(tensorflow = "1.5") install_keras(tensorflow = "1.5-gpu")
Für weitere Details, siehe hier.
Das Unterstützungspaket tfruns ist für Experimente mit TensorFlow konzipiert. Dies ist ein Toolkit zur Verwaltung von TensorFlow Training und Experimenten von R.
- Verfolgen Sie die Hyperparameter, Metriken, Ausgabedaten und den Quellcode jedes Trainingslaufs.
- Vergleichen Sie Hyperparameter und Metriken über mehrere Läufe hinweg, um das leistungsstärkste Modell zu finden.
- Automatische Generierung von Berichten zur Visualisierung einzelner Trainingsläufe oder Vergleiche zwischen den Läufen.
- Es sind keine Änderungen am Quellcode notwendig (Die Startdaten werden automatisch für alle Modelle von Keras und tfestimators erfasst).
Die beste Visualisierungsqualität des Trainingsprozessen des DNNs und der Ergebnisse bietet TensorBoard.
Experten des tiefen Lernens erhalten die Gelegenheit direkt mit der low-level Bibliothek von TensorFlow unter Verwendung des Pakets tensorflow zu arbeiten.
Alle diese Pakete basieren auf dem Hauptpaket reticulate, das eine R-Schnittstelle zu den Modulen, Funktionen und Klassen von Python ist. Beim Aufruf von Python werden R-Datentypen automatisch in ihre entsprechenden Python-Typen umgewandelt. Die von Python zurückgegebenen Werte werden wieder in R-Typen umgewandelt.
Alle diese Pakete sind gut dokumentiert, mit zahlreichen Beispielen versehen und werden ständig weiterentwickelt. Dies macht es möglich, die fortschrittlichsten Modelle des tiefen Lernens (DNN, RNN, CNN, LSTM, VAE, etc.), Verstärkungslernen (RL) und viele andere Python Entwicklungen in den Experten und Indikatoren des Terminals zu verwenden. Die einzige Einschränkung ist das Wissen und die Erfahrung des Entwicklers.
Hier sind noch zwei weitere interessante Pakete, die es zu beachten gilt: kerasR und kerasformel. Es gibt Tests für die erste, die eine höhere Arbeitsgeschwindigkeit als die des Originals "tensorflow-1.5" bestätigen. Die zweite bietet eine vereinfachte Version des Modells unter Verwendung einer Formel.
Dieser Artikel soll nur Beispiele für einen einfachen Einstieg in ein neues Feld geben. Seine Aufgabe ist es nicht, die ganze Vielfalt der Möglichkeiten abzudecken und eine hohe Qualitätsnoten des Modells zu erreichen.
Vor Beginn der Experimente ist zu prüfen, ob Python installiert ist und ob R mit ihm interagiert.
> library(reticulate)
> py_config()
python: K:\Anaconda3\envs\r-tensorflow\python.exe
libpython: K:/Anaconda3/envs/r-tensorflow/python36.dll
pythonhome: K:\ANACON~1\envs\R-TENS~1
version: 3.6.5 | packaged by conda-forge | (default, Apr 6 2018, 16:13:55)
[MSC v.1900 64 bit (AMD64)]
Architecture: 64bit
numpy: K:\ANACON~1\envs\R-TENS~1\lib\site-packages\numpy
numpy_version: 1.14.2
tensorflow: K:\ANACON~1\envs\R-TENS~1\lib\site-packages\tensorflow
python versions found:
K:\Anaconda3\envs\r-tensorflow\python.exe
K:\ANACON~1\python.exe
K:\Anaconda3\python.exe
Schauen wir, wie diese Version von tensorflow arbeitet:
> library(tensorflow) > tf_config() TensorFlow v1.5.1 (K:\ANACON~1\envs\R-TENS~1\lib\site-packages\tensorflow) Python v3.6 (K:\Anaconda3\envs\r-tensorflow\python.exe)
Alles ist bereit, um mit den Experimenten fortzufahren.
4. Der Kombinator der Ausgabe des Bagging-Ensembles — Neuronales Netz
Führen wir zwei Experimente durch. Im ersten Fall verwenden wir die Funktion softmax, anstatt die besten Ergebnisse des Ensembles zu mitteln. Im zweiten Fall ersetzen wir die Bereinigung und die Mittelwertbildung durch ein neuronales Netz, das alle 500 Ausgänge des Ensembles als Eingang speist. Das Strukturschema des Experiments ist in der folgenden Abbildung dargestellt.
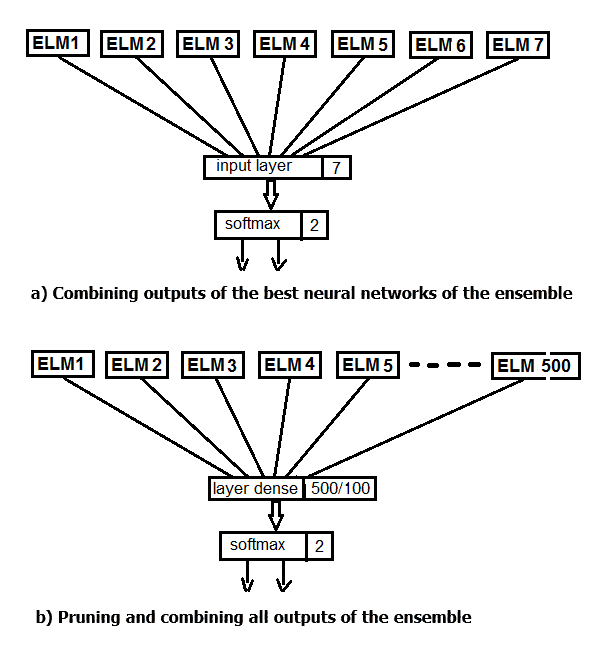
Abb. 2. Ersatz der Mittelung der Ausgabe des Ensembles mit einem Neuronalen Netz
Die Hauptdatenstruktur in Keras ist ein Modell, eine Art, Ebenen zu organisieren. Der einfachste Typ ist ein Sequentielles Modell, das einen linearen Stapel von Schichten darstellt.
Wir erstellen zunächst ein einfaches sequentielles Modell und fügen es mit dem Operator pipe (%>%) dem Layer hinzu. Wir erstellen für das erste Experiment ein neuronales Netzwerk, das nur aus der Ein- und Ausgabeschicht besteht. Die Ausgänge des Ensembles nach der Bereinigung, die mit dem Testset erhalten wurden, werden als Input zugeführt. 20% des Trainingssets werden für die Validierung verwendet. Das Erstellen, Trainieren und Testen von neuronalen Netzen in diesem Paket ist extrem einfach.
Wir stellen die konstanten Parameter des Modells ein und definieren die Trainings- und Testsets für den DNN.
#===========Keras=========================================== library(keras) num_classes <- 2L batch_size <- 32L epochs <- 300L #--------- bestNN <- env$resBest$bestNN x_train <- env$res$InputTrain[ ,bestNN] y_train <- env$Ytest %>% to_categorical() x_test <- env$res$InputTest[ ,bestNN] y_test <- env$Ytest1 %>% to_categorical() x_test1 <- env$res$InputTest1[ ,bestNN] y_test1 <- env$Ytest2 %>% to_categorical()
Erstellen wir das Modell. Der Skriptcode ist unten aufgeführt. Wir definieren und kompilieren ein Modell mit der Struktur NN(7, 2) - 7 Neuronen am Eingang und 2 am Ausgang. Optimierer - die "rmsprop"-Funktion, Verlustfunktion - 'binäre'_Crossentropie', Metriken für die Testergebnisse - "Genauigkeit".
##----model--keras------------------------- # define model model <- keras_model_sequential() # add layers and compile model %>% layer_dense(units = num_classes, input_shape = dim(x_train)[2]) %>% layer_activation(activation = 'softmax') %>% compile( loss = 'binary_crossentropy', optimizer = optimizer_rmsprop(), metrics = 'accuracy' )
Wir trainieren und testen das Modell (das Skript ist weiter unten). Wir speichern die Trainingshistorie. Zusätzlich legen wir fest:
- Es ist nicht notwendig, das Ergebnis jeder Iteration an das Terminal auszugeben;
- Es ist nicht notwendig, Echtzeit-Charts im Viewer/Rstudio anzuzeigen;
- Es ist notwendig, die Eingabedaten nach jeder Trainingsepoche zu mischen.
Für die Validierung verwenden wir 20% des Trainingssets.
## Training & Evaluation --------------------------- # Fit model to data model %>% fit( x_train, y_train, batch_size = batch_size, epochs = epochs, verbose = 0, view_metrics = FALSE, shuffle = TRUE, validation_split = 0.2) -> history # Output metrics score <- model %>% evaluate(x_test, y_test, verbose = 0) cat('Test loss:', score[[1]] %>% round(3), '\n') Test loss: 0.518 cat('Test accuracy:', score[[2]] %>% round(3), '\n') Test accuracy: 0.754 #--------------- score1 <- model %>% evaluate(x_test1, y_test1, verbose = 0) cat('Test loss:', score1[[1]] %>% round(3), '\n') Test loss: 0.55 cat('Test accuracy:', score1[[2]] %>% round(3), '\n') Test accuracy: 0.737
Die quantitativen Ergebnisse sind nicht schlecht, sie sind virtuell gleich den gemittelten Ergebnissen des Ensembles. Schauen wir uns den Trainingsablauf und die Tests dieses Modells an:
#--plot------------------------
plot(history)
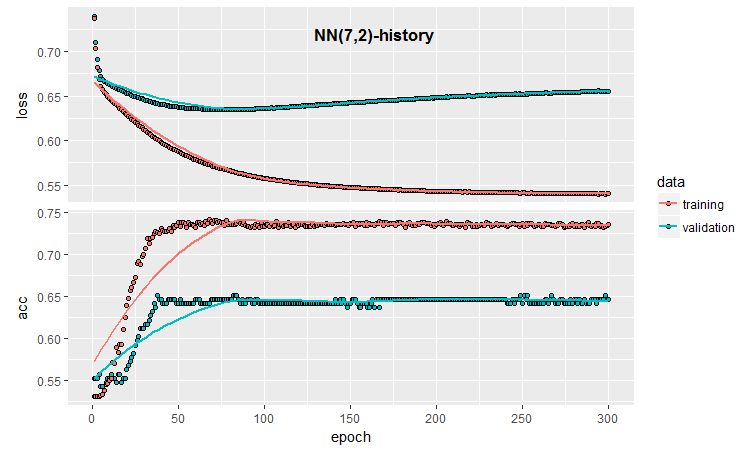
Abb. 3. Model Trainingsablauf (7, 2)
Die Grafik zeigt, dass das Modell nach 30 Epochen deutlich überangepasst ist, und nach 50 Epochen erreicht die Genauigkeit ein Plateau.
Wie Sie sich erinnern, ist der Prozess der Initialisierung des neuronalen Netzwerks zufällig. Das heißt, jedes neu erstellte, trainierte und getestete Modell führt zu unterschiedlichen Ergebnissen.
Selbst in dieser minimalen Konfiguration eines neuronalen Netzes gibt es viele Möglichkeiten, die Klassifizierungsqualität und die Überpassung zu beeinflussen. Hier sind einige davon: frühes Beenden (early stopping); Neuroneninitialisierungsmethode; Regularisierung der Aktivierungsfunktion, etc. Davon werden wir nur das frühzeitige Beenden, das Hinzufügen von Rauschen zu den Eingabedaten, die Regularisierung der Aktivierungsfunktion und die Ausgabe einer detaillierteren grafischen Darstellung der Trainingsergebnisse überprüfen. Um dies zu tun, verwenden wir die Fähigkeit, einen Callback während des Trainings anzuwenden, bereitgestellt von keras.
callback_early_stopping(monitor = "val_loss", min_delta = 0, patience = 0, verbose = 0, mode = c("auto", "min", "max")) callback_tensorboard(log_dir = NULL, histogram_freq = 0, batch_size = 32, write_graph = TRUE, write_grads = FALSE, write_images = FALSE, embeddings_freq = 0, embeddings_layer_names = NULL, embeddings_metadata = NULL)
Definieren der Callback-Funktion.
early_stopping <- callback_early_stopping(monitor = "val_acc", min_delta = 1e-5, patience = 20, verbose = 0, mode = "auto") log_dir <- paste0(getwd(),"/run_1") tensboard <- callback_tensorboard(log_dir = log_dir, histogram_freq = 1, batch_size = 32, write_graph = TRUE, write_grads = TRUE, write_images = FALSE)
In der ersten haben wir angegeben, dass es notwendig ist, den Genauigkeitswert zu beobachten. Wird dieser Wert kleiner als min_delta in patiente Epochen, dann sollte das Training abgebrochen werden. Im zweiten Schritt legen wir den Pfad zu dem Verzeichnis fest, in dem die Trainingsergebnisse für das spätere Playback gespeichert werden sollen, und geben auch an, wo genau sie gespeichert werden sollen. Schreiben wir ein komplettes Skript mit diesen Funktionen und schauen uns das Ergebnis an.
##=====Variant earlystopping================================= #--prepare data-------------------------- library(reticulate) library(keras) py_set_seed(12345) num_classes <- 2L batch_size <- 32L learning_rate <- 0.005 epochs <- 100L #--------- bestNN <- env$resBest$bestNN x_train <- env$res$InputTrain[ ,bestNN] y_train <- env$Ytest %>% to_categorical() x_test <- env$res$InputTest[ ,bestNN] y_test <- env$Ytest1 %>% to_categorical() x_test1 <- env$res$InputTest1[ ,bestNN] y_test1 <- env$Ytest2 %>% to_categorical() ##----model--keras------------------------- # define model model <- keras_model_sequential() # add layers and compile model %>% layer_gaussian_noise(stddev = 0.05, input_shape = dim(x_train)[2], name = "GN") %>% layer_dense(units = num_classes, name = "dense1") %>% layer_activation_softmax(name = "soft") %>% layer_activity_regularization(l2 = 1.0, name = "reg") %>% #l1 = 0.01, compile( loss = 'binary_crossentropy', optimizer = optimizer_rmsprop(lr = learning_rate, decay = 0.01), metrics = 'accuracy' ) ## Training & Evaluation --------------------------- # Fit model to data model %>% fit( x_train, y_train, batch_size = batch_size, epochs = epochs, verbose = 0, view_metrics = TRUE , shuffle = TRUE, validation_split = 0.2, callbacks = list(early_stopping, tensboard)) -> history
Die Metriken von zwei Testsets und dem Trainingsablauf mit der frühen Beendigung.
# Output metrics > score <- model %>% evaluate(x_test, y_test, verbose = 0) > cat('Test loss:', score[[1]] %>% round(3), '\n') Test loss: 0.539 > cat('Test accuracy:', score[[2]] %>% round(3), '\n') Test accuracy: 0.756 > #--------------- > score1 <- model %>% evaluate(x_test1, y_test1, verbose = 0) > cat('Test loss:', score1[[1]] %>% round(3), '\n') Test loss: 0.571 > cat('Test accuracy:', score1[[2]] %>% round(3), '\n') Test accuracy: 0.713
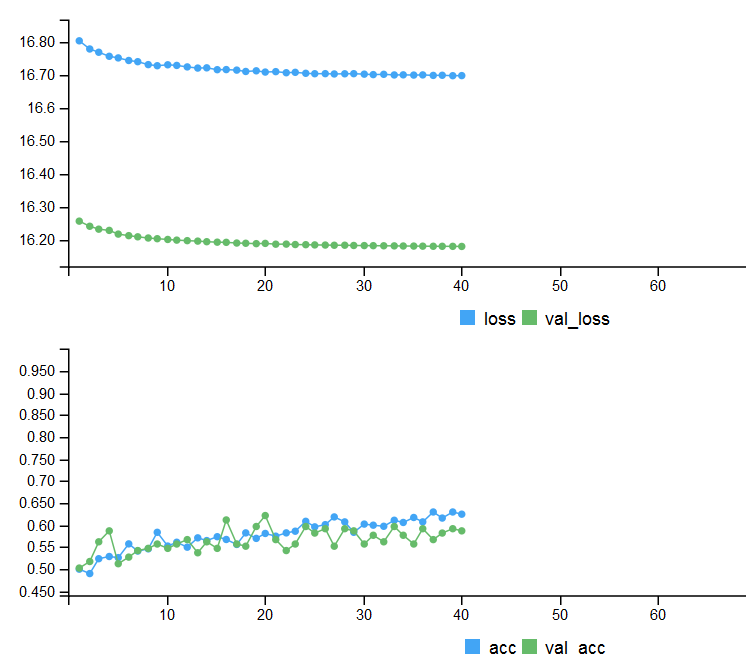
Abb. 4. Trainingsablauf mit früher Beendigung
Um eine detaillierte grafische Information des Trainingsablaufs des Neuronalen Netzes anzuzeigen, verwenden wir die Möglichkeiten von tensorboard:
> tensorboard(log_dir = log_dir) TensorBoard 1.7.0 at http://127.0.0.1:7451 (Press CTRL+C to quit) Started TensorBoard at http://127.0.0.1:7451
Der Browser öffent eine Seite, auf der alle internen Details des Neuronalen Netzes angezeigt werden. Hier sind einige beispielhafte Bildschirmfotos:
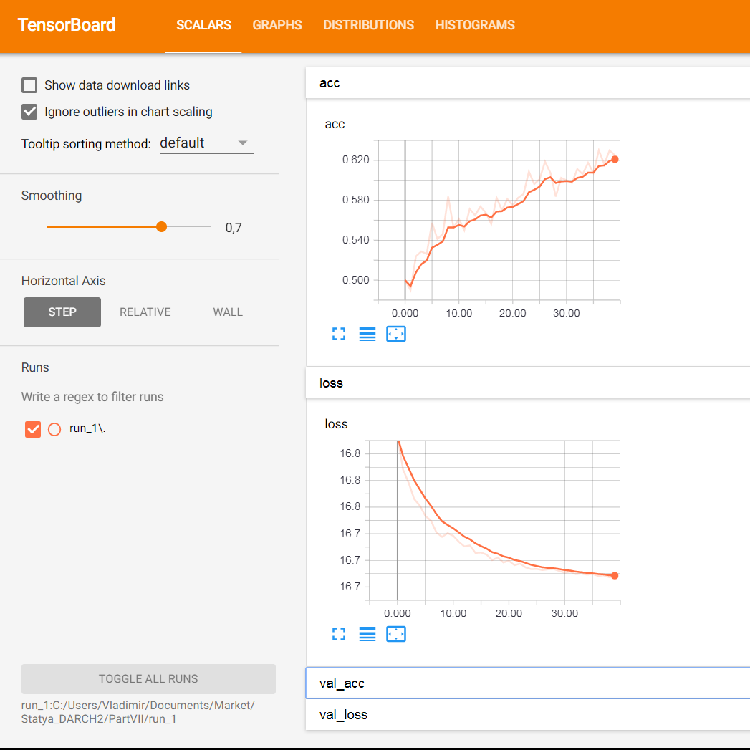
Abb. 5. Die Grafiken von Verlust (loss) und Genauigkeit (acc) des Trainings mit dem Trainingsset und der Validierung mit val_acc und val_loss
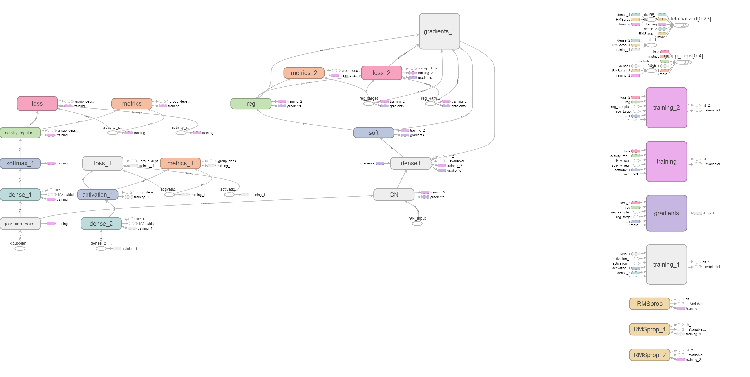
Abb. 6. Das Diagramm des Computernetzwerk
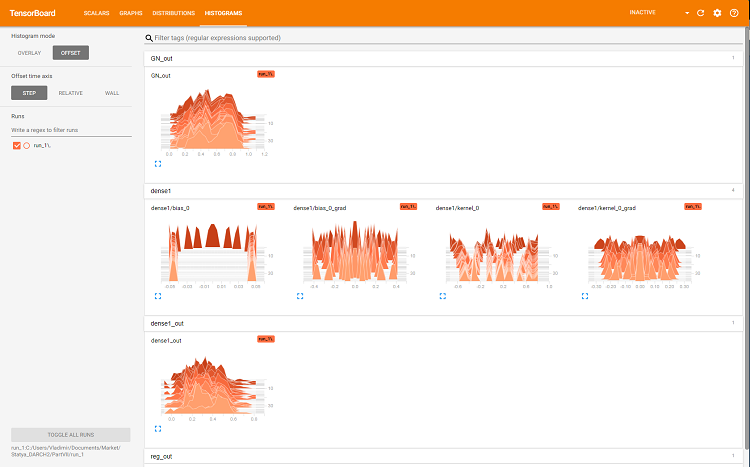
Abb. 7. Histogramm der Dichte
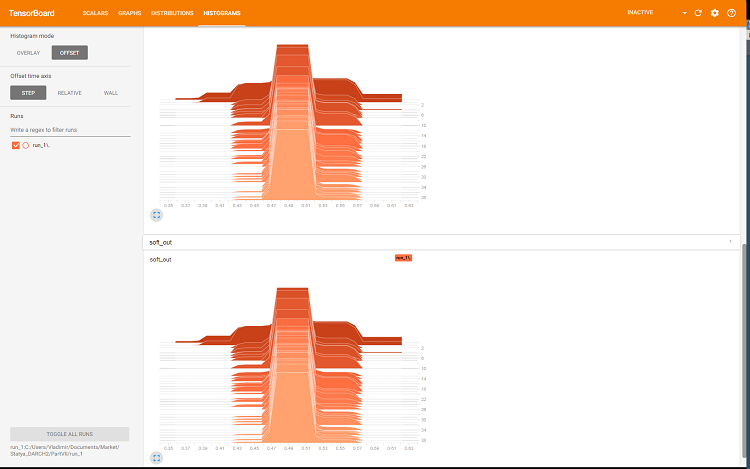
Abb. 8. Histogramm der Ausgänge von sotmax und der Regularisierung
Diese Diagramme sind ein mächtiges Werkzeug zur Anpassung der Parameter des neuronalen Netzes, aber ihre detaillierte Analyse geht über den Rahmen dieses Artikels hinaus.
Bei jedem Neustart der Tensorboard muss der Speicherpfad log_dir geändert oder der zuvor verwendete gelöscht werden.
Schauen wir, wie sich die Qualität der Klassifizierung mit den gleichen Parametern ändern würde, aber mit dem Testset für die Validierung. Das Skript wird unten gezeigt und ist in der Datei verfügbar:
library(reticulate) library(keras) py_set_seed(12345) num_classes <- 2L batch_size <- 32L learning_rate <- 0.005 epochs <- 100L #--------- bestNN <- env$resBest$bestNN x_train <- env$res$InputTrain[ ,bestNN] y_train <- env$Ytest %>% to_categorical() x_test <- env$res$InputTest[ ,bestNN] y_test <- env$Ytest1 %>% to_categorical() x_test1 <- env$res$InputTest1[ ,bestNN] y_test1 <- env$Ytest2 %>% to_categorical() #---------------------------------------- early_stopping <- callback_early_stopping(monitor = "val_acc", min_delta = 1e-5, patience = 20, verbose = 0, mode = "auto") log_dir <- paste0(getwd(),"/run_2") tensboard <- callback_tensorboard(log_dir = log_dir, histogram_freq = 1, batch_size = 32, write_graph = TRUE, write_grads = TRUE, write_images = FALSE) ##----model--keras------------------------- # define model model <- keras_model_sequential() # add layers and compile model %>% layer_gaussian_noise(stddev = 0.05, input_shape = dim(x_train)[2], name = "GN") %>% layer_dense(units = num_classes, name = "dense1") %>% layer_activation_softmax(name = "soft") %>% layer_activity_regularization(l2 = 1.0, name = "reg") %>% #l1 = 0.01, compile( loss = 'binary_crossentropy', optimizer = optimizer_rmsprop(lr = learning_rate, decay = 0.01), metrics = 'accuracy' ) ## Training & Evaluation --------------------------- # Fit model to data model %>% fit( x_train, y_train, batch_size = batch_size, epochs = epochs, verbose = 0, view_metrics = TRUE , shuffle = TRUE, validation_data = list(x_test, y_test), callbacks = list(early_stopping, tensboard)) -> history
Schauen wir uns jetzt die Metriken des zweiten Testsets an:
#--model--test1------------------------------------------------- predict(model, x_test1) -> Ypr.test1 Ypr.test1 %>% max.col()-1 -> y_pr_test1 #Ypr.test1 %>% apply(1, function(x) which.max(x)) %>% subtract(1) -> y_pr_test1 evalq(res_mod_test1 <- Eval(Ytest2, y_pr_test1), env) > env$res_mod_test1 $metrics Accuracy Precision Recall F1 0 0.713 0.704 0.826 0.760 1 0.713 0.730 0.575 0.644 $confMatr Confusion Matrix und Statistik predicted actual 0 1 0 114 24 1 48 65 Accuracy : 0.7131 95% CI : (0.6529, 0.7683) No Information Rate : 0.6454 P-Value [Acc > NIR] : 0.013728 Kappa : 0.4092 Mcnemar's Test P-Value : 0.006717 Sensitivity : 0.7037 Specificity : 0.7303 Pos Pred Value : 0.8261 Neg Pred Value : 0.5752 Prevalence : 0.6454 Detection Rate : 0.4542 Detection Prevalence : 0.5498 Balanced Accuracy : 0.7170 'Positive' Class : 0
Virtuell sind sie identisch mit denen der ersten Variante. Wir könne beide Varianten mittels tensorboard visuell vergleichen.
#-----plot------------------ tensorboard(log_dir = c(paste0(getwd(),"/run_1"), paste0(getwd(),"/run_2")))
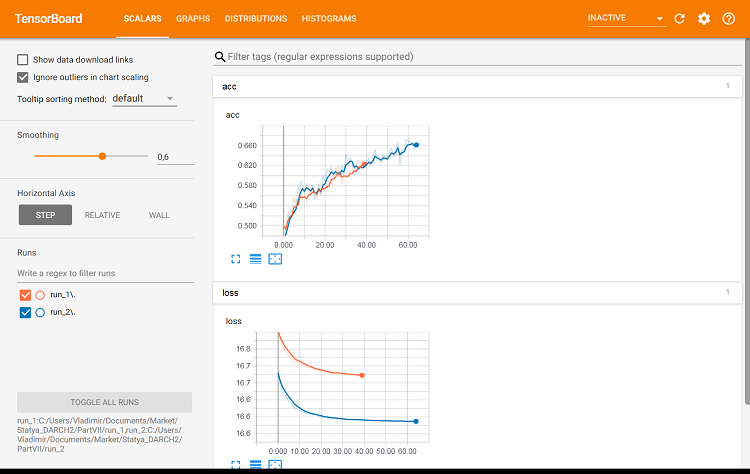
Abb. 9. Metriken der Trainingssets
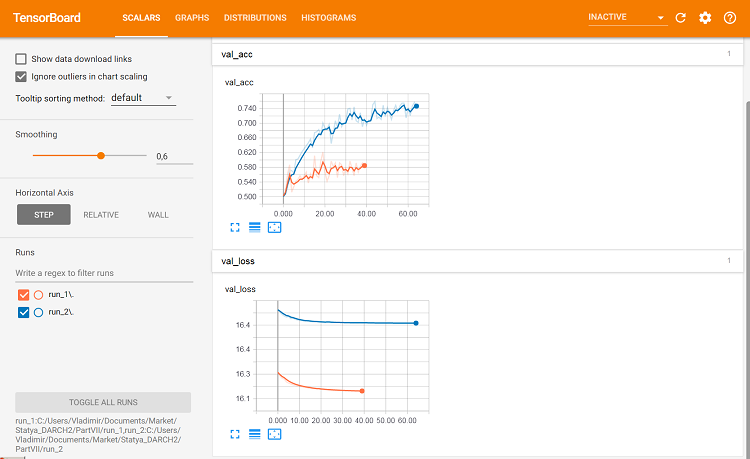
Abb. 10. Metriken der Validierungssets
Hier zeigen sich die Unterschiede.
Führen wir jetzt das letzte Experiment durch. Alle 500 Ausgänge des Ensembles werden als Eingang in das mehrschichtige neuronale Netzwerk eingespeist. So führt das neuronale Netz die Bereinigung und die Kombination gleichzeitig durch. Das Skript ist unten aufgeführt und steht auch in der Datei modelDNNN_500.R zur Verfügung.
library(reticulate) library(keras) py_set_seed(12345) num_classes <- 2L batch_size <- 32L learning_rate <- 0.0001 epochs <- 100L #--------- x_train <- env$res$InputTrain y_train <- env$Ytest %>% to_categorical() x_test <- env$res$InputTest y_test <- env$Ytest1 %>% to_categorical() x_test1 <- env$res$InputTest1 y_test1 <- env$Ytest2 %>% to_categorical() #---------------------------------------- early_stopping <- callback_early_stopping(monitor = "val_acc", min_delta = 1e-5, patience = 20, verbose = 0, mode = "auto")
Wir habe die Bibliotheken, Konstanten geladen, die Sets des Trainings und der Tests definiert und ebenso die Funktion der frühen Beendigung.
##----modelDNN--keras------------------------- # define model modDNN <- keras_model_sequential() # add layers and compile modDNN %>% layer_gaussian_noise(stddev = 0.001, input_shape = dim(x_train)[2], name = "GN") %>% layer_batch_normalization() %>% layer_dense(units = 100, activation = "elu", name = "dense1") %>% layer_dropout(rate = 0.5, name = "dp1") %>% layer_batch_normalization() %>% layer_dense(units = 50, activation = "elu", name = "dense2") %>% layer_batch_normalization() %>% layer_dropout(rate = 0.5, name = "dp2") %>% layer_dense(units = 10, activation = "elu", name = "dense3") %>% layer_batch_normalization() %>% layer_dropout(rate = 0.2, name = "dp3") %>% layer_dense(units = num_classes, activation = "softmax", name = "soft") %>% compile( loss = 'binary_crossentropy', optimizer = optimizer_rmsprop(lr = learning_rate, decay = 0.0001), metrics = 'accuracy' )
Also haben wir das neuronale Netz definiert, indem wir die Reihenfolge und die Parameter der Schichten festgelegt haben. Wir haben den Compiler auch angewiesen, welche Verlustfunktion, Optimierer und Metrik er beim Training des Modells verwenden soll. Jetzt trainieren wir das Modell:
## Training & Evaluation --------------------------- # Fit model to data modDNN %>% fit( x_train, y_train, batch_size = batch_size, epochs = epochs, verbose = 0, view_metrics = TRUE , shuffle = TRUE, validation_split = 0.2, #validation_data = list(x_test, y_test), callbacks = list(early_stopping)) -> history
Während des Trainings geben wir die Metriken aus und mischen die Eingabedaten, 20% des Trainingssatzes werden für die Validierung verwendet, und die frühe Beendigung wird angewendet. Testen Sie das Modell am Testset:
#--model--test------------------------- predict(modDNN, x_test) -> Ypr.test Ypr.test %>% apply(1, function(x) which.max(x)) %>% subtract(1) -> y_pr_test evalq(res_mod_test <- Eval(Ytest1, y_pr_test), env)
Wir betrachten das Ergebnis in Zahlen auf der Ebene der Mittelwertbildung des Ensembles:
> env$res_mod_test $metrics Accuracy Precision Recall F1 0 0.752 0.702 0.800 0.748 1 0.752 0.808 0.712 0.757 $confMatr Confusion Matrix und Statistik predicted actual 0 1 0 184 46 1 78 193 Accuracy : 0.7525 95% CI : (0.7123, 0.7897) No Information Rate : 0.523 P-Value [Acc > NIR] : < 2.2e-16 Kappa : 0.5068 Mcnemar's Test P-Value : 0.005371 Sensitivity : 0.7023 Specificity : 0.8075 Pos Pred Value : 0.8000 Neg Pred Value : 0.7122 Prevalence : 0.5230 Detection Rate : 0.3673 Detection Prevalence : 0.4591 Balanced Accuracy : 0.7549 'Positive' Class : 0
Zeichnen wir den Trainingsablauf:
plot(history)
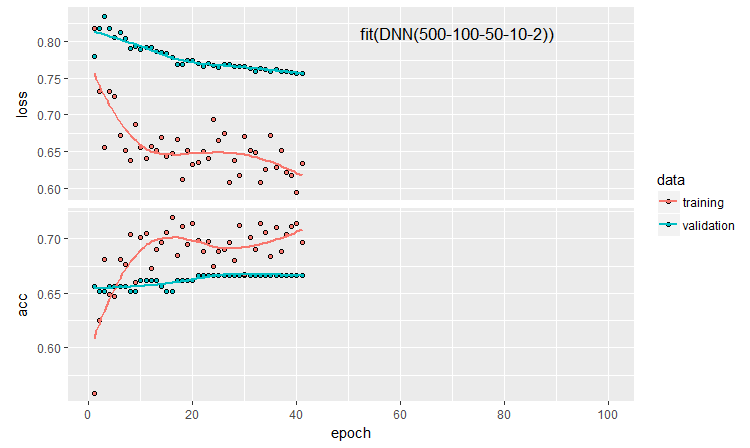
Abb. 11. Der Trainingsablauf des Neuronalen Netzes DNN500
Zur Verbesserung der Klassifikationsqualität können zahlreiche Hyperparameter modifiziert werden: Neuroneninitialisierungsmethode, Regularisierung der Aktivierung der Neuronen und ihrer Gewichte, etc. Die Ergebnisse, die mit fast intuitiv ausgewählten Parametern erzielt werden, haben eine vielversprechende Qualität, aber auch eine enttäuschende Seite. Ohne Optimierung war es nicht möglich, die Genauigkeit über 0,82 zu erhöhen. Fazit: Es ist notwendig, die Hyperparameter des neuronalen Netzes zu optimieren. In den vorangegangenen Artikeln haben wir mit der Bayes'schen Optimierung experimentiert. Das kann auch hier angewendet werden, aber es ist ein anderes schwieriges Thema.
Die sequentielle Definition eines Modells ermöglicht das Testen und Konfigurieren von Modellen beliebiger Komplexität und Tiefe. Aber mit der funktionalen API von keras ist es möglich, komplexere Strukturen neuronaler Netze zu erzeugen: zum Beispiel mit zahlreichen Ein- und Ausgängen. Dies wird im nächsten Artikel besprochen.
5. Analyse der experimentellen Ergebnisse
Wir haben jetzt die Trainings- und Testergebnisse von fünf Modellen:
- Ensemble mit Mittelung (EnsAver);
- Ensemble mit Stimmenmehrheit (EnsVot);
- Logistisches Regressionsmodell varb;
- Neuronales Netzwerk DNN(7,2);
- Neuronales Netzwerk DNN500.
Fassen wir die Qualitätswerte all dieser Modelle in einer Tabelle zusammen, zerlegen den Klassifizierungsfehler in Komponenten und schätzen ihren Beitrag zum Gesamtfehler. Wir verwenden die Funktion randomUniformForest::biasVarCov() (Bias-Varianz-Kovarianz-Zerlegung). Weitere Informationen zu dieser Funktion finden Sie in der Paketbeschreibung. Der Code für die Zerlegung des Klassifizierungsfehlers der EnsAver- und EnsVot-Ensembles ist unten dargestellt. Die Skripte sind für andere Modelle ähnlich.
#---bias--test------------------------------- import_fun(randomUniformForest, biasVarCov, BiasVar) evalq({ target = Ytest1 biasAver <- BiasVar(predictions = ScoreAver$clAver, target = target, regression = FALSE, idx = 1:length(target)) biasVot <- BiasVar(predictions = ScoreVot$ClVot, target = target, regression = FALSE, idx = 1:length(target)) }, env) ----------------------------- Noise: 0.2488224 Squared bias: 0.002107561 Variance of estimator: 0.250475 Covariance of estimator and target: 0.1257046 Assuming binary classification with classes {0,1}, where '0' is the majority class. Misclassification rate = P(Y = 1)P(Y = 0) + {P(Y = 1) - P(Y_hat = 1)}^2 + P(Y_hat = 0)P(Y_hat = 1) - 2*Cov(Y, Y_hat) Misclassification rate = P(Y = 1) + P(Y_hat = 1) - 2*E(Y*Y_hat) = 0.2499958 --------------------- Noise: 0.2488224 Squared bias: 0.004079665 Variance of estimator: 0.2499721 Covariance of estimator and target: 0.1274411 Assuming binary classification with classes {0,1}, where '0' is the majority class. Misclassification rate = P(Y = 1)P(Y = 0) + {P(Y = 1) - P(Y_hat = 1)}^2 + P(Y_hat = 0)P(Y_hat = 1) - 2*Cov(Y, Y_hat) Misclassification rate = P(Y = 1) + P(Y_hat = 1) - 2*E(Y*Y_hat) = 0.2479918
Zusammengefasste Ausgabe:
> env$biasAver $predError [1] 0.2499958 $squaredBias [1] 0.002107561 $predictionsVar [1] 0.250475 $predictionsTargetCov [1] 0.1257046
| 95%CI Acc | Precision | Recall | F1 | PredErr | sqBias | predVar | predTargCov | |
|---|---|---|---|---|---|---|---|---|
| EnsAver | 0.7102, 0.7880 (0.7500) | 0.708 0.794 |
0.778 0.727 |
0.741 0.759 |
0.2499 | 0.0021 | 0.2505 | 0.1257 |
| EnsVot | 0.7123, 0.7897 (0.7525) | 0.702 0.808 |
0.800 0.712 |
0.748 0.757 |
0.248 | 0.0041 | 0.25 | 0.1274 |
| varb | 0.7416, 0.8159 (0.7804) | 0.790 0.808 |
0.783 0.779 |
0.766 0.793 |
0.2199 | 0.000398 | 0.25 | 0.13964 |
| DNN(7, 2) | 0.7165, 0.7935 (0.7565) | 0.765 0.751 |
0.678 0.823 |
0.719 0.785 |
0.2460 | 0.000195 | 0.2498 | 0.1264 |
| DNN500 | 0.7123, 0.7897 (0.7525) | 0.702 0.808 |
0.800 0.712 |
0.748 0.757 |
0.2779 | 0.01294 | 0.2452 | 0.1145 |
Informationen der zusammenfassenden Tabelle:
- Der beste Wert für Accuracy unter den Basismodellen wurde durch varb erreicht, wobei 500 Ausgänge des Ensembles kombiniert wurden. Das beste Modell unter den trainierbaren Kombinatoren ist DNN(7,2), das die 7 besten Ergebnisse des Ensembles vereint.
- Der kleinste Testfehler für die Testprobe (PredErr) wurde durch varb und DNN(7,2) erreicht.
- Die quadrierten Bias (sqBias) der beiden gleichen Modelle ist eine Größenordnung besser als die der anderen.
- Die Fehlervarianz (PredVar) ist bei allen Modellen nahezu gleich. Das sieht merkwürdig aus: Das Ensemble hätte für eine Verringerung der Varianz sorgen sollen, aber wir haben eine geringe Verzerrung erhalten.
- Die beste Kovarianz zwischen der Schätzung und der Antwort (predictionTargetCov) wird durch varb angezeigt. Das ist keine Einzelvariable, sondern dient nur dem Vergleich von Modellen.
- Alle Werte des Modells DNN500 sind die niedrigsten. Fazit: Die Erhöhung der Komplexität von Modellen für einfache Aufgaben führt nicht zu besseren Ergebnissen.
Schlussfolgerung
Das Ensemble der neuronalen Netzwerkklassifikatoren ELM mit Mittelwertbildung oder einfacher Mehrheitsabstimmung zeigen eine gute Klassifikationsqualität bei sehr hoher Rechengeschwindigkeit. Es ist möglich, die Qualität zu verbessern, indem man die Schwelle für die Umwandlung von kontinuierlichen in nominale Größen optimiert und die Ausgänge vor der Mittelwertbildung kalibriert. Es wurde keine merkliche Abnahme der Abweichung des Fehlers festgestellt.
Das Ersetzen der Mittelung der Ensembleausgänge durch die Funktion Softmax eines einfachen neuronalen Netzes reduziert die Vorspannung um eine Größenordnung, ohne dass die Varianz merklich abnimmt. Die Verwendung von komplexeren neuronalen Netzmodellen als Ersatz für die Bereinigung und Mittelwertbildung brachte keine guten Ergebnisse.
Das mit Hilfe der Bayes'schen Variablenauswahl (varbvs-Paket) gewonnene logistische Regressionsmodell zeigt sehr gute Ergebnisse. Sie können die besten von diesem Paket ermittelten Ausgaben für das neuronale Netz verwenden.
24% des Rauschens, das seit der Vorverarbeitung nicht mehr entfernbar zu sein scheint, führt wieder einmal dazu, dass die verrauschten Proben irgendwann in eine eigene Klasse umbenannt werden sollten.
Es ist notwendig, die Möglichkeiten von keras zu nutzen und mit Sequenzen (Zeitreihen) zu arbeiten, wie es unsere Daten sind. Dies kann die Qualität der Klassifizierung verbessern.
Anlagen
GitHub/PartVII enthält folgende Dateien:
- Importar.R — Paket-Import Funktionen.
- Library.R — benötigte Bibliotheken.
- FunPrepareData_VII.R — Funktionen zur Vorbereitung der Anfangsdaten.
- FunStacking.R — Funktionen zum Erstellen und Testen der Ensembles.
- Prepare.R — Funktion und Skripts zur Vorbereitung der Anfangsdaten des trainierbaren Kombinators.
- Varb.R — Skripte des Modells varb base.
- model_DNN7_2.R — Skripte des Neuronalen Netzes DNN(7-2).
- model_DNN_500.R — Skripte des Neuronalen Netzes DNN500.
- SessionInfo_VII.txt — Liste der in diesem Artikel verwendeten Pakete.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/4228
Testen von Mustern von Währungspaaren: Praktische Anwendung und echte Handelsperspektiven. Teil IV
So formulieren Sie das Pflichtenheft eines Auftrages für einen Handelsroboter
Integration von MQL-basierten Expert Advisors und Datenbanken (SQL Server, .NET und C#)
Die Visualisierung von Optimierungsergebnissen nach dem ausgewählten Kriterium
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.