
Bewertung und Auswahl von Variablen für Modelle für maschinelles Lernen
Einführung
Dieser Artikel konzentriert sich auf die Besonderheiten der Auswahl, Vorkonditionierung und Bewertung der Eingabevariablen für den Einsatz in Modellen für maschinelles Lernen. Mehrere Methoden zur Normalisierung und deren Features werden hier beschrieben. Wichtige Phasen des Prozesses, die das Endergebnis der Trainingsmodelle erheblich beeinflussen werden ebenso genannt. Wir müssen uns neue und wenig bekannte Methoden zur Bestimmung der Informativität und Visualisierung der Eingabedaten genauer betrachten und bewerten.
Mit dem Paket "RandomUniformForests" berechnen und analysieren wir das Bedeutungskonzept einer Variablen auf verschiedenen Ebenen und in verschiedenen Kombinationen, die Übereinstimmung der Prädiktoren sowie ein Ziel und das Zusammenspiel zwischen Prädiktoren und der Auswahl eines optimalen Satzes von Prädiktoren unter Berücksichtigung aller Aspekte der Bedeutung.
Mit dem Paket "RoughSets" werden wir die gleiche Frage der Wahl Prädiktoren aus einem anderen Blickwinkel und basierend auf anderen Konzept betrachten. Wir zeigen, dass nicht nur eine Reihe von Prädiktoren optimal sein kann, eine Reihe von Beispielen für das Training kann ebenfalls optimiert werden.
Alle Berechnungen und Experimente erfolgen in der Sprache R um genauer zu sein Revolution R Open 3.2.1 .
1. Eingabevariablen (Vorzeichen, Prädiktoren)
Alle Variablen, sowhl Eingabe (unabhängig, Prädiktoren) und Ausgabe (Ziel) können vom folgenden Typ sein:
Binär — hat zwei Werte: {0,1}, {-1,1}, {"ja", "nein"}, {"männlich", "weiblich"}.
Nominal (Faktoren) mit einer endlichen Zahl von Ebenen. Zum Beispiel hat der Faktor "Wochentag" sieben Ebenen und jede von ihnen kann benannt werden (Montag, Dienstag etc). Faktoren können geordnet und ungeordnet sein. Zum Beispiel hat der Faktor "Stunde des Tages" 24 Ebenen und ist geordnet. Der Faktor "Bezirk einer Stadt" mit 32 Ebenen ist ungeordnet, da alle Ebenen von gleicher Bedeutung sind. Es sollte explizit angegeben werden, wenn ein geordneter Faktor deklariert wird.
Quantitative (numerische) fortlaufende. Der Bereich von fortlaufenden Variablen geht von Inf (unendlich) bis +Inf.
Die "rohen" Quotierungen (OHLC) werden niht als numerische Eingabevariablen verwendet. Der Unterschied des Logarithmus oder der Logarithmus der Quotierungsverhältnisse werden angewendet. Verschiedene Indikatoren, die zu Gruppen zusammengefasst werden jedoch am häufigsten verwendet. In der Regel wird eine Reihe von Eingabedaten als Matrix gebildet, wenn alle Variablen einheitlich sind, oder häufiger, als ein Datenframe, wobei jede Spalte eine Variable ist und eine Linie ein Zustand der Variablen an einem bestimmten Punkt ist. Eine Zielvariable wird in der letzten (oder ersten) Spalte platziert.
1.1. Bereinigung
Die Bereinigung beinhaltet Folgendes:
(a) Entfernung oder Umwandlung von fehlenden (unsicheren) Daten "NA".
Viele Modelle erlauben keine Lücken in den Eingabedaten. Daher löschen wir entweder die Zeilen mit fehlenden Daten oder füllen die Lücken mit interpolierten Daten auf. Für solche Zwecke werden die jeweiligen Funktionen in vielen Paketen zur Verfügung gestellt. Entfernen von unsicheren Daten NA ist in der Regel standardmäßig integriert, aber es ist besser, es selbst durch na.omit(dt) vor dem eigentlichen Training zu erledigen.
(b) Entfernung der "Null-optional" Variablen (numerische und nominale).
In einigen Fällen (vor allem während der Transformation oder Konvertierung von Variablen) können Prädiktoren mit einzigartigem Einzelwert oder mehrerer solcher Werte in einer sehr niedrigen Frequenz auftreten. Bei vielen Modellen kann dies zu einem Zusammenbruch oder instabilen Betrieb führen. Diese nahe-Null-Varianz Prädiktoren müssen vor der Simulation identifiziert und beseitigt werden. Um solche Prädiktoren zu identifizieren und entfernen kann eine Sonderfunktion Caret:: nearZeroVar() des "caret" Paketes verwendet werden. Die Notwendigkeit dieses Punktes steht zur Debatte.
(c) Ermittlung und Beseitigung der korrelierten Prädiktoren (numerisch).
Während einige Modelle die korrelierten Prädiktoren außergewöhnlich gut behandeln (z.B. PLS, LARS und ähnliche mit der Regularisierung L1), können andere Modelle Vorteile aus der Reduzierung des Korrelationslevels zwischen Prädiktoren ziehen. Zur Identifizierung und Entfernung von stark korrelierten Prädiktoren (Schwellwert für Korrelationskoeffizient ist zum Beispiel > 0,9 gesetzt) verwenden wir die caret:: findCorrelation() Funktion aus dem gleichen "caret"-Paket. Dies ist ein sehr leistungsfähiges Paket, von dem ich dringend empfehle, es zu analysieren.
(d) Ermittlung und Beseitigung der linearen Abhängigkeiten (Faktoren).
Die caret::findLinearCombos() Funktion nutzt die QR-Erweiterung von Matrix-Transfers um deren lineare Kombinationen (sofern vorhanden) zu ermitteln. Lassen Sie uns zum Beispiel die folgende Matrix analysieren:
ltfrDesign <- matrix(0, nrow = 6, ncol = 6) ltfrDesign[, 1] <- c(1, 1, 1, 1, 1, 1) ltfrDesign[, 2] <- c(1, 1, 1, 0, 0, 0) ltfrDesign[, 3] <- c(0, 0, 0, 1, 1, 1) ltfrDesign[, 4] <- c(1, 0, 0, 1, 0, 0) ltfrDesign[, 5] <- c(0, 1, 0, 0, 1, 0) ltfrDesign[, 6] <- c(0, 0, 1, 0, 0, 1)
Bitte beachten Sie, dass Spalten 2 und 3 Ergänzungen zur ersten sind. Ebenso werden die Spalten 4, 5 und 6 in der ersten Spalte gebildet. Die caret::findLinearCombos() Funktion gibt eine Liste zurück, die diese Abhängigkeiten zusammen mit dem Vektor der Spaltenpositionen aufzählt, die gelöscht werden kann, um lineare Abhängigkeiten zu entfernen.
comboInfo <- findLinearCombos(ltfrDesign) comboInfo $linearCombos $linearCombos[[1]] [1] 3 1 2 $linearCombos[[2]] [1] 6 1 4 5 $remove [1] 3 6 ltfrDesign[, -comboInfo$remove] [,1] [,2] [,3] [,4] [1,] 1 1 1 0 [2,] 1 1 0 1 [3,] 1 1 0 0 [4,] 1 0 1 0 [5,] 1 0 0 1 [6,] 1 0 0 0
Diese Art von Abhängigkeiten kann auftreten, wenn eine große Anzahl von binären Prädiktoren benutzt wird, oder Faktor-Prädiktoren in einen "dummy" umgewandelt werden.
1.2. Transformation, Daten-Vorverarbeitung
Viele Modelle erfordern, dass numerische Eingabe-Daten in einem bestimmten Bereich (Normierung, Standardisierung) sind oder in einer bestimmten Weise konvertiert werden (Faktoren). Beispielsweise akzeptieren neuronalen Netzen und Support-Vector-Machinen (SVM) Eingangsdaten im Bereich [-1, 1] oder [0, 1]. Viele Pakete in der Sprache R bieten spezielle Features für solche Transformation oder führen die Umwandlung selbst durch. Bitte denken Sie daran, dass die Definition der Vorverarbeitungsparameter nur auf eine Trainingsmenge von Eingabedaten durchgeführt wird. Testen und Validierung von Mengen, neue Daten, eingehende Vorhersagemodelle, werden mit Parametern, die durch die Trainingsmenge gewonnen wurden, umgewandelt.
Normalisierung (Skalierung)
Eine allgemeine Formel eine Variable in Bereich {+ h, -l} umzuwandeln. Je nach gewünschtem Bereich h = + 1; l = (-1 oder 0). Einige Quellen empfehlen, den Bereich auf {-0,9; 0,9} oder {0,1; 0,9} einzugrenzen, um die Verwendung von Sättigungsabschnitten der Aktivierungsfunktionen (Tanh/Sig) zu vermeiden. Dies bezieht sich auf neuronale Netze, SVMs und andere Modelle mit den genannten Aktivierungsfunktionen.
Xn = (x - min(x)) / (max(x) - min(x)) * (h - l) + l;
Die inverse Transformation (Denormalisierung) erfolgt anhand der Formel:
x = (x - l) / (h - l) * (max(x) - min(x)) + min(x);
Standardisierung
Wenn man weiß, dass die Verteilung einer Variable nahe Normal ist, ist es möglich, mithilfe der folgenden Formel zu normalisieren:
x = (x - mean(x)) / sd(x)
Einige Pakete haben spezielle Funktionen für die Vorverarbeitung. Damit bietet die preProcess() Funktion des Pakets "caret" die folgenden Methoden der Vorverarbeitung: "BoxCox", "YeoJohnson", "ExpoTrans", "Center", "Scale", "range", "KnnImpute", "BagImpute", "MedianImpute", "PKA", "Ica" und "SpatialSign".
"BoxCox", "YeoJohnson", "expoTrans"
Die Yeо-Johnson-Konvertierung ähnlich leicht dem Box-Cox-Modell, aber es kann Prädiktoren mit Null oder negativen Werten annehmen (während Prädiktor-Werte für die Box-Cox-Transformation strikt positiv sein müssen). Die exponentielle Transformation von Manly (1976) kann auch für positive und negative Daten verwendet werden.
"Range" Transformation skaliert Daten innerhalb des Bereichs [0, 1]. Das ist wichtig! Wenn neue Proben höhere oder niedrigere Werte als in der Trainingsmenge haben, dann werden die Werte außerhalb dieses Bereichs liegen und das Prognoseergebnis somit falsch.
"center" – der Durchschnitt wird abgezogen, "scale" wird geteilt durch die Standardabweichung (Skalierung). In der Regel werden sie gemeinsam verwendet, das nennt man "Standardisierung".
"KnnImpute", "BagImpute", "MedianImpute" – Berechnung der fehlenden oder undefinierten Daten mit verschiedenen Algorithmen.
"SpatialSign" – Transformation, projiziert Prädiktordaten auf dem Einheitskreis in р Dimensionen, wobei р eine Reihe von Prädiktoren ist. Im Wesentlichen werden Vektordaten durch ihre Norm dividiert. Daten sollten vor der Umwandlung zentriert und skaliert werden.
"Pca" – in einigen Fällen muss die Hauptkomponentenanalyse für die Umwandlung von Daten in einen kleineren Subraum verwendet werden wo neue Variablen nicht miteinander korrelieren. Mit dieser Methode, werden Zentrierung und Skalierung automatisch durchgeführt und die Spaltennamen werden auf PC1, PC2 usw. geändert.
"isa" — in ähnlicher Weise kann eine unabhängige Komponente Analyse verwendet werden, um neue Variablen zu finden, die lineare Kombinationen der ursprünglichen Menge sind, wobei die Komponenten unabhängig sind (im Gegensatz zu unkorrelierten in PCA). Neue Variablen werden als IC1, IC2, etc. gekennzeichnet.
Das ausgezeichnete "ClusterSim" -Paket, gedacht zur Suche nach den optimalen Clustering Verfahren, hat die dataNormalization()-Funktion, die Daten auf 18 Arten sowohl von Spalten als auch Zeilen normalisiert. Ich werde einfach alle aufzählen:
n1 — standardization ((x – mean) / sd);
n2 — positional standardization ((x – median) / mad);
n3 — unitization ((x – mean) / range);
n3а — positional unitization ((x – median) / range);
n4 — unitization with zero minimum ((x – min) / range);
n5 — normalization in range <-1, 1> ((x – mean) / max(abs(x – mean)));
n5a — positional normalization in range <-1,1> ((x – median) / max(abs(x-median)));
n6 — quotient transformation (x/sd);
n6a — positional quotient transformation (x/mad);
n7 — quotient transformation (x/range);
n8 — quotient transformation (x/max);
n9 — quotient transformation (x/mean);
n9a — positional quotient transformation (x/median);
n10 — quotient transformation (x/sum);
n11 — quotient transformation (x/sqrt(SSQ));
n12 — normalization ((x-mean)/sqrt(sum((x-mean)^2)));
n12a — positional normalization ((x-median)/sqrt(sum((x-median)^2)));
n13 - Normalisierung bei der Null der zentrale Punkt ist ((x-midrange)/(range/2)).
"Dummy-Variablen" - viele Modelle erfordern eine Umwandlung von Faktor Prädiktoren nach "Dummies". Die Funktion dummyVar() aus dem Paket "caret" kann für diesen Zweck verwendet werden. Die Funktion nimmt Formel und Datenmenge und zeigt das Objekt, das zum Erstellen von dummy-Variablen verwendet werden kann.
2. Ausgabedaten (Zielvariable)
Da wir ein Klassifizierungsproblem lösen, ist die Zielvariable ein Faktor mit mehreren Ebenen (Klassen). Mehrheit der Modelle zeigen bessere Ergebnisse beim Training auf ein Ziel mit zwei Klassen. Mit einer Menge von Sonderklassen werden zusätzliche Maßnahmen getroffen, um diese Probleme anzugehen. Die Zielvariable ist in den Prozess der Trainingsdatenaufbereitung kodiert und wird nach der Vorhersage dekodiert.
Die Klassen werden auf verschiedene Weise codiert. Das RSNNS-Paket "Simulation von neuronalen Netzen in der Universität Stuttgart" bietet zwei Funktionen – decodeClassLabels() , die die Vektor-Klassen in der Matrix, die Spalten für die Klassen enthalten kodiert, und EncodeClassLabels (), die die inverse Transformation nach der Modell-Vorhersage erledigt. Zum Beispiel:
> data(iris) > labels <- decodeClassLabels(iris[,5]) > class <- encodeClassLabels(labels) > head(labels) setosa versicolor virginica [1,] 1 0 0 [2,] 1 0 0 [3,] 1 0 0 [4,] 1 0 0 [5,] 1 0 0 [6,] 1 0 0 > head(class) [1] 1 1 1 1 1 1
Die Anzahl der Modell-Ausgaben ist daher gleich der Anzahl der Klassen. Dies ist nicht die einzige Kodierungsmethode (eins zu eins) die für das Ziel gilt. Wenn das Ziel über zwei Klassen verfügt, können Sie es mit einem Output verwalten. Die Codierung der Zielvariablen in der Matrix hat auf jeden Fall eine Reihe von Vorteilen.
3. Bewertung und Auswahl der Prädiktoren
Erfahrungen haben gezeigt, dass die Erhöhung der Eingabedaten (Prädiktor) nicht immer zu einer Modell Verbesserung führt, im Gegenteil. Das Ergebnis wird tatsächlich von 3-5 Prädiktoren beeinflusst. In vielen Aggregationspaketen wie "rminer", "caret", "SuperLearner" und "mlr" gibt es integrierte Funktionen für die Berechnung der Bedeutung der Variablen und deren Auswahl. Die meisten Ansätze zur Reduzierung der Prädiktoren können in zwei Kategorien (unter Verwendung der Terminologie von John, Kohavi und Pfleger, 1994) unterteilt werden:
- Filtern. Filtermethoden bewerten die Relevanz der Prädiktoren außerhalb von Vorhersagemodellen, und möglicherweise verwendet das Modell nur die Prädiktoren, die bestimmte Kriterien erfüllen. Beispielsweise kann für Klassifikationsaufgaben jeder Prädiktor individuell ausgewertet werden um zu überprüfen, ob es eine plausible Beziehung zwischen einem Prädiktor und den beobachteten Klassen gibt. Nur Prädiktoren mit wichtigen prognostischen Abhängigkeiten werden dann in das Klassifizierungsmodell aufgenommen.
Wrapper. Wrapping-Methoden bewerten verschiedene Modelle mit Verfahren, die Prädiktoren hinzufügen und/oder entfernen, um die optimale Kombination zu finden, die die Modelleffizienz optimiert. Im Wesentlichen sind Wrapping-Methoden Suchalgorithmen die Prädiktoren als Eingänge betrachten und die Modelleffizienz als Ausgabe, die optimiert werden muss. Es gibt viele Möglichkeiten, Prädiktoren (rekursives entfernen/hinzufügen, genetische Algorithmen, simuliertes Abkühlen und viele andere) durchlaufen.
In diesem Artikel werden wir Wrapping-Techniken nicht beachten, stattdessen werden wir neue Methoden und Ansätze der Filtermethoden analysieren, die meines Erachtens alle der oben genannten Nachteile beseitigen.
3.1. Filtern
Durch die Verwendung von verschiedenen externen Methoden und Kriterien ist die Bedeutung (Informationsfähigkeit) von Prädiktoren etabliert. Der Beitrag der einzelnen Variablen bei der Verbesserung der Vorhersage des Modells wird hier unter der Bedeutung impliziert.
Danach stehen in der Regel drei Optionen zur Verfügung:
Verwendung einer bestimmte Anzahl von Prädiktoren der höchsten Bedeutung.
Verwendung eines Prozentsatzes der Gesamtzahl der Prädiktoren mit der höchsten Bedeutung.
- Verwendung der Prädiktoren, deren Bedeutung die Schwelle überschreitet .
Alle Fällen ermöglichen die Optimierung von Menge, Prozentsatz oder Schwelle.
Lassen Sie uns die Eingabe- und Ausgabe-Daten unter Berücksichtigung spezifischer Methoden bilden und Experimente durchführen.
Eingabedaten
Wir werden 11 Indikatoren (Oszillatoren) ohne vorherige Einstellungen in der Eingabe einbinden. Wir werden mehrere Variablen aus einigen Indikatoren nehmen. Dann werden wir eine Funktion schreiben, die die Eingabemenge von 17 Variablen bildet.
Die Quotierungen aus den letzten 4000 Balken auf TF = M30 / EUR/USD werden genommen.
In <- function(p = 16){ require(TTR) require(dplyr) require(magrittr) adx <- ADX(price, n = p) %>% as.data.frame %>% mutate(.,oscDX = DIp -DIn) %>% transmute(.,DX, ADX, oscDX) %>% as.matrix() ar <- aroon(price[ ,c('High', 'Low')], n = p)%>% extract(,3) atr <- ATR(price, n = p, maType = "EMA") %>% extract(,1:2) cci <- CCI(price[ ,2:4], n = p) chv <- chaikinVolatility(price[ ,2:4], n = p) cmo <- CMO(price[ ,'Med'], n = p) macd <- MACD(price[ ,'Med'], 12, 26, 9) %>% as.data.frame() %>% mutate(., vsig = signal %>% diff %>% c(NA,.) %>% multiply_by(10)) %>% transmute(., sign = signal, vsig) %>% as.matrix() rsi <- RSI(price[ ,'Med'], n = p) stoh <- stoch(price[ ,2:4], nFastK = p, nFastD =3, nSlowD = 3, maType = "EMA")%>% as.data.frame() %>% mutate(., oscK = fastK - fastD)%>% transmute(.,slowD, oscK)%>% as.matrix() smi <- SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9) vol <- volatility(price[ ,1:4], n = p, calc = "yang.zhang", N = 144) In <- cbind(adx, ar, atr, cci, chv, cmo, macd, rsi, stoh, smi, vol) return(In) }
Diese Indikatoren sind sehr bekannt und weit verbreitet, daher werden wir sie nicht wieder diskutieren. Ich werde einfach die Berechnung "pipe"(%>%) Methode aus den ""nagrittr " Paket basierend auf dem Beispiel für den MACD-Indikator kommentieren. Die Reihenfolge wird wie folgt lauten:
Der Indikator, der zwei Variablen (Macd, Signal) zurückgibt wird berechnet.
Die erhaltenen Matrix wird in ein Dataframe konvertiert.
Eine neue Variable vsig wird dem Dataframe hinzugefügt (in folgender Reihenfolge):
- Die Variable Signal wird geholt;
- Der erste Unterschied errechnet;
- Die NA-Vektoren werden am Anfang hinzugefügt da bei der Berechnung des ersten Unterschieds der Vektor eine Einheit kürzer ist als das Original;
- Es wird mit 10 multipliziert.
Nur die erforderlichen Variablen (Spalten) vsig, Signal werden aus dem Dataframe ausgewählt.
Das Dataframe wird in die Matrix umgewandelt.
Diese Berechnungsmethode ist sehr bequem, wenn Zwischenergebnisse nicht erforderlich sind. Darüber hinaus sind die Formeln leichter zu lesen und zu verstehen.
Wir holen die Matrix der Eingabedaten und betrachten den Inhalt.
x <- In(p = 16) > summary(x) DX ADX oscDX Min. : 0.02685 Min. : 5.291 Min. :-93.889 1st Qu.: 8.11788 1st Qu.:14.268 1st Qu.: -9.486 Median :16.63550 Median :18.586 Median : 5.889 Mean :20.70162 Mean :20.716 Mean : 4.227 3rd Qu.:29.90428 3rd Qu.:24.885 3rd Qu.: 19.693 Max. :79.80812 Max. :59.488 Max. : 64.764 NA's :16 NA's :31 NA's :16 ar tr atr Min. :-100.0000 Min. :0.0000000 Min. :0.000224 1st Qu.: -50.0000 1st Qu.:0.0002500 1st Qu.:0.000553 Median : -6.2500 Median :0.0005600 Median :0.000724 Mean : -0.8064 Mean :0.0008031 Mean :0.000800 3rd Qu.: 50.0000 3rd Qu.:0.0010400 3rd Qu.:0.000970 Max. : 100.0000 Max. :0.0150300 Max. :0.003104 NA's :16 NA's :1 NA's :16 cci chv cmo Min. :-515.375 Min. :-0.67428 Min. :-88.5697 1st Qu.: -84.417 1st Qu.:-0.33704 1st Qu.:-29.9447 Median : -5.674 Median : 0.03057 Median : -2.4055 Mean : -1.831 Mean : 0.11572 Mean : -0.6737 3rd Qu.: 83.517 3rd Qu.: 0.44393 3rd Qu.: 28.0323 Max. : 387.814 Max. : 3.25326 Max. : 94.0649 NA's :15 NA's :31 NA's :16 sign vsig rsi Min. :-0.38844 Min. :-0.43815 Min. :12.59 1st Qu.:-0.07124 1st Qu.:-0.05054 1st Qu.:39.89 Median :-0.00770 Median : 0.00009 Median :49.40 Mean :-0.00383 Mean :-0.00013 Mean :49.56 3rd Qu.: 0.05075 3rd Qu.: 0.05203 3rd Qu.:58.87 Max. : 0.38630 Max. : 0.34871 Max. :89.42 NA's :33 NA's :34 NA's :16 slowD oscK SMI Min. :0.0499 Min. :-0.415723 Min. :-74.122 1st Qu.:0.2523 1st Qu.:-0.043000 1st Qu.:-33.002 Median :0.4720 Median : 0.000294 Median : -5.238 Mean :0.4859 Mean :-0.000017 Mean : -4.089 3rd Qu.:0.7124 3rd Qu.: 0.045448 3rd Qu.: 22.156 Max. :0.9448 Max. : 0.448486 Max. : 75.079 NA's :19 NA's :17 NA's :25 signal vol Min. :-71.539 Min. :0.003516 1st Qu.:-31.749 1st Qu.:0.008204 Median : -5.319 Median :0.011274 Mean : -4.071 Mean :0.012337 3rd Qu.: 19.128 3rd Qu.:0.015312 Max. : 71.695 Max. :0.048948 NA's :33 NA's :16
Ausgabedaten (Ziel)
Als Zielvariable werden von ZZ empfangenen Signale verwendet. Es folgt die Formel für die Berechnung von zigzag und Signal:
ZZ <- function(pr = price, ch = ch , mode="m") { require(TTR) if(ch > 1) ch <- ch/(10 ^ (Dig - 1)) if(mode == "m"){pr <- pr[ ,'Med']} if(mode == "hl") {pr <- pr[ ,c("High", "Low")]} if(mode == "cl") {pr <- pr[ ,c("Close")]} zz <- ZigZag(pr, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) for(i in n) { if(is.na(zz[i])) zz[i] = zz[i-1]} dz <- zz %>% diff %>% c(0,.) sig <- sign(dz) return(cbind(zz, sig)) }
Die Funktionsparameter:
- PR = Preis - Matrix OHLCMed Quotierungen;
- ch – minimale Länge einer ZigZag-Kurve in Punkten (4 Zeichen);
- mode – angewandter Preis (m — durchschnittlich, hl — Hoch und Tief, cl-Schluss). Standardmäßig wird der Mittelwert verwendet.
Die Funktion gibt die Matrix mit zwei Variablen zurück - ZigZag und das Signal das sich aus der ZigZag-Neigung im Bereich [-1; 1] ergibt.
Wir berechnen die Signale von zwei ZZ mit einer unterschiedlichen Beinlänge:
out1 <- ZZ(ch = 25) out2 <- ZZ(ch = 50)
Auf dem Chart sehen sie entsprechend aus:
> matplot(tail(cbind(out1[ ,1], out2[ ,1]), 500), t="l")
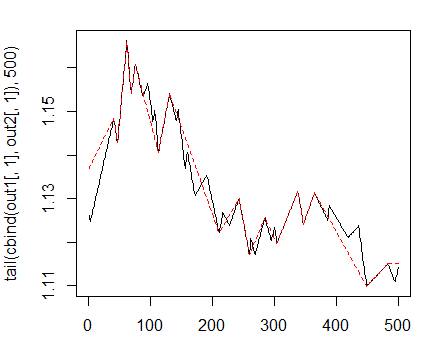
Abb. 1. ZigZags mit minimaler Länge der Kurven 25/75 p
Als nächstes werden wir den ersten ZZ mit einem kürzeren Bein verwenden. Wir werden die Eingabevariablen und das Ziel im allgemeinen Dataframe kombinieren, undefinierte Daten mit der Bedingung = "0" und die Klasse "0" aus dem Ziel entfernen.
> data <- cbind(as.data.frame(x) , Class = factor(out1[ ,2])) %>% + na.omit > data <- data[data$Class != 0, ] > data$Class <- rminer::delevels(data$Class, c("0", "1"), "1")
Sehen wir uns die Verteilung der Klassen im Ziel an:
> table(data$Class) -1 1 1980 1985
Was wir sehen können ist, dass die Klassen gut ausbalanciert sind. Da wir eine Reihe von Eingabe- und Ausgabe-Daten vorbereitet haben, können wir beginnen, die Bedeutung der Prädiktoren zu bewerten.
Zunächst werden wir prüfen, wie korreliert die Eingabedaten sind:
> descCor <- cor(data[ ,-ncol(data)]) > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.20170 0.03803 0.26310 0.31750 0.57240 0.95730
Welche Eingangsgrößen haben Korrelationen über 90%?
> highCor <- caret::findCorrelation(descCor, cutoff = .90) > highCor [1] 12 15
Die Antwort lautet – rsi und SMI. Wir bilden einen Satz von Daten ohne diese beiden und prüfen die Korrelation von den restlichen.
> data.f <- data[ ,-highCor] > descCor <- cor(data.f[ ,-ncol(data.f)]) > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.20170 0.03219 0.21610 0.27060 0.47820 0.89880
Um die Bedeutung der Variable (VI) zu bestimmen, verwenden wir ein neues Paket "Random Uniform Forests", welches eine große Auswahl an Instrumenten für tiefe Analyse und Visualisierung hat. Nach Absicht der Entwickler des Pakets ist das Hauptziel der Bestimmung der Bedeutung der Variablen zu beurteilen, was, wann, wo und wie sie das zu lösende Problem beeinflussen.
Das Paket enthält verschiedene Bedeutungmasszahlen einer Variablen in der Tiefe. Wir werden diese betrachten bevor wir eine eingehendere Evaluierung vornehmen.
Die globale Variablenbedeutung setzt Variablen, die die Vorhersagefehler auf das äußerste reduzieren, aber sie sagt uns nicht, wie die wichtige Variable sich auf die Antworten auswirkt.
Wir möchten zum Beispiel wissen, welche Variablen einen stärkeren Einfluss auf die separate Klasse haben, oder wie die Wechselwirkung zwischen Variablen aussieht.
Die Variablenbedeutung wird durch alle Einheiten und Bäume gemessen, und das erlaubt allen Variablen einen Wert aufzuweisen wobei die Schnittpunkte zufällig sind. Jede Variable hat daher gleiche Chancen ausgewählt zu werden, aber nur die wird die Bedeutung wiedergeben, wenn sie jene ist, die die Entropie in jedem Knoten am meisten reduzierte.
Lokale Variable Bedeutung
Definition: ein Prädiktor ist lokal wichtig in der ersten Ordnung, wenn er für die gleiche Beobachtung und alle Bäume jener ist, der die höchste Häufigkeit des Auftretens in einem Terminalknoten ist.
Partielle Bedeutung
Definition: ein Prädiktor ist partiell wichtig, wenn er für die gleiche Beobachtung, Klasse und für alle Ordnungen derjenige ist, der die höchste Häufigkeit des Auftretens am Terminalknoten hat.
Wechselwirkungen
Wir wollen wissen, wie Prädiktoren das Problem beeinflussen, wenn wir sie berücksichtigen. Beispielsweise können einige Variablen nur relativ geringe Auswirkungen auf das Problem haben, aber einen starken Einfluss auf weitere relevantere Variablen haben, oder eine Variable kann viel Interaktion mit anderen haben, wodurch diese Variable Einfluss haben kann. Lassen Sie uns definieren, was Interaktion ist.
Definition: ein Prädiktor interagiert mit anderen, wenn beide für die gleiche Beobachtung und für alle Bäume, bzw. erst- und zweithäfigstes Auftreten im Terminalknoten haben.
Partielle Abhängigkeiten
Dies sind die Werkzeuge, die es ermöglichen zu bestimmen, wie eine Variable (oder ein Variablenpaar) die die Werte aller anderen Variablen kennt, den Wert der Antwort beeinflusst. Um genauer zu sein, ist eine partielle Abhängigkeit der Bereich wo der maximale Wirkungseinfluss der Variablen basierend auf dem Wert der Antwort ausgeübt wird. Das Konzept einer partiellen Abhängigkeit kam von Friedman (2002), der es in Gradient Boosting Machines (GBM) verwendete, jedoch wurde es in Random Uniform Forests anders umgesetzt.
Nach den Vorstellungen des Pakets Random Uniform Forests können wir die Bedeutung einer Variablen basierend auf folgendem Schema bestimmen: Bedeutung = Beitrag + Interaktion, wobei Beitrag der Einfluss einer Variablen (in Bezug auf alle zu beeinflussenden) auf Vorhersagefehler ist und Interaktion ist eine Auswirkung auf andere Variablen.
Lassen Sie zu Experimenten übergehen
Wir unterteilen unsere Datensatz [data.f] in die Trainings- und Testmengen im Verhältnis 2/3, normalisieren im Bereich von -1;1 und testen das Modells. Für die Trennung verwenden wir die rminer::holdout()-Funktion , die die Menge in zwei Teile teilt. Für die Normalisierung verwenden wir die caret::preProcess() Funktion und die -Methode = c("spatialSign"). Beim Trainieren des Modells wird das Paket automatisch die Berechnungen zwischen den verfügbaren Prozessorkernen minus einem der das "-DoParallel" Paket verwendet parallelisieren . Sie können mit der "treads" Option angeben, dass eine bestimmte Anzahl von Kernen für die Berechnung verwendet wird.> idx <- rminer::holdout(y = data.f$Class)
> prep <- caret::preProcess(x = data.f[idx$tr, -ncol(data.f)],
+ method = c("spatialSign"))
> x.train <- predict(prep, data.f[idx$tr, -ncol(data.f)])
> x.test <- predict(prep, data.f[idx$ts, -ncol(data.f)])
> y.train <- data.f[idx$tr, ncol(data.f)]
> y.test <- data.f[idx$ts, ncol(data.f)]
> ruf <- randomUniformForest( X = x.train,
+ Y = y.train,
+ xtest = x.test,
+ ytest = y.test,
+ mtry = 1, ntree = 300,
+ threads = 2,
+ nodesize = 2
+ )
Die Labels -1 1 wurden nach 1 2 für eine einfache Berechnung konvertiert und werden intern als Ersatz verwendet.
> print(ruf)
Aufruf:
randomUniformForest.default(X = x.train, Y = y.train, xtest = x.test,
ytest = y.test, ntree = 300, mtry = 1, nodesize = 2, threads = 2)
Typ von random uniform forest: Klassifizierung
paramsObject
ntree 300
mtry 1
nodesize 2
maxnodes Inf
replace TRUE
bagging FALSE
depth Inf
depthcontrol FALSE
OOB TRUE
importance TRUE
subsamplerate 1
classwt FALSE
classcutoff FALSE
oversampling FALSE
outputperturbationsampling FALSE
targetclass -1
rebalancedsampling FALSE
randomcombination FALSE
randomfeature FALSE
categorical variables FALSE
featureselectionrule entropy
Out-of-bag (OOB) Evaluierung
OOB geschätzte Fehlerrate: 20.2%
OOB Fehlerrate gebunden (mit 1% Abweichung): 21.26%
OOB Konfusionsmatrix:
Reference
Prädiktion -1 1 class.error
-1 1066 280 0.2080
1 254 1043 0.1958
OOB Schätzung des AUC: 0.798
OOB Schätzung des AUPR: 0.7191
OOB Schätzung des F1-Score: 0.7962
OOB (angepasste) Schätzung des geometrisches Mittels: 0.7979
Breiman's Grenzen
Erwarteter Pärdiktionsfehler (unter annähernd ausbalancierten Klassen): 18.42%
Obere Grenze: 27.76%
Mittlere Korrelation zwischen Bäumen: 0.0472
Stärke (margin): 0.4516
Standardabweichung der Stärke: 0.2379
Testmennge
Fehlerrate: 19.97%
Konfusionsmatrix:
Reference
Prädiktion -1 1 class.error
-1 541 145 0.2114
1 119 517 0.1871
Bereich unter ROC Kurve: 0.8003
Bereich unter Precision-Recall Kurve: 0.7994
F1 Score: 0.7966
Geometrisches Mittel: 0.8001
Wir werden dies etwas entschlüsseln:
- Trainingsfehler (interner Fehler) gegeben 1 % Abweichung = 21.26 %.
- Breiman Grenzen - theoretische von Breiman (2001) vorgeschlagene Eigenschaften. Da Random Uniform Forests die Eigenschaften von Random Forests erben, sind sie hier anwendbar. Für die Klassifizierung gibt es zwei Grenzen des Vorhersagefehlers, durchschnittliche Korrelation zwischen Bäumen und Stärke samt Standardabweichung der Stärke.
- Erwartet Vorhersagefehler = 18,42 %. Fehler der oberen Grenze = 27.76 %.
- Testfehler = 19.97% (externer Fehler). (Wenn die externe Evaluierung kleiner ist oder gleich der internen Evaluierung und kleiner als die Obergrenze von Breimans Grenzen, dann wird ein Neutraining höchstwahrscheinlich nicht auftreten.)
Schauen Sie den Chart eines Trainingsfehlers an:
> plot(ruf)
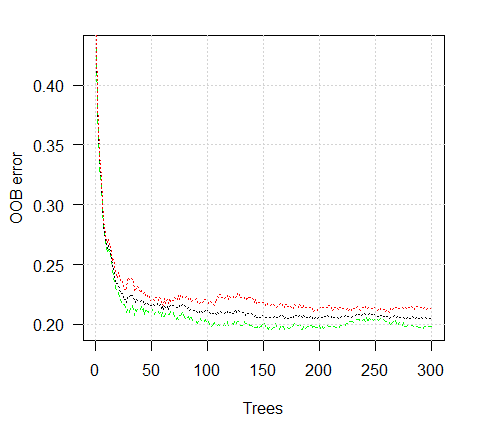
Abb. 2. Trainingsfehler abhängig von der Anzahl der Bäume
> summary(ruf) Globale Variable Bedeutung: Hinweis: die meisten prädiktiven Funktionen sind sortiert nach "Score" und werden geplottet. Die am meisten diskriminanten sollten auch in durch Überprüfung von 'class' und 'class.frequency' berücksichtigt werden. variables score class class.frequency percent 1 cci 2568 1 0.50 100.00 2 signal 2438 1 0.51 94.92 3 slowD 2437 1 0.51 94.90 4 oscK 2410 1 0.50 93.85 5 ADX 2400 -1 0.51 93.44 6 vol 2395 1 0.51 93.24 7 atr 2392 -1 0.51 93.15 8 sign 2388 1 0.50 92.97 9 vsig 2383 1 0.50 92.81 10 ar 2363 -1 0.51 92.01 11 chv 2327 -1 0.50 90.62 12 cmo 2318 -1 0.51 90.28 13 DX 2314 1 0.50 90.10 14 oscDX 2302 -1 0.51 89.64 15 tr 2217 1 0.52 86.31 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 6 14 6 15 6 Durchschnittlichen Baumgröße (Anzahl der Knoten) Zusammenfassung: Min. 1st Qu. Median Mean 3rd Qu. Max. 3 1044 1313 1213 1524 1861 Durchschnittliche Blattknoten (Anzahl der Endknoten) Zusammenfassung: Min. 1st Qu. Median Mean 3rd Qu. Max. 2 522 657 607 762 931 Blattknoten Größe (Anzahl der Beobachtungen pro Blattknoten) Zusammenfassung: Min. 1st Qu. Median Mean 3rd Qu. Max. 1.000 1.000 2.000 4.355 3.000 2632.000 Durchschnittliche Baumtiefe: 10 Theoretische (ausgewogene) Baumtiefe: 11
Wir sehen, dass unsere Eingabevariablen signifikatn und wichtig sind. Es wird angezeigt, in welchen Klassen die Variablen am häufigsten auftreten.
Und einige weitere Statistiken:
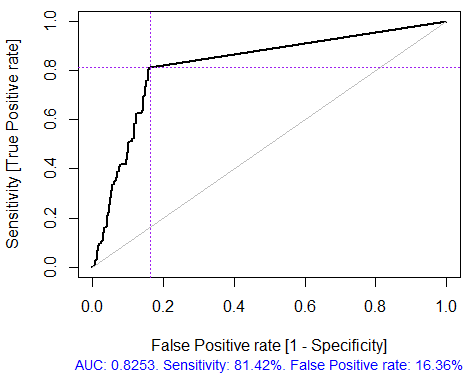
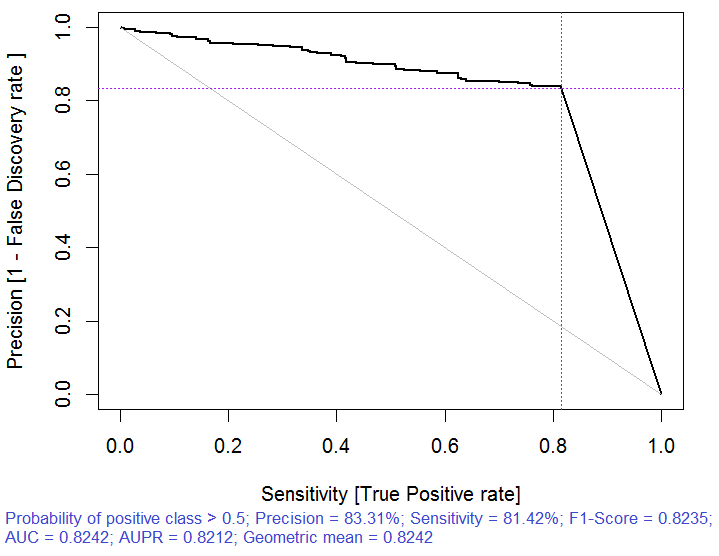
> pr.ruf <- predict(ruf, x.test, type = "response"); > ms.ruf <- model.stats(pr.ruf, y.test) Testmennge Fehlerrate: 19.97% Konfusionsmatrix: Reference Prädiktion -1 1 class.error -1 540 144 0.2105 1 120 518 0.1881 Bereich unter ROC Kurve: 0.8003 Bereich unter Precision-Recall Kurve: 0.7991 F1-Score: 0.7969 Geometrisches Mittel: 0.8001
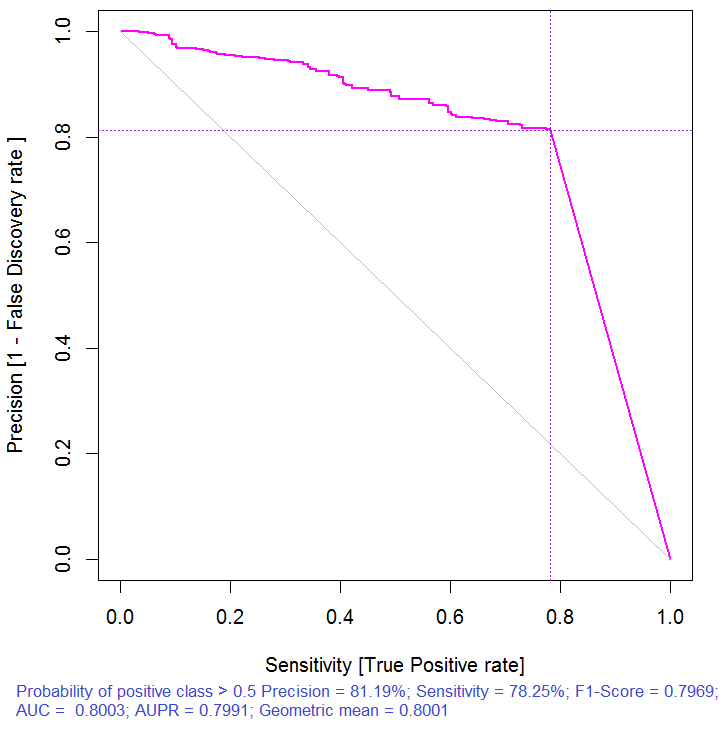
Abb. 3. Precision-recall curve
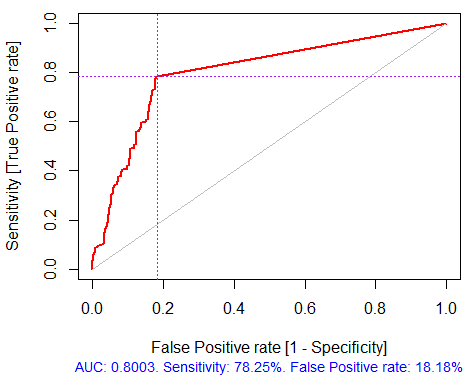
Abb. 4. ROC Kurve oder Fehlerkurve
Wenn wir hier aufhören würden, was normalerweise viele Filter Pakete so vorsehen, müssten wir mehrere Prädiktoren mit den besten Indikatoren von globaler Bedeutung auswählen. Diese Wahl bietet keine gute Ergebnisse, da sie die gegenseitige Beeinflussung der Prädiktoren nicht berücksichtigt.
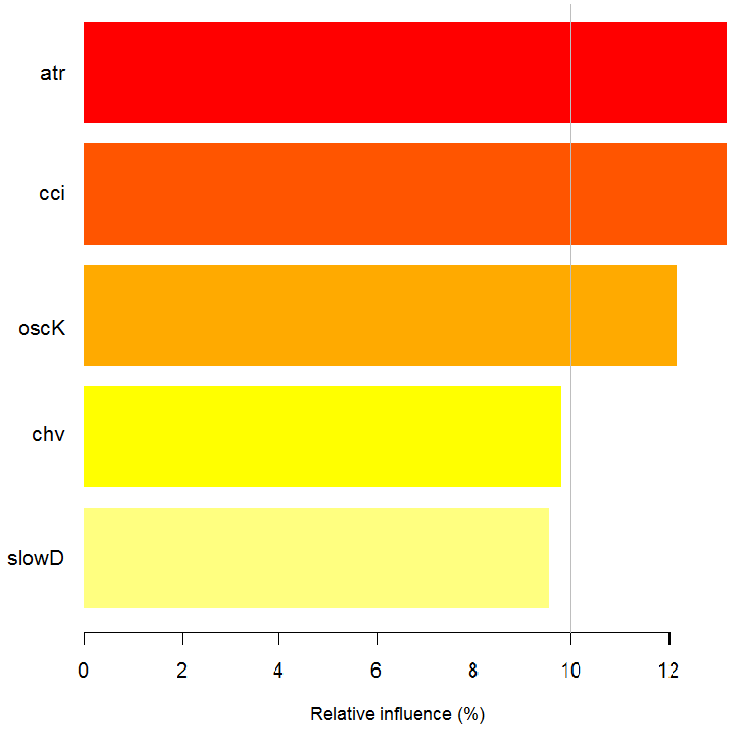
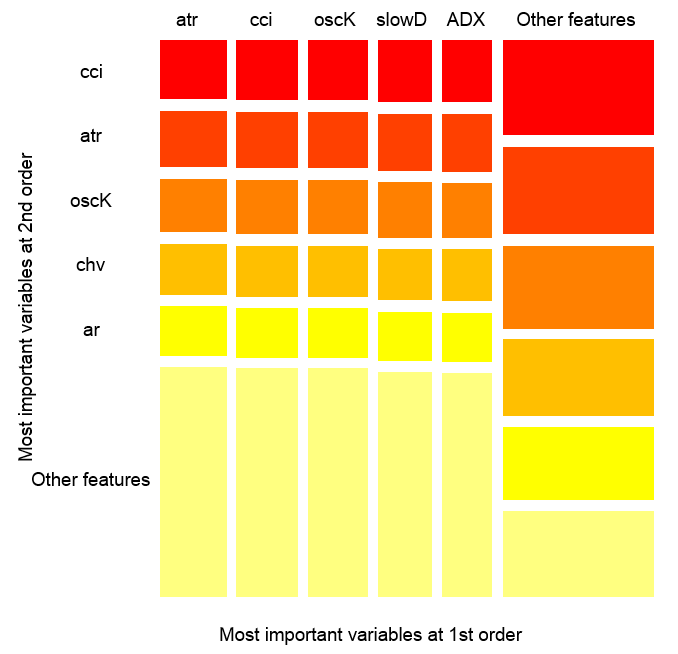
> imp.ruf <- importance(ruf, Xtest = x.test, maxInteractions = 3) 1 - Global Variable Bedeutung (15 größte Bedeutung basieren auf Informationsgewinn) : Hinweis: die meisten prädiktiven Funktionen sind sortiert nach "Score" und werden geplottet. Die am meisten diskriminanten sollten auch in durch Überprüfung von 'class' und 'class.frequency' berücksichtigt werden. variables score class class.frequency percent 1 cci 2568 1 0.50 100.00 2 signal 2438 1 0.51 94.92 3 slowD 2437 1 0.51 94.90 4 oscK 2410 1 0.50 93.85 5 ADX 2400 -1 0.51 93.44 6 vol 2395 1 0.51 93.24 7 atr 2392 -1 0.51 93.15 8 sign 2388 1 0.50 92.97 9 vsig 2383 1 0.50 92.81 10 ar 2363 -1 0.51 92.01 11 chv 2327 -1 0.50 90.62 12 cmo 2318 -1 0.51 90.28 13 DX 2314 1 0.50 90.10 14 oscDX 2302 -1 0.51 89.64 15 tr 2217 1 0.52 86.31 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 6 14 6 15 6 2 - lokale Variable Bedeutung Variablen-Interaktionen (10 wichtigste Variablen in erster (Spalten) und zweiter (Zeilen) Reihenfolge): Für jede Variable (bei jeder Reihenfolge), wird ihre Interaktion mit anderen berechnet. cci cmo slowD oscK signal atr chv cmo 0.1933 0.1893 0.1345 0.1261 0.1146 0.1088 0.1062 cci 0.1770 0.1730 0.1182 0.1098 0.0983 0.0925 0.0899 slowD 0.1615 0.1575 0.1027 0.0943 0.0828 0.0770 0.0744 signal 0.1570 0.1530 0.0981 0.0897 0.0782 0.0725 0.0698 atr 0.1490 0.1450 0.0902 0.0818 0.0703 0.0646 0.0619 ADX 0.1468 0.1428 0.0879 0.0795 0.0680 0.0623 0.0596 ar 0.1452 0.1413 0.0864 0.0780 0.0665 0.0608 0.0581 oscK 0.1441 0.1401 0.0853 0.0769 0.0654 0.0596 0.0570 DX 0.1407 0.1367 0.0819 0.0735 0.0620 0.0562 0.0536 oscDX 0.1396 0.1356 0.0807 0.0723 0.0608 0.0551 0.0524 avg1rstOrder 0.1483 0.1443 0.0895 0.0811 0.0696 0.0638 0.0612 ADX tr ar vsig DX oscDX sign cmo 0.1026 0.1022 0.1013 0.1000 0.0977 0.0973 0.0964 cci 0.0864 0.0859 0.0850 0.0837 0.0815 0.0810 0.0802 slowD 0.0708 0.0704 0.0695 0.0682 0.0660 0.0655 0.0647 signal 0.0663 0.0659 0.0650 0.0637 0.0614 0.0610 0.0601 atr 0.0584 0.0579 0.0570 0.0557 0.0535 0.0531 0.0522 ADX 0.0561 0.0557 0.0548 0.0534 0.0512 0.0508 0.0499 ar 0.0546 0.0541 0.0533 0.0519 0.0497 0.0493 0.0484 oscK 0.0534 0.0530 0.0521 0.0508 0.0486 0.0481 0.0473 DX 0.0500 0.0496 0.0487 0.0474 0.0452 0.0447 0.0439 oscDX 0.0489 0.0485 0.0476 0.0463 0.0440 0.0436 0.0427 avg1rstOrder 0.0577 0.0572 0.0563 0.0550 0.0528 0.0524 0.0515 vol avg2ndOrder cmo 0.0889 0.1173 cci 0.0726 0.1010 slowD 0.0571 0.0855 signal 0.0526 0.0810 atr 0.0447 0.0730 ADX 0.0424 0.0707 ar 0.0409 0.0692 oscK 0.0397 0.0681 DX 0.0363 0.0647 oscDX 0.0352 0.0636 avg1rstOrder 0.0439 0.0000 Variablenbedeutung anhand von Interaktionen (10 wichtigsten): cmo cci slowD signal oscK atr ADX ar 0.1447 0.1419 0.0877 0.0716 0.0674 0.0621 0.0563 0.0533 chv DX 0.0520 0.0485 Variable Bedeutung über Lables (10 wichtigsten Variablen bedingt für jeden Label): Class -1 Class 1 cci 0.16 0.23 cmo 0.20 0.18 slowD 0.09 0.10 oscK 0.09 0.07 signal 0.05 0.07 tr 0.02 0.07 ADX 0.06 0.03 chv 0.06 0.04 atr 0.05 0.06 ar 0.05 0.03
Von dem was wir sehen, wird die Bedeutung der Top 10 der Variablen auf Basis der Interaktion mit anderen, die mit der Reihenfolge der globalen Bedeutungnicht übereinstimmen, hervorgehoben.. Und schließlich die Bedeutung der Variablen von Klassen unter Berücksichtigung ihres Beitrags und Beteiligung. Bitte beachten Sie, dass die Variable tr, die auf der Grundlage von globaler Bedeutung an letzter Stelle war, und laut Theorie daher verworfen werden sollte, durch die starke Wechselwirkung tatsächlich auf den sechsten Platz gestiegen ist.
Also lauten die Top 10 Variablen:
> best <- Cs(cci, cmo, slowD, oscK, signal, tr, ADX. chv, atr, ar)Lassen Sie uns prüfen, wie sich die Modellqualität mit den wichtigsten Prädiktoren verbessert hat.
> x.tr <- x.train[ ,best] > x.tst <- x.test[ ,best] > ruf.opt <- randomUniformForest(X = x.tr, + Y = y.train, + xtest = x.tst, + ytest = y.test, + ntree = 300, + mtry = "random", + nodesize = 1, + threads = 2) Labels -1 1 wurden für eine einfache Berechnung in 1 2 konvertiert und werden intern als Ersatz verwendet werden. > ruf.opt Aufruf: randomUniformForest.default(X = x.tr, Y = y.train, xtest = x.tst, ytest = y.test, ntree = 300, mtry = "random", nodesize = 1, threads = 2) Typ von random uniform forest: Klassifizierung paramsObject ntree 300 mtry random nodesize 1 maxnodes Inf replace TRUE bagging FALSE depth Inf depthcontrol FALSE OOB TRUE importance TRUE subsamplerate 1 classwt FALSE classcutoff FALSE oversampling FALSE outputperturbationsampling FALSE targetclass -1 rebalancedsampling FALSE randomcombination FALSE randomfeature FALSE categorical variables FALSE featureselectionrule entropy Out-of-bag (OOB) Evaluierung OOB Schätzung der Fehlerquote: 18,69 % OOB Fehlerquote begrenzt (mit 1 % Abweichung): 19,67 % OOB Konfusionsmatrix: Reference Prädiktion -1 1 class.error -1 1079 253 0.1899 1 241 1070 0.1838 OOB Schätzung von AUC: 0.8131 OOB Schätzung von AUPR: 0.7381 OOB Schätung des F1-Score: 0.8125 OOB (angepasste) Schätzung des geometrischen Mittels: 0.8131 Breiman's Grenzen Erwartet Vorhersagefehler (unter annähernd ausbalancierten Klassen): 14,98 % Obere Grenze: 28.18% Mittlere Korrelation zwischen Bäumen: 0.0666 Stärke (margin): 0.5548 Standardabweichung der Stärke: 0.2945 > pr.ruf.opt <- predict(ruf.opt, x.tst, type = "response") > ms.ruf.opt <- model.stats(pr.ruf.opt, y.test) Testmennge Fehlerquote: 17,55 % Konfusionsmatrix: Reference Prädiktion -1 1 class.error -1 552 124 0.1834 1 108 538 0.1672 Bereich unter ROC Kurve: 0.8245 Bereich unter Precision-Recall Kurve: 0.8212 F1-Score: 0.8226 Geometrisches Mittel: 0.8244
Abb. 5. ROC Kurve oder Fehlerkurve
Abb. 6. Precision-recall curve
Die Qualität hat sich deutlich verbessert. Die Vorhersagefehler auf der Testmenge 17,55 % ist niedriger als der obere Level 28,18 %, daher ist ein Neutraining höchst unwahrscheinlich. Das Modell hat viele andere Hyperparameter, deren Tuning weitere Verbesserung der Qualität des Modells ermöglichen kann, dies ist jedoch nicht Ziel des aktuellen Artikels.
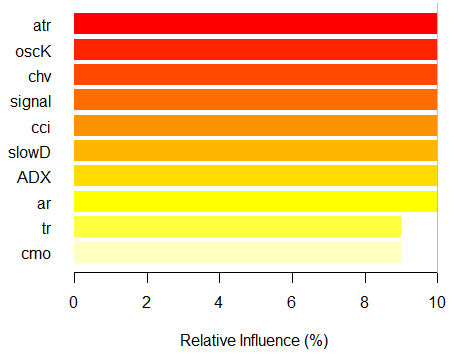
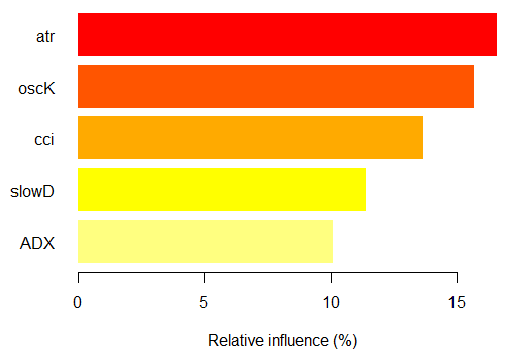
> imp.ruf.opt <- importance(ruf.opt, Xtest = x.tst) Relevante Variablen wurden extrahiert. 1 - Globale Variable Bedeutung (10 wichtigste basierend auf Informationsgewinn): Hinweis: die meisten prädiktiven Funktionen sind sortiert nach "Score" und werden geplottet. Die am meisten diskriminanten sollten auch in durch Überprüfung von 'class' und 'class.frequency' berücksichtigt werden. variables score class class.frequency percent 1 atr 3556 -1 0.50 100.00 2 oscK 3487 -1 0.51 98.07 3 chv 3465 1 0.51 97.45 4 signal 3432 1 0.51 96.51 5 cci 3424 1 0.50 96.30 6 slowD 3415 1 0.51 96.04 7 ADX 3397 -1 0.50 95.52 8 ar 3369 -1 0.50 94.76 9 tr 3221 1 0.53 90.59 10 cmo 3177 -1 0.50 89.36 percent.importance 1 10 2 10 3 10 4 10 5 10 6 10 7 10 8 10 9 9 10 9 2 - lokale Variable Bedeutung Variablen-Interaktionen (10 wichtigste Variablen in erster (Spalten) und zweiter (Zeilen) Reihenfolge): Für jede Variable (bei jeder Reihenfolge), wird ihre Interaktion mit anderen berechnet. atr cci oscK slowD ADX tr chv cci 0.1748 0.1625 0.1620 0.1439 0.1411 0.1373 0.1349 atr 0.1650 0.1526 0.1522 0.1341 0.1312 0.1274 0.1251 oscK 0.1586 0.1462 0.1457 0.1277 0.1248 0.1210 0.1186 chv 0.1499 0.1375 0.1370 0.1190 0.1161 0.1123 0.1099 ar 0.1450 0.1326 0.1321 0.1140 0.1112 0.1074 0.1050 signal 0.1423 0.1300 0.1295 0.1114 0.1085 0.1047 0.1024 ADX 0.1397 0.1273 0.1268 0.1088 0.1059 0.1021 0.0997 slowD 0.1385 0.1262 0.1257 0.1076 0.1048 0.1010 0.0986 cmo 0.1276 0.1152 0.1147 0.0967 0.0938 0.0900 0.0876 tr 0.1242 0.1118 0.1113 0.0932 0.0904 0.0866 0.0842 avg1rstOrder 0.1466 0.1342 0.1337 0.1156 0.1128 0.1090 0.1066 signal ar cmo avg2ndOrder cci 0.1282 0.1182 0.1087 0.1412 atr 0.1184 0.1084 0.0989 0.1313 oscK 0.1120 0.1020 0.0925 0.1249 chv 0.1033 0.0933 0.0838 0.1162 ar 0.0984 0.0884 0.0789 0.1113 signal 0.0957 0.0857 0.0762 0.1086 ADX 0.0931 0.0831 0.0736 0.1060 slowD 0.0919 0.0819 0.0724 0.1049 cmo 0.0810 0.0710 0.0615 0.0939 tr 0.0776 0.0676 0.0581 0.0905 avg1rstOrder 0.0999 0.0900 0.0804 0.0000 Variable Importance based on interactions (10 most important) : atr cci oscK chv slowD ADX signal ar 0.1341 0.1335 0.1218 0.0978 0.0955 0.0952 0.0898 0.0849 tr cmo 0.0802 0.0672 Variable Bedeutung über Labels (10 wichtigste Variablen bedingt für jeden Label): Class -1 Class 1 atr 0.17 0.14 oscK 0.16 0.11 tr 0.03 0.16 cci 0.14 0.13 slowD 0.12 0.09 ADX 0.10 0.10 chv 0.08 0.10 signal 0.09 0.07 cmo 0.07 0.03 ar 0.06 0.06
Abb. 7. Die Bedeutung der Variablen basierend auf dem Informationsgewinn
Wie wir sehen können, hat sich die globale Bedeutung der Variablen fast eingependelt, aber die Bedeutung der Variablen nach Klassen wird anders eingestuft. Die tr -Variable nimmt den dritten Platz ein.
Partielle Abhängigkeit über Prädiktor
Die partielle Abhängigkeit der wichtigsten Variablen wird berücksichtigt.
> plot(imp.ruf.opt, Xtest = x.tst)
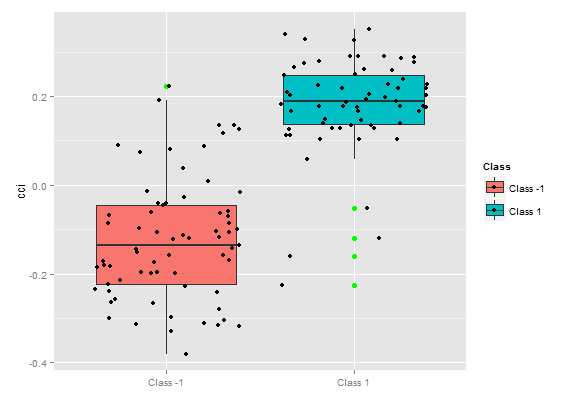
Abb. 8. Partielle Abhängigkeit der CCI Variable
> pd.signal <- partialDependenceOverResponses(x.tst, + imp.ruf.opt, + whichFeature = "signal", + whichOrder = "all" + )
Abb. 9. Partielle Abhängigkeit der signal Variablen
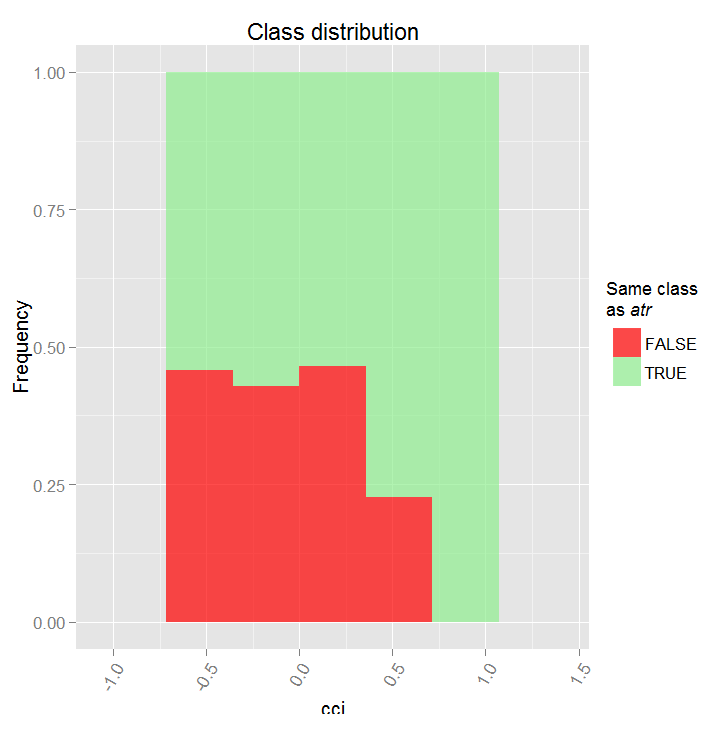
Es zeigt sich ein ganz anderes Bild einer partiellen Abhängigkeit für den Signal Prädiktor in der Abbildung oben. Fast komplette Datenabdeckung für beide Klassen ist zu beobachten.
> pd.tr <- partialDependenceOverResponses(x.tst,
imp.ruf.opt,
whichFeature = "tr",
whichOrder = "all"
)
Eine teilweise Abhängigkeit vom tr Prädiktor zeigt eine angemessene Trennung von Klassen, es gibt hier noch immer eine beträchtliche Abdeckung.
Abb. 10. Partielle Abhängigkeit der tr -variable
> pd.chv <- partialDependenceOverResponses(x.tst,
imp.ruf.opt,
whichFeature = "chv",
whichOrder = "all")
Eine partielle Abhängigkeit vom CHV Prädiktor ist absolut bedauerlich. Eine komplette Datenabdeckung von Klassen ist zu beobachten.
Abb. 11. Partielle Abhängigkeit der Chv -Variablen
Auf diese Weise können wir visuell bestimmen, wie die Prädiktordaten mit den Klassen verknüpft sind, und wie trennbar sie sind.
Die Bedeutung der Variable über Klassen
"Die Bedeutung der Variable" über Klassen bietet eine lokale Perspektive: die Klasse ist fixiert, was bedeutet, dass die erste Entscheidung ist, die Klasse unter Berücksichtigung der Variablen, die wichtig sind und als Konstanten fungieren zu fixieren und eventuell werden die wichtigen Variablen für jede Klasse berücksichtigt. Daher hat jede Variable Bedeutung, als gäbe es keine anderen Klassen.
Hier sind wir nicht an Variablen, die zur Wahl einer Klasse führen, interessiert sondern an Variablen, die in der Klasse wichtig sein werden, wenn diese ausgewählt werden. Die Reihenfolge der Variablen gibt ihr freies Ranking wider hinsichtlich ihres Ranges in jeder Klasse ohne Rücksicht auf Bedeutung der Klasse.
Was zeigt das Diagramm? Der tr -Prädiktor ist wesentlich wichtiger für die "1" Klasse als für die "-1"-Klasse. Und umgekehrt, der OscK Prädiktor für die Klasse "-1" ist wichtiger als für die "1"-Klasse. Prädiktoren haben unterschiedlichen Bedeutung in verschiedenen Klassen.
Abb. 12. Bedeutung der Variablen von Klassen
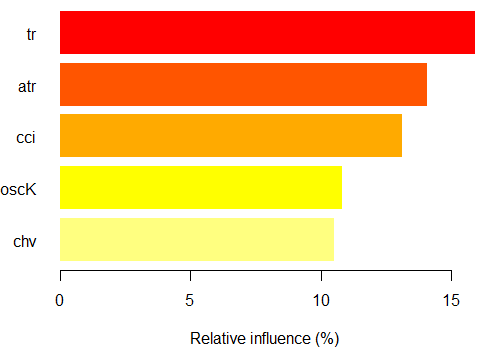
Die Bedeutung der Variablen basierend auf Interaktion
Das Diagramm unten zeigt, wie jede Variable in der gemeinsamen Interaktion mit anderen Variablen dargestellt wird. Eine wichtige Bemerkung: die erste Variable ist nicht unbedingt die wichtigste, sondern es ist diejenige, die die größte wechselseitige Beeinflussung mit anderen hat.
Abb. 13. Die Bedeutung der Variablen basierend auf Interaktionen
Variablen-Interaktionen über Beobachtungen
Abb. 14. Die Bedeutung der Variablen über Beobachtungen
Die obige Abbildung zeigt das Zusammenspiel von erster und zweiter Ordnung für alle Prädiktoren im Einklang mit der Definition, die wir für die Interaktiongegeben haben. Ihre Fläche entspricht Einheit. Der erste Ordnung bedeutet, dass Variablen (sortiert nach absteigendem Einfluss) am wichtigsten sind, wenn die Entscheidung unter Berücksichtigung nur einer Variable getroffen werden muss. Der zweite Ordnung zeigt, dass die unbekannte Variable bereits in der ersten Ordnung ausgewählt ist, dann wird die zweitwichtigste Variable eine von denen in der zweiten Ordnung.
Zur Klarstellung: die Interaktion liefert eine Tabelle von geordneten Features. Die erste Ordnung liefert geordnete Möglichkeiten der wichtigsten Variablen. Die zweite Ordnung liefert geordnete Möglichkeiten der zweitwichtigsten Variablen. Der Schnittpunkt eines Variablenpaares gibt ihre relative gegenseitige Beeinflussung aus allen möglichen gegenseitigen Einflüssen wider. Bitte beachten Sie, dass diese Messungen abhängig von Modell und Daten. sind Daher hängt das Vertrauen in Messungen direkt vom Vertrauen in Vorhersagen ab. Wir können auch hinzufügen, dass eine Meta-variable namens "andere Zeichen" auftritt, was bedeutet, dass wir dem Algorithmus erlauben, die Standardansicht für die Visualisierung der weniger relevanten gruppierten Variablen zu zeigen.
Partielle Bedeutung
Die partielle Bedeutung basierend auf x.tst Beobachtungen über die Klasse "-1" können Sie hier anschauen.
> par.imp.ruf <- partialImportance(X = x.tst, + imp.ruf.opt, + whichClass = "-1") Relativen Einfluss: 67.41% Basierend auf x.tst und Klasse «-1»
Abb. 15. Partielle Bedeutung der Variablen basierend auf Beobachtungen über die Klasse "-1"
Wie wir sehen, sind die wichtigsten Prädiktoren für die Klasse "-1" fünf Prädiktoren ersichtlich auf der Abbildung oben.
Jetzt das gleiche für die Klasse "+ 1"
> par.imp.ruf <- partialImportance(X = x.tst, + imp.ruf.opt, + whichClass = "1") Relativer Einfluss: 64,45%
Abb. 16. Partielle Bedeutung der Variablen basierend auf Beobachtungen über die Klasse "+ 1"
Wir sehen, dass die Prädiktoren sowohl in Struktur als auch Rankings unterscheiden.
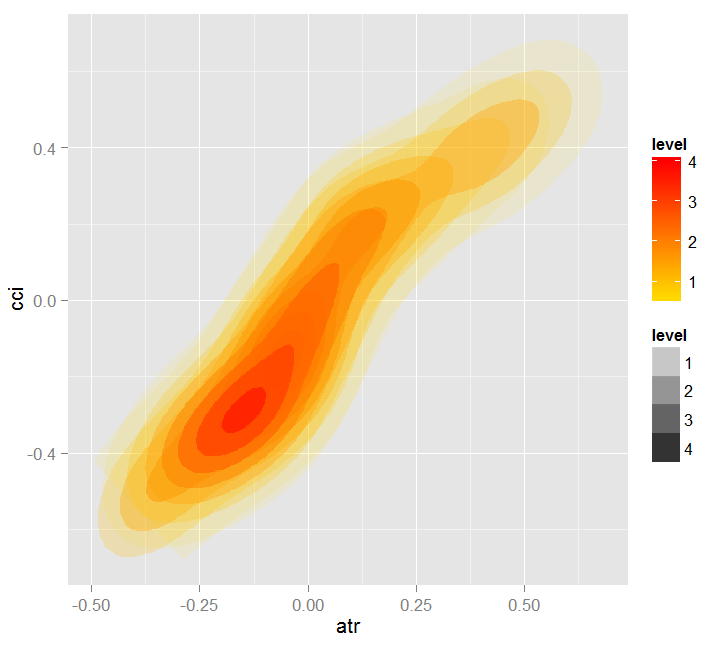
Sehen wir uns die teilweise Abhängigkeit zwischen den Prädiktoren cci und atr an, die die wichtigsten in der ersten und der zweiten Ordnung der Prädiktorinteraktion sind.
> par.dep.1 <- partialDependenceBetweenPredictors(Xtest = x.tst, + imp.ruf.opt, + features = Cs(atr, cci), + whichOrder = "all", + perspective = T) Level von Interaktionen zwischen atr und cci bei der ersten Ordnung: 0.1748 (99,97% der Features mit höchstem Level) Level von Interaktionen zwischen atr und cci an zweiter Ordnung: 0.1526 (87.28% der Features mit höchstem Level) Klassen-Verteilung : für eine Variable des Paares, zeigt die geschätzte Wahrscheinlichkeit das die betrachtete Variable die selbe Klasse hat wie die andere. Wenn dieselbe Klasse tendenziell WAHR ist, hat die Variable möglicherweise einen Einfluss auf die andere (für die betrachteten Kategorien oder Werte) bei der Vorhersage eines Labels. Abhängigkeit : für das Paar von Variablen, zeigt die Form ihrer Abhängigkeit und die geschätzte Übereinstimmung in der Vorhersage derselben Klasse für die Werte, die Abhängigkeit definieren. Im Fall der kategorialen Variablen wird Kreuztabellierung verwendet. Heatmap : für das Paar von Variablen, zeigt den Bereich, wo die Abhängigkeit die effektivste ist . Je dunkler die Farbe, die stärker ist die Abhängigkeit. Aus dem Paar von Variablen, ist diejenige die dominiert, möglicherweise jene die am meisten diskriminiert ist (wenn man die "Globale Variable Bedeutung" betrachtet) bzw. diejenige, die das höhere Niveau der Interaktionen hat (wenn man "Variable Bedeutung anhand von Interaktionen").
Abb. 17. Partielle Abhängigkeit zwischen Prädiktoren cci und atr
Abb. 18. Abhängigkeit zwischen Prädiktoren atr und cci
Abb. 19. Heatmap der Abhängigkeit zwischen Prädiktoren atr und cci
Es sollte durch die Bedeutung der globalen Variable beschrieben werden welche globale Variablen den größten Einfluss auf die Verringerung der Vorhersagefehlers hat.
Die Bedeutung der lokalen Variable beschreibt was eine Variable - durch Verwendung ihrer Interaktion mit anderen - einflussreich macht .
Dies führt zu einer teilweisen Bedeutung die zeigt, wann eine Variable wichtiger ist. Der letzte Schritt bei der Analyse der Bedeutung der Variablen ist eine partielle Abhängigkeit, die auftritt, wenn und/oder wie jede Variable mit einer Antwort verknüpft ist.
Zusammenfassung: die Bedeutung einer Variablen in den Random Uniform Forests geht mit der Detaillierung vom höchsten bis zum niedrigsten Level. Zuerst finden wir heraus, welche Variablen wichtig sind und lernen Gewichtungs-Nuancen in jeder Klasse. Dann finden wir heraus, was sie angesichts ihrer Wechselwirkung einflussreich macht und wählen zuerst eine Variable die alle Klassen als eine betrachtet. Der nächste Schritt – wir lernen, unter Betrachtung innerhalb einer Klasse wenn sie fixiert wurde wo sie ihren Einfluss erhalten. Zu guter Letzt ermitteln wir mit Blick auf die "partielle Abhängigkeit" wann und wie die Variable wichtig sein kann/ist . Alle Messungen, mit Ausnahme von "globale Variable der Bedeutung", arbeiten bei jeder Trainings- oder Restmenge.
Eine vorgestellte mehrstufige Bewertung der Prädiktoren ermöglicht, die wichtigsten Prädiktoren zu wählen und durch deutliche Reduktion von Datendimension und Verbesserung der Qualität der Vorhersagen optimale Mengen zu erstellen.
Sie können nicht nur Prädiktoren bewerten und auswählen, sondern auch die informativsten Beobachtungselemente.
Schauen wir uns ein weiteres interessantes Paket an — "RoughSet".
Kurze Beschreibung: Es gibt zwei Hauptbereiche, die in diesem Paket abgedeckt werden: die Rough Set Theory (RST) und die Fuzzy Rough Set Theory (FRST)). RST wurde von Z. Pawlak vorgeschlagen (1982, 1991), sie bietet anspruchsvolle mathematische Instrumente für die Modellierung und Analyse von Informationssystemen, die Heterogenität und Ungenauigkeiten enthalten. Mit Hilfe der Ununterscheidbarkeits-Beziehungen zwischen Objekten erfordert RST keine zusätzliche Parameter um Informationen zu extrahieren.
Die FRST Theorie, RST-Erweiterung, wurde von D. Dubois und H. Prade (1990) vorgeschlagen, sie verbindet die Begriffe Unsicherheit und Ununterscheidbarkeit die in von L.A. vorgeschlagenen Fuzzy-Mengen zum Ausdruck gebracht werden. Zadeh (1965) und RST. Dieses Konzept erlaubt kontinuierliche Attribute (Variablen) ohne vorherige Daten-Diskretisierung zu analysieren. Basierend auf den oben beschriebenen Konzepten wurdenviele Methoden vorgeschlagen und in verschiedenen Bereichen verwendet. Um Probleme zu lösen verwenden die Methoden das Verhältnis von Ununterscheidbarkeit und das Konzept der unteren und oberen Annäherung.
Bitte gestatten Sie mir einen kleinen Exkurs.
Eine Methode der Wissensrepräsentation spielt in der Regel eine wichtige Rolle in Informationssystemen. Die bekanntesten Methoden der Präsentation von Wissen in den Systemen der induktiven Begriffsbildung sind: Erstellungsvorschriften, Entscheidungsbäume, Prädikatenberechnung und semantische Netze.
Für Extraktion und Generalisierung von Wissen das in den eigentlichen Informations-Arrays gespeichert ist, treten folgende Hauptprobleme auf:
- Die Daten sind unterschiedlich (quantitativ, qualitativ, strukturell).
- Heutge Datenbanken sind normalerweise groß, daher können Algorithmen mit exponentieller Komplexität für das Abrufen von Wissen aus der Datenbank nicht akzeptabel erscheinen.
- Die Angaben in den eigentlichen Daten-Arrays kann unvollständig, übertrieben, verzerrt, kontrovers sein und einige Werte einer Reihe von Attributen kann völlig fehlen. Für den Bau der Klassifizierungsregeln verwenden Sie daher nur die vorhandenen Attribute.
Derzeit wird zunehmend für die Gewinnung von Wissen aus der Datenbank (Data Mining) die Rough Sets Theorie als ein theoretischer Rahmen und eine Menge von praktischen Methoden eingesetzt.
Approximierte Mengen haben nicht definierte Grenzen, d.h. sie können nicht genau durch eine Reihe von verfügbaren Features beschrieben werden .
Eine Theorie für approximative Mengen wurde von Zdzislaw Pawlak 1982 vorgeschlagen und wurde ein neues mathematisches Instrument für die Arbeit mit unvollständigen Informationen. Das wichtigste Konzept dieser Theorie ist eine so genannte obere und untere Annäherung der approximativen Mengen, die es erlaubt, die Möglichkeit oder die Notwendigkeit der Zugehörigkeit der Elemente einer Menge mit "fuzzy" Grenzen zu bewerten.
Die unteren Annäherung besteht aus Elementen, die auf jeden Fall zu X gehören, eine höhere Annäherung enthält Elemente, die möglicherweise zu X gehören. Der Randbereich der X-Reihe ist der Unterschied zwischen höherer und unterer Annäherung, d.h. der Grenzbereich hat Elemente aus der X-Menge, die zu einer höheren Annäherung gehören als zu einer niedrigeren Annäherung.
Ein einfaches, aber leistungsfähiges Konzept der approximativen Mengen wurde eine Basis für mehrere theoretische Studien – Logik, Algebra, Topologie und angewandte Studien – künstliche Intelligenz, approximative Argumentation, Analyse von intellektuellen Daten, Entscheidungstheorie, Bildverarbeitung und Mustererkennung.
Das Konzept von "approximativen Mengen" befasst sich mit "Daten Unvollkommenheit" im Zusammenhang mit "Granularität" der Information. Dieses Konzept ist von Natur aus topologisch und ergänzt andere bekannte Ansätze für die Arbeit mit unvollständigen Informationen, z. B. Fuzzy-Mengen, Bayesian Argumentation, neuronale Netze, evolutionäre Algorithmen, statistische Methoden der Datenanalyse.
Lassen Sie uns forsetzen. Alle Methoden, die in diesem Paket bereitgestellt werden, können entsprechend gruppiert werden:
Grundbegriffe der RST und FRST. In diesem Teil können wir vier verschiedene Aufgaben beobachten: Fehlerunerkennbarkeits-Beziehung, untere und obere Annäherung, positive Region und Fehlererkennbarkeits-Matrix.
Diskretisierung. Sie wird zur Konvertierung physikalischer Daten in nominale verwendet. Aus der Perspektive der RST versucht diese Aufgabe, die Fehlererkennbarkeit zwischen Objekten aufrechtzuerhalten.
Featureauswahl. Dies ist ein Prozess des Findens von Teilmengen von Prädiktoren, die versuchen, die gleiche Qualität wie die ganze Menge von Prädiktoren zu erhalten. Das heißt das Ziel ist, die wesentlichen Merkmale auszuwählen und ihre Abhängigkeit zu beseitigen. Es ist nützlich und notwendig, wenn wir mit einer Menge von Daten die mehrere Features enthält konfrontiert sind. In Begriffen von RST und FRST bezieht sich die Auswahl der Prädiktoren auf die Suche nach Superreduktionen und Reduktionen.
Auswahl der Instanz. Dieser Prozess zielt darauf ab, verrauschte, unnötige oder widersprüchliche Kopien aus der Trainingsdatenmenge zu enttfernen während die Kohäerenz erhalten bleibt. Daher wird eine gute Klassifizierungsgenauigkeit durch die Entfernung von Mustern, die keinen positiven Beitrag leisten, erreicht.
Regel-Induktion. Wie wir bereits erwähnt haben, wird die Aufgabe der Erzeugung von Regeln verwendet, um Regeln zu Generieren, die Wissen aus der Lösungstabelle bereitsstellen. In der Regel wird dieser Prozess als Trainingsphase im maschinellen Lernen bezeichnet.
Vorhersage/Klassifizierung. Diese Aufgabe wird verwendet, um die Werte einer Variablen aus dem neuen Datensatz (Testmenge) vorherzusagen.
Wir werden aus dieser Liste nur zwei Kategorien erkunden – Auswahl der Prädiktoren und Auswahl der Muster.
Lassen Sie uns die Ein- und Ausgabedaten bilden. Wir werden die gleichen Daten, die wir zuvor erhalten haben verwenden, werden sie aber in eine "DecisionTable"-Klasse transformieren mit der das Paket arbeitet.> library(RoughSets) Erforderliche Paket laden: Rcpp > require(magrittr) > data.tr <- SF.asDecisionTable(data.f[idx$tr, ], + decision.attr = 16, + indx.nominal = 16) > data.tst <- SF.asDecisionTable(data.f[idx$ts, ], + decision.attr = 16, + indx.nominal = 16 + ) > true.class <- data.tst[ ,ncol(data.tst)]Wie wir bereits erwähnt haben, verwendet RST nominale Daten. Da wir kontinuierliche numerische Daten haben, wollen wir diese mit Hilfe einer spezialisierten Diskretisierungs-Funktion aus dem Paket in nominale Daten konvertieren.
> cut.values <- D.global.discernibility.heuristic.RST(data.tr) > data.tr.d <- SF.applyDecTable(data.tr, cut.values)
Mal sehen, was wir als Ergebnis erhalten:
> summary(data.tr.d) DX ADX (12.5,20.7]: 588 (17.6,19.4]: 300 (20.7, Inf]:1106 (19.4,25.4]: 601 [-Inf,12.5]: 948 (25.4,31.9]: 294 (31.9, Inf]: 343 [-Inf,17.6]:1104 oscDX ar (1.81, Inf]:1502 (-40.6,40.6]:999 [-Inf,1.81]:1140 (40.6,71.9] :453 (71.9, Inf] :377 [-Inf,-40.6]:813 tr atr (0.000205,0.000365]:395 (0.00072,0.00123]:1077 (0.000365,0.0005] :292 (0.00123, Inf] : 277 (0.0005,0.00102] :733 [-Inf,0.00072] :1288 (0.00102,0.00196] :489 (0.00196, Inf] :203 [-Inf,0.000205] :530 cci chv (-6.61, Inf]:1356 (-0.398,0.185]:1080 [-Inf,-6.61]:1286 (0.185,0.588] : 544 (0.588, Inf] : 511 [-Inf,-0.398] : 507 cmo sign (5.81,54.1]: 930 [-Inf, Inf]:2642 (54.1, Inf]: 232 [-Inf,5.81]:1480 vsig slowD (0.0252, Inf]:1005 [-Inf, Inf]:2642 [-Inf,0.0252]:1637 oscK signal (-0.0403,0.000545]:633 (-11.4, Inf]:1499 (0.000545,0.033] :493 [-Inf,-11.4]:1143 (0.033, Inf] :824 [-Inf,-0.0403] :692 vol Klasse (0.0055,0.00779]:394 -1:1319 (0.00779,0.0112]:756 1 :1323 (0.0112,0.0154] :671 (0.0154, Inf] :670 [-Inf,0.0055] :151
Wir sehen, dass die Prädiktoren anders diskretisiert werden. Variablen wie slowD, sign sind überhaupt nicht getrennt. Variablen signal, vsig, cci, oscDX sind einfach in zwei Bereiche unterteilt. Die anderen Variablen sind zwischen 3 und 6 Klassen unterteilt.
Wir wählen die wichtigen Variablen:
> reduct1 <- FS.quickreduct.RST(data.tr.d, control = list()) > best1 <- reduct1$reduct > best1 DX ADX oscDX ar tr atr cci 1 2 3 4 5 6 7 chv cmo vsig oscK signal vol 8 9 11 13 14 15
Daten, die nicht geteilt waren (slowD, sign( ) werden aus der Gruppe entfernt. Wir führen die Testmengen Diskretisierung aus und verwandeln sie entsprechend der durchgeführten Reduktion .
> data.tst.d <- SF.applyDecTable(data.tst, cut.values) > new.data.tr <- SF.applyDecTable(data.tr.d, reduct1) > new.data.tst <- SF.applyDecTable(data.tst.d, reduct1)
Nun werden wir mit Hilfe einer ausgezeichnete Funktion des Pakets "indcution rules" eine Reihe von Regeln extrahieren, die Prädiktoren und ein Ziel zusammenbinden. Eine der folgenden Optionen wird verwendet:
> rules <- RI.AQRules.RST(new.data.tr, confidence = 0.9, timesCovered = 3)
Wir prüfen auf der Testmenge, wie diese Regeln bei der Vorhersage arbeiten :
> pred.vals <- predict(rules, new.data.tst) > table(pred.vals) pred.vals -1 1 655 667
Metriken:
> caret::confusionMatrix(true.class, pred.vals[ ,1]) Konfusionsmatrix und Statistiken Reference Prädiktion -1 1 -1 497 163 1 158 504 Genauigkeit: 0.7572 95% CI : (0.7331, 0.7801) Rate von fehlenden Informationen: 0.5045 P-Value [Acc > NIR] : <2e-16 Kappa : 0.5144 Mcnemar's Test P-Wert : 0.8233 Sensitivität : 0.7588 Besonderheit: 0.7556 Pos Pred Wert : 0.7530 Neg Pred Wert : 0.7613 Prävalenz: 0.4955 Erkennungsrate: 0.3759 Erkennung-Prävalenz: 0.4992 Ausgewogene Genauigkeit: 0.7572 'Positive' Class : -1
Und jetzt – eine Auswahl an signifikanten Beispielen:
> ##-----Instanz Auswahl----------- > res.1 <- IS.FRIS.FRST(decision.table = data.tr, control = list(threshold.tau = 0.5, alpha = 1, type.aggregation = c("t.tnorm", "lukasiewicz"), t.implicator = "lukasiewicz")) > new.data.tr <- SF.applyDecTable(data.tr, res.1) > nrow(new.data.tr) [1] 2353Rund 300 Beispiele wurden als unwesentlich bewertet und verworfen. Wir werden eine Menge von Reihe von Regeln aus dieser Menge extrahieren und Qualität der Vorhersage mit einer vorherigen Menge vergleichen.
> rules <- RI.AQRules.RST(new.data.tr, confidence = 0.9,
timesCovered = 3)
> pred.vals <- predict(rules, new.data.tst)
> table(pred.vals)
pred.vals
-1 1
638 684
> caret::confusionMatrix(true.class, pred.vals[ ,1])
Konfusionsmatrix und Statistiken
Reference
Prädiktion -1 1
-1 506 154
1 132 530
Genauigkeit: 0.7837
95% CI : (0.7605, 0.8056)
Keine Informationen Preis: 0.5174
P-Value [Acc > NIR] : <2e-16
Kappa : 0.5673
Mcnemar's Test P-Wert : 0.2143
Empfindlichkeit: 0.7931
Besonderheit: 0.7749
Pos Pred Wert : 0.7667
Neg Pred Wert : 0.8006
Prävalenz: 0.4826
Erkennungsrate: 0.3828
Erkennung-Prävalenz: 0.4992
Ausgewogene Genauigkeit: 0.7840
'Positive' Class : -1
Die Qualität ist höher als im vorherigen Fall. Es sei darauf hingewiesen, dass es, wie im Fall mit RandomUniformForests, unmöglich ist, reproduzierbare Ergebnisse bei wiederholten Versuchen zu erhalten. Jede neue Ausführung ergibt leicht unterschiedliche Ergebnisse.
Wie sehen die Regeln aus? Mal sehen:> head(rules) [[1]] [[1]]$idx [1] 6 4 11 [[1]]$values [1] "(85.1, Inf]" "(0.00137, Inf]" "(0.0374, Inf]" [[1]]$consequent [1] "1" [[1]]$support [1] 1335 1349 1363 1368 1372 1390 1407 1424 1449 1454 [11] 1461 1472 1533 1546 1588 1590 1600 1625 1630 1661 [21] 1667 1704 1720 1742 1771 1777 1816 1835 1851 1877 [31] 1883 1903 1907 1912 1913 1920 1933 1946 1955 1981 [41] 1982 1998 2002 2039 2040 2099 2107 2126 2128 2191 [51] 2195 2254 2272 2298 2301 2326 2355 2356 2369 2396 [61] 2472 2489 2497 2531 2564 2583 2602 2643 [[1]]$laplace 1 0.9857143
Dies ist eine Liste mit den folgenden Daten:
- $idx - Index der Prädiktoren, die an dieser Regel teilnehmen. Im obigen Beispiel sind diese 6 ("atr") , 4 ("ar") und 11 ("vsig").
- $values — eine Reihe von Wertindikatoren bei denen diese Regel angewendet wird.
- $consequent — solution: class = "1". Um es verständlicher klingen zu lassen: if "atr" is in the range "(85.1, Inf]" UND "ar" is in the range "(0.00137, Inf]" UND "vsig" is in the range "(0.0374, Inf]", THEN Class = "1".
- $support - Indizes der Beispiele für diese Lösung.
- $laplace – eine Bewertung des Konfidenzlevels für diese Regel.
Eine Berechnung der Regeln nimmt sehr viel Zeit in Anspruch.
Fazit
Wir haben neue Möglichkeiten basierend auf der Bewertung von Prädiktoren, ihrer Visualisierung und Auswahl der wertvollsten betrachtet. Wir haben auch verschiedene Ebenen von Bedeutung, Prädiktor Abhängigkeiten und ihre Auswirkungen auf Antworten untersucht. Die Ergebnisse der Experimente werden im nächsten Artikel angewendet werden, wo wir tiefe Netzwerke mit RBM betrachten.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/2029
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Selbst-organisierende Feature Maps (Kohonen Maps) - Wiederaufgreifen des Themas
Selbst-organisierende Feature Maps (Kohonen Maps) - Wiederaufgreifen des Themas
 Arbeit mit einem GSM-Modem über einen Expert Advisor in MQL5
Arbeit mit einem GSM-Modem über einen Expert Advisor in MQL5
 Indikator für Renko-Diagramme
Indikator für Renko-Diagramme
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
in der Echtzeit, verwenden Sie "ohne die letzten 300 Takte"!
Sie sieht so dumm, können Sie es in der Echtzeit zu verwenden.?
Alle Ihre Artikel sind falsch, weil Ihr Ziel zu definieren ist falsch.alle kann nicht in der Echtzeit arbeiten, wie folgen Sie Ihren Punkt, Sie singal wird nach 300 Bars später passieren.
All canot Arbeit in der Echtzeit, als folgen Sie Ihren Punkt, Sie singal wird nach 300 Bars später passiert.
in der Echtzeit, verwenden Sie "ohne die letzten 300 Takte"!
Sie sieht so dumm, können Sie es in der Echtzeit zu verwenden.?
Alle Ihre Artikel sind falsch, weil Ihr Ziel zu definieren ist falsch.alle kann nicht in der Echtzeit arbeiten, wie folgen Sie Ihren Punkt, Sie singal wird nach 300 Bars später passieren.
All canot Arbeit in der Echtzeit, als folgen Sie Ihren Punkt, Sie singal wird nach 300 Bars später passiert.
Sie verstehen die Vision des Autors nicht wirklich, Sie sind zu naiv in Ihrer eigenen Vorstellung, und die Dummheit dessen, was Sie sagen, ist nur auf Sie selbst gemünzt, bitte blamieren Sie Ihr Land nicht mehr, nicht nur dumm, sondern hässlich.
an Vladimir Perervenko: danke nochmals für diese wunderbaren Artikel, Sie haben wirklich gut recherchiert! dieses dumme Ding von "freewalk", nicht alle Chinesen mögen ihn.
Ich habe Ihnen im nächsten Zweig geantwortet.
Hallo Vladimir,
Ich habe deine Antwort auf diese Frage nicht gefunden. Ich bin mir auch nicht sicher, was der Wert von Dig ist. könnten Sie plz spezifizieren. danke!
Liebe Leute,
Kann mir jemand sagen, was die in der Funktion ZZ definierte Variable --Dig-- bedeutet. Handelt es sich um eine Konstante? Wenn ja, was sollte der Wert dieser Konstante sein?
Dig - die Anzahl der Stellen nach dem Dezimalpunkt in Anführungszeichen. Vielleicht 5 oder 3.
Es tut mir leid, dass ich zu spät antworte. Ich habe die Frage nicht gesehen. Die Diskussion ist über viele Zweige verstreut. Ich habe keine Zeit, sie zu verfolgen.
Entschuldigen Sie mich.
Der Artikel ist sehr umfangreich, danke für die Arbeit.
Er ist jedoch fragwürdig:
1. die Verwendung einer Schichtung mit einem ausgewählten Ziel, das auf jedem Balken angegeben ist. Das Mischen von zwei nicht repräsentativen Stichproben verbessert in der Regel das Ergebnis, was es verzerrt.
2. Die auf konstruierten Modellen basierende Merkmalsauswahl, insbesondere angesichts der ersten Split-Randoms und der Greedy-Methode, ist eher eine Methode zur Merkmalsreduzierung für die Modellbildungsmethode. Die gierige Methode ist nicht immer korrekt und stabil. In diesem Fall müssen Sie vielleicht zumindest andere Teilstichproben verwenden.
Die zweite Methode habe ich bis zum Schluss nicht verstanden - ist es das Gleiche mit einem zufälligen ersten Prädiktor, und dann versuchen wir, ein Blatt zu bilden, oder bilden wir einen Baum und lassen das beste Blatt übrig, das für die Auswertung verwendet wird?