
Neuronale Netzwerke der dritten Generation: Tiefe Netzwerke
Inhalt
- Neuronale Netzwerke der zweiten Generation
- 1.1. Die Architektur der Verknüpfungen
- 1.2. Wichtigste Typen neuronaler Netzwerke
- 1.3. Einlernmethoden
- 1.4. Nachteile
- Tiefes Lernen
- 2.1. Hintergrund
- 2.2. Autoencoder. Autoencoder und beschränkte Boltzmann-Maschine. Unterschiede und Besonderheiten
- 2.3. Gestackte autoassoziative Netzwerke. Gestackte Autoencoder (SAE), gestackte beschränkte Boltzmann-Maschine (Stacked RBM)
- 2.4. Einlernen tiefer Netzwerke (DN). Phasen. Besonderheiten
- Praktische Experimente
- 3.1. Die Sprache R
- 3.2. Umsetzungsvarianten und betrachtete Aufgaben
- 3.3. Vorbereitung der Daten für das Experiment
- 3.3.1. Quelldaten
- 3.3.2. Eingabedaten (Prädiktoren)
- 3.3.2.1. Welles Wilder's Directional Movement Index - ADX(HLC, n)
- 3.3.2.2. aroon(HL, n)
- 3.3.2.3. Commodity Channel Index - CCI(HLC, n)
- 3.3.2.4. chaikinVolatility (HLC, n)
- 3.3.2.5. Chande Momentum Oscillator - CMO(Med, n)
- 3.3.2.6. MACD oscillator
- 3.3.2.7. OsMA(Med,nFast, nSlow, nSig)
- 3.3.2.8. Relative Strength Index - RSI(Med,n)
- 3.3.2.9. Stochastic Oscillator - stoch(HLC, nFastK=14, nFastD=3, nSlowD=3)
- 3.3.2.10. Stochastic Momentum Index - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9)
- 3.3.2.11. Volatility (Yang and Zhang) - volatility(OHLC, n, calc="yang.zhang", N=96)
- 3.3.3. Ausgangsdaten (Ziel)
- 3.3.4. Bereinigen von Daten
- 3.3.5. Formen der Stichproben zum Einlernen und Testen
- 3.3.6. Ausgleich von Klassen
- 3.3.7. Vorverarbeitung
- 3.4. Aufbauen, Einlernen und Testen von Modellen
- Umsetzung (Indikator und Expert Advisor)
Einleitung
In diesem Beitrag behandeln wir ohne komplexe Berechnungen und in Laienbegriffen die grundlegenden Ideen der Themen tiefes Lernen (Deep Learning) und tiefe Netzwerke (Deep Network).
Experimente mit realen Daten bestätigen (oder auch nicht) die theoretischen Vorteile tiefer neuronaler Netzwerke gegenüber oberflächlichen Netzwerken durch die Definition und den Vergleich von Messwerten. Die vorliegende Aufgabe ist die Klassifizierung. Wir erstellen einen Indikator und einen Expert Advisor auf Basis des Modells eines tiefen neuronalen Netzwerks, die gemäß dem Client-Server-Schema zusammen arbeiten, und testen sie anschließend.
Es wird davon ausgegangen, dass sich der Leser mit den grundlegenden Konzepten neuronaler Netzwerke auskennt.
1. Neuronale Netzwerke der zweiten Generation
Neuronale Netzwerke sollen auf eine große Bandbreite an Aufgaben im Zusammenhang mit der Verarbeitung von Bildern eingehen.
Nachfolgend sehen Sie eine Liste von Aufgaben, die klassischerweise von neuronalen Netzwerken gelöst werden:
- Approximation von Funktionen durch einen Satz von Punkten (Regression);
- Datenklassifizierung nach dem festgelegten Satz von Klassen;
- Daten-Clustering mit der Identifizierung vorher unbekannter Klassenprototypen;
- Komprimierung von Informationen;
- Wiederherstellung verlorener Daten;
- Assoziativer Speicher;
- Optimierung, optimale Steuerung usw.
Aus der obigen Liste wird in diesem Beitrag nur die "Klassifizierung" besprochen.
1.1. Die Architektur der Verknüpfungen
Die Art der Verarbeitung von Informationen wird wesentlich durch das Fehlen oder Vorhandensein von Feedbackschleifen im Netzwerk beeinflusst. Falls keine Feedbackschleifen zwischen Neuronen bestehen (d. h. das Netzwerk hat eine Struktur von aufeinanderfolgenden Lagen, bei der jedes Neuron nur Informationen von der vorherigen Lage enthält), ist die Verarbeitung von Informationen im Netzwerk unidirektional. Ein Eingabesignal wird durch eine Sequenz von Lagen verarbeitet und die Antwort wird über die Anzahl von Takten gleich der Anzahl von Lagen erhalten.
Das Vorhandensein von Feedbackschleifen kann die Dynamik eines neuronalen Netzwerks (in diesem Fall als rekurrent bezeichnet) unberechenbar machen. Tatsächlich kann das Netzwerk in der Schleife "hängenbleiben" und nie eine Antwort geben. Gleichzeitig gibt es laut Turing keinen Algorithmus, der es einem willkürlich rekurrenten Netzwerk ermöglicht, zu bestimmen, ob seine Elemente ein Gleichgewicht finden werden (das Halteproblem).
Allgemein gesprochen, ermöglicht die Tatsache, dass Neuronen in rekurrenten Netzwerken viele Male an der Verarbeitung von Informationen teilnehmen, solchen Netzwerken eine tiefere und vielfältigere Verarbeitung von Informationen. In diesem Fall müssen spezielle Maßnahmen ergriffen werden, damit das Netzwerk nicht in einer Endlosschleife hängenbleibt. Verwenden Sie beispielsweise symmetrische Verknüpfungen wie in einem Hopfield-Netz oder erzwingen Sie eine Begrenzung der Anzahl an Iterationen.
| Art des Einlernens Art der Verknüpfung | Mit "Aufseher" | Ohne "Aufseher" |
|---|---|---|
| Ohne Feedbackschleifen | Mehrlagige Perzeptrons (Approximation von Funktionen, Klassifizierung) | Konkurrierendes Netzwerk, selbstorganisierende Karten (Datenkomprimierung, Abtrennung von Merkmalen) |
| Mit Feedbackschleifen | Rekurrentes Perzeptron (Vorhersage von Zeitreihen, Online-Einlernen) | Hopfield-Netz (assoziativer Speicher, Daten-Clustering, Optimierung) |
Tabelle 1. Klassifizierung von neuronalen Netzwerken nach Art der Verknüpfung und des Einlernens
1.2. Wichtigste Typen neuronaler Netzwerke
Seit dem Perzeptron haben neuronale Netzwerke eine starke Entwicklung durchgemacht. Heute werden zahlreiche neuronale Netzwerke mit unterschiedlichen Strukturen und Einlernmethoden verwendet.
Die bekanntesten sind:
1.2.1. Mehrlagige voll verknüpfte Feedforward-Netzwerke (Multilayer Perceptron, MLP)
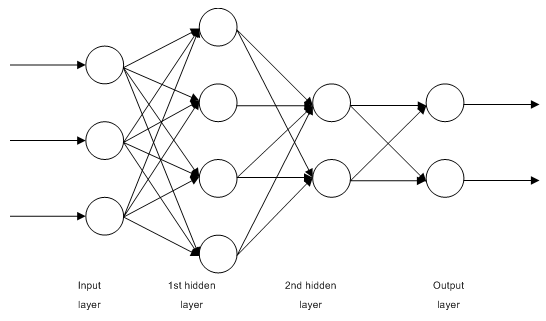
Abb. 1. Struktur eines mehrlagigen neuronalen Netzwerks
1.2.2. Jordan-Netze sind teilweise rekurrente Netzwerke und ähneln Elman-Netzen.
Sie können als Feedforward-Netzwerke mit zusätzlichen Kontextneuronen in der Eingangslage behandelt werden.
Diese Kontextneuronen werden durch sich selbst (direktes Feedback) und die Eingangsneuronen gespeist. Kontextneuronen bewahren den aktuellen Zustand des Netzwerks. In einem Jordan-Netz muss die Menge der Kontext- und Eingangsneuronen gleich sein.
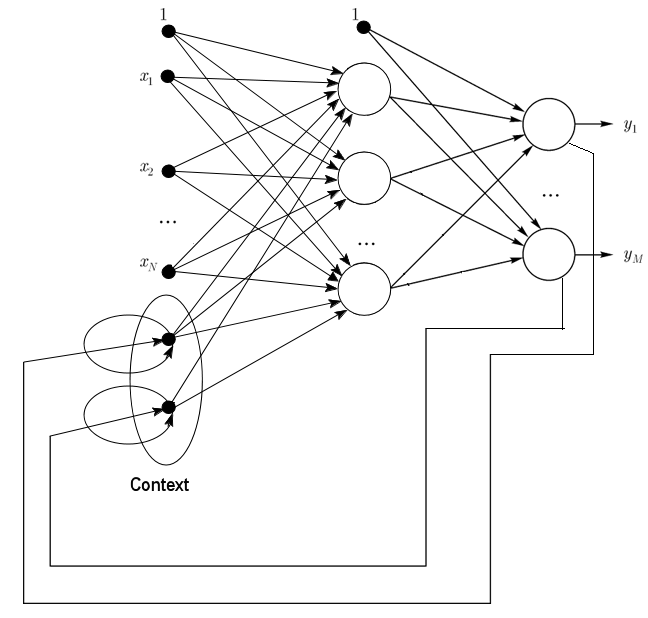
Abb. 2. Struktur eines Jordan-Netzes
1.2.3. Elman-Netze sind teilweise rekurrente Netzwerke und ähneln Jordan-Netzen. Der Unterschied zwischen Elman- und Jordan-Netzen liegt darin, dass Kontextneuronen in einem Elman-Netz nicht durch Ausgangsneuronen gespeist werden, sondern durch verborgene Neuronen. Davon abgesehen haben Kontextneuronen kein direktes Feedback.
In einem Elman-Netz muss die Menge der Kontext- und verborgenen Neuronen gleich sein. Der wichtigste Vorteil von Elman-Netzen ist, dass die Menge der Kontextneuronen nicht durch die Menge der Ausgänge bestimmt wird wie im Jordan-Netz, sondern durch die Menge der verborgenen Neuronen, was das Netzwerk flexibler macht. Im Gegensatz zur Menge der Ausgänge können verborgene Neuronen einfach hinzugefügt oder entfernt werden.
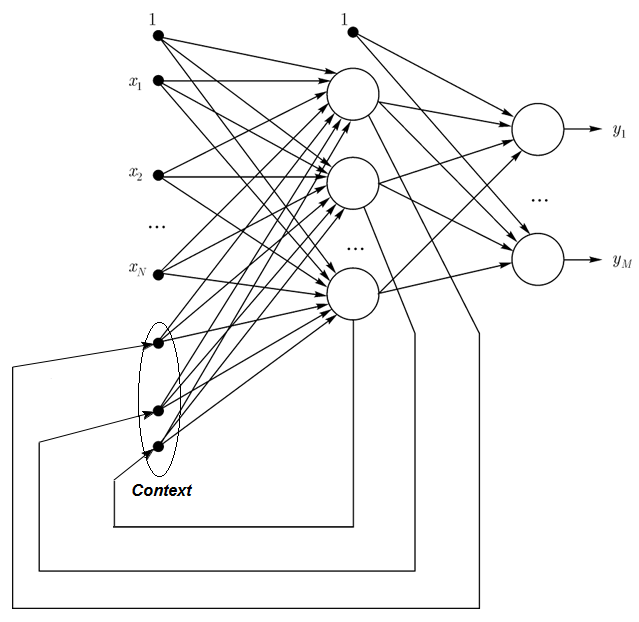
Abb. 3. Struktur eines Elman-Netzes
1.2.4. Das radiale Basisfunktionsnetzwerk (RBF) ist ein neuronales Feedforward-Netzwerk, das eine (verborgene) Zwischenlage aus radial symmetrischen Neuronen enthält. Ein solches Neuron konvertiert die Distanz von einem bestimmten Eingangsvektor zu seinem entsprechenden Mittelpunkt durch ein nichtlineares Gesetz, für gewöhnlich das gauss'sche.
Das RBF-Netzwerk hat zahlreiche Vorteile gegenüber mehrlagigen Feedforward-Netzwerken. Erstens emulieren sie eine beliebige nichtlineare Funktion mit nur einer Zwischenlage, was dem Entwickler die Notwendigkeit erspart, über die Menge der Lagen entscheiden zu müssen. Außerdem können die Parameter in der linearen Kombination in der Ausgangslage mithilfe weit verbreiteter linearer Optimierungsmethoden optimiert werden. Diese arbeiten schnell und haben keine Schwierigkeiten mit lokalen Minima, die die Backpropagation stark stören. Aus diesem Grund lernt das RBF-Netzwerk viel schneller als bei der Nutzung von Backpropagation.
Nachteile des RBF: Diese Netzwerke haben schwache Extrapolationseigenschaften und erweisen sich als mühselig, wenn der Eingangsvektor sehr groß ist.
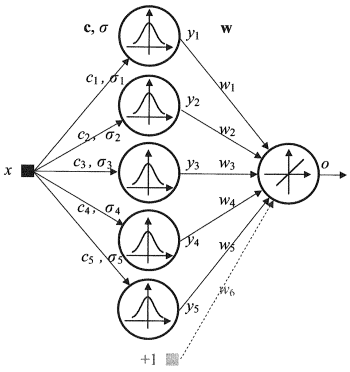
Abb. 4. Struktur eines RBF
1.2.5. Netzwerke mit dynamischem Einlernen der Vektorquantisierung (Dynamic learning vector quantization, DLVQ) sind selbstorganisierenden Karten (SOM) sehr ähnlich. Im Gegensatz zu SOM beherrschen DLVQ das beaufsichtigte Lernen und weisen kein Nachbarschaftsverhältnis zwischen den Prototypen auf. Die Vektorquantisierung hat einen breiteren Einsatzbereich als Clustering.
1.2.6. Das Hopfield-Netz ist ein voll verknüpftes Netzwerk mit symmetrischer Verknüpfungsmatrix. Während des Betriebs laufen die Dynamiken solcher Netzwerke zu einem der Gleichgewichtszustände zusammen. Bei diesen Gleichgewichtszuständen handelt es sich um lokale Minima der Funktionalität, die als Energie des Netzwerks bezeichnet werden. Ein solches Netzwerk kann als inhaltsadressiertes assoziatives Speichersystem, als Filter und zum Angehen bestimmter Optimierungsherausforderungen verwendet werden.
Im Gegensatz zu vielen neuronalen Netzwerken, die arbeiten, bis sie eine Antwort in einer bestimmten Anzahl von Takten erhalten, arbeiten Hopfield-Netze, bis sie den Gleichgewichtszustand erreichen, das heißt, wenn der nächste Zustand eines Netzwerks genau der gleiche ist wie der vorherige. In diesem Fall ist der ursprüngliche Zustand ein Eingangsmuster und im Gleichgewichtszustand wird das Ausgangsbild erhalten. Das Einlernen eines Hopfield-Netzes erfordert ein Einlernmuster, das an den Eingangs- und Ausgangslagen gleichzeitig vorgelegt wird.
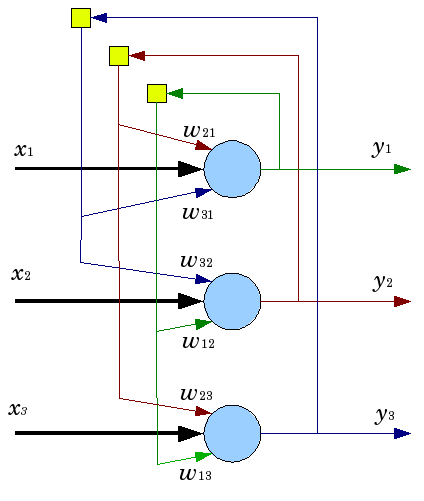
Abb. 5. Struktur eines Hopfield-Netzes mit drei Neuronen
Trotz der ansprechenden Eigenschaften ist das klassische Hopfield-Netz alles andere als ideal. Es verfügt nur über begrenzten Speicher, etwa 15 % der Anzahl der Neuronen im Netzwerk N, während Systeme von adressiertem Speicher bis zu 2N verschiedener Bilder mithilfe von N Bits speichern können.
Außerdem können Hopfield-Netze nicht erkennen, ob das Bild in Bezug auf seine ursprüngliche Speicherposition bewegt oder gedreht wird. Diese und weitere Nachteile definieren die allgemeine Wahrnehmung des Hopfield-Netzes als theoretisches Modell, das für Studien besser geeignet ist als im täglichen Einsatz als praktisches Instrument.
Viele andere Netzwerke (rekurrentes Hemming-Netz, Grossberg-Netz, Netzwerke der adaptiven Resonanztheorie (ART-1, ART-2) usw.) wurden in diesem Beitrag nicht erwähnt, da sie außerhalb unseres Interessensbereichs liegen.
1.3. Einlernmethoden
Die Fähigkeit, Neues zu lernen, ist das Hauptmerkmal eines menschlichen Gehirns. Im Fall künstlicher neuronaler Netzwerke ist das Einlernen ein Prozess, bei dem die Netzwerkstruktur (die Struktur der Verknüpfungen zwischen Neuronen) und die Gewichtungen synaptischer Verbindungen (mit Wirkung auf Koeffizientensignale) konfiguriert werden, um eine wirksame Lösung für die vorliegende Aufgabe zu erhalten. Für gewöhnlich werden neuronale Netzwerke anhand von Musterdaten eingelernt. Der Einlernprozess befolgt einen bestimmten Algorithmus und mit seinem Fortschreiten sollte die Reaktion des Netzwerks auf Eingangssignale besser werden.
Es gibt drei wesentliche Einlernparadigmen: beaufsichtigt, unbeaufsichtigt und kombiniert. Im ersten Fall sind die richtigen Antworten für jedes Eingabebeispiel bekannt und die Gewichtungen versuchen, den Fehler zu vermindern. Das unbeaufsichtigte Einlernen ermöglicht eine Kategorisierung von Stichproben durch Erklären der internen Struktur und Art der Daten. Beim kombinierten Einlernen werden beide der vorher genannten Herangehensweisen genutzt.
1.3.1. Hauptregeln des Einlernens neuronaler Netzwerke
Es gibt vier Hauptregeln für das Einlernen auf Basis der mit dem Netzwerk verbundenen Architektur: Fehlerbehebung, Boltzmannsche Regel, Hebbsche Regel und Competitive Learning.
1.3.1.1. Fehlerbehebung
Jedes Eingangsbeispiel hat einen festgelegten gewünschten Ausgangswert (Zielwert), der möglicherweise nicht mit einem realen (prognostizierten) Wert übereinstimmt. Die Regel der Fehlerbehebung nutzt die Differenz zwischen dem Ziel- und dem prognostizierten Wert für die direkte Anpassung von Gewichtungen, um den Fehler zu vermindern. Das Einlernen wird nur bei einem fehlerhaften Ergebnis durchgeführt. Für diese Einlernregel gibt es zahlreiche Modifikationen.
1.3.1.2. Boltzmannsche Regel
Die Boltzmannsche Regel ist eine stochastische Einlernregel, bedingt durch die Analogie mit thermodynamischen Prinzipien. Dies führt zu einer Anpassung der Gewichtungskoeffizienten der Neuronen gemäß der gewünschten Wahrscheinlichkeitsverteilung. Das Einlernen nach der Boltzmannschen Regel kann als Einzelfall der Korrektur nach Fehler betrachtet werden, bei dem ein Fehler eine Korrelationsdiskrepanz zwischen den Zuständen in zwei Modi bedeutet.
1.3.1.3. Hebbsche Regel
Die Hebbsche Regel ist der bekannteste Algorithmus für das Einlernen neuronaler Netzwerke. Die Grundidee dieser Methode ist, dass wenn Neuronen auf beiden Seiten einer Synapse gleichzeitig und regelmäßig aktiviert werden, die Stärke der synaptischen Verbindung dadurch steigt. Eine wichtige Besonderheit dabei ist, dass die Änderung der synaptischen Gewichtung nur von der Aktivität der mit dieser Synapse verknüpften Neuronen abhängt. Es gibt zahlreiche Varianten dieser Regel, die sich durch Besonderheiten bei der Modifizierung der synaptischen Gewichtung unterscheiden.
1.3.1.4. Competitive Learning
Im Gegensatz zur Hebbschen Regel, bei der mehrere Ausgangsneuronen gleichzeitig aktiviert werden können, stehen die Ausgangsneuronen hier in einem Konkurrenzverhältnis (Competition) zueinander. Das Ausgangsneuron mit dem maximalen Wert der gewichteten Summe ist der "Sieger" und "the winner takes it all". Die Ausgänge der restlichen Ausgangsneuronen werden in den inaktiven Zustand versetzt. Beim Einlernen werden nur die Gewichtungen des "Siegers" in Richtung der Erhöhung der Nähe zur aktuellen Ausgangsinstanz modifiziert.
Es gibt zahlreiche Einlernalgorithmen, die auf unterschiedliche Aufgaben eingehen. Backpropagation, einer der effizientesten modernen Algorithmen, ist einer davon. Das Prinzip dahinter ist, dass die Änderung der synaptischen Gewichtung unter Berücksichtigung des lokalen Gradienten der Fehlerfunktion stattfindet.
Der Unterschied zwischen den realen und korrekten Antworten eines neuronalen Netzwerks, die in der Ausgangslage bewertet werden, wird rückwärts, in Richtung des Signalstroms, propagiert (Abb. 5). Auf diese Weise kann jedes Neuron den Beitrag seiner Gewichtung zum kumulativen Fehler des Netzwerks definieren. Die einfachste Einlernregel ist die Methode des steilsten Abstiegs, das heißt, die synaptischen Gewichtungen verändern sich proportional zu ihrem Beitrag zum kumulativen Fehler.
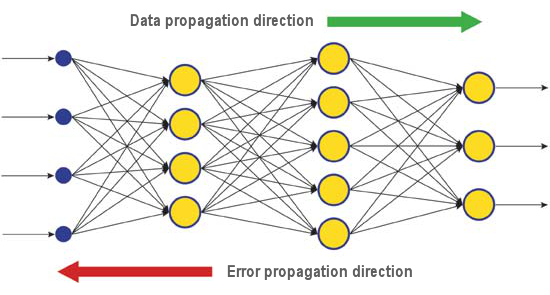
Abb. 6. Muster der Verbreitung von Daten und Fehlern in einem Netzwerk beim Einlernen durch Backpropagation
Natürlich gewährleistet diese Art des Einlernens eines neuronalen Netzwerks nicht das beste Einlernergebnis, da immer die Möglichkeit besteht, dass der Algorithmus in ein lokales Minimum gerät. Es gibt spezielle Techniken, die es ermöglichen, die gefundene Lösung aus einem lokalen Extremalpunkt "herauszuschlagen". Wenn das neuronale Netzwerk nach einigen Durchläufen dieser Technik weiterhin zu derselben Entscheidung kommt, lässt sich schlussfolgern, dass die gefundene Lösung höchstwahrscheinlich die optimale ist.
1.4. Nachteile
- Die größte Schwierigkeit bei der Verwendung von neuronalen Netzwerken ist der sogenannte "Fluch der Dimensionalität". Wenn Eingangsdimensionen und die Menge der Lagen erhöht werden, steigen die Komplexität des Netzwerks und die Einlernzeit exponentiell und das erhaltene Ergebnis ist nicht immer optimal.
- Eine weitere Schwierigkeit bei der Verwendung von neuronalen Netzwerken ist, dass das herkömmliche neuronale Netzwerk nicht in der Lage ist, zu erklären, wie es Aufgaben löst. In einigen Einsatzbereichen, z. B. in der Medizin, ist diese Erklärung aber wichtiger als das Ergebnis selbst. Die innere Darstellung der Ergebnisse ist oft so komplex, dass sie unmöglich zu analysieren ist, ausgenommen einfachste Fälle, die für gewöhnlich uninteressant sind.
2. Tiefes Lernen
Heute erleben Theorie und Praxis des maschinellen Lernens eine "tiefe Revolution", die durch die erfolgreiche Umsetzung der Methoden des tiefen Lernens verursacht wird und neuronale Netzwerke der dritten Generation darstellt. Im Gegensatz zu herkömmlichen Netzwerken der zweiten Generation aus den 80er und 90er Jahren des vergangenen Jahrhunderts lösen die neuen Lernparadigmen eine Reihe von Problemen, die die Verbreitung und erfolgreiche Umsetzung herkömmlicher neuronaler Netzwerke einschränkten.
Netzwerke, die mit Algorithmen des tiefen Lernens eingelernt wurden, übertrafen nicht nur die besten alternativen Methoden in puncto Genauigkeit, sondern deckten in einigen Fällen Rudimente des Verstehens des Sinnes der Eingangsinformationen auf. Die besten Beispiele dafür sind Bilderkennung und die Analyse von Textinformationen.
Heute basieren die fortschrittlichsten industriellen Methoden der Bild- und Spracherkennung auf tiefen Netzwerken. Riesen der IT-Branche wie Apple, Google oder Facebook beschäftigen Forscher, die tiefe neuronale Netzwerke entwickeln.
2.1. Hintergrund
Ein Team von Graduierten von der Universität von Toronto gewann unter der Leitung von Professor Geoffrey E. Hinton den ersten Preis in einem von Merck gesponserten Wettbewerb. Unter Verwendung eines begrenzten Datensatzes, der die chemische Struktur von 15 Molekülen beschrieb, konnte Hintons Gruppe ein spezielles Programmsystem entwickeln und anwenden, das definierte, welches dieser Moleküle sich mit der höchsten Wahrscheinlichkeit als wirksame Medizin erweisen würde.
Die Besonderheit dieser Arbeit war, dass die Entwickler ein künstliches neuronales Netzwerk auf Basis des tiefen Einlernens nutzten. Als Ergebnis konnte dieses System Berechnungen und Forschungen auf Basis eines stark begrenzten Satzes von Quelldaten durchführen, während das Einlernen eines neuronalen Netzwerks normalerweise die Eingabe einer hohen Menge von Informationen ins System erfordert.
Die Errungenschaft von Hintons Team war besonders beeindruckend, weil das Team in letzter Minute beschloss, am Wettbewerb teilzunehmen. Zudem wurde das System des tiefen Einlernens ohne besonderes Wissen darüber entwickelt, wie sich die Moleküle an ihre Ziele anbinden. Die erfolgreiche Umsetzung des tiefen Einlernens war eine weitere Errungenschaft auf dem Gebiet der Entwicklung der künstlichen Intelligenz im ereignisreichen Jahr 2012.
So präsentierten Jeff Dean und Andrew Y. Ng von Google im Sommer 2012 ein neues Bilderkennungssystem mit einer Trefferquote von 15,8 %, wobei sie zum Einlernen eines Cluster-Systems aus 16.000 Knoten das ImageNet-Netzwerk mit einer Bibliothek von 14 Millionen Bildern von 20.000 verschiedenen Objekten nutzten. Letztes Jahr übertraf ein von Schweizer Wissenschaftlern entwickeltes Programm einen Menschen beim Erkennen von Bildern von Verkehrsschildern. Das Gewinnerprogramm erkannte 99,46 % der Bilder aus einem Satz von 50.000. Die höchste Trefferquote in einer Gruppe aus 32 menschlichen Teilnehmern lag bei 99,22 %, der Durchschnitt der menschlichen Teilnehmer betrug 98,84 %. Im Oktober 2012 präsentierte Richard F. Rashid, ein Koordinator für wissenschaftliche Programme bei Microsoft, auf einer Konferenz im chinesischen Tianjin eine Technologie für das simultane Dolmetschen aus dem Englischen in Mandarin, begleitet von einer Simulation seiner eigenen Stimme.
All diese Technologien, die einen Durchbruch auf dem Gebiet der künstlichen Intelligenz demonstrieren, basieren zu einem gewissen Grad auf der Methode des tiefen Lernens. Der größte Beitrag zur Theorie des tiefen Lernens stammt von Professor Hinton, einem Ururenkel von George Boole, einem englischen Wissenschaftler und Begründer der booleschen Algebra, die auch heutigen Computern zugrunde liegt.
Die Theorie des tiefen Lernens ergänzt herkömmliche Methoden des maschinellen Lernens mit speziellen Algorithmen für die Analyse von Eingangsinformationen auf mehreren Darstellungsebenen. Die Besonderheit dieser neuen Herangehensweise ist, dass das tiefe Lernen das Thema studiert, bis es genügend informative Darstellungsebenen findet, um alle Faktoren zu berücksichtigen, die sich auf die Parameter des zugrunde liegenden Objekts auswirken können.
Somit benötigt ein neuronales Netzwerk, das auf dieser Herangehensweise basiert, weniger Eingangsinformationen zum Lernen und ein eingelerntes Netzwerk kann Informationen mit einer höheren Genauigkeit analysieren als ein herkömmliches neuronales Netzwerk. Professor Hinton und seine Kollegen erklären, dass ihre Technologie besonders gut für die Suche nach Besonderheiten in multidimensionalen, gut strukturierten Arrays von Informationen geeignet ist.
Die Technologien der künstlichen Intelligenz (KI), insbesondere das tiefe Lernen, werden in unterschiedlichsten Systemen genutzt, darunter der intelligente persönliche Assistent Siri auf Basis der Nuance-Communications-Technologien und die Erkennung von Adressen in Google Street View. Dennoch gehen Wissenschaftler mit Erfolgen auf diesem Gebiet sehr vorsichtig um, da es in der Geschichte der Erschaffung einer künstlichen Intelligenz bereits zahlreiche Fälle optimistischer Versprechen und Enttäuschungen gab.
In den 60er Jahren glaubten Wissenschaftler, dass es nur 10 Jahre dauern würde, um eine voll funktionsfähige künstliche Intelligenz zu erschaffen. Später, in den 80er Jahren, gab es eine Welle von jungen Unternehmen, die eine "gebrauchsfertige künstliche Intelligenz" anboten, worauf eine "Eiszeit" auf diesem Gebiet folgte, die erst kürzlich zu Ende ging. Heute ermöglichen hohe Berechnungskapazitäten in Cloud-Services ein ganz neues Niveau der Umsetzung leistungsfähiger neuronaler Netzwerke unter Verwendung einer neuen theoretischen und algorithmischen Basis.
Es muss berücksichtigt werden, dass neuronale Netzwerke, auch solche der dritten Generation wie Convolutional Neural Networks, autoassoziative Netzwerke, Boltzmann-Maschinen, außer dem Namen nichts mit biologischen Neuronen gemeinsam haben.
Das neue Lernparadigma setzt die Lernidee in zwei Phasen um. In der ersten Phase werden Informationen über die interne Struktur der Eingangsdaten aus einem großen Array aus unformatierten Daten mithilfe von Autoassoziatoren, die Lage für Lage unbeaufsichtigt eingelernt wurden, extrahiert. Dann durchlaufen diese Informationen in einem mehrlagigen neuronalen Netzwerk ein beaufsichtigtes Einlernen durch bekannte Methoden mithilfe formatierter Daten. Gleichzeitig sollte die Menge unformatierter Daten so groß wie möglich sein. Die Menge formatierter Daten kann wesentlich kleiner sein. In unserem Fall ist das nicht unmittelbar wichtig.
2.2. Autoencoder. Autoencoder und beschränkte Boltzmann-Maschine. Unterschiede und Besonderheiten
2.2.1. Autoencoder
Der erste Autoassoziator (AA) war ein Fukushima-Neocognitron.
Seine Struktur wird in Abb. 7 vorgestellt.
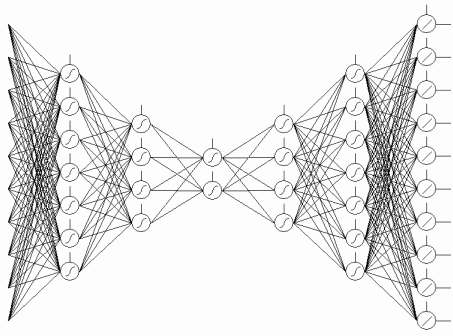
Abb. 7. Ein Fukushima-Neocognitron
Der Zweck eines Autoassoziators (AA) ist der Erhalt eines möglichst genauen Abbilds des Eingangs am Ausgang.
Es gibt zwei Arten von AA: generierende und synthetisierende. Eine beschränkte Boltzmann-Maschine gehört zum ersten Typen und ein Autoencoder repräsentiert den zweiten Typen.
Ein Autoencoder ist ein neuronales Netzwerk mit einer offenen Lage. Mithilfe eines unbeaufsichtigten Einlernalgorithmus und Backpropagation legt er einen Zielwert gleich dem Eingangsvektor fest, d. h. y = x.
Ein Beispiel eines Autoencoders ist in Abb. 8. dargestellt.
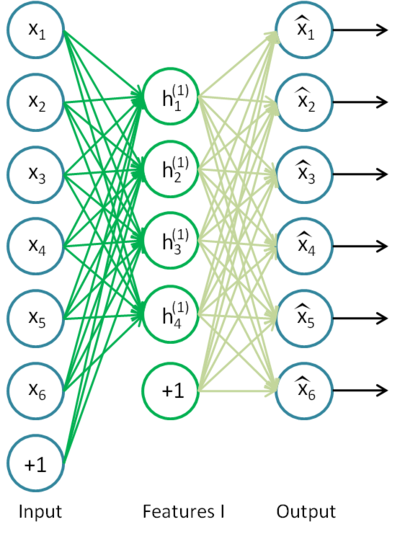
Abb. 8. Struktur eines Autoencoders
Der Autoencoder versucht, die Funktion h(x)=x zu konstruieren. In anderen Worten: Er versucht, eine Approximation einer Funktion zu finden, die sicherstellt, dass das Feedback eines neuronalen Netzwerks den Werten der Eingangsparameter ungefähr entspricht. Damit die Lösung der Aufgabe nicht trivial ist, muss die Anzahl der Neuronen in der offenen Lage geringer sein als die Dimension der Eingangsdaten (wie abgebildet).
Dies ermöglicht eine Komprimierung der Daten, wenn das Eingangssignal an den Netzwerkeingang übergeben wird. Zum Beispiel: Wenn der Eingangsvektor einen Satz von Helligkeitsstufen eines 10x10 Pixel großen Bildes darstellt (100 Merkmale) und die Menge der Neuronen der verborgenen Lage 50 beträgt, wird das Netzwerk gezwungen, zu lernen, das Bild zu komprimieren. Die Anforderung h(x)=x bedeutet, dass die Ausgangslage basierend auf den Aktivierungsebenen von fünfzig Neuronen der verborgenen Lage 100 Pixel des ursprünglichen Bildes wiederherstellen muss. Eine solche Komprimierung ist möglich, wenn verborgene Verbindungen, eine Korrelation der Merkmale oder irgendeine Struktur vorliegen. Auf diese Art erinnert die Arbeit des Autoencoders sozusagen die Analysemethode der wesentlichen Komponenten (Principal Component Analysis, PCA) daran, dass Eingangsdaten reduziert werden.
Überraschenderweise zeigten Experimente von Bengio et al., (2007), dass beim Einlernen mit stochastischem Gradientenverfahren nichtlineare Autocoding-Netzwerke mit mehr verborgenen Neuronen als Eingängen (auch als "überreichlich" bezeichnet) angesichts des Übereinstimmungsfehlers des Netzwerks, das die Darstellung aus dem Eingang bezog, nützliche Darstellungen aufwiesen.
Als später die Idee der dünnen Besetzung (sparsity) auftrat, wurden dünnbesetzte Autoencoder häufig verwendet.
Beim dünnbesetzten Autoencoder handelt es sich um einen Autoencoder, dessen Menge an verborgenen Neuronen wesentlich größer ist als die Eingangsdimension, die aber selten aktiviert werden. Eine seltene Aktivierung liegt vor, wenn die Menge der inaktiven Neuronen in der verborgenen Lage wesentlich größer ist als die Menge der aktiven. Wenn wir die dünne Besetzung formlos beschreiben sollen, lässt sich sagen, dass ein Neuron als aktiv betrachtet werden kann, wenn der Wert seiner Funktion nahe an 1 liegt. Wird eine Sigmoidfunktion genutzt, muss der Wert des inaktiven Neurons nahe an 0 liegen (für die Funktion des Tangens hyperbolicus muss der Wert nahe an -1 sein).
Es gibt eine Variante des Autoencoders, die als Denoising-Autoencoder bezeichnet wird (Vincent et al., 2008). Dabei handelt es sich um den gleichen Autoencoder, doch sein Einlernprozess weist einige Besonderheiten auf. Beim Einlernen dieses Netzwerks werden "korrumpierte" Daten eingegeben (einige Werte werden durch 0 ersetzt). Gleichzeitig gibt es "korrekte" Daten zum Vergleich mit den Ausgangsdaten. Auf diese Weise kann ein Autoencoder beschädigte Daten wiederherstellen.
2.2.2. Beschränkte Boltzmann-Maschine (Restricted Boltzmann Machine, RBM)
Wir werden nicht auf die Geschichte der beschränkten Boltzmann-Maschine (RBM) eingehen. Wir müssen nur wissen, dass ihre Existenz mit rekurrenten neuronalen Netzwerken mit Feedback begann, die sehr schwer einzulernen waren. Aufgrund dieser Schwierigkeit des Einlernens erschienen beschränktere rekurrente Modelle, sodass einfachere Einlernalgorithmen angewendet werden konnten. Das neuronale Hopfield-Netz war eines dieser Modelle. John Hopfield stellte das Konzept der Netzwerkenergie vor, indem er die Dynamiken von neuronalen Netzwerken mit Thermodynamik verglich.
Der nächste Schritt auf dem Weg zur RBM waren herkömmliche Boltzmann-Maschinen. Sie unterscheiden sich dadurch vom Hopfield-Netz, dass sie stochastischer Natur sind und ihre Neuronen in zwei Gruppen aufgeteilt sind, die sichtbare und verborgene Zustände beschreiben (ähnlich einem verborgenen Markov-Modell). Eine beschränkte Boltzmann-Maschine unterscheidet sich durch das Fehlen von Verknüpfungen zwischen den Neuronen einer Lage von einer herkömmlichen Boltzmann-Maschine.
Abb. 9 zeigt die Struktur der RBM.
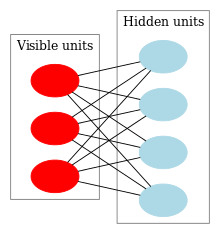
Abb. 9. Struktur einer RBM
Die Besonderheit dieses Modells ist, dass im aktuellen Zustand der Neuronen einer Gruppe die Zustände der Neuronen einer anderen Gruppe voneinander unabhängig sind. Nun können wir zur Theorie übergehen, an welchen Stellen diese Eigenschaft eine wichtige Rolle spielt.
Interpretation und Ziel
Eine RBM wird ähnlich einem verborgenen Markov-Modell interpretiert. Wir haben eine Reihe von Zuständen, die wir beobachten können (sichtbare Neuronen), und eine Reihe von verborgenen Zuständen, die wir nicht direkt sehen können (verborgene Neuronen). Wir können zu einem wahrscheinlichkeitsbasierten Schluss über die verborgenen Zustände kommen, indem wir uns auf die Zustände stützen, die wir beobachten können. Nach dem Einlernen eines solchen Modells erhalten wir eine Gelegenheit, Schlussfolgerungen über sichtbare Zustände zu ziehen, weil wir wissen, dass die verborgenen den Satz von Bayes befolgen. Dies ermöglicht die Erzeugung von Daten aus der für das Einlernen des Modells verwendeten Wahrscheinlichkeitsverteilung.
Somit können wir das Ziel des Einlernens eines Modells formulieren: Die Parameter des Modells müssen so angepasst werden, dass ein wiederhergestellter Vektor aus dem ursprünglichen Zustand so nahe wie möglich am Original ist. Ein wiederhergestellter Vektor ist ein Vektor, der sich aus dem Wahrscheinlichkeitsschluss aus verborgenen Zuständen ergibt, die sich ihrerseits aus dem Wahrscheinlichkeitsschluss aus sichtbaren Zuständen, d. h. dem Originalvektor, ergeben haben.
Der Einlernalgorithmus ist die kontrastive Divergenz CD-k
Dieser Algorithmus wurde 2002 von Professor Hinton erfunden und ist erstaunlich simpel. Die Grundidee ist, dass mathematische Erwartungswerte durch definierte Werte ersetzt werden. Es wird die Idee des Gibbs-Sampling eingeführt.
Der CD-k-Prozess sieht so aus:
- Der Zustand der sichtbaren Neuronen wird mit dem Eingangsmuster gleichgesetzt;
- Die Wahrscheinlichkeiten der Zustände der verborgenen Lagen werden gezeichnet;
- Jedes Neuron der verborgenen Lage erhält den Zustand "1" mit einer Wahrscheinlichkeit gleich seinem aktuellen Zustand;
- Die Wahrscheinlichkeiten der Zustände der sichtbaren Lage werden auf Basis der verborgenen Lage gezeichnet;
- Falls die aktuelle Iteration weniger als k ist, kehren Sie zu Schritt 2 zurück;
- Die Wahrscheinlichkeiten der Zustände der verborgenen Lagen werden gezeichnet;
In Hintons Lektionen sieht es so aus:
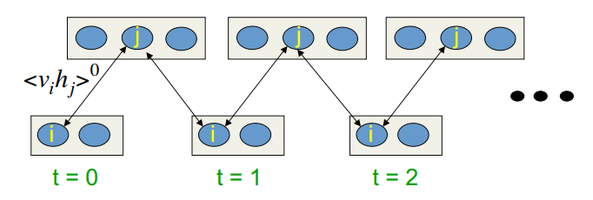
Abb. 10. Algorithmus des CD-k-Einlernens
In anderen Worten: Je länger wir das Sampling durchführen, desto genauer ist der Gradient. Der Professor erklärt, dass das Ergebnis für CD-1, also aus nur einer Sampling-Iteration, bereits ausreicht.
2.3. Gestackte autoassoziative Netzwerke. Gestackte Autoencoder (SAE), gestackte beschränkte Boltzmann-Maschine (Stacked RBM)
Zum Extrahieren von Abstraktionen aus dem Eingangsdatensatz auf hoher Ebene werden Autoassoziatoren zu einem Netzwerk kombiniert.
Abb. 11 stellt die Struktur eines gestackten Autoencoders und eines neuronalen Netzwerks dar, die zusammen ein tiefes neuronales Netzwerk mit durch einen gestackten Autoencoder initialisierten Gewichtungen darstellen.
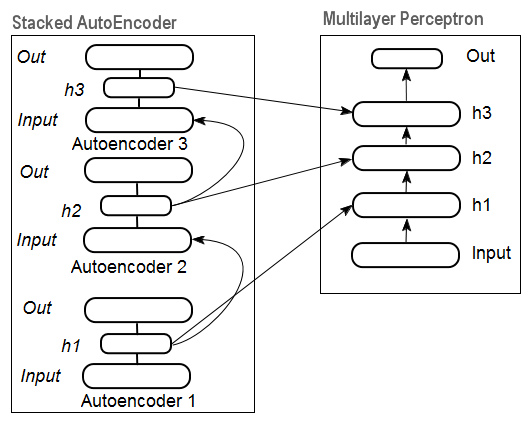
Abb. 11. Struktur eines SAE-DN
In Abb. 12 sehen Sie ein Muster einer gestackten RBM (SRBM) und eines neuronalen Netzwerks, die zusammen ein tiefes neuronales Netzwerk mit durch die SRBM initialisierten Gewichtungen darstellen.
Diese Illustrationen von Strukturen eines tiefen neuronalen Netzwerks betonen, dass die Informationen von unten nach oben extrahiert werden.
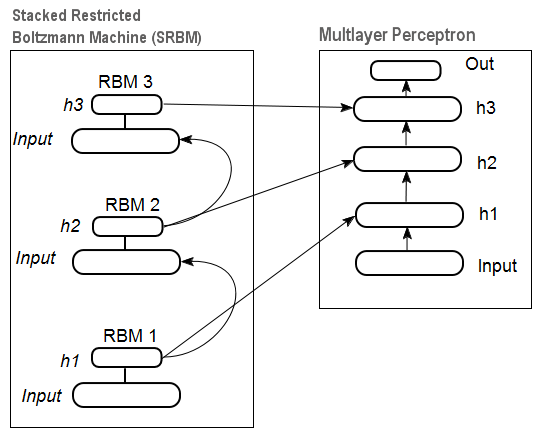
Abb. 12. Struktur eines SRBM-DN
2.4. Einlernen tiefer Netzwerke (DN). Phasen. Besonderheiten
Das Einlernen tiefer Netzwerke umfasst zwei Phasen. In der ersten Phase wird ein autoassoziatives Netzwerk (SAE oder SRBM, je nach DN-Typ) unbeaufsichtigt auf einem Array von unformatierten Daten eingelernt. Anschließend werden die Neuronen der verborgenen Lage eines herkömmlichen MLP durch die Gewichtungen der verborgenen Lage initialisiert, die nach dem Einlernen erhalten wurden. Abb. 11 und Abb. 12 zeigen ein Muster der Einlern- und Transferprozesse. Nach dem Einlernen der ersten AE/RBM werden die Neuronengewichtungen der verborgenen Lage zu Eingängen der zweiten usw. Auf diese Weise werden verallgemeinernde Informationen über die Struktur (Linie, Kontur, Muster usw.) aus den Daten extrahiert.
In der zweiten Phase findet die Feinabstimmung des MLP (beaufsichtigtes Einlernen) auf einem formatierten Datensatz mithilfe wohlbekannter Methoden statt. Die Praxis zeigt, dass eine solche Initialisierung die Neuronengewichte der verborgenen Lagen des MLP auf das globale Minimum setzt und die darauffolgende Feinabstimmung sehr wenig Zeit in Anspruch nimmt.
Ferner schlug D. Hinton für tiefe Netzwerke mit mehr als drei Lagen vor, die Feinabstimmung in zwei Phasen durchzuführen. In der ersten Phase sollten nur die beiden oberen Lagen eingelernt werden, in der zweiten der Rest des Netzwerks.
Es sollte erwähnt werden, dass die Ergebnisse des unbeaufsichtigten Einlernens einer SRBM weniger stabil sind als die eines SAE.
Hinweis. Diese Begriffe werden häufig verwechselt. Eine SRBM wird mit einem Deep Belief Network (DBN) identifiziert. Obwohl die RBM aus einem DBN abgeleitet wird, handelt es sich dabei um völlig unterschiedliche Strukturen. Ein DBN ist ein mehrlagiges neuronales Netzwerk, dessen Neuronengewichtungen von verborgenen Lagen zufällig durch binäre Muster initialisiert werden.
3. Praktische Experimente
Tiefe Netzwerke werden in R ausgeführt.
3.1. Die Sprache R
Zur Geschichte. R ist eine Programmiersprache und eine Umgebung für statistische Berechnungen und Diagramme, die 1996 von den neuseeländischen Wissenschaftlern Ross Ihaka und Robert Gentleman an der University of Auckland entwickelt wurde.
R ist ein GNU-Projekt, das heißt, eine frei zugängliche Software, deren Philosophie die folgenden Prinzipien befolgt:
- Freiheit, Programme zu jedem Zweck auszuführen (Freiheit 0);
- Freiheit, zu lernen, wie ein Programm funktioniert, und es an die eigenen Bedürfnisse anzupassen (Freiheit 1);
- Freiheit, Kopien zu verbreiten, um einander zu unterstützen (Freiheit 2);
- Freiheit, das Programm zu verbessern und die Gesellschaft von den Verbesserungen profitieren zu lassen.
Historisch betrachtet, ist R eine alternative Umsetzung von S. S wurde 1976 von John Chambers und seinen Kollegen bei Bell Labs entwickelt. R wird bis heute durch das R Development Core Team mit John Chambers weiterentwickelt.
Um die Experimente zu wiederholen, müssen Sie R und Rstudio installieren. Informationen dazu, wo und wie Sie die Sprache und die Software herunterladen können, finden Sie im Internet. Falls Sie Fragen haben sollten, können wir in den Kommentaren zu diesem Beitrag darauf eingehen.
Vorteile von R:
- R gilt heute als Standard für statistische Berechnungen.
- Es wird durch die globale wissenschaftliche Gemeinschaft von Universitäten entwickelt und unterstützt.
- Zahlreiche Pakete für alle modernen Gebiete des Data-Mining. Zwischen der Veröffentlichung einer Idee und ihrer Umsetzung im R-Paket vergehen für gewöhnlich nicht mehr als 2 Wochen.
- Und zu guter Letzt: Es ist absolut kostenlos. Ein berühmter Entwickler eines kostenlosen Betriebssystems sagte einst: "Programme sind wie Sex – sie sind besser, wenn sie kostenlos sind."
3.2. Umsetzungsvarianten und betrachtete Aufgaben
Es sind zwei Arten der Umsetzung möglich.
Zur ersten gehört die Nutzung besonderer Programme von John Hilton für Matlab. Dafür wird "R.matlab" benötigt. Dieses Paket beinhaltet die Methoden writeMat() und readMat() zum Lesen und Schreiben der MAT-Dateien. Es ermöglicht die Kommunikation (Ausführung von Code, Senden und Empfangen von Objekten usw.) aus Matlab v6 und höher, das lokal oder auf einem Remote-Host in der Client-Server-Verbindung ausgeführt wird. Details finden Sie in der Beschreibung des Pakets. Diese Variante ist für jene geeignet, die mit dem Gebrauch von Matlab vertraut sind. Ich habe diese Methode nicht ausprobiert, doch es gibt eine Möglichkeit, Matlab und MQL auf diese Weise zu verbinden.
Die zweite Variante der Umsetzung ist die Nutzung von R-Paketen zu diesem Thema. Dies sehen wir uns näher an.
Es gibt drei Pakete, von denen ich weiß, dass sie mit dem Thema dieses Beitrags in Verbindung stehen:
"deepnet" ist ein einfaches Paket, das die Modelle DN SAE und DN SRBM umsetzt. Die Länge des Eingangsdatensatzes beim beaufsichtigten und unbeaufsichtigten Einlernen ist gleich. Es gibt keine Möglichkeit der Feinabstimmung des Systems in zwei Phasen. Wird zum Erforschen und Testen der Modelle am Anfang genutzt.
"darh" ist ein fortschrittliches und breit gefächertes Paket für die Modellierung für DN SRBM. Es gibt ein Modell für DN SAE, doch ich konnte es nicht starten. Dieses Paket richtet sich an erfahrene Benutzer und ermöglicht die Erschaffung und Abstimmung eines beliebig komplexen Modells. Es basiert auf den besonderen Programmen von Hinton in der Sprache m für MatLab.
"H2O" ist ein umfangreiches Paket zum Einlernen von (nicht nur) tiefen Netzwerken auf großen Datensätzen (>1 GB) in csv-Dateien.
In den nachfolgenden Experimenten nutzen wir das "deepnet"-Paket.
3.3. Vorbereitung der Eingangs- und Zieldaten für das Experiment
Data-Mining befolgt heutzutage eine bestimmte Reihenfolge:
- Auswahl von Eingangsdaten (Betrachtung, Analyse, vorläufige Vorbereitung, Bewertung). Aufteilen der Daten in Einlern-, Validierungs- und Testsätze (Stichproben);
- Einlernen eines Modells auf dem Einlerndatensatz und Auswahl eines Modells/mehrerer Modelle für den Validierungssatz;
- Bewertung der Qualität des Modells/der Modelle anhand der Teststichprobe und Definition der optimalen Modellparameter oder des besten Modells aus dem Satz anhand bestimmter Messungen;
- Aufnahme der Arbeit des Modells/der Modelle.
Die erste Phase ist die zeitintensivste und äußerst wichtig für das Endergebnis. Der Gerechtigkeit halber muss man sagen, dass diese Phase nicht formalisiert und im Allgemeinen fast eine Kunstform ist. Viel hängt von der Erfahrung des Forschers ab. Aber! Es ist äußerst wichtig, quantitative Bewertungen des Eingangsdatensatzes zu erhalten, um die wichtigsten auszuwählen. Die automatische Auswahl der besten Variablen für ein bestimmtes Modell ist in diesem Fall sogar besser. R liefert eine umfassende Funktionalität, um auf Herausforderungen in allen Phasen einzugehen.
Quelldaten sind nicht nur sehr wichtig, sondern haben auch viele zu berücksichtigende Aspekte. Sie verdienen einen eigenen Beitrag. Da es das Ziel dieses Beitrags ist, einen komplexen Sachverhalt in einfachen Worten zu beschreiben, werden wir wichtige Punkte betrachten, aber nicht sehr ins Detail gehen.
3.3.1. Quelldaten
Für unsere Klassifizierung benötigen wir einen Satz von unabhängigen (Eingangs-)Variablen und eine Zielvariable. Da der große Vorteil von tiefen Netzwerken ihre Fähigkeit ist, schnell anhand großer Eingangsstichproben zu lernen, erstellen wir einen Satz von Eingangsdaten aus 17 Prädiktoren (11 Indikatoren). ZigZag übernimmt die Rolle der Zielvariable. Laden Sie in der R-Umgebung Vektoren der Open-, High-, Low- und Close-Gebote mit einer Tiefe von 4000 Balken herunter. Wie das bewerkstelligt wird, wird nachfolgend in der Beschreibung zum Schreiben eines Indikators besprochen. Aktuell ist es unwichtig. Alle weiteren Berechnungen werden in R durchgeführt.
Konstruieren Sie eine Matrix aus 4 Vektoren, dem Durchschnittspreis und der Größe des Balkenkörpers. Machen Sie daraus eine Funktion:
pr.OHLC <- function (o, h, l, c)
{
#Unite quote vectors into a matrix having previously expanded them
#Indexing of time series of vectors in R starts with 1.
#Direction of indexing is from old to new ones.
price <- cbind(Open = rev(o), High = rev(h), Low = rev(l), Close = rev(c))
Med <- (price[, 2] + price[, 3])/2
CO <- price[, 4] - price[, 1]
#add Med and CO to the matrix
price <- cbind(price, Med, CO)
} Sehen Sie sich das Ergebnis an (Zustand am 08.10.14 12:00):
> head(price)
Open High Low Close Med CO
[1,] 1.33848 1.33851 1.33824 1.33844 1.338375 -4e-05
[2,] 1.33843 1.33868 1.33842 1.33851 1.338550 8e-05
[3,] 1.33849 1.33862 1.33846 1.33859 1.338540 1e-04
[4,] 1.33858 1.33861 1.33856 1.33859 1.338585 1e-05
[5,] 1.33862 1.33868 1.33855 1.33855 1.338615 -7e-05
[6,] 1.33853 1.33856 1.33846 1.33855 1.338510 2e-05 3.3.2. Eingabedaten (Prädiktoren)
Listen Sie die Indikatoren auf. Indikatoren wurden zufällig und ohne jegliche Präferenz ausgewählt, um eine größtmögliche Differenz der Eingangsgrößen zu erzielen.
Die Berechnung aller Indikatoren wird mithilfe des Pakets "TTR" durchgeführt, das zahlreiche Indikatoren enthält.
3.3.2.1. Welles Wilder's Directional Movement Index – ADX(HLC, n) – 4 out (Dip, Din,DX, ADX)
Führen Sie die Berechnung durch und sehen Sie sich an, wie es auf den ersten 200 Balken aussieht:
> library(TTR)
> adx<-ADX(price, n = 16)
> plot.ts(head(adx, 200)) 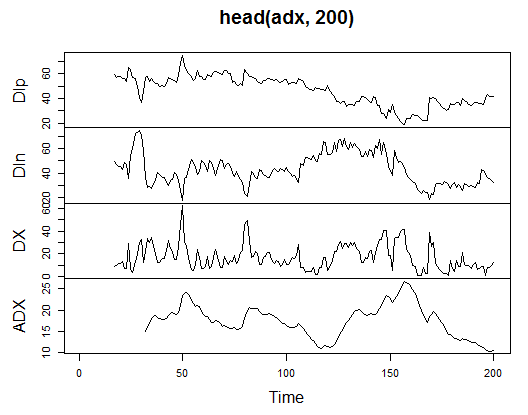
Abb. 13. Indikator Welles Wilder's Directional Movement Index – ADX(HLC, n)
> summary(adx) DIp DIn DX ADX Min. :15.90 Min. : 5.468 Min. : 0.00831 Min. : 5.482 1st Qu.:41.21 1st Qu.: 33.599 1st Qu.: 8.05849 1st Qu.:14.046 Median :47.36 Median : 43.216 Median :16.95423 Median :18.099 Mean :47.14 Mean : 46.170 Mean :19.73032 Mean :19.609 3rd Qu.:53.31 3rd Qu.: 55.315 3rd Qu.:27.97471 3rd Qu.:23.961 Max. :80.12 Max. :199.251 Max. :81.08751 Max. :52.413 NA's :16 NA's :16 NA's :16 NA's :31
Am Anfang der Matrix gibt es 31 undefinierte Werte (NA). Führen Sie anschließend die gleichen Berechnungen für alle Indikatoren ohne detaillierte Beschreibungen durch.
3.3.2.2. aroon(HL, n) – 1 out (oscillator)
Führen Sie die Berechnung durch und Sehen Sie sich die ersten 200 Balken von nur einer Variable, "oscillator", an:
> ar<-aroon(price[ , c('High', 'Low')], n = 16)[ ,'oscillator']
> plot(head(ar, 200), t = "l")
> abline(h = 0) 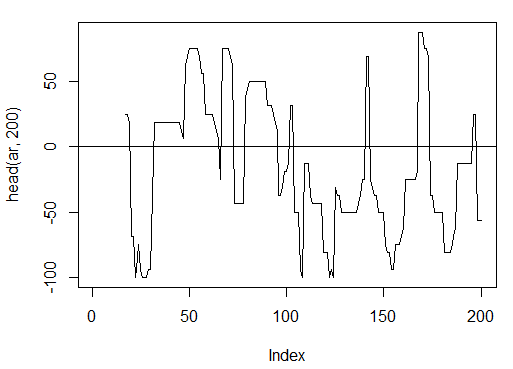
Abb. 14. Indikator aroon(HL, n)
> summary(ar) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -100.00 -56.25 -18.75 -7.67 43.75 100.00 16
3.3.2.3. Commodity Channel Index – CCI(HLC, n) – 1 out
> cci<-CCI(price[ ,2:4], n = 16)
> plot.ts(head(cci, 200))
> abline(h = 0) 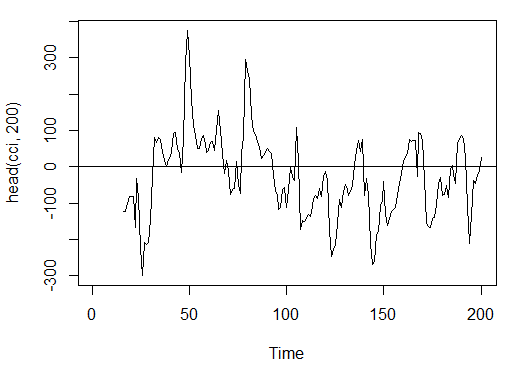
Abb. 15. Indikator Commodity Channel Index – CCI(HLC, n)
> summary(cci) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -469.10 -90.95 -18.74 -14.03 66.91 388.20 15
3.3.2.4. Chaikin Volatility – chaikinVolatility (HLC, n) – 1 out
> chv<-chaikinVolatility(price[ , 2:4], n = 16)
> summary(chv)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
-0.67570 -0.29940 0.02085 0.12890 0.41580 5.15700 31
> plot(head(chv, 200), t = "l")
> abline(h = 0) 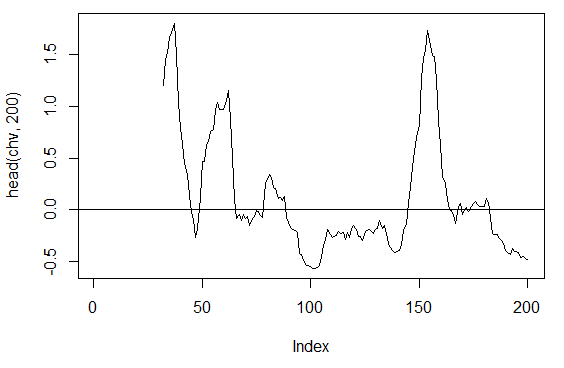
Abb. 16. Indikator chaikinVolatility (HLC, n)
3.3.2.5. Chande Momentum Oscillator – CMO(Med, n) – 1 out
> cmo<-CMO(price[ ,'Med'], n = 16)
> plot(head(cmo, 200), t = "l")
> abline(h = 0) 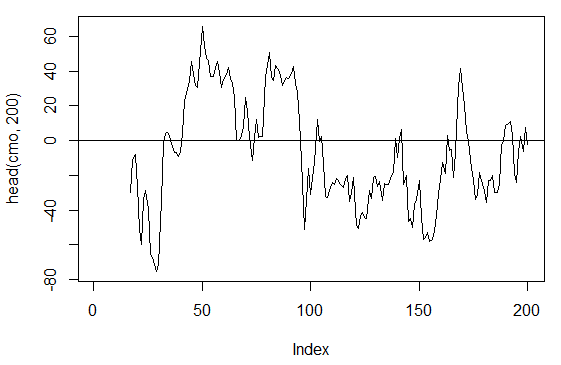
Abb. 17. Indikator Chande Momentum Oscillator – CMO(Med, n)
> summary(cmo) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -97.670 -32.650 -5.400 -6.075 19.530 93.080 16
3.3.2.6. MACD oscillator – MACD(Med, nFast, nSlow, nSig) 1 out wird verwendet (macd)
> macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd'] > plot(head(macd, 200), t = "l") > abline(h = 0)
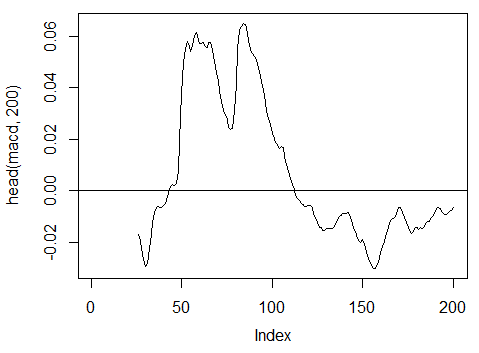
Abb. 18. Indikator MACD oscillator
> summary(macd) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -0.346900 -0.025150 -0.005716 -0.011370 0.013790 0.088880 25
3.3.2.7. OsMA(Med,nFast, nSlow, nSig) – 1 out
> osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal'] > plot(head(osma, 200), t = "l") > abline(h = 0)
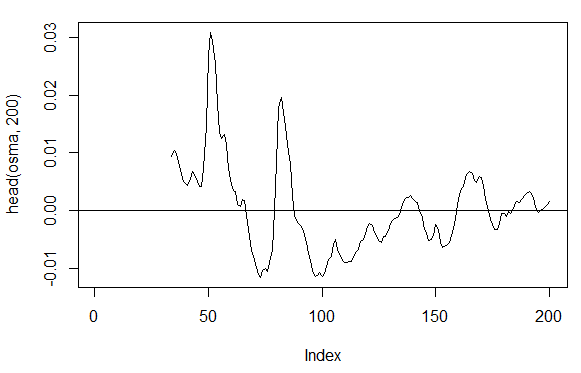
Abb. 19. Indikator OsMA(Med,nFast, nSlow, nSig)
> summary(osma) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -0.10560 -0.00526 0.00034 0.00007 0.00646 0.05922 33
3.3.2.8. Relative Strength Index – RSI(Med,n) – 1 out
> rsi<-RSI(price[ ,'Med'], n = 16)
> plot(head(rsi, 200), t = "l")
> abline(h = 50) 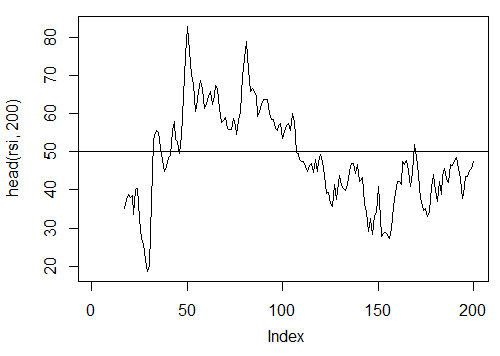
Abb. 20. Indikator Relative Strength Index – RSI(Med,n)
> summary(rsi) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 5.32 37.33 47.15 46.53 55.71 84.82 16
3.3.2.9. Stochastic Oscillator – stoch(HLC, nFastK=14, nFastD=3, nSlowD=3) – 3 out
> stoh<-stoch(price[ ,2:4], 14, 3, 3) > plot.ts(head(stoh, 200))
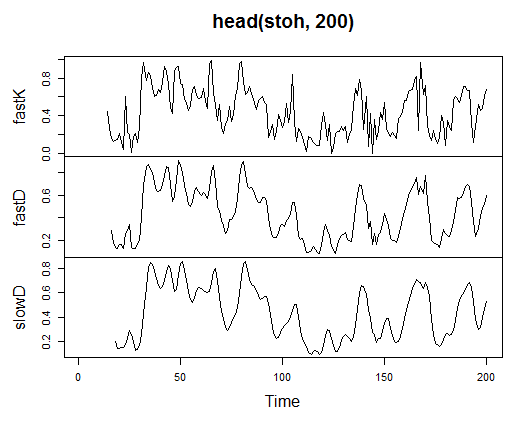
Abb. 21. Indikator Stochastic Oscillator – stoch(HLC, nFastK=14, nFastD=3, nSlowD=3)
> summary(stoh) fastK fastD slowD Min. :0.0000 Min. :0.01782 Min. :0.02388 1st Qu.:0.2250 1st Qu.:0.23948 1st Qu.:0.24873 Median :0.4450 Median :0.44205 Median :0.44113 Mean :0.4622 Mean :0.46212 Mean :0.46207 3rd Qu.:0.6842 3rd Qu.:0.67088 3rd Qu.:0.66709 Max. :1.0000 Max. :0.99074 Max. :0.97626 NA's :13 NA's :15 NA's :17
3.3.2.10. Stochastic Momentum Index – SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9) – 2 out
> smi<-SMI(price[ ,2:4],n = 13, nFast = 2, nSlow = 25, nSig = 9) > plot.ts(head(smi, 200))
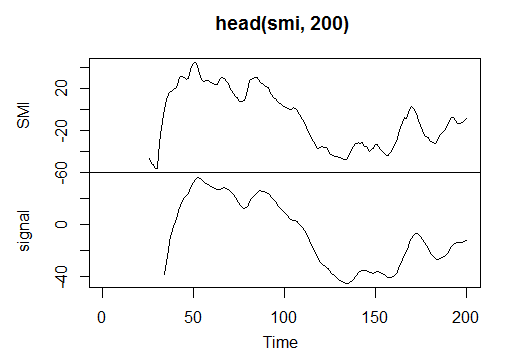
Abb. 22. Indikator Stochastic Momentum Index – SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9)
> summary(smi) SMI signal Min. :-82.185 Min. :-78.470 1st Qu.:-33.392 1st Qu.:-31.307 Median : -9.320 Median : -8.839 Mean : -8.942 Mean : -8.985 3rd Qu.: 15.664 3rd Qu.: 14.069 Max. : 71.878 Max. : 63.865 NA's :25 NA's :33
3.3.2.11. Volatility (Yang and Zhang) – volatility(OHLC, n, calc="yang.zhang", N=96) – 1 out
> vol<-volatility(price[ ,1:4],n = 16,calc = "yang.zhang", N =96) > plot.ts(head(vol, 200))
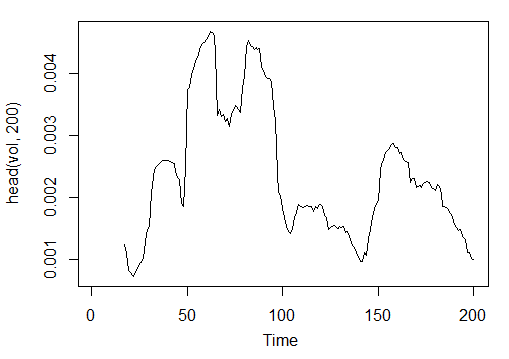
Abb. 23. Indikator Volatility (Yang and Zhang) – volatility(OHLC, n, calc="yang.zhang", N=96)
> summary(vol) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 0.000599 0.001858 0.002638 0.003127 0.004015 0.012840 16
Somit haben wir 17 Variablen aus 11 Indikatoren für EURUSD auf dem M15-Timeframe für die OHLC-Stichprobe mit einer Tiefe von 4000 Balken.
Nutzen Sie sie, um eine Matrix zu formen, und schreiben Sie die oben aufgeführten Parameter in eine Funktion mit einem formalen Parameter p, der für die Optimierung benötigt wird.
Berechnen Sie die Matrix der Eingangsparameter mithilfe der folgenden Formel:
In<-function(p = 16){
adx<-ADX(price, n = p);
ar<-aroon(price[ ,c('High', 'Low')], n=p)[ ,'oscillator'];
cci<-CCI(price[ ,2:4], n = p);
chv<-chaikinVolatility(price[ ,2:4], n = p);
cmo<-CMO(price[ ,'Med'], n = p);
macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd'];
osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal'];
rsi<-RSI(price[ ,'Med'], n = p);
stoh<-stoch(price[ ,2:4],14, 3, 3);
smi<-SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9);
vol<-volatility(price[ ,1:4],n = p,calc="yang.zhang", N=96);
In<-cbind(adx, ar, cci, chv, cmo, macd, osma, rsi, stoh, smi, vol);
return(In)
} > X<-In()
> tail(X)
DIp DIn DX ADX ar cci chv
[3995,] 46.49620 36.32411 12.28212 18.17544 25.0 168.0407 0.1835102
[3996,] 52.99009 31.61164 25.26952 18.61882 37.5 227.7030 0.3189822
[3997,] 58.11948 28.16241 34.72000 19.62515 37.5 145.2337 0.3448520
[3998,] 56.00323 30.48687 29.50206 20.24245 37.5 118.5831 0.3068059
[3999,] 55.96197 28.78737 32.06467 20.98134 37.5 116.5376 0.3517668
[4000,] 54.97777 26.85440 34.36713 21.81795 62.5 160.0767 0.6169701
cmo macd osma rsi fastK
[3995,] 29.71342 -0.020870825 0.01666593 52.91932 0.8832685
[3996,] 41.89526 -0.009654368 0.02230591 61.49793 0.8833819
[3997,] 30.98237 -0.002051532 0.02392699 58.94513 0.7259475
[3998,] 33.84813 0.003454534 0.02354645 58.00549 0.7930029
[3999,] 38.84892 0.009590136 0.02374564 60.63806 0.8367347
[4000,] 54.71698 0.019303110 0.02676689 66.64815 0.9354120
fastD slowD SMI signal vol
[3995,] 0.7773581 0.7735064 -35.095406 -47.27712 0.003643196
[3996,] 0.7691688 0.7761507 -26.482951 -43.11828 0.003858942
[3997,] 0.8308660 0.7924643 -19.699762 -38.43458 0.003920541
[3998,] 0.8007775 0.8002707 -13.141932 -33.37605 0.003916109
[3999,] 0.7852284 0.8056239 -6.569699 -28.01478 0.003999789
[4000,] 0.8550499 0.8136852 2.197810 -21.97226 0.004293766 Die rohen Eingangsdaten sind vorbereitet.
3.3.3. Ausgangsdaten (Ziel)
Nun formen wir Ausgangsdaten (Zieldaten). Wie bereits erwähnt, werden wir ZigZag verwenden.
Wir verwenden ZigZag mit einer Kanalbreite von 37 großen Punkten. ZigZag wird nach dem Durchschnittspreis berechnet. Der Indikator kann auch anhand der HL-Preise berechnet werden, allerdings ist der Durchschnittspreis vorzuziehen, da der Indikator in diesem Fall stabiler ist. Nach der Extraktion des Signals (0 – Buy, 1 – Sell) konvertieren Sie es in eine Eingangsmatrix, die vom Netzwerkmodell übernommen wird.
Schreiben Sie eine Funktion:
Out<-function(ch=0.0037){ # ZigZag has values on each bar and not only in the points zz<-ZigZag(price[ ,'Med'], change = ch, percent = F, retrace = F, lastExtreme = T); n<-1:length(zz); # On the last bars substitute the undefined values for the last known ones for(i in n) { if(is.na(zz[i])) zz[i] = zz[i-1];} #Define the speed of ZigZag changes and move one bar forward dz<-c(diff(zz), NA); #If the speed >0 - signal = 0(Buy), if <0, signal = 1 (Sell) otherwise NA sig<-ifelse(dz>0, 0, if else(dz<0, 1, NA)); return(sig); }
Berechnen Sie die Signale.
> Y<-Out() > table(Y) Y 0 1 1567 2423
Das Klassenverhältnis ist nicht ausbalanciert. Die Anzahl der Beispiele einer Klasse ist größer als die der anderen. Alle Modelle der Klassifizierung sind solchen Sätzen nicht wohlgesonnen.
Wir beheben diese Situation beim Trennen der Daten in Einlern- und Teststichproben.
3.3.4. Bereinigen von Daten
Lassen Sie uns unsere Datensätze von undefinierten Daten bereinigen. Die Bereinigung umfasst in diesem Fall einen größeren Aufgabenbereich. Dazu gehört die Bereinigung von "Variablen, die praktisch Null sind", und solchen, die zu stark korreliert sind, sowie weitere Aufgaben, die wir an dieser Stelle nicht besprechen werden.
Schreiben Sie eine Funktion und bereinigen Sie die Daten.
Clearing<-function(x, y){
dt<-cbind(x,y);
n<-ncol(dt)
dt<-na.omit(dt)
return(dt);
}
> dt<-Clearing(X,Y); nrow(dt)
[1] 3957 Die Matrix hat sich um 43 Balken verkürzt.
3.3.5. Formen der Stichproben zum Einlernen und Testen
Es gibt mehrere Arten, die Quelldaten in Einlern- und Teststichproben aufzuteilen. Wir wenden eine herkömmliche zufällige Aufteilung der Quelldaten in Einlern- und Testdaten in einem Verhältnis von 8/10 an. Es ist wichtig, dass die Stichproben geschichtet sind, das heißt, das Verhältnis der Klasseninstanzen in Einlern- und Teststichproben muss dem Klassenverhältnis im Quelldatensatz entsprechen. Es wäre auch vorteilhaft, die Ungleichheit von Klassen im Quelldatensatz auszugleichen. Es gibt zwei Möglichkeiten dafür: entweder nach der kleineren oder nach der größeren Klasse ausgleichen. Da wir mehr Beispiele brauchen, gleichen wir nach der größeren Klasse "1" aus. In diesem Fall nutzen wir das Paket "caret".
Formen wir einen neuen ausgeglichenen Satz, bei dem die Menge der Instanzen beider Klassen gleich ist und der größeren entspricht.
3.3.6. Ausgleich von Klassen
Nachfolgend sehen Sie die Funktion, die die Menge der Klasse anhand der größeren Klasse ausgleicht (falls der Unterschied größer als 15 % ist) und eine ausgeglichene Matrix ausgibt:
Balancing<-function(DT){
#Calculate a table with a number of classes
cl<-table(DT[ ,ncol(DT)]);
#If the divergence is less than 15%, return the initial matrix
if(max(cl)/min(cl)<= 1.15) return(DT)
#Otherwise level by the greater side
DT<-if(max(cl)/min(cl)> 1.15){
upSample(x = DT[ ,-ncol(DT)],y = as.factor(DT[ , ncol(DT)]), yname = "Y")
}
#Convert у (factor) into a number
DT$Y<-as.numeric(DT$Y)
#Recode у from 1,2 into 0,1
DT$Y<-ifelse(DT$Y == 1, 0, 1)
#Convert dataframe to matrix
DT<-as.matrix(DT)
return(DT);
} Erklärung. Im ersten String wird die Menge der Instanzen jeder Klasse berechnet (Vektor, dessen Dimension gleich der Menge der Klassen ist).
Finden Sie das Verhältnis des größeren Vektors zum kleineren und falls es kleiner als der Schwellenwert ist, verlassen Sie die Funktion. Falls das Verhältnis größer ist, berechnen Sie die Funktion, indem Sie x und y separat eingeben. y muss vorher in einen Faktor konvertiert werden.
Dies ist die Anforderung an die formalen Parameter der Funktion upSample(). Da wir die Zielvariable nicht als Faktor brauchen, konvertieren wir sie zurück zu einer numerischen Variable mit den Werten 0 und 1. Bitte beachten Sie, dass wir bei der Konvertierung einer numerischen Variable (0,1) in einen Faktor die Textvariablen "0" und "1" erhalten. Bei der umgekehrten Konvertierung in numerische Variablen erhalten wir 1 und 2 (!). Wir ersetzen sie durch 0 und 1. Unser Datensatz wird vom "Datenrahmen" zur "Matrix" der Klasse konvertiert. Berechnen Sie sie:
dt.b<-Balancing(dt) x<-dt.b[ ,-ncol(dt.b)] y<-dt.b[ , ncol(dt.b)]
Somit haben wir den Quelldatensatz dt (Eingang und Ausgang) und den ausgeglichenen Satz dt.b.
Teilen Sie ihn in die Einlern- und Teststichproben auf
Erhalten Sie die Indizes der Einlern- und Teststichproben aus dem Paket "rminer" mithilfe der Funktion holdout().
> library('rminer')
> t<-holdout(y, ratio = 8/10, mode = "random") Beim Objekt t handelt es sich um eine Liste mit den Indizes der Datensätze für das Einlernen (t$tr) und Testen (t$ts). Die erhaltenen Sätze sind geschichtet.
3.3.7. Vorverarbeitung
Unsere Eingangsdatenquelle enthält Variablen mit unterschiedlichen Wertbereichen. Im Wesentlichen handelt es sich bei tiefen Netzwerken um herkömmliche Netzwerke mit einer besonderen Art der Initialisierung von Gewichtungen.
Neuronale Netzwerke können Eingangsvariablen im Bereich (-1; 1) oder (0, 1) erhalten. Normalisieren Sie die Eingangsvariablen in den Bereich [-1, 1].
Nutzen Sie dazu die Funktion preProcess() aus dem Paket "caret". Bitte beachten Sie, dass die Parameter der Vorverarbeitung auf dem Einlerndatensatz berechnet werden müssen, und speichern Sie sie für die weitere Vorverarbeitung des Testdatensatzes und neuer Eingangsdaten.
> spSign<-preProcess(x[t$tr, ], method = "spatialSign")
> x.tr<-predict(spSign, x[t$tr, ])
> x.ts<-predict(spSign, x[t$ts, ]) Nun ist alles fertig, was wir für den Aufbau, das Einlernen und das Testen eines tiefen neuronalen Netzwerks benötigen.
3.4. Aufbauen, Einlernen und Testen von Modellen
Wir werden das Modell DN SAE aufbauen und einlernen. Die Formel des Modells und Beschreibung der Variablen:
sae.dnn.train(x, y, hidden = c(10), activationfun = "sigm", learningrate = 0.8, momentum = 0.5, learningrate_scale = 1, output = "sigm", sae_output = "linear", numepochs = 3, batchsize = 100, hidden_dropout = 0, visible_dropout = 0)
wobei:
- x ist eine Matrix aus Eingangsdaten;
- y ist ein Vektor oder eine Matrix aus Zielvariablen;
- hidden ist ein Vektor mit einer Menge von Neuronen in jeder verborgenen Lage. Standardmäßig c(10);
- activationfun ist eine Funktion zum Aktivieren von verborgenen Neuronen. Kann "sigm", "linear", "tanh" sein. Standardmäßig "sigm";
- learningrate ist eine Einlernebene für das Gradientenverfahren. Standardmäßig 0.8;
- momentum ist ein Momentum für das Gradientenverfahren. Standardmäßig 0.5;
- learningrate_scale ist ein Wert, mit dem die Einlernebene nach jeder Iteration multipliziert werden kann. Standardmäßig 1.0;
- numepochs ist eine Menge von Iterationen für das Einlernen. Standardmäßig 3;
- batchsize ist die Größe einer kleinen Menge von Daten, die eingelernt werden. Standardmäßig 100;
- output ist die Aktivierungsfunktion für Ausgangsneuronen. Kann "sigm", "linear", "softmax" sein. Standardmäßig "sigm";
- sae_output ist die Aktivierungsfunktion von Ausgangsneuronen von SAE. Kann "sigm", "linear", "softmax" sein. Standardmäßig "linear";
- hidden_dropout ist ein löschbarer Teil für verborgene Lagen. Standardmäßig 0;
- visible_dropout ist ein löschbarer Teil der sichtbaren (Eingangs-)Lage. Standardmäßig 0.
Wir werden ein Modell mit den Dimensionen (17, 100, 100, 100, 1) erstellen, einlernen, die Einlerndauer notieren und die Prognose beobachten.
> system.time(SAE<-sae.dnn.train(x= x.tr, y= y[t$tr], hidden=c(100,100,100), activationfun = "tanh", learningrate = 0.6, momentum = 0.5, learningrate_scale = 1.0, output = "sigm", sae_output = "linear", numepochs = 10, batchsize = 100, hidden_dropout = 0, visible_dropout = 0)) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. user system elapsed 12.92 0.00 13.09
Wie wir sehen können, geschieht dies in zwei Phasen. Als Erstes wird der Autoencoder Lage für Lage eingelernt und anschließend das neuronale Netzwerk.
Die geringe Anzahl von Einlerndurchläufen und die riesige Menge verborgener Neuronen in den drei Lagen wurden absichtlich festgelegt. Der gesamte Prozess hat 13 Sekunden gedauert!
Sehen wir uns die Prognosen zum Testsatz von Prädiktoren an.
> pr.sae<-nn.predict(SAE, x.ts); > summary(pr.sae) V1 Min. :0.2649 1st Qu.:0.2649 Median :0.5881 Mean :0.5116 3rd Qu.:0.7410 Max. :0.7410
Konvertieren Sie sie in die Ebenen 0,1 und berechnen Sie die Messwerte:
> pr<-ifelse(pr.sae>mean(pr.sae), 1, 0) > confusionMatrix(y[t$ts], pr) Confusion Matrix and Statistics Reference Prediction 0 1 0 316 128 1 134 378 Accuracy : 0.7259 95% CI : (0.6965, 0.754) No Information Rate : 0.5293 P-Value [Acc > NIR] : <2e-16 Kappa : 0.4496 Mcnemar's Test P-Value : 0.7574 Sensitivity : 0.7022 Specificity : 0.7470 Pos Pred Value : 0.7117 Neg Pred Value : 0.7383 Prevalence : 0.4707 Detection Rate : 0.3305 Detection Prevalence : 0.4644 Balanced Accuracy : 0.7246 'Positive' Class : 0
Das ist kein überragender Koeffizient. Wir interessieren uns mehr für den Gewinn, den wir mit diesen Signalen erzielen werden, nicht den Koeffizienten. Prüfen Sie dies auf den letzten 500 Balken (etwa eine Woche). Wir erhalten Signale auf den letzten 500 aufeinanderfolgenden Balken aus unserem eingelernten Netzwerk.
Normalisieren Sie die letzten 500 Balken von Eingangsdaten, erhalten Sie die Prognosen aus dem eingelernten neuronalen Netzwerk und konvertieren Sie sie in die Signale -1 = (Sell) und 1 = (Buy).
> new.x<-predict(spSign,tail(dt[ ,-ncol(dt)], 500)) > pr.sae1<-nn.predict(SAE, new.x) > pr.sig<-ifelse(pr.sae1>mean(pr.sae1), -1, 1) > table(pr.sig) pr.sig -1 1 235 265 > new.y<-ifelse(tail(dt[ , ncol(dt)], 500) == 0, 1, -1) > table(new.y) new.y -1 1 201 299 > cm1<-confusionMatrix(new.y, pr.sig) > cm1 Confusion Matrix and Statistics Reference Prediction -1 1 -1 160 41 1 75 224 Accuracy : 0.768 95% CI : (0.7285, 0.8043) No Information Rate : 0.53 P-Value [Acc > NIR] : < 2.2e-16 Kappa : 0.5305 Mcnemar's Test P-Value : 0.002184 Sensitivity : 0.6809 Specificity : 0.8453 Pos Pred Value : 0.7960 Neg Pred Value : 0.7492 Prevalence : 0.4700 Detection Rate : 0.3200 Detection Prevalence : 0.4020 Balanced Accuracy : 0.7631 'Positive' Class : -1
Der Koeffizient Accuracy ist nicht schlecht, doch wir interessieren uns eher für den Gewinn als den Koeffizienten.
Testen sie den Gewinn für die letzten 500 Balken mithilfe unserer prognostizierten Signale und erhalten Sie die Bilanzkurve:
> bal<-cumsum(tail(price[ , 'CO'], 500) * pr.sig) > plot(bal, t = "l") > abline(h = 0)
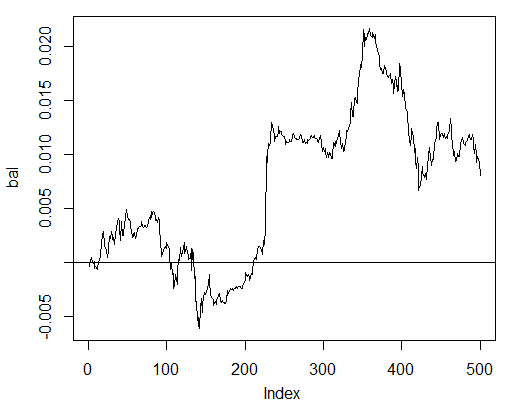
Abb. 24. Bilanz der letzten 500 Balken nach den Signalen des neuronalen Netzwerks
Die Bilanz wurde ohne Berücksichtigung des Spreads, der Abweichung und sonstiger Reize eines realen Marktes berechnet.
Vergleichen Sie sie nun mit der Bilanz, die Sie aus den idealen Signalen von ZZ erhalten hätten. Die rote Linie ist die Bilanz nach den Signalen des neuronalen Netzwerks:
> bal.zz<-cumsum(tail(price[ , 'CO'], 500) * new.y) > plot(bal.zz, t = "l") > lines(bal, col = 2)
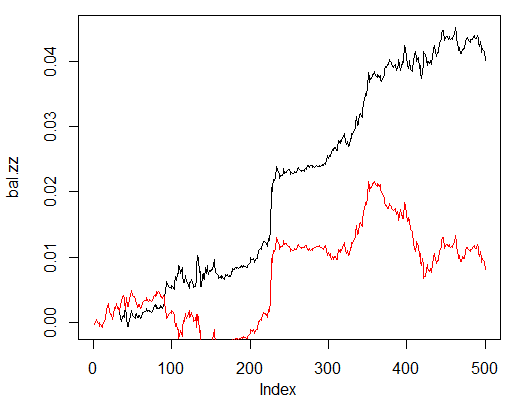
Abb. 25. Bilanz der letzten 500 Balken nach den Signalen des neuronalen Netzwerks und den ZigZag-Signalen
Es gibt definitiv Verbesserungspotenzial.
Schreiben Sie die zwei Hilfsfunktionen Estimation() und Testing(), um das Testen zu erleichtern. Erstere erzeugt die Koeffizienten Accuracy/Err, letztere die Bilanz Bal/BalZZ.
Dies ermöglicht den sofortigen Erhalt eines Ergebnisses, wodurch einige Netzwerkparameter verändert werden, und man kann sehen, welche Parameter die Qualität des Netzwerks beeinflussen.
Nach dem Schreiben einer Fitness-Funktion lassen sich die optimalen Netzwerkparameter mithilfe evolutionärer (genetischer) Algorithmen ohne jegliche Unterbrechungen des Handelsprozesses finden. Darauf gehen wir in diesem Beitrag nicht weiter ein und betrachten es ein andermal detailliert.
Nachfolgend sehen Sie die Funktion Estimation() zum Berechnen der Koeffizienten Err/Accuracy:
Estimation<-function(X, Y, r = 8/10, m = "random", norm = "spatialSign", h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, out = "sigm", sae = "linear", Ep = 10, Bs = 50, CM=F){ #Indices of the training and test data set t<-holdout(Y, ratio = r, mode = m) #Parameters of preprocessing prepr<-preProcess(X[t$tr, ], method = norm) #Divide into train and test data sets with preprocessing x.tr<-predict(prepr, X[t$tr, ]) x.ts<-predict(prepr, X[t$ts, ]) y.tr<- Y[t$tr]; y.ts<- Y[t$ts] #Train the model SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs) #Obtain a forecast on the test data set pr.sae<-nn.predict(SAE, x.ts) #Recode it into signals 1,0 pr<-ifelse(pr.sae>mean(pr.sae), 1, 0) #Calculate the Accuracy coefficient or classification error if(CM) err<-unname(confusionMatrix(y.ts, pr)$overall[1]) if(!CM) err<-nn.test(SAE, x.ts, y.ts, mean(pr.sae)) return(err) }
Formale Parameter:
- X – Matrix roher Eingangsprädiktoren;
- Y – Vektor der Zielvariable;
- r – Verhältnis train/test;
- m – Modus der Formierung von Stichproben (zufällig oder aufeinanderfolgend);
- norm – Modus der Normalisierung von Parametern ([-1, 1]= "spatialSign";[0, 1]="range");
- h – Vektor mit der Menge der Neuronen in den verborgenen Schichten;
- act – Aktivierungsfunktion von verborgenen Neuronen;
- LR – Einlernebene;
- Mom – Momentum;
- out – Aktivierungsfunktion der Ausgangslage;
- sae – Aktivierungsfunktion des Autoencoders;
- Ep – Menge der Einlerndurchläufe;
- Bs – Größe der kleinen Stichprobe;
- CM – boolesche Variable, falls TRUE, wird Accuracy ausgegeben. Andernfalls Err.
Als Beispiel berechnen wir den Klassifizierungsfehler auf dem unausgeglichenen Datensatz dt anhand des Netzwerks mit drei verborgenen Lagen mit je 30 Neuronen:
> Err<-Estimation(X = dt[ ,-ncol(dt)], Y = dt[ ,ncol(dt)], h=c(30, 30, 30), LR= 0.7) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > Err [1] 0.1376263
Die Funktion Testing() berechnet die Bilanz nach den Prognosesignalen oder nach den idealen Signalen (ZigZag):
Testing<-function(dt1, dt2, r=8/10, m = "random", norm = "spatialSign", h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, out = "sigm", sae = "linear", Ep = 10, Bs=50, pr = T, bar = 500){ X<-dt1[ ,-ncol(dt1)] Y<-dt1[ ,ncol(dt1)] t<-holdout(Y, ratio = r, mode = m) prepr<-preProcess(X[t$tr, ], method = norm) x.tr<-predict(prepr, X[t$tr, ]) y.tr<- Y[t$tr]; SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs) X<-dt2[ ,-ncol(dt2)] Y<-dt2[ ,ncol(dt2)] x.ts<-predict(prepr, tail(X, bar)) y.ts<-tail(Y, bar) pr.sae<-nn.predict(SAE, x.ts) sig<-ifelse(pr.sae>mean(pr.sae), -1, 1) sig.zz<-ifelse(y.ts == 0, 1,-1 ) bal<-cumsum(tail(price[ ,'CO'], bar) * sig) bal.zz<-cumsum(tail(price[ ,'CO'], bar) * sig.zz) if(pr) return(bal) if(!pr) return(bal.zz) }
Formale Parameter:
- dt1 – Matrix der Eingangs- und Zielvariablen zum Einlernen des Netzwerks;
- dt2 – Matrix der Eingangs- und Zielvariablen zum Testen des Netzwerks;
- pr – boolesche Variable, falls TRUE, wird die Bilanz nach den Prognosesignalen ausgegeben, andernfalls nach ZigZag;
- bar – Menge der letzten zu verwendenden Balken zur Berechnung der Bilanz.
Berechnen Sie die Bilanz auf den letzten 500 Balken unseres Datensatzes dt beim Einlernen auf dem ausgeglichen Datensatz dt.b anhand des neuronalen Netzwerks mit den gleichen Parametern wie oben aufgeführt:
> Bal<-Testing(dt.b, dt, h=c(30, 30, 30), LR= 0.7) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > plot(Bal, t = "l") > abline(h = 0)
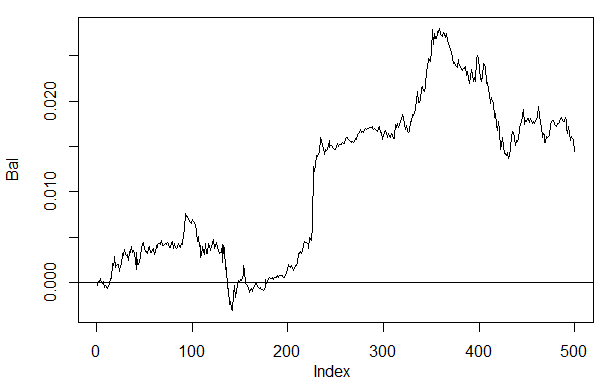
Abb. 26. Bilanz der letzten 500 Balken nach den Signalen des neuronalen Netzwerks h(30,30,30)
Wenn wir das Ergebnis mit der vorher erhaltenen Bilanz vergleichen, sehen wir eine wesentliche Verbesserung. Doch das ist hier nicht der interessanteste Punkt.
Wenn wir uns die Preisdarstellung auf den letzten 500 Balken ansehen, können wir sehen, welche Teile davon von unserem Netzwerk am besten aufgenommen wurden (Balken 150-350).
> plot(tail(price[ ,'Close'], 500), t = "l") > abline(v = c(150,350), col=2)
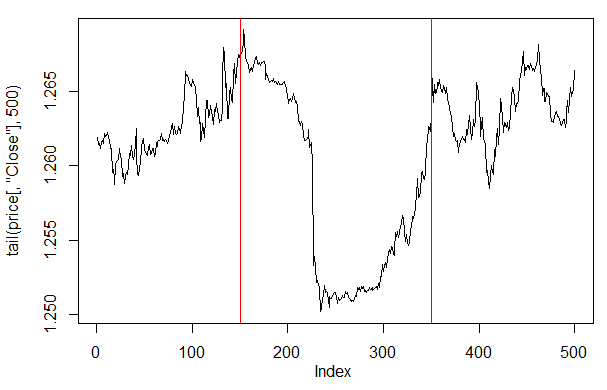
Abb. 27. Darstellung des Close-Preises auf den letzten 500 Balken
Hinweis: Beim Dekodieren der prognostizierten Ausgänge haben wir eine vereinfachte Version größer/kleiner als der Durchschnitt verwendet. Es können auch andere Versionen verwendet werden.
Wenn die Werte größer als 0,6 oder kleiner als 0,4 sind, wird das instabile Segment von 0,4-0,6 abgeschnitten. Genauere Klassengrenzen können bei der Kalibrierung erhalten werden. Das wird später besprochen.
Unsere Funktion Testing() wird geringfügig abgeändert, wenn der zusätzliche Parameter dec eingeführt wird. Dies ermöglicht uns die Auswahl einer Methode zum Dekodieren ("mean" oder "60/40") und die Prüfung auf den prognostizierten Werten, welche Auswirkung dies auf die Bilanz haben wird.
Testing.1<-function(dt1, dt2, r = 8/10, m = "random", norm = "spatialSign", h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, out = "sigm", sae = "linear", Ep = 10, Bs = 50, pr = T, bar = 500, dec=1){ X<-dt1[ ,-ncol(dt1)] Y<-dt1[ ,ncol(dt1)] t<-holdout(Y, ratio = r, mode = m) prepr<-preProcess(X[t$tr, ], method = norm) x.tr<-predict(prepr, X[t$tr, ]) y.tr<- Y[t$tr]; SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs) X<-dt2[ ,-ncol(dt2)] Y<-dt2[ ,ncol(dt2)] x.ts<-predict(prepr, tail(X, bar)) y.ts<-tail(Y, bar) pr.sae<-nn.predict(SAE, x.ts) #Вариант +/- mean if(dec == 1) sig<-ifelse(pr.sae>mean(pr.sae), -1, 1) #Вариант 60/40 if(dec == 2) sig<-ifelse(pr.sae>0.6, -1, ifelse(pr.sae<0.4, 1, 0)) sig.zz<-ifelse(y.ts == 0, 1,-1 ) bal<-cumsum(tail(price[ ,'CO'], bar) * sig) bal.zz<-cumsum(tail(price[ ,'CO'], bar) * sig.zz) if(pr) return(bal) if(!pr) return(bal.zz) }
Berechnen und bewerten Sie die Bilanz mit der ersten und zweiten Variante der Dekodierung.
Damit sich die Ergebnisse wiederholen, richten Sie einen Generator von Pseudozufallszahlen in der gleichen Position ein.
> set.seed<-1245 > Bal1<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 1) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > set.seed<-1245 > Bal2<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > plot(Bal2, t = "l") > lines(Bal1, col = 2)
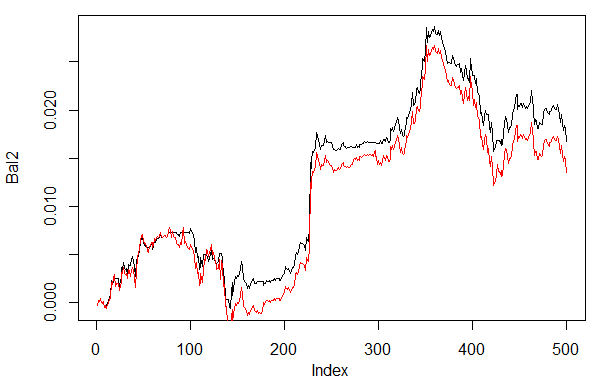
Abb. 28. Bilanz der letzten 500 Balken nach den Signalen des neuronalen Netzwerks mit unterschiedlichen Varianten der Dekodierung von Prognosen
Die Bilanz nach der zweiten Variante (60/40) sieht deutlich besser aus. Doch auch hier gibt es noch Verbesserungspotenzial.
Hier ist der letzte zu überprüfende Punkt. Theoretisch führt ein Ensemble aus mehreren neuronalen Netzwerken zu einem besseren und stabileren Ergebnis. Wir testen ein Ensemble aus mehreren Netzwerken, die auf den gleichen Stichproben eingelernt werden, obwohl sie auch auf unabhängigen Stichproben eingelernt werden können. Das Ergebnis der Prognose des Ensembles ist ein einfacher Durchschnittswert der Prognosen aller Netzwerke. Es gibt aber auch komplexere Arten der Mittelung.
Wir verbessern unsere Funktion Testing(), indem wir einen weiteren Parameter hinzufügen, ans=1, der die Anzahl der Netzwerke im Ensemble festlegt.
3.4.1. Parallele Berechnungen
Da sich die Berechnungen nach mehreren unabhängigen Modellen einfach parallel ausrichten lassen, nutzen wir die von der Sprache R bereitgestellte Möglichkeit und erstellen ein Cluster aus mehreren Prozessorkernen oder Computern in einem lokalen Netzwerk, unabhängig davon, welche Betriebssysteme auf diesen Computern installiert sind.
Dazu brauchen wir die Pakete "foreach" und "doParallel". Nachfolgend sehen Sie eine sehr einfache Funktion, die ein Cluster für alle Kerne unseres Prozessors ausführt.
library(doParallel) library(foreach) puskCluster<-function(){ cores<-detectCores() cl<-makePSOCKcluster(cores) registerDoParallel(cl) clusterSetRNGStream(cl) return(cl) }
Im Nachfolgenden werden mehrere Punkte erörtert. In den ersten zwei Strings laden wir die erforderlichen Bibliotheken. Diese müssen vorher auf Ihrem Computer installiert werden. Anschließend definieren wir, wie viele Kerne unser Prozessor hat, erstellen ein Cluster, registrieren ein Paket für parallele Berechnungen, richten einen unabhängigen Generator von Pseudozufallszahlen in jedem Strom von Berechnungen ein und geben das Handle des Clusters aus. Die Qualität des Generators von Pseudozufallszahlen für die Berechnungen jedes Modells ist äußerst wichtig, doch das ist ein separates Thema.
Nachdem das Cluster gestartet und alle erforderlichen Berechnungen ausgeführt wurden, müssen wir daran denken, es anzuhalten:
cl<-puskCluster() stopCluster(cl)
Parallele Berechnungen werden durch die folgende Formel aus dem Paket "foreach" ausgeführt:
SAE<-foreach(times(ans), .packages = "deepnet") %dopar% sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs)
wobei times(ans) eine Anzahl von Netzwerken ist, die wir erhalten möchten, und .packages auf das Paket deutet, aus dem die berechnete Funktion entnommen wird.
Das Ergebnis hat die Form einer Liste und beinhaltet die von uns benötigte Anzahl von eingelernten Netzwerken.
Anschließend erhalten wir die Prognose aus jedem Netzwerk und berechnen den Durchschnitt.
pr.sae<-(foreach(i = 1:ans, .combine = "+") %do% nn.predict(SAE[[i]], x.ts))/ans
Hier ist i ein Vektor der Indizes der eingelernten Netzwerke, .combine="+" legt fest, in welcher Form die Prognosen in allen neuronalen Netzwerken ausgegeben werden müssen. In diesem Fall müssen wir eine Summe ausgeben und diese Berechnungen sequenziell, nicht parallel, durchführen (Operator %do%). Die erhaltene Summe wird durch die Anzahl der neuronalen Netzwerke geteilt und stellt das Endergebnis dar. Das ist einfach und elegant.
Berechnen Sie die Bilanz aus Ensembles aus 3 und 4 neuronalen Netzwerken mit den gleichen Parametern wie die obigen und der Dekodierungsvariante 60/40. Vergleichen Sie das Ergebnis mit den Ergebnissen von einem neuronalen Netzwerk. Um die Effektivität von parallelen Berechnungen zu bewerten, erhöhen Sie die Anzahl der Durchläufe auf 300 und messen Sie, wie lange der Prozess zum Erhalten der Prognose dauert.
1. Ein neuronales Netzwerk:
> system.time(Bal21<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000057 ####loss on step 20000 is : 0.000043 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000081 ####loss on step 20000 is : 0.000086 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000072 ####loss on step 20000 is : 0.000066 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.069451 ####loss on step 20000 is : 0.079629 deep nn has been trained. user system elapsed 115.78 0.00 116.96 > plot(Bal21, t = "l") > abline(h = 0)
2. Ensemble aus 3 neuronalen Netzwerken:
> system.time(Bal41<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=3)) user system elapsed 0.22 0.06 233.64 > lines(Bal41, col=4)
3. Ensemble aus 4 neuronalen Netzwerken:
> system.time(Bal44<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=4)) user system elapsed 0.13 0.03 247.86 > lines(Bal44, col=2)
Die Ausführungsdauer bei paralleler Berechnung ist optimal, wenn die Menge der Ströme ein Vielfaches der Menge der Kerne ist. Ich habe 2 Kerne verwendet.
Allerdings gibt es keine wesentlichen Vorteile in der Bilanz. Im nachfolgenden Diagramm stellt die blaue Linie 3 Netzwerke dar, die rote 4 und die schwarze ein Netzwerk.
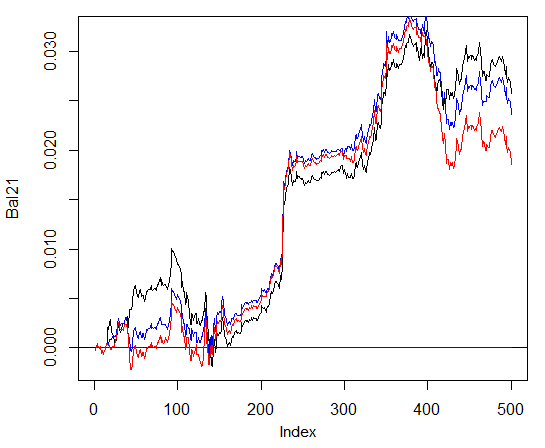
Abb. 29. Bilanz der letzten 500 Balken nach den Signalen der Ensembles aus 3 und 4 neuronalen Netzwerken und von einem Netzwerk
Im Allgemeinen hängt das Ergebnis von vielen Parametern ab, angefangen bei den Eingangs- und Ausgangsdaten, der Art ihrer Normalisierung, der Menge verborgener Lagen und der Anzahl der Neuronen in diesen Lagen, der Einlernebene, der Anzahl der Einlerndurchläufe und vielen weiteren.
Die letzten drei Beispiele. Berechnen Sie die Bilanz der letzten 1000 Balken mit drei neuronalen Netzwerken mit unterschiedlichen Mengen von verborgenen Neuronen in drei verborgenen Lagen.
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300, bar=1000)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000054 ####loss on step 20000 is : 0.000044 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000078 ####loss on step 20000 is : 0.000079 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000090 ####loss on step 20000 is : 0.000072 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.072633 ####loss on step 20000 is : 0.057917 deep nn has been trained. user system elapsed 116.09 0.02 116.26 > max(Bal0) [1] 0.04725 > plot(Bal0, t="l") > tail(Bal0,1) [1] 0.03514
Der maximale Gewinn beträgt 472 Punkte, auf dem letzten Balken 351 Punkte. Im Diagramm wird er in Schwarz dargestellt.
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(13, 8, 5), LR = 0.7, dec = 2, Ep=300, bar=1000)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.005217 ####loss on step 20000 is : 0.004846 training layer 2 autoencoder ... ####loss on step 10000 is : 0.051324 ####loss on step 20000 is : 0.046230 training layer 3 autoencoder ... ####loss on step 10000 is : 0.023292 ####loss on step 20000 is : 0.026113 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.057788 ####loss on step 20000 is : 0.056932 deep nn has been trained. user system elapsed 64.04 0.01 64.24 Warning message: In sae$encoder[[i - 1]]$W[[1]] %*% t(train_x) + sae$encoder[[i - : longer object length is not a multiple of shorter object length > lines(Bal0, col="blue")
Das ist definitiv eine unwirksame Variante.
Die dritte Variante:
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=1000)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000018 ####loss on step 20000 is : 0.000013 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000062 ####loss on step 20000 is : 0.000048 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000053 ####loss on step 20000 is : 0.000055 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.096490 ####loss on step 20000 is : 0.084860 deep nn has been trained. user system elapsed 186.18 0.00 186.39 > lines(Bal0, col="red") > max(Bal0) [1] 0.0543
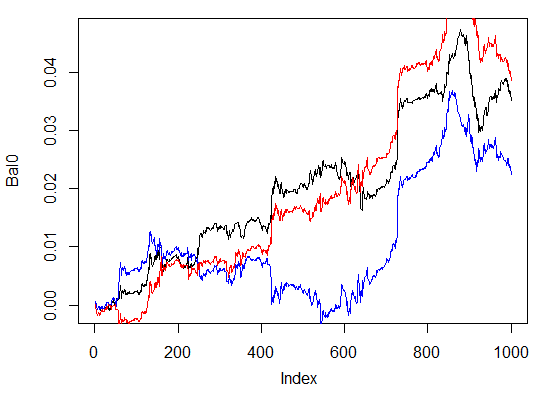
Abb. 30. Bilanz der letzten 1000 Balken nach den Signalen von drei neuronalen Netzwerken mit unterschiedlichen Mengen von verborgenen Neuronen
Die Ergebnisse zeigen, dass die dritte Variante die beste dieser drei mit einem maximalen Gewinn von 543 Punkten ist. Wir haben lediglich die Menge der verborgenen Neuronen verändert, was zu einer wesentlichen Verbesserung geführt hat. Die Suche nach den optimalen Parametern sollte mithilfe von evolutionären Algorithmen durchgeführt werden. Dies zu erforschen, ist die Aufgabe des Lesers.
Denken Sie daran, dass der Algorithmus des Verfassers in diesem Paket nicht vollständig umgesetzt wurde.
4. Umsetzung (Indikator und Expert Advisor)
Nun schreiben wir ein Programm für den Indikator und den Expert Advisor mit einem tiefen Netzwerk zum Erhalten von Handelssignalen.
Es gibt zwei Möglichkeiten, dies umzusetzen:
- Die erste. Das Einlernen des neuronalen Netzwerks wird manuell in Rstudio durchgeführt. Speichern Sie das Netzwerk im jeweiligen Katalog, nachdem Sie akzeptable Ergebnisse erhalten haben. Führen Sie dann den EA und Indikator im Diagramm aus. Der EA lädt das eingelernte Netzwerk. Der Indikator bereitet einen Vektor von neuen Eingangsdaten auf jedem neuen Balken vor und übergibt ihn an den EA. Der EA präsentiert die Daten des Netzwerks, erhält ein Signal und führt es aus. Der EA fährt mit seinen üblichen Aktivitäten wie dem Öffnen und Schließen von Ordern, Trailing usw. fort. Das Ziel des Indikators ist es, neue Eingangsdaten auf jedem neuen Balken vorzubereiten und an den EA zu übergeben, und vor allem, Signale, die vom Netzwerk prognostiziert werden, auf einem Diagramm zu präsentieren. Die Praxis zeigt, dass eine Sichtprüfung die effizienteste Art ist, ein neuronales Netzwerk zu beurteilen.
- Die zweite Art. Führen Sie den EA und Indikator im Diagramm aus. Beim ersten Start übergibt der Indikator einen vorbereiteten großen Satz von Eingangs- und Ausgangsdaten an den EA. Der EA führt das Einlernen, das Testen und die Auswahl des besten neuronalen Netzwerks aus. Anschließend geht alles weiter wie bei der ersten Variante.
Wir schreiben die Verknüpfung Indikator-EA unter Befolgung des ersten Algorithmus. Der EA hat nur das nötige Minimum an "Rüschen und Schleifen".
Warum ist das so schwierig? Diese Art der Umsetzung ermöglicht eine Verknüpfung von mehreren Indikatoren auf unterschiedlichen Symbolen/Timeframes mit einem EA und die darauffolgende Arbeit mit ihnen. Dafür muss der EA ein wenig modernisiert werden. Darüber sprechen wir später.
Nachfolgend sehen Sie die Struktur der Interaktion zwischen dem Indikator und dem EA:
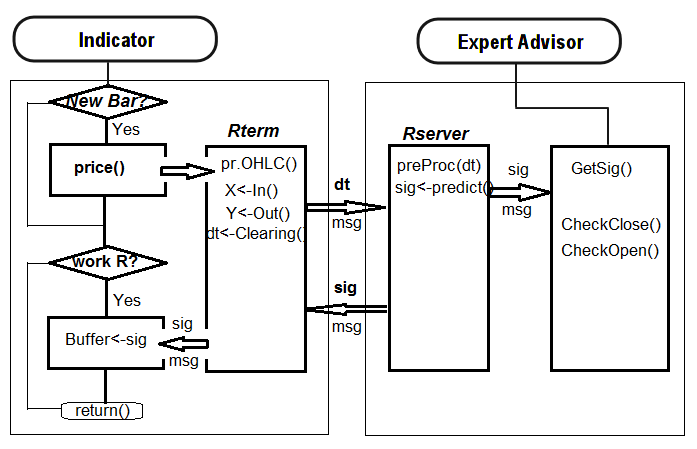
Abb. 31. Struktur der Interaktion zwischen dem Indikator und dem EA
4.1. Einlernen und Speichern des Modells
Rufen Sie die erforderlichen Quelldaten mithilfe des Indikators auf dem von uns betrachteten Diagramm ab. Platzieren Sie dazu den Indikator auf dem Diagramm, nachdem Sie die Eingangsvariable send=false festgelegt haben, d. h. die optische Darstellung soll nicht an den Server gesendet werden. Beim ersten Ausführen auf diesem Symbol oder Timeframe soll der Indikator die Verzeichnisse /Symbol/TF/Test_Data/ in der Datendatei des Terminals (/MQL4/Files) erstellen.
Diese Anordnung der Verzeichnisse gibt Ihnen eine Gelegenheit, die Ergebnisse von Experimenten nicht beim vorläufigen Einlernen von Modellen an einem Ort anzuhäufen und alte Daten nicht durch neue zu überschreiben. Zwischenergebnisse werden im Verzeichnis /Symbol/TF/Test_Data gespeichert und das Modell, das der EA für die Arbeit nutzen wird, befindet sich in /Symbol/TF (es muss manuell dort abgelegt werden). Das gleiche Ergebnis erhalten Sie beim ersten Ausführen auf einem neuen Symbol oder dem Timeframe des EAs.
Somit gibt es für EURUSD, M30 am 14.10.2014 4000 Balken. Wir brauchen den Datenrahmen dt[].
Gleichen Sie die Klassen aus:
> dt.b<-Balancing(dt) > table(dt.b[ ,ncol(dt.b)]) 0 1 2288 2288
Lernen Sie nun mithilfe der vorher geschriebenen Funktion Testing.1() das tiefe neuronale Netzwerk mit 500 und 300 Durchläufen ein und bewerten Sie Bilanz auf den letzten 500 Balken anhand der durch das neuronale Netzwerk prognostizierten Signale.
> system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=500, bar=500)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000017 ####loss on step 20000 is : 0.000015 ####loss on step 30000 is : 0.000015 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000044 ####loss on step 20000 is : 0.000041 ####loss on step 30000 is : 0.000039 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000042 ####loss on step 20000 is : 0.000042 ####loss on step 30000 is : 0.000036 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.089417 ####loss on step 20000 is : 0.043276 ####loss on step 30000 is : 0.069399 deep nn has been trained. user system elapsed 267.59 0.08 269.37 > plot(bal, t="l")
Speichern Sie das neuronale Netzwerk unter einem anderen Namen und lernen Sie ein weiteres ein.
> SAE1<-SAE > system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=500)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000020 ####loss on step 20000 is : 0.000016 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000050 ####loss on step 20000 is : 0.000050 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000051 ####loss on step 20000 is : 0.000043 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.083888 ####loss on step 20000 is : 0.083941 deep nn has been trained. user system elapsed 155.32 0.02 156.25 > lines(bal, col=2)
Sehen Sie sich die Bilanzdiagramme an (das letzte Ergebnis ist rot gekennzeichnet).
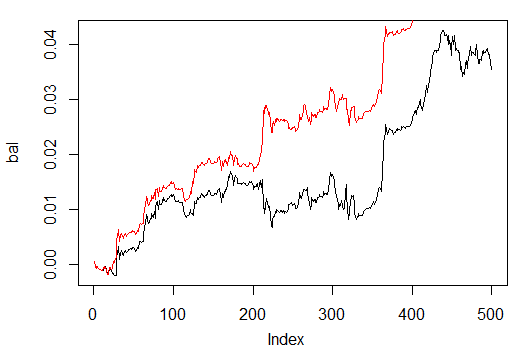
Abb. 32. Bilanz der letzten 500 Balken nach den Signalen von in 500 und 300 Durchläufen eingelernten neuronalen Netzwerken
Wie wir sehen können, zeigte das in 300 Durchläufen eingelernte neuronale Netzwerk ein besseres Ergebnis als das in 500 Durchläufen eingelernte.
Die Einlerndauer des letzteren ist für das schnelle Neueinlernen während einer Handelssitzung auf diesem Timeframe geeignet.
Für die weitere Arbeit auf einem realen Diagramm brauchen wir zwei Objekte: das eingelernte Modell "SAE" und die Normalisierungsparameter "prepr" für die Eingangsdaten. Speichern Sie sie im jeweiligen Verzeichnis, in meinem Fall "D:/Alpari Limited MT4/MQL4/Files/EURUSD/M30/Test_2014-10-14". Dieses ist bereits definiert und wird als Arbeitsverzeichnis genutzt, wenn Sie in Rstudio den durch den Indikator gespeicherten Arbeitsbereich "i_SAE_EURUSD_30.Rdata" geöffnet haben.
save(SAE, prepr, file="SAE.model") In der Datei "SAE.model" haben wir das Modell selbst und die Normalisierungsparameter gespeichert. Eine Verwendung des Modells ohne sie ist nicht sinnvoll. Sie können gerne experimentieren und Modelle, die Ihnen gefallen, jeden Tag speichern. Sie werden im Ordner "/File/Symbol/TF/Test_Data" gespeichert. Damit der EA das Modell nutzt, legen Sie die Datei "SAE.model" manuell in den Ordner "File/Symbol/TF". Dieser Ordner kann nur ein Modell enthalten und der EA wird es für seine Arbeit nutzen.
Nachdem Sie die Datei "SAE.model" geladen haben, lädt der EA diese Objekte im Arbeitsbereich für die Verwendung bei seiner Arbeit. An dieser Stelle ist der manuelle Teil der Arbeit abgeschlossen. Sie können den Indikator-EA im Diagramm platzieren und in Echtzeit testen.
Um die Wirksamkeit der Arbeit des EAs zu beurteilen, werden quantitative Kriterien benötigt. Der Koeffizient Accuracy ist für diesen Zweck nicht sehr gut geeignet.
Geeignet wäre der Durchschnitt des prognostizierten Bilanzverhältnisses zur Bilanz nach ZigZag oder das Bilanzverhältnis des letzten Balkens zur Anzahl der Balken. In unserem Fall ist es die Bilanz nach ZigZag:
sig.zz<-ifelse(tail(dt[ , ncol(dt)], 500) == 0, 1, -1) bal.zz<-cumsum(tail(price[ , 'CO'], 500) * sig.zz) Kzz<-mean(bal.zz / bal) > Kzz [1] 0.9173312
Das ist eine sehr hohe Punktzahl, doch sie ist relativ.
Wenn wir uns ansehen, wie sie im Verlauf der Zeit aussieht, stellen wir fest, dass dies für die ersten 50-100 Balken ein instabiler Index ist, wobei er später fast konstant wird. Die Statistiken sehen Sie unten:
> plot(bal/bal.zz, t="l") > summary(bal/bal.zz) Min. 1st Qu. Median Mean 3rd Qu. Max. -15.2500 0.7341 0.7844 0.9173 0.8833 55.0000
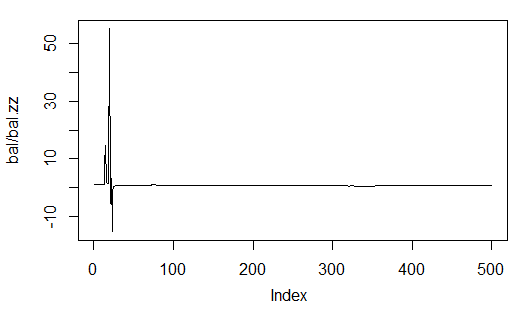
Abb. 33. Verhältnis der prognostizierten Bilanz zur Bilanz nach ZigZag
Die zweite ist präziser, da sie zeigt, wie viele Gewinnpunkte es pro Balken über eine Strecke von N Balken gibt.
Zum Beispiel für die Bilanz nach der Prognose des neuronalen Netzwerks auf der Strecke von 500 Balken:
> Kb<-tail(bal,1)/length(bal)*10^Dig > Kb [1] 11.508
nach ZigZag-Signalen:
> Kbz<-tail(bal.zz,1)/length(bal)*10^Dig > Kbz [1] 13.784
Wenn die Untergrenze der Wirksamkeit auf einem der Parameter definiert ist, kennen wir den Zeitpunkt, zu dem wir das neuronale Netzwerk neu einlernen oder seine Parameter optimieren müssen.
Der EA zeigt die folgenden Parameter im Diagramm an: OP – auszuführende Operation, Acc – Accuracy, K – ist der früher definierte Kb, Kmax – der gleiche Parameter wie Kb, allerdings auf dem Höchstpunkt der Bilanz definiert und gibt eine Vorstellung davon, wie stark sich dieser Parameter auf dem letzten Balken vom Maximum unterscheidet.
4.2. Reihenfolge der Installation und des Starts
Im angehängten Archiv SAE.zip finden Sie:
- Den Indikator i_SAE.mq4. Legen Sie ihn in den Ordner ~/MQL4/Indicators.
- Den EA e_SAE.mq4. Legen Sie ihn in den Ordner ~/MQL4/Experts.
- Die Bibliothek mt4Rb7.dll. Legen Sie sie in den Ordner ~/MQL4/Libraries.
- Die Header-Datei mt4Rb7.mqh. Legen Sie sie in den Ordner ~/MQL4/Include. Die Bibliothek und Header-Datei wurden von Bernd Kreuss entwickelt und freundlicherweise zur Verfügung gestellt. Der Name enthält den Index der letzten Änderung (b7). Wenn es viele Versionen mit dem gleichen Namen gibt, führt dies zu Verwechslungen, deren Behebung viel Zeit in Anspruch nimmt.
- Scripts in R: i_SAE.r (Hauptscript des Indikators), i_SAE_fun.r (Funktionen des Indikatorscripts), e_SAE.r (EA-Script), e_SAE_init.r (Initialisierungsscript des EAs), SAE_SetDir.r (Script für die Validierung und Erstellung notwendiger Verzeichnisse). Da Scripts weder vom Symbol noch vom Timeframe abhängig sind, können sie sich in einem separaten Verzeichnis befinden. In meinem Fall ist es "C:Rdata/SAE/". Das Verzeichnis "C:Rdata/" enthält verschiedene Scripts, die an kein bestimmtes Projekt angehängt sind. Falls Sie Scripts in einen Ordner legen, der sich von meinem unterscheidet, nehmen Sie die entsprechenden Korrekturen im Indikator und im EA vor, damit der Pfad zu den Scripts korrekt ist.
- SAE.model ist eine Datei mit dem Modell "SAE" und den Normalisierungsparametern "prepr". Das Modell wurde auf EURUSD (M30) mit dem letzten Datum 14.10.14 eingelernt. Der Einlernprozess wurde weiter oben beschrieben.
Vergessen Sie auch nicht den Pfad zum Verzeichnis, in dem die Sprache R auf Ihrem Computer abgelegt wurde.
Für den Beginn der Arbeit wird die folgende Reihenfolge empfohlen. Platzieren Sie den EA auf dem Diagramm. Falls Sie beschließen, den EA auf einem anderen Symbol zu platzieren, muss ein Port angegeben werden, der sich von vorher gestarteten Servern unterscheidet. Beispielsweise Port 8886 (standardmäßig Port 8888).
Hinweis. Das ist eine absolut ineffiziente Vorgehensweise. Jeder Server hat eine Größe von 120-130 Mb. Doch so laufen die Dinge heute.
Nach der normalen Initialisierung des EAs erscheint der Alarm "No calculation results! Symbol". Richten Sie dann den Indikator mit dem externen Parameter send = true und dem festgelegten Server-Port ein, mit dem sich der Indikator verbinden soll (siehe oben). Wenn alles richtig funktioniert, erscheinen die realen Daten "Operation", Accuracy, K und Kmax im Ausgangsstring und der Handel beginnt.
Die Kontrolle über den Prozess ist über den Windows Task Manager am effizientesten. Wenn Rterm nach dem Start des EAs oder Indikators nicht in der Liste erscheint, wurde der R-Prozess unterbrochen. Der Hauptgrund für solche Unterbrechungen ist ein Syntaxfehler in Scripts, Nichtentsprechung der Länge des empfangenden MQL-Vektors und der aus Rterm extrahierte Vektor.
Scripts können in Rstudio debuggt werden, indem die Scripts Zeile für Zeile von Anfang bis Ende ausgeführt werden.
Leider konnte ich den EA nicht im Tester starten, deshalb muss er auf einem Demokonto getestet werden.
4.3. Wege und Methoden zur Verbesserung der Qualitätsmerkmale
- Ändern des am Eingang verwendeten Satzes von Indikatoren.
- Ändern der Methode der Normalisierung der Eingangsdaten.
- Optimieren der Parameter des "Aufsehers" und der Indikatoren am Eingang.
- Ändern der Kodierung der Eingangsvariable für die Matrix mit zwei Spalten. Kalibrieren des prognostizierten Signals.
- Optimieren der Netzwerkparameter (Anzahl der Neuronen in den verborgenen Lagen, Anzahl der Lagen, Ebene des Einlernens, Anzahl der Durchläufe).
Fazit
Wir haben tiefe Netzwerkmodelle mit Initialisierung der Neuronengewichtungen in den verborgenen Lagen von SAE erstellt, eingelernt und getestet. Netzwerke lassen sich sehr schnell neu einlernen, was ein Neueinlernen ohne Unterbrechung des Handelsprozesses ermöglicht.
In Bezug auf ihre Metriken sind die von neuronalen Netzwerken gezeigten Ergebnisse durchschnittlich. Das ideale Ergebnis war nicht das ursprüngliche Ziel.
Mithilfe eines solchen Modells und der permanenten Bewertung des Effektivitätskoeffizienten lässt sich das Modell ohne Unterbrechung des Handelsprozesses neu einlernen und optimieren.
Anhang:
- SAE.zip – Indikator, EA und begleitende Dateien.
- R_intro.zip – Literatur zu R und Rstudio in russischer Sprache.
- DeepLearning.zip – Literatur zum tiefen Lernen.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/1103
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 MQL5-Kochbuch: Verarbeitung des TradeTransaction-Ereignisses
MQL5-Kochbuch: Verarbeitung des TradeTransaction-Ereignisses
 Regressionsanalyse des Einflusses makroökonomischer Daten auf Fluktuationen des aktuellen Kurses
Regressionsanalyse des Einflusses makroökonomischer Daten auf Fluktuationen des aktuellen Kurses
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Hallo.
Sie erwähnen in Ihrem Artikel die Möglichkeit der Parallelisierung von Rechenprozessen mit Hilfe der R-Bibliothek. Könnten Sie mir mehr dazu sagen, wie man das für Rechner in einem gemeinsamen Netzwerk organisieren kann. So wie ich das verstanden habe, muss man dafür keinen Cluster mit der entsprechenden Software erstellen und keine großen Änderungen im R-Skriptcode vornehmen - die Bibliothek organisiert die Client-Server-Kommunikation. Oder habe ich das falsch verstanden?
Ich habe ein Skript, das auf einem lokalen Rechner parallelisiert ist, aber ich muss Computer in einem Netzwerk verwenden, wie kann ich das tun?
Hallo.
Sie erwähnen in Ihrem Artikel die Möglichkeit der Parallelisierung von Rechenprozessen mit Hilfe der R-Bibliothek. Könnten Sie mir mehr dazu sagen, wie man das für Rechner in einem gemeinsamen Netzwerk organisieren kann. So wie ich das verstanden habe, muss man dafür keinen Cluster mit der entsprechenden Software erstellen und keine großen Änderungen im R-Skriptcode vornehmen - die Bibliothek organisiert die Client-Server-Kommunikation. Oder habe ich das falsch verstanden?
Ich habe ein Skript, das auf einem lokalen Rechner parallelisiert ist, aber ich muss Computer im Netzwerk verwenden, wie kann ich das machen?
Guten Tag!
Es ist richtig, dass Sie in einer privaten Nachricht angeklopft haben. Ich kann nur nicht in allen Artikeln den Überblick über die letzten Beiträge behalten.
Zur Parallelisierung. Ich benutze einen Computer. Es gab keine Aufgaben, die nicht in einer vernünftigen Zeit gelöst werden konnten. Um mehrere Rechner zu verwenden, müssen Sie einen Cluster erstellen (Pakete snow, foreach, doSnow). Ich habe diese Option nicht getestet.
Bei rechenintensiven Aufgaben ist es besser, diese an die GPU auszulagern. Das Paket gpuR.
Viel Erfolg!
Hallo Fabio,
es tut mir leid.
Ich schreibe nicht über MKL5.
Mit freundlichen Grüßen
Vladimir
Hallo Fabio,
Was ist nicht klar?
Hallo Vladimir,
Ich habe nicht den Vektor von (o,h,l,c) in RStudio, Wie kann ich Daten in R herunterladen und mit ihnen in RStudio arbeiten? wenn ich "head(price)" ausführe, wird dieses Massge angezeigt:
> head(price)
Fehler in head(price): Objekt 'price' nicht gefunden
> Der MT4 nummeriert die Balken vom jüngsten zum ältesten. Der R dagegen,
> # vom alten zum neuen, neuer Balken zuletzt, dann verwenden Sie die Funktion "rev", um dies umzukehren.
> Preis <- cbind(Open = rev(o), High = rev(h), Low = rev(l), Close = rev(c))
Fehler in rev(o) : Objekt 'o' nicht gefunden
Hallo!
Danke für die Informationen
Zu diesem Thema:
save(SAE, prepr, file="SAE.model")Wie können wir die Prepr speichern?
Ich fürchte, die, die ich speichere, ist nicht dieselbe wie die in Ihrem Modell.
Könnten Sie das bitte etwas näher erläutern.
Vielen Dank!
Hallo/
Ich freue mich, dass Sie sich für den Artikel interessieren.
Idebugcasesfall Rterma wie folgt:
- Kommentieren Sie alles in der start () aus , außer der Inspektion workRterma
- Kommentieren Sie in der init () alles außer runRterm() aus
- Wenn Rterm läuft, seitInit()einen Operatorauskommentieren und überprüfen. Sie geben an,waspassiert, wenn der Operator abstürzt.
Danach ist es einfacher , die Ursache des Absturzes zu bestimmen,in der Regelsind es zwei: der Syntaxfehler des Skripts oder das Fehlender notwendigen Bibliotheken.
Ich verweise nochmals auf den Anhang zumArtikel.
Ich bin bereit, Ihnen in Zukunft zu helfen , wenn Sie mir sagen, welcherRterm abstürzt.
Mit freundlichen Grüßen
Konnten Sie das Problem lösen, ich habe den gleichen Fehler. Hier ist ein Schnappschuss. In meinem Fall ist die Funktion RIsRunning(hR) von vornherein falsch. Also stürzt sie in der if-Anweisung ab. Müssen wir diese Funktion RIsRunning(hR) ausführen? Was bewirkt sie? Gibt es eine Möglichkeit, es vorher auszuführen, indem wir auf die ausführbare Datei klicken?
Wie haben Sie das Problem gelöst?