Neuronale Netze im Handel: Ein Ensemble von Agenten mit Aufmerksamkeitsmechanismen (letzter Teil)

Einführung

Das Portfoliomanagement spielt eine entscheidende Rolle bei Investitionsentscheidungen, da es darauf abzielt, durch die dynamische Umverteilung von Kapital auf verschiedene Vermögenswerte die Rendite zu steigern und die Risiken zu verringern. Die Studie „Developing an attention-based ensemble learning framework for financial portfolio optimisation“ stellt einen innovativen adaptiven Multi-Agenten-Rahmen, MASAAT, vor, der Aufmerksamkeitsmechanismen und Zeitreihenanalyse integriert. Mit diesem Ansatz wird eine Reihe von Handelsagenten geschaffen, die eine Kreuzanalyse von direktionalen Preisbewegungen auf mehreren Granularitätsebenen durchführen. Ein solches Konzept ermöglicht eine kontinuierliche Neugewichtung des Portfolios, wodurch ein wirksames Gleichgewicht zwischen Rentabilität und Risiko auf hochvolatilen Finanzmärkten erreicht wird.

Um signifikante Preisverschiebungen zu erfassen, setzen die Agenten Richtungsfilter mit unterschiedlichen Schwellenwerten ein. Dies ermöglicht die Extraktion wichtiger Trendmerkmale aus den analysierten Preiszeitreihen und verbessert die Interpretation von Marktübergängen unterschiedlicher Intensität. Die vorgeschlagene Methode führt eine neuartige Technik zur Generierung von Sequenz-Token ein, die es den Modulen für die „cross-sectional attention“ (Querschnitts-Aufmerksamkeit, CSA) und die zeitliche Analyse (TA) ermöglicht, verschiedene Korrelationen effektiv zu erkennen. Bei der Rekonstruktion von Merkmalskarten werden die Sequenz-Token im Modul CSA auf der Grundlage individueller Asset-Indikatoren generiert und durch Aufmerksamkeitsmechanismen optimiert. Parallel dazu werden Tokens im Modul TA aus zeitlichen Merkmalen konstruiert, was es ermöglicht, sinnvolle Beziehungen über verschiedene Zeitpunkte hinweg zu identifizieren.

Die aus den Modulen CSA und TA abgeleiteten Korrelationsbewertungen von Vermögenswerten und Zeitpunkten werden dann von den MASAAT-Agenten mit Hilfe eines Aufmerksamkeitsmechanismus kombiniert, mit dem Ziel, Abhängigkeiten für jeden Vermögenswert in Bezug auf jeden Zeitpunkt über den Beobachtungszeitraum zu erkennen.

Die ursprüngliche Visualisierung des MASAAT-Rahmens ist unten zu sehen.

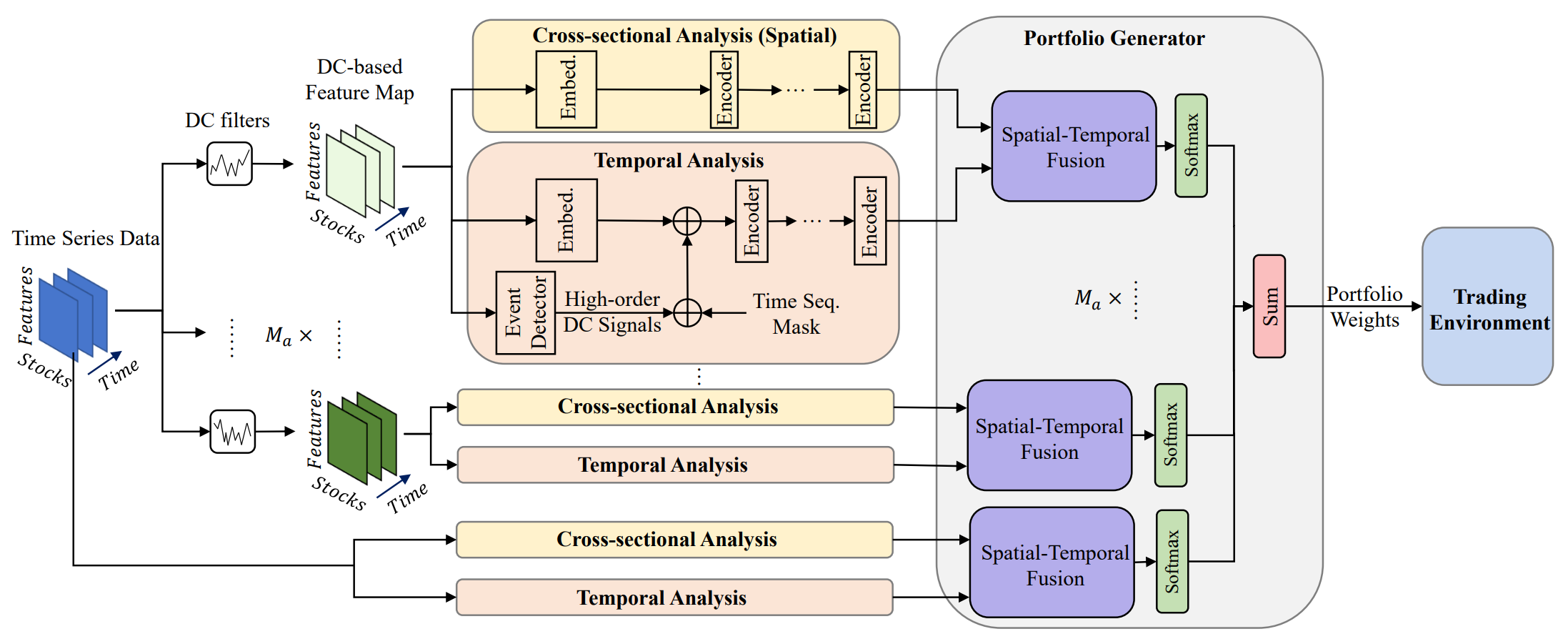
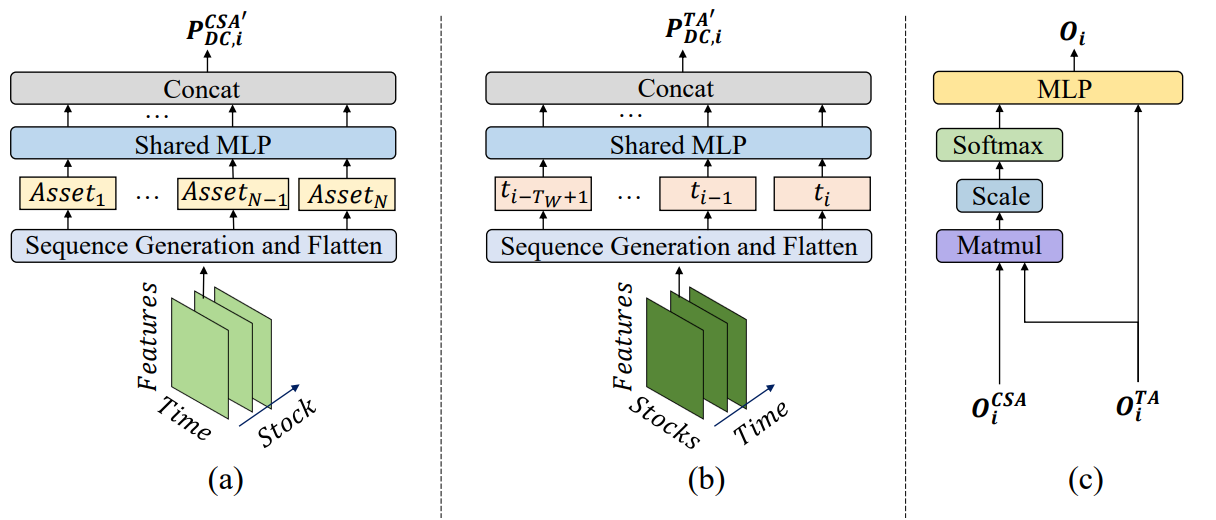
Das System von MASAAT weist eine klar definierte modulare Architektur auf. Dadurch ist es möglich, jedes Modul als unabhängige Klasse zu implementieren und die daraus resultierenden Objekte in eine einheitliche Struktur zu integrieren. Im vorigen Artikel haben wir die Implementierungsalgorithmen für das Multiagentenobjekt CNeuronPLRMultiAgentsOCL vorgestellt, das die analysierten multimodalen Zeitreihen in mehrskalige, stückweise lineare Darstellungen transformiert. Wir haben auch den Algorithmus des CSA-Moduls CNeuronCrossSectionalAnalysis überprüft. In diesem Artikel setzen wir diese Arbeit fort.

Das Modul der Zeitanalyse

Zum Abschluss des vorigen Artikels haben wir das Objekt CNeuronCrossSectionalAnalysis untersucht, das das CSA-Modul implementiert. Daneben umfasst das MASAAT-Framework das Modul für die zeitliche Analyse (TA). Es ist darauf ausgelegt, Abhängigkeiten zwischen einzelnen Zeitpunkten innerhalb der analysierten multimodalen Sequenz aufzudecken. Ein genauerer Blick auf die Strukturen dieser beiden Module zeigt, dass sie sich nahezu vollständig ähneln. Sie führen jedoch eine Queranalyse der Originaldaten durch. Mit anderen Worten: Sie analysieren die Sequenz aus verschiedenen Perspektiven.

Dies legt natürlich eine einfache Lösung nahe: die ursprüngliche Sequenz zu transponieren, bevor sie in das zuvor entwickelte Objekt CNeuronCrossSectionalAnalysis eingespeist wird. An diesem Punkt müssen wir jedoch zwei Dimensionen innerhalb eines dreidimensionalen Tensors transponieren. Es ist wichtig, daran zu erinnern, dass wir eine parallele Analyse mehrerer multimodaler Zeitsequenzen durchführen wollen. Genauer gesagt verarbeitet jeder Agent seine eigene Skala der stückweise linearen Darstellung der multimodalen Ausgangssequenz. Folglich wird erwartet, dass der Input für das Objekt ein 3D-Tensor in der Form [Agent, Asset, Time] ist. Für die Analyse der Abhängigkeiten über die Zeitpunkte hinweg müssen wir die letzten beiden Dimensionen transponieren. Da unsere Bibliothek diese Funktion noch nicht unterstützt, muss sie implementiert werden.

Für die Transposition eines dreidimensionalen Tensors in die letzten beiden Dimensionen gibt es mehrere Möglichkeiten. Die direkteste Lösung wäre die Entwicklung eines neuen Kerns innerhalb des OpenCL-Programms, gefolgt von der Erstellung einer neuen Klasse im Hauptprogramm zur Verwaltung dieses Kerns. Dieser Ansatz ist wahrscheinlich der effizienteste in Bezug auf die Rechenleistung. Allerdings ist es auch die arbeitsintensivste Variante für den Entwickler. Um die Komplexität der Programmierung auf Kosten der Rechenressourcen zu verringern, haben wir uns stattdessen dafür entschieden, das Verfahren mit drei nacheinander angelegten Transpositionsschichten zu implementieren, die zuvor erstellt wurden. Genauer gesagt, wenden wir zunächst eine 2D-Matrixtranspositionsebene an, indem wir die letzten beiden Dimensionen zu einer einzigen zusammenfassen:

[Agent, [Asset, Time]] → [[Time, Asset], Agent]

Als Nächstes verwenden wir das Objekt CNeuronTransposeRCDOCL, um den dreidimensionalen Tensor in die ersten beiden Dimensionen zu transponieren:

[Time, Asset, Agent] → [Asset, Time, Agent]

Abschließend wird eine weitere 2D-Matrix-Transpositionsebene angewandt, um die Dimension des Agenten wieder in die erste Position zu bringen, indem die beiden anderen Dimensionen zu einer zusammengefasst werden:

[[Asset, Time], Agent] → [Agent, [Time, Asset]]

Dieser Prozess ist in der neuen Klasse CNeuronTransposeVRCOCL implementiert, deren Struktur unten dargestellt ist.

class CNeuronTransposeVRCOCL  :  public CNeuronTransposeOCL
  {
protected:
   CNeuronTransposeOCL     cTranspose;
   CNeuronTransposeRCDOCL  cTransposeRCD;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;

public:
                     CNeuronTransposeVRCOCL(void) {};
                    ~CNeuronTransposeVRCOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint variables, uint count, uint window, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)  const override    {  return defNeuronTransposeVRCOCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Als übergeordnetes Objekt verwenden wir die zweidimensionale Matrix-Transpositionsschicht, die gleichzeitig die letzte Stufe der Datenpermutation durchführt. Dieses Design erlaubt es uns, nur zwei statische Objekte innerhalb des Körpers der neuen Klasse zu deklarieren. Die Initialisierung aller Objekte erfolgt in der Methode Init, die alle drei Dimensionen des zu transponierenden Tensors als Parameter erhält.

bool CNeuronTransposeVRCOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                  uint variables, uint count, uint window,
                                  ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronTransposeOCL::Init(numOutputs, myIndex, open_cl, count * window, variables, optimization_type, batch))
      return false;

Innerhalb dieser Methode rufen wir die gleichnamige Methode der übergeordneten Klasse auf. Es ist jedoch wichtig zu beachten, dass das übergeordnete Objekt ausschließlich für die endgültige Neuordnung der Daten verwendet wird. Daher müssen wir beim Aufruf der übergeordneten Methode die richtigen Parameter angeben. Konkret ist die erste Dimension als das Produkt der beiden letzten Dimensionen des ursprünglichen Tensors definiert. Die verbleibende Dimension ist überschaubar.

Nach erfolgreicher Ausführung der Methode der übergeordneten Klasse fahren wir mit der Initialisierung der internen Objekte fort. Zunächst initialisieren wir die primäre Matrixtranspositionsschicht. Seine Parameter sind die Umkehrung der Parameter, die zuvor der übergeordneten Klasse übergeben wurden.

   if(!cTranspose.Init(0, 0, OpenCL, variables, count * window, optimization, iBatch))
      return false;

Als Nächstes initialisieren wir das Objekt, das für die Transposition der ersten beiden Dimensionen des dreidimensionalen Tensors verantwortlich ist. Bei diesem Schritt werden die Dimensionen Vermögenswert und Zeit effektiv vertauscht.

   if(!cTransposeRCD.Init(0, 1, OpenCL, count, window, variables, optimization, iBatch))
      return false;
//---
   return true;
  }

Schließlich geben wir das logische Ergebnis dieser Operationen an das aufrufende Programm zurück und schließen damit die Ausführung der Methode ab.

Die hier vorgestellte Initialisierungsmethode ist einfach und leicht zu befolgen. Dasselbe gilt für die anderen Methoden dieser dreidimensionalen Tensortranspositionsklasse. In der Methode feedForward werden beispielsweise nacheinander die entsprechenden Methoden der internen Objekte aufgerufen, wobei der Prozess durch die gleichnamige Methode der Elternklasse abgeschlossen wird.

bool CNeuronTransposeVRCOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;
   if(!cTransposeRCD.FeedForward(cTranspose.AsObject()))
      return false;
//---
   return CNeuronTransposeOCL::feedForward(cTransposeRCD.AsObject());
  }

Die Algorithmen für die Methoden für den Rückwärtsdurchlauf sind separat in der Anlage aufgeführt. Da dieses Objekt keine trainierbaren Parameter enthält, werden sie hier nicht im Detail untersucht.

Nachdem wir nun das notwendige Objekt für die Datentransposition haben, können wir mit der Implementierung des Moduls für die zeitliche Analyse (TA) fortfahren, dessen Algorithmen in der Klasse CNeuronTemporalAnalysis implementiert sind. Die Funktionalität dieser neuen Klasse ist bewusst einfach gehalten. Wir transponieren die Eingabedaten und wenden dann die Mechanismen des Moduls für die Querschnitts-Aufmerksamkeit (CSA) an. Die Struktur des neuen Objekts wird im Folgenden dargestellt.

class CNeuronTemporalAnalysis :  public CNeuronCrossSectionalAnalysis
  {
protected:
   CNeuronTransposeVRCOCL  cTranspose;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTemporalAnalysis(void) {};
                    ~CNeuronTemporalAnalysis(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint heads, uint heads_kv,
                          uint units_count, uint layers, uint layers_to_one_kv,
                          uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) override;
   //---
   virtual int       Type(void)   const override   {  return defNeuronTemporalAnalysis;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Als übergeordnete Klasse verwenden wir das Modul Querschnitts-Aufmerksamkeit. Wie bereits erwähnt, bildet die Funktionalität dieses Moduls die Grundlage für unseren Algorithmus. Wir fügen nur ein internes Objekt für die Transposition des dreidimensionalen Tensors über seine letzten beiden Dimensionen hinzu. Die Initialisierung der neuen und geerbten Objekte wird in der Methode Init durchgeführt, die die Parameterstruktur des Gegenstücks der Elternklasse widerspiegelt.

bool CNeuronTemporalAnalysis::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                   uint window, uint window_key, uint heads, uint heads_kv,
                                   uint units_count, uint layers, uint layers_to_one_kv, uint variables,
                                   ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronCrossSectionalAnalysis::Init(numOutputs, myIndex, open_cl, 3 * units_count, window_key, heads, heads_kv,
                                           window / 3, layers, layers_to_one_kv, variables, optimization_type, batch))
      return false;

Innerhalb dieser Methode rufen wir sofort die Initialisierungsmethode des Elternteils auf und übergeben alle erhaltenen Parameter.

An dieser Stelle sind einige Besonderheiten unserer Umsetzung zu erwähnen. Zunächst geben die externen Parameter die Dimensionen der Originaldaten an. Erinnern Sie sich daran, dass wir den dreidimensionalen Tensor über seine letzten beiden Dimensionen transponieren wollen. Daher werden bei der Übergabe von Parametern an die Initialisierungsmethode der übergeordneten Klasse die entsprechenden Dimensionen vertauscht.

Zweitens müssen wir die Struktur der Eingabedaten berücksichtigen. Dieses Objekt empfängt die Ausgabe des Trenderkennungsblocks der Multi-Agenten. Dementsprechend besteht die Modelleingabe aus einem Tensor, der die stückweise lineare Approximation der multimodalen Zeitreihe darstellt. In unserer Implementierung wird jedes gerichtete Segment einer univariaten Zeitreihe durch drei Elemente dargestellt. Logischerweise sollten diese bei der Analyse als eine einzige Einheit behandelt werden. Wir verdreifachen also die Größe des Analysefensters und reduzieren entsprechend die Sequenzlänge um den Faktor drei.

Nachdem die Initialisierung der übergeordneten Klasse erfolgreich abgeschlossen ist, rufen wir die Initialisierungsmethode des internen dreidimensionalen Tensortranspositionsobjekts auf.

   if(!cTranspose.Init(0, 0, OpenCL,variables, units_count, window, optimization_type, batch))
      return false;
//---
   return true;
  }

Anschließend wird die Methode abgeschlossen, indem das logische Ergebnis der Operationen an das aufrufende Programm zurückgegeben wird.

Die Algorithmen für den Vorwärts- und den Rückwärtsdurchlauf des Objekts CNeuronTemporalAnalysis sind recht einfach. Deshalb werden wir in diesem Artikel nicht näher darauf eingehen. Den vollständigen Quellcode für diese Klasse und alle ihre Methoden finden Sie im Anhang zu diesem Artikel.

Modul zur Erstellung von Portfolios

Am Ausgang der Blöcke von CSA und TA erhalten wir Daten, die mit Informationen über die Abhängigkeiten von Asset-to-Asset bzw. Time-to-Time angereichert sind. Diese Informationen werden über einen Aufmerksamkeitsmechanismus kombiniert, der es jedem Agenten ermöglicht, seine eigene Version eines Investitionsportfolios zu erstellen. Genauer gesagt, bildet jeder Agent zunächst eine Einbettung von Vermögenswerten, die die zeitlichen Abhängigkeiten berücksichtigt. Diese Einbettungen werden dann durch eine vollständig verknüpfte Schicht geleitet, um einen Gewichtsvektor zu erzeugen, der die Portfoliozuordnung darstellt, wobei die Summe aller Vektorelemente gleich 1 ist.

Die mathematische Darstellung der Portfolio-Generierungsfunktion lautet wie folgt:

Auf der Grundlage der Portfolio-Vorschläge wird eine endgültige Portfoliodarstellung erstellt.

Hier weichen wir leicht von der ursprünglichen Darstellung von MASAAT durch die Autoren ab. Diese Abweichung ist jedoch eher logischer als mathematischer Natur. In der Praxis halten wir uns zwar eng an die ursprüngliche Funktion, aber wir interpretieren die resultierenden Ergebnisse neu.

Unsere Aufgabe unterscheidet sich etwas von derjenigen der MASAAT-Autoren. Am Ausgang des Modells wollen wir den Aktionsvektor eines Agenten erhalten, der die Handelsrichtung, die Positionsgröße und die Stop-Loss- und Take-Profit-Niveaus angibt. Um die Positionsgröße zu bestimmen, benötigen wir neben der Dynamik des Finanzinstruments auch Informationen über den Kontostand, die jedoch in den Eingabedaten nicht enthalten sind. Daher erwarten wir in unserer Implementierung von MASAAT, dass die Ausgabe eine versteckte Zustandseinbettung ist, die eine umfassende Analyse der aktuellen Marktsituation beinhaltet.

Die endgültige Funktionalität von MASAAT wird durch das Objekt CNeuronPortfolioGenerator realisiert, dessen Struktur unten dargestellt ist.

class CNeuronPortfolioGenerator  :  public CNeuronBaseOCL
  {
protected:
   uint              iAssets;
   uint              iTimePoints;
   uint              iAgents;
   uint              iDimension;
   //---
   CNeuronBaseOCL          cAssetTime[2];
   CNeuronTransposeVRCOCL  cTransposeVRC;
   CNeuronSoftMaxOCL       cSoftMax;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)  override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                                                   CBufferFloat *SecondGradient, 
                                                ENUM_ACTIVATION SecondActivation = None) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronPortfolioGenerator(void) {};
                    ~CNeuronPortfolioGenerator(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint assets, uint time_points, uint dimension,
                          uint agents,  uint projection,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const override   {  return defNeuronPortfolioGenerator;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Innerhalb der Struktur dieser neuen Klasse deklarieren wir mehrere interne Objekte, deren Funktionen bei der Implementierung der Methoden beschrieben werden. Alle internen Objekte werden statisch deklariert, sodass wir den Konstruktor und Destruktor der Klasse leer lassen können. Die Initialisierung dieser deklarierten und abgeleiteten, internen Objekte wird in der Methode Init durchgeführt. Bitte beachten Sie hier einige Nuancen.

bool CNeuronPortfolioGenerator::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                     uint assets, uint time_points, uint dimension,
                                     uint agents, uint projection,
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(assets <= 0 || time_points <= 0 || dimension <= 0 || agents <= 0)
      return false;

Die Methode erhält mehrere Parameter, die einer Klärung bedürfen:

• assets – die Anzahl der im CSA-Modul analysierten Anlagen;
• time_points – die Anzahl der im TA-Modul analysierten Zeitpunkte;
• dimension – die Größe des Einbettungsvektors für jedes Element der analysierten Sequenz (gemeinsam für die Module CSA und TA);
• agents – die Anzahl der Agenten;
• projection – die Projektionsgröße des analysierten Zustands am Modulausgang.

Innerhalb der Methode validieren wir zunächst die Parameterwerte. Sie müssen alle größer als Null sein. Anschließend rufen wir die Initialisierungsmethode der Elternklasse auf und übergeben die Projektionsgröße des analysierten Zustands. Er entspricht dem Tensor, der am Ausgang des Moduls erwartet wird.

   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, projection, optimization_type, batch))
      return false;

Nachdem die Initialisierung der übergeordneten Klasse erfolgreich durchgeführt wurde, werden die Werte der externen Parameter in internen Variablen gespeichert.

   iAssets = assets;
   iTimePoints = time_points;
   iDimension = dimension;
   iAgents = agents;

Dann fahren wir mit der Initialisierung der internen Objekte fort. Unter Bezugnahme auf die zuvor vorgestellte Formel stellen wir fest, dass der Output des TA-Moduls zweimal verwendet wird: einmal in seiner transponierten Form und einmal in seiner ursprünglichen Form.

Erinnern Sie sich, dass das TA-Modul einen dreidimensionalen Tensor mit den Dimensionen [Agent, Time, Embedding] ausgibt. Folglich müssen wir in diesem Fall ein dreidimensionales Tensortranspositionsobjekt für die letzten beiden Dimensionen verwenden.

   if(!cTransposeVRC.Init(0, 0, OpenCL, iAgents, iTimePoints, iDimension, optimization, iBatch))
      return false;

Anschließend multiplizieren wir die Ergebnisse des CSA-Moduls mit den transponierten TA-Ausgängen. Die Methode der Matrixmultiplikation wird von der übergeordneten Klasse geerbt. Um die Ergebnisse zu speichern, initialisieren wir eine interne, vollständig verbundene Schicht.

   if(!cAssetTime[0].Init(0, 1, OpenCL, iAssets * iTimePoints * iAgents, optimization, iBatch))
      return false;
   cAssetTime[0].SetActivationFunction(None);

Die resultierenden Werte werden mit der Funktion Softmax normalisiert.

   if(!cSoftMax.Init(0, 2, OpenCL, cAssetTime[0].Neurons(), optimization, iBatch))
      return false;
   cSoftMax.SetHeads(iAssets * iAgents);

Es ist zu betonen, dass die Normalisierung pro Asset und pro Agent durchgeführt wird. Daher ist die Anzahl der Normalisierungsköpfe gleich dem Produkt aus der Anzahl der Vermögenswerte und der Anzahl der Bearbeiter.

Die normalisierten Koeffizienten dienen als Aufmerksamkeitsgewichte für jeden Zeitpunkt auf der Ebene der einzelnen Vermögenswerte über die Akteure hinweg. Durch Multiplikation dieser Koeffizientenmatrix mit den Outputs von TA erhalten wir die Einbettungen der analysierten Vermögenswerte. Um diese Einbettungen zu speichern, initialisieren wir eine weitere vollständig verbundene Schicht.

   if(!cAssetTime[1].Init(Neurons(), 3, OpenCL, iAssets * iDimension * iAgents, optimization, iBatch))
      return false;
   cAssetTime[1].SetActivationFunction(None);
//---
   return true;
  }

Um die von allen Agenten erzeugten Einbettungen in eine einheitliche Darstellung der analysierten Umgebung zu projizieren, verwenden wir eine vollständig verbundene Schicht. Hier ist es wichtig zu beachten, dass diese vollständig verbundene Schicht das übergeordnete Objekt unserer Klasse ist. Aus diesem Grund vermeiden wir die Erstellung einer zusätzlichen internen Schicht und nutzen stattdessen die Funktionalität der übergeordneten Klasse. In der letzten internen Schicht geben wir nur die Anzahl der Ausgangsverbindungen an, die der vom externen Programm gelieferten Projektionsgröße entspricht.

Nachdem alle internen Objekte erfolgreich initialisiert wurden, geben wir das logische Ergebnis dieser Operationen an das aufrufende Programm zurück und beenden die Methode.

Der nächste Schritt unserer Arbeit besteht in der Entwicklung der Algorithmen für den Vorwärtsdurchlauf im der Methode feedForward. Es ist wichtig zu beachten, dass wir es in diesem Fall mit zwei Quellen von Eingangsdaten zu tun haben. Dabei ist zu beachten, dass die Ergebnisse des Moduls der zeitlichen Analyse doppelt verwendet werden. Dieser Umstand zwingt uns dazu, diesen Informationsstrom als den primären zu bezeichnen.

bool CNeuronPortfolioGenerator::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!SecondInput)
      return false;
//---
   if(!cTransposeVRC.FeedForward(NeuronOCL))
      return false;

Innerhalb der Methode validieren wir zunächst den Zeiger auf die zweite Datenquelle und führen eine Transposition der ersten Datenquelle durch. Nach diesen vorbereitenden Schritten gehen wir zu den eigentlichen Berechnungen über. Zunächst multiplizieren wir den Tensor aus der zweiten Datenquelle mit dem transponierten Tensor der ersten.

   if(!MatMul(SecondInput, cTransposeVRC.getOutput(), cAssetTime[0].getOutput(), iAssets, iDimension, 
                                                                                 iTimePoints, iAgents))
      return false;

Die Ergebnisse werden mit der Funktion SoftMax normalisiert.

   if(!cSoftMax.FeedForward(cAssetTime[0].AsObject()))
      return false;

Anschließend werden sie mit den Originaldaten des primären Informationsstroms multipliziert.

   if(!MatMul(cSoftMax.getOutput(), NeuronOCL.getOutput(), cAssetTime[1].getOutput(), iAssets, iTimePoints,
                                                                                      iDimension, iAgents))
      return false;

Schließlich projizieren wir die gewonnenen Daten mithilfe der Funktion der übergeordneten Klasse in den angegebenen Unterraum.

   return CNeuronBaseOCL::feedForward(cAssetTime[1].AsObject());
  }

Das logische Ergebnis dieser Operationen wird an das aufrufende Programm zurückgegeben, und die Methode ist beendet.

Nach Abschluss der Implementierung der Vorwärtsdurchläufe gehen wir zu den Algorithmen für die Rückwärtsdurchläufe über. Hier untersuchen wir zunächst die Methode calcInputGradients zur Verteilung der Fehlergradienten.

bool CNeuronPortfolioGenerator::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                     CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!NeuronOCL || !SecondGradient || !SecondInput)
      return false;

Die Methodenparameter enthalten Zeiger auf die Eingangsdatenobjekte und die entsprechenden Fehlergradienten für beide Informationsströme. Im Hauptteil der Methode wird sofort die Gültigkeit der Zeiger überprüft. Wenn die Zeiger ungültig sind, wären alle weiteren Operationen sinnlos.

Wie Sie wissen, folgt die Ausbreitung von Fehlergradienten genau der Struktur des Informationsflusses eines Vorwärtsdurchlaufs, nur in umgekehrter Richtung. Die Operationen in dieser Methode beginnen mit einem Aufruf der gleichnamigen Methode der übergeordneten Klasse, die den Gradienten auf das interne Objekt überträgt.

   if(!CNeuronBaseOCL::calcInputGradients(cAssetTime[1].AsObject()))
      return false;

Als Nächstes rufen wir die Methode der Fehlergradientenverteilung für die Matrixmultiplikation auf und geben die Daten an die Eingabeebene und die interne Softmax-Schicht weiter.

   if(!MatMulGrad(cSoftMax.getOutput(), cSoftMax.getGradient(),
                  NeuronOCL.getOutput(), cTransposeVRC.getPrevOutput(),
                  cAssetTime[1].getGradient(),
                  iAssets, iTimePoints, iDimension, iAgents))
      return false;

Es ist jedoch wichtig, daran zu denken, dass der Fehlergradient für die Eingangsebene des primären Informationsstroms aus zwei verschiedenen Strömen stammen muss. Daher werden die in dieser Phase ermittelten Werte in einem Hilfspuffer des Datenumsetzungsobjekts gespeichert.

Anschließend propagieren wir den Fehlergradienten durch die Softmax-Schicht zurück auf die Ebene der nicht normalisierten Koeffizienten.

   if(!cAssetTime[0].calcHiddenGradients(cSoftMax.AsObject()))
      return false;

Anschließend verteilen wir den resultierenden Gradienten auf die zweite Datenquelle und auf unsere Transpositionsebene.

   if(!MatMulGrad(SecondInput, SecondGradient,
                  cTransposeVRC.getOutput(), cTransposeVRC.getGradient(),
                  cAssetTime[0].getGradient(),
                  iAssets, iDimension, iTimePoints, iAgents))
      return false;

An dieser Stelle überprüfen wir sofort die Aktivierungsfunktion der zweiten Datenquelle und passen gegebenenfalls den Fehlergradienten über die entsprechende Ableitung an.

   if(SecondActivation != None)
      if(!DeActivation(SecondInput, SecondGradient, SecondGradient, SecondActivation))
         return false;

In diesem Stadium wurde der Gradient an das Modul von CSA (das in diesem Fall als zweite Datenquelle dient) weitergegeben. Nun gilt es, die Übertragung des Gradienten auf das Modul für die zeitliche Aufmerksamkeit (den primären Informationsstrom) zu vervollständigen. Dieses Modul erhält Gradienten über zwei Informationsflüsse: von den Aufmerksamkeitskoeffizienten und direkt von den Ergebnissen. Die Daten aus diesen beiden Strömen werden derzeit in verschiedenen Puffern des Datenumsetzungsobjekts gespeichert. Im primären Gradientenpuffer finden wir die transponierten Werte aus dem Strom der Aufmerksamkeitskoeffizienten. Mit Hilfe der Kernfunktionalität des dreidimensionalen Tensortranspositionsobjekts werden diese Werte zurück auf die Eingabeebene übertragen.

   if(!NeuronOCL.calcHiddenGradients(cTransposeVRC.AsObject()) ||
      !SumAndNormilize(NeuronOCL.getGradient(), cTransposeVRC.getPrevOutput(), NeuronOCL.getGradient(),
                                                                        iDimension, false, 0, 0, 0, 1))
      return false;

Als Nächstes summieren wir die Daten aus beiden Informationsströmen. Schließlich wird der resultierende Gradient entsprechend der Ableitung der Aktivierungsfunktion des Primärstroms angepasst.

   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(), cTransposeVRC.getPrevOutput(), cTransposeVRC.getPrevOutput(), 
                                                                                   NeuronOCL.Activation()))
         return false;
//---
   return true;
  }

Die Methode schließt mit der Rückgabe des logischen Ergebnisses der Operationen an das aufrufende Programm ab.

Ich schlage vor, die Methode, die für die Aktualisierung der Parameter des Modells verantwortlich ist, unabhängig zu überprüfen. Der vollständige Quellcode der Klasse CNeuronPortfolioGenerator und alle ihre Methoden sind im Anhang enthalten.

Zusammenstellung des Systems von MASAAT

Wir haben die Funktionalität der einzelnen Systemblöcke von MASAAT bereits implementiert, nun ist es an der Zeit, sie zu einer einheitlichen Struktur zusammenzufügen. Diese Integration ist in der Klasse CNeuronMASAAT implementiert. Als übergeordnetes Objekt haben wir den zuvor erstellten CNeuronPortfolioGenerator ausgewählt, der den letzten Block unserer Implementierung von MASAAT darstellt. Damit entfällt die Notwendigkeit, dieses Modul als internes Objekt der neuen Klasse zu deklarieren, da alle erforderlichen Funktionen vererbt werden. Die Struktur der neuen Klasse ist unten dargestellt.

class CNeuronMASAAT  :  public CNeuronPortfolioGenerator
  {
protected:
   CNeuronTransposeOCL              cTranspose;
   CNeuronPLRMultiAgentsOCL         cPLR;
   CNeuronBaseOCL                   cConcat;
   CNeuronCrossSectionalAnalysis    cCrossSectionalAnalysis;
   CNeuronTemporalAnalysis          cTemporalAnalysis;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)  override
     { return        feedForward(NeuronOCL); }
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                       CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override
     { return        calcInputGradients(NeuronOCL); }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMASAAT(void)  {};
                    ~CNeuronMASAAT(void)  {};
   //---
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint heads, uint units_cout,
                          uint layers, vector<float> &min_distance, uint projection,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const override   {  return defNeuronMASAAT;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

In dieser Klassenstruktur sehen wir die Deklaration aller zuvor erstellten Objekte. Wie Sie sehen können, werden die Algorithmen für alle Methoden auf dem sequentiellen Aufruf der entsprechenden Methoden der internen Objekte aufgebaut. Die Ausführungsreihenfolge wird deutlicher, wenn wir mit den Methodenimplementierungen fortfahren.

Alle internen Objekte werden statisch deklariert, was uns erlaubt, den Konstruktor und den Destruktor der Klasse leer zu lassen. Die Initialisierung aller deklarierten und geerbten Objekte wird in der Methode Init durchgeführt.

bool CNeuronMASAAT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                         uint window, uint window_key, uint heads, uint units_cout,
                         uint layers, vector<float> &min_distance, uint projection,
                         ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronPortfolioGenerator::Init(numOutputs, myIndex, open_cl, window, units_cout / 3,
                                       window_key, (uint)min_distance.Size() + 1, projection, optimization_type, batch))
      return false;

Die Parameter dieser Methode umfassen die Schlüsselkonstanten, die die Struktur der Eingabedaten beschreiben und die Architektur des zu initialisierenden Objekts definieren.

Im Methodenrumpf rufen wir, der gängigen Praxis folgend, sofort die Initialisierungsmethode der Elternklasse auf, die bereits die Logik für die Initialisierung geerbter Objekte und grundlegender Schnittstellen enthält. Es sei jedoch darauf hingewiesen, dass wir in diesem Fall die übergeordnete Klasse als einen voll funktionsfähigen Block innerhalb des umfassenderen Algorithmus verwenden. Dieses Modul wird für die endgültige Ausgabe unserer Implementierung von MASAAT verwendet. Daher müssen wir ein wenig vorausschauen, um die richtigen Initialisierungsparameter für das übergeordnete Objekt zu bestimmen.

Als Eingabe des übergeordneten Objekts planen wir die Ergebnisse der Module CSA und TA bereitstellen. Bei diesen Modulen entspricht die Anzahl der analysierten Assets der Größe des Eingabefensters, während die Anzahl der Zeitpunkte der Länge der Eingabesequenz entspricht. Aber halt – wir wenden eine Transformation der ursprünglichen multimodalen Zeitreihe in ihre stückweise lineare Darstellung an. Das bedeutet, dass die Anzahl der Zeitpunkte um den Faktor drei reduziert wird. Daher wird bei der Übergabe von Parametern an die Initialisierungsmethode der Elternklasse die Länge der ursprünglichen Sequenz durch drei geteilt.

Wenn man die Parameter weiter untersucht, kommt man auf die Anzahl der Agenten. Wie bereits erwähnt, wird beim Aufbau des Multi-Agenten-Transformationsobjekts die Anzahl der Agenten durch die Länge des Vektors der Schwellenwertabweichungen bestimmt. Betrachtet man jedoch die Analyse der Autoren von MASAAT zu den einzelnen Rahmenkomponenten, so stellt man fest, dass die Kombination der stückweise linearen Darstellung einer Zeitreihe mit der ursprünglichen Reihe die Modelleffizienz verbessert. Daher erhöhen wir die Anzahl der Agenten um einen und beauftragen den zusätzlichen Agenten mit der Arbeit an der unveränderten ursprünglichen Zeitreihe.

Alle anderen Parameter werden unverändert übergeben.

Nachdem die Initialisierung der übergeordneten Klasse erfolgreich durchgeführt wurde, fahren wir mit der Initialisierung der neu deklarierten Objekte fort. Zunächst initialisieren wir das Objekt für die Datenumsetzung.

   if(!cTranspose.Init(0, 0, OpenCL, units_cout, window, optimization, iBatch))
      return false;

Als Nächstes initialisieren wir das Multi-Agenten-Transformationsobjekt, das die stückweise linearen Darstellungen der analysierten Sequenz erzeugt.

   if(!cPLR.Init(0, 1, OpenCL, window, units_cout, false, min_distance, optimization, iBatch))
      return false;

Die Transformationsergebnisse werden mit den Originaldaten verkettet. Dazu initialisieren wir eine vollverknüpfte Schicht mit der entsprechenden Größe.

   if(!cConcat.Init(0, 2, OpenCL, cTranspose.Neurons() + cPLR.Neurons(), optimization, iBatch))
      return false;

Schließlich initialisieren wir die Module CSA und TA. Beide arbeiten mit denselben Quelldaten und erhalten daher identische Parameter.

   if(!cCrossSectionalAnalysis.Init(0, 3, OpenCL, units_cout, window_key, heads, heads / 2, window, layers, 1, 
                                                                                 iAgents, optimization, iBatch))
      return false;
   if(!cTemporalAnalysis.Init(0, 4, OpenCL, units_cout, window_key, heads, heads / 2, window, layers, 1, 
                                                                                  iAgents, optimization, iBatch))
      return false;
//---
   return true;
  }

Nach erfolgreicher Initialisierung aller internen Objekte geben wir das logische Ergebnis der Operationen an das aufrufende Programm zurück und beenden die Methode.

Wir fahren nun mit dem Algorithmus des Vorwärtsdurchlaufs innerhalb der Methode feedForward fort. Hier ist alles ganz einfach. Die Methodenparameter liefern einen Zeiger auf das Eingabedatenobjekt, das wir sofort an die gleichnamige Methode des Transpositionsobjekts übergeben.

bool CNeuronMASAAT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;

Die resultierenden Daten werden dann in mehrere Versionen der stückweise-linearen Zeitreihendarstellung transformiert, und die Ergebnisse werden mit den ursprünglichen Daten verkettet, allerdings in transponierter Form.

   if(!cPLR.FeedForward(cTranspose.AsObject()))
      return false;
   if(!Concat(cTranspose.getOutput(), cPLR.getOutput(), cConcat.getOutput(), cTranspose.Neurons(), cPLR.Neurons(), 1))
      return false;

Die aufbereiteten Daten werden anschließend an die Module von CSA und TA weitergegeben, deren Ergebnisse dann an die entsprechende Methode der Elternklasse geliefert werden.

   if(!cCrossSectionalAnalysis.FeedForward(cConcat.AsObject()))
      return false;
   if(!cTemporalAnalysis.FeedForward(cConcat.AsObject()))
      return false;
//---
   return CNeuronPortfolioGenerator::feedForward(cTemporalAnalysis.AsObject(), cCrossSectionalAnalysis.getOutput());
  }

Die Methode schließt mit der Rückgabe des logischen Ergebnisses der Operation an den Aufrufer ab.

Hinter der scheinbaren Einfachheit der Methode des Vorwärtsdurchlaufs verbirgt sich eine komplexe Verzweigung der Informationsflüsse. Beachten Sie, dass die transponierten Originaldaten und der verkettete Tensor jeweils zweimal verwendet werden. Dies führt zu Komplikationen bei der Organisation der Fehlergradientenverteilung innerhalb der Methode calcInputGradients.

In den Parametern dieser Methode erhalten wir einen Zeiger auf das Eingabedatenobjekt, das den Fehlergradienten enthalten muss. Und im Hauptteil der Methode prüfen wir sofort die Relevanz des empfangenen Zeigers.

bool CNeuronMASAAT::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

Anschließend rufen wir die gleichnamige Methode der Elternklasse auf, um den Fehlergradienten zwischen den Modulen CSA und TA entsprechend ihrem Einfluss auf die Modellausgabe zu verteilen.

   if(!CNeuronPortfolioGenerator::calcInputGradients(cTemporalAnalysis.AsObject(),
         cCrossSectionalAnalysis.getOutput(),
         cCrossSectionalAnalysis.getGradient(),
         (ENUM_ACTIVATION)cCrossSectionalAnalysis.Activation()))
      return false;

Beide Module arbeiten mit dem verketteten Tensor. Daher muss der Gradient aus zwei verschiedenen Strömen auf diesen Tensor übertragen werden. Zunächst übergeben wir den Gradienten von einem Modul.

   if(!cConcat.calcHiddenGradients(cCrossSectionalAnalysis.AsObject()))
      return false;

Durch Anwendung einer Puffersubstitutionstechnik rufen wir dann die Gradientenwerte aus dem zweiten Datenstrom ab und summieren anschließend die Informationen aus beiden Quellen.

   CBufferFloat *grad = cConcat.getGradient();
   if(!cConcat.SetGradient(cConcat.getPrevOutput(), false) ||
      !cConcat.calcHiddenGradients(cTemporalAnalysis.AsObject()) ||
      !SumAndNormilize(grad, cConcat.getGradient(), grad, 1, 0, 0, 0, 0, 1) ||
      !cConcat.SetGradient(grad, false))
      return false;

Der Gradient des verketteten Tensors wird dann auf die verketteten Objekte verteilt. An dieser Stelle sei daran erinnert, dass das Objekt „Datentransposition“ seinen Gradienten über einen anderen Stream erhalten soll. Daher verwenden wir in dieser Phase einen zusätzlichen Datenpuffer.

   if(!DeConcat(cTranspose.getPrevOutput(), cPLR.getGradient(), cConcat.getGradient(), cTranspose.Neurons(), 
                                                                                         cPLR.Neurons(), 1))
      return false;

Bevor wir mit der Gradientenverteilung zwischen den Objekten fortfahren, überprüfen wir, ob die Korrektur durch die Ableitung der Aktivierungsfunktion notwendig ist.

   if(cPLR.Activation() != None)
      if(!DeActivation(cPLR.getOutput(), cPLR.getGradient(), cPLR.getGradient(), cPLR.Activation()))
         return false;

Als Nächstes propagieren wir den Gradienten durch das stückweise lineare Transformationsobjekt des Multiagenten und summieren die Werte aus beiden Strömen.

   if(!cTranspose.calcHiddenGradients(cPLR.AsObject()) ||
      !SumAndNormilize(cTranspose.getGradient(), cTranspose.getPrevOutput(), cTranspose.getGradient(), iDimension, 
                                                                                               false, 0, 0, 0, 1))
      return false;

Bei Bedarf passen wir den Gradienten entsprechend der Ableitung der Aktivierungsfunktion an und geben ihn dann an die Eingabeebene zurück.

   if(cTranspose.Activation() != None)
      if(!DeActivation(cTranspose.getOutput(), cTranspose.getGradient(), cTranspose.getGradient(), 
                                                                         cTranspose.Activation()))
         return false;
   if(!prevLayer.calcHiddenGradients(cTranspose.AsObject()))
      return false;
//---
   return true;
  }

Zum Schluss gibt die Methode das logische Ergebnis der Operationen an das aufrufende Programm zurück.

An dieser Stelle schließen wir unsere Untersuchung der algorithmischen Umsetzung der Ansätze von MASAAT ab. Der vollständige Quellcode für alle vorgestellten Klassen und Methoden befindet sich im Anhang. Dort finden Sie auch alle Programme, die bei der Erstellung dieses Artikels verwendet wurden, sowie die Modellarchitekturen. Wir werden kurz auf die Modellarchitekturen eingehen. Unsere Systemimplementierung von MASAAT wurde in das Akteursmodell integriert. Wir werden hier nicht die gesamte Architektur untersuchen. Sie ist fast vollständig aus unseren früheren Arbeiten übernommen worden. Sehen wir uns stattdessen die Deklaration der neuen Ebene an.

Im dynamischen Array der Fenstergrößen geben wir die Größe des analysierten Datenfensters und die Länge des von der Ausgabeschicht erzeugten verborgenen Zustandstensors an. 

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMASAAT;
//--- Windows
     {
      int temp[] = {BarDescr, LatentCount};
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }

Die Schwellenwerte für unsere drei Wirkstoffe wurden als geometrische Progression ermittelt.

//--- Min Distance
     {
      vector<float> ones = vector<float>::Ones(3);
      vector<float> cs = ones.CumSum() - 1;
      descr.radius = pow(ones * 2, cs) * 0.01f;
     }

Alle anderen Parameter behalten ihre Standardwerte bei.

   descr.window_out = 32;
   descr.count = HistoryBars;
   descr.step = 4;               //Heads
   descr.layers = 3;             //Layers
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Die vollständige Architektur der Modelle ist, wie bereits erwähnt, im Anhang zu finden.

Test

Unsere Arbeit an der Implementierung von MASAAT in MQL5 hat ihren logischen Abschluss erreicht. Wir gehen nun zum wichtigsten Schritt über – der Bewertung der Effektivität der implementierten Methoden an realen historischen Daten.

Es ist wichtig zu betonen, dass wir die *implementierten* Ansätze bewerten, nicht das System von MASAAT in seiner ursprünglichen Form. Dies ist darauf zurückzuführen, dass während der Durchführung Änderungen vorgenommen wurden.

Die Modelle wurden mit historischen Daten aus dem Jahr 2023 für EURUSD trainiert, mit einem Zeitrahmen H1. Alle analysierten Indikatoren wurden mit ihren Standardparametereinstellungen verwendet.

Für die erste Trainingsphase haben wir einen Datensatz verwendet, der im Rahmen früherer Studien gesammelt wurde und während des Trainings regelmäßig aktualisiert wurde, um ihn an die aktuelle Strategie des Akteurs anzupassen.

Nach mehreren Trainingszyklen und Aktualisierungen der Datensätze erhielten wir eine Strategie, die sowohl in den Trainings- als auch in den Testdatensätzen profitabel war.

Der abschließende Test der trainierten Strategie wurde mit historischen Daten vom Januar 2024 durchgeführt, wobei alle anderen Parameter konstant gehalten wurden. Die Testergebnisse sind wie folgt:

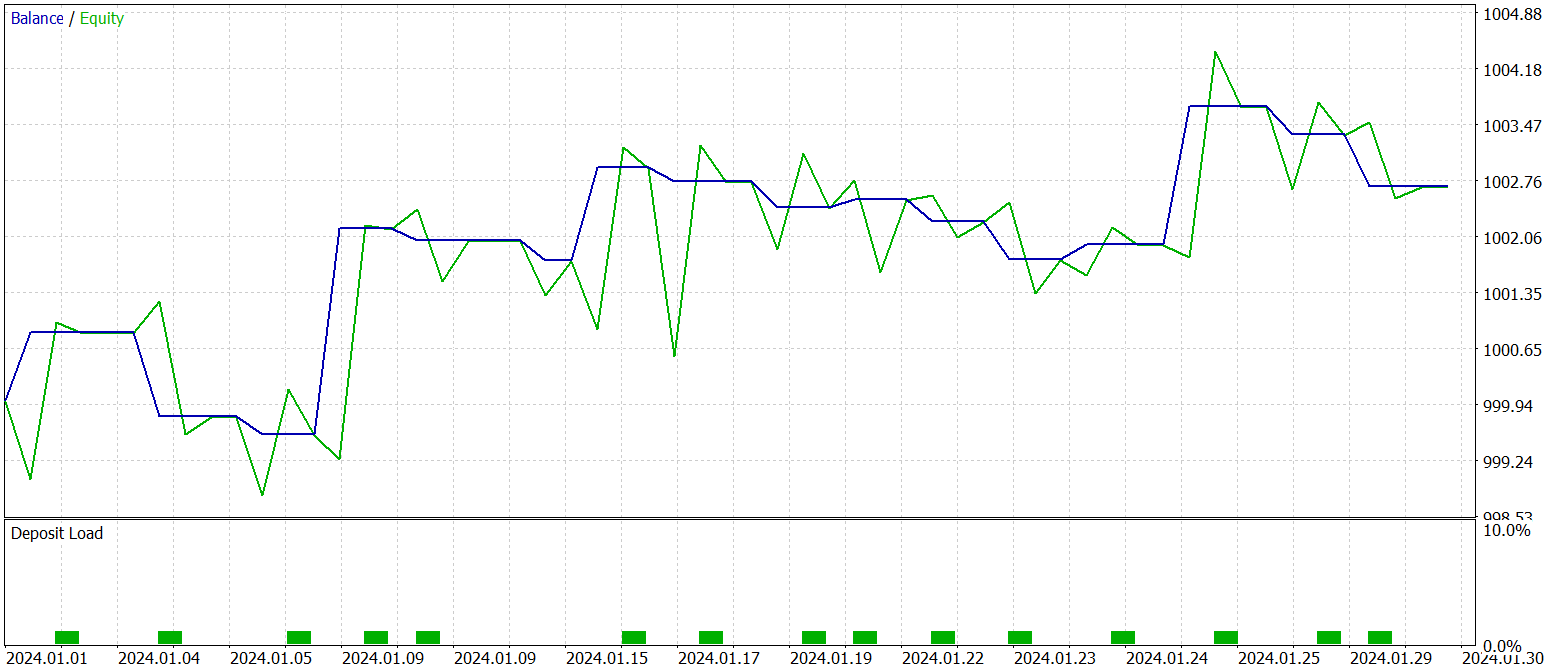
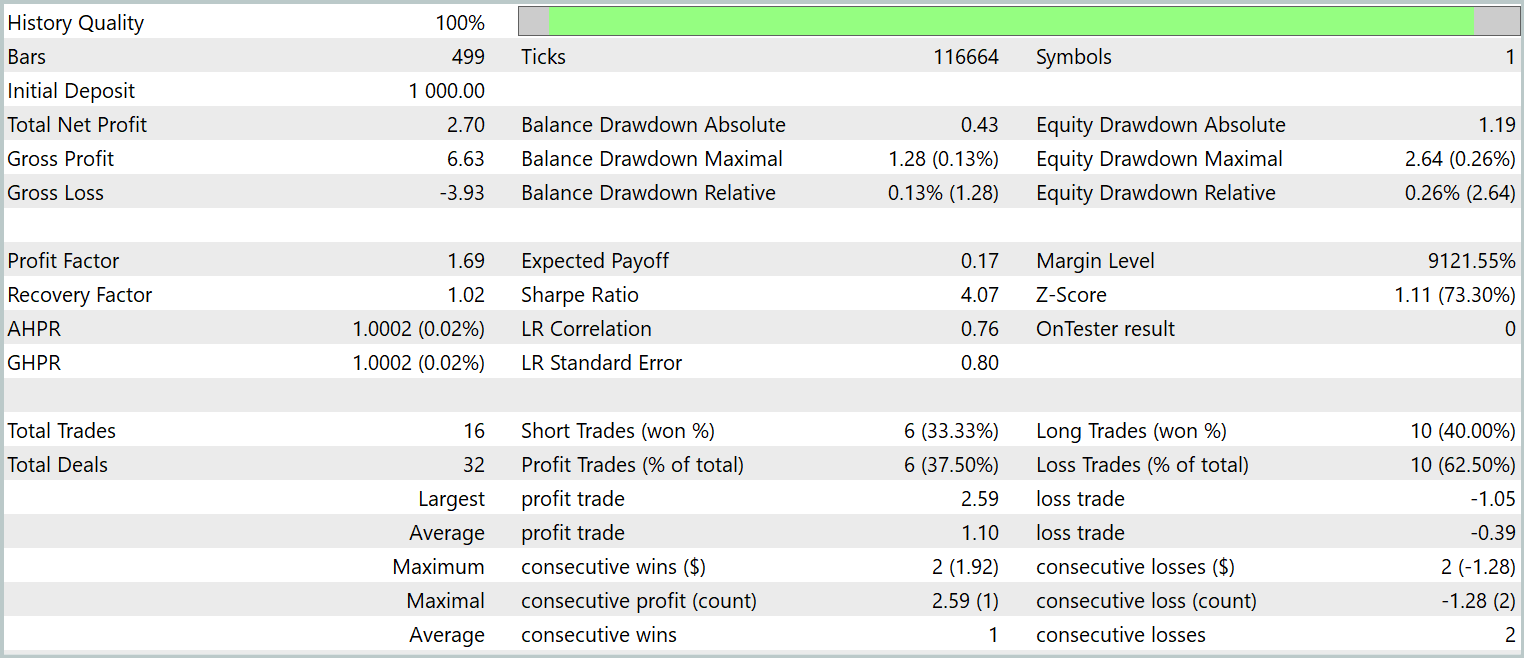
Wie die Daten zeigen, führte das Modell während des Testzeitraums 16 Handelsgeschäfte aus. Etwas mehr als ein Drittel von ihnen schloss mit Gewinn ab. Allerdings überstieg der maximale Gewinn den größten Verlust um das 2,5-fache. Außerdem war der durchschnittliche Gewinn pro Handel dreimal so hoch wie der durchschnittliche Verlust. Infolgedessen ist ein deutlicher Aufwärtstrend beim Kontostand zu beobachten.

Schlussfolgerung

In dieser Arbeit haben wir das adaptive Multi-Agenten-System MASAAT untersucht, das für die Optimierung von Investitionsportfolios entwickelt wurde. MASAAT kombiniert Aufmerksamkeitsmechanismen mit Zeitreihenanalysen. Der Rahmen setzt ein Ensemble von Handelsagenten ein, um eine vielschichtige Analyse von Preisdaten durchzuführen und dadurch die Verzerrung von Handelsentscheidungen zu verringern. Jeder Agent wendet einen aufmerksamkeitsbasierten Querschnittsanalysemechanismus an, um Korrelationen zwischen Vermögenswerten und Zeitpunkten innerhalb des Beobachtungszeitraums zu ermitteln. Diese Informationen werden dann mithilfe eines Moduls für die räumlich-zeitliche Fusion zusammengeführt, was eine effektive Datenintegration ermöglicht und die Handelsstrategien verbessert.

Im praktischen Teil haben wir unsere eigene Interpretation der vorgeschlagenen Methoden mit MQL5 umgesetzt. Wir haben diese Ansätze in ein Modell integriert und es auf realen historischen Daten trainiert. Die Testergebnisse des trainierten Modells zeigen das Potenzial der vorgeschlagenen Methoden.

Referenzen

• Developing An Attention-Based Ensemble Learning Framework for Financial Portfolio Optimisation
• Andere Artikel aus dieser Reihe

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	Expert Advisor für die Probennahme
2	ResearchRealORL.mq5	Expert Advisor	Expert Advisor für die Probennahme mit der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modellausbildung Expert Advisor
4	Test.mq5	Expert Advisor	Modellprüfung Expert Advisor
5	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
6	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
7	NeuroNet.cl	Code Base	OpenCL-Programmcode-Bibliothek