Neuronale Netze im Handel: Ein Ensemble von Agenten mit Aufmerksamkeitsmechanismen (MASAAT)

Einführung

Das Portfoliomanagement von Finanzinstrumenten ist eine Schlüsselkomponente der Anlageentscheidung, die darauf abzielt, die Rendite zu steigern und gleichzeitig die Risiken durch die dynamische Verteilung des Kapitals auf die verschiedenen Vermögenswerte zu minimieren. Die hohe Volatilität der Finanzmärkte, auf denen die Preise von Vermögenswerten von einer Vielzahl von Faktoren abhängen, erschwert die Konstruktion eines optimalen Portfolios, das gleichzeitig zwei gegensätzliche Ziele verfolgt: Gewinnmaximierung und Risikominimierung. Traditionelle Finanzmodelle, die auf verschiedenen Anlagegrundsätzen beruhen, bewähren sich oft auf einem einzelnen Markt, können aber unter den komplexen und dynamischen Bedingungen moderner Märkte versagen.

In den letzten Jahren wurde den Methoden des maschinellen Lernens zur Analyse nicht-stationärer Preisreihen immer mehr Aufmerksamkeit geschenkt. Deep Learning und Reinforcement Learning-Strategien haben in der Finanzinformatik bemerkenswerte Erfolge erzielt. Bei den Preisdaten auf den Finanzmärkten handelt es sich jedoch in der Regel um verrauschte Zeitreihen, bei denen es schwierig ist, Signale zu extrahieren, die auf zukünftige Trends hinweisen.

Ein vielversprechender Ansatz wird in dem Artikel „Developing an attention-based ensemble learning framework for financial portfolio optimisation“ vorgestellt. Die Autoren stellen einen innovativen adaptiven Handelssystem vor, der Aufmerksamkeitsmechanismen und Zeitreihenanalyse integriert (Multi-Agent and Self-Adaptive portfolio optimisation framework integrated with Attention mechanisms and Time series - MASAAT). Innerhalb dieses Systems werden mehrere Agenten eingesetzt, um Richtungsänderungen von Vermögenspreisen auf verschiedenen Granularitätsebenen zu beobachten und zu analysieren. Ziel ist es, ein gründliches Rebalancing des Portfolios zu ermöglichen, um Renditen und Risiken in hochvolatilen Märkten auszugleichen.

Durch die Anwendung von Filtern für Richtungsbewegungen mit unterschiedlichen Schwellenwerten zur Erfassung signifikanter Preisänderungen extrahieren die Agenten zunächst Trendmerkmale aus rohen Zeitreihen. Auf diese Weise können sie die Veränderungen des Marktregimes aus verschiedenen Perspektiven verfolgen. Ein solcher Ansatz führt eine neuartige Methode zur Generierung von Token in Sequenzen ein, die es den Modulen Cross-Sectional Attention (CSA, Querschnittsanalyse) und Temporal Attention (TA, Zeitanalyse), innerhalb der Agenten ermöglicht, sowohl Korrelationen zwischen Vermögenswerten als auch zeitliche Abhängigkeiten effektiv zu erfassen. Bei der Rekonstruktion von Feature-Maps basieren die Sequenz-Token im CSA-Modul auf individuellen Merkmalen der Vermögenswerte und optimieren die Einbettung der Aufmerksamkeit über die Vermögenswerte hinweg, während die Token im TA-Modul auf individuellen Zeitpunkten basieren und die Relevanz zwischen aktuellen und vergangenen Beobachtungen erfassen.

Darüber hinaus werden Informationen über sachliche und zeitliche Abhängigkeiten in einen räumlich-zeitlichen Aufmerksamkeitsblock integriert. Mit klar definierten Rollen für CSA und TA verfügen die Agenten über umfassendere Einblicke in Vermögenstrends, die es ihnen ermöglichen, Portfolios auf der Grundlage ihrer einzigartigen Perspektiven vorzuschlagen. Letztendlich werden die von verschiedenen Agenten erstellten Portfolios zu einem neuen Gesamtportfolio kombiniert, das sich dynamisch an die aktuellen Marktbedingungen anpasst. Selbst wenn ein einzelner Agent Markttrends falsch interpretiert und voreingenommene Empfehlungen abgibt, kann MASAAT durch seine Multi-Agenten-Integration das endgültige Portfolio adaptiv verfeinern, um negative Ergebnisse abzumildern.

Der Algorithmus von MASAAT

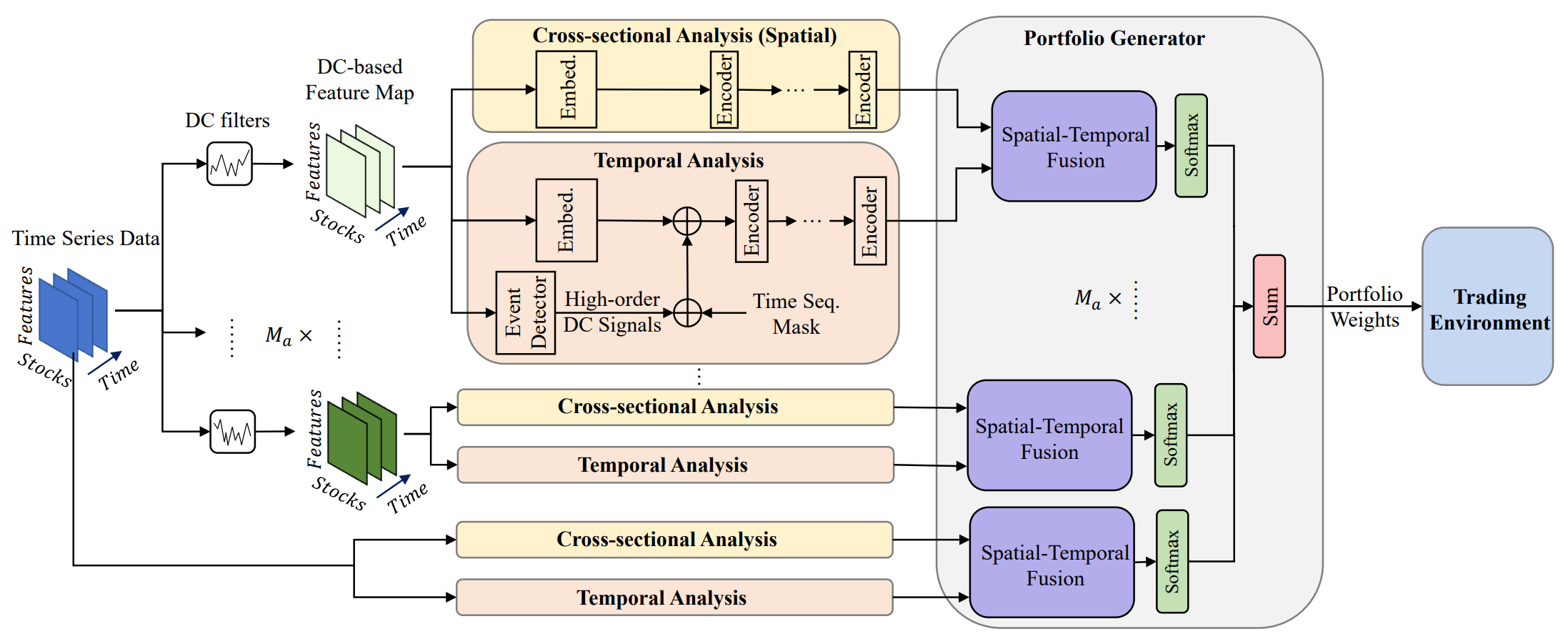
MASAAT wendet mehrere direktionale Bewegungsfilter mit unterschiedlichen Schwellenwerten an, um signifikante Preisschwankungen in rezeptiven Feldern mit mehreren Skalen zu erfassen, was die Analyse potenzieller Einflüsse auf zukünftige Preisbewegungen ermöglicht. Diese rezeptiven Felder repräsentieren unterschiedliche Niveaus der Volatilität von Vermögenswerten und geben den Agenten eine intuitive Wahrnehmung der Marktdynamik. Durch die Rekonstruktion von vermögenswertorientierten, richtungsbezogenen Bewegungsmerkmalen im CSA-Modul und zeitpunktorientierten Merkmalen im TA-Modul in Sequenz-Token sammelt das Multi-Agenten-MASAAT-System gleichzeitig räumliche und zeitliche Informationen über verschiedene Skalen von Preisänderungen. Dies erleichtert es, sowohl die Richtung als auch das Ausmaß der kommenden Trends zu erkennen. Die rohen Preisreihen werden direkt in vermögens- und zeitorientierte Merkmale umgewandelt, gefolgt von einer Querschnitts- und Zeitanalyse innerhalb der Module CSA und TA.

Die CSA- und TA-Module basieren auf Encodern der Selbstaufmerksamkeit (Self-Attention), bei denen die Aufmerksamkeitswerte für die gesamte Token-Sequenz berechnet werden. Dies ermöglicht eine faire Schätzung der Ähnlichkeit über alle Handelsinstrumente hinweg, im Gegensatz zu Faltungsneuronalen Netzen (CNN), die sehr empfindlich auf lokale Positionsstrukturen in Feature-Maps reagieren und auf Kernelgrößen angewiesen sind. Durch die Verwendung von Aufmerksamkeitsscores, die explizit die Ähnlichkeit von Token quantifizieren, sind die von MASAAT generierten Handelssignale von Natur aus besser interpretierbar. Mit Hilfe von räumlich-zeitlichen Aufmerksamkeitsblöcken werden Zuordnungen zwischen Vermögenswertesequenzen und historischen Zeitpunktsequenzen hergestellt. Dieser Prozess erzeugt Einbettungen, die die Aufmerksamkeitswerte jedes Vermögenswerts über alle Zeitpunkte innerhalb des Beobachtungsfensters darstellen. Diese Einbettungen werden dann verwendet, um Portfolioallokationen vorzuschlagen. Ein Portfolio-Generator konsolidiert Vorschläge auf Agentenebene zu einem überarbeiteten Gesamtportfolio und ermöglicht so adaptive Reaktionen auf sich verändernde Marktbedingungen.

N sei die Anzahl der Vermögenswerte, M die Anzahl der beobachtbaren Marktmerkmale und Ma die Anzahl der Handelsagenten. Bei einer bestimmten historischen Tiefe beobachtet jeder Agent zunächst die Preismerkmale 𝐏 ∈ RN×M×Tw über das Beobachtungsfenster Tw. Dann werden trendbasierte Funktionen 𝐏DC={𝐏DC,1, 𝐏DC,2,…,𝐏DC,𝐌a} ∈ RMa, 𝐏DC,i ∈ RN×M×Tw werden mit Hilfe von Filtern für gerichtete Bewegungen extrahiert. Wie oben erwähnt, ist die Methode 𝐏DC,i nach 𝐏DC,i,CSA ∈ RN×MTw transformiert für das Modul CSA und 𝐏DC,i,TA ∈ RTw×NM für das Modul ТА. Die Interdependenzen werden dann im Transformer-Encoder analysiert. In ähnlicher Weise wird die rohe Preisreihe 𝐏 in 𝐏CSA ∈ RN×MTw transformiert und 𝐏TA ∈ RTw×NM.

Nach der Analyse von Token-Abhängigkeiten geben Ausgaben der Module CSA und TA von vermögensorientierten Einbettungen 𝐎CSA ∈ RN×D und zeitorientierte Einbettungen 𝐎TA ∈ RTw×D, wobei D die Dimension des Einbettungsvektors ist. Diese Einbettungen werden zusammengeführt, um ein aktualisiertes Portfolio zu erstellen, das dann mit den Ergebnissen der anderen Agenten integriert wird, um den endgültigen Abhängigkeitsvektor W𝐭 zu erhalten und das Portfolio zu verfeinern.

Nach der Ausführung der Handelsoperationen werden die Belohnungen rt gesammelt und im Erfahrungswiedergabepuffer Ď zusammen mit W𝐭, 𝐏 und 𝐏DC gespeichert. Außerdem wird die Akteurspolitik π iterativ durch Stichproben aus Ď unter Verwendung einer Politik-Gradienten-Methode aktualisiert.

Da höhere Renditen in der Regel mit höheren Risiken einhergehen, ist eine Diversifizierung sowohl entscheidend als auch eine Herausforderung. Die Akteure müssen heterogenen Vermögenswerten eine angemessene Gewichtung zuweisen, um Absicherungseffekte zu erzielen. Das kontinuierliche Erlernen von Korrelationen zwischen Vermögenswerten ermöglicht es den Akteuren also, Risiken unter turbulenten Marktbedingungen besser zu steuern.

Die Trendmerkmale werden vor der Korrelationsanalyse durch den Encoder der Selbstaufmerksamkeit in Sequenz-Token umgewandelt. Der optimierte Aufmerksamkeitsvektor quantifiziert Korrelationen zwischen Vermögenswerten, wobei von Vermögenswerten mit ähnlichen Aufmerksamkeitsvektoren auf gemeinsame relevante Merkmale geschlossen wird.

Über die Korrelation von Vermögenswerten hinaus untersucht MASAAT auch die zeitliche Relevanz über Beobachtungsfenster hinweg und zielt darauf ab, Preistrends auf mehreren Ebenen vorherzusagen. In diesem Fall wird jeder Zeitpunkt als ein Sequenz-Token behandelt, und die Korrelationen zwischen den Zeitpunkten werden mit Hilfe von Transformer-Encodern gelernt. Bei zwei Zeitpunkten mit ähnlichen Aufmerksamkeitsvektoren wird davon ausgegangen, dass sie eine vergleichbare Trenddynamik aufweisen.

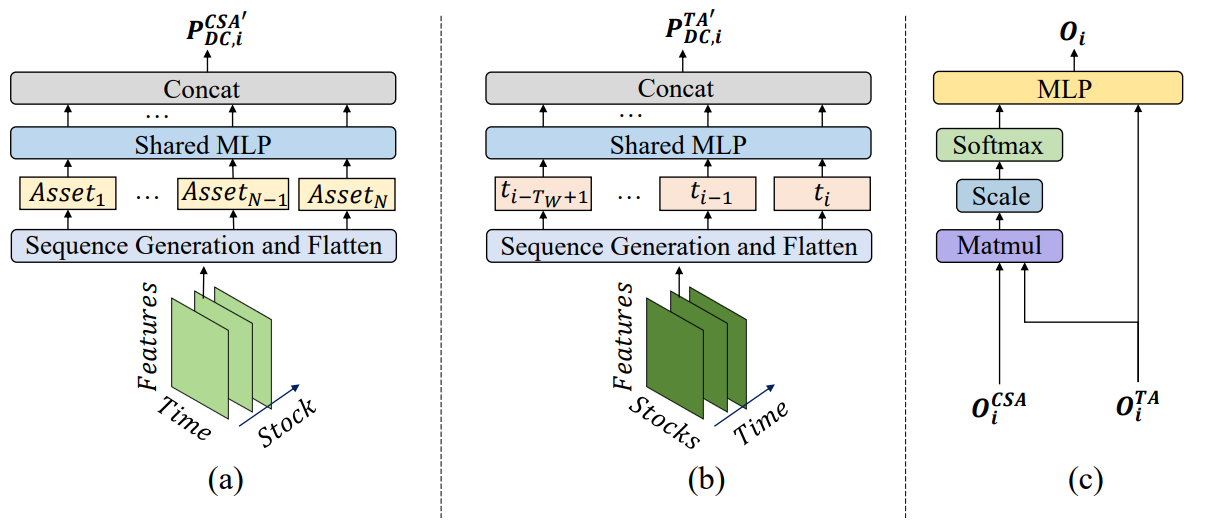
Durch die Aggregation der Informationen aus den Modulen CSA und TA kombinieren die MASAAT-Agenten Aufmerksamkeitsbewertungen auf Vermögensebene und auf Zeitebene und schätzen die Bedeutung jedes Vermögenswertes im Verhältnis zu jedem Zeitpunkt des Beobachtungszeitraums. Das von jedem Agenten vorgeschlagene Portfolio kann wie folgt ausgedrückt werden:

wobei 𝐕i undbi lernbare Parameter von MLP sind.

Die Ergebnisse mehrerer Agenten, die jeweils Preisschwankungen in unterschiedlicher Granularität beobachten, werden dann integriert, um ein Gesamtportfolio zu bilden, das auf das aktuelle Finanzumfeld reagiert. Im Vergleich zu Portfolios, die von einzelnen Agenten erstellt werden, bietet die Multi-Agenten-Struktur von MASAAT mehrere Kandidatenportfolios, die aus verschiedenen Perspektiven abgeleitet werden. Dadurch wird die Anpassungsfähigkeit des Systems, insbesondere auf stark schwankenden Märkten, erheblich verbessert.

Die ursprüngliche Visualisierung des Systems von MASAAT ist unten zu sehen.

Implementation in MQL5

Nachdem wir die theoretischen Aspekte von MASAAT erörtert haben, wenden wir uns nun dem praktischen Teil dieses Artikels zu, in dem wir eine Implementierung unserer Interpretation des vorgeschlagenen Ansatzes mit MQL5 vorstellen. Wie bereits erwähnt, ist MASAAT ein umfassendes System. Um eine klare Trennung der Funktionalität zwischen den verschiedenen Blöcken zu gewährleisten, werden wir eine modulare Struktur aus unabhängigen Objekten entwickeln, die jeweils für einen Teil der MASAAT-Funktionalität verantwortlich sind.

Wir beginnen mit dem Mechanismus der Trenderkennung. Eine stückweise lineare Repräsentation (PLR) für Zeitreihen ist gut geeignet, um lokale Trends zu erkennen. Es gibt jedoch eine Einschränkung: Das zuvor implementierte Objekt kann nur als ein einziger Agent agieren. Da MASAAT flexible Funktionen für die Erstellung von Modellen mit mehreren Agenten benötigt, brauchen wir eine skalierbare Lösung.

Eine Möglichkeit wäre die Verwendung eines dynamischen Arrays mit Zeigern auf mehrere PLR-Objekte der analysierten Zeitreihen, die jeweils mit unterschiedlichen Schwellenwerten arbeiten. Dieser Ansatz führt jedoch zu einer sequenziellen Ausführung, die nicht optimal ist. Stattdessen werden wir ein neues Objekt entwickeln, das den parallelen Betrieb mehrerer Trenderkennungsagenten ermöglicht. Um dies zu erreichen, müssen wir zunächst das Programm OpenCL um neue Kernel erweitern.

Programmerweiterung von OpenCL

Bei dem Versuch, die bestehenden PLR-Kerne anzupassen, sahen wir uns mit der Notwendigkeit konfrontiert, einen einzigen Schwellenwertparameter durch einen Vektor von Schwellenwerten zu ersetzen, einen für jeden Agenten. Diese Änderung erfordert nicht nur eine Modifizierung des Kernel-Algorithmus, sondern auch eine Umstrukturierung der abhängigen Objekte. Um die Entwicklung zu vereinfachen, haben wir neue Kernel für die Vorwärts- und Rückwärtsdurchläufe entwickelt und dabei die Logik der bestehenden Implementierung teilweise wiederverwendet.

Für den Vorwärtsdurchlauf haben wir den Kernel PLRMultiAgents entwickelt. Er empfängt vier Datenpuffer-Zeiger. Zwei Puffer enthalten die rohen Zeitreihen und agentenspezifische Schwellenwerte. In den beiden anderen Puffern werden die Analyseergebnisse und Trendumkehrflags gespeichert.

__kernel void PLRMultiAgents(__global const float *inputs,
                             __global float *outputs,
                             __global int *isttp,
                             const int transpose,
                             __global const float *min_step
                            )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);
   const size_t a = get_global_id(2);
   const size_t agents = get_global_size(2);

Dieser Kernel wird in einem 3D-Aufgabenraum ausgeführt. Die erste Dimension entspricht der Größe der analysierten Sequenz. Die zweite Dimension entspricht der Anzahl der univariaten Reihen in einer multimodalen Sequenz. Die dritte Dimension entspricht der Anzahl der Agenten. Innerhalb des Kerns identifiziert jeder Thread seine Position über alle Aufgabendimensionen hinweg. Danach bestimmen wir den Offset in den Datenpuffern.

//--- constants
   const int shift_in = ((bool)transpose ? (i * variables + v) : (v * lenth + i));
   const int step_in = ((bool)transpose ? variables : 1);
   const int shift_ag = a * lenth * variables;

Es ist wichtig zu beachten, dass alle Agenten die gleiche multimodale Sequenz analysieren. Die Kennung des Agenten wirkt sich also nur auf den Pufferversatz für Ergebnisse und Schwellenwerte aus.

Nach der Initialisierung beginnt der Kernel mit der Suche nach Trendumkehrpunkten (Extrema). Jeder Fluss bestimmt das Vorhandensein eines Trendumkehrpunktes an der Position des aktuellen Elements. Die Extrempunkte der analysierten Zeitreihe erhalten automatisch den Status eines Trendumkehrpunktes, da sie a priori die Extrempunkte des Segments sind.

//--- look for ttp
   float value = IsNaNOrInf(inputs[shift_in], 0);
   bool bttp = false;
   if(i == 0 || i == lenth - 1)
      bttp = true;

Bei anderen Punkten sucht der Algorithmus rückwärts nach dem nächstgelegenen Element, dessen Abweichung den Schwellenwert überschreitet. Dabei werden die Mindest- und Höchstwerte im geprüften Intervall aufgezeichnet.

   else
     {
      float prev = value;
      int prev_pos = i;
      float max_v = value;
      float max_pos = i;
      float min_v = value;
      float min_pos = i;
      while(fmax(fabs(prev - max_v), fabs(prev - min_v)) < min_step[a] && prev_pos > 0)
        {
         prev_pos--;
         prev = IsNaNOrInf(inputs[shift_in - (i - prev_pos) * step_in], 0);
         if(prev >= max_v && (prev - min_v) < min_step[a])
           {
            max_v = prev;
            max_pos = prev_pos;
           }
         if(prev <= min_v && (max_v - prev) < min_step[a])
           {
            min_v = prev;
            min_pos = prev_pos;
           }
        }

Wir suchen vorwärts nach dem nächsten Element mit der gewünschten Abweichung.

      float next = value;
      int next_pos = i;
      while(fmax(fabs(next - max_v), fabs(next - min_v)) < min_step[a] && next_pos < (lenth - 1))
        {
         next_pos++;
         next = IsNaNOrInf(inputs[shift_in + (next_pos - i) * step_in], 0);
         if(next > max_v && (next - min_v) < min_step[a])
           {
            max_v = next;
            max_pos = next_pos;
           }
         if(next < min_v && (max_v - next) < min_step[a])
           {
            min_v = next;
            min_pos = next_pos;
           }
        }

Bestimmen wir, ob das aktuelle Element als Extremum zu betrachten ist.

      if(
         (value >= prev && value > next) ||
         (value > prev && value == next) ||
         (value <= prev && value < next) ||
         (value < prev && value == next)
      )
         if(max_pos == i || min_pos == i)
            bttp = true;
     }

Dabei ist jedoch zu bedenken, dass bei der Suche nach Elementen mit der geringsten erforderlichen Abweichung ein Korridor von Werten aus mehreren Elementen der Sequenz gesammelt werden könnte, die ein bestimmtes Extremwertplateau bilden. Daher erhält ein Element nur dann das Flag für einen Trendumkehrpunkt, wenn es ein Extremum in diesem Bereich ist. Wenn es mehrere Elemente mit demselben Wert gibt, wird das Extremum-Flag dem ersten von ihnen zugewiesen.

Wir speichern das erhaltene Flag und löschen den Ausgabepuffer. Gleichzeitig synchronisieren wir die Abläufe in den Arbeitsgruppen.

   isttp[shift_in + shift_ag] = (int)bttp;
   outputs[shift_in + shift_ag] = 0;
   barrier(CLK_LOCAL_MEM_FENCE);

Nachfolgende Schritte werden nur von Threads durchgeführt, die mit einer bestätigten Trendumkehr verbunden sind. Die übrigen erfüllen die Bedingungen nicht und schließen die Vorgänge praktisch ab.

Zunächst bestimmen wir die Position des aktuellen Extremwerts. Dazu zählen wir anhand der gespeicherten Flags alle vorangegangenen Extrema bis zur analysierten Position und speichern die Position des vorangegangenen Extremums aus dem Quelldatenpuffer in einem lokalen Puffer.

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int prev_ttp = 0;
   if(bttp)
     {
      pos = 0;
      for(int p = 0; p < i; p++)
        {
         int current_in = ((bool)transpose ? (p * variables + v) : (v * lenth + p));
         if((bool)isttp[current_in + shift_ag])
           {
            pos++;
            prev_ttp = p;
            prev_in = current_in;
           }
        }
     }

Dann berechnen wir die Parameter der linearen Approximation für das Segment.

//--- cacl tendency
   if(pos > 0 && pos < (lenth / 3))
     {
      float sum_x = 0;
      float sum_y = 0;
      float sum_xy = 0;
      float sum_xx = 0;
      int dist = i - prev_ttp;
      for(int p = 0; p < dist; p++)
        {
         float x = (float)(p);
         float y = IsNaNOrInf(inputs[prev_in + p * step_in], 0);
         sum_x += x;
         sum_y += y;
         sum_xy += x * y;
         sum_xx += x * x;
        }
      float slope = IsNaNOrInf((dist * sum_xy - sum_x * sum_y) / (dist > 1 ? (dist * sum_xx - sum_x * sum_x) : 1), 0);
      float intercept = IsNaNOrInf((sum_y - slope * sum_x) / dist, 0);

Danach speichern wir die erhaltenen Werte im Ergebnispuffer.

      int shift_out = ((bool)transpose ? ((pos - 1) * 3 * variables + v) : (v * lenth + (pos - 1) * 3)) + shift_ag;
      outputs[shift_out] = slope;
      outputs[shift_out + step_in] = intercept;
      outputs[shift_out + 2 * step_in] = ((float)dist) / lenth;
     }

Jedes erhaltene Segment wird durch 3 Parameter charakterisiert:

• slope – der Winkel der Trendlinie,
• intercept – der Linienversatz im Datenraum,
• dist – die normierte Länge des Segments.

Die Speicherung der Sequenzlänge als Integer-Wert ist in diesem Fall nicht die beste Option. Denn für den effizienten Betrieb des Modells ist ein normalisiertes Datenpräsentationsformat vorzuziehen. Daher übersetzen wir die ganzzahlige Segmentgröße in einen Bruchteil der Länge der zu analysierenden univariaten Sequenz. Dazu wird die Anzahl der Elemente im Segment durch die Anzahl der Elemente in der gesamten Sequenz der univariaten Zeitreihe geteilt. Um nicht in die „Falle“ der Integer-Operationen zu tappen, wandeln wir zunächst die Anzahl der Elemente im Segment von int in den Typ float um.

Außerdem werden wir für das letzte Segment einen eigenen Handlungszweig einrichten. Zu diesem Zeitpunkt kennen wir die Anzahl der Segmente, die zu einem bestimmten Zeitpunkt gebildet werden, noch nicht. Hypothetisch gesehen können in extremen Szenarien (z. B. bei kleinen Schwellenwerten und hoher Volatilität) bei fast jedem Element Umkehrungen auftreten. Dieser Fall ist zwar unwahrscheinlich, würde aber das Datenvolumen erheblich vergrößern. Gleichzeitig wollen wir aber auch keine Daten verlieren.

Daher gehen wir von einem A-priori-Wissen über die Darstellung von Zeitreihen in MQL5 aus und verstehen die Struktur der analysierten Daten: Die zeitlich jüngsten Daten stehen am Anfang unserer Zeitreihe. Gehen wir näher auf sie ein. Die Daten am Ende der untersuchten Sequenz sind zu einem früheren Zeitpunkt in der Geschichte entstanden und haben daher weniger Einfluss auf spätere Ereignisse. Allerdings werden wir solche Abhängigkeiten nicht ausschließen.

Daher verwenden wir zum Schreiben der Ergebnisse eine Datenpuffergröße, die der Größe des eingegebenen Zeitreihentensors entspricht. Dadurch können wir Segmente schreiben, die dreimal kleiner sind als die Sequenzlänge (3 Elemente für 1 Segment). Wir gehen davon aus, dass dieses Volumen mehr als ausreichend ist. Wenn es jedoch mehr Segmente gibt, werden die Daten der letzten Segmente zu 1 zusammengeführt, um Datenverluste zu vermeiden.

   else
     {
      if(pos == (lenth / 3))
        {
         float sum_x = 0;
         float sum_y = 0;
         float sum_xy = 0;
         float sum_xx = 0;
         int dist = lenth - prev_ttp;
         for(int p = 0; p < dist; p++)
           {
            float x = (float)(p);
            float y = IsNaNOrInf(inputs[prev_in + p * step_in], 0);
            sum_x += x;
            sum_y += y;
            sum_xy += x * y;
            sum_xx += x * x;
           }
         float slope = IsNaNOrInf((dist * sum_xy - sum_x * sum_y) / (dist > 1 ? (dist * sum_xx - sum_x * sum_x) : 1),0);
         float intercept = IsNaNOrInf((sum_y - slope * sum_x) / dist, 0);
         int shift_out = ((bool)transpose ? ((pos - 1) * 3 * variables + v) : (v * lenth + (pos - 1) * 3)) + shift_ag;
         outputs[shift_out] = slope;
         outputs[shift_out + step_in] = intercept;
         outputs[shift_out + 2 * step_in] = IsNaNOrInf((float)dist / lenth, 0);
        }
     }
  }

In den meisten Fällen erwarten wir weniger Segmente, dann werden die letzten Elemente unseres Ergebnispuffers mit Nullwerten gefüllt sein.

Wie Sie sehen können, verwenden wir im Algorithmus für den Vorwärtsdurchlauf keine trainierbaren Parameter. Der Rückwärtsdurchlauf wird also auf die Fehlergradientenverteilung reduziert. Diese Funktion ist im Kernel PLRMultiAgentsGradient implementiert.

Alle Agenten analysieren die gleichen Zeitreihen. Daher müssen die Gradienten aller Agenten auf der Ebene der Rohdaten aggregiert werden. In Anbetracht der zu erwartenden geringen Anzahl von Agenten haben wir uns dafür entschieden, den Kernel nicht übermäßig zu verkomplizieren. Stattdessen verwenden wir den Algorithmus der Gradientenverteilung für Einzelagenten. Wir fügen jedoch auch eine Schleife hinzu, um die Gradienten aller Agenten zu sammeln und einen Parameter, der ihre Anzahl angibt. Ich möchte Sie dazu ermutigen, ihre Implementierungen selbst zu erkunden. Das vollständige OpenCL-Programm, einschließlich dieser Kernel, ist im Anhang enthalten.

Das Objekt mit dem Mechanismus zur Trenderkennung

Nachdem wir die OpenCL-seitige Implementierung abgeschlossen haben, gehen wir nun zu unserer Hauptbibliothek über und implementieren den Algorithmus zur Erkennung von Multiagententrends im Objekt CNeuronPLRMultiAgentsOCL. Wie Sie vielleicht bemerken, erweitert dieses Objekt im Wesentlichen die zuvor entwickelte stückweise lineare Darstellung (PLR) einer Zeitreihe. Aus diesem Grund haben wir sie als übergeordnete Klasse ausgewählt. Die Struktur des neuen Objekts wird im Folgenden dargestellt.

class CNeuronPLRMultiAgentsOCL  :  public CNeuronPLROCL
  {
protected:
   int               iAgents;
   CBufferFloat      cMinDistance;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);

public:
                     CNeuronPLRMultiAgentsOCL(void)  : iAgents(1) {};
                    ~CNeuronPLRMultiAgentsOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window_in, uint units_count, bool transpose,
                          vector<float> &min_distance,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronPLRMultiAgentsOCL;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

In dieser neuen Klasse deklarieren wir eine Konstante, die die Anzahl der aktiven Agenten (iAgents) definiert, und einen Puffer für die Speicherung der Schwellenwerte der Merkmalsänderungen in der analysierten Zeitreihe (cMinDistance).

Da alle internen Objekte statisch deklariert werden, können wir den Konstruktor und den Destruktor leer lassen. Die Initialisierung dieser deklarierten und geerbten Objekte wird in der Methode Init durchgeführt.

bool CNeuronPLRMultiAgentsOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                    uint window_in, uint units_count, bool transpose,
                                    vector<float> &min_distance,
                                    ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   iAgents = (int)min_distance.Size();
   if(iAgents <= 0)
      return false;

Beachten Sie, dass die Methode nur einen Vektor von Schwellenwerten als Eingabe benötigt. Wir geben die Anzahl der Agenten nicht explizit an. Die Zahl ergibt sich aus der Größe des Schwellenwertvektors selbst. Dadurch wird die Anzahl der externen Parameter reduziert und die Konsistenz zwischen dem Schwellenwertparameter und der Pufferlänge gewährleistet.

Innerhalb der Methode wird, nachdem die Anzahl der Agenten in einer internen Variablen gespeichert und validiert wurde (für einen ordnungsgemäßen Betrieb ist mindestens ein Agent erforderlich), die Initialisierungsmethode des Basisobjekts aufgerufen, die die wichtigsten Schnittstellen einrichtet.

   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_in * units_count * iAgents, optimization_type, batch))
      return false;

Wichtig ist, dass wir die Init-Methode des Basisobjekts aufrufen, nicht die des direkten Elternobjekts. Der Grund dafür ist, dass die Größe des Ergebnispuffers proportional zur Anzahl der Agenten skaliert wird. Dies erfordert jedoch eine tiefere Neuinitialisierung der vererbten Komponenten.

Zunächst speichern wir die Werte der empfangenen Parameter in geerbten Variablen.

   iVariables = (int)window_in;
   iCount = (int)units_count;
   bTranspose = transpose;

Und dann initialisieren wir den Puffer der Extremum-Flags.

   icIsTTP = OpenCL.AddBuffer(sizeof(int) * Neurons(), CL_MEM_READ_WRITE);
   if(icIsTTP < 0)
      return false;

Beachten Sie, dass diese Flags nach jedem Vorwärtsdurchlauf neu berechnet werden. Ihre Größe entspricht der des Ergebnispuffers. Offensichtlich besteht keine Notwendigkeit, ihre Werte dauerhaft zu speichern. Der Puffer wird also nur im Kontextspeicher von OpenCL erstellt. Das Objekt behält nur einen Zeiger darauf.

Als Nächstes wird der Schwellenwertpuffer initialisiert.

   if(!cMinDistance.AssignArray(min_distance) ||
      !cMinDistance.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Danach schließen wir die Methode ab, indem wir das logische Ergebnis des Initialisierungsprozesses an das aufrufende Programm zurückgeben.

Die Methoden des Vorwärtsdurchlaufs und des Rückwärtsdurchlaufs werden ebenfalls überschrieben. Ihre einzige Funktion besteht jedoch darin, die zuvor beschriebenen OpenCL-Kernel aufzurufen. Da ihre Logik einfach ist, überlassen wir sie einer unabhängigen Untersuchung.

Damit ist die Implementierung des Trenderkennungsobjekts der Multi-Agenten CNeuronPLRMultiAgentsOCL abgeschlossen. Der vollständige Quellcode der Methoden ist in der Anlage enthalten.

Das Modul Cross-Sectional Attention (CSA)

Sobald wir die stückweise linearen Darstellungen der analysierten Zeitreihen erhalten, verarbeitet jeder Agent die ihm zugewiesene Skala für eine eingehende Analyse. Im System von MASAAT werden Zeitreihen in zwei Projektionen analysiert: über Vermögenswerte und über Zeitpunkte.

Die Zeitreihenanalyse innerhalb des Systems von MASAAT wird durch das Modul der Aufmerksamkeit von Kreuzsymbolen durchgeführt, das wir als Objekt CNeuronCrossSectionalAnalysis implementieren. Doch bevor wir uns mit der Implementierung befassen, wollen wir den Algorithmus zur Konstruktion der CSA-Module erläutern.

Wie im theoretischen Teil der Beschreibung von MASAAT erläutert, verwendet das CSA-Modul einen Selbstaufmerksamkeits-Encoder zur Erfassung der Abhängigkeiten von Handelsinstrumenten. Unsere Bibliothek enthält bereits mehrere Encoder-Implementierungen. Es gibt jedoch eine Nuance: In MASAAT arbeiten mehrere Agenten parallel, wobei jeder nur die Abhängigkeiten innerhalb der ihm zugewiesenen Teilmenge der Daten analysiert. Nach der Prüfung können wir eine geeignete Lösung finden.

Zum Beispiel im Block CNeuronMVMHAttentionMLKV für die unabhängige Kanalanalyse, ursprünglich entwickelt für das System InjectTST entwickelt wurde. Keine schlechte Lösung. Während dieser Block für die Analyse von Abhängigkeiten zwischen verschiedenen Maßstäben eines einzelnen Vermögenswerts konzipiert ist, besteht unsere Aufgabe darin, Abhängigkeiten zwischen verschiedenen Vermögenswerten innerhalb eines Maßstabs zu finden. Um ihn anzupassen, transponieren wir zunächst den dreidimensionalen Eingangstensor entlang seiner ersten beiden Achsen. Wir haben bereits eine solche Transpositionsebene in unserer Bibliothek: CNeuronTransposeRCDOCL.

Wir haben uns für den Encoder entschieden. Doch bevor wir die Daten in den Encoder einspeisen, müssen wir auch die Einbettung der Trajektorien der Handelsinstrumente erstellen. Die Autoren von MASAAT schlagen die Verwendung eines MLP mit gemeinsamen Parametern für alle Vermögenswerte vor. Unserer Konvention folgend, ersetzen wir den MLP durch eine Faltungsschicht. Konkret fügen wir eine einzelne Faltungsschicht mit GELU-Aktivierung hinzu. Die zweite Rolle von MLP (Generierung der Entitäten von Query, Key und Value) wird intern vom Encoder selbst übernommen.

Dies wird die Struktur unseres Moduls CSA sein. Darin verwenden wir nacheinander eine Datentranspositionsschicht, eine Faltungseinbettungsschicht und einen unabhängigen Kanalanalyseblock (Selbstaufmerksamkeit-Encoder). Aus Gründen der Effizienz platzieren wir die Faltungsschicht vor der Transposition. Das Ergebnis der Vorgänge ändert sich nicht. Dies wirkt sich jedoch positiv auf die Wirksamkeit der Lösung aus.

Wir füttern das Modul CSA mit einer Darstellung der Zeitreihen mit den Preisbewegungen der analysierten Vermögenswerte. Mit zunehmender Tiefe der analysierten Historie steigt also auch das Volumen der Quelldaten. Da die PLR oft viele mit Nullen gefüllte Elemente enthält, können kleinere Einbettungen verwendet werden. Dadurch verringert sich die Größe des Tensors, der nach den Operationen der Faltungseinbettungsschicht transponiert werden muss, was den Rechenaufwand verringert und die Leistung verbessert.

Nachdem wir die wichtigsten Aspekte der Implementierung identifiziert haben, können wir mit der Konstruktion unseres neuen Objekts CNeuronCrossSectionalAnalysis fortfahren. Seine Struktur wird im Folgenden dargestellt.

class CNeuronCrossSectionalAnalysis :  public CNeuronMVMHAttentionMLKV
  {
protected:
   CNeuronConvOCL          cEmbeding;
   CNeuronTransposeRCDOCL  cTransposeRCD;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronCrossSectionalAnalysis(void) {};
                    ~CNeuronCrossSectionalAnalysis(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint heads, uint heads_kv,
                          uint units_count, uint layers, uint layers_to_one_kv,
                          uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) override;
   //---
   virtual int       Type(void)   const override   {  return defNeuronCrossSectionalAnalysis;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Beachten Sie, dass wir den Block Independent Channel Analysis als übergeordnete Klasse verwenden. Diese Lösung ermöglicht es uns, seine Methoden direkt wiederzuverwenden, anstatt sie als interne Komponente einzubetten. Wir deklarieren andere Objekte als statisch und können daher den Konstruktor und Destruktor der Klasse leer lassen. Die Initialisierung erfolgt in der Methode Init, deren Parameter die der übergeordneten Klasse widerspiegeln.

bool CNeuronCrossSectionalAnalysis::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                         uint window, uint window_key, uint heads, uint heads_kv,
                                         uint units_count, uint layers, uint layers_to_one_kv, uint variables,
                                         ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronMVMHAttentionMLKV::Init(numOutputs, myIndex, open_cl, window_key, window_key, heads, heads_kv,
                                      variables, layers, layers_to_one_kv, units_count, optimization_type, batch))
      return false;

Im Methodenkörper rufen wir wie üblich zunächst die entsprechende Methode der übergeordneten Klasse auf. Es gibt jedoch einen Vorbehalt. Bei der Implementierung der Funktionalität des Moduls CSA planen wir, alle geerbten Methoden in vollem Umfang zu nutzen. Im System des Vorwärtsdurchlaufs wird die Eingabe der übergeordneten Klassenmethode mit transponierten Einbettungen der Rohdaten gefüttert. Daher wird beim Aufruf der Initialisierungsmethode der übergeordneten Klasse die Größe des Quelldatenfensters an die Einbettungsdimension angepasst und die Parameter der analysierten Sequenzlänge mit der Anzahl der unabhängigen Variablen vertauscht.

Nachdem die Initialisierungsoperationen der übergeordneten Klassenobjekte erfolgreich abgeschlossen wurden, werden nacheinander die Faltungseinbettungs- und Datentranspositionsschicht initialisiert.

   if(!cEmbeding.Init(0, 0, OpenCL, window, window, window_key, units_count, variables, optimization, iBatch))
      return false;
   cEmbeding.SetActivationFunction(GELU);
   if(!cTransposeRCD.Init(0,1,OpenCL,variables,units_count,window_key,optimization,iBatch))
      return false;

Danach deaktivieren wir die Aktivierungsfunktion zwangsweise und beenden die Methode, nachdem wir zuvor das logische Ergebnis der Operationen an das aufrufende Programm zurückgegeben haben.

   SetActivationFunction(None);
//---
   return true;
  }

Als Nächstes bauen wir den Algorithmus für den Vorwärtsdurchlauf unseres CSA-Moduls in der Methode feedForward auf. Hier ist alles ganz einfach. In den Methodenparametern erhalten wir einen Zeiger auf das Eingabedatenobjekt, das wir sofort an die gleichnamige Methode der Faltungsschicht übergeben.

bool CNeuronCrossSectionalAnalysis::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cEmbeding.FeedForward(NeuronOCL))
      return false;
   if(!cTransposeRCD.FeedForward(cEmbeding.AsObject()))
     return false;
//---
   return CNeuronMVMHAttentionMLKV::feedForward(cTransposeRCD.AsObject());
  }

Wir transponieren die Ausgaben der Faltungsschicht und übergeben sie an die gleichnamige Methode der übergeordneten Klasse. Die Methode schließt mit der Rückgabe des logischen Ergebnisses der Operation an das aufrufende Programm ab.

Der Algorithmus des Rückwärtsdurchlaufs ist ebenfalls einfach. Deshalb schlage ich vor, dass Sie es selbst erkunden. Wir schließen unsere Arbeit an dem Objekt CNeuronCrossSectionalAnalysis ab. Den vollständigen Code für alle diese Methoden finden Sie im Anhang.

Unser Arbeitstag ist nun vorbei. Die Arbeit ist jedoch noch nicht abgeschlossen. Lassen Sie uns eine kurze Pause einlegen, und im nächsten Artikel werden wir das Projekt zu einem logischen Abschluss bringen.

Schlussfolgerung

In diesem Artikel haben wir das Multi-Agent Self-Adaptive Attention-based Time Series System (MASAAT) zur Portfolio-Optimierung untersucht, das ein Ensemble von Handelsagenten einsetzt, um Preisdaten aus mehreren Perspektiven zu analysieren. Dadurch wird die Verzerrung der generierten Handelsaktionen verringert. Jeder Agent führt Querschnitts- und Zeitanalysen durch, indem er Aufmerksamkeitsmechanismen einsetzt, um Korrelationen zwischen Vermögenswerten und Zeitpunkten zu erfassen, gefolgt von einem Modul für die räumlich-zeitliche Fusion zur Integration der extrahierten Informationen.

Im praktischen Teil begannen wir damit, unsere eigene Interpretation von MASAAT in MQL5 zu implementieren, einschließlich des Multi-Agenten-Trenderkennungsmechanismus und des Moduls für querschnittliche Aufmerksamkeit. Im nächsten Artikel werden wir diese Arbeit fortsetzen und die Leistung der implementierten Lösung anhand echter historischer Daten bewerten.

Referenzen

• Developing An Attention-Based Ensemble Learning Framework for Financial Portfolio Optimisation
• Andere Artikel dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	Expert Advisor für das Sammeln von Stichproben
2	ResearchRealORL.mq5	Expert Advisor	Expert Advisor für die Probenahme mit der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modellausbildung Expert Advisor
4	Test.mq5	Expert Advisor	Modellprüfung Expert Advisor
5	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
6	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
7	NeuroNet.cl	Code Base	OpenCL-Programmcode-Bibliothek