Trendkriterien im Handel

Einführung

Alle Händler kennen die Redewendung „Der Trend ist dein Freund“. In der Tat können tendenzielle Kursbewegungen recht hohe Gewinne bringen. Der Trendhandel basiert auf der Annahme, dass sich die Kursbewegung in dieselbe Richtung fortsetzen wird. Das Hauptproblem bei dieser Art des Handels besteht darin, den Anfangs- und Endzeitpunkt des Trends mit ausreichender Genauigkeit zu bestimmen.

Heute gibt es viele Ansätze zur Definition und Berechnung von Trendparametern. In diesem Artikel werden wir uns die interessantesten von ihnen ansehen und versuchen, sie in der Praxis anzuwenden.

Glättung und Trends

Die Preisentwicklung lässt sich anhand eines einfachen Modells darstellen. Es gibt eine deterministische Komponente, die von der Zeit abhängt. Ihm wird eine zufällige Komponente hinzugefügt, die von nichts abhängt und sich unvorhersehbar verhält. Eine der Aufgaben eines Händlers besteht darin, den Einfluss dieser Komponente irgendwie zu reduzieren.

Einer der einfachsten Filter ist der einfache gleitende Durchschnitt. Dieser Indikator hat jedoch einen gravierenden Nachteil – er hinkt hinterher. Simulieren wir den Trend und wenden wir SMA mit einer Periode von 3 an.

Trend	0	1	2	3	4	5
SMA	-	-	1	2	3	4

Versuchen wir nun, die Verzögerung zu beseitigen. Die SMA-Gleichung sieht wie folgt aus:

Fügen wir eine Korrektur hinzu, die der durchschnittlichen Preisänderung für einen Balken entspricht:

Schauen wir uns an, wie sich die Koeffizienten unseres neuen Indikators verändern:

Der Indikator mit solchen Koeffizienten wird den Trend genau treffen. Verallgemeinern wir diesen Indikator auf eine beliebige Anzahl von gehandhabten Preisen. Die Berechnung eines Indikators mit einer Periode von 4 sieht folgendermaßen aus.

Ermitteln wir zunächst den SMA-Wert:

Es gibt jetzt zwei Korrekturen für die durchschnittliche Preisänderung:

Mit anderen Worten: Wir berechnen die durchschnittliche Kursänderung relativ zur SMA-Mitte. Die Indikatorgleichung lautet dann wie folgt:

Der Unterschied zwischen diesem Indikator und dem SMA ist vor allem bei kurzen Zeiträumen spürbar.

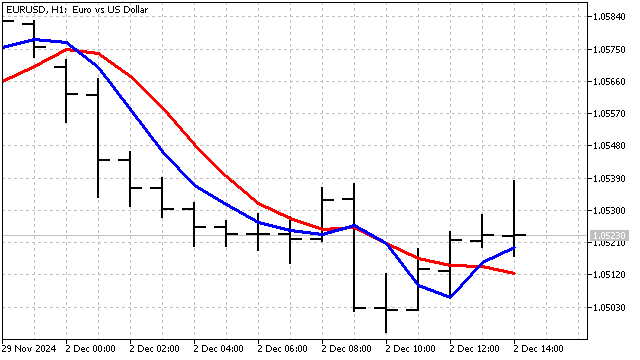
Der größte Nachteil dieses Ansatzes ist, dass es keine Kriterien für die Auswahl des Indikatorzeitraums gibt. Die Händler sollten ihn willkürlich und nach eigenen Überlegungen wählen.

Versuchen wir, einen Indikator zu entwickeln, der nicht von der Periode abhängt. Angenommen, wir haben die Zeitreihe V, die wir einen Schritt voraus prognostizieren möchten. Für die Vorhersage werden wir die einfachste Methode verwenden – frühere Aktionen bestimmen die zukünftigen. Wenn wir beispielsweise den Ausgangswert von V haben, dann entspricht die Ein-Schritt-Vorhersage diesem Wert:

Sobald der neue Wert von V erscheint, ermitteln wir die Halbsumme zwischen der Prognose und V. Der daraus resultierende Wert ist die Prognose für den nächsten Schritt:

Mit anderen Worten: Die Vorhersage wird angepasst, wenn neue Werte der Zeitreihe erscheinen. Diese Prognosemethode führt zu einer exponentiellen Glättung mit einem Koeffizienten von 0,5.

Nun ändern wir ein wenig den Ansatz für die Vorhersagen. Gehen wir davon aus, dass die Änderung der Vorhersage mit der gleichen Intensität eintritt:

Mit anderen Worten: Alle Prognosewerte gehören zum linearen Trend. Die Indikatorgleichung, die auf diesem Prinzip beruht, sieht wie folgt aus:

Wir haben einen rekursiven Indikator – um den aktuellen Wert des Indikators zu berechnen, werden seine früheren Werte verwendet. Aber in dieser Form wird sie instabil sein – eine der Koeffizienten ist gleich 1. Um dieses Problem zu lösen, werden wir dieselbe Rekursion auf Indicator[i+1] anwenden:

Der Indikator besteht nun aus zwei Teilen – SMA mit einer Periode von 2 und der Hälfte der Geschwindigkeit des Indikators in den vorherigen Messwerten. Nehmen wir eine weitere Änderung vor, um den Indikator robuster zu machen:

So sieht unser neuer Indikator im Vergleich zu einem ähnlichen EMA mit einer Periode von 3 aus.

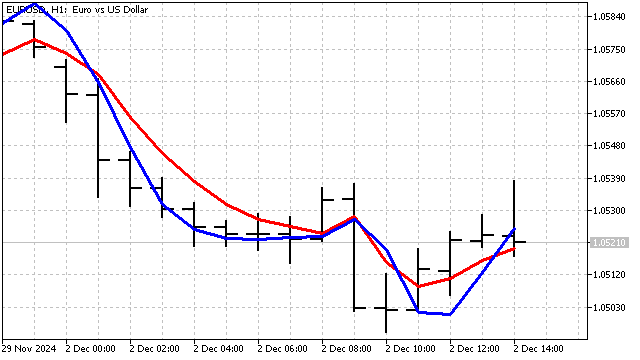
Leider ist das vollständige Unterdrücken des Rauschens eine nahezu unmögliche Aufgabe. Es ist jedoch durchaus möglich, die Trendkomponente in der Preisbewegung zu erkennen. Beide Indikatoren reagieren empfindlich auf Veränderungen der Trendparameter. Gleichzeitig wird ihre Verzögerung auf ein Minimum reduziert. Diese Indikatoren können sowohl unabhängig voneinander zur Preisglättung als auch als Datenquelle für andere Indikatoren verwendet werden.

Trend-Kriterien

Richtiger ist es, Trendkriterien als Zufallskriterien zu bezeichnen. Das Wesen ihrer Anwendung ist sehr einfach. Anhand dieses Kriteriums lässt sich überprüfen, wie zufällig die Preisreihen sind. Wenn das Kriterium zeigt, dass die Reihe nicht zufällig ist, dann kann man sagen, dass es sich um einen Trend handelt. Schauen wir uns die möglichen Kriterien an und wie sie in der technischen Analyse angewendet werden können.

Abbe-Kriterium. Dieses Kriterium basiert auf der Berechnung der Varianz auf zwei verschiedene Arten. Die normale Varianz einer Stichprobe reagiert auf einen Trend. Bei der Varianz von Allan tendiert der Einfluss des Trends gegen Null. Durch den Vergleich dieser Streuungen kann man den Beitrag der Trendkomponente zur Preisänderung abschätzen.

Ich werde die Berechnung dieses Kriteriums für den Handel leicht abändern:

Dieses Kriterium zeigt nur das Vorhandensein eines Trends an. Die Richtung des Trends muss auf andere Weise bestimmt werden.

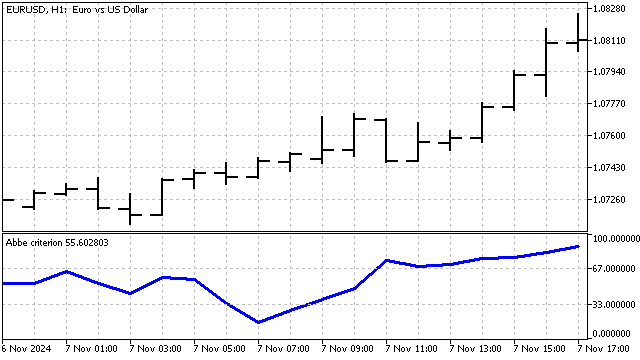
Dieses Kriterium kann helfen, Momente von Trendänderungen zu erkennen.

Kriterium der Anzeichen für eine erste Änderung. Dieses Kriterium ist sehr einfach und intuitiv. Wir nehmen N Preise. Wir unterteilen sie in aufeinanderfolgende Paare, von denen es N-1 gibt. Wir wenden die Vorzeichenfunktion auf jedes Paar an:

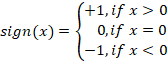
Danach erhalten wir den Kriteriumwert:

Beim RSI wird derselbe Ansatz verwendet, aber die Kursbewegungen nach oben und unten werden getrennt berechnet, ohne die Vorzeichen zu berücksichtigen.

Diese Statistik hat einen Nachteil: Sie unterscheidet nicht nach der Reihenfolge, in der die Vorzeichen erscheinen. Mit anderen Worten: Wir können die Preise vertauschen und erhalten das gleiche Ergebnis. Um diesen Nachteil zu beseitigen, können wir jedem Vorzeichen eine Gewichtung zuweisen, die vom Zeitpunkt seines Auftretens abhängt. Dann sieht die Berechnung des Kriteriums wie folgt aus:

In diesem Fall wird die Vorzeichenfolge eindeutig, und das gleiche Ergebnis ist nur möglich, wenn sich beiden Zeitreihen einander ähneln.

Schauen wir uns an, wie dieses Kriterium für die technische Analyse verwendet werden kann. Die Werte, die mit diesem Kriterium ermittelt werden können, liegen in einem eng begrenzten Rahmen. Die Intuition legt nahe, dass Werte nahe Null häufiger vorkommen. Aber es ist besser, die notwendigen Kontrollen durchzuführen.

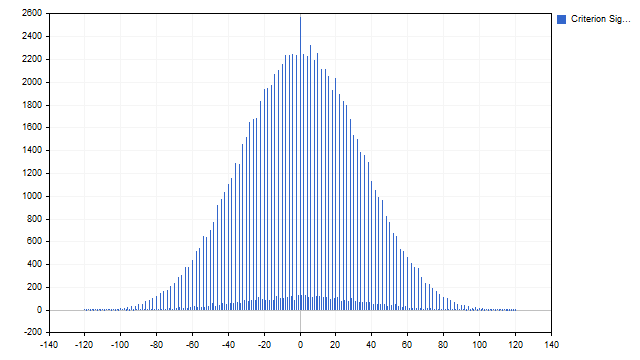
Die Vermutung erwies sich als richtig. In strenger Handelssprache: Wir haben eine empirische Wahrscheinlichkeitsfunktion erhalten. Was lässt sich aus dieser Funktion lernen? Wir können überkaufte/überverkaufte Niveaus erreichen. Ich habe diesen Wert auf 33 % gesetzt – der Indikator sortiert ein Drittel der niedrigsten und höchsten Werte aus. Das Drittel, das in der Mitte bleibt, ist flach. Der Indikator selbst sieht wie folgt aus:

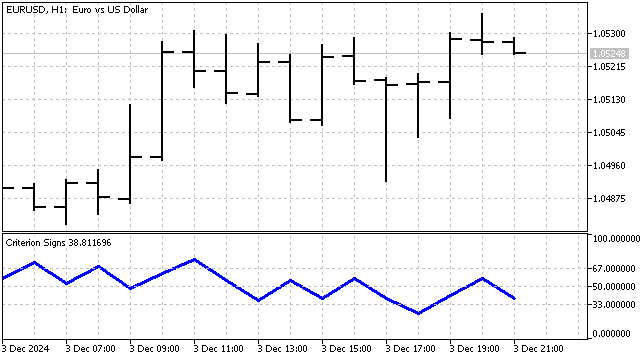
Das Vorzeichenkriterium ist nicht parametrisch. Der Hauptvorteil solcher Kriterien ist ihre Stabilität und Unempfindlichkeit gegenüber plötzlichen Preisänderungen.

Kendall-Kriterium. Auch dieses Kriterium beruht auf der Funktion von Vorzeichen. Diese Funktion wird jedoch ein wenig anders angewandt.

Die Berechnung dieses Kriteriums kann in zwei Schritten durchgeführt werden. Zunächst wird für jeden Preis die Summe der Vorzeichen mit allen vorangehenden Preisen ermittelt:

Anschließend wird die Gesamtsumme dieser Werte ermittelt:

Mit diesem Kriterium vergleichen wir die Anzahl der Kursbewegungen nach oben und unten für alle paarweisen Kurskombinationen. Auf diese Weise können wir die Richtung und Stärke des Trends genauer einschätzen.

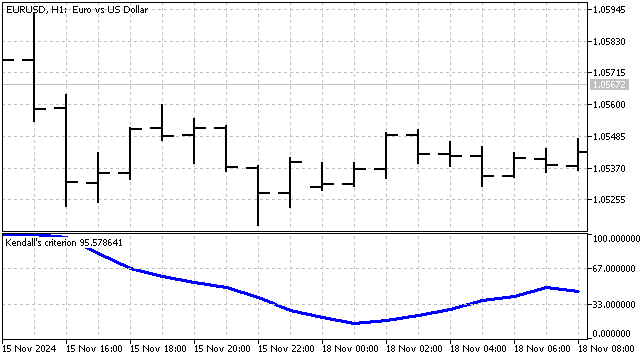
Wald-Wolfowitz-Rangtest. Um dieses Kriterium zu berechnen, müssen wir den Rang der einzelnen Preise kennen. Der Rang ist die Anzahl der Preise, die unter dem aktuellen Preis liegen. Ich nehme zum Beispiel 5 Preiswerte:

Index	0	1	2	3	4
Preis	1.05702	1.05910	1.05783	1.05761	1.05657
Rang	1	4	3	2	0

Der Preis mit Index 0 ist höher als ein Einzelpreis mit Index 4. Das bedeutet, dass der Rang dieses Preises 1 ist. Der Preis mit dem Index 1 ist höher als alle anderen, und sein Rang ist 4. Die Ränge aller anderen Preise werden auf die gleiche Weise berechnet.

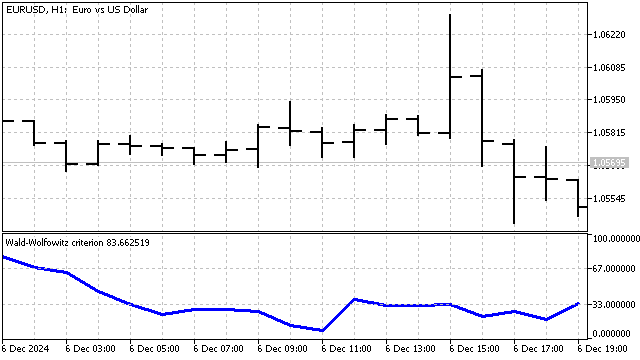
Das Wesen dieses Kriteriums ist sehr einfach – wenn die Preise einen Trend bilden, dann werden auch ihre Ränge organisiert sein. Umgekehrt, wenn die Ränge auf unverständliche Weise durcheinander gebracht werden, dann passiert auch mit den Preisen etwas Unverständliches. In diesem Beispiel sind die Preise teilweise geordnet, was auf das Vorhandensein eines Trends hinweisen kann.

Der Wert dieses Kriteriums wird anhand der folgenden Gleichung berechnet:

Im Wesentlichen ist dieses Kriterium eine robuste Variante der Autokorrelation. Der darauf aufbauende Indikator sieht wie folgt aus:

Foster-Stewart-Kriterium. Dieses Kriterium ermöglicht es, gleichzeitig das Vorhandensein eines Trends bei den Mittelwerten und Varianzen zu bewerten. Sie basiert auf dem Zählen der Anzahl der oberen und unteren Datensätze. Für jede Preisabfrage bestimmen wir den Wert von zwei Variablen H und L.

Die Variable H ist gleich 1, wenn der aktuelle Preis höher ist als alle vorherigen. Die Variable L ist gleich 1, wenn der Preis niedriger ist als alle vorherigen Preise. In allen anderen Fällen sind diese Variablen gleich Null. Die Parameter des Kriteriums werden wie folgt berechnet:

Der Parameter T gibt die Stärke und Richtung des Trends an. Der Parameter D ähnelt dem Abbe-Kriterium und zeigt nur das Vorhandensein eines Trends an. Diese Parameter können entweder einzeln oder in Kombination miteinander verwendet werden.

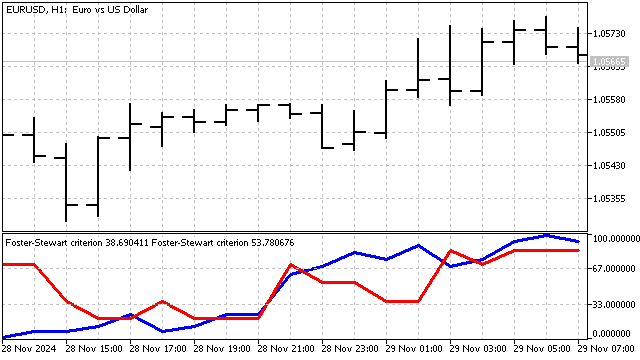
Dieses Kriterium kann modernisiert werden, um beide Parameter gleichzeitig zu berücksichtigen. In der klassischen Version kann ein Trend als etabliert angesehen werden, wenn der Wert von T oder D groß genug ist (natürlich muss man den absoluten Wert für T nehmen). Bei einem Trend weicht das Produkt dieser Parameter also maximal von Null ab. Mit diesem Ansatz können wir die stärksten Trends ermitteln.

Schauen wir uns nun an, wie diese Kriterien beim Handel verwendet werden können.

Handelsstrategien

Leider sagen die Trendkriterien nichts über den Beginn eines Trends aus. Sie zeigen nur an, dass der Trend stattgefunden hat. Diese Eigenschaft kann beim Handel genutzt werden – nach einem starken Trend kann sich die Richtung der Kursbewegung ins Gegenteil verkehren.

Wir können diese Annahme nutzen, um eine einfache Strategie zu entwickeln. Wenn das Trendkriterium einen bestimmten Mindestwert erreicht hat, sollen wir eine Kaufposition eröffnen. Um Verkaufspositionen zu eröffnen, muss das Kriterium seinen Höchstwert erreichen. Mit anderen Worten, es werden Trendkriterien verwendet, um überkaufte/überverkaufte Bedingungen zu bestimmen. Dieser Ansatz sieht vielversprechend aus.

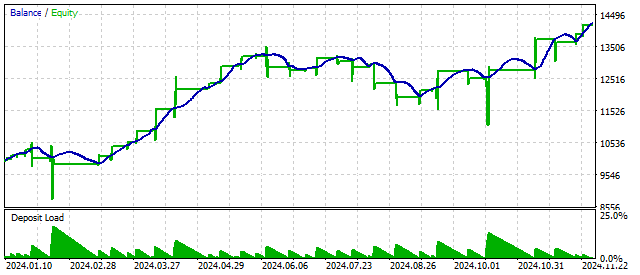
Die Verwendung zusätzlicher Filter kann die Leistung der Strategie verbessern. Das Abbe-Kriterium kann als solcher Filter verwendet werden. Ich möchte Sie daran erinnern, dass dieses Kriterium nur das Vorhandensein eines Trends feststellt. Die Richtung des Trends muss auf andere Weise bestimmt werden. Ich werde zum Beispiel den Trend anhand der durchschnittlichen Geschwindigkeit der Kursbewegung bestimmen:

Liegt der ermittelte Wert über oder unter einem bestimmten Niveau, so betrachte ich den Trend als etabliert. Um diese Annahme zu bestätigen, verwende ich das Abbe-Kriterium. Liegt der Wert über einem bestimmten Niveau, so ist die Trendannahme zutreffend. Ich belasse das Öffnen und Schließen von Positionen wie im vorherigen Beispiel. Das Ergebnis einer solchen Strategie sieht folgendermaßen aus:

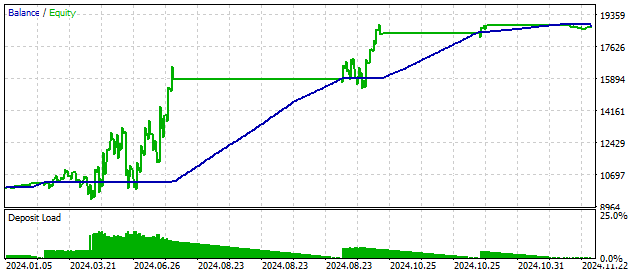
Anhand des Foster-Stewart-Kriteriums lassen sich sowohl das Vorhandensein eines Trends als auch dessen Richtung unmittelbar beurteilen. Mit anderen Worten: Dieses Kriterium kann gleichzeitig als Signal und als Filter dienen. Die Anwendung dieses Kriteriums kann zu den folgenden Ergebnissen führen:

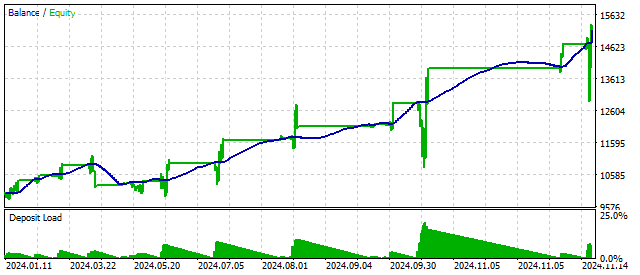
Eine modernisierte Version dieses Kriteriums ermöglicht es uns, andere Ergebnisse zu erzielen.

Die Verwendung von Trendkriterien ist durchaus gerechtfertigt, aber mit einigen Schwierigkeiten verbunden:

• Erstens müssen zusätzliche Filter eingesetzt werden, um die Anzahl der falschen Signale zu reduzieren.
• Zweitens sind gesonderte Vorschriften für die Schließung von Positionen erforderlich, um die Risiken und die Belastung der Einlagen zu verringern.
• Drittens können die Trendkriterien von der Anzahl der verarbeiteten Preise abhängen. Daher kann ihre Anwendung eine vorherige Glättung der Zeitreihen erfordern. Für kleine Zeiträume sollte die Glättung obligatorisch sein.

Schlussfolgerung

Derzeit gibt es mehrere Dutzend Trendkriterien. Die Anwendung dieser Kriterien kann sowohl bei der Analyse von Marktsituationen als auch beim Handel nützlich sein.

Die folgenden Programme wurden bei der Erstellung dieses Artikels verwendet.

Name	Typ	Beschreibung
tSMA	Indikator	Trendanalogie zu SMA iPeriod – Periodenlänge des Indikators, Mindestwert 3
tEMA	Indikator	Trendanalogie des EMA mit Periodenlänge von 3
Abbe-Kriterium	Indikator	Abbe-Kriterium
Vorzeichen-Kriterium	Indikator	Kriterium der Vorzeichen für erste Änderungen
scr Vorzeichen-Kriterium	Skript	Das Skript ermöglicht die Auswertung der Verteilung der Vorzeichenkriterienwerte iPeriode – Periodenlänge des Kriteriums Bildschirmfoto – ermöglicht das Speichern des Bildes im Ordner der Dateien
Kendall-Kriterium	Indikator	Kendall-Kriterium
Foster-Stewart-Kriterium	Indikator	Foster-Stewart-Kriterium Typ – Parameterauswahl iPeriode – Kriterium der Periodenlänge
Foster-Stewart-Kriterium I	Indikator	Eine modernisierte Version des Foster-Stewart-Kriteriums
Wald-Wolfowitz-Kriterium	Indikator	Wald-Wolfowitz-Kriterium
EA 3-Kriterien	EA	Der EA handelt nach 3 Kriterien Typ – Kriterium Auswahl Period Kriterium - Periodenlänge Kriterium Ebene – Antwortniveau, zulässige Werte 1 – 49
EA-Abbe-Kriterium	EA	Durchschnittliche Geschwindigkeit Abbe-Niveau – Kriterium Niveau, zulässige Werte 1 – 99
EA Foster-Stewart-Kriterium	EA	T-Ebene – Niveau des Trendparameters, zulässige Werte 1 – 49 D-Pegel – Niveau des Dispersionsparameters, zulässige Werte 1 – 99
EA Foster-Stewart-Kriterium I	EA	Ebene – Kriteriumsebene, zulässige Werte 1 – 49