
Neuronale Netze im Handel: Ein Multi-Agent Self-Adaptive Modell (letzter Teil)
Einführung
Im vorangegangenen Artikel haben wir den MASA-Rahmen vorgestellt – ein Multiagentensystem, das auf einer einzigartigen Integration interagierender Agenten beruht. Innerhalb der MASA-Architektur optimiert der RL-Agent auf der Grundlage von Reinforcement Learning (RL) die Gesamtrendite eines Anlageportfolios. Gleichzeitig versucht ein alternativer, auf einem Algorithmus basierender Agent, das vom RL-Agenten vorgeschlagene Portfolio zu optimieren, wobei der Schwerpunkt auf der Minimierung potenzieller Risiken liegt.
Dank einer klaren Aufgabenteilung zwischen den Akteuren lernt das Modell ständig dazu und passt sich an das zugrunde liegende Finanzmarktumfeld an. Das Multi-Agenten-System MASA führt zu ausgewogeneren Portfolios, sowohl in Bezug auf die Rentabilität als auch auf die Risikoexposition.
Die ursprüngliche Visualisierung von MASA ist unten zu sehen.
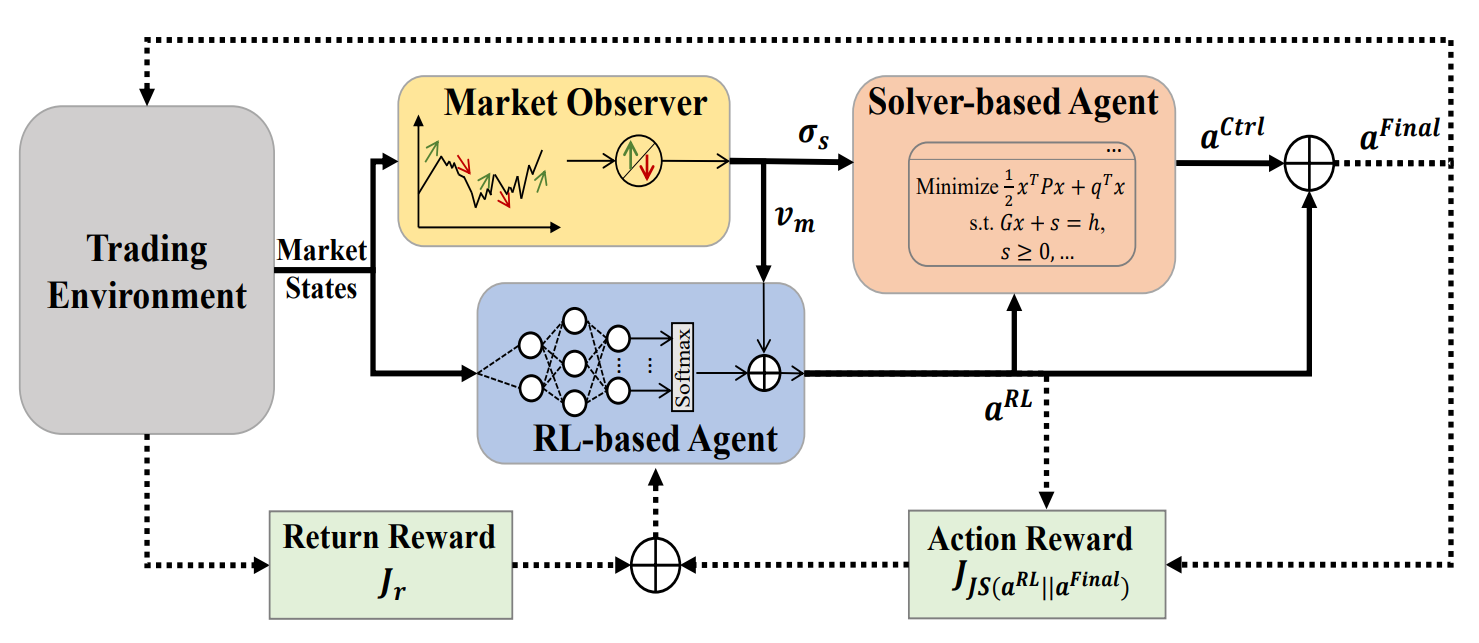
Im praktischen Teil des vorangegangenen Artikels haben wir die Algorithmen untersucht, die die Funktionalität der einzelnen Agenten von MASA implementieren, die als separate Objekte entwickelt wurden. Heute setzen wir diese Arbeit fort.
1. Die MASA-Verbundschicht
Im vorangegangenen Artikel haben wir drei separate Agenten erstellt, die jeweils eine bestimmte Funktion innerhalb von MASA haben. Jetzt werden wir sie in einem einzigen System zusammenfassen. Zu diesem Zweck erstellen wir ein neues Objekt CNeuronMASA, dessen Struktur unten dargestellt ist.
class CNeuronMASA : public CNeuronBaseSAMOCL { protected: CNeuronMarketObserver cMarketObserver; CNeuronRevINDenormOCL cRevIN; CNeuronRLAgent cRLAgent; CNeuronControlAgent cControlAgent; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMASA(void) {}; ~CNeuronMASA(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers_mo, uint forecast, uint segments_rl, float rho, uint layers_rl, uint n_actions, uint heads_contr, uint layers_contr, int NormLayer, CNeuronBatchNormOCL *normLayer, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronMASA; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; virtual void SetActivationFunction(ENUM_ACTIVATION value) override; //--- virtual int GetNormLayer(void) { return cRevIN.GetNormLayer(); } virtual bool SetNormLayer(int NormLayer, CNeuronBatchNormOCL *normLayer); };
Mehrere Aspekte der Struktur dieses neuen Objekts verdienen besondere Aufmerksamkeit.
Zunächst fällt die relativ große Anzahl von Parametern bei der Initialisierungsmethode Init auf. Dies ist darauf zurückzuführen, dass alle drei Akteure mit ihren jeweiligen architektonischen Besonderheiten untergebracht werden müssen.
Eine weitere Nuance widerspricht der allgemeinen Philosophie unserer Bibliothek. Die Methode des Vorwärtsdurchlaufs hat eine einzige Eingangsquelle, was mit dem MASA-Rahmenwerk vereinbar ist. Sowohl der RL-Agent als auch der Marktbeobachtungsagent erhalten den aktuellen Marktzustand als Input. Bei der Gradientenverteilungsmethode führen wir jedoch eine zweite Datenquelle ein – eine, die sowohl im Vorwärtsdurchlauf als auch in MASA, wie ursprünglich beschrieben, fehlt.
Diese unkonventionelle Lösung wurde gewählt, um einen alternativen Trainingsprozess für den Marktbeobachtungsagenten zu ermöglichen. Zu diesem Zweck haben wir auch ein internes Objekt für die Umkehrnormalisierung der Daten hinzugefügt. Wir werden diese Entscheidung bei der Entwicklung unserer Klassenmethoden noch ausführlicher diskutieren.
Alle internen Objekte unserer neuen Klasse werden als statisch deklariert, sodass wir den Konstruktor und Destruktor leer lassen können. Die Initialisierung einer neuen Klasseninstanz wird ausschließlich von der Methode Init durchgeführt. Wie bereits erwähnt, benötigt diese Methode viele Parameter, die jedoch im Wesentlichen die Initialisierungsparameter der zuvor erstellten Agenten duplizieren.
bool CNeuronMASA::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads_mo, uint layers_mo, uint forecast, uint segments_rl, float rho, uint layers_rl, uint n_actions, uint heads_contr, uint layers_contr, int NormLayer, CNeuronBatchNormOCL *normLayer, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseSAMOCL::Init(numOutputs, myIndex, open_cl, n_actions, rho, optimization_type, batch)) return false;
Innerhalb der Methode rufen wir zunächst die gleichnamige Methode der übergeordneten Klasse auf. In diesem Fall ist die übergeordnete Klasse eine vollständig verbundene neuronale Schicht mit SAM-Optimierung.
Erinnern Sie sich, dass die endgültige Ausgabe von MASA vom Controller-Agenten als Aktionstensor erzeugt wird. Dementsprechend stellen wir bei der Initialisierung der Elternklasse die Größe der Ebene so ein, dass sie dem Aktionsraum des Akteurs entspricht.
Als Nächstes initialisieren wir unsere Agenten nacheinander. Der erste ist der Agent für die Marktbeobachtung.
Es erhält den aktuellen Marktzustandstensor als Eingabe und liefert Prognosewerte im gleichen multimodalen Sequenzformat für den angegebenen Planungshorizont.
//--- Market Observation if(!cMarketObserver.Init(0, 0, OpenCL, window, window_key, units_count, heads_mo, layers_mo, forecast, optimization, iBatch)) return false; if(!cRevIN.Init(0, 1, OpenCL, cMarketObserver.Neurons(), NormLayer, normLayer)) return false;
Unmittelbar danach initialisieren wir die Umkehrnormierungsschicht, deren Größe dem Output des Marktbeobachtungsagenten entspricht.
Anschließend initialisieren wir den RL-Agenten, der ebenfalls den Marktzustandstensor als Input erhält. Aber es gibt den Aktionstensor des Akteurs in Übereinstimmung mit der erlernten Politik zurück.
//--- RL Agent if(!cRLAgent.Init(0, 2, OpenCL, window, units_count, segments_rl, fRho, layers_rl, n_actions, optimization, iBatch)) return false;
Schließlich initialisieren wir den Controller-Agenten, der die Ausgaben der beiden vorherigen Agenten übernimmt und den angepassten Aktions-Tensor des Akteurs erzeugt.
if(!cControlAgent.Init(0, 3, OpenCL, 3, window_key, n_actions / 3, heads_contr, window, forecast, layers_contr, optimization, iBatch)) return false;
Es ist wichtig zu beachten, dass in unserer Implementierung der RL-Agent und der Controller-Agent den Aktionstensor des Akteurs unterschiedlich interpretieren. Die Unterscheidung ist nicht nur funktional.
Für die Ausgabe des RL-Agenten wird eine vollständig verknüpfte Schicht verwendet, die jedes Element des Aktionstensors auf der Grundlage der Marktanalyse und der erlernten Strategie unabhängig erzeugt. Wir wissen jedoch, dass sich entgegengesetzte Handlungen (Kauf und Verkauf desselben Vermögenswerts) gegenseitig ausschließen. Außerdem belegen die Handelsparameter in jeder Richtung drei Elemente im Aktionsvektor.
Unter Berücksichtigung dieser Tatsache weisen wir den Controller-Agenten an, den Aktionstensor als multimodale Sequenz zu interpretieren, bei der jedes Element einen durch einen 3-Elemente-Vektor beschriebenen Handel darstellt. Auf diese Weise kann der Controller-Agent die Risiken für jede Handelsrichtung getrennt bewerten.
Am Ende der Initialisierungsmethode werden Zeiger auf externe Schnittstellenpuffer neu zugewiesen und die Sigmoid-Aktivierungsfunktion als Standard eingestellt.
if(!SetOutput(cControlAgent.getOutput(), true) || !SetGradient(cControlAgent.getGradient(), true)) return false; SetActivationFunction(SIGMOID); //--- return true; }
Die Methode gibt dann ein logisches Flag zurück, das die erfolgreiche Ausführung anzeigt.
Zur Aktivierungsfunktion sollten einige Worte gesagt werden. Die Ausgabe unserer Klasse ist der Aktionstensor des Akteurs, der zunächst vom RL-Agenten erzeugt und dann vom Controller-Agenten angepasst wird. Es liegt auf der Hand, dass die Ausgabebereiche sowohl für die Bearbeiter als auch für die Klasse selbst konsistent sein müssen. Aus diesem Grund setzen wir die Aktivierungsfunktion außer Kraft, um die Synchronisierung aller Komponenten zu gewährleisten.
void CNeuronMASA::SetActivationFunction(ENUM_ACTIVATION value) { cControlAgent.SetActivationFunction(value); cRLAgent.SetActivationFunction((ENUM_ACTIVATION)cControlAgent.Activation()); CNeuronBaseSAMOCL::SetActivationFunction((ENUM_ACTIVATION)cControlAgent.Activation()); }
Nachdem die Initialisierung abgeschlossen ist, gehen wir zum Algorithmus des Vorwärtsdurchlaufs über. Dieser Teil ist ganz einfach. Wir rufen einfach die Methoden der Vorwärtsdurchläufe unserer Agenten nacheinander auf. Zunächst erhalten wir die Ergebnisse der Marktanalyse und den vorläufigen Aktionstensor.
bool CNeuronMASA::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cMarketObserver.FeedForward(NeuronOCL.AsObject())) return false; if(!cRLAgent.FeedForward(NeuronOCL.AsObject())) return false;
Anschließend geben wir diese Ergebnisse an den Controller-Agenten weiter, um die endgültige Entscheidung zu treffen.
if(!cControlAgent.FeedForward(cRLAgent.AsObject(), cMarketObserver.getOutput())) return false; //--- return true; }
Die Methode endet mit der Rückgabe eines logischen Ausführungsergebnisses.
Wenn Sie sich noch einmal die frühere Visualisierung von MASA ansehen, werden Sie feststellen, dass der endgültige Aktionsvektor als die Summe der Ausgaben des RL-Agenten und des Controller-Agenten dargestellt wird. In unserer Implementierung behandeln wir jedoch den Output des Controller-Agenten als das Endergebnis, ohne die Verbindungen der Residuen zum RL-Agenten. Erinnern Sie sich an die Architektur unseres Controller-Agenten?
Unser Controller-Agent ist als Transformer-Decoder implementiert. Wie Sie wissen, enthält die Transformer-Architektur bereits Verbindungen der Residuen sowohl in den Aufmerksamkeitsmodulen als auch im Block von FeedForward. Daher ist der restliche Informationsfluss vom RL-Agenten in den Controller-Agenten integriert, und zusätzliche Verbindungen sind nicht erforderlich.
Wir wenden uns nun dem Verfahren der Backpropagation, dem Rückwärtsdurchlauf zu. Speziell für den Algorithmus zur Verteilung von Fehlergradienten (calcInputGradients). Hier kommen einige unserer früheren Nicht-Standard-Entscheidungen, die wir im CNeuronMASA begonnen haben, ins Spiel.
Schauen wir uns zunächst die erwarteten Ergebnisse unserer Agenten an. Zwei unserer Agenten geben den Aktionstensor des Akteurs zurück. Es ist logisch, beim Training die Menge der optimalen Handlungen als Ziel (beim überwachten Lernen) oder ihre Projektion auf Belohnungen (beim verstärkenden Lernen) zu verwenden.
Der Marktbeobachtungsagent gibt jedoch Prognosewerte einer multimodalen Zeitreihe für das analysierte Finanzinstrument aus. Dies wirft die Frage nach den Trainingszielen für dieses Mittel auf. Wir könnten Gradienten durch den Controller-Agenten leiten, um indirekt die Entscheidung des Marktbeobachters zu beeinflussen, den Output des RL-Agenten anzupassen. Ein solcher Ansatz würde jedoch nicht mit dem Ziel der Prognose übereinstimmen.
Eine angemessenere Lösung wäre es, den Marktbeobachter-Agenten separat auf die Vorhersage der Zeitreihen zu trainieren, wie wir es zuvor mit dem Account State Encoder getan haben. Die Herausforderung besteht jedoch darin, dass der Beobachter nun in unser zusammengesetztes Modell integriert ist. Dies macht ein separates Training unpraktisch. Dies bringt uns auf die Idee, zwei Trainingsziele auf der Ebene der Schichten anzubieten. Das ist eine grundlegende Änderung des Arbeitsablaufs in unserer Bibliothek. Dies würde eine umfassende Neugestaltung erfordern.
Um dies zu vermeiden, können wir eine nicht standardisierte Lösung wählen. Verwenden wir den zweiten Mechanismus der Eingabequelle, um eine zusätzliche Gruppe von Zielwerten zu liefern. Wir definieren also die Methode der Fehlergradientenverteilung unter Verwendung von zwei Eingangsdatenquellen neu, nur dass dieses Mal die Puffer des zweiten Objekts verwendet werden, um den Zielwerttensor an den Marktbeobachtungsagenten weiterzugeben.
bool CNeuronMASA::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1) { if(!NeuronOCL) return false;
Dieser Ansatz hat jedoch seine Tücken, vor allem die Vergleichbarkeit der Daten. Normalerweise füttern wir das Modell mit rohen, unbearbeiteten Eingabedaten, die wir vom Terminal erhalten. Diese Daten vom Terminal werden in der Vorverarbeitung normalisiert, und alle neuronalen Schichten arbeiten mit normalisierten Werten. Dies gilt auch für das CNeuronMASA-Objekt, das wir erstellen. Die Ausgabe des Beobachteragenten wird daher ebenfalls normalisiert, um die Verarbeitung durch den Controller-Agenten zu erleichtern. Die zukünftigen Ist-Werte der analysierten multimodalen Zeitreihen (unsere Ziele) liegen dagegen nur in Rohform vor. Um dieses Problem zu lösen, haben wir die Umkehrnormierungsschicht eingeführt, die wir im Vorwärtsdurchlauf nicht verwendet haben. Sie wird jedoch bei der Gradientenverteilung eingesetzt. Es wendet die statistischen Parameter der Eingabedaten auf die Vorhersagen des Beobachters an.
if(!cRevIN.FeedForward(cMarketObserver.AsObject())) return false;
Dies ermöglicht einen validen Vergleich mit Rohzielen und eine korrekte Gradientenfortpflanzung.
if(!cRevIN.FeedForward(cMarketObserver.AsObject())) return false; float error = 1.0f; if(!cRevIN.calcOutputGradients(SecondGradient, error)) return false; if(!cMarketObserver.calcHiddenGradients(cRevIN.AsObject())) return false;
Danach wird der Gradient des Controller-Agenten zwischen dem RL-Agenten und dem Marktbeobachter aufgeteilt. Um die zuvor angesammelten Gradienten zu erhalten, speichern wir den Fehler des Beobachters in einem Puffer und summieren dann die Beiträge beider Informationsflüsse.
if(!cRLAgent.calcHiddenGradients(cControlAgent.AsObject(), cMarketObserver.getOutput(), cMarketObserver.getPrevOutput(), (ENUM_ACTIVATION)cMarketObserver.Activation()) || !SumAndNormilize(cMarketObserver.getGradient(), cMarketObserver.getPrevOutput(), cMarketObserver.getGradient(), 1, false, 0, 0, 0, 1)) return false;
Ein weiterer wichtiger Punkt: Sowohl der RL-Agent als auch der Controller-Agent geben Aktions-Tensoren des Akteurs zurück. Er gibt sie auf der Grundlage der Ergebnisse seiner eigenen Analyse der aktuellen Marktlage zurück. Und letztere – nach Bewertung der Risiken des bereitgestellten Aktionstensors unter Berücksichtigung der vom Marktbeobachtungsagenten erhaltenen Prognosewerte für die bevorstehende Preisbewegung. Im Idealfall sollten ihre Ergebnisse übereinstimmen. Daher führen wir einen Fehlerterm für den RL-Agenten ein, der die Abweichung von den Ergebnissen des Controller-Agenten darstellt.
CBufferFloat *temp = cRLAgent.getGradient(); if(!cRLAgent.SetGradient(cRLAgent.getPrevOutput(), false) || !cRLAgent.calcOutputGradients(cControlAgent.getOutput(), error) || !SumAndNormilize(temp, cRLAgent.getPrevOutput(), temp, 1, false, 0, 0, 0, 1) || !cRLAgent.SetGradient(temp, false)) return false;
Auch hier gilt, dass diese Fehleroperationen die zuvor aufgelaufenen Gradienten nicht löschen dürfen. Um dies sicherzustellen, verwenden wir Puffersubstitution und Summierung über beide Datenströme.
Nachdem die Gradienten auf alle internen Agenten verteilt wurden, besteht der nächste Schritt darin, sie an die Eingangsebene zurückzugeben. Auch hier müssen wir Gradienten aus zwei Quellen aggregieren: dem RL-Agenten und dem Marktbeobachtungsagenten. Wie zuvor propagieren wir zunächst den Gradienten des Beobachters.
if(!NeuronOCL.calcHiddenGradients(cMarketObserver.AsObject())) return false;
Dann ersetzen wir die Puffer und propagieren den Gradienten des RL-Agenten.
temp = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(NeuronOCL.getPrevOutput(), false) || !NeuronOCL.calcOutputGradients(cRLAgent.getOutput(), error) || !SumAndNormilize(temp, NeuronOCL.getPrevOutput(), temp, 1, false, 0, 0, 0, 1) || !NeuronOCL.SetGradient(temp, false)) return false; //--- return true; }
Wir addieren beide Beiträge und stellen den ursprünglichen Pufferzustand wieder her.
In diesem Stadium wurde der Fehlergradient auf alle Komponenten entsprechend ihrem Beitrag zur Leistung des Modells verteilt. Der letzte Schritt besteht darin, die Modellparameter zu aktualisieren, um den Fehler zu minimieren. Diese Funktion wird in der Methode updateInputWeights ausgeführt. Der Algorithmus der Methode ist recht einfach. Wir rufen einfach die Methoden der Vorwärtsdurchläufe unserer Agenten nacheinander auf. Wir werden hier nicht ins Detail gehen. Man muss nur bedenken, dass alle Agenten die SAM-Optimierung nutzen. Daher müssen diese Aktualisierungen in umgekehrter Reihenfolge des Vorwärtsdurchlaufs ausgeführt werden.
Damit schließen wir unsere Diskussion über die Algorithmen hinter den neuen Methoden der Klasse CNeuronMASA ab. Der vollständige Code dieses Objekts und alle seine Methoden werden im Anhang zur weiteren Untersuchung bereitgestellt.
2. Modell der Architektur
Nachdem wir nun die Konstruktion neuer Objekte abgeschlossen haben, wenden wir uns der Architektur der trainierbaren Modelle zu. Auch hier haben wir einige Änderungen vorgenommen und einige unkonventionelle Lösungen eingeführt.
Erstens haben wir auf die Verwendung eines separaten Encoders des Umgebungszustands verzichtet. Dies ist kein Zufall. In unserer Klasse CNeuronMASA führen bereits zwei Agenten parallel eine Analyse der aktuellen Umgebung durch.
Die zweite Änderung betrifft die Einbeziehung von Kontostandsinformationen. Zuvor haben wir diese Daten in das Akteursmodell als zweite Eingabequelle eingespeist. Nun ist dieser Eingangskanal aber durch die Zielwerte des Marktbeobachteragenten belegt. Um dieses Problem zu lösen, haben wir die Kontostandsinformationen einfach an das Ende des Umgebungszustandstensors angehängt.
Somit erhält der Akteur nun einen kombinierten Eingabetensor, der sowohl aus der Beschreibung des Umgebungszustands als auch aus der Kontostandsinformation besteht.
bool CreateDescriptions(CArrayObj *&actor, CArrayObj *&critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } //--- Actor actor.Clear(); //--- if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr + AccountDescr); descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Diese rohen Eingabedaten werden zunächst von einer Batch-Normalisierungsschicht verarbeitet.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
In diesem Stadium ist zu beachten, dass der Zustandsvektor des Kontos die Struktur des Zustandstensors der Umgebung stört. Ihre Länge kann von der Beschreibungsgröße eines einzelnen Elements in der multimodalen Sequenz der analysierten Zeitreihe abweichen, was mit der Struktur der von uns verwendeten Aufmerksamkeitsmodule nicht vereinbar ist. Um dieses Problem zu lösen, wandeln wir die Eingabedaten mithilfe einer trainierbaren Einbettungsschicht in eine Matrixform um.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronEmbeddingOCL; descr.count = 1; descr.window_out = BarDescr; { int temp[HistoryBars + 1]; if(ArrayInitialize(temp, BarDescr) < (HistoryBars + 1)) return false; temp[HistoryBars] = AccountDescr; if(ArrayCopy(descr.windows, temp) < (HistoryBars + 1)) return false; } descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Diese Schicht unterteilt den Eingangsvektor in Blöcke fester Länge und projiziert jeden Block in einen Unterraum mit vordefinierter Dimensionalität, unabhängig von der ursprünglichen Größe des Blocks. Jeder Block hat seine eigene, unabhängig trainierbare Projektionsmatrix.
Wir wissen, dass der größte Teil des Eingabetensors aus homogenen Vektoren besteht, die einzelne Umgebungszustände (Balken) beschreiben, und dass nur das letzte Element (Kontostand) unterschiedlich ist. Daher initialisieren wir die Sequenz mit Analysefenstern fester Länge und passen dann nur die Größe des letzten Elements an.
Wichtig ist, dass wir die Ausgabegröße jedes eingebetteten Sequenzelements auf die Größe einer einzelnen Balkenbeschreibung festlegen. Das ist eine sehr wichtige Sache. Dies ist von entscheidender Bedeutung: Wir könnten theoretisch jede beliebige Dimensionalität für die Einbettungsausgabe wählen. Der Marktbeobachtungsagent liefert jedoch Prognosen in der ursprünglichen Eingangsdimension. Daher müssen die prognostizierten multimodalen Zeitreihen mit den beim Training verwendeten Zielwerten übereinstimmen, die mit den Rohdaten identisch sind. Der Kreis schließt sich.
Die Verwendung trainierbarer Einbettungen bietet implizit eine Positionskodierung. Wie wir bereits erwähnt haben, hat jedes Sequenzelement seine eigene Projektionsmatrix. Auf diese Weise werden identische Vektoren an unterschiedlichen Positionen in unterschiedliche Unterraumdarstellungen projiziert, sodass sie bei der Analyse unterscheidbar bleiben.
Die resultierenden Einbettungen werden dann an unser Rahmenobjekt MASA übergeben. Hier sind einige wichtige Details zu beachten.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMASA; //--- Windows { int temp[] = {BarDescr, NForecast, 2 * NActions}; if(ArrayCopy(descr.windows, temp) < (int)temp.Size()) return false; } descr.window_out = 32; descr.count = HistoryBars+1; //--- Heads { int temp[] = {4, 4}; if(ArrayCopy(descr.heads, temp) < (int)temp.Size()) return false; } //--- Layers { int temp[] = {3, 3, 3}; if(ArrayCopy(descr.units, temp) < (int)temp.Size()) return false; } descr.window = BarDescr; descr.probability = Rho; descr.step = 1; // Normalization layer descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
In dem dynamischen Array descr.windows werden die wichtigsten Parameter der von den internen Agenten analysierten Sequenzen angegeben. Hier geben wir nacheinander die Dimensionalität eines Elements der Eingabesequenz, den Prognosehorizont der nachfolgenden Zeitreihe und den Aktionsraum des Akteurs an.
Besondere Aufmerksamkeit sollte dem letzten Parameter gewidmet werden. Bei der Konzeption der internen Agentenarchitektur haben wir zunächst eine direkte Abhängigkeit zwischen dem Zustand der Umgebung und der erzeugten Aktion beschrieben und dabei die Stochastizität im Verhalten des Akteurs ausgeschlossen. In der Praxis wenden wir jedoch eine stochastische Akteurspolitik an. Um dies zu erreichen, verdoppeln wir die Dimensionalität des Ausgangsaktionsraums von dem System MASA. Dies entspricht dem Ansatz, den wir zuvor bei der Organisation der stochastischen Politik verwendet haben. Der resultierende Aktionsvektor wird logischerweise in zwei gleiche Teile geteilt, die die Mittelwerte und Varianzen des Aktionsraums des Akteurs unter dem analysierten Umgebungszustand darstellen. Aus diesem Grund ist die Aktivierungsfunktion dieser Schicht deaktiviert.
Jedes von uns verwendete Aufmerksamkeitsmodul verfügt über vier Köpfe. Und jeder Agent enthält drei Encoder/Decoder-Schichten.
Wie bereits erwähnt, wird die Ausgabe des MASA-Rahmens in die latente Zustandsschicht eines Variations-Autoencoders geleitet, der stochastische Akteurshandlungen entsprechend der vorgegebenen Verteilung erzeugt.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Der resultierende Aktionsvektor wird mit Hilfe einer Faltungsschicht und einer anschließenden Sigmoid-Aktivierungsfunktion in den gewünschten Bereich projiziert.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvSAMOCL; descr.count = NActions / 3; descr.window = 3; descr.step = 3; descr.window_out = 3; descr.activation = SIGMOID; descr.optimization = ADAM; descr.probability = Rho; if(!actor.Add(descr)) { delete descr; return false; }
Bei der endgültigen Ausgabe des Modells wenden wir eine Frequenzabgleichsschicht an, um die Ergebnisse des Modells mit den Zielwerten abzugleichen.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NActions; descr.count = 1; descr.step = int(false); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Der nächste Schritt ist der Aufbau der Architektur des Kritikers. Im Großen und Ganzen ähnelt er den früheren Entwürfen. Allerdings gibt es eine wichtige Änderung: Durch die Abschaffung des separaten Environment State Encoders mussten wir dem Kritiker-Modell direkt einen Block zur Umgebungsanalyse hinzufügen. Hierfür verwenden wir das PSformer-Framework, um den aktuellen Zustand zu analysieren. Insbesondere enthalten die Eingabedaten des Kritikers keine Informationen zum Kontostand. Meines Erachtens haben diese Informationen für den Kritiker wenig Wert. Die Ergebnisse des Handels hängen in erster Linie von den Marktbedingungen ab, nicht vom Kontostand zum Zeitpunkt des Abschlusses.
Man könnte argumentieren, dass übermäßig große oder kleine Handelsvolumina zu Ausführungsfehlern führen könnten, die keine offene Position zur Folge haben. Die Bestimmung des Handelsvolumens liegt jedoch in der Verantwortung des Akteurs. Sollte der Kritiker solche Grenzfälle behandeln? Dies ist im Wesentlichen eine Frage der funktionalen Trennung zwischen den Modellen.
Ein weiterer Aspekt sind die offenen Positionen und die kumulierten Gewinne oder Verluste, d. h. die Ergebnisse vergangener Handelsgeschäfte. Der Kritiker bewertet den aktuellen Handel (oder die Politik), nicht die früheren Ergebnisse. Selbst wenn wir davon ausgehen, dass der Kritiker die Politik als Ganzes bewertet, erstreckt sich seine Bewertung auf das Ende der Episode, nicht rückwirkend.
Daher erhält der Kritiker nur den aktuellen Zustand der Umgebung als Eingabe.
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Wie zuvor werden die rohen Eingabedaten in einer Batch-Normalisierungsschicht verarbeitet.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Dann wird es in 3 aufeinanderfolgende Schichten des PSformer-Frameworks eingespeist.
//--- layer 2 - 4 for(int i = 0; i < 3; i++) { if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronPSformer; descr.window = BarDescr; descr.count = HistoryBars; descr.window_out = Segments; descr.probability = Rho; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } }
Als Nächstes werden sukzessive Faltungsschichten und voll verknüpfte Schichten verwendet, um die Dimensionalität des resultierenden Tensors zu reduzieren.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvSAMOCL; descr.count = HistoryBars; descr.window = BarDescr; descr.step = BarDescr; descr.window_out = int(LatentCount / descr.count); descr.probability = Rho; descr.activation = GELU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseSAMOCL; descr.count = LatentCount; descr.probability = Rho; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Wir kombinieren die Ergebnisse der Umgebungsanalyse mit den Aktionen des Agenten in der Datenverkettungsschicht.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = LatentCount; descr.step = NActions; descr.activation = GELU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
Danach folgt das Entscheidungsfindungsmodul, das aus 4 vollständig verbundenen Schichten besteht.
//--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseSAMOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; descr.probability = Rho; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseSAMOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; descr.probability = Rho; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 10 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseSAMOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; descr.probability = Rho; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 11 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseSAMOCL; descr.count = NRewards; descr.activation = None; descr.optimization = ADAM; descr.probability = Rho; if(!critic.Add(descr)) { delete descr; return false; }
In der Ausgabestufe verwenden wir eine Frequenzabgleichsschicht, um die Ergebnisse des Modells mit den Zielwerten in Einklang zu bringen.
//--- layer 12 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = NRewards; descr.count = 1; descr.step = int(false); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
Nachdem wir die Architekturen der beiden trainierbaren Modelle erfolgreich definiert haben, schließen wir die Methode ab, indem wir ein logisches Ergebnis an das aufrufende Programm zurückgeben.
3. Modellschulungsprogramm
Wir nähern uns nun zuversichtlich dem logischen Abschluss unserer Arbeit und wenden uns der Konstruktion des Modellschulungsprogramms zu. Natürlich hat das Entfernen eines der trainierbaren Modelle seine Spuren im Trainingsalgorithmus hinterlassen. Darüber hinaus haben wir uns bei der Entwicklung von MASA darauf geeinigt, den Informationsstrom aus der zweiten Datenquelle als zusätzlichen Strom von Zielwerten zu verwenden. In diesem Sinne gehen wir direkt zum Trainingsalgorithmus über, der in der Methode Train implementiert ist.
Wie zuvor beginnen wir mit einigen vorbereitenden Arbeiten. Aus dem Erfahrungswiederholungspuffer bilden wir einen Vektor von Bahnauswahlwahrscheinlichkeiten, gewichtet nach der Effektivität vergangener Läufe.
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9); //--- vector<float> result, target, state; bool Stop = false; //--- uint ticks = GetTickCount();
Anschließend deklarieren wir die erforderlichen lokalen Variablen.
Als Nächstes richten wir die Trainingsschleife ein, wobei die Anzahl der Iterationen durch die externen Parameter unseres Expert Advisors bestimmt wird.
for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++) { int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast)); if(i <= 0) { iter --; continue; } if(!state.Assign(Buffer[tr].States[i].state) || MathAbs(state).Sum() == 0 || !bState.AssignArray(state)) { iter --; continue; } if(!state.Assign(Buffer[tr].States[i+NForecast].state) || !state.Resize(NForecast*BarDescr) || MathAbs(state).Sum() == 0 || !bForecast.AssignArray(state)) { iter --; continue; }
Innerhalb der Schleife werden eine Trajektorie und ihr Umgebungszustand erfasst. An dieser Stelle überprüfen wir auch, ob sowohl historische als auch zukünftige Daten in der erforderlichen Analysetiefe und mit dem erforderlichen Prognosehorizont vorhanden sind. Wenn die Prüfung an irgendeinem Punkt fehlschlägt, wird eine neue Trajektorie und ein neuer Zustand gewählt.
Sobald die erforderlichen Daten verfügbar sind, werden sie in die entsprechenden Puffer übertragen. Die Informationen zum Kontostand werden dann zum Zeitpunkt der Analyse an die Zustandsbeschreibung der Umgebung angehängt.
//--- Account float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; bState.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); bState.Add(Buffer[tr].States[i].account[1] / PrevBalance); bState.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); bState.Add(Buffer[tr].States[i].account[2]); bState.Add(Buffer[tr].States[i].account[3]); bState.Add(Buffer[tr].States[i].account[4] / PrevBalance); bState.Add(Buffer[tr].States[i].account[5] / PrevBalance); bState.Add(Buffer[tr].States[i].account[6] / PrevBalance);
Außerdem fügen wir dem analysierten Umgebungsstatus einen Zeitstempel hinzu.
//--- double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); bState.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); bState.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); bState.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); bState.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
Nach der Vorbereitung der Eingabedaten beginnen wir mit dem Modelltraining. Der erste Schritt ist das Training des Kritikers. Der Kritiker erhält als Input den analysierten Umgebungszustand und den Aktionsvektor, den der Actor bei der Erhebung der Trainingsstichprobe tatsächlich ausgeführt hat. Wir nutzen diese Aktionen, weil wir bereits wissen, welche realen Belohnungen die Umgebungs für sie bereithält. Wir führen einen Vorwärtsdurchlauf durch, bei dem wir die vergangenen Aktionen des Akteurs auswerten.
//--- Critic bActions.AssignArray(Buffer[tr].States[i].action); Critic.TrainMode(true); if(!Critic.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)GetPointer(bActions))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Wie erwartet, wollen wir, dass der Ausgang des Vorwärtsdurchlauf vom Kritiker ein Belohnungs-Tensor ist, der den tatsächlich beobachteten Belohnungen nahe kommt. Daher extrahieren wir die tatsächliche Belohnung aus dem Wiederholungspuffer und führen den Rückwärtsdurchlauf-Prozess des Kritikers durch, um den Fehler gegenüber diesem Ziel zu minimieren.
result.Assign(Buffer[tr].States[i + 1].rewards); target.Assign(Buffer[tr].States[i + 2].rewards); result = result - target * DiscFactor; Result.AssignArray(result); if(!Critic.backProp(Result, (CBufferFloat *)GetPointer(bActions), (CBufferFloat *)GetPointer(bGradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Als Nächstes folgt die Schulung zur Akteurspolitik, die wir in zwei Phasen durchführen. Zunächst führt der Akteur einen Vorwärtsdurchlauf durch, um einen Aktionstensor zu erzeugen.
//--- Actor Policy if(!Actor.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Es folgt ein Vorwärtsdurchlauf des Kritikers, bei dem die vom Akteur generierten Aktionen bewertet werden.
Critic.TrainMode(false); if(!Critic.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CNet*)GetPointer(Actor), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
In diesem Stadium ist das Kritikertraining deaktiviert. Dadurch wird verhindert, dass falsche Werte das Lernen der Belohnungspolitik des Akteurs beeinflussen.
Anschließend bewerten wir das Ergebnis der analysierten Trajektorie. Wenn die Politik des Akteurs zu einem positiven Ergebnis geführt hat, verschieben wir die aktuelle Politik des Akteurs in Richtung dieses positiven Verlaufs in einem überwachten Lernstil. Dies ist die erste Stufe des Trainings des Akteurs.
if(Buffer[tr].States[0].rewards[0] > 0) if(!Actor.backProp(GetPointer(bActions),(CBufferFloat*)GetPointer(bForecast),GetPointer(bGradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
In der zweiten Stufe beauftragen wir den Kritiker mit der Maximierung der Belohnung und übertragen den Fehlergradienten auf die Aktionsebene des Akteurs.
Critic.getResults(Result); for(int c = 0; c < Result.Total(); c++) { float value = Result.At(c); if(value >= 0) Result.Update(c, value * 1.01f); else Result.Update(c, value * 0.99f); } if(!Critic.backProp(Result, (CNet *)GetPointer(Actor), LatentLayer) || !Actor.backPropGradient((CBufferFloat*)GetPointer(bForecast),GetPointer(bGradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
So kann der Kritiker angeben, in welche Richtung die Politik des Akteurs angepasst werden sollte, um den Gesamtertrag zu steigern. Die Politik des Akteurs wird dann entsprechend aktualisiert.
Wir informieren den Nutzer weiterhin über den Trainingsprozess und fahren mit der nächsten Iteration des Trainingszyklus fort.
//--- if(GetTickCount() - ticks > 500) { double percent = double(iter) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, Actor.getRecentAverageError()); str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Critic", percent, Critic.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
Nach erfolgreichem Abschluss aller Iterationen löschen wir das Kommentarfeld auf dem Chart des Handelsistruments (das zur Anzeige von Nutzerinformationen dient).
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic", Critic.getRecentAverageError()); ExpertRemove(); //--- }
Wir geben die Ergebnisse des Modelltrainings im Protokoll aus und leiten den Beendigungsprozess des EAs ein.
An dieser Stelle schließen wir unsere Diskussion über die Algorithmen von MASA und die Implementierung von Modelltrainingsprogrammen ab. Der vollständige Quellcode ist im Anhang verfügbar.
4. Tests
Unsere Arbeit an der Umsetzung der von den Autoren des MASA-Rahmens vorgeschlagenen Ansätze unter Verwendung von MQL5 ist somit zu einem logischen Abschluss gekommen. Wir haben nun die letzte Phase unserer Arbeit erreicht – die Evaluierung der implementierten Ansätze an realen historischen Daten.
Es ist wichtig zu betonen, dass wir die Effektivität der implementierten Ansätze bewerten, nicht nur die der vorgeschlagenen, da unsere Implementierung mehrere Änderungen am ursprünglichen MASA-Rahmenwerk beinhaltete.
Die Modelle wurden mit EURUSD H1-Daten aus dem Jahr 2023 trainiert. Alle Indikatorparameter wurden auf ihre Standardwerte gesetzt.
Für das anfängliche Training wurde ein in früheren Arbeiten zusammengestellter Datensatz verwendet, der während des Trainings regelmäßig aktualisiert wurde, um ihn mit der sich entwickelnden Politik des Akteurs in Einklang zu bringen.
Nach mehreren Zyklen des Modelltrainings und der Datenaktualisierung erhielten wir eine Strategie, die sich sowohl bei den Trainings- als auch bei den Testdaten als rentabel erwies.
Die trainierte Strategie wurde mit historischen Daten vom Januar 2024 getestet, wobei alle anderen Parameter unverändert blieben. Die Ergebnisse sind wie folgt:
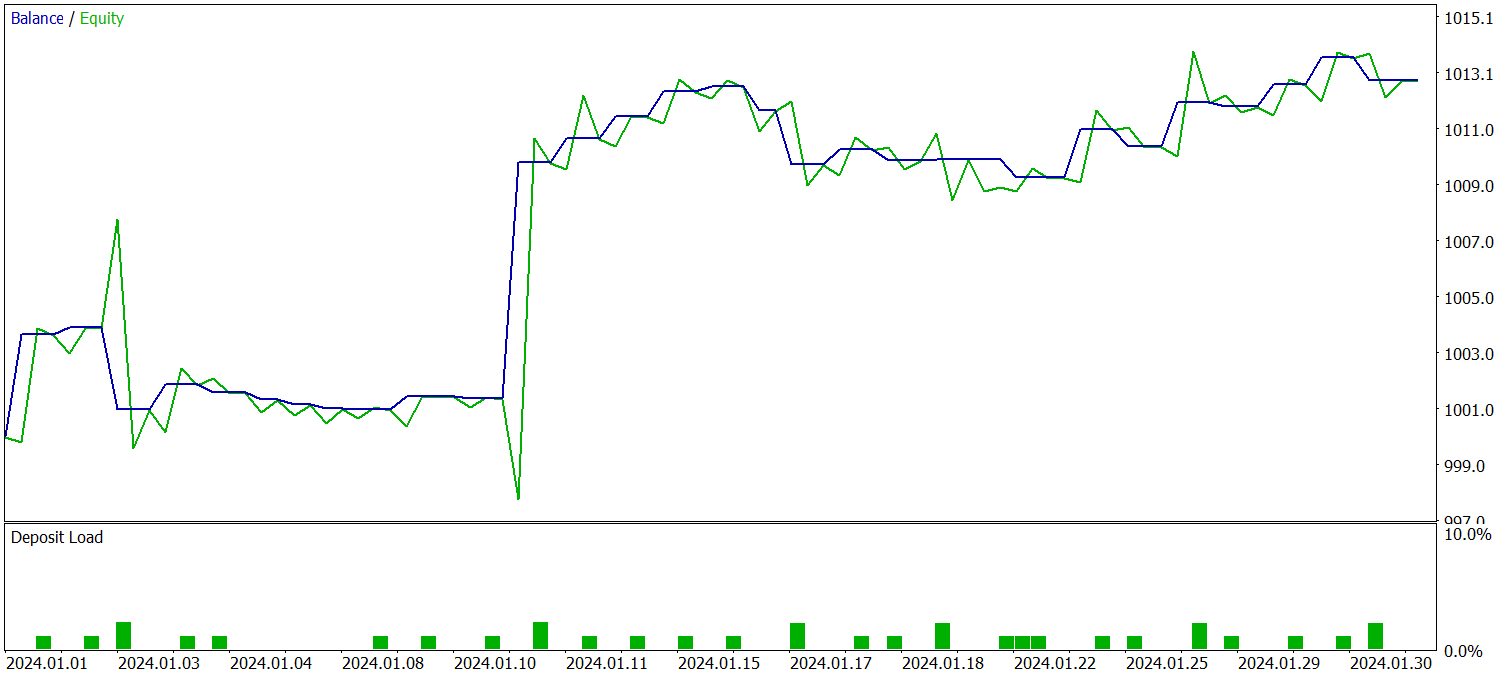
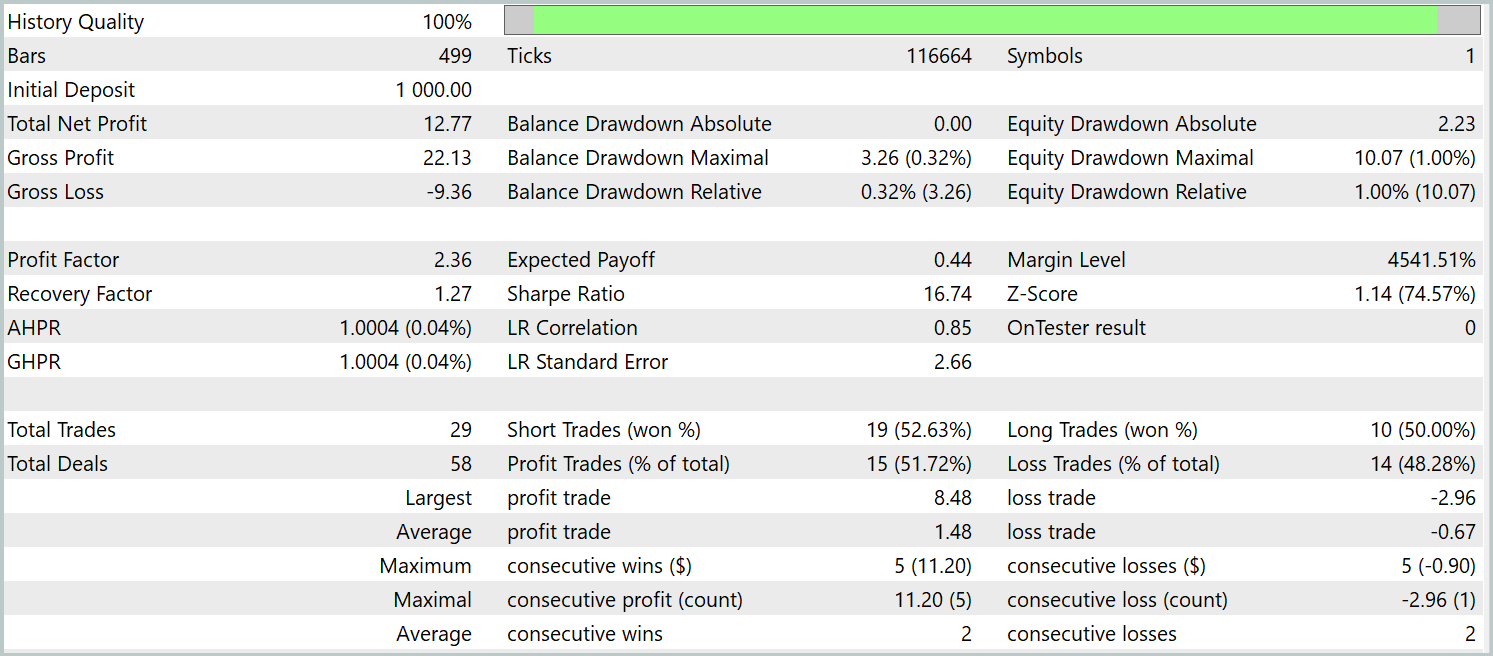
Während des Testzeitraums führte das Modell 29 Handelsgeschäfte aus, von denen die Hälfte mit Gewinn abgeschlossen wurde. Dank der Tatsache, dass der Durchschnitt der Handelsgeschäfte mit Gewinn mehr als doppelt so groß war wie der Durchschnitt jener mit Verlust, erzielte das Modell einen deutlichen Aufwärtstrend beim Kontostand. Diese Ergebnisse weisen auf das Potenzial des implementierten Rahmens hin.
Schlussfolgerung
Wir haben eine innovative Methodik für das Portfoliomanagement auf instabilen Finanzmärkten erforscht – das adaptive Multi-Agenten-System MASA. Dieser Rahmen kombiniert effektiv die Stärken von RL-Algorithmen und adaptiven Optimierungsmethoden, sodass die Modelle gleichzeitig die Rentabilität verbessern und das Risiko reduzieren können.
Im praktischen Teil haben wir unsere Interpretation der vorgeschlagenen Ansätze in MQL5 umgesetzt. Wir haben die Modelle anhand echter historischer Daten trainiert und die daraus resultierenden Maßnahmen getestet. Die Ergebnisse deuten auf ein vielversprechendes Potenzial hin. Vor dem Einsatz im Live-Handel ist es jedoch unerlässlich, weitere Trainings mit repräsentativeren Datensätzen durchzuführen und umfangreiche Tests unter verschiedenen Bedingungen vorzunehmen.
Referenzen
- Developing A Multi-Agent and Self-Adaptive Framework with Deep Reinforcement Learning for Dynamic Portfolio Risk Management
- Andere Artikel aus dieser Reihe
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Expert Advisor zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | Expert Advisor für das Sammeln von Beispielen nach der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Expert Advisor für das Modelltraining |
| 4 | Test.mq5 | Expert Advisor | Expert Advisor für die Modellprüfung |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16570
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Trendkriterien im Handel
Trendkriterien im Handel
 Marktsimulation (Teil 02): Kreuzaufträge (II)
Marktsimulation (Teil 02): Kreuzaufträge (II)
 Marktsimulation (Teil 03): Eine Frage der Leistung
Marktsimulation (Teil 03): Eine Frage der Leistung
 Von der Grundstufe bis zur Mittelstufe: Template und Typename (IV)
Von der Grundstufe bis zur Mittelstufe: Template und Typename (IV)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.