取引におけるニューラルネットワーク：マルチエージェント自己適応モデル（最終回）

MetaTrader 5 — トレーディングシステム | YYYY年10月DD日, 08:15

はじめに

前回の記事では、MASA（マルチエージェント自己適応、Multi Agent Self Adaptive）フレームワークを紹介しました。本フレームワークは、相互に連携する複数のエージェントを統合したマルチエージェントシステムです。MASAの構造においては、強化学習(RL)に基づくRLエージェントが投資ポートフォリオの総合リターンの最適化を担当します。一方で、別のアルゴリズムベースのエージェントは、RLエージェントが提案するポートフォリオの最適化を補助し、潜在的なリスクの最小化に注力します。

エージェントごとの役割が明確に分かれていることで、モデルは金融市場の環境に応じて継続的に学習し、適応することが可能です。MASAのマルチエージェント構造は、収益性だけでなくリスク面においても、よりバランスの取れたポートフォリオを実現します。

MASAフレームワークのオリジナルの視覚化を以下に示します。

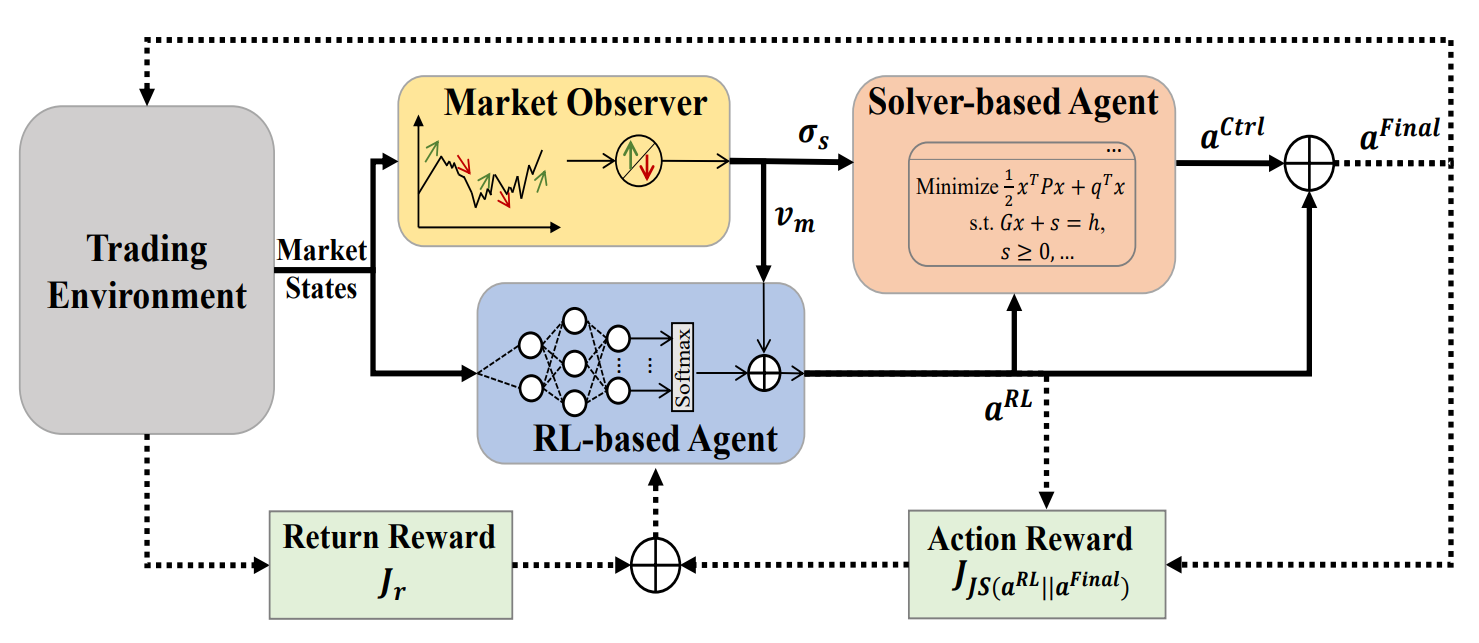
前回の記事の実践編では、MASAフレームワークの各エージェントの機能を個別のオブジェクトとして実装するアルゴリズムについて詳しく解説しました。本記事では、その作業をさらに進めていきます。

1. MASA複合層

前回の記事では、MASAフレームワーク内でそれぞれ特定の機能を持つ3つのエージェントを作成しました。今回はこれらを単一のシステムに統合します。そのために、新しいオブジェクト「CNeuronMASA」を作成します。構造は以下の通りです。

class CNeuronMASA    :  public CNeuronBaseSAMOCL
  {
protected:
   CNeuronMarketObserver   cMarketObserver;
   CNeuronRevINDenormOCL   cRevIN;
   CNeuronRLAgent          cRLAgent;
   CNeuronControlAgent     cControlAgent;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                                                   CBufferFloat *SecondGradient, 
                                                        ENUM_ACTIVATION SecondActivation = None) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMASA(void) {};
                    ~CNeuronMASA(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers_mo, uint forecast,
                          uint segments_rl, float rho,
                          uint layers_rl, uint n_actions,
                          uint heads_contr,
                          uint layers_contr,
                          int NormLayer, CNeuronBatchNormOCL *normLayer,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMASA; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   virtual void      SetActivationFunction(ENUM_ACTIVATION value) override;
   //---
   virtual int       GetNormLayer(void)   {  return cRevIN.GetNormLayer(); }
   virtual bool      SetNormLayer(int NormLayer, CNeuronBatchNormOCL *normLayer);
  };

この新しいオブジェクトの構造には、特に注目すべき点がいくつかあります。

まず、初期化メソッド「Init」に比較的多くのパラメータが存在することがすぐにわかります。これは、各エージェントがそれぞれ独自のアーキテクチャ特性を持つため、3つのエージェントすべてに対応する必要があるからです。

もう一つの注意点として、ライブラリの一般的な哲学に反する部分があります。フィードフォワードパスのメソッドは単一の入力ソースしか持たず、これはMASAフレームワークと整合しています。RLエージェントと市場オブザーバーエージェントの両方が、現在の市場状態を入力として受け取ります。しかし、勾配分配メソッドでは第二のデータソースを導入しています。これは、フィードフォワードパスや元々のMASAフレームワークには存在しないものです。

この非標準的な解決策は、市場オブザーバーエージェントの代替学習プロセスを可能にするために採用されました。そのため、内部的にデータの逆正規化用オブジェクトも追加しています。この判断については、クラスメソッドを構築する際にさらに詳しく説明します。

新しいクラスの内部オブジェクトはすべてstaticとして宣言されており、コンストラクタとデストラクタは空のままにできます。新しいクラスインスタンスの初期化はInitメソッドのみでおこなわれます。前述の通り、このメソッドは多数のパラメータを受け取りますが、基本的には以前作成した各エージェントの初期化パラメータを複製したものです。

bool CNeuronMASA::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                       uint window, uint window_key, uint units_count,
                       uint heads_mo, uint layers_mo, uint forecast, uint segments_rl,
                       float rho, uint layers_rl, uint n_actions, uint heads_contr,
                       uint layers_contr, int NormLayer, CNeuronBatchNormOCL *normLayer,
                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseSAMOCL::Init(numOutputs, myIndex, open_cl, n_actions, rho, optimization_type, batch))
      return false;

メソッド内では、まず親クラスの同名メソッドを呼び出します。ここでの親クラスは、SAM最適化を持つ全結合ニューラル層です。

masaフレームワークの最終出力は、コントローラーエージェントによって行動テンソルとして生成されます。したがって、親クラスの初期化時には、層のサイズをActorの行動空間に合わせます。

次に、各エージェントを順に初期化します。まずは市場オブザーバーエージェントです。

このエージェントは現在の市場状態テンソルを入力として受け取り、指定した計画期間におけるマルチモーダルシーケンス形式で予測値を返します。

//--- Market Observation
   if(!cMarketObserver.Init(0, 0, OpenCL, window, window_key, units_count, heads_mo, layers_mo, forecast,
                                                                                    optimization, iBatch))
      return false;
   if(!cRevIN.Init(0, 1, OpenCL, cMarketObserver.Neurons(), NormLayer, normLayer))
      return false;

直後に、市場オブザーバーエージェントの出力に合わせて、逆正規化層を初期化します。

続いて、RLエージェントを初期化します。こちらも市場状態テンソルを入力として受け取り、学習済み方策に従ってActor行動テンソルを出力します。

//--- RL Agent
   if(!cRLAgent.Init(0, 2, OpenCL, window, units_count, segments_rl, fRho, layers_rl, n_actions, optimization, iBatch))
      return false;

最後に、コントローラーエージェントを初期化します。このエージェントは、前の2つのエージェントの出力を受け取り、調整済みのactor行動テンソルを生成します。

   if(!cControlAgent.Init(0, 3, OpenCL, 3, window_key, n_actions / 3, heads_contr, window, forecast, layers_contr,
                                                                                            optimization, iBatch))
      return false;

実装上、rlエージェントとコントローラーエージェントではactor行動テンソルの解釈が異なる点に注意が必要です。この違いは単なる機能上の差ではありません。

RLエージェントの出力は、全結合層を使用して市場分析と学習済み方策に基づき各要素を独立して生成します。しかし、同じ資産の買いと売りは互いに排他的であることが事前にわかっています。さらに、各方向の取引パラメータは行動ベクトル内の3つの要素で表されます。

そこで、コントローラーエージェントには、行動テンソルを各要素が3要素ベクトルで表される取引として扱うマルチモーダルシーケンスとして解釈させます。これにより、コントローラーエージェントは各取引方向のリスクを個別に評価できます。

初期化メソッドの最後で、外部インターフェースバッファのポインタを再割り当てし、デフォルトでシグモイド活性化関数を設定します。

   if(!SetOutput(cControlAgent.getOutput(), true) ||
      !SetGradient(cControlAgent.getGradient(), true))
      return false;
   SetActivationFunction(SIGMOID);
//---
   return true;
  }

このメソッドは、実行の成功を示す論理フラグを返して終了します。

活性化関数についても少し触れます。本クラスの出力はactorの行動テンソルであり、まずrlエージェントによって生成され、次にコントローラーエージェントによって調整されます。出力空間は、両エージェントおよびクラス自体で整合している必要があります。そのため、活性化関数メソッドをオーバーライドして、すべてのコンポーネントで同期を保証します。

void CNeuronMASA::SetActivationFunction(ENUM_ACTIVATION value)
  {
   cControlAgent.SetActivationFunction(value);
   cRLAgent.SetActivationFunction((ENUM_ACTIVATION)cControlAgent.Activation());
   CNeuronBaseSAMOCL::SetActivationFunction((ENUM_ACTIVATION)cControlAgent.Activation());
  }

初期化が完了したら、フィードフォワードパスのアルゴリズムに移ります。この部分は単純で、エージェントのフィードフォワードメソッドを順番に呼び出すだけです。まず、市場分析結果と初期Actor行動テンソルを取得します。

bool CNeuronMASA::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cMarketObserver.FeedForward(NeuronOCL.AsObject()))
      return false;
   if(!cRLAgent.FeedForward(NeuronOCL.AsObject()))
      return false;

次に、これらの結果をコントローラーエージェントに渡して最終決定を生成します。

   if(!cControlAgent.FeedForward(cRLAgent.AsObject(), cMarketObserver.getOutput()))
      return false;
//---
   return true;
  }

このメソッドは、論理的な実行結果を返して終了します。

先ほどのmasaの可視化をもう一度見ると、最終的な行動ベクトルがrlエージェントとコントローラーエージェントの出力の和として描かれています。しかし、実装上はコントローラーエージェントの出力を最終結果として扱い、rlエージェントへの残差接続はおこないません。コントローラーエージェントのアーキテクチャを覚えていらっしゃるでしょうか。

コントローラーエージェントはtransformerデコーダとして実装されており、ご存知のとおり、TransformerにはすでにアテンションモジュールやFeedForwardブロック内に残差接続が組み込まれているため、rlエージェントからの残留情報フローは、コントローラーエージェントに本質的に組み込まれているため、追加の接続は不要です。

次に、バックプロパゲーション処理について説明します。具体的には、誤差勾配分布のアルゴリズム(calcInputGradients)です。ここで、CNeuronMASAで採用した一部の非標準的な判断が関わってきます。

まず、各エージェントの期待される出力を確認します。2つのエージェントはActor行動テンソルを返します。学習時には、最適行動セットをターゲット（教師あり学習）として使用するか、報酬への射影（強化学習）を使用するのが理にかなっています。

しかし、市場オブザーバーエージェントは、分析対象となる金融商品のマルチモーダル時系列予測値を出力します。この場合、学習ターゲットの設定方法が問題となります。コントローラーエージェントを通して勾配を渡してrlエージェントの出力調整に間接的に影響を与えることも可能ですが、この方法は予測目的には適合しません。

より適切な解決策は、以前にAccount State Encoderでおこなったように、市場オブザーバーエージェントを個別に時系列予測で学習させることです。しかし、オブザーバーは現在コンポジットモデルに統合されているため、個別学習は現実的ではありません。そこで、層レベルで二重の学習ターゲットを提供するという発想に至ります。これはライブラリのワークフローに根本的な変更を伴い、大規模な再設計が必要です。

これを回避するために、非標準的な解決策を採用します。第二入力ソースの仕組みを用いて追加のターゲット値セットを渡すのです。すなわち、勾配分配メソッドを2つの入力データソースを使う形で再定義し、第二オブジェクトのバッファで市場オブザーバーエージェントにターゲット値テンソルを渡します。

bool CNeuronMASA::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                                             CBufferFloat *SecondGradient, 
                                                     ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!NeuronOCL)
      return false;

この方法には注意点があります。主にデータの比較可能性です。通常、モデルにはターミナルから受け取った未処理の生データを入力します。ターミナルデータは前処理で正規化され、ニューラル層は正規化された値で動作します。これは、作成しているCNeuronMASAオブジェクトでも同様です。オブザーバーエージェントの出力は、コントローラーエージェントが扱いやすいよう正規化済みです。一方で、分析対象のマルチモーダル時系列の将来実値（ターゲット）は生データしか存在しません。これを解決するため、逆正規化層を導入しました。フィードフォワードパスでは使用しませんが、勾配分配時に使用され、オブザーバーの予測値に入力データの統計パラメータを再適用します。

   if(!cRevIN.FeedForward(cMarketObserver.AsObject()))
      return false;

これにより、生データターゲットとの有効な比較と勾配伝播が可能になります。

   if(!cRevIN.FeedForward(cMarketObserver.AsObject()))
      return false;
   float error = 1.0f;
   if(!cRevIN.calcOutputGradients(SecondGradient, error))
      return false;
   if(!cMarketObserver.calcHiddenGradients(cRevIN.AsObject()))
      return false;

その後、コントローラーエージェントの勾配をrlエージェントと市場オブザーバーの間で分配します。以前に蓄積された勾配を保持するため、オブザーバーの誤差をバッファに保存し、両情報フローからの寄与を合算します。

   if(!cRLAgent.calcHiddenGradients(cControlAgent.AsObject(), cMarketObserver.getOutput(),
                                    cMarketObserver.getPrevOutput(),
                                    (ENUM_ACTIVATION)cMarketObserver.Activation()) ||
      !SumAndNormilize(cMarketObserver.getGradient(), cMarketObserver.getPrevOutput(), 
                                 cMarketObserver.getGradient(), 1, false, 0, 0, 0, 1))
      return false;

もう1つの重要なポイントは、rlエージェントとコントローラーエージェントの両方がactor行動テンソルを返すということです。前者は自身の市場分析に基づき、後者はオブザーバーエージェントからの予測値を考慮してリスク評価後のテンソルを返します。理想的には、両者の出力は一致するべきです。そこで、rlエージェントの誤差項として、コントローラーエージェントの出力との差を導入します。

   CBufferFloat *temp = cRLAgent.getGradient();
   if(!cRLAgent.SetGradient(cRLAgent.getPrevOutput(), false) ||
      !cRLAgent.calcOutputGradients(cControlAgent.getOutput(), error) ||
      !SumAndNormilize(temp, cRLAgent.getPrevOutput(), temp, 1, false, 0, 0, 0, 1) ||
      !cRLAgent.SetGradient(temp, false))
      return false;

ここでも、既存の勾配が消去されないよう、バッファ置換と両データストリームの合算をおこないます。

内部エージェント全体に勾配が分配された後、次に入力レベルに勾配を戻します。この場合も、RLエージェントと市場オブザーバーエージェントの2つのソースから勾配を集約します。以前と同様に、オブザーバーの勾配を伝播させます。

   if(!NeuronOCL.calcHiddenGradients(cMarketObserver.AsObject()))
      return false;

次にバッファを置換し、RLエージェントの勾配を伝播させます。

   temp = NeuronOCL.getGradient();
   if(!NeuronOCL.SetGradient(NeuronOCL.getPrevOutput(), false) ||
      !NeuronOCL.calcOutputGradients(cRLAgent.getOutput(), error) ||
      !SumAndNormilize(temp, NeuronOCL.getPrevOutput(), temp, 1, false, 0, 0, 0, 1) ||
      !NeuronOCL.SetGradient(temp, false))
      return false;
//---
   return true;
  }

両寄与を合算し、元のバッファ状態を復元します。

この段階で、誤差勾配はモデルの性能への寄与に応じてすべてのコンポーネントに分配されました。最後のステップは、モデルパラメータを更新して誤差を最小化することです。この機能はupdateInputWeightsメソッドで実行されます。このメソッドのアルゴリズムは非常にシンプルです。エージェントのフィードフォワードメソッドを順番に呼び出すだけです。ここでは詳細に触れませんが、すべてのエージェントがSAM最適化を使用していることを覚えておいてください。したがって、これらの更新はフィードフォワードパスの逆順で実行する必要があります。

これで、新しいCNeuronMASAクラスメソッドのアルゴリズムに関する解説を終了します。オブジェクトとその全メソッドの完全なコードは、付録にて参照可能です。

2. モデルアーキテクチャ

新しいオブジェクトの構築が完了したので、次に学習可能なモデルのアーキテクチャについて説明します。ここでも、いくつかの変更と非標準的な解決策を導入しています。

まず、従来使用していたEnvironment State Encoderの利用を廃止しました。これは偶然ではありません。CNeuronMASAクラスでは、すでに2つのエージェントが現在の環境を並行して分析しています。

次の変更点は、口座状態情報の取り扱いです。以前は、Actorモデルに第二の入力ソースとしてこの情報を入力していました。しかし、現在では、この入力チャネルは市場オブザーバーエージェントのターゲット値によって占有されています。これを解決するため、単純に口座状態情報を環境状態テンソルの末尾に追加しました。

したがって、Actorは現在、環境状態の記述と口座状態情報の両方を含む結合入力テンソルを受け取ります。

bool CreateDescriptions(CArrayObj *&actor, CArrayObj *&critic)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }
//--- Actor
   actor.Clear();
//---
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr + AccountDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

これらの生データは、まずバッチ正規化層で処理されます。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

この段階で注意すべき点があります。口座状態ベクトルは環境状態テンソルの構造を乱します。その長さは、分析対象の時系列のマルチモーダルシーケンス内の単一要素の記述サイズと異なる場合があり、使用するアテンションモジュールの構造と整合しません。この問題を解決するため、入力データを学習可能な埋め込み層によって行列形式に変換します。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronEmbeddingOCL;
   descr.count = 1;
   descr.window_out = BarDescr;
     {
      int temp[HistoryBars + 1];
      if(ArrayInitialize(temp, BarDescr) < (HistoryBars + 1))
         return false;
      temp[HistoryBars] = AccountDescr;
      if(ArrayCopy(descr.windows, temp) < (HistoryBars + 1))
         return false;
     }
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

この層は、入力ベクトルを固定長ブロックに分割し、各ブロックを元のサイズに関係なく事前定義された次元の部分空間に射影します。各ブロックには独立して学習可能な射影行列があります。

入力テンソルのほとんどは、個々の環境状態（バー）を表す同質のベクトルで構成されており、最後の要素（口座状態）のみが異なります。したがって、シーケンスは固定長の分析ウィンドウで初期化し、最後の要素のサイズのみを調整します。

重要なのは、埋め込み後の各シーケンス要素の出力サイズを、単一バーの記述サイズに設定することです。これはとても重要なことです。これは非常に重要です。理論的には埋め込み出力の次元は任意に選べますが、市場オブザーバーエージェントは元の入力次元で予測値を返します。そのため、予測されたマルチモーダル時系列は、学習時に使用されるターゲット値と一致する必要があります。ここでループが閉じます。

学習可能な埋め込みを使用することで、暗黙的に位置情報エンコーディングが提供されます。前述の通り、各シーケンス要素は独自の射影行列を持つため、異なる位置の同一ベクトルも異なる部分空間表現に射影され、分析中に識別可能となります。

得られた埋め込みは、その後MASAフレームワークオブジェクトに渡されます。ここでもいくつか重要な詳細があります。

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMASA;
//--- Windows
     {
      int temp[] = {BarDescr, NForecast, 2 * NActions};    
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }
   descr.window_out = 32;
   descr.count = HistoryBars+1;
//--- Heads
     {
      int temp[] = {4, 4};
      if(ArrayCopy(descr.heads, temp) < (int)temp.Size())
         return false;
     }
//--- Layers
     {
      int temp[] = {3, 3, 3};
      if(ArrayCopy(descr.units, temp) < (int)temp.Size())
         return false;
     }
   descr.window = BarDescr;
   descr.probability = Rho;
   descr.step = 1; // Normalization layer
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

動的配列descr.windowsでは、内部エージェントが分析するシーケンスの主要パラメータを指定します。ここでは、入力シーケンス要素の次元、時系列の予測期間、Actorの行動空間を順に指定しています。

最後のパラメータには特に注意が必要です。内部エージェントのアーキテクチャ設計では、環境状態と生成される行動の直接依存関係を記述し、Actorの行動に確率性を含めない設計でした。しかし、実際には確率的Actor方策を実装しています。そのため、MASAフレームワークの出力行動空間の次元を倍にしています。これは、以前確率的方策を組織する際のアプローチと一致します。生成される行動ベクトルは論理的に2等分され、分析対象となる環境状態におけるActor行動空間の平均と分散を表します。そのため、この層の活性化関数は無効化されています。

使用する各アテンションモジュールは4つのヘッドを持ち、各エージェントは3層のエンコーダ/デコーダを含みます。

前述の通り、MASAフレームワークの出力は、指定された分布に従って確率的Actor行動を生成する変分オートエンコーダの潜在状態層に渡されます。

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

得られた行動ベクトルは、畳み込み層とシグモイド活性化関数を用いて必要な範囲に射影されます。

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvSAMOCL;
   descr.count = NActions / 3;
   descr.window = 3;
   descr.step = 3;
   descr.window_out = 3;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   descr.probability = Rho;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

最終モデル出力では、モデル結果をターゲット値に合わせるために頻度整合層を適用します。

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = NActions;
   descr.count =  1;
   descr.step = int(false);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

次のステップは、Criticアーキテクチャを構築することです。全体としては以前の設計と類似していますが、一つ大きな変更点があります。Environment State Encoderを廃止したため、Criticモデル内に直接環境分析ブロックを追加する必要がありました。これにはPSformerフレームワークを使用して現在の状態を分析します。なお、Criticの入力データには口座状態情報を含めません。私見では、Criticにとってこの情報はほとんど価値がありません。取引結果は主に市場状況に依存し、エントリー時点の口座状態には依存しません。

過剰または過少な取引量が実行エラーを引き起こし、ポジションが開かれない可能性があると主張することもできます。しかし、取引量の決定はActorの役割です。Criticがこのようなエッジケースを扱うべきでしょうか。これは本質的にモデル間の機能分離の問題です。

さらに、ポジションや累積損益（過去の取引結果）も考慮されます。Criticは現在の取引（または方策）を評価し、過去の結果を評価するわけではありません。Criticが方策全体を評価すると仮定しても、その評価はエピソードの終了までに及ぶものであり、過去に遡るものではありません。

したがって、Criticは現在の環境状態のみを入力として受け取ります。

//--- Critic
   critic.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

入力層の生データは、前回と同様にバッチ正規化層で処理されます。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

その後、PSformerフレームワークの3層に順次入力されます。

//--- layer 2 - 4
   for(int i = 0; i < 3; i++)
     {
      if(!(descr = new CLayerDescription()))
         return false;
      descr.type = defNeuronPSformer;
      descr.window = BarDescr;
      descr.count = HistoryBars;
      descr.window_out = Segments;
      descr.probability = Rho;
      descr.batch = 1e4;
      descr.activation = None;
      descr.optimization = ADAM;
      if(!critic.Add(descr))
        {
         delete descr;
         return false;
        }
     }

得られたテンソルの次元を圧縮するため、順次畳み込み層と全結合層を使用します。

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvSAMOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.step = BarDescr;
   descr.window_out = int(LatentCount / descr.count);
   descr.probability = Rho;
   descr.activation = GELU;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseSAMOCL;
   descr.count = LatentCount;
   descr.probability = Rho;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

環境分析の結果とエージェントの行動をデータ結合層で統合します。

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = LatentCount;
   descr.step = NActions;
   descr.activation = GELU;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

その後、意思決定モジュールとして4層の全結合層を適用します。

//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseSAMOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   descr.probability = Rho;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseSAMOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   descr.probability = Rho;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseSAMOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   descr.probability = Rho;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 11
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseSAMOCL;
   descr.count = NRewards;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.probability = Rho;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }

最終出力段階では、頻度整合層を使用してモデル結果をターゲット値と整合させます。

//--- layer 12
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = NRewards;
   descr.count =  1;
   descr.step = int(false);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!critic.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

これで、2つの学習可能モデルのアーキテクチャ定義が完了し、呼び出しプログラムに論理結果を返してメソッドを終了します。

3. モデル学習プログラム

ここまでで、私たちは自信を持って作業の論理的な結論に近づき、モデルの学習プログラムの構築に取りかかります。当然ながら、学習可能モデルのひとつを削除したことは、学習アルゴリズムに影響を与えています。さらに、MASAフレームワークモジュールを設計する際、第2のデータソースからの情報ストリームをターゲット値の補助的なフローとして使用することに合意しました。この点を踏まえたうえで、TrainTrainメソッドとして実装された学習アルゴリズムの内容に進みましょう。

従来と同様、まずはいくつかの準備作業から始めます。リプレイバッファから、過去の実行の効果に基づいて重み付けされた軌道選択確率のベクトルを作成します。

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
//---
   vector<float> result, target, state;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

次に、必要なローカル変数を宣言します。

続いて、外部パラメータで指定された反復数に基づく学習ループを設定します。

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast));
      if(i <= 0)
        {
         iter --;
         continue;
        }
      if(!state.Assign(Buffer[tr].States[i].state) ||
         MathAbs(state).Sum() == 0 ||
         !bState.AssignArray(state))
        {
         iter --;
         continue;
        }
      if(!state.Assign(Buffer[tr].States[i+NForecast].state) ||
         !state.Resize(NForecast*BarDescr) ||
         MathAbs(state).Sum() == 0 ||
         !bForecast.AssignArray(state))
        {
         iter --;
         continue;
        }

ループ内では、ひとつの軌道とその環境状態をサンプリングします。この時点で、必要な分析深度と予測期間において、過去および将来のデータが存在するかどうかも確認します。いずれかのチェックに失敗した場合は、新しい軌道と状態を再サンプリングします。

必要なデータが利用可能になったら、それらを適切なバッファに転送します。その後、分析時点の環境状態記述に口座状態情報を追加します。

      //--- Account
      float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
      float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
      bState.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
      bState.Add(Buffer[tr].States[i].account[1] / PrevBalance);
      bState.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
      bState.Add(Buffer[tr].States[i].account[2]);
      bState.Add(Buffer[tr].States[i].account[3]);
      bState.Add(Buffer[tr].States[i].account[4] / PrevBalance);
      bState.Add(Buffer[tr].States[i].account[5] / PrevBalance);
      bState.Add(Buffer[tr].States[i].account[6] / PrevBalance);

さらに、分析対象の環境状態にタイムスタンプを付加します。

      //---
      double time = (double)Buffer[tr].States[i].account[7];
      double x = time / (double)(D'2024.01.01' - D'2023.01.01');
      bState.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_MN1);
      bState.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_W1);
      bState.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_D1);
      bState.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));

入力データの準備が整ったら、モデル学習プロセスを開始します。最初のステップはCriticの学習です。Criticは、分析対象の環境状態と、学習サンプル収集時にActorが実際に実行した行動ベクトルを入力として受け取ります。この行動を使用するのは、それに対して環境が実際に返した報酬をすでに知っているためです。フィードフォワード処理を実行し、Actorの過去の行動を評価します。

      //--- Critic
      bActions.AssignArray(Buffer[tr].States[i].action);
      Critic.TrainMode(true);
      if(!Critic.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)GetPointer(bActions)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

期待通り、Criticのフィードフォワード出力は、観測された実際の報酬に近い報酬テンソルであることが望ましいです。そのため、リプレイバッファから実際の報酬を抽出し、これをターゲットとしてCriticの誤差逆伝播を実行し、誤差を最小化します。

      result.Assign(Buffer[tr].States[i + 1].rewards);
      target.Assign(Buffer[tr].States[i + 2].rewards);
      result = result - target * DiscFactor;
      Result.AssignArray(result);
      if(!Critic.backProp(Result, (CBufferFloat *)GetPointer(bActions), (CBufferFloat *)GetPointer(bGradient)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

次に、Actor方策の学習に移ります。この学習は2段階でおこないます。まず、Actorが順伝播を実行し、行動テンソルを生成します。

      //--- Actor Policy
      if(!Actor.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

次に、Criticがフィードフォワード処理をおこない、今回はActorが生成した行動を評価します。

      Critic.TrainMode(false);
      if(!Critic.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CNet*)GetPointer(Actor), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

この段階ではCriticの学習が無効化されています。これは、誤った値がActorの報酬方策学習に影響を与えることを防ぐためです。

続いて、分析対象の軌道の結果を評価します。Actorの方策が正の成果をもたらした場合、その方策を教師あり学習的なスタイルでその正の軌道方向へとシフトさせます。これがActor学習の第一段階となります。

      if(Buffer[tr].States[0].rewards[0] > 0)
         if(!Actor.backProp(GetPointer(bActions),(CBufferFloat*)GetPointer(bForecast),GetPointer(bGradient)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

第二段階では、Criticに報酬の最大化を指示し、誤差勾配をActorの行動層まで伝播させます。

      Critic.getResults(Result);
      for(int c = 0; c < Result.Total(); c++)
        {
         float value = Result.At(c);
         if(value >= 0)
            Result.Update(c, value * 1.01f);
         else
            Result.Update(c, value * 0.99f);
        }
      if(!Critic.backProp(Result, (CNet *)GetPointer(Actor), LatentLayer) ||
         !Actor.backPropGradient((CBufferFloat*)GetPointer(bForecast),GetPointer(bGradient)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

これにより、CriticはActorの方策をどの方向に調整すれば全体のリターンを増やせるかを示します。Actorの方策はその指示に従って更新されます。

学習プロセスの進捗は、ユーザーに逐次通知され、次の学習サイクルの反復処理へと進みます。

      //---
      if(GetTickCount() - ticks > 500)
        {
         double percent = double(iter) * 100.0 / (Iterations);
         string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, Actor.getRecentAverageError());
         str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Critic", percent, Critic.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

すべての反復処理が正常に完了した後、銘柄チャート上のコメント欄（ユーザー情報表示用）をクリアします。

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic", Critic.getRecentAverageError());
   ExpertRemove();
//---
  }

モデル学習の結果をログに出力し、EAの終了プロセスを開始します。

これをもって、MASAフレームワークのアルゴリズムおよびモデル学習プログラムの実装に関する説明を完結します。完全なソースコードは添付ファイルとして提供されています。

4. テスト

これまで進めてきた、MASAフレームワークの提案手法をMQL5で実装する作業は、ついにその論理的な結論に到達しました。ここからは、最終段階である「実装した手法の実データによる評価」に移ります。

ここで強調しておきたいのは、私たちが評価するのは提案された手法そのものではなく、実際に実装された手法の有効性であるという点です。なぜなら、今回の実装では、元のMASAフレームワークに対していくつかの修正を加えているためです。

モデルの学習には、EURUSDのH1データ（2023年）を使用しました。すべてのインジケーターのパラメータはデフォルト値のままとしています。

初期学習では、以前の研究で作成したデータセットを用い、学習中も定期的に更新を行いました。これは、学習が進むにつれてActorの方策が変化するため、それに合わせてデータセットを最新の状態に保つためです。

モデルの学習とデータセットの更新を複数回繰り返した結果、学習セットおよびテストセットの両方で収益性を示す方策を得ることができました。

学習済み方策は、2024年1月のヒストリカルデータを用いてテストされました。その他のパラメータはすべて変更していません。以下が結果です。

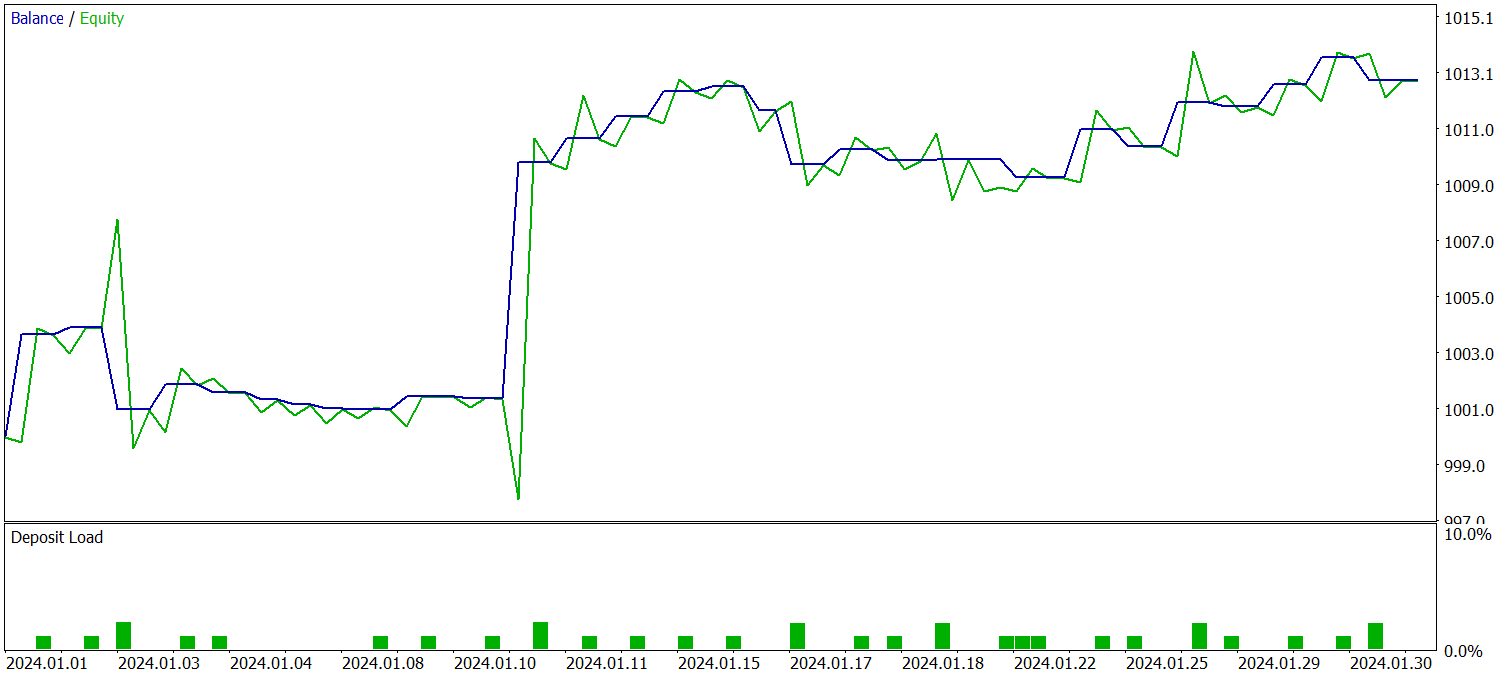
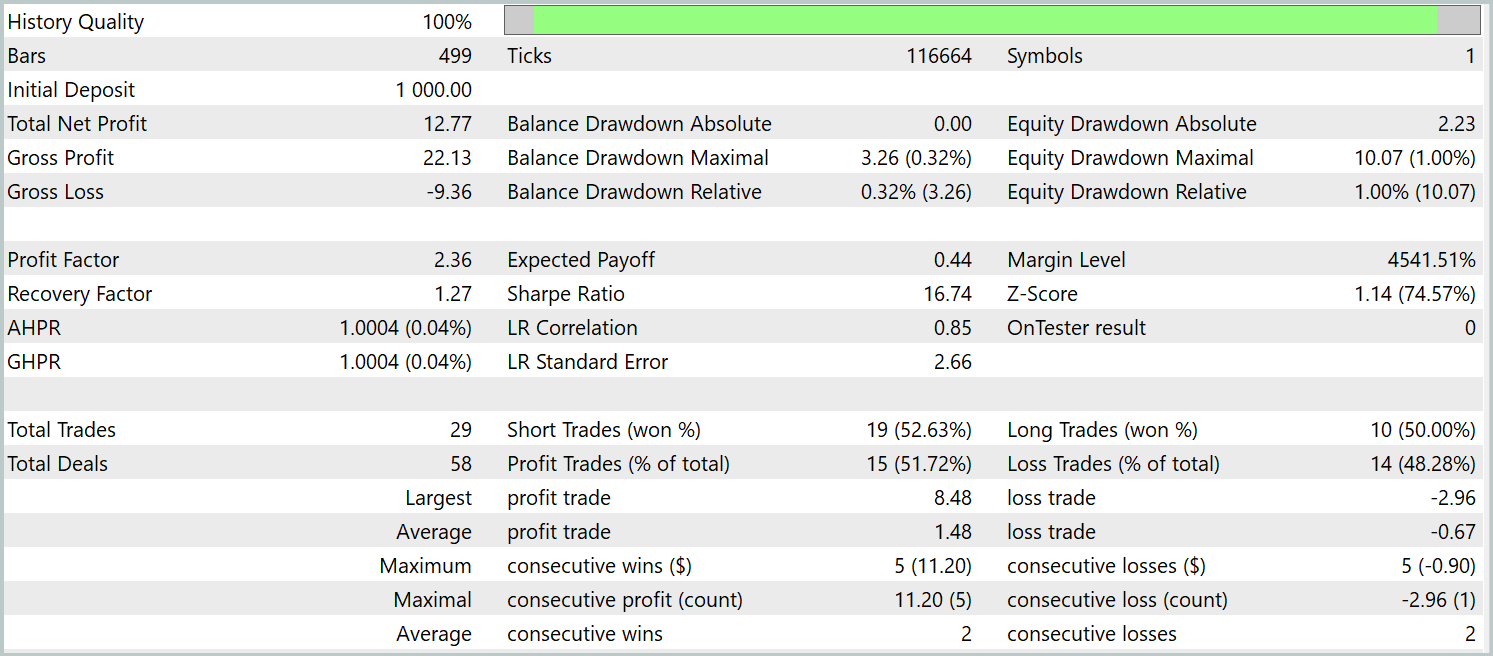
テスト期間中、モデルは29回の取引を実行し、そのうち半数が利益で終了しました。平均利益取引の大きさが平均損失取引の2倍以上であったため、口座残高は明確な上昇傾向を示しました。これらの結果は、本実装フレームワークの高い潜在能力を示唆しています。

結論

本記事では、不安定な金融市場におけるポートフォリオ管理のための革新的な手法、すなわちMASAマルチエージェント自己適応システムを検討しました。このフレームワークは、強化学習(RL)アルゴリズムの強みと自己適応型最適化手法の特長を効果的に融合させることで、収益性の向上とリスク低減を同時に実現することを可能にしています。

実践的なセクションでは、提案手法を私たちの解釈に基づいてMQL5上で実装しました。モデルを実際のヒストリカルデータで学習させ、その結果得られた方策を検証しました。得られた結果は非常に有望な可能性を示しています。とはいえ、実運用環境への導入に先立ち、より代表性の高いデータセットを用いた追加学習および、多様な市場条件下での包括的なテストを実施することが不可欠です。

参照文献

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	事例収集用EA
2	ResearchRealORL.mq5	EA	Real-ORL法を用いた例収集用のEA
3	Study.mq5	EA	モデル学習用EA
4	Test.mq5	EA	モデルテスト用EA
5	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
6	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
7	NeuroNet.cl	ライブラリ	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16570

添付されたファイル |

ZIPをダウンロード

MQL5.zip (2195.86 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

ディスカッションに移動

取引におけるニューラルネットワーク：Attentionメカニズムを備えたエージェントのアンサンブル(MASAAT)

アテンション機構と時系列解析を組み合わせたマルチエージェント自己適応型ポートフォリオ最適化フレームワーク(MASAAT: Multi-Agent Self-Adaptive Portfolio Optimization Framework)を提案します。MASAATは、価格系列や方向性の変化を分析する複数のエージェントを生成し、異なる詳細レベルで資産価格の重要な変動を特定できるように設計されています。

リプレイシステムの開発（第77回）：新しいChart Trade (IV)

この記事では、通信プロトコルを作成する際に考慮すべきいくつかの対策や注意点について説明します。内容は比較的シンプルでわかりやすいものなので、詳細には触れません。しかし、この記事の内容を理解することで、今後の展開が把握しやすくなります。

リプレイシステムの開発（第78回）：新しいChart Trade(V)

本記事では、受信側コードの一部の実装方法について解説します。ここでは、プロトコルの相互作用をテストし理解するためのエキスパートアドバイザー(EA)を実装します。ここで提示されるコンテンツは、教育目的のみに使用されることを意図しています。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを利用することは避けてください。

初級から中級まで：定義(II)

本記事では、前回に引き続き#defineディレクティブについて理解を深めていきますが、今回はその第2の使用形態、すなわちマクロの作成に焦点を当てます。このテーマはやや複雑であるため、これまで学習を進めてきたアプリケーションを題材として取り上げながら説明していきます。この記事も楽しんでいただけたら幸いです。