
Redes neuronales en el trading: Transformador contrastivo de patrones (Final)
Introducción
El framework Atom-Motif Contrastive Transformer(AMCT) puede considerarse un sistema capaz de mejorar la calidad de predicción de las tendencias del mercado combinando dos niveles de análisis: objetos elementales y estructuras complejas. La idea básica consiste en que las velas y los patrones formados por ellas suponen diferentes representaciones de la misma situación de mercado. Esto permite una alineación natural de las dos representaciones durante el entrenamiento del modelo, mientras que la extracción de la información adicional inherente a las representaciones de distintos niveles ayudará a mejorar la calidad de las predicciones generadas.
Además, los patrones de mercado similares en gráficos de distintos marcos temporales o instrumentos suelen proporcionar señales similares. Por consiguiente, el uso de técnicas de aprendizaje contrastivo puede identificar patrones clave y mejorar la calidad de su interpretación. Y para lograr una identificación más precisa de los patrones que desempeñan un papel importante en la identificación de las tendencias del mercado, los desarrolladores del framework AMCT han introducido un mecanismo de atención basado en propiedades que explota los enfoques de atención cruzada.
A continuación le mostramos la visualización del autor del framework Atom-Motif Contrastive Transformer.
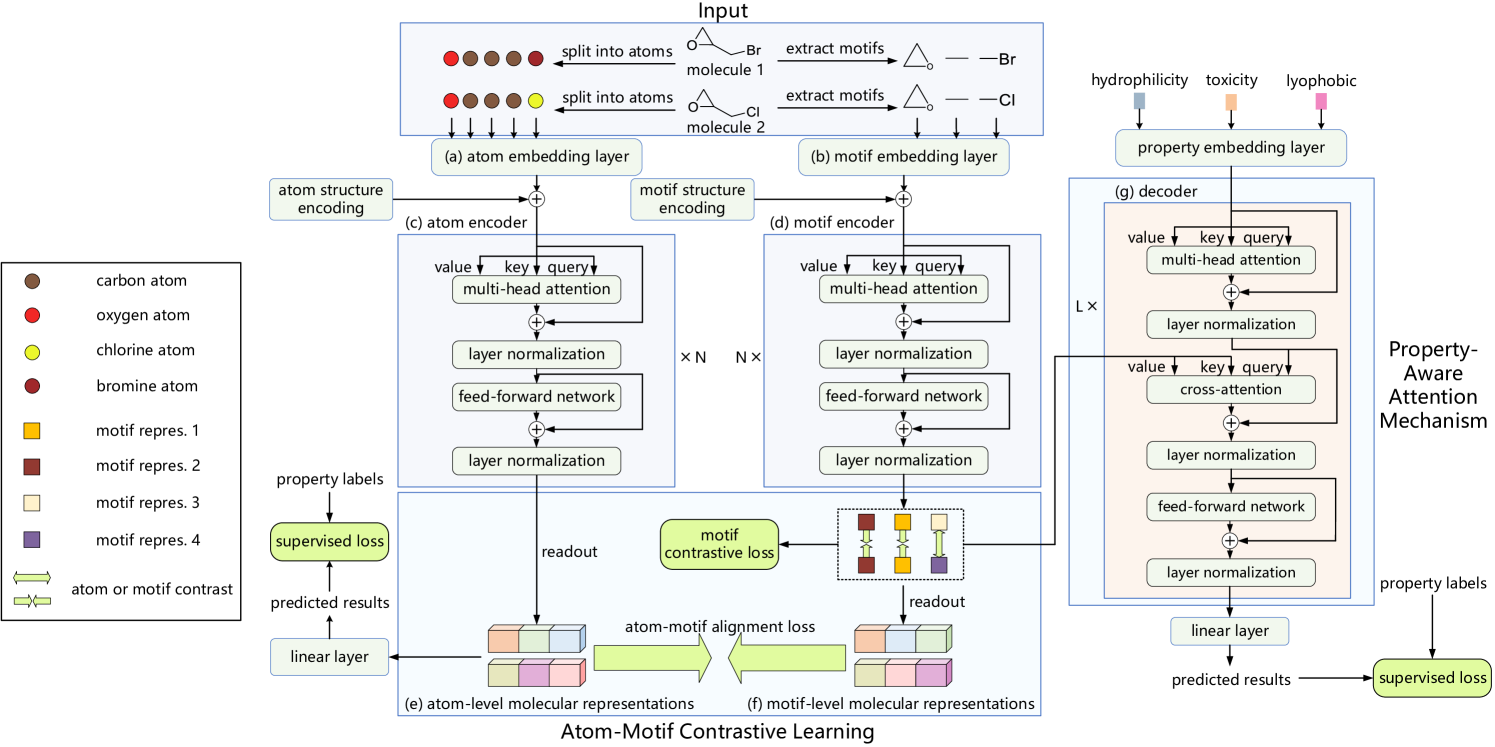
En el artículo anterior, analizamos la implementación de los pipelines de velas y patrones, y también construimos una clase de atención cruzada relativa que planeamos utilizar en el módulo para analizar las interdependencias entre las propiedades de las situaciones de mercado y los patrones de velas. Hoy continuaremos la labor iniciada.
1. Análisis de las interdependencias entre Propiedades y Motivos
Vamos a hablar un poco del módulo de análisis de las interdependencias de propiedades y motivos. Una de las cuestiones clave es qué entendemos exactamente por "propiedades". A primera vista, puede parecer una pregunta sencilla, pero en la práctica resulta bastante complicada. Los autores del framework AMCT usaron distintas propiedades de las sustancias que querían identificar y analizar en moléculas. Sin embargo, ¿cómo definimos las propiedades en el contexto de las situaciones de mercado y, además, cómo podemos describirlas correctamente?
Tomaremos como ejemplo una tendencia. En la literatura clásica sobre el análisis técnico de los mercados, las tendencias suelen dividirse en tres categorías: alcista, bajista y lateral (plana). Pero entonces nos surge la pregunta: ¿resulta suficiente esta clasificación para un análisis en profundidad? ¿Cómo podemos describir con precisión la dinámica del movimiento de los precios y la fuerza de la tendencia?
Y más cuestiones aún se plantean a la hora de seleccionar propiedades características de la situación del mercado en el contexto de la resolución de problemas prácticos concretos.
Pero si no tenemos una solución aceptable para este asunto, podemos enfocarlo desde otro ángulo. Así que le pediremos al modelo que aprenda de forma independiente las propiedades de las situaciones de mercado presentadas en la muestra de entrenamiento relevantes para la tarea que nos ocupa. Similar a las primitivas lingüísticas entrenadas en el framework RefMask3D, generaremos un tensor entrenable de propiedades relevantes para un problema práctico concreto. Implementaremos un algoritmo de este tipo en la clase CNeuronPropertyAwareAttention, cuya estructura se muestra a continuación.
class CNeuronPropertyAwareAttention : public CNeuronRMAT { protected: CBufferFloat cTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronPropertyAwareAttention(void) {}; ~CNeuronPropertyAwareAttention(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint properties, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronPropertyAwareAttention; } };
Así, usaremos CNeuronRMAT como clase padre que implementará el algoritmo del modelo lineal. Como ya sabe, los objetos internos de nuestra clase padre están empaquetados en un único array dinámico. Esto nos permite no declarar nuevos objetos en la estructura de clases al cambiar la arquitectura interna que estamos construyendo. Bastará con redefinir el método virtual de inicialización de objetos, en el que se creará la secuencia necesaria de objetos internos. La única limitación será la linealidad de la arquitectura.
Desafortunadamente, la arquitectura de atención cruzada se sale un poco de la linealidad porque utiliza 2 fuentes de datos de origen. Por consiguiente, nos veremos obligados a redefinir los métodos virtuales de pasada directa e inversa. Le propongo estudiar algoritmos para los métodos redefinidos.
En los parámetros del método Init de inicialización de un nuevo objeto, obtendremos constantes que nos permitirán definir inequívocamente la arquitectura del objeto que se va a crear.
bool CNeuronPropertyAwareAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint properties, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * properties, optimization_type, batch)) return false;
Y en el cuerpo del método llamaremos inmediatamente al método homónimo de la clase básica de la capa neuronal totalmente conectada CNeuronBaseOCL.
Tenga en cuenta que en este caso se llamará al método de la capa neuronal básica, no la directa del padre. Al fin y al cabo, solo queremos inicializar las interfaces básicas llamando al método especificado. Y redefiniremos completamente la secuencia de objetos internos.
A continuación, prepararemos un array dinámico de registros de punteros a los objetos internos.
cLayers.Clear(); cLayers.SetOpenCL(OpenCL);
Y declararemos las variables locales para almacenar temporalmente los punteros a los objetos creados.
CNeuronBaseOCL *neuron=NULL; CNeuronRelativeSelfAttention *self_attention = NULL; CNeuronRelativeCrossAttention *cross_attention = NULL; CResidualConv *ff = NULL;
Aquí terminaremos el trabajo preparatorio y procederemos a la construcción de la secuencia de objetos internos. En primer lugar, crearemos 2 capas consecutivas totalmente conectadas para generar un tensor entrenable de propiedades que puedan caracterizar la situación del mercado.
int idx = 0; neuron = new CNeuronBaseOCL(); if (!neuron || !neuron.Init(window * properties, idx, OpenCL, 1, optimization, iBatch) || !cLayers.Add(neuron)) return false; CBufferFloat *temp = neuron.getOutput(); if (!temp.Fill(1)) return false; idx++; neuron = new CNeuronBaseOCL(); if (!neuron || !neuron.Init(0, idx, OpenCL, window * properties, optimization, iBatch) || !cLayers.Add(neuron)) return false;
Aquí utilizaremos los enfoques que hemos probado con éxito en trabajos anteriores. La primera capa contendrá una sola neurona con un valor fijo de "1". Mientras que la segunda capa neuronal generará la secuencia de incorporaciones que necesitamos, para cuyo entrenamiento utilizaremos la funcionalidad básica del objeto creado. Luego añadiremos los punteros a ambos objetos a nuestro array dinámico, según la secuencia en la que son llamados.
Luego tendremos que construir la estructura del decodificador del Transformer casi vainilla. Solo sustituiremos en él los módulos de atención por los correspondientes con codificación relativa de la estructura de la secuencia analizada. Para ello, crearemos un ciclo con un número de iteraciones igual a un número determinado de capas interiores.
for (uint i = 0; i < layers; i++) { idx++; self_attention = new CNeuronRelativeSelfAttention(); if (!self_attention || !self_attention.Init(0, idx, OpenCL, window, window_key, properties, heads, optimization, iBatch) || !cLayers.Add(self_attention) ) { delete self_attention; return false; }
En el cuerpo del ciclo, primero crearemos e inicializaremos una capa de Self-Attention relativa que analizará las interdependencias entre las incorporaciones de nuestras propiedades aprendidas que describen la situación del mercado en el contexto del problema a resolver. Por lo tanto, la longitud de la secuencia analizada vendrá determinada por el parámetro properties. También añadiremos el puntero al objeto creado a nuestro array dinámico.
A continuación, crearemos una capa de atención cruzada relativa.
idx++; cross_attention = new CNeuronRelativeCrossAttention(); if (!cross_attention || !cross_attention.Init(0, idx, OpenCL, window, window_key, properties, heads, window, units_count, optimization, iBatch) || !cLayers.Add(cross_attention) ) { delete cross_attention; return false; }
Aquí, también utilizaremos la información de incorporación de las propiedades como flujo principal, que en realidad determinará el tamaño del tensor resultante. Por ello, también especificaremos que la longitud de la secuencia de bloques FeedForward será igual al número de propiedades generadas.
idx++; ff = new CResidualConv(); if (!ff || !ff.Init(0, idx, OpenCL, window, window, properties, optimization, iBatch) || !cLayers.Add(ff) ) { delete ff; return false;}
}
Luego añadiremos los punteros a los objetos creados al array dinámico y procederemos a la siguiente iteración del ciclo.
Tras ejecutar con éxito el número necesario de iteraciones del ciclo, nuestro array dinámico contendrá el conjunto completo de objetos necesarios para ejecutar correctamente el algoritmo del módulo de análisis de interdependencias entre las propiedades entrenadas y los patrones encontrados. Solo necesitaremos sustituir los punteros a los búferes de datos, lo cual nos permitirá reducir significativamente el número de operaciones durante el entrenamiento del modelo.
if (!SetOutput(ff.getOutput()) || !SetGradient(ff.getGradient())) return false; //--- return true;}
Y finalizaremos el método transmitiendo el resultado lógico de las operaciones al programa que realiza la llamada.
Una vez que hayamos terminado de inicializar el nuevo objeto de nuestra clase, construiremos el algoritmo de pasada directa, que se implementará en el método feedForward. Y aquí deberemos observar inmediatamente que, a pesar de usar el módulo de atención cruzada en nuestra arquitectura de bloques, el método de pasada directa solo obtiene el puntero al objeto de datos de origen. Esto se debe a que la segunda fuente de datos de origen ("propiedades") es generada directamente por los objetos de nuestra clase.
bool CNeuronPropertyAwareAttention::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
En el cuerpo del método comprobaremos directamente la relevancia del puntero obtenido. Al fin y al cabo, usaremos el objeto resultante como fuente de datos adicional. Esto significa que accederemos directamente a los búferes de este objeto y, en caso de obtener un puntero irrelevante al objeto, nos arriesgaremos a obtener un error crítico.
Luego declararemos una variable local para almacenar temporalmente los punteros al objeto.
CNeuronBaseOCL *neuron = NULL;
Tenga en cuenta que estamos declarando una variable de nuestro tipo de capa neuronal básica. Y debemos recordar que es el ancestro común de todos nuestros objetos de capa neuronal. Esto nos permitirá almacenar el puntero a cualquiera de los objetos internos de la capa neuronal en una variable declarada y utilizar sus interfaces básicas y métodos redefinidos.
A continuación, comenzaremos a trabajar con nuestro modelo de generación de incorporación de propiedades. Además, conviene recordar que sus objetos se escribirán en los dos primeros elementos de nuestro array dinámico. Nuestra primera capa neuronal contendrá un valor fijo, por lo que inmediatamente procederemos a llamar al método de pasada directa del segundo objeto, transmitiéndole como datos de entrada el puntero al objeto de la primera capa.
if (bTrain) { neuron = cLayers[1]; if (!neuron || !neuron.FeedForward(cLayers[0])) return false; }
Sin embargo, llamaremos el método de pasada directa de la segunda capa solo durante el entrenamiento del objeto, ya que en la fase de entrenamiento examinaremos los estados del mercado de la muestra de entrenamiento en busca de propiedades relevantes para la tarea en cuestión. Durante el funcionamiento, sin embargo, utilizaremos las propiedades de incorporación aprendidas previamente, lo que significa que el resultado de esta capa será siempre constante. Y no necesitaremos realizar operaciones de generación del tensor de incorporación en cada pasada. En consecuencia, omitiremos este pasada en la explotación, lo cual nos permitirá reducir el tiempo de decisión del modelo.
A continuación, simplemente organizaremos un ciclo de iteración de las capas internas restantes con sucesivas llamadas a sus métodos de pasada directa. Y como fuentes de datos de origen transmitiremos los resultados de la capa anterior y el búfer de resultados del objeto obtenido en los parámetros del método.
for (int i = 2; i < cLayers.Total(); i++) { neuron = cLayers[i]; if (!neuron.FeedForward(cLayers[i - 1], NeuronOCL.getOutput())) return false; } //--- return true; }
Tenga en cuenta que los resultados de la capa anterior se usarán como fuente principal de datos de entrada. A través de esta línea troncal se transmitirán las propiedades aprendidas de las situaciones de mercado. Y se analizarán en todos los módulos de atención y en el bloque FeedForward de nuestro descodificador. Las incorporaciones de patrones encontradas en la descripción de la situación del mercado analizado, obtenidas en los parámetros del método, nos ayudarán a hacer hincapié en las propiedades relevantes para la situación actual del mercado. Así, a la salida del descodificador obtendremos otra representación de la situación del mercado en forma de propiedades con acentos.
Una vez ejecutadas todas las iteraciones de nuestro ciclo, finalizaremos el método de pasada directa transmitiendo el resultado lógico de las operaciones al programa que realiza la llamada.
A continuación, tendremos que trabajar en la organización de los procesos de pasada inversa de nuestra clase. La organización del método updateInputWeights para actualizar los parámetros del modelo no supone ninguna dificultad. Aquí, simplemente llamaremos secuencialmente a los métodos de los objetos internos homónimos. Pero el método de distribución de gradientes de error calcInputGradients tiene sus matices.
Como usted sabrá, el algoritmo del método de distribución del gradiente de error debe replicar por entero el flujo de información de la pasada directa, pero en orden inverso, distribuyendo el gradiente de error a todos los objetos según su influencia en la salida global del modelo. Y si un objeto es la fuente de datos de entrada de varios flujos de información, deberá recibir su parte de gradiente de error de cada uno de ellos.
Echemos un vistazo a la implementación del método de pasada directa. En él, se transmitirá el puntero al objeto de incorporación de patrones en los parámetros de todas las capas neuronales internas de nuestro Decodificador. Obviamente, los módulos de Self-Attention y FeedForward simplemente lo ignorarán, ya que no utilizan una segunda fuente de datos de origen. Pero aquí, el módulo de atención cruzada los utilizará en cada capa interna de nuestro Decodificador. Por lo tanto, en el proceso de distribución de errores, tendremos que sumar al objeto de incorporación de patrones su parte del gradiente de error de cada módulo de atención cruzada.
En los parámetros del método, obtendremos el puntero al objeto de representación de los patrones detectados. Y en el cuerpo del método comprobaremos inmediatamente la relevancia del puntero recibido.
bool CNeuronPropertyAwareAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
A continuación tendremos que hacer algunos preparativos. Aquí comprobaremos primero la presencia del búfer de datos auxiliar previamente inicializado en el que pensamos escribir los valores intermedios de los gradientes de error. Y asegurarnos de que su tamaño resulte suficiente. Si el resultado es negativo, en cualquier punto de control inicializaremos un nuevo búfer de datos de tamaño suficiente.
if (cTemp.GetIndex() < 0 || cTemp.Total() < NeuronOCL.Neurons()) { cTemp.BufferFree(); if (!cTemp.BufferInit(NeuronOCL.Neurons(), 0) || !cTemp.BufferCreate(OpenCL)) return false; }
Y luego pondremos a cero el búfer de gradiente de error obtenido en los parámetros del objeto.
if (!NeuronOCL.getGradient() || !NeuronOCL.getGradient().Fill(0)) return false;
Por lo común, no realizamos semejante operación porque, al realizar las operaciones de distribución del gradiente de error, sustituimos los valores almacenados previamente por valores nuevos. Y esta es una buena solución para los modelos lineales. Pero, por otra parte, esta implementación nos obliga a buscar soluciones si recogemos gradientes de error de varias líneas troncales.
Una vez efectuado con éxito el trabajo preparatorio, organizaremos un ciclo de iteración inversa de las capas internas de nuestro bloque para distribuir el gradiente de error sobre ellas.
CNeuronBaseOCL *neuron = NULL; for (int i = cLayers.Total() - 2; i > 0; i--) { neuron = cLayers[i]; if (!neuron.calcHiddenGradients(cLayers[i + 1], NeuronOCL.getOutput(), GetPointer(cTemp), (ENUM_ACTIVATION)NeuronOCL.Activation())) return false;
En el cuerpo del ciclo, llamaremos al método de distribución de gradientes de error de cada capa interna, transmitiéndole los parámetros correspondientes. Solo que en lugar de un búfer de gradiente de error, transmitiremos el puntero a nuestro búfer de almacenamiento temporal de datos. Y después de ejecutar con éxito las operaciones del método llamado del objeto interno, comprobaremos el tipo de la capa neuronal. Después de todo, debemos recordar que no todas las capas neuronales internas utilizan una segunda fuente de datos. En el caso de encontrar un módulo de atención cruzada, añadiremos el gradiente de error resultante de la segunda fuente de datos a los valores acumulados previamente en el búfer del objeto de incorporación de patrones.
if (neuron.Type() == defNeuronRelativeCrossAttention) { if (!SumAndNormilize(NeuronOCL.getGradient(), GetPointer(cTemp), NeuronOCL.getGradient(), 1, false, 0, 0, 0, 1)) return false; } //--- return true;}
Tras ejecutar con éxito todas las iteraciones de nuestro ciclo, retornaremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.
Con esto concluirá nuestro trabajo sobre el bloque de atención basado en propiedades. Podrá ver el código completo de esta clase y todos sus métodos en el archivo adjunto.
2. El framework AMCT
Hemos trabajado mucho para implementar los bloques individuales que componen el framework Atom-Motif Contrastive Transformer. Ahora ha llegado el momento de combinar los módulos creados en una única estructura. Para realizar esta tarea, crearemos un objeto CNeuronAMCT, cuya estructura le mostramos a continuación.
class CNeuronAMCT : public CNeuronBaseOCL { protected: CNeuronRMAT cAtomEncoder; CNeuronMotifEncoder cMotifEncoder; CLayer cMotifProjection; CNeuronPropertyAwareAttention cPropertyDecoder; CLayer cPropertyProjection; CNeuronBaseOCL cConcatenate; CNeuronMHAttentionPooling cPooling; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronAMCT(void) {}; ~CNeuronAMCT(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint properties, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronAMCT; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
En la estructura presentada, vemos la declaración de los objetos que hemos implementado, a los que añadiremos dos arrays dinámicos. Hablaremos de su funcionalidad un poco más adelante. Todos los objetos se declararán de forma estática, lo cual nos permitirá dejar vacíos el constructor y el destructor de la clase, La inicialización de todos los objetos heredados y declarados se realizará en el método Init.
En los parámetros del método de inicialización obtendremos las constantes básicas que nos permitirán definir de forma inequívoca la arquitectura del objeto que vamos a crear.
bool CNeuronAMCT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint properties, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Y en el cuerpo del método llamaremos inmediatamente al método homónimo de la clase padre, transmitiéndole algunos de los parámetros obtenidos.
Creo que habrá notado que en la estructura de objetos presentada no hay variables internas para almacenar los valores de los parámetros obtenidos. Todas las constantes que definen la arquitectura de nuestra clase se usarán para inicializar objetos internos, en cuyo fondo se almacenarán los valores necesarios. En los métodos de pasada directa e inversa operaremos solo con objetos internos. Por lo tanto, no crearemos variables innecesarias.
A continuación, inicializaremos los objetos internos. Y primero inicializaremos los objetos de nuestras dos líneas troncales: las velas y los patrones.
int idx = 0; if (!cAtomEncoder.Init(0, idx, OpenCL, window, window_key, units_count, heads, layers, optimization, iBatch)) return false; idx++; if (!cMotifEncoder.Init(0, idx, OpenCL, window, window_key, units_count, heads, layers, optimization, iBatch)) return false;
A pesar de las diferencias en la arquitectura de las líneas troncales, ambas trabajarán con la misma fuente de datos de origen y recibirán parámetros idénticos en esta fase.
A la salida de las líneas troncales esperamos obtener dos representaciones de la situación del mercado analizado: a nivel de velas y a nivel de patrones. Y los autores del framework proponen compararlos para enriquecerse mutuamente y aclarar ideas. Pero aquí deberemos prestar atención a que los tamaños de los tensores resultantes en ambos casos son diferentes. Y este hecho sin duda complica el proceso de comparación de resultados. Por lo tanto, usaremos un modelo de escalado de datos pequeños que aplicaremos a los resultados de la línea troncal del patrón. Luego almacenaremos los punteros a los objetos del modelo de escala en el array dinámico cMotifProjection.
En primer lugar, prepararemos el array dinámico especificado.
cMotifProjection.Clear(); cMotifProjection.SetOpenCL(OpenCL);
Y determinaremos la longitud de la secuencia de patrones. Como ya sabe, a la salida de la línea troncal de patrones obtendremos un tensor concatenado de incorporaciones de dos niveles.
int motifs = int(cMotifEncoder.Neurons() / window);
Obsérvese que los tensores de representación solo se distinguen en la longitud de la secuencia. En este caso, además, hemos preservado el tamaño del vector de la descripción de un único elemento de la secuencia. Por lo tanto, resulta lógico que trabajemos con filas de secuencias unitarias individuales en el proceso de escalado. Para ello, primero transpondremos el tensor de representación a nivel de patrones.
idx++; CNeuronTransposeOCL *transp = new CNeuronTransposeOCL(); if (!transp || !transp.Init(0, idx, OpenCL, motifs, window, optimization, iBatch) || !cMotifProjection.Add(transp)) return false;
Y luego usaremos la capa de convolución para escalar secuencias unitarias.
idx++; CNeuronConvOCL *conv = new CNeuronConvOCL(); if (!conv || !conv.Init(0, idx, OpenCL, motifs, motifs, units_count, 1, window, optimization, iBatch) || !cMotifProjection.Add(conv)) return false; conv.SetActivationFunction((ENUM_ACTIVATION)cAtomEncoder.Activation());
Tenga en cuenta que el tamaño de la ventana de datos de origen y su tamaño de pasada serán iguales a la longitud de la secuencia de representación a nivel de patrones. En este caso, el número de filtros será igual a la longitud de la secuencia de presentación en el nivel de las velas.
Otra cosa a la que deberemos prestar atención son los parámetros de longitud de secuencia y número de secuencias unitarias. En este caso, hemos especificado que la secuencia de datos de origen constará de un único elemento, mientras que el número de filas unitarias de la secuencia será igual al tamaño del vector de descripción de un elemento de la secuencia de datos original. Este conjunto de parámetros nos permitirá crear matrices de pesos entrenables independientes para cada secuencia unitaria de los datos de origen resultantes. En otras palabras, para escalar secuencias de diferentes elementos, se utilizarán distintas matrices de escalado para describir un elemento de la secuencia original. Esto nos permitirá establecer un proceso de escalado más flexible.
Y no nos olvidaremos de sincronizar las funciones de activación en las salidas de la capa convolucional de escalado y la línea troncal de presentación en el nivel de las velas.
Después, retornaremos los datos ya escalados a la representación original utilizando la capa de transposición de datos.
idx++; transp = new CNeuronTransposeOCL(); if (!transp || !transp.Init(0, idx, OpenCL, window, units_count, optimization, iBatch) || !cMotifProjection.Add(transp)) return false; transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
A continuación, inicializaremos un bloque de atención cruzada de propiedades y patrones, cuya salida planeamos para obtener una representación a nivel de propiedad del estado del mercado analizado.
idx++; if (!cPropertyDecoder.Init(0, idx, OpenCL, window, window_key, properties, motifs, heads, layers, optimization, iBatch)) return false;
Y aquí llegamos al momento culminante. El resultado de los tres bloques nos ofrece tres representaciones diferentes del mismo estado del mercado analizado. Además, todos ellos están representados por tensores de distintos tamaños. ¿Y ahora qué? ¿Cómo pueden usarse para resolver problemas concretos? ¿Cuál elegimos para obtener los resultados de máxima calidad?
Creo que deberíamos usar los resultados de los tres bloques. Ya hemos inicializado el modelo de escalado de representación de patrones. Ahora crearemos uno similar para escalar la representación de propiedades. Almacenaremos los punteros a los objetos de este modelo de escalado en el array dinámico cPropertyProjection.
cPropertyProjection.Clear(); cPropertyProjection.SetOpenCL(OpenCL); idx++; transp = new CNeuronTransposeOCL(); if (!transp || !transp.Init(0, idx, OpenCL, properties, window, optimization, iBatch) || !cPropertyProjection.Add(transp)) return false; idx++; conv = new CNeuronConvOCL(); if (!conv || !conv.Init(0, idx, OpenCL, properties, properties, units_count, 1, window, optimization, iBatch) || !cPropertyProjection.Add(conv)) return false; conv.SetActivationFunction((ENUM_ACTIVATION)cAtomEncoder.Activation()); idx++; transp = new CNeuronTransposeOCL(); if (!transp || !transp.Init(0, idx, OpenCL, window, units_count, optimization, iBatch) || !cPropertyProjection.Add(transp)) return false; transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
Las tres representaciones convertidas a una sola dimensionalidad las concatenaremos en un único tensor.
idx++; if (!cConcatenate.Init(0, idx, OpenCL, 3 * window * units_count, optimization, iBatch)) return false;
Como puede ver ahora, hemos obtenido un tensor concatenado que combina tres puntos de vista diferentes de una misma situación de mercado. ¿No le recuerda esto a los resultados de la atención multicabeza? De hecho, tenemos los resultados de las tres cabezas, y para obtener los valores finales, usaremos la capa de agrupación basada en la dependencia.
idx++; if(!cPooling.Init(0, idx, OpenCL, window, units_count, 3, optimization, iBatch)) return false;
Ahora solo nos quedará sustituir los búferes de datos de las interfaces heredadas por el objeto de pooling correspondiente, lo que nos permitirá eliminar operaciones innecesarias de copiado de datos.
if (!SetOutput(cPooling.getOutput(), true) || !SetGradient(cPooling.getGradient(), true)) return false; //--- return true; }
Y finalizar el método de inicialización, habiendo transmitido previamente el resultado lógico de las operaciones al programa que realiza la llamada.
Una vez finalizado el trabajo de construcción del método de inicialización de nuestro objeto, organizaremos los procesos de pasada directa. Como de costumbre, implementaremos su algoritmo en el método feedForward.
bool CNeuronAMCT::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cAtomEncoder.FeedForward(NeuronOCL)) return false; if(!cMotifEncoder.FeedForward(NeuronOCL)) return false;
En los parámetros del método obtendremos el puntero al objeto de datos de origen, que transmitiremos inmediatamente a nuestras líneas troncales de representación de la situación del mercado a nivel de velas y patrones.
Luego transmitiremos los resultados de la línea troncal de patrones al módulo de atención cruzada de propiedades y patrones.
if(!cPropertyDecoder.FeedForward(cMotifEncoder.AsObject())) return false;
En esta fase, hemos obtenido tres representaciones de la situación analizada. Vamos a convertirlos a una escala de datos común. Para ello, primero escalaremos la representación a nivel de patrones.
//--- Motifs projection CNeuronBaseOCL *prev = cMotifEncoder.AsObject(); CNeuronBaseOCL *current = NULL; for(int i = 0; i < cMotifProjection.Total(); i++) { current = cMotifProjection[i]; if(!current || !current.FeedForward(prev, NULL)) return false; prev = current; }
Y organizaremos un proceso similar para la representación a nivel de propiedades.
//--- Property projection prev = cPropertyDecoder.AsObject(); for(int i = 0; i < cPropertyProjection.Total(); i++) { current = cPropertyProjection[i]; if(!current || !current.FeedForward(prev, NULL)) return false; prev = current; }
Ahora podremos combinar las tres representaciones en un único tensor.
//--- Concatenate uint window = cAtomEncoder.GetWindow(); uint units = cAtomEncoder.GetUnits(); prev = cMotifProjection[cMotifProjection.Total() - 1]; if(!Concat(cAtomEncoder.getOutput(), prev.getOutput(), current.getOutput(), cConcatenate.getOutput(), window, window, window, units)) return false;
Y utilizaremos la capa de agrupación para resumir los resultados de las tres representaciones de forma ponderada.
//--- Out if(!cPooling.FeedForward(cConcatenate.AsObject())) return false; //--- return true; }
Gracias a la sustitución de punteros del búfer de datos realizada en el método de inicialización, no necesitaremos copiar los datos en los búferes de interfaz de nuestra clase. Simplemente finalizaremos el método devolviendo el resultado lógico de las operaciones al programa que realiza la llamada.
La siguiente etapa en nuestro trabajo consistirá en construir los métodos de pasada inversa. Y el más interesante en cuanto a la construcción de los algoritmos será el método de distribución del gradiente de error calcInputGradients. La cuestión es que la estructura ramificada de dependencias entre flujos de información propuesta por los autores del marco AMCT, ha dejado su impronta en el algoritmo del método anterior. Le sugiero echar un vistazo más de cerca a su implementación en el código.
En los parámetros del método, como es habitual, obtendremos el puntero al objeto de la capa anterior, al que deberemos transmitir el gradiente de error según la influencia de los datos de origen en el resultado final.
bool CNeuronAMCT::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Después comprobaremos directamente la pertinencia del puntero recibido. Y si no fuera válido, todas las demás operaciones carecerán de sentido.
A continuación, distribuiremos secuencialmente el gradiente de error entre los objetos internos. Aquí cabe señalar que, al sustituir los punteros a los búferes de datos de las interfaces, no necesitaremos copiar los datos de las interfaces externas a los objetos internos. Y podremos empezar inmediatamente a distribuir el gradiente de error a los objetos internos. En primer lugar, definiremos el gradiente de error a nivel del tensor concatenado de las tres representaciones del estado del entorno analizado.
if(!cConcatenate.calcHiddenGradients(cPooling.AsObject())) return false;
Y luego distribuiremos el gradiente de error entre las líneas troncales de las representaciones individuales. Luego transmitiremos directamente al Codificador el gradiente del error de representación al nivel de la vela. Y pasaremos los otros dos a sus respectivos modelos de escalado.
uint window = cAtomEncoder.GetWindow(); uint units = cAtomEncoder.GetUnits(); CNeuronBaseOCL *motifs = cMotifProjection[cMotifProjection.Total() - 1]; CNeuronBaseOCL *prop = cPropertyProjection[cPropertyProjection.Total() - 1]; if (!motifs || !prop || !DeConcat(cAtomEncoder.getGradient(), motifs.getGradient(), prop.getGradient(), cConcatenate.getGradient(), window, window, window, units)) return false;
A continuación, corregiremos los gradientes de error de las representaciones individuales con las funciones de activación correspondientes.
if (cAtomEncoder.Activation() != None) { if (!DeActivation(cAtomEncoder.getOutput(), cAtomEncoder.getGradient(), cAtomEncoder.getGradient(), cAtomEncoder.Activation())) return false; if (motifs.Activation() != None) { if (!DeActivation(motifs.getOutput(), motifs.getGradient(), motifs.getGradient(), motifs.Activation())) return false; if (prop.Activation() != None) { if (!DeActivation(prop.getOutput(), prop.getGradient(), prop.getGradient(), prop.Activation())) return false;
Y añadiremos el gradiente de error de coincidencia de las representaciones de velas y patrones.
if(!motifs.calcAlignmentGradient(cAtomEncoder.AsObject(), true)) return false;
Después, distribuiremos el gradiente de error entre los modelos de escalado organizando ciclos de iteración inversa de las capas neuronales de los modelos.
for (int i = cMotifProjection.Total() - 2; i >= 0; i--) { motifs = cMotifProjection[i]; if (!motifs || !motifs.calcHiddenGradients(cMotifProjection[i + 1])) return false; }
for (int i = cPropertyProjection.Total() - 2; i >= 0; i--) { prop = cPropertyProjection[i]; if (!prop || !prop.calcHiddenGradients(cPropertyProjection[i + 1])) return false; }
Luego pasaremos el gradiente de error del modelo de escalado de representación de propiedades al módulo de atención cruzada de propiedades y patrones. Y a continuación por el Codificador de patrones.
if (!cPropertyDecoder.calcHiddenGradients(cPropertyProjection[0]) || !cMotifEncoder.calcHiddenGradients(cPropertyDecoder.AsObject())) return false;
Pero debemos señalar que los resultados del Codificador de patrones también se han usado para el modelo de escalado de representación de patrones. Por ello, deberemos añadir el gradiente de error del segundo flujo de información. Para ello, primero almacenaremos el puntero al objeto de búfer de gradiente de error de nuestro Codificador de patrones en una variable local. Y luego lo sustituiremos por el búfer "donante".
Después seleccionaremos la capa de concatenación de las tres representaciones como objeto donante. El gradiente de error de la misma ya lo habremos distribuido a los flujos de información correspondientes. La capa en sí no tendrá parámetros entrenables. Por consiguiente, podremos eliminar sin problemas los valores del búfer. También será la capa con el mayor tamaño de búfer de todos los objetos internos de nuestro bloque, lo cual la convertirá en la mejor candidata a "donante".
Tras la sustitución de los búferes, obtendremos el gradiente de error del modelo de escalado. Luego sumaremos los datos de los dos flujos de información y devolveremos los punteros a los búferes de datos al estado inicial. Y luego pasaremos el gradiente de error a la capa de datos de origen.
CBufferFloat *temp = cMotifEncoder.getGradient(); if (!cMotifEncoder.SetGradient(cConcatenate.getGradient(), false) || !cMotifEncoder.calcHiddenGradients(cMotifProjection[0]) || !SumAndNormilize(temp, cMotifEncoder.getGradient(), temp, window, false, 0, 0, 0, 1) || !cMotifEncoder.SetGradient(temp, false) || !NeuronOCL.calcHiddenGradients(cMotifEncoder.AsObject())) return false;
Una situación similar nos esperará en el nivel de datos de origen: al gradiente de error obtenido del codificador de patrones, tendremos que añadirle la parte de influencia en el resultado por parte de la línea troncal del codificador de velas. Luego repetiremos el truco con la sustitución del puntero por el búfer de datos, pero para un objeto diferente.
temp = NeuronOCL.getGradient(); if (!NeuronOCL.SetGradient(cConcatenate.getGradient(), false) || !NeuronOCL.calcHiddenGradients(cAtomEncoder.AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, window, false, 0, 0, 0, 1) || !NeuronOCL.SetGradient(temp, false)) return false; //--- return true; }
Bueno, ya hemos distribuido completamente el gradiente de error entre todos los objetos del modelo y los datos de origen, ahora podemos finalizar el método, pero antes devolveremos el resultado lógico de las operaciones al programa que realiza la llamada.
Me gustaría llamar su atención sobre dos puntos de la aplicación presentada. En primer lugar, al sustituir los punteros a los búferes de gradiente, aquí resultará obligatorio que primero guardemos el puntero al búfer de datos original. Y luego, al llamar al método de sustitución del puntero, deberemos establecer la bandera false, que impedirá la eliminación del objeto escrito anteriormente. Esto nos permitirá guardar el objeto de búfer y, en un momento posterior, devolver el puntero a su lugar. Si utilizáramos la bandera true, como hicimos en el método de inicialización, borraríamos el objeto de búfer de datos existente y recibiríamos un error crítico en accesos posteriores al mismo.
El segundo punto se refiere a la arquitectura de la construcción del método. En el algoritmo presentado, no existe la creación de representaciones de patrones contrastados proporcionada por los autores del framework AMCT. Pero le recuerdo que hemos añadido la diversificación de representaciones en el objeto de atención cruzada relativa. Así que, en efecto, acabamos de trasladar el punto de adición del error de aprendizaje contrastivo.
Con esto concluimos nuestra revisión de los algoritmos para construir el framework Atom-Motif Contrastive Transformer. Podrá ver el código completo de todas las clases presentadas y sus métodos en el archivo adjunto. También le mostramos ahí la interacción con el entorno y los programas de entrenamiento del modelo. Todos ellos se mantendrán sin cambios respecto a los artículos anteriores. Solo hemos realizado modificaciones puntuales en la arquitectura del codificador del entorno. Aquí hemos sustituido una capa.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronAMCT; descr.window = BarDescr; // Window (Indicators to bar) { int temp[] = {HistoryBars, 100}; // Bars, Properties if(ArrayCopy(descr.units, temp) < (int)temp.Size()) return false; } descr.window_out = EmbeddingSize / 2; // Key Dimension descr.layers = 5; // Layers descr.step = 4; // Heads descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
En el anexo figura una descripción completa de la arquitectura de los modelos entrenados.
3. Simulación
Hemos trabajado mucho para implementar el framework Atom-Motif Contrastive Transformer utilizando herramientas MQL5, y ha llegado el momento de probar en la práctica la eficacia de los enfoques implementados. Para ello, entrenaremos el modelo utilizando los nuevos objetos con datos históricos reales y luego probaremos la política entrenada en el probador de estrategias de MetaTrader 5 en un periodo de tiempo fuera de la muestra de entrenamiento.
Como de costumbre, entrenaremos el modelo offline con una muestra de entrenamiento previamente recopilada de pasadas para todo el año 2023. El entrenamiento será iterativo y, tras varias iteraciones de entrenamiento de los modelos, realizaremos una actualización de la muestra de entrenamiento. Esto nos permitirá lograr la evaluación más precisa de las acciones del Agente según la política vigente.
Durante el entrenamiento, hemos logrado obtener un modelo capaz de generar beneficios tanto en la muestra de entrenamiento como en la de prueba. No obstante, debemos considerar un pequeño detalle: El modelo obtenido realiza muy pocas transacciones. Hemos ampliado incluso el periodo de prueba a 3 meses. Ahora le presentaremos los resultados de las pruebas.
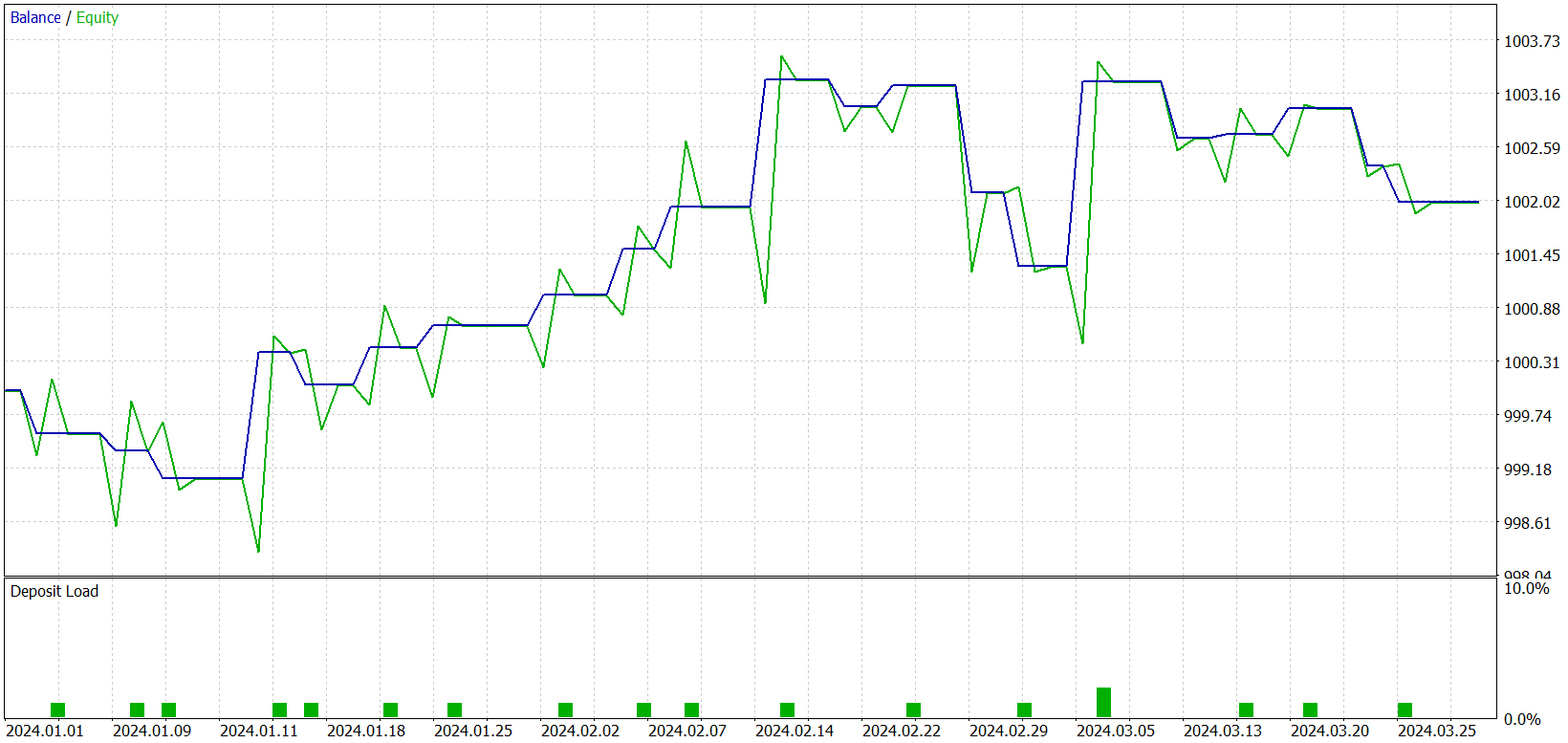
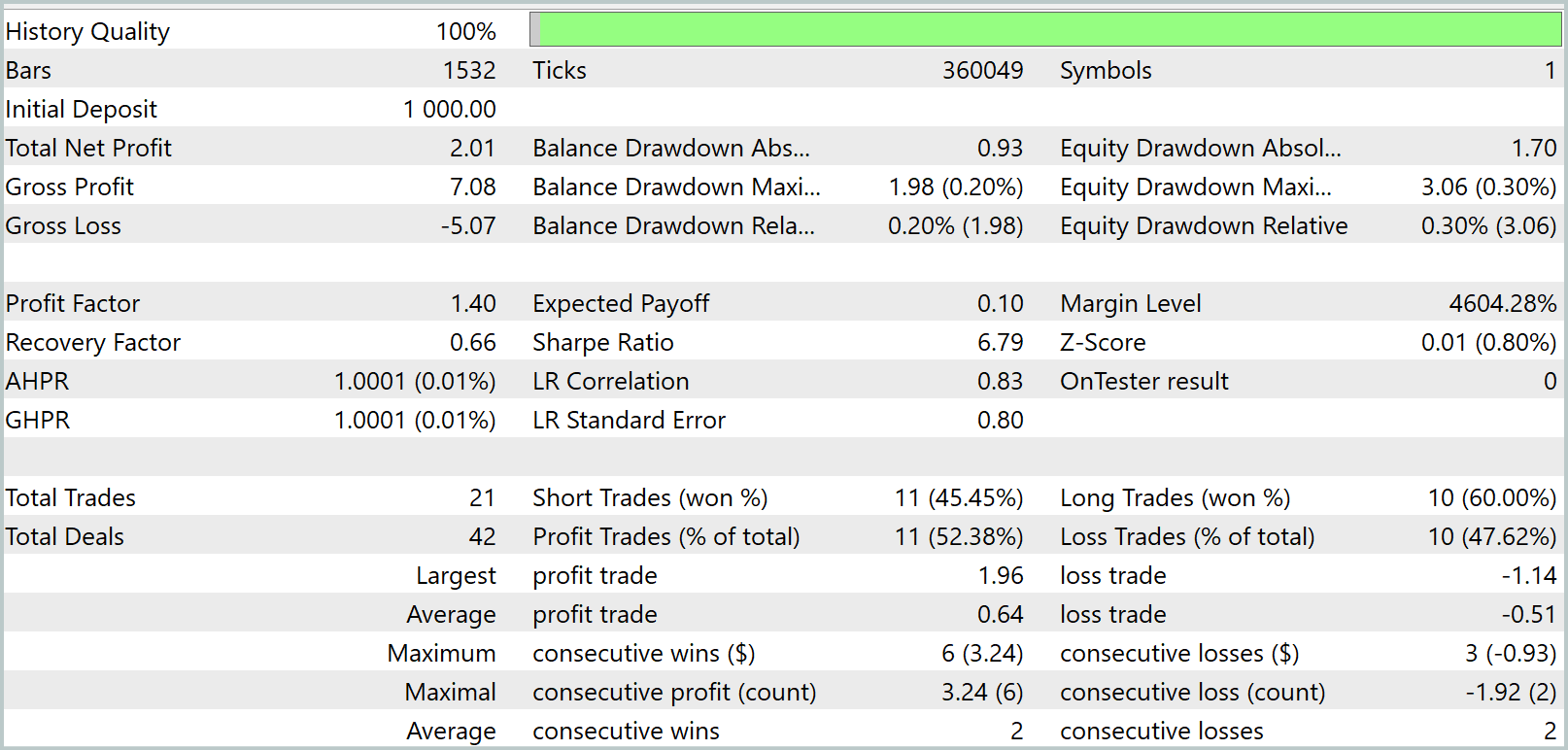
Como se desprende de los datos presentados, durante el intervalo de tres meses del periodo de prueba el modelo ha realizado solo 21 transacciones y algo más de la mitad de ellas se han cerrado con beneficios. Pero echemos un vistazo al gráfico de balance. Vemos un crecimiento del balance en el primer mes y medio, que luego es sustituido por un movimiento lateral. De hecho, es un comportamiento bastante esperado. Nuestro modelo solo recopila las estadísticas de los estados del mercado de la muestra de entrenamiento. Y como en cualquier modelo estadístico, la muestra de entrenamiento debe ser representativa. Y del gráfico de balance podemos concluir que la muestra de entrenamiento de 1 año resulta representativa para los siguientes 1,2 - 1,5 meses.
Entonces podemos asumir que el entrenamiento del modelo con una muestra de entrenamiento de 10 años es capaz de producir un modelo con un rendimiento estable en 1 año. También cabe suponer que una muestra de entrenamiento más amplia permitirá identificar más patrones clave y propiedades entrenables. Y esto aumentará potencialmente el número de transacciones realizadas. Sin embargo, deberemos seguir trabajando con el modelo para confirmar o refutar estas hipótesis.
Conclusión
En los dos últimos artículos, hemos introducido el framework Atom-Motif Contrastive Transformer (AMCT), que se basa en los conceptos de elementos atómicos (velas) y motivos (patrones). La idea principal del método consiste en aplicar el aprendizaje por contraste para distinguir patrones informativos y no informativos a distintos niveles: desde los constituyentes elementales hasta las estructuras complejas. Esto permite al modelo no solo considerar los movimientos locales de los precios en el mercado, sino también identificar patrones significativos que pueden ofrecer información adicional para una previsión más precisa del futuro comportamiento del mercado. La arquitectura del Transformer subyacente a este marco reconoce eficazmente las dependencias a largo plazo y las relaciones complejas entre velas y patrones.
En la parte práctica, hemos implementado nuestra visión de los enfoques propuestos utilizando herramientas MQL5, hemos entrenado los modelos y los hemos probado con datos históricos reales. Por desgracia, el modelo obtenido ha resultado un poco "tacaño" con las transacciones. Sin embargo, se aprecia cierto potencial que esperamos desarrollar en futuros trabajos.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 5 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 6 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16192
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Creación de un modelo de restricción de tendencia de velas (Parte 9): Asesor Experto de múltiples estrategias (I)
Creación de un modelo de restricción de tendencia de velas (Parte 9): Asesor Experto de múltiples estrategias (I)
 Obtenga una ventaja sobre cualquier mercado (Parte V): Datos alternativos de FRED (Federal Reserve Economic Data) sobre el EURUSD
Obtenga una ventaja sobre cualquier mercado (Parte V): Datos alternativos de FRED (Federal Reserve Economic Data) sobre el EURUSD
 Redes neuronales en el trading: Representación adaptativa de grafos (NAFS)
Redes neuronales en el trading: Representación adaptativa de grafos (NAFS)
 Métodos de optimización de la biblioteca ALGLIB (Parte I)
Métodos de optimización de la biblioteca ALGLIB (Parte I)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso