交易中的神经网络：对比形态变换器（终章）

MetaTrader 5 — 交易系统 | 23 七月 2025, 07:43

136

Dmitriy Gizlyk

概述

原子-基序对比变换器（AMCT）框架可视作一个系统，设计通过集成两个层级的分析来增强市场趋势和形态预测的准确性：原子元素、和复杂结构。核心思路是烛条、及由它们形成的形态，只是同一市场场景的不同表征。这允许在模型训练过程中两种表征的性质统调。提取这些不同层级表征所固有的附加信息，可以显著提高生成预测的品质。

进而，在不同时间帧或金融产品中观察到的相似市场形态典型情况下会产生相似的信号。因此，对比学习方法的应用能够识别关键形态，并强化其解释品质。在判定市场趋势时，为了更准确地甄别扮演关键角色的形态，AMCT 框架的开发人员引入了一种属性感知注意力机制，可协同交叉注意力技术。

下面提供了作者所提议的 原子-基序对比变换器 框架的原始可视化。

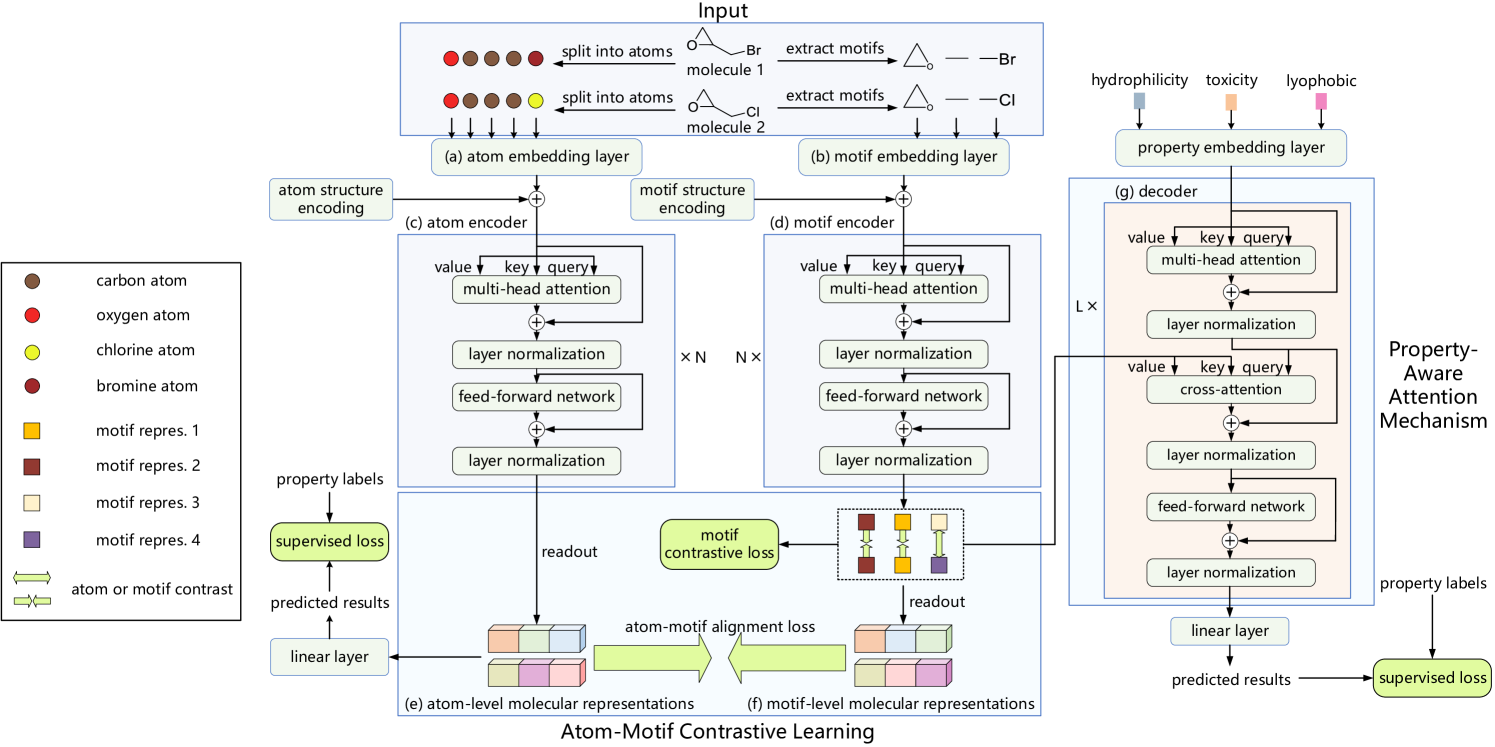
在上一篇文章中，我们讨论了烛条和形态管道的实现，我们还构造了一个相对交叉注意力类，我们计划在分析市场状况属性、及烛条形态之间相互依赖关系的模块中使用它。今天，我们将继续这项工作。

1. 分析属性和基序之间的相互依赖关系

我们就近查看负责分析属性和基序之间相互依赖关系的模块。此处的关键问题之一是：“属性”到底是什么意思？初看，这看似是一个直截了当的问题，但在实践中，它被证明是相当复杂的。AMCT 框架的作者最初把用它们用在各种化学属性，旨在检测和分析分子结构。但我们如何在市场情景的上下文中定义“属性” — 更重要的是，我们如何准确描述它们？

以趋势的概念为例。在经典的技术分析文献中，趋势通常分为三种类型：上行趋势、下行趋势、及横盘整理。但问题浮现 — 这种分类是否足以深入分析？我们如何能准确描述价格走势的动态、以及趋势的强度？

在解决特定实际任务的背景下，选择刻画市场状况的属性时，会出现更多问题。

如果我们还没有针对该问题的明确解决方案，我们就从不同的角度来处置它。我们可允许模型从训练数据集中自主学习市场属性，取代手工定义 — 从而识别出与手头任务相关的特征。更多像在 RefMask3D 框架中学到的语言基元一样，我们将生成一个可学习属性张量，用于解决特定的应用问题。这是我们在 CNeuronPropertyAwareAttention 类中实现的算法，其结构如下所示。

class CNeuronPropertyAwareAttention    :  public CNeuronRMAT
  {
protected:
   CBufferFloat      cTemp;
//---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronPropertyAwareAttention(void) {};
                    ~CNeuronPropertyAwareAttention(void) {};

   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint properties,
                          uint units_count, uint heads, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronPropertyAwareAttention; }
  };

我们以 CNeuronRMAT 作为父类，其实现了一个线性模型算法。您或许知道，我们的父类的内部组件被封装在一个动态数组之中。这种设计允许我们修改内部架构，无需在类结构中声明新的成员对象。所有需做的就是重写虚拟对象初始化方法，其中已创建了必要的内部组件序列。唯一的约束是架构必须保持线性。

不幸的是，交叉注意力架构并不完全符合线性需求，在于它的操作会用到两个独立的输入源。如是结果，我们需要覆盖前馈和反向传播通验的虚拟方法。我们就近查看在这些重写方法中实现的算法。

在初始化新对象的 Init 方法中，我们接收定义所创建对象架构唯一性的常量。

bool CNeuronPropertyAwareAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                         uint window, uint window_key, uint properties,
                                         uint units_count, uint heads, uint layers,
                                         ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * properties, optimization_type, batch))
      return false;

在方法主体中，我们立即调用全连接神经层基类 — CNeuronBaseOCL 中的相关方法。

重点要注意，在这种情况下，我们调用来自基础神经层的方法，而非调用直接父类中的方法。这是因为我们的目标是仅初始化基本接口。内部组件的顺序在我们的实现中会被彻底重新定义。

接下来，我们准备一个动态数组，存储指向内部组件的指针。

cLayers.Clear();
cLayers.SetOpenCL(OpenCL);

我们还声明了局部变量来临时存储指向我们将要创建对象的指针。

CNeuronBaseOCL *neuron=NULL;
CNeuronRelativeSelfAttention *self_attention = NULL;
CNeuronRelativeCrossAttention *cross_attention = NULL;
CResidualConv *ff = NULL;

如此这般，我们的准备工作完成，并转去构造内部对象的序列。首先，我们创建 2 个连续的全连接层，以便生成一个可训练特征嵌入张量，其嫩巩固刻画市场状况。

int idx = 0;
neuron = new CNeuronBaseOCL();
if (!neuron ||
    !neuron.Init(window * properties, idx, OpenCL, 1, optimization, iBatch) ||
    !cLayers.Add(neuron))
    return false;
CBufferFloat *temp = neuron.getOutput();
if (!temp.Fill(1))
    return false;
idx++;
neuron = new CNeuronBaseOCL();
if (!neuron ||
    !neuron.Init(0, idx, OpenCL, window * properties, optimization, iBatch) ||
    !cLayers.Add(neuron))
    return false;

于此，我们应用了在之前工作中已成功验证过的方法。第一层包含一个固定值为 1 的神经元。第二个神经层生成所需的嵌入序列，其将使用所创建对象的基本功能来训练。指向这两个对象的指针将按它们的调用顺序添加到我们的动态数组之中。

然后，我们继续构造一个与原版变换器解码器非常相似的结构。唯一的修改是，我们把标准的注意力模块替换为支持所分析序列结构的相对位置编码的等效模块。为达成这一点，我们创建了一个循环，迭代次数等于指定内层数量。

for (uint i = 0; i < layers; i++) 
  {
    idx++;
    self_attention = new CNeuronRelativeSelfAttention();
    
    if (!self_attention ||
        !self_attention.Init(0, idx, OpenCL, window, window_key, properties, heads, optimization, iBatch) ||
        !cLayers.Add(self_attention)
       ) 
       {
        delete self_attention;
        return false;
       }

在循环主体内部，我们首先创建、并初始化一个相对自注意力层，分析所解决任务的上下文中表征市场状况的可学习属性嵌入之间的相互依赖关系。因此，正在分析的序列的长度由 properties 参数决定。然后把指向新创建对象的指针添加到我们的动态数组之中。

接下来，我们创建一个相对交叉注意力层。

idx++;
cross_attention = new CNeuronRelativeCrossAttention();

if (!cross_attention ||
    !cross_attention.Init(0, idx, OpenCL, window, window_key, properties, heads, window, units_count,
                          optimization, iBatch) ||
    !cLayers.Add(cross_attention)
   ) 
   {
    delete cross_attention;
    return false;
  }

在此，属性的嵌入再次当作主要输入流，它决定了结果张量的形状。由此，FeedForward 模块中的序列长度也设置为等于所生成属性的数量。

idx++;
ff = new CResidualConv();
if (!ff ||
    !ff.Init(0, idx, OpenCL, window, window, properties, optimization, iBatch) ||
    !cLayers.Add(ff)
   ) 
   {
    delete ff;
    return false;



   }}

我们将指向这些新创建对象的指针添加到动态数组之中，并继续循环的下一次迭代。

所需次数的迭代成功完成后，我们的动态数组将包含正确实现模块所需的完整对象集，即分析可学习属性与检测到形态之间的相互依赖关系。最后一步是替换数据缓冲区指针，这令我们能够显著减少模型训练期间的操作数量。

if (!SetOutput(ff.getOutput()) ||
    !SetGradient(ff.getGradient()))
    return false;
//---
   return true;



  }

我们在结束该方法时向调用程序返回一个布尔结果，指示操作成功。

初始化类的新对象完成之后，我们继续实现 feedForward 方法中定义的前馈通验算法。重点要注意，即使我们的模块架构包括一个价差注意力模块，前馈通验方法仅接收单一指向输入数据对象的指针。这是因为第二个输入源（“属性”）是由我们的类对象于其内部生成。

bool CNeuronPropertyAwareAttention::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

在方法主体中，我们立即检查接收指针的相关性。由于该对象将用作附加数据源，故我们将直接访问其数据缓冲区。该阶段的无效指针可能会导致严重故障。

我们声明一个局部变量来临时存储指向输入对象的指针。

CNeuronBaseOCL *neuron = NULL;

注意，我们用神经层的基本类型来声明该变量。这种基本类型当作我们所有内部神经层对象的共同祖先。这允许我们在声明的变量中存储指向任何内部组件的指针，并使用它们的基本接口、及重写方法。

然后，我们继续配合属性嵌入生成模型工作。其对象存储在动态数组的前两个元素当中。第一个神经层包含一个固定值，故我们立即调用第二个对象的前馈方法，传递指向第一层的指针作为输入。

if (bTrain) 
   {
    neuron = cLayers[1];
    if (!neuron || 
        !neuron.FeedForward(cLayers[0]))
        return false;
   }

不过，我们仅在训练期间调用第二层的前馈方法，因为在该阶段，模型会学习从训练数据中提取出来的、与当前任务相关的属性嵌入。在操作使用期间，我们改用之前学习的属性嵌入。如是结果，该层的输出维持不变。而且无需在每次传递时重新生成嵌入张量。在实际操作期间跳过该步骤可减少模型的决策延迟。

之后，我们简单地遍历剩余的内层，按顺序调用它们的前馈方法。作为输入，我们提供前一层的输出、以及方法参数中所接收输入对象的结果缓冲区。

for (int i = 2; i < cLayers.Total(); i++) 
  {
    neuron = cLayers[i];
    if (!neuron.FeedForward(cLayers[i - 1], NeuronOCL.getOutput()))
        return false;
  }
//---
   return true;
  }

此处的主数据源是上一层的输出。这是主要数据流，其中传递的是市场状况的可学习属性的嵌入。这些嵌入由所有注意力模块、和解码器中的 FeedForward 模块处理。形态嵌入，在方法中作为接收的参数，表示在所分析市场状况描述中检测到的形态。它们突显把与当前上下文最相关的属性。如是结果，解码器将市场状况的精细表征输出为一组属性，并强调最重要的特征。

循环的所有迭代完成后，前馈方法最后向调用函数返回一个布尔值，指示操作成功。

接下来，我们需要构造反向传播过程。更新模型参数的 updateInputWeights 方法非常简单。我们只需按顺序在每个内部对象上调用相应方法。不过，用于分派误差梯度的 calcInputGradients 方法包含更多细致的细节。

如您所知，梯度分布算法必须完全镜像前馈通验的信息流，但顺序相反，基于对最终输出的贡献在所有分量之间分派误差梯度。如果一个对象当作多个信息流的数据源，则它必须从每个流中接收其误差梯度份额。

再看一下前馈通验实现。形态嵌入对象指针作为参数传递给解码器的所有内部神经层。当然，自注意力和 FeedForward 模块将会忽略它，因为它们不用第二个输入源。不过，交叉注意力模块将在解码器的每个内部层用到这些嵌入。因此，在误差反向传播期间，我们必须从每个交叉注意力模块中累积误差梯度的相应部分，并将总和应用到形态嵌入对象。

该方法接收指向形态嵌入对象的指针作为其参数之一。方法主体的第一步是验证指针，从而确保它是最新的，且可安全使用。

bool CNeuronPropertyAwareAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

接下来，我们有一些准备工作要做。此处，我们首先检查是否存在之前已初始化的辅助数据缓冲区，我们计划将误差梯度的中间值写入其中。我们还要确保它的大小足够。如果结果是否定的，我们在任何控制点初始化一个足够大小的新数据缓冲区。

if (cTemp.GetIndex() < 0 || cTemp.Total() < NeuronOCL.Neurons()) 
   {
    cTemp.BufferFree();
    if (!cTemp.BufferInit(NeuronOCL.Neurons(), 0) ||
        !cTemp.BufferCreate(OpenCL))
        return false;
   }

然后我们重置在对象参数中获得的误差梯度缓冲区。

if (!NeuronOCL.getGradient() ||
    !NeuronOCL.getGradient().Fill(0))
    return false;

我们通常不执行该操作，因为在执行误差梯度分派操作时，我们会用新值替换以前存储的值。对于线性模型来说，这是一个优秀的解决方案。但另一方面，如此实现迫使我们在从若干路径收集误差梯度的情况下寻找变通之法。

准备工作成功完成之后，我们运行逆向循环遍历模块内层，以便在它们之间分派误差梯度。

CNeuronBaseOCL *neuron = NULL;
for (int i = cLayers.Total() - 2; i > 0; i--) 
  {
    neuron = cLayers[i];
    if (!neuron.calcHiddenGradients(cLayers[i + 1], NeuronOCL.getOutput(),
                                    GetPointer(cTemp),
                                    (ENUM_ACTIVATION)NeuronOCL.Activation()))
        return false;

在循环主体中，我们调用每个内层的误差梯度分派方法，并将相应的参数传递给它。不过，我们取代提供标准的梯度缓冲区，而是传递一个指向临时数据存储缓冲区的指针。一旦内部组件的方法成功执行，我们就继续检查神经层的类型。正如我们所知，并非所有内层都会用到第二个数据源。如果当前层被识别为交叉注意力模块，我们把第二个输入源相关的误差梯度累积到形态嵌入对象的缓冲区当中，与先前收集的数值相加。

if (neuron.Type() == defNeuronRelativeCrossAttention) {
    if (!SumAndNormilize(NeuronOCL.getGradient(), GetPointer(cTemp), NeuronOCL.getGradient(), 1, false, 0, 0, 0, 1))
        return false;
}
//---
return true;



}

循环的所有迭代成功完成之后，我们将操作的布尔结果返回给调用函数，并结束该方法的执行。

据此，我们就完成了属性感知注意力模块的实现。附件中提供了该类及其所有方法的完整源代码。

2. AMCT 框架

我们已经取得了重大进展，并实现了构造原子-基序对比转换器（AMCT）框架的独立构建模块。现在是时候将这些模块集成到一个有凝聚力的架构之中了。为此，我们将创建一个名为 CNeuronAMCT 的对象。其结构如下所示。

class CNeuronAMCT    :  public CNeuronBaseOCL
  {
protected:
   CNeuronRMAT                   cAtomEncoder;
   CNeuronMotifEncoder           cMotifEncoder;
   CLayer                        cMotifProjection;
   CNeuronPropertyAwareAttention cPropertyDecoder;
   CLayer                        cPropertyProjection;
   CNeuronBaseOCL                cConcatenate;
   CNeuronMHAttentionPooling     cPooling;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronAMCT(void) {};
                    ~CNeuronAMCT(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint properties,
                          uint units_count, uint heads, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronAMCT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

在所呈现结构中，我们看到已实现对象的声明、和两个额外的动态数组。我们稍后会讨论它们的功能。所有对象都声明为静态，这允许我们将类构造函数和析构函数留空。继承成员、及新声明成员的初始化都在 Init 方法中执行。

在初始化方法参数中，我们收到主常量，允许我们确定正创建对象的唯一架构。

bool CNeuronAMCT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                       uint window, uint window_key, uint properties,
                       uint units_count, uint heads, uint layers,
                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

在方法主体中，我们立即调用父类的同名方法，并将接收参数的一部分传递给它。

您可能已经注意到，该对象的结构不包括存储所接收参数值的内部变量。定义我们类架构的所有常量仅用于内部对象的初始化，必要数值都存储在这些对象之中。在前馈和反向传播方法中，我们仅与这些内部组件交互。因此，我们避免引入不必要的类级变量。

接下来，我们转到初始化内部对象。我们从初始化两个管道开始：一个针对烛条，另一个针对形态。

int idx = 0;
if (!cAtomEncoder.Init(0, idx, OpenCL, window, window_key, units_count, heads, layers, optimization, iBatch))
    return false;
idx++;
if (!cMotifEncoder.Init(0, idx, OpenCL, window, window_key, units_count, heads, layers, optimization, iBatch))
    return false;

尽管这些管道之间存在架构差异，但两者的操作都在同一输入数据源上，并且在该阶段它们接收雷同的初始化参数。

从这两条管道中，我们期望获得所分析市场状况的两种表征：烛台级别、和形态级别。AMCT 框架提议统调这些表征，从而丰富和完善它们的相互理解。不过，重点要注意，这两条管道的输出张量维度不同。这一事实令统调过程非常复杂。为了解决这个问题，我们使用轻量级扩展模型来转换形态管道的输出。指向这些缩放模型对象的指针存储在名为 cMotifProjection 的动态数组之中。

我们首先初始化这个动态数组。

cMotifProjection.Clear();
cMotifProjection.SetOpenCL(OpenCL);

我们判定形态序列的长度。如您所知，在形态管道的输出中，我们得到一个两级的级联嵌入张量。

int motifs = int(cMotifEncoder.Neurons() / window);

注意，表征张量仅在其序列的长度上有所不同。描述每个序列元素的向量大小维持不变。因此，为达到完美意义缩放过程将依据张量内的单个单变量序列操作。为此，我们首先转置形态级别表征张量。

idx++;
CNeuronTransposeOCL *transp = new CNeuronTransposeOCL();
if (!transp ||
    !transp.Init(0, idx, OpenCL, motifs, window, optimization, iBatch) ||
    !cMotifProjection.Add(transp))
    return false;

然后，我们应用卷积层来缩放这些单变量序列。

idx++;
CNeuronConvOCL *conv = new CNeuronConvOCL();
if (!conv ||
    !conv.Init(0, idx, OpenCL, motifs, motifs, units_count, 1, window, optimization, iBatch) ||
    !cMotifProjection.Add(conv))
    return false;
conv.SetActivationFunction((ENUM_ACTIVATION)cAtomEncoder.Activation());

要注意，输入窗口大小及其步幅都等于形态级别表征中的序列长度。同时，过滤器的数量被设置为与烛条级别表征的序列长度相匹配。

另一个重要层面是我们如何定义序列长度和单变量序列的数量。在这种情况下，我们指定输入序列由单个元素组成。单变量序列的数量等于输入中单个序列元素的向量大小。这种配置允许我们分配单独的可学习权重矩阵，来缩放输入数据的每个正交序列。换言之，原始输入序列的每个元素都将靠其自己的专用矩阵进行缩放。这可启用更灵活和精细的变换过程。

同步卷积缩放层的输出和烛条级别表征管道之间的激活函数也很重要。

该操作完成后，我们用一个数据转置层将缩放后的数据转置回其原始布局。

idx++;
transp = new CNeuronTransposeOCL();
if (!transp ||
    !transp.Init(0, idx, OpenCL, window, units_count, optimization, iBatch) ||
    !cMotifProjection.Add(transp))
    return false;
transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

接下来，我们初始化属性和形态的交叉注意力模块，它旨在输出所分析市场状态的属性级别表示。

idx++;
if (!cPropertyDecoder.Init(0, idx, OpenCL, window, window_key, properties, motifs, heads, layers, optimization, iBatch))
    return false;

现在，我们已经抵达关键时刻。在三个主要区块的输出中，我们获得了所分析单一市场场景的三种不同表征。甚至，这些表征中的每一个都被构造成不同维度的张量。那么下一步是什么？我们如何用它们来解决实际问题？我们应该选择哪一个才能达到最高的预测品质？

我认为我们应该使用所有三种表征形式。我们已经初始化了形态表征的缩放模型。现在，我们将创建一个类似的模型来缩放基于属性的表征。指向这些缩放模型对象的指针将存储在 cPropertyProjection 动态数组之中。

cPropertyProjection.Clear();
cPropertyProjection.SetOpenCL(OpenCL);
idx++;
transp = new CNeuronTransposeOCL();
if (!transp ||
    !transp.Init(0, idx, OpenCL, properties, window, optimization, iBatch) ||
    !cPropertyProjection.Add(transp))
    return false;
idx++;
conv = new CNeuronConvOCL();
if (!conv ||
    !conv.Init(0, idx, OpenCL, properties, properties, units_count, 1, window, optimization, iBatch) ||
    !cPropertyProjection.Add(conv))
    return false;
conv.SetActivationFunction((ENUM_ACTIVATION)cAtomEncoder.Activation());
idx++;
transp = new CNeuronTransposeOCL();
if (!transp ||
    !transp.Init(0, idx, OpenCL, window, units_count, optimization, iBatch) ||
    !cPropertyProjection.Add(transp))
    return false;
transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

这三种表征形式被带至一个统一的维度，被级联成单一张量。

idx++;
if (!cConcatenate.Init(0, idx, OpenCL, 3 * window * units_count, optimization, iBatch))
    return false;

我们获得了一个级联的张量，它结合了单一市场状况的三种不同观点。这会不会令您想起来自多头注意力的结果？事实上，我们基本上有三个头的输出，为了得出最终值，我们利用了一个基于依赖关系的池化层。

idx++;
if(!cPooling.Init(0, idx, OpenCL, window, units_count, 3, optimization, iBatch))
   return false;

接下来，我们简单地将继承的接口中的数据缓冲区替换为相应的池化对象。这令我们能够避免不必要的数据复制操作。

if (!SetOutput(cPooling.getOutput(), true) ||
    !SetGradient(cPooling.getGradient(), true))
    return false;
//---
return true;
}

然后，我们结束初始化方法，给调用程序返回一个布尔状态，指示成功。

完成对象的初始化方法之后，我们继续组织前馈通验过程。如常，前向通验算法是在 feedForward 方法中实现的。

bool CNeuronAMCT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cAtomEncoder.FeedForward(NeuronOCL))
      return false;
   if(!cMotifEncoder.FeedForward(NeuronOCL))
      return false;

在方法参数中，我们收到一个指向原始输入数据对象的指针，我们立即将其传递给我们的两个表征管道：烛台级别、和形态级别。

形态管道的输出被转发到处理属性和形态的交叉注意力模块。

if(!cPropertyDecoder.FeedForward(cMotifEncoder.AsObject()))
   return false;

在该阶段，我们对于所分析市场状况有三种不同的表征形式。我们将它们带至一个统一的数据尺度。为此，我们首先将伸缩应用于形态级别的表征。

//--- Motifs projection
   CNeuronBaseOCL *prev = cMotifEncoder.AsObject();
   CNeuronBaseOCL *current = NULL;
   for(int i = 0; i < cMotifProjection.Total(); i++)
     {
      current = cMotifProjection[i];
      if(!current ||
         !current.FeedForward(prev, NULL))
         return false;
      prev = current;
     }

然后，我们对属性级表征执行类似的伸缩过程。

//--- Property projection
   prev = cPropertyDecoder.AsObject();
   for(int i = 0; i < cPropertyProjection.Total(); i++)
     {
      current = cPropertyProjection[i];
      if(!current ||
         !current.FeedForward(prev, NULL))
         return false;
      prev = current;
     }

现在，我们可将三种表征合并为单一张量。

//--- Concatenate
   uint window = cAtomEncoder.GetWindow();
   uint units = cAtomEncoder.GetUnits();
   prev = cMotifProjection[cMotifProjection.Total() - 1];
   if(!Concat(cAtomEncoder.getOutput(), prev.getOutput(), current.getOutput(), cConcatenate.getOutput(),
                                                                         window, window, window, units))
      return false;

我们使用一个池化层计算来自这三种表征结果的加权聚合。

//--- Out
   if(!cPooling.FeedForward(cConcatenate.AsObject()))
      return false;
//---
   return true;
  }

由于在初始化期间替换了缓冲区指针，我们避免了将数据复制到类接口缓冲区，我们简单地完成该方法，将布尔成功标志返回给调用者。

下一步是开发反向传播方法。在算法上特别有趣的是梯度分派方法 calcInputGradients。正如 AMCT 框架作者所提议那样，信息流之间的分支依赖关系结构严重影响了该方法的算法。我们详细验证一下它的实现。

如常，该方法接收一个指向前一层对象的指针，其中必须根据输入数据对最终结果的贡献传播误差梯度。

bool CNeuronAMCT::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

我们立即验证指针的有效性，因为如果指针无效，则任何进一步的操作都将变得毫无意义。

然后，我们按顺序在内部对象之间分派误差梯度。值得注意的是，由于替换了接口缓冲区的缓冲区指针，故无需将数据从外部接口复制到内部对象。因此，我们可立即开始在内部对象之间分派误差梯度。我们首先计算代表所分析环境状态的三个视角的级联张量的误差梯度。

if(!cConcatenate.calcHiddenGradients(cPooling.AsObject()))
   return false;

然后，我们将误差梯度传播到各个管道。烛条级别表征的梯度立即转发到编码器。其它两个则传递给各自的缩放模型。

uint window = cAtomEncoder.GetWindow();
uint units = cAtomEncoder.GetUnits();
CNeuronBaseOCL *motifs = cMotifProjection[cMotifProjection.Total() - 1];
CNeuronBaseOCL *prop = cPropertyProjection[cPropertyProjection.Total() - 1];
if (!motifs || !prop ||
    !DeConcat(cAtomEncoder.getGradient(), motifs.getGradient(), prop.getGradient(), cConcatenate.getGradient(),
              window, window, window, units))
    return false;

接下来，我们根据各个表示的激活函数调整它们的误差梯度。

if (cAtomEncoder.Activation() != None) {
    if (!DeActivation(cAtomEncoder.getOutput(), cAtomEncoder.getGradient(), cAtomEncoder.getGradient(),
                      cAtomEncoder.Activation()))
        return false;
if (motifs.Activation() != None) {
    if (!DeActivation(motifs.getOutput(), motifs.getGradient(), motifs.getGradient(),
                      motifs.Activation()))
        return false;
if (prop.Activation() != None) {
    if (!DeActivation(prop.getOutput(), prop.getGradient(), prop.getGradient(),
                      prop.Activation()))
        return false;

我们还添加了来自烛条和形态表征之间统调产生的误差梯度。

if(!motifs.calcAlignmentGradient(cAtomEncoder.AsObject(), true))
   return false;

随后，我们在缩放模型中分派误差梯度，向后迭代遍历它们的神经层。

for (int i = cMotifProjection.Total() - 2; i >= 0; i--) 
  {
    motifs = cMotifProjection[i];
    if (!motifs || 
        !motifs.calcHiddenGradients(cMotifProjection[i + 1]))
        return false;
  }

for (int i = cPropertyProjection.Total() - 2; i >= 0; i--) 
  {
    prop = cPropertyProjection[i];
    if (!prop || 
        !prop.calcHiddenGradients(cPropertyProjection[i + 1]))
        return false;
  }

来自属性缩放模型的误差梯度被传递到属性和形态的交叉注意力模块，然后传递给形态编码器。

if (!cPropertyDecoder.calcHiddenGradients(cPropertyProjection[0]) ||
    !cMotifEncoder.calcHiddenGradients(cPropertyDecoder.AsObject()))
    return false;

应该注意的是，形态编码器的输出也用于形态表征缩放模型。因此，我们必须协同来自这个二级信息流的误差梯度。为此，我们首先将指向形态编码器的误差梯度缓冲区的指针保存在一个局部变量之中。然后我们将其替换为 “双精度” 缓冲区。

作为供体对象，我们选择了三种表征的计量层。它的误差梯度已分派在相应的信息流当中。由于该层没有可学习参数，故我们可安全地清除其缓冲区。此外，在我们区块中的所有内部对象中，该层拥有最大的缓冲区尺寸，令其成为最优供体候选者。

替换缓冲区之后，我们从缩放模型中提取误差梯度。我们还对汇总两个信息流的梯度，恢复原始缓冲区指针。最后，我们将误差梯度传播到输入数据级别。

CBufferFloat *temp = cMotifEncoder.getGradient();
if (!cMotifEncoder.SetGradient(cConcatenate.getGradient(), false) ||
    !cMotifEncoder.calcHiddenGradients(cMotifProjection[0]) ||
    !SumAndNormilize(temp, cMotifEncoder.getGradient(), temp, window, false, 0, 0, 0, 1) ||
    !cMotifEncoder.SetGradient(temp, false) ||
    !NeuronOCL.calcHiddenGradients(cMotifEncoder.AsObject()))
    return false;

类似的情况出现在输入数据级别：自形态编码器接收的误差梯度，必须按其来自烛条编码器管道的贡献来增益。我们相应地针对另一个缓冲区对象重复指针替换技巧。

temp = NeuronOCL.getGradient();
if (!NeuronOCL.SetGradient(cConcatenate.getGradient(), false) ||
    !NeuronOCL.calcHiddenGradients(cAtomEncoder.AsObject()) ||
    !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, window, false, 0, 0, 0, 1) ||
    !NeuronOCL.SetGradient(temp, false))
    return false;
//---
return true;
}

现在，误差梯度已在所有模型组件和输入数据之间彻底分派，该方法以返回布尔结果给调用方完结。

我想强调该实现中的两个关键点。首先，在替换缓冲区指针期间，我们始终提前保存原始缓冲区指针。在调用指针替换方法时，我们显式设置了一个 false 标志，以便防止删除以前存储的缓冲区对象。该方式预留缓冲区，并允许稍后还原其指针。如果我们如同在初始化方法中那样用 true，我们将删除现有的缓冲区对象，从而导致将来访问时出现严重错误。

其二，关于方法架构：所呈现算法没有实现 AMCT 作者提议的形态对比表征学习。然而，回想一下，我们在相对交叉注意力对象中整合了表征多样化。因此，效果上，我们重新定位了对比学习误差注入点。

我们回顾 原子-基序对比变换器 框架的算法结构至此完毕。附件中提供了全部呈现的类及方法的完整源代码。在那里，您还可找到环境互动和模型训练程序的完整代码。它们都是从之前的工作中原封不动地复制而来的。还包括环境交互程序和训练脚本。在此，我们替换了一层。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronAMCT;
   descr.window = BarDescr;                           // Window (Indicators to bar)
     {
      int temp[] = {HistoryBars, 100};                // Bars, Properties
      if(ArrayCopy(descr.units, temp) < (int)temp.Size())
         return false;
     }
   descr.window_out = EmbeddingSize / 2;              // Key Dimension
   descr.layers = 5;                                  // Layers
   descr.step = 4;                                    // Heads
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

附件中提供了可训练模型的完整架构描述。

3. 测试

我们已利用 MQL5 完成了 原子-基序对比变换器 框架的大量工作，现在是时候评估我们的方式在实践中的有效性了。为此，我们在真实历史数据上用新对象来训练模型，然后在 MetaTrader 5 策略测试器中取训练集之外的一个区间验证已训练策略。

如常，模型训练是依据预先收集的涵盖整个 2023 年的离线训练数据集上执行的。训练是迭代的，经过若干次迭代后，训练数据集会更新。这可以根据当前政策对代理人的操作进行最准确的评估。

在训练期间，我们获得了一个能够在训练和测试数据集上均产生盈利的模型。但这里有一个警告。出品的模型只执行了很少量的交易。我们甚至将测试期延长至 3 个月。测试结果呈现如下。

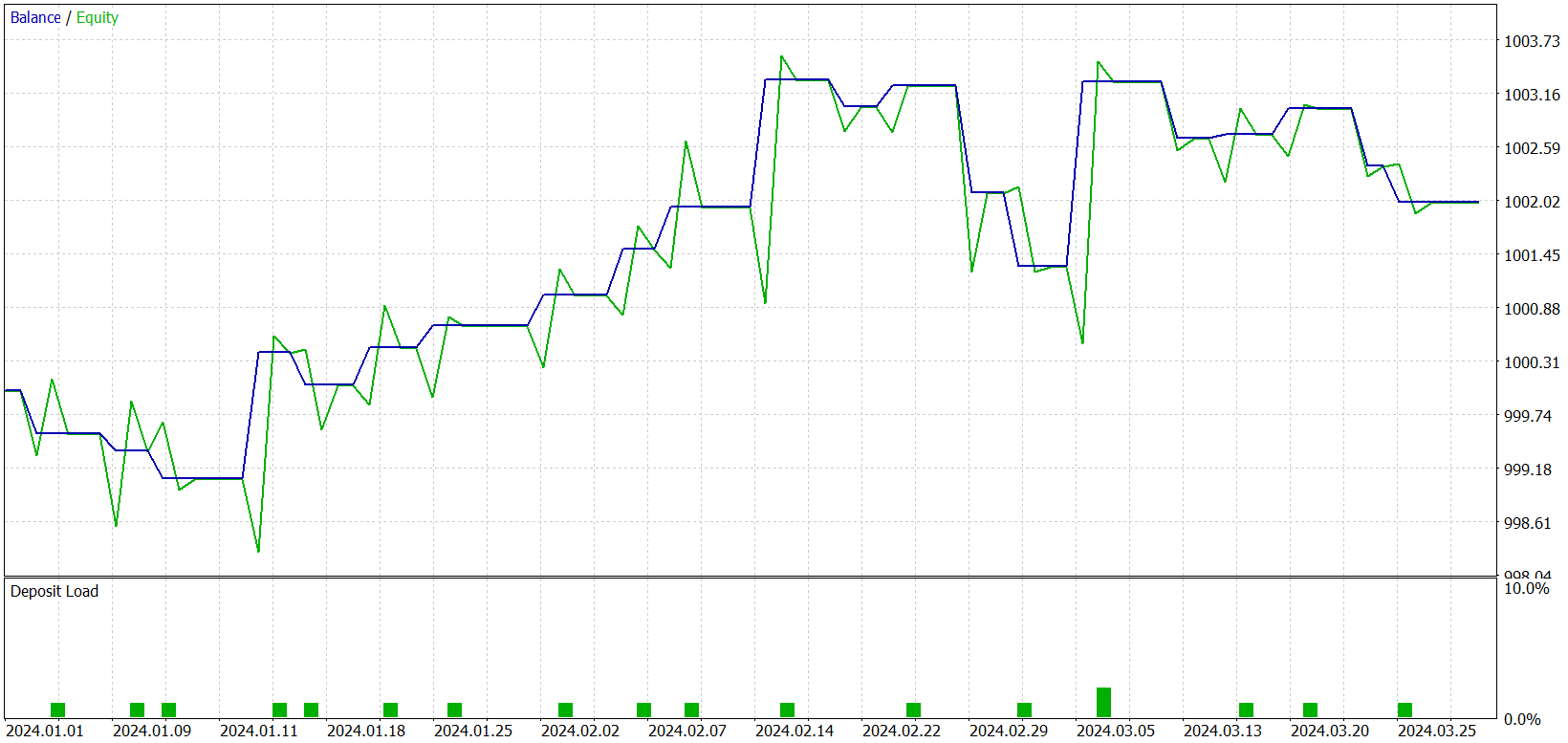
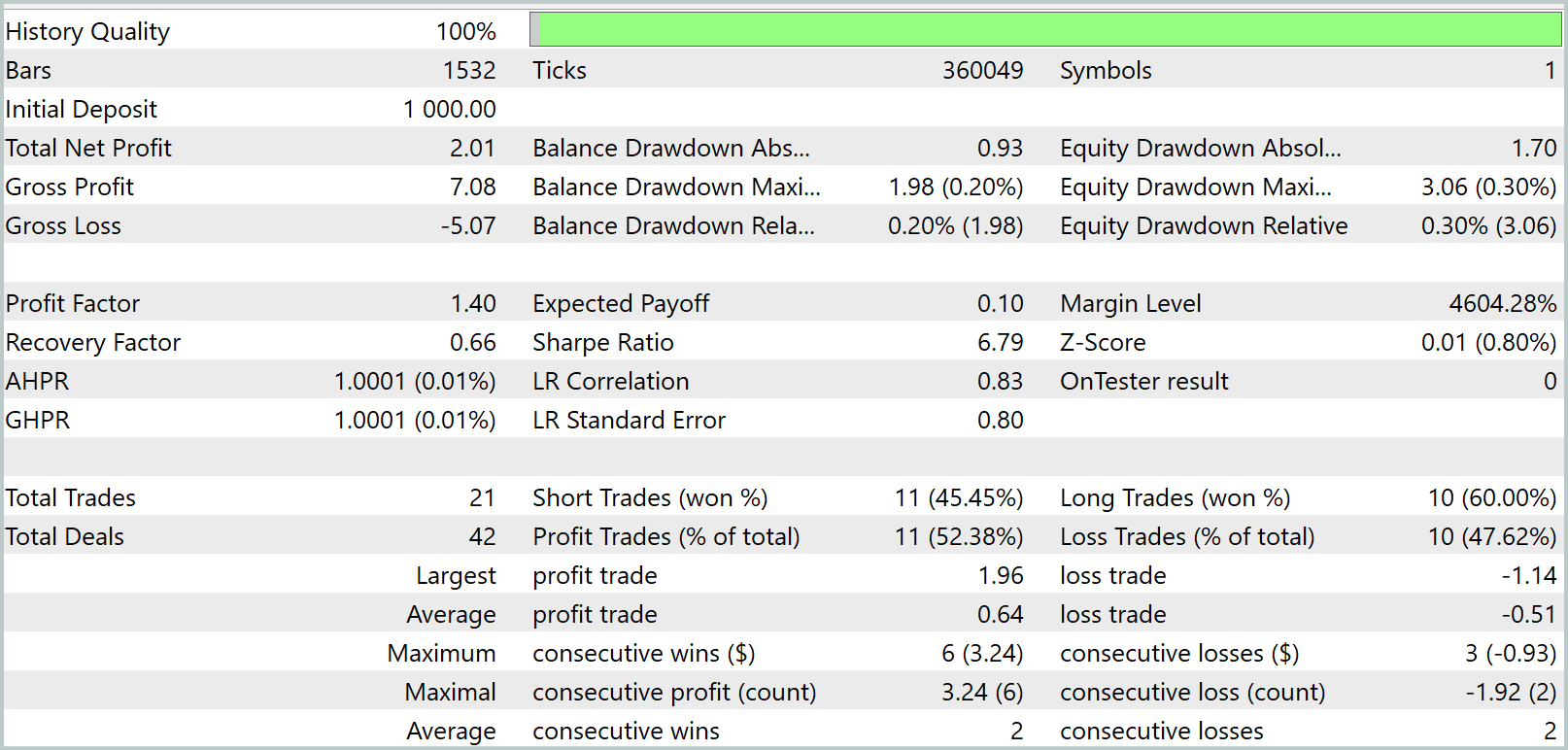
如结果中所见，在三个月的测试间隔内，该模型只执行了 21 笔交易，且只有一半稍多获利了结。检查余额图，我们观察到前一个半月的初始增长，然后是横盘走势。这是完全符合预期的行为。我们的模型仅从训练数据集中存在的市场状态收集统计数据。与任何统计模型一样，训练集必须具有代表性。从余额图中，我们可以得出结论，一年的训练数据集提供了大约 1.2 到 1.5 个月的表象。

因此，可以假设在十年数据集上训练模型或许会产生一年内性能稳定的模型。甚至，更大的训练集应该允许识别更多的关键形态和可学习属性，潜在增加交易频率。不过，确认或反驳这些假设需要对模型进行深入工作。

结束语

在最后两篇文章中，我们探讨了原子-基序对比变换器（AMCT）框架，该框架以原子元素（烛条）和基序（形态）的概念为基础。该方法的主要思路是应用对比学习来区分多个级别的信息性、和非信息性形态：从基本成分到复杂结构。这令该模型不仅能够捕获局部价格走势，还可检测出重要形态，从而为更准确的市场行为预测提供额外的见解。该框架底层的 变换器 架构有效地识别出烛条和形态之间的长期依赖关系、及错综复杂的关系。

在实践部分，我们利用 MQL5 实现了这些方式的解释，训练了模型，并在真实历史数据上进行了测试。不幸的是，出品的模型只有很少的交易活动。无论如何，它仍具有明显的潜力，我们希望在未来的研究中进一步发展。

参考

文章中所用程序

#	名称	类型	说明
1	Research.mq5	智能系统	收集样本的 EA
2	ResearchRealORL.mq5	智能系统	利用 Real ORL方法收集样本的 EA
3	Study.mq5	智能系统	模型训练 EA
4	Test.mq5	智能系统	模型测试 EA
5	Trajectory.mqh	类库	系统状态描述结构
6	NeuroNet.mqh	类库	创建神经网络的类库
7	NeuroNet.cl	函数库	OpenCL 程序代码库