MQL5 Wizard Techniques you should know (Part 43): Reinforcement Learning with SARSA

Introduction

Reinforcement Learning (RL) allows trading systems to learn from their environment or market data and thus improve their ability to trade over time. RL enables adaptation to changing market conditions, making it suitable for certain dynamic financial markets and securities. Financial markets are unpredictable, as often they feature a high degree of uncertainty. RL excels at making decisions under uncertainty by continuously adjusting its actions based on received feedback (rewards), thus being very helpful to traders when handling volatile market conditions.

A parallel comparison to this could be an Expert Advisor that is attached to a chart and also self optimizes periodically on recent price history to fine tune its parameters. RL aims to do the same thing but with less fanfare. For the segment of these series that has looked at RL this far, we have been using it from its strict definition sense as a 3^rd approach to training in machine learning (besides supervised and unsupervised learning). We have not yet looked at it as an independent model that can be used in forecasting.

That changes in this article. We do not just introduce a different RL algorithm, SARSA, but we seek to implement this within another custom signal class of wizard assembled Expert Advisors as an independent signal model. When used as a signal model, RL automates the process of decision-making, reducing the need for constant human intervention, which in turn (in theory at least) could allow for high-frequency trading and real-time response to market movements. Also, by having continuous feedback from its reward mechanism, RL models tend to learn to manage risk better. This is realized via penalizing high-risk actions with low rewards, the net effect of this being RL minimizes exposure to volatile or loss-making trades.

RL though, in principle, is also about balancing exploration and exploitation aka the balancing of trying new strategies vs using already profitable ones. This is made possible thanks to an ‘epsilon-greedy’ approach at updating the Q-Map, which is a matrix of actions across the possible environmental states from which an agent gets to select an action.

There are also a few other pros to RL that may seem anecdotal, but are still worth mentioning given RL’s burgeoning role in AI.

It can help to optimize trade execution by learning the best timing and price points for buying or selling, based on historical data and real-time feedback, thus improving profitability. This can be achieved when as a base signal model, as is the case for this article, it is paired with another signal, such that its role comes down to determining the how, in situations where pending orders are being used. If the Q-Map features, say, 3 actions of limit-orders, stop-orders, and market orders, one’s entry points of an already established and familiar strategy can be fine-tuned.

RL is being a bit non-conventional, unlike traditional linear models, is perhaps suited to learn and execute complex, nonlinear trading strategies, which are arguably more reflective of real-world market behaviour. RL is also scalable to handle multiple asset classes or strategies simultaneously, depending on how one defines their Q-Map and attendant actions, making it a versatile solution for portfolio management or algorithmic trading across diverse financial instruments. Finally, it is particularly suited for real-time decision-making systems, which not only include fully automated Expert Advisors, but can scale to even include part manual trading systems and Expert Advisors depending on one’s strategy and currents setups.

Introduction to the SARSA

SARSA which is an acronym for State-Action-Reward-State-Action, derives its name from the way the Q-Map values are updated. This method of updating the Q-Values clearly differs from the Q-Learning approach we looked at in an earlier article in that it is on-policy as opposed to the off-policy approach we examined then. In fact, our SARSA implementation for this article is identical to what we used in that article when we introduced Q-Learning, save for the way the Q-Map values are updated.

SARSA’s on-policy algorithm, means it learns the Q-values based on the actions it has already taken, following its current policy and not the actions it’s about to take based on the current environment state. It updates the Q-values using the action that was chosen by the same policy it follows. Q-Learning, on the other hand, is an off-policy algorithm, meaning it updates Q-values using the best possible action from the next environment state, regardless of the action the current policy has taken. It learns the optimal policy independently of the agent's current actions. We implement this on-policy update of Q-Values for SARSA as follows:

//+------------------------------------------------------------------+
// Update Q-value using On-policy
//+------------------------------------------------------------------+
void Cql::SetOnPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 1 represents the current Q-action from Q-Map
   double _action = Q[act[1]][e_row[0]][e_col[0]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _action *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  if(i == act[0])
      {  continue;
      }
      Q[i][e_row[1]][e_col[1]] += THIS.alpha * (Reward + (THIS.gamma * _action) - Q[act[0]][e_row[1]][e_col[1]]);
   }
}

The SARSA update rule uses the actual action taken in the next state (State → Action → Reward → State → Action). It follows the epsilon-greedy policy for exploration and learning. This is very similar to what looked at with Q-Learning, however what was not clear then, but was brought to the forefront now is how the epsilon-greedy selection can lead to very inconsistent results since the process of updating the Q-Map is randomized. As a rule, the smaller the epsilon value is, the less the random effects.

When it comes to balancing exploration vs. exploitation, SARSA has a more balanced approach because it follows the same policy during both learning and action-taking, which on paper means it’s safer in uncertain environments like some financial markets. Q-Learning, on the other hand, tends to be more aggressive, as it always seeks the maximum reward from the next state, potentially making it more prone to high-risk decisions in volatile environments.

SARSA is therefore better suited for scenarios where maintaining a balance between exploration and exploitation is critical, and the environment is risky or non-stationary, and the best scenario that comes to mind for this would be trading any of the JPY pairs for instance. Conversely, Q-Learning is better suited when the environment is relatively stable, and finding the optimal strategy is more important than managing ongoing risk. Again, a probably the best example for this could be the EUR CHF pair.

We also did consider another RL algorithm, Deep-Q-Networks in this article, and it too differs from SARSA in a number of ways. Off the bat, the main distinction would be with how SARSA, like Q-Learning, uses a Q-table for storing state-action values. This limits SARSA to environments with small state spaces, as larger environments make maintaining a Q-table impractical. However, DQNs, as we saw in that article, utilize neural networks to approximate Q-values for each state-action pair, making them more scalable and effective in environments with large or continuous state spaces.

When it comes to experience replay, SARSA does not use this, since it learns from each experience in sequence. This can lead to inefficient learning, as the agent only learns from the most recent experience. On the flip side, though, DQN can implements experience replay, where past experiences are buffered and sampled randomly during training. This can go a long way in reducing correlation between consecutive experiences, which in turn may lead to more stable learning.

Another distinction between SARSA and DQN stems from the use of target networks. SARSA has no such concept, since it updates Q-values directly in each step based on the current policy. On the other hand, as we saw in the DQN article, the use of a target network alongside the main Q-network to stabilize learning is mandatory. With DQNs, the target network is updated periodically which provides stable Q-value updates, preventing large oscillations in learning.

Scalability & complexity are another abstruse way DQN and SARSA do vary, since SARSA is best suited for smaller, simpler problems due to the limitations of Q-table size and on-policy learning. While DQN is designed for more complex, high-dimensional problems like those encountered in image-based tasks or environments with a vast number of states. In this article on SARSA, just like we had on the Q-Learning article, we are restricting our environment states to 9 for brevity.

To recap, these are based on 3 simplified market states of bullishness, bearishness, and whipsaw market. Each of these states is then applied on a short time-frame and long time-frame to create a 3 x 3 matrix which implies 9 possible states. In cases where extra parameters such as economic news data or related security price action needs to be factored in, then the continuum of values this data can take to limit SARSA’s applicability.

Finally, learning Speed, presents another major difference between SARSA and DQN, given that SARSA can be slower in complex environments due to the sequential update process and lack of neural network generalization. DQN, though, tends to be faster in large environments due to the ability to generalize across similar states using a neural network, especially when this is coupled with batch learning via experience replay.

Setting Up the MQL5 Environment for SARSA

To implement our custom signal class that uses RL and not an MLP or another machine learning algorithm as the base model, we, in essence, need to simplify the signal class we saw in the introductory article to RL that focused on Q-Learning. That article relied on an MLP for its forecasts, with RL restricted to processing the loss function during training. The RL then and just like now with SARSA use epsilon-greedy approach which guides when to randomly choose the best action for the agent.

When we were simply using the RL to guide the training process of an MLP, these often-random choices were ‘tolerable’ since the provided loss value from training was not as sensitive to the overall performance of the MLP. However now that the RL is the model and not another MLP, the selection of random actions has a disproportionate impact on overall performance.

Often in machine learning, there is a training sample and a testing sample. I though, as a habit, do not provide these, but do mention them and invite the reader to get these two independent data sets. Typically, the training data set will be slightly larger than the testing data set and when we follow this protocol of separating training from testing, then the use of epsilon can actually be constructive to the model as a whole. The Q-Map which is simply a matrix array is not exported by any function in the attached code, but this is relatively straightforward and anyone interested in taking this further to independent training and testing would need to export this matrix array as a bin, or CSV file on their system after training, before reading it when testing.

Coding the Custom Signal Class

Our custom signal class, as mentioned above, is a simplification of what we had in the Q-Learning algorithm article and one of the major adjustments is the get output function which we have revised as indicated below:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalSARSA::GetOutput(int &Output, Cql *QL)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float);
      QL.SetOnPolicy(_reward, _in_e);
      Output = QL.transition_act;
   }
}

Assembly of this code into an Expert Advisor can be done by following guidelines that are here and here for new readers. The assembled Expert Advisor will be tested with an optimized epsilon value simply because we are only demonstrating usability of the Expert Advisor. In practice, this value should ideally be guided by one’s own knowledge of the relative importance and significance of the various environment states and their respective actions.

Testing and Debugging Your SARSA-Based Signal

To better test and harness the SARSA custom signal, some changes would have to be made to this signal class, and perhaps most important of which is the addition of a function to export the Q-Map matrix array. This will enable independent testing and training in the traditional sense. These cross-validation abilities though are inbuilt into strategy tester since forward walk testing is available.

Additional adjustments can be made to the way we have defined the environment states as well by considering alternative market states such as absolute price levels, indicator values of RSI or Bollinger Bands, and crossing this with alternative timeframes for each of these data points. Debugging will start with checking how these state variables are being captured and updated.

The reward function should also accurately reflect trading outcomes. For this article, our code uses favourable excursion as a percentage of price range, on each new bar. This is because we are simultaneously training a Q-Map and placing trade decisions based on its Q-Value weightings at that time.  This is certainly not ideal, as one ought to seek proper independent testing and training data sets. But the reward metrics though can be more long term than what we are using here if for instance they consider profitability and the performance of an Expert Advisor over longer periods of time.

In order to not blindly chase Expert Advisor profitability, it would also be a good idea to test individual state-action pairs and ensure that the EA reacts correctly to market conditions, as expected. For example, checking the Q-Value weightings in the Q-Map in our simplified version for this article at the first grid coordinate of 0 & 0 which marks bearish short-term and long-term conditions, should have the highest weighting for action 0 which represents selling, and not a ‘curve-fit value’ which is inconsistent with what one should do in bearish markets.

Verification of a proper exploration-exploitation balance as implemented via the epsilon-greedy policy is also vital, however this can be got from optimization for the ideal epsilon value. This optimization though would need to be performed on a separate training data set where Q-Maps are backed up on passes with better performance. After training, on a separate data set, testing (forward walking) can then confirm or refute the used epsilon value.

Back-training should be performed on data sets of reasonable quality. Strategy tester reports indicate the quality of used data after a strategy tester pass, and so this is always a good proxy of how reliable the training has been. This training though will involve the export of Q-Maps at the end of each pass if the test results are better than previous benchmarks, and the exported Q-Maps would then be re-used in subsequent back-training rounds such that these additional train passes act as epochs when training neural networks.

At the end of the training process, the final Q-Map that provides most satisfactory Expert Advisor performance would then be used in a single forward-test pass to see if past training performance with this particular Q-Map can be replicated on as yet ‘unseen’ test data-set. Forward walks are native to strategy tester, and this article here can serve as a guide to readers that are new to this.

Besides cross validation on historical data sets, the same could be considered for live accounts before full deployment. Performance Logging, where different Q-Maps are tabulated next to their respective tester performance. This can be taken a step further by implementing detailed logging in real-time forward tests to capture market states, actions, rewards, and Q-value updates which should, on paper at least, help trace decision-making flaws and adjust parameters, such as learning rate or ε-decay if needed.

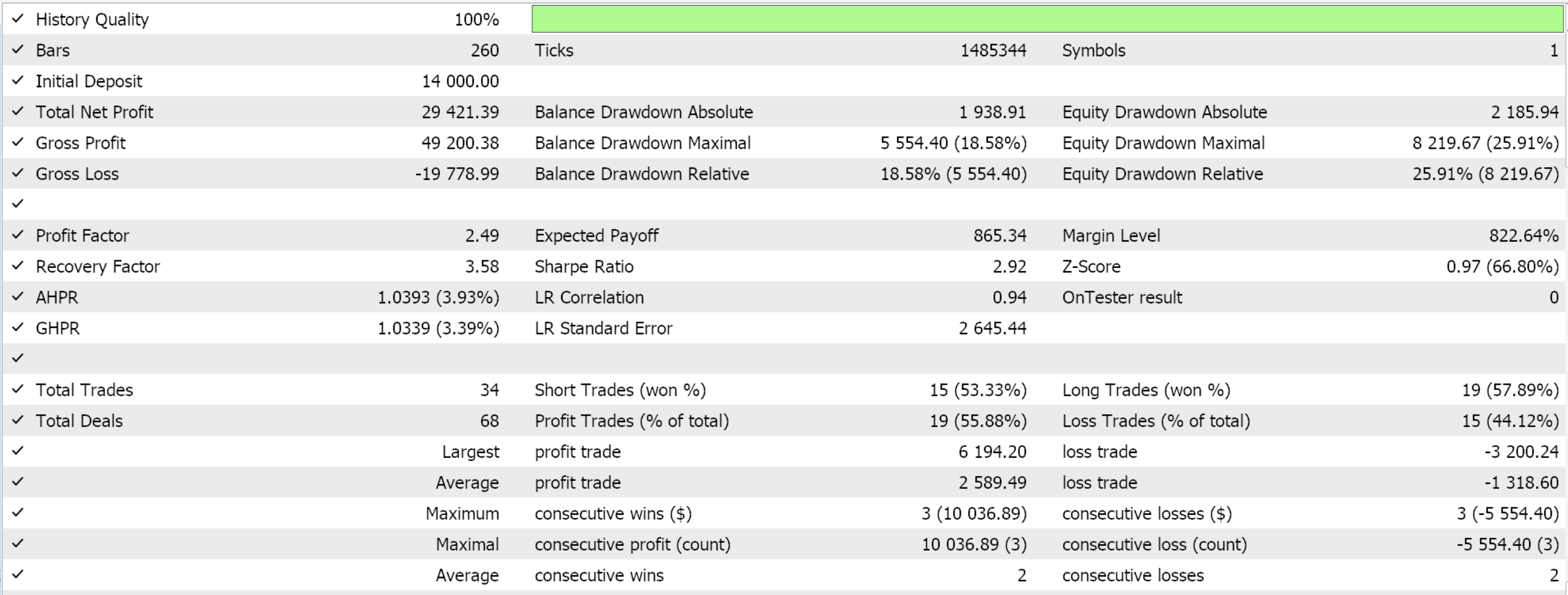
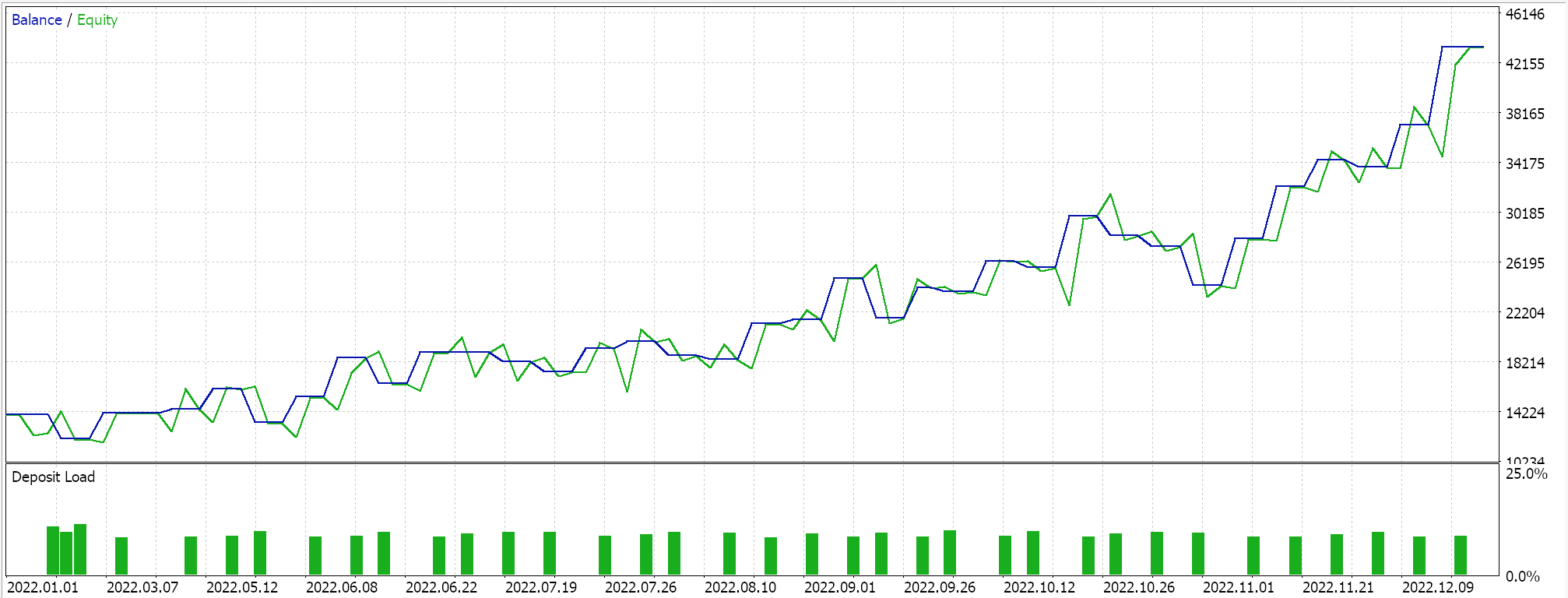
Strategy Tester Reports

Test runs on the daily time frame for EUR JPY for the year 2022 that are strictly meant to demonstrate usability of the Expert Advisor do give us the following results:

Practical Considerations for SARSA in Live Trading

Since SARSA is an on-policy algorithm, it directly incorporates the policy’s actions during learning, making it more adaptable to noisy data. The Q-Map value method we use updates all Q-Values in the map in proportion to their gap from the current action, as shown in the on-policy code above. This update follows the epsilon-greedy update performed in the Action-function, to balance exploration (discovery of new strategies) and exploitation (using of known strategies), to assist the model in avoiding overfitting to short-term noise in market data. The selection of the next action to be used by the agent happens through a Markov decision process, regardless of whether Markov weighting will be applied to the Q-Value update process as we had in the Q-Learning article earlier. This is handled in the Action-function as shown below:

//+------------------------------------------------------------------+
// Choose an action using epsilon-greedy approach
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//
   int _e_row_new = 0, _e_col_new = 0;
   SetMarkov(int(E[E.Size() - 1]), _e_row_new, _e_col_new);
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   e_row[0] = _e_row_new;
   e_col[0] = _e_col_new;
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   transition_act = 0;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q[i][_next_row][_next_col] > Q[transition_act][_next_row][_next_col])
      {  transition_act = i;
      }
   }
}

Temporal smoothing through a reward Mechanism helps smooth out short-term noise by focusing on the cumulative reward over multiple time iterations. This gives the algorithm the capacity to learn patterns beyond the immediate noise in the data. Also, a continuous-policy-adjustment ensures the policy is based on both current and future states. This can help mitigate the effects of noisy data by allowing the algorithm to adapt as more data becomes available, especially when market conditions are rapidly changing.

SARSA is quite robust in handling Volatile Markets given its inherent structure in selecting the transition action as indicated in the Action-function whose code is shared above. Given a pair of coordinates for the current environment state, these two values would need to be converted into a single index, recognizable by the QL class’s Markov matrix. This we do by using the ‘Get Markov’ function, whose code is listed below:

//+------------------------------------------------------------------+
// Getting markov index from environment row & col
//+------------------------------------------------------------------+
int Cql::GetMarkov(int Row, int Col)
{  return(Row + (THIS.environments * Col));
}

Once armed with this index, we can then proceed to read from our Markov matrix row (as represented by this index) for which column has the highest probability value. This Markov matrix is particularly suited for this because it is not buffered or stored in any way like most common indicators. It is memoryless and this makes it very adaptable to uncertain environments like when volatility is high. So, from the row of the Markov matrix for the current environment state, we read off the column with the highest probability and its index would give us the integer for the next environment state. This integer again would need to be decomposed into two values similar to what we started with, which we call a row index and column index.

Once we have these row and column values, which represent the coordinates for the next state, we can then proceed to read off the action with the highest Q-Value from our Q-Map. The index of this action would represent what we have called the ‘transition action’. To recap, we are faced with three possible actions namely 0-sell, 1-do nothing, and 2-buy. Also, the environment is restricted to 3 states on the 3 ‘time frames’ that the Q-Map considers.

I refer to ‘time frames’ because we are really using only one-time frame. The reader, can, of course modify the code and make changes accordingly. The input parameter ‘m_scale’ defines by how much the larger ‘time frame’ changes are tracked when getting these two-tier changes that we use in mapping and defining the environment states.

SARSA considers both actions and rewards within the current policy, helping to stabilize the learning process during periods of high market volatility. This prevents extreme swings in decision-making that could arise from sudden market changes, making it better suited for volatile markets compared to off-policy algorithms like Q-learning. As can be seen from our on-policy function code shared above, we update the values for the action indexed 1 and not index 0 as had been the case for the Q-Learning algorithm.

Because SARSA directly evaluates the actions taken by the current policy, it, without much fuss, becomes more cautious in highly volatile environments, thus avoiding overly optimistic action-value estimates that could lead to poor decisions during unexpected market shifts. Also, in volatile markets, SARSA’s ε-greedy exploration allows the model to explore safer strategies rather than taking high-risk actions. This reduces the likelihood of large losses during periods of extreme price swings, while still giving the model opportunities to discover new profitable strategies. The exploration of safer strategies comes from epsilon allowing for a random choice of actions and not necessarily the current best rewarding actions which given a volatile setting could quickly dematerialize into dismal rewards. 

SARSA’s long-term convergence to the optimal policy depends on continuous interaction with the environment. In financial markets, where long-term trends and structural changes are a norm, SARSA’s iterative policy evaluation ensures that Q-values will tend to converge over time, thus reflecting these long-term patterns. 

Customizing SARSA for More Complex Strategies

State-Space Aggregation in SARSA can be a way of breaking down complex state spaces, especially in financial markets, where the state space (price movements, indicators, market conditions, economic calendar news) can be very large and continuous. State-space aggregation would reduce this complexity by grouping similar states into "aggregated" or "abstract" states. The crudest example of this would be our environment states for this article, which are simply 3 across immediate changes and longer spanning changes. However, a more resourceful use of this could also be when considering an environment that is more multifaceted such as a Q-Map that has on each axis, say 10yr yield value information, benchmark interest rates, PPI, CPI and unemployment rate, for instance.

Since Q-Maps are dual axed, this information would be applicable for each currency in a traded forex pair. So rather than grappling with the individual value readings for each of these metrics, it could be put together in the same way we did for this article by simply considering whether each of these metrics increased, remained flat or decreased. These results would then go on to determine what sort of index that needs to be assigned at each point in the Q-Map matrix, in the same way as we have assigned index values in the Q-Map for this article.

Conclusion

We have considered another algorithm for reinforcement learning, SARSA, in this article, and it is worth mentioning the implementation we had for the first RL algorithm that considered Q-Learning as well as the subsequent one that looked at Deep-Q-Networks, did not properly use the Markov Decision Process when selecting the next action. Instead, Markov chains were simply provided as a mechanism for weighting the update process. This has been corrected for this article, with apologies, and the complete source code is attached.