Von der Grundstufe bis zur Mittelstufe: Fließkommazahlen

Einführung

Im vorherigen Artikel „Von der Grundstufe zur Mittelstufe: Definitionen (II)“, haben wir darüber gesprochen, wie wichtig Makros sind und wie wir sie effektiv einsetzen können, um unseren Code noch lesbarer zu machen.

Nach allem, was wir bisher besprochen haben, verfügen wir nun über genügend Material und geeignete Werkzeuge, um zu erklären, wie Fließkommazahlen funktionieren. Ich weiß, dass viele Leute denken, dass Double- oder Float-Werte in verschiedenen Situationen die beste Wahl sind. Es gibt jedoch ein Problem mit dieser Art von Werten, das nur sehr wenige Menschen verstehen, insbesondere diejenigen, die keine Programmierer sind.

Und da solche Werte in MQL5 weit verbreitet sind und wir mit Informationen arbeiten, bei denen das Fließkomma fast ein Konsens ist, ist es notwendig, sehr gut zu verstehen, wie diese Art von Werten von der CPU verarbeitet wird.

Warum sagen Sie das? Es ist klar, dass Bruchzahlen wie 2,5 immer sehr leicht zu verstehen sind, da niemand diese Art von Werten mit anderen verwechseln wird. Aber, liebe Leserin, lieber Leser, wenn es um Berechnungen geht, sind die Dinge nicht so einfach. Tatsächlich sind Fließkommazahlen in einer Reihe von Situationen recht nützlich. Sie sollten jedoch nicht in der gleichen Weise wie Ganzzahlen betrachtet oder verstanden werden.

Viele von Ihnen sind es vielleicht gewohnt, mit Fließkommazahlen in zwei Arten von Notationen umzugehen: in der wissenschaftlichen Notation, in der wir Werte wie 1-e2 notieren, und in der gebräuchlicheren, arithmetischen Notation, in der wir Werte wie 0,01 notieren. Beide Werte sind in der Größenordnung gleich, werden aber unterschiedlich notiert. Ebenso gibt es eine gebrochene Schreibweise für denselben Wert, die 1/100 entspricht.

Bitte beachten Sie, dass es sich in allen Fällen um denselben Wert handelt. Verschiedene Programme oder Programmiersprachen behandeln diese Werte jedoch unterschiedlich.

Kurze Geschichte

In den Anfängen der Computertechnik gab es noch keine Fließkommazahlen, wie wir sie heute kennen. Oder besser gesagt, es gab keine standardisierte Art und Weise, mit ihnen umzugehen. Jeder Programmierer, jedes Betriebssystem und sogar jedes Programm handhabte diese Art von Zahlen auf eine sehr spezifische und individuelle Weise.

In den 1960er und 1970er Jahren gab es keine Möglichkeit für ein Programm, mit einem anderen zu interagieren, um die Faktorisierung solcher Werte zu teilen und zu beschleunigen. Stellen Sie sich vor: Zu Beginn des Raumfahrtzeitalters, als solche Zahlen von größter Bedeutung gewesen wären, war es UNMÖGLICH, auf den damaligen Computern Fließkommazahlen zu berechnen. Und selbst wenn eine solche Kapazität zur Verfügung stand, war es unmöglich, die Aufgabe auf eine große Anzahl von Computern aufzuteilen, um die Berechnungen zu beschleunigen.

Dann begann IBM, das damals fast den gesamten Markt beherrschte, eine Möglichkeit zur Darstellung dieser Art von Werten anzubieten. Aber der Markt nimmt nicht immer an, was ihm angeboten wird. Daher haben andere Hersteller ihre eigenen Methoden zur Darstellung solcher Werte entwickelt. Es war ein echtes CHAOS. Bis irgendwann das Institute of Electrical and Electronics Engineers (IEEE) begann, die Dinge zu bereinigen, indem es den heute als IEEE 754 bekannten Standard einführte. Am Ende dieses Artikels, im Abschnitt „Links“, werde ich einige Links für diejenigen hinterlassen, die sich eingehender mit diesem Thema beschäftigen möchten.

Die erste Norm, die erstellt wurde, war IEEE 754-1985, ein Versuch, dieses Problem zu lösen. Heutzutage verwenden wir einen wesentlich moderneren Standard, der jedoch auf demselben, ursprünglich festgelegten Schema beruht.

Ein wichtiges Detail: Trotz der Existenz dieser Norm, die die verteilte Faktorisierung normalisieren und ermöglichen soll, gibt es Fälle, in denen diese Norm nicht verwendet wird und die Berechnungen - oder genauer gesagt die Faktorisierung - nach anderen Prinzipien durchgeführt werden, auf die wir hier nicht eingehen werden, da sie den Rahmen des Themas völlig sprengen. Das liegt daran, dass MQL5, wie mehrere andere Sprachen auch, diesen IEEE 754-Standard verwendet.

Ursprünglich konnte die CPU diese Art von Berechnungen nicht bewältigen, sodass es einen separaten Prozessor gab, der damals als FPU bezeichnet wurde und ausschließlich diesem Zweck diente. Diese FPU wurde separat gekauft, da ihre Kosten nicht immer ihre Verwendung rechtfertigten. Das Modell 80387 kann als Beispiel für eine FPU dienen. Und ja, das ist kein Tippfehler. Im Wesentlichen ist dieses Modell dem berühmten 80386 sehr ähnlich, der gemeinhin als 386 bezeichnet wird. Dies war jedoch eher eine Marketinglösung von Intel, um die CPU (80386) von der FPU (80387) zu unterscheiden. Der Computer konnte nur mit der zentralen Prozessoreinheit arbeiten, nicht aber mit der FPU allein, da diese nur für die Durchführung von Fließkommaberechnungen ausgelegt war.

OK, aber was ist mit diesem Fließkomma falsch? Warum ist ein ganzer Artikel nur diesem Thema gewidmet? Der Grund dafür ist, dass Sie eine Reihe von Fehlern machen können, wenn Sie nicht verstehen, wie die Fließkommadarstellung funktioniert. Das liegt nicht an einer schlechten Programmierung, sondern an der Vorstellung, dass die durchgeführten Berechnungen wörtlich zu nehmen sind, während die Verwendung der Norm IEEE 754 bereits einen potenziellen Fehler im berechneten Endwert verursacht.

Das mag absurd erscheinen, denn Computer sind Maschinen, die uns immer genaue Werte liefern müssen. Es ist nicht schwerwiegend zu sagen, dass das Ergebnis des Vorgangs einen Fehler enthält, außerdem ist es inakzeptabel. Vor allem, wenn unser Ziel darin besteht, mit diesen Daten auf dem Finanzmarkt zu handeln. Wenn unsere Berechnungen falsch sind, können wir Geld verlieren, auch wenn alles darauf hindeutet, dass wir einen Gewinn erzielen. Aus diesem Grund ist dieser Artikel so wichtig.

Es gibt eine Reihe von Aspekten im Zusammenhang mit der Fließkommaberechnung, die im Rahmen unseres Vorhabens nicht so wichtig sind. Aber es gibt noch eine andere Sache, die sehr wichtig und entscheidend ist, und das ist die Rundung.

Ich weiß, dass viele Leute sagen oder sogar prahlen und behaupten: 

Ich verwende bei meinen Berechnungen KEINE Rundungen. Sie sind immer genau und fehlerfrei.

Aber diese Idee zeugt meiner Meinung nach von einem völlig falschen Verständnis des Programmierens, das die Menschen zu falschen Annahmen verleitet, obwohl in Wirklichkeit alles anders ist. Die Rundung muss nicht unbedingt von einem Programmierer vorgenommen werden. Sie existiert einfach unabhängig davon, ob der Programmierer es will oder nicht. Daher ist es wichtig, dass Sie die Materialien auf den Links lesen, die ich am Ende dieses Textes angegeben habe. Ich tue dies, weil das Thema Fließkommazahlen nicht in einem einzigen Artikel erklärt werden kann. Denken Sie daran: Es gibt Experten, die sich seit den Anfängen der Entwicklung der Computertechnologie mit diesem Thema beschäftigt haben.

Hier werden wir uns eine andere Art von Dingen ansehen, die viel einfacher sind und sich darauf konzentrieren, genau zu verstehen, was ein Double oder Float ist, da alle anderen Datentypen viel einfacher sind und bereits in früheren Artikeln erklärt worden sind.

Die Darstellung einer Fließkommazahl

Wir werden hier also über den Typ sprechen, der in MQL5 tatsächlich verwendet wird. Bei diesem Typ orientieren wir uns grundsätzlich an der IEEE 754-Spezifikation, die zwei Formate - oder genauer gesagt, zwei Präzisionen - vorsieht. Und ja, wenn wir über Fließkommazahlen sprechen, ist es richtig, den Begriff „Präzision“ und nicht „Format“ oder „Anzahl der beteiligten Bits“ zu verwenden. Um die Dinge aber nicht zu verkomplizieren, da dies für viele Menschen recht verwirrend sein kann, werden wir hier den Begriff „Anzahl der Bits“ verwenden, aber nur, damit die meisten Leser die Materie besser verstehen können und um weitere Erklärungen zu vereinfachen. Ich glaube, dass ich mich nicht an Ingenieure oder Spezialisten mit umfangreichen und umfassenden Kenntnissen auf dem Gebiet der Elektronik und des Chipdesigns wende, sondern eher an Menschen, die sich für die Programmierung in der Sprache MQL5 interessieren und wissbegierig sind.

Schauen wir uns zunächst einen sehr einfachen Code an. Trotz seiner Einfachheit benötigen Sie alle Kenntnisse, die Sie in den vorangegangenen Artikeln dieser Reihe erworben haben, um ihn vollständig zu verstehen. Kommen wir zur Sache.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define typeFloating float
05. //+----------------+
06. void OnStart(void)
07. {
08.     union un_1
09.     {
10.         typeFloating v;
11.         uchar arr[sizeof(typeFloating)];
12.     }info;
13. 
14.     info.v = 741;
15. 
16.     PrintFormat("Floating point value: [ %f ] Hexadecimal representation: [ %s ]", info.v, ArrayToHexadecimal(info.arr));
17. }
18. //+------------------------------------------------------------------+
19. string ArrayToHexadecimal(const uchar &arr[])
20. {
21.     const string szChars = "0123456789ABCDEF";
22.     string sz = "0x";
23. 
24.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
25.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
26. 
27.     return sz;
28. }
29. //+------------------------------------------------------------------+

Code 01

Nun, mein lieber Leser, dieser Code ist recht interessant, außerdem ist er recht neugierig und es macht Spaß, damit zu experimentieren. Trotzdem setzen wir hier nur den ersten Teil dessen um, was wir wirklich wollen und tun werden.

Bitte beachten Sie: In der vierten Zeile geben wir an, welche Art von Wert wir als Fließkommazahl verwenden werden. Wir können angeben, dass wir einen Double- oder Float-Typ benötigen. Der Unterschied zwischen ihnen liegt in der Präzision, die sie jeweils ermöglichen. Doch bevor wir ins Detail gehen, sollten wir herausfinden, was dieser Code bewirkt.

Nachdem wir also den Typ deklariert haben, können wir eine Union verwenden, um einen Weg zu finden, Speicher zu lesen. Zu diesem Zweck verwenden wir die Zeile 8. Bereits innerhalb der Union verwenden wir Zeile 10, um eine Variable zu erstellen, und Zeile 11, um ein Array mit gemeinsamem Zugriff zu erstellen. Ähnliche Strukturen wurden bereits in früheren Artikeln erörtert und erläutert. Bitte lesen Sie diese für weitere Informationen, wenn Sie sich nicht im Klaren darüber sind, was hier vor sich geht und was der Zweck der Gründung dieser Vereinigung ist.

Für uns ist 14 die wichtigste Zeile, denn in ihr legen wir den Wert fest, den wir visualisieren wollen. Und Zeile 16 bietet lediglich eine Möglichkeit, den Inhalt des Speichers darzustellen, was im Moment unser Ziel ist, denn wir wollen verstehen, wie eine Fließkommazahl im Speicher dargestellt wird, bis der Computer sie interpretieren kann.

Nach der Ausführung von Code 01 erhalten wir also das in der folgenden Abbildung gezeigte Ergebnis.

Abbildung 01

Hmm ... Was ist das für eine seltsame Darstellung im hexadezimalen Format, die wir gerade sehen? Nun, mein lieber Leser, das ist genau die Art und Weise, wie der Computer eine Fließkommazahl nach der Norm IEEE 754 interpretiert. Ein wichtiges Detail: Dieser Wert wird als Wert im Little-Endian-Format notiert. Wir werden später mehr über dieses Format erfahren. Aber jetzt müssen Sie nur Folgendes verstehen: Dieser Hexadezimalwert wird in umgekehrter Reihenfolge notiert und muss von rechts nach links gelesen werden.

Nun, auf jeden Fall glauben Sie es wahrscheinlich nicht. Daher können wir ein anderes Programm verwenden, um dies zu klären. Lassen Sie uns den Hex-Editor verwenden. ist eine der einfachsten kostenlosen Optionen. Wenn Sie die Werte im Hexadezimalfeld von Bild 01 eingeben, sie markieren und sehen, welcher Wert dort dargestellt wird, erhalten Sie ein ähnliches Bild wie das unten abgebildete.

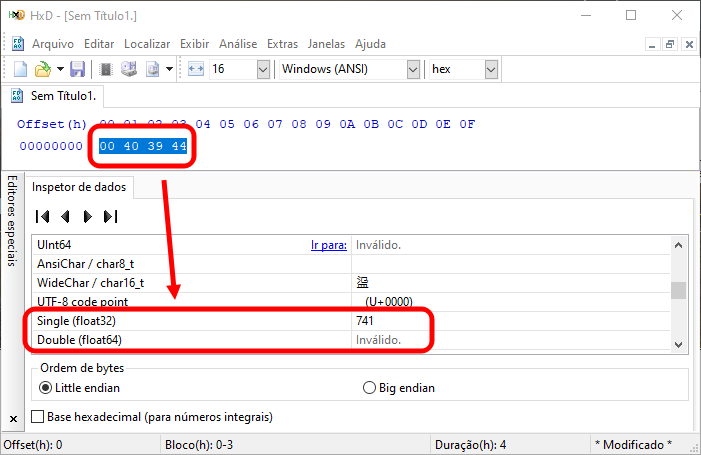
Abbildung 02

Beachten Sie, dass wir tatsächlich einen erwarteten Wert haben, der visualisiert werden kann. Ich persönlich ziehe es jedoch vor, die Erweiterung meiner Entwicklungsumgebung zu verwenden, um solche Dinge zu sehen, was es ermöglicht, die Installation vieler verschiedener Programme auf dem Computer zu vermeiden. Der Fairness halber möchte ich jedoch anmerken, dass HxD nicht installiert werden muss. Was wir auf jeden Fall sehen können, ist in der folgenden Abbildung dargestellt.

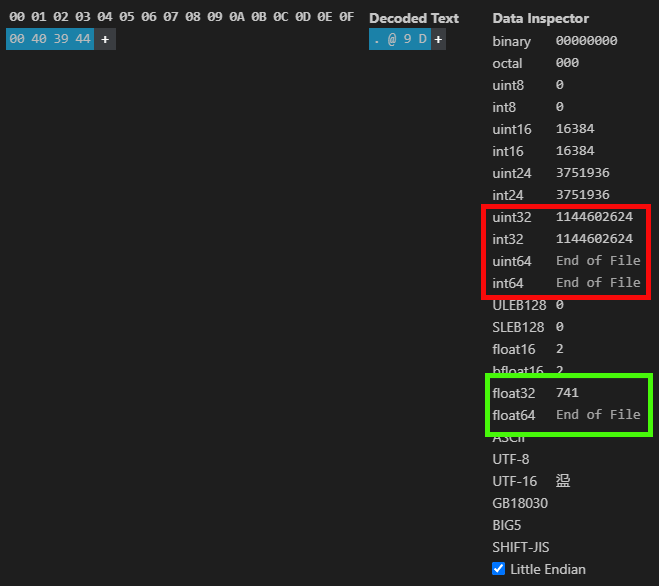
Abbildung 03

Diese Informationen können sowohl im MetaTrader 5 als auch im HxD abgerufen werden. Aber ich möchte, dass Sie sich genau ansehen, was ich in Bild 03 zeige. Beachten Sie, dass ein und derselbe Fließkommawert ein anderer Wert ist, der als Ganzzahl dargestellt wird. Aber warum ist das so? Der Grund dafür ist, dass es für einen Computer keinen Unterschied macht, ob ein Wert durch eine ganze Zahl oder einen anderen Typ repräsentiert wird - es macht für ihn keinen Unterschied. Für uns und für den Compiler ist dies jedoch von grundlegender Bedeutung - der Datentyp beeinflusst, ob wir ein vernünftiges Ergebnis oder etwas völlig Unerwartetes erhalten.

Das Beispiel, das wir gerade in Code 01 betrachtet haben, ist jedoch nur ein einfacher Fall. Ersetzen wir den Code 01 durch ein leicht abgewandeltes Beispiel, das im Folgenden zu sehen ist.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. // #define Floating_64Bits
05. //+----------------+
06. #ifdef Floating_64Bits
07.     #define typeFloating double
08. #else
09.     #define typeFloating float
10. #endif
11. //+----------------+
12. void OnStart(void)
13. {
14.     union un_1
15.     {
16.         typeFloating v;
17. #ifdef Floating_64Bits
18.         ulong integer;
19. #else
20.         uint integer;
21. #endif
22.         uchar arr[sizeof(typeFloating)];
23.     }info;
24. 
25.     info.v = 42.25;
26. 
27.     PrintFormat("Using a type with %d bits\nFloating point value: [ %f ]\nHexadecimal representation: [ %s ]\nDecimal representation: [ %I64u ]",
28. #ifdef Floating_64Bits
29.         64,
30. #else
31.         32,
32. #endif
33.         info.v, ArrayToHexadecimal(info.arr), info.integer);
34. }
35. //+------------------------------------------------------------------+
36. string ArrayToHexadecimal(const uchar &arr[])
37. {
38.     const string szChars = "0123456789ABCDEF";
39.     string sz = "0x";
40. 
41.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
42.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
43. 
44.     return sz;
45. }
46. //+------------------------------------------------------------------+

Code 02

Nun gut, Code 02 erscheint vielleicht etwas komplizierter. Es ist jedoch so einfach wie Code 01, aber hier haben wir die Gelegenheit, einige zusätzliche Punkte bezüglich der Anzeige von Fließkommazahlen zu diskutieren. Dies ist dank Zeile 4 möglich, bei dem wir wählen können, ob wir einen Typ mit einfacher (float) oder doppelter Präzision verwenden wollen. Wenn wir jedoch den oben gezeigten Code ausführen, erhalten wir die unten gezeigte Antwort.

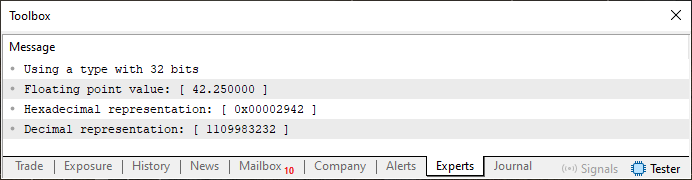
Abbildung 04

Und wie wir bereits gesehen haben, erhalten wir bei Verwendung der in Abbildung 04 angegebenen Werte das in der folgenden Abbildung gezeigte Ergebnis:

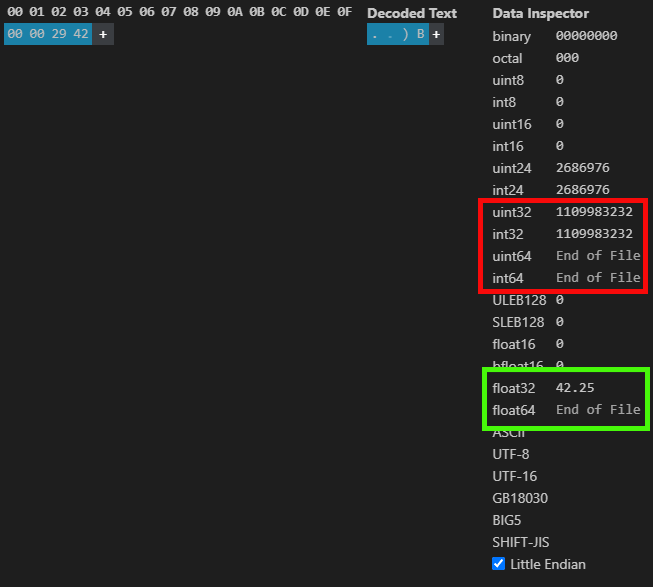
Abbildung 05

Mit anderen Worten: Hier ist wirklich etwas im Gange. Aber wie funktioniert das IEEE 754 System? Nun, lieber Leser, um dies zu erklären, sollten wir uns die interne Struktur des Systems selbst genauer ansehen. Ich werde mich bemühen, die Dinge nicht zu sehr zu verkomplizieren, denn das kann letztlich jeden Versuch zunichte machen, zu erklären, was passiert, und helfen, alles zu verstehen.

Ursprünglich - und das ist auch heute noch so - gibt es zwei IEEE-754-Formate: eines für einfache Präzision (bei dem 32 Bits verwendet werden) und das andere für doppelte Präzision (bei dem 64 Bits verwendet werden). Der Unterschied zwischen ihnen besteht nicht darin, dass die eine präziser ist als die andere; der Unterschied liegt in der Bandbreite der Werte, innerhalb derer gearbeitet werden muss. Daher kann der Begriff „Präzision“ oft irreführend sein. Aus diesem Grund ziehe ich es vor, ihn nicht zu verwenden, auch wenn er als korrekt angesehen wird.

In der Abbildung unten sehen Sie zwei in der Norm definierte Typen:

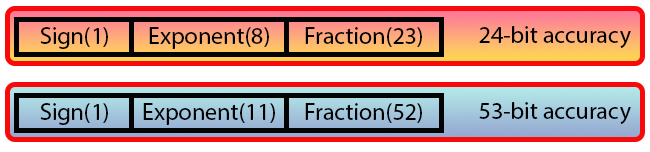
Bild 06

„Moment mal... Haben Sie nicht gesagt, dass wir 32 Bit für den einen und 64 für den anderen Typ verwenden? Aber es scheint, dass hier etwas verwendet wird, das überhaupt keinen Sinn macht. Was sind das für Daten und Werte, die wir in Bild 06 sehen?“

Das ist die Art und Weise, wie ein Fließkommawert nach dem IEEE 754-Standard dargestellt wird. Hier ist jeder der angezeigten Werte ein BIT. Bitte beachten Sie, dass wir Brocken mit einer ungewöhnlichen Breite haben, die sich von den bisher bekannten unterscheidet. Das hindert uns jedoch nicht daran, das System selbst zu verstehen. Obwohl die Erklärungen einfacher sein könnten, wenn wir die Sprachen C oder C++ verwenden würden. Das liegt daran, dass wir in MQL5 nicht die Möglichkeit haben, Bits einzeln zu benennen, was in C oder C++ möglich ist. Wir können jedoch Makros und Definitionen verwenden, um dem näher zu kommen, was in diesen Sprachen getan wird.

Deshalb werde ich versuchen, sie bereits in diesem Artikel zu erklären. Wenn es nicht klappt, werde ich einen separaten Artikel schreiben, um alles genau zu erklären. Ich möchte mich nicht auf eine kursorische Erklärung beschränken. Ich möchte, dass Sie, lieber Leser, wirklich verstehen, was das Problem bei der Verwendung von Fließkommazahlen in unseren Codes ist. Denn ich sehe, wie viele Menschen behaupten und sogar ernsthaft glauben, dass es möglich ist, Berechnungen durchzuführen, die eigentlich unmöglich sind. Das liegt daran, dass es eine leichte Diskrepanz zwischen dem erwarteten und dem tatsächlichen Ergebnis gibt, die zu Problemen führen kann, wenn wir nicht darauf vorbereitet sind.

Beginnen wir mit folgendem: Wenn Sie die Anzahl der Bits in Abbildung 06 addieren, werden Sie feststellen, dass das erste Format 32 Bits und das zweite 64 Bits enthält. An dieser Stelle stellen sich die ersten Fragen. Der Einfachheit halber wollen wir uns daher nur auf eines der Formate konzentrieren, da der Unterschied zwischen ihnen mit dem Wert zusammenhängt, der bei der Anpassung verwendet wird. Aber darüber werden wir später sprechen.

Das in Abbildung 06 als Vorzeichen bezeichnete Bit ist das Vorzeichenbit. Das heißt, es zeigt an, ob der Wert negativ oder positiv ist, genau wie bei den ganzzahligen Typen, wo das ganz linke Bit angibt, ob die Zahl negativ oder positiv ist.

Auf das Vorzeichenbit (Sign) folgen also unmittelbar acht Bits, die Exponent genannt werden. Dieser Wert erzeugt einen sogenannten Bias gleich 127, der den Exponenten kodiert. Im Falle der doppelten Präzision (double) werden elf Bits verwendet, was zu einem Bias von 1023 führt. Bitte beachten Sie, dass trotz der Bezeichnung „double precision“ der Bias-Wert hier deutlich höher ist.

Der wichtigste Teil für uns ist jedoch der Teil, der direkt nach dem Exponenten kommt. Dieses Feld heißt Fraction (Bruchzahl). Es bestimmt die Präzision des darzustellenden Wertes. Beachten Sie, dass dieses Feld bei 32 Bits (einfache Präzision) 23 Bits enthält, was eine Präzision von 24 Bits ergibt. Im Falle der doppelten Präzision enthält dieses Feld 52 Bits, was eine Präzision von 53 Bits ergibt. Auch hier ist der Wert mehr als doppelt so hoch wie der vorherige, weshalb der Begriff „doppelte Präzision“ wieder etwas irreführend ist.

Wenn Sie sich jedoch eingehender mit Fließkommazahlen befassen, werden Sie feststellen, dass das Feld, das wir hier Fraction nennen, oft Mantisse genannt wird. Die Mantisse ist der wichtigste Teil bei der Bildung von Fließkommazahlen.

Es gibt viele Aspekte, die hier eine Rolle spielen, aber da viele Menschen das Interesse verlieren, wenn sie zu viele technische Details sehen, lassen Sie uns, um den Prozess angenehmer zu gestalten, zu einem praktischen Beispiel übergehen. In Code 01 haben wir in Zeile 14 den Wert 741 verwendet und ihn in eine Fließkommazahl umgewandelt. In diesem Fall in einen 32-Bit-Wert, d. h. in ein einfaches Präzisionsformat. Daher können wir das orangefarbene Schema aus Abbildung 06 verwenden. Ich möchte, dass Sie versuchen, sich auf das zu konzentrieren, was gezeigt wird, damit Sie dieses einfache Modell zunächst verstehen können.

Wir wollen also zunächst den Wert 741 in das Binärformat umwandeln. Hierfür können verschiedene Methoden eingesetzt werden. Für die meisten Menschen ist es jedoch am verständlichsten, durch zwei zu dividieren. Wenn Sie nicht wissen, wie man eine Zahl in ein binäres System umwandelt, machen Sie sich keine Sorgen, denn dieser erste Wert ist ganz einfach. Und es wird leicht zu verstehen sein, wie man es macht. Die folgende Abbildung 07 zeigt, wie dies gemacht wird.

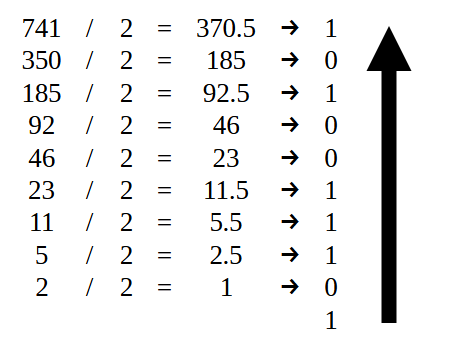
Abbildung 07

Nachdem alle Divisionen abgeschlossen sind, erhalten wir eine Folge von Nullen und Einsen. Damit der Wert aber richtig notiert wird, muss er in der Reihenfolge notiert werden, die der Pfeil anzeigt. Als Ergebnis erhalten wir das untenstehende Bild.

Bild 08

Okay, das ist der erste Teil. Sobald Sie dieses Bild 08 erreicht haben, können wir zur zweiten Phase übergehen, der darin besteht, diesen Binärwert in eine Fließkommazahl umzuwandeln. Seien Sie nun vorsichtig, denn dies ist der einfachste Fall, der möglich ist. Es ist jedoch notwendig, sie sehr gut zu verstehen, um später mit komplexeren Situationen umgehen zu können.

Wir müssen unsere Mantisse, d. h. den Bruchteil, erstellen. Dazu müssen wir den Punkt, der sich an der äußersten rechten Position befindet, nach links verschieben. Damit bleibt nur noch ein Bit übrig, das den Wert Eins hat. Diese Umwandlung führt zu dem Ergebnis, das Sie in der Abbildung unten sehen.

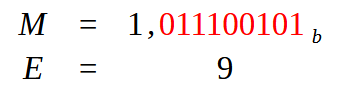
Bild 09

Betrachten wir nun das Folgende: M ist die so genannte Mantisse, d. h. der gebrochene Teil einer Fließkommazahl. E wird unser Exponent sein. Aber woher kommt dieser Wert von neun? Nun, das kommt daher, dass wir neun rote Werte in der Mantisse haben. Aber an diesem Wert von 9 muss noch gearbeitet werden. Und hier beginnt die dritte Phase der Umstellung. Je nachdem, welchen Ansatz wir wählen, werden wir diesen Wert von 9 auf die eine oder andere Weise verarbeiten und dadurch unterschiedliche Werte erzeugen. Dies ist notwendig, um eine Fließkommazahl im Hexadezimalformat darzustellen.

Doch bevor wir uns überlegen, was wir mit dem Wert 9 machen, sollten wir herausfinden, wie der Bruchteil einer Fließkommazahl gebildet wird.

Erinnern Sie sich, dass wir 23 Bits für einen Wert mit einfacher Präzision und 52 Bits für einen Wert mit doppelter Präzision haben? Die Präzision hingegen beträgt 24 Bit für einfache Präzision und 53 Bit für doppelte Präzision, nicht wahr? Genau dieses Bit mit dem Wert 1, das in Bild 09 schwarz hervorgehoben ist, ist also das zusätzliche Bit, das erscheint. Das heißt, es ist NICHT VORHANDEN, sondern ist im Feld Bruchteil impliziert. Das Feld Fraction wird also wie folgt gebildet:

Abbildung 10

Die Anzahl der grünen Nullen in Bild 10 hängt von der Anzahl der Bits im Feld Fraktion ab. Der Rest des Feldes wird mit so vielen Nullen wie nötig ausgefüllt. Jetzt haben wir also den gebrochenen Teil der Fließkommazahl. Es bleibt ein Teil des Exponenten zu bilden. Da der Wert positiv ist, ist das Vorzeichenfeld Sign Null. Bei der Bildung des Exponententeils muss die Art der verwendeten Präzision berücksichtigt werden. Wenn es sich um eine einfache Präzision handelt, addieren wir den in Abbildung 09 gezeigten Wert E (in diesem Fall neun) zum Bias-Wert, der für diesen Typ 127 beträgt. Daraus ergibt sich der Wert von 136. Dieser Vorgang ist in der nachstehenden Abbildung dargestellt.

Abbildung 11

Jetzt können wir endlich einen Wert mit einfacher Präzision bilden, um die Zahl 741 im Fließkommaformat darzustellen. Dieser Wert wird direkt darunter angezeigt.

Abbildung 12

Dividiert man die Bits aus Abbildung 12, um eine hexadezimale Darstellung zu erhalten, erhält man das in Abbildung 13 dargestellte Ergebnis.

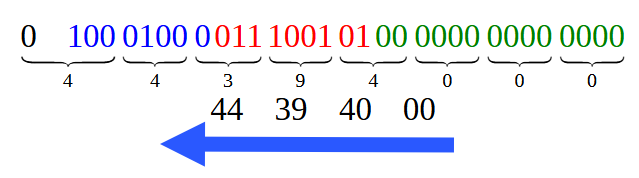
Abbildung 13

Beachten Sie, dass jeder der in Abbildung 13 gezeigten Hexadezimalwerte mit dem übereinstimmt, was wir in Bild 01 sehen. Sie sollten jedoch daran denken, sie in der durch den Pfeil angegebenen Reihenfolge zu lesen.  Dies hängt mit einem Merkmal zusammen, das wir in einem anderen, zukünftigen Artikel behandeln werden. Okay, das war der einfachste Fall von allen. Aber in diesem Artikel haben wir auch einen anderen Fall betrachtet, einen etwas komplizierteren, wenn ich so sagen darf. Dies ist der Fall, der in Code 02 betrachtet wird, wo wir im Wesentlichen einen Dezimalpunktwert haben. Und was sollten wir in dieser Situation tun?

Nun, mein lieber Leser, wenn ein Dezimalpunkt in einem numerischen Wert verwendet wird, sind die Dinge ein wenig anders, aber nicht viel. Die Wahrheit ist, dass wir in diesem Fall den Schritt der Binärkonvertierung in zwei Teile aufteilen sollten: einen für den Teil links vom Dezimalpunkt und den anderen für den Teil rechts davon. Das scheint kompliziert zu sein, oder? Aber in Wirklichkeit ist alles ganz einfach und logisch, man muss nur darauf achten, was man tut.

Zunächst sollte der Teil, der sich LINKS vom Dezimalpunkt befindet, wie in Abbildung 07 dargestellt umgerechnet werden. Das heißt, wir sollten nur den Wert 42 verwenden, wie unten dargestellt.

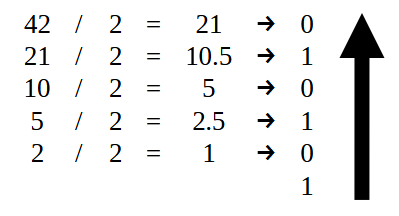
Abbildung 14

Der Teil RECHTS vom Dezimalpunkt sollte jedoch wie in Abbildung 15 gezeigt umgerechnet werden. Das heißt, wir nehmen 0,25 und wandeln den Dezimalteil des in Code 02 angegebenen Wertes in das Binärformat um.

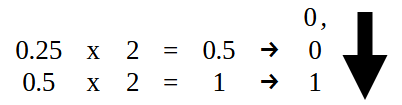
Abbildung 15

Daraus ergibt sich die folgende Darstellung der Zahl 42,25 im Binärformat, die unmittelbar darunter gezeigt wird.

Abbildung 16

Achten Sie sehr genau auf die Tatsache, dass wir in Bild 16 BEREITS EINEN PUNKT HABEN. Dies wird die nächsten Schritte etwas verändern - dies ist nämlich die in Abbildung 09 gezeigte Phase, in der wir den Wert der Mantisse und des Exponenten bestimmen. Da der Dezimalpunkt in Abbildung 16 bereits angegeben ist, müssen wir ihn nur noch so beeinflussen, dass nur noch ein Bit mit dem Wert 1 an der äußersten linken Position übrig bleibt. Genau dasselbe wie in Abbildung 09. Als Ergebnis erhalten wir das folgende Bild, das in der folgenden Abbildung dargestellt ist.

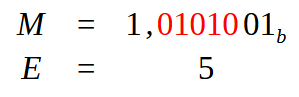
Abbildung 17

Beachten Sie, dass die in Abbildung 17 rot hervorgehobenen Werte genau die Werte sind, die verändert werden müssen, damit der Punkt die richtige Position einnimmt. Der Wert für die Einstellung des Exponenten ist also fünf. Wir haben auch schon den Mantissenwert, der zur Bildung des Feldes „Bruch“ verwendet wird. Nach der Berechnung des Wertes für die einfache Präzision ergibt sich das unten dargestellte Ergebnis.

Abbildung 18

Bitte beachten Sie, dass der gefundene Hexadezimalwert genau mit dem in Abbildung 04 dargestellten Wert übereinstimmt. Bitte denken Sie daran, dass der Text in Pfeilrichtung gelesen werden muss, und zwar in Gruppen von zwei Bytes. Gut, aber würden wir das gleiche Ergebnis erhalten, wenn wir doppelte Präzision verwenden würden? Das heißt, wenn die Zeile 4 in Code 02 unkommentiert bliebe, damit diese Richtlinie angewendet werden kann, würden wir 64 Bits anstelle von 32 Bits verwenden und damit die doppelte Präzision im System anwenden.

Erhalten wir in diesem Fall die gleichen Daten wie in Abbildung 18? Nun, wir werden so ziemlich das Gleiche bekommen, mein lieber Leser. Der Bruchteil bleibt nämlich gleich. Natürlich müssen wir weitere Nullen hinzufügen, um alle 52 Bits für das Feld des Bruchteils im doppelten Präzisionsformat aufzufüllen. Der Exponent wird jedoch völlig anders sein, da wir statt 127 (für einfache Präzision) 1023 verwenden werden. Der einzige Teil, der sich in Bild 18 visuell unterscheidet, ist also der blaue Bereich, der den Exponenten anzeigt. Um dies zu verdeutlichen, sehen Sie sich die folgende Abbildung an, die zeigt, wie die Werteingabe bei Verwendung der doppelten Präzision aussehen wird.

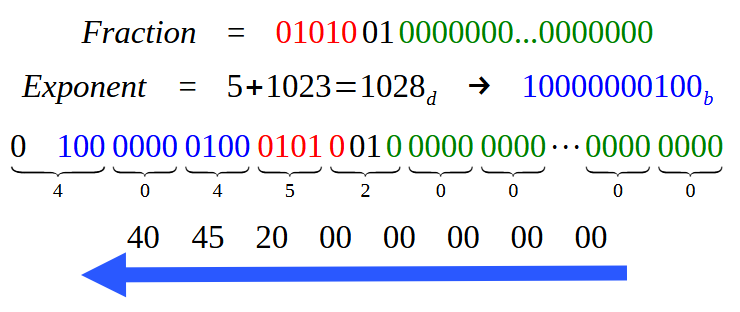
Abbildung 19

Und um zu überprüfen, ob unsere Schätzung richtig ist, führen wir Code 02 mit der vorgeschlagenen Änderung aus. Das Ergebnis sieht dann wie unten dargestellt aus.

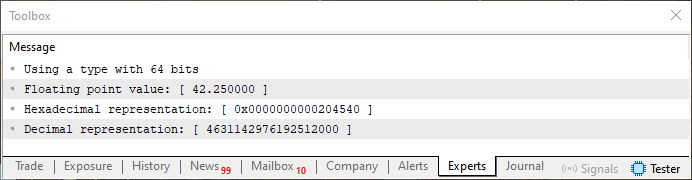
Abbildung 20

Abschließende Überlegungen

In diesem Artikel, der eine kurze Einführung in das Thema Fließkommazahlen darstellt, haben wir uns angesehen, wie eine solche Zahl im Speicher dargestellt wird und wie Sie mit dieser Art von Werten arbeiten können. Ich weiß, dass Sie, liebe Leserin, lieber Leser, an dieser Stelle vielleicht ein wenig verwirrt sind über verschiedene Aspekte im Zusammenhang mit Fließkommawerten. Und das ist nicht überraschend. Ich selbst habe viel Zeit damit verbracht, herauszufinden, wie diese Art von Daten erstellt wird, aber vor allem, wie man mit diesen Daten Berechnungen durchführen kann. Das ist zwar nicht mein Hauptziel hier, aber wer weiß, vielleicht kann ich in Zukunft erklären, wie man Berechnungen mit Fließkommazahlen durchführt. Dies ist in der Tat ein sehr faszinierendes Thema, vor allem mit Blick auf die Norm IEEE 754.

Natürlich gibt es auch andere Formate und Möglichkeiten zur Darstellung von Zahlen mit einem Dezimalpunkt. Da MQL5 jedoch, wie viele andere Programmiersprachen auch, genau das Format verwendet, das in diesem Artikel besprochen wird, empfehlen wir Ihnen, diese Art von Daten sorgfältig zu studieren. Schließlich entsprechen solche Zahlen oft nicht genau dem Wert, den wir zu berechnen glauben. Und ich schlage vor, Sie schauen sich die Links unten an und lernen, wie man Fließkommazahlen rundet, denn dafür gibt es klare Regeln, und das geschieht nicht umsonst.

Es liegt jedoch in Ihrem Ermessen. Ausgehend von dem, was wir hier betrachtet haben, ist es bereits möglich, mit Fließkommazahlen zu arbeiten. Aber zusätzliche Aspekte wie Rundungsregeln und eine Liste von Werten, die dargestellt werden können oder nicht, sind nur für diejenigen notwendig, die eine hohe Präzision und Korrektheit der in ihren Anwendungen verwendeten Werte anstreben. Und das ist in dem vorliegenden Artikel nicht zwingend vorgeschrieben.

Links:

• 754
• Arbeiten mit ONNX-Modellen in den Datenformaten float16 und float8