Der Kalman-Filter für Forex-Strategien der Rückkehr zur Mitte

Einführung

Der Kalman-Filter ist ein rekursiver Algorithmus, der im algorithmischen Handel verwendet wird, um den wahren Zustand einer Finanzzeitreihe durch Herausfiltern von Rauschen aus den Preisbewegungen zu schätzen. Er aktualisiert die Vorhersagen dynamisch auf der Grundlage neuer Marktdaten, was ihn für adaptive Strategien wie Mean Reversion wertvoll macht. In diesem Artikel wird zunächst der Kalman-Filter vorgestellt und seine Berechnung und Anwendung erläutert. Als nächstes wenden wir den Filter auf eine klassische Devisenstrategie, der Rückkehr zur Mitte, als Beispiel an. Schließlich führen wir verschiedene statistische Analysen durch, indem wir den Filter mit einem gleitenden Durchschnitt für verschiedene Devisenpaare vergleichen.

Der Kalman-Filter

Der Kalman-Filter, der 1960 von Rudolf E. Kalman eingeführt wurde, ist ein optimaler, rekursiver Schätzer, der für die Verfolgung und Vorhersage dynamischer Systeme verwendet wird. Ursprünglich für die Luft- und Raumfahrt sowie für Kontrollsysteme entwickelt, wurde es inzwischen auch in den Bereichen Finanzen, Robotik und Signalverarbeitung eingesetzt. Der Filter arbeitet in zwei Schritten: einem Vorhersageschritt, in dem er den nächsten Zustand des Systems schätzt, und einem Aktualisierungsschritt, in dem er die Schätzung auf der Grundlage neuer Beobachtungen verfeinert und dabei das Rauschen minimiert. 

Im Bereich des algorithmischen Handels kann man ihn einfach als einen allgemeinen Systemfilter betrachten, den Händler normalerweise verwenden, ähnlich wie gleitende Durchschnitts- oder lineare Regressionsmodelle. Der Kalman-Filter passt sich dynamisch an neue Daten an, reduziert das Rauschen und aktualisiert die Schätzungen effizient in Echtzeit, was ihn zu einem effektiven Instrument zur Erkennung von Marktverschiebungen macht. Es geht jedoch von einer linearen Dynamik aus, erfordert eine sorgfältige Parameterabstimmung, kann bei der Erkennung abrupter Veränderungen zurückbleiben und ist rechnerisch komplexer als einfachere Filter wie gleitende Durchschnitte.

Einige gängige Verwendungszwecke für den Kalman-Filter im algorithmischen Handel:

• Die Rückkehr zur Mitte handeln: Verwendung des aktuellen Preises im Vergleich zum geschätzten Preis als Einstiegsfilter.
• Handeln von Paaren: Schätzt dynamisch den Spread zwischen korrelierten Vermögenswerten und passt die Absicherungsquoten an die sich ändernden Marktbedingungen an.
• Trendfolge: Filtert kurzfristiges Rauschen, um langfristige Preistrends genauer zu erkennen.
• Schätzung der Volatilität: Bietet adaptive Schätzungen der Marktvolatilität für das Risikomanagement und die Positionsgrößenbestimmung.

Die Formel zur Berechnung des Kalman-Filterwertes lautet wie folgt:

Um die komplexe Formel auf einfache Weise zu verstehen, lassen Sie uns ein Beispiel zur Visualisierung heranziehen.

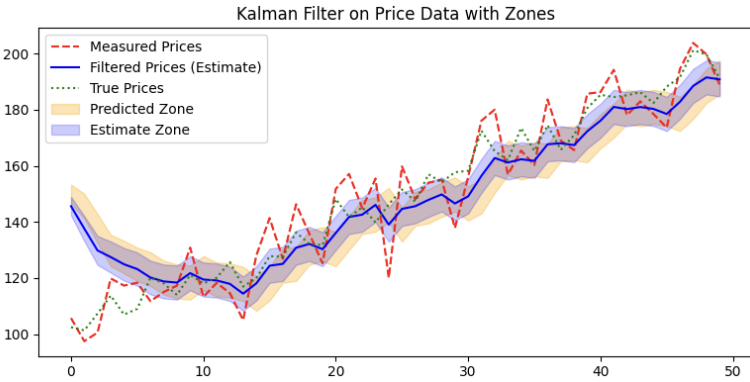
Der Kalman-Filter funktioniert, indem er seine Schätzung des wahren Preises auf der Grundlage von verrauschten Messungen und Vorhersagen aktualisiert. Sie wird in der Regel in drei Schritten gewonnen:

1. Vorhersage: Der Filter beginnt mit einer ersten Schätzung des Preises (vorhergesagter Preis) und seiner Unsicherheit (vorhergesagte Kovarianz). Dies wird durch die orangefarbene prognostizierte Zone dargestellt, d. h. den Bereich, in dem der Filter unter Berücksichtigung der vorherigen Schätzung und des Prozessrauschens den wahren Preis erwartet.

2. Aktualisierung: Wenn neue Preisdaten (gemessene Preise) verfügbar sind, vergleicht der Kalman-Filter diese mit dem vorhergesagten Preis. Anschließend wird die so genannte Kalman-Verstärkung (lila Linie) berechnet, um zu entscheiden, wie viel Gewicht die neue Messung gegenüber der Vorhersage haben soll. Wenn die Messung sehr verrauscht ist, vertraut der Filter seiner Vorhersage mehr. 

3. Schätzung: Der Filter aktualisiert den prognostizierten Preis unter Einbeziehung der neuen Messung. Der aktualisierte Preis (dargestellt durch den blauen Schätzbereich) weist eine geringere Unsicherheit auf als die Vorhersage. Dieser Bereich wird kleiner, wenn der Filter seine Schätzung verfeinert. 

Hier ist die Vorhersageunsicherheit durch die Kovarianz zwischen Messung und Vorhersage definiert. Eine größere Kovarianz bedeutet eine weniger sichere Schätzung, während eine kleinere Kovarianz bedeutet, dass der Filter mit seiner Schätzung sicherer ist. Wenn die Messung zuverlässig ist, ist die Kalman-Verstärkung hoch, und der Filter vertraut den neuen Daten mehr (was die Unsicherheit verringert). Wenn die Messung verrauscht ist, ist die Verstärkung geringer, und der Filter verlässt sich mehr auf die vorherige Vorhersage.

Die Geringfügigkeit wird durch die Varianz definiert, nämlich die Messabweichung und die Prozessabweichung. Sie passen sich nicht selbst an wie die Kovarianz, sondern werden von Anfang an festgelegt, je nachdem, wie glatt der Kalman-Filter sein soll.

Hier sind einige Beispiele dafür, wie sich die Abweichungen auf die Glätte der Kurve auswirken:

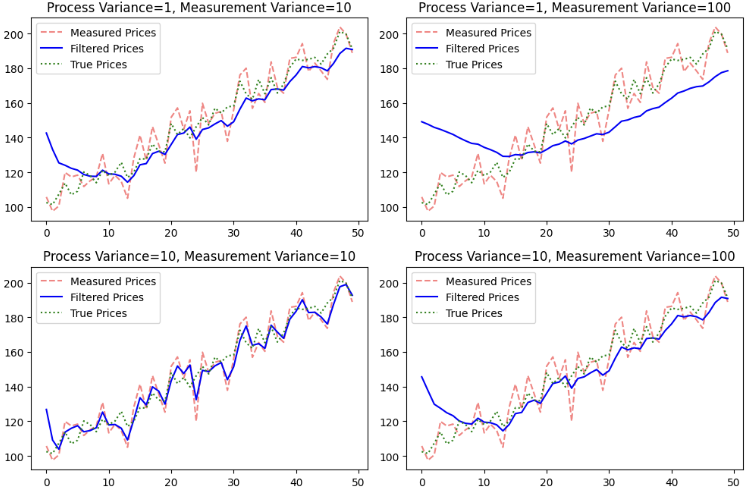
Im Allgemeinen stellt die Prozessvarianz (Q) dar, wie sehr das Modell erwartet, dass sich der wahre Zustand im Laufe der Zeit ändert, während die Messvarianz (R) das Vertrauen in die beobachteten Daten widerspiegelt. Ein höheres Q lässt den Filter besser auf plötzliche Veränderungen reagieren, erhöht aber auch die Volatilität. Ein höheres R glättet die Vorhersagen, indem es den Schätzungen der Vergangenheit mehr Vertrauen schenkt, was allerdings mit verzögerten Anpassungen einhergeht. Ein niedriger Q-Wert und ein moderater R-Wert führen zu stabilen Vorhersagen, während ein hoher Q-Wert und ein niedriger R-Wert den Filter reaktiver, aber auch stärker verrauscht machen.

Programmieren der Strategie

Die Strategien der Rückkehr zur Mitte verfolgen häufig den Ansatz, zu kaufen, wenn der Kurs überverkauft ist, zu verkaufen, wenn er überkauft ist, und auszusteigen, wenn der Kurs zum Mittelwert zurückgekehrt ist. Diese Strategie basiert auf der Annahme, dass die Preisdaten im Allgemeinen stabil sind und nicht zu extremen Niveaus neigen. Wenn sich der Preis in einem Extrem befindet, wird erwartet, dass er schließlich zum Gleichgewichtspunkt zurückkehrt. Diese Theorie gilt insbesondere für semistationäre Daten wie Devisen, bei denen sich Strategien zur Umkehrung des Mittelwerts über Jahre hinweg als profitabel erwiesen haben.

Wir werden unseren Ansatz anhand von Bollinger-Bändern mit 100 Perioden und einer Abweichung von 2,0 quantifizieren. Der detaillierte Plan sieht wie folgt aus:

• Wir kaufen, wenn der letzte Schlusskurs unter dem unteren Band liegt.
• Wir verkaufen, wenn der letzte Schlusskurs höher ist als das obere Band.
• Wir schließen die Position, sobald der Kurs das mittlere Band kreuzt.
• Jeweils nur eine Position, um einen übermäßigen Handel zu vermeiden.
• Wir legen den Stop-Loss auf 1 % des Kurses fest, um die für die Strategie der Rückkehr zur Mitte übliche Risiko der dicken Ränder zu vermeiden .

Wir planen, Forex-Paare auf dem 15-Minuten-Zeitrahmen zu handeln, einem gängigen Zeitrahmen, der genügend Handelsgeschäfte bietet und gleichzeitig eine angemessene Handelsqualität gewährleistet.

Wir beginnen immer damit, zuerst die notwendigen Funktionen zu definieren, da dies die spätere Kodierung der Handelslogik erleichtert. In diesem Fall brauchen wir nur die Kauf- und Verkaufsfunktionen wie folgt zu kodieren:

#include <Trade/Trade.mqh>
CTrade trade;
//+------------------------------------------------------------------+
//| Buy Function                                                     |
//+------------------------------------------------------------------+
void executeBuy(string symbol) {
       double ask = SymbolInfoDouble(symbol, SYMBOL_ASK);
       double lots=0.01;
       double sl = ask*(1-0.01);
       trade.Buy(lots,symbol,ask,sl);
}

//+------------------------------------------------------------------+
//| Sell Function                                                    |
//+------------------------------------------------------------------+
void executeSell(string symbol) {      
       double bid = SymbolInfoDouble(symbol, SYMBOL_BID);
       double lots=0.01;
       double sl = bid*(1+0.01);
       trade.Sell(lots,symbol,bid,sl);     
}

Dann initialisieren wir hier die globalen Variablen und den Initialisierer. Damit wird die magische Zahl für den Expert Advisor initialisiert, ebenso wie der Griff des Bollinger Bandes, den wir später verwenden werden.

input int Magic = 0;
input int bbPeriod = 100;
input double d = 2.0;

int barsTotal = 0;
int handleMa;

//+------------------------------------------------------------------+
//| Initialization                                                   |
//+------------------------------------------------------------------+
int OnInit()
{   handleBb = iBands(_Symbol,PERIOD_CURRENT,bbPeriod,0,d,PRICE_CLOSE);  
    trade.SetExpertMagicNumber(Magic);
    return INIT_SUCCEEDED;
}

In der Funktion OnTick() schließlich stellen wir damit sicher, dass wir die Handelslogik nur bei jedem Balken und nicht bei jedem Tick verarbeiten:

int bars = iBars(_Symbol,PERIOD_CURRENT);
  
if (barsTotal!= bars){
   barsTotal = bars;

Wir erhalten die aktuellen Werte der Bollinger-Bänder, indem wir Puffer-Arrays erstellen, die die aktuellen Werte durch Kopieren vom Handle speichern können.

double bbLower[], bbUpper[], bbMiddle[];
CopyBuffer(handleBb,UPPER_BAND,1,1,bbUpper);
CopyBuffer(handleBb,LOWER_BAND,1,1,bbLower);
CopyBuffer(handleBb,0,1,1,bbMiddle);

Diese Prüfung durchläuft alle aktuell geöffneten Positionen des Handelskontos, um zu prüfen, ob die Position von diesem speziellen EA geöffnet wurde. Wenn bereits eine Position von diesem EA eröffnet wurde, setzen wir die Variable NotInPosition auf false. Für jede geöffnete Position, die wieder zum mittleren Band zurückgekehrt ist, schließen wir sie.

bool NotInPosition = true;
for(int i = 0; i<PositionsTotal(); i++){
    ulong pos = PositionGetTicket(i);
    string symboll = PositionGetSymbol(i);
    if(PositionGetInteger(POSITION_MAGIC) == Magic&&symboll== _Symbol){
       NotInPosition = false;
       if((PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY&&price>bbMiddle[0])
       ||(PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL&&price<bbMiddle[0]))trade.PositionClose(pos);  
  }
}  

Die endgültige Handelslogik wird folgendermaßen ausgeführt:

if(price<bbLower[0]&&NotInPosition) executeBuy(_Symbol);
if(price>bbUpper[0]&&NotInPosition) executeSell(_Symbol);

Wir kompilieren den EA und starten den Strategietester im visuellen Modus, um zu sehen, ob der EA wie erwartet funktioniert.

Ein typischer Handel im Visualizer sollte wie folgt aussehen:

Anschließend kehren wir zu MetaEditor zurück und codieren die Filter der Strategie.

Erstens wollen wir, dass die Strategie der Rückkehr zur Mitte beim Einstieg in den 500-EMA mit dem Trend übereinstimmt, um eine zusätzliche Bestätigung zu erhalten. Wir fügen diese Zeilen dem ursprünglichen EA hinzu:

int handleMa;
handleMa = iMA(_Symbol,PERIOD_CURRENT,maPeriod,0,MODE_EMA,PRICE_CLOSE);
 
double ma[];
CopyBuffer(handleMa,0,1,1,ma);
    
if(price<bbLower[0]&&price>ma[0]&&NotInPosition) executeBuy(_Symbol);
if(price>bbUpper[0]&&price<ma[0]&&NotInPosition) executeSell(_Symbol);

 Danach codieren wir die Funktion zur Ermittlung des Kalman-Filterwerts:

//+------------------------------------------------------------------+
//| Kalman Filter Function                                           |
//+------------------------------------------------------------------+
double KalmanFilter(double price,double measurement_variance,double process_variance)
{
    // Prediction step (state does not change)
    double predicted_state = prev_state;
    double predicted_covariance = prev_covariance + process_variance;

    // Kalman gain calculation
    double kalman_gain = predicted_covariance / (predicted_covariance + measurement_variance);

    // Update step (incorporate new price observation)
    double updated_state = predicted_state + kalman_gain * (price - predicted_state);
    double updated_covariance = (1 - kalman_gain) * predicted_covariance;

    // Store updated values for next iteration
    prev_state = updated_state;
    prev_covariance = updated_covariance;

    return updated_state;
}

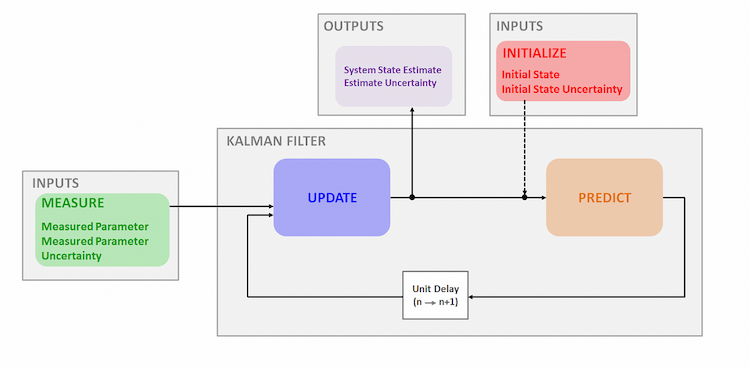
Diese Funktion erlaubt eine rekursive Funktion wie auf diesem Diagramm:

Um Kalman als Systemfilter im EA zu implementieren, fügen wir diese Zeilen in OnTick() ein:

double kalman = KalmanFilter(price,mv,pv);
if(price<bbLower[0]&&price>kalman&&NotInPosition) executeBuy(_Symbol);
if(price>bbUpper[0]&&price<kalman&&NotInPosition) executeSell(_Symbol);

Der Kalman-Filter funktioniert, indem er seine Schätzung des wahren Preises ständig aktualisiert, das Rauschen glättet und sich an die Preisbewegungen im Laufe der Zeit anpasst. Im Wesentlichen prognostiziert er den Preis. Wenn der Kurs unter das untere Band der Bollinger-Bänder fällt, signalisiert dies, dass der Markt überverkauft ist und voraussichtlich zum Mittelwert zurückkehren wird. Hier verwenden wir den Kalman-Filter als Bestätigung der Umkehrung. Wenn der Kurs im überverkauften Szenario über der Kalman-Schätzung liegt, deutet dies darauf hin, dass der Kurs bereits Anzeichen einer potenziellen Aufwärtsbewegung gezeigt hat. Im Verkaufsszenario ist das Gegenteil der Fall.

Der gleitende Durchschnitt ist zwar auch ein gängiger Systemfilter, sein Zweck unterscheidet sich jedoch leicht von dem des Kalman-Filters. Gleitende Durchschnitte dienen als Trendindikator, wobei die Position des Preises im Verhältnis zum MA die aktuelle Trendrichtung anzeigt.

Der vollständige Code lautet wie folgt:

#include <Trade/Trade.mqh>
CTrade trade;

input double mv = 10;
input double pv = 1.0;
input int Magic = 0;
input int bbPeriod = 100;
input double d = 2.0;
input int maPeriod = 500;

double prev_state;       // Previous estimated price
double prev_covariance = 1;  // Previous covariance (uncertainty)
int barsTotal = 0;
int handleMa;
int handleBb;

//+------------------------------------------------------------------+
//| Initialization                                                   |
//+------------------------------------------------------------------+
int OnInit()
{   handleMa = iMA(_Symbol,PERIOD_CURRENT,maPeriod,0,MODE_EMA,PRICE_CLOSE);
    handleBb = iBands(_Symbol,PERIOD_CURRENT,bbPeriod,0,d,PRICE_CLOSE);
    prev_state = iClose(_Symbol,PERIOD_CURRENT,1);  
    trade.SetExpertMagicNumber(Magic);
    return INIT_SUCCEEDED;
}

//+------------------------------------------------------------------+
//| Deinitializer function                                           |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
  }

//+------------------------------------------------------------------+
//| OnTick Function                                                  |
//+------------------------------------------------------------------+
void OnTick()
{
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  
  if (barsTotal!= bars){
     barsTotal = bars;
     bool NotInPosition = true;
     double price = iClose(_Symbol,PERIOD_CURRENT,1); 
     double bbLower[], bbUpper[], bbMiddle[];
     double ma[];
     double kalman = KalmanFilter(price,mv,pv);
     
     CopyBuffer(handleMa,0,1,1,ma);
     CopyBuffer(handleBb,UPPER_BAND,1,1,bbUpper);
     CopyBuffer(handleBb,LOWER_BAND,1,1,bbLower);
     CopyBuffer(handleBb,0,1,1,bbMiddle);
     
     for(int i = 0; i<PositionsTotal(); i++){
         ulong pos = PositionGetTicket(i);
         string symboll = PositionGetSymbol(i);
         if(PositionGetInteger(POSITION_MAGIC) == Magic&&symboll== _Symbol){
            NotInPosition = false;
            if((PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY&&price>bbMiddle[0])
            ||(PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL&&price<bbMiddle[0]))trade.PositionClose(pos);  
      }
    }  
    
     if(price<bbLower[0]&&price>kalman&&NotInPosition) executeBuy(_Symbol);
     if(price>bbUpper[0]&&price<kalman&&NotInPosition) executeSell(_Symbol);
    }
}

//+------------------------------------------------------------------+
//| Kalman Filter Function                                           |
//+------------------------------------------------------------------+
double KalmanFilter(double price,double measurement_variance,double process_variance)
{
    // Prediction step (state does not change)
    double predicted_state = prev_state;
    double predicted_covariance = prev_covariance + process_variance;

    // Kalman gain calculation
    double kalman_gain = predicted_covariance / (predicted_covariance + measurement_variance);

    // Update step (incorporate new price observation)
    double updated_state = predicted_state + kalman_gain * (price - predicted_state);
    double updated_covariance = (1 - kalman_gain) * predicted_covariance;

    // Store updated values for next iteration
    prev_state = updated_state;
    prev_covariance = updated_covariance;

    return updated_state;
}

//+------------------------------------------------------------------+
//| Buy Function                                                     |
//+------------------------------------------------------------------+
void executeBuy(string symbol) {
       double ask = SymbolInfoDouble(symbol, SYMBOL_ASK);
       double lots=0.01;
       double sl = ask*(1-0.01);
       trade.Buy(lots,symbol,ask,sl);
}

//+------------------------------------------------------------------+
//| Sell Function                                                    |
//+------------------------------------------------------------------+
void executeSell(string symbol) {      
       double bid = SymbolInfoDouble(symbol, SYMBOL_BID);
       double lots=0.01;
       double sl = bid*(1+0.01);
       trade.Sell(lots,symbol,bid,sl);     
} 

Um den Systemfilter zu ändern, passen wir einfach die endgültigen Kauf-/Verkaufskriterien an.

Statistische Analyse

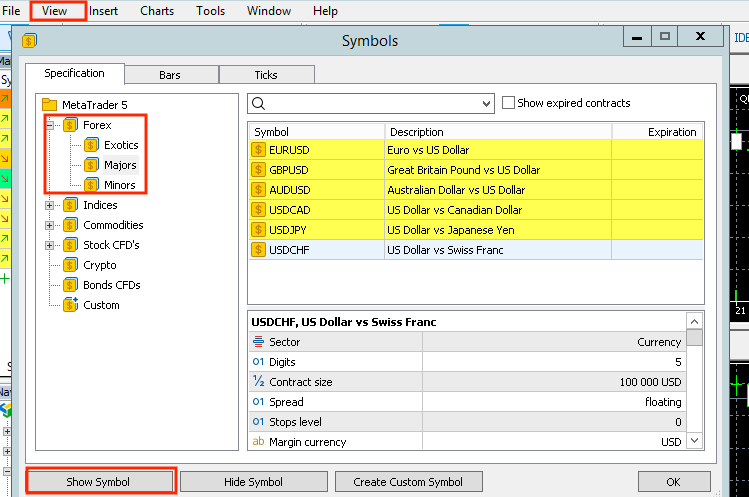
Wir kompilieren den EA und gehen zum MetaTrader 5 Terminal, klicken oben links auf Ansicht->Symbole->Forex und wählen Sie „Symbol anzeigen“ für alle Haupt- und Nebenpaare. Dadurch werden sie in Ihre Marktbeobachtungsliste aufgenommen, damit Sie den Markt später beobachten können.

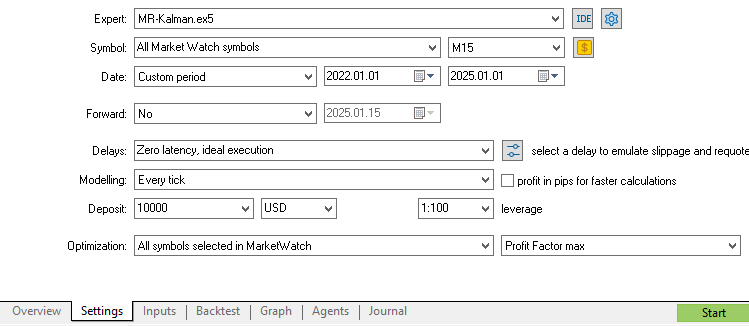
Dann gehen wir zum Markt-Scanner im Bereich Strategietester und führen einen Backtest der Strategie mit den Daten der letzten 3 Jahre durch. Dies wird uns helfen, ein Gefühl dafür zu bekommen, ob die Filter der Strategie die Rentabilität für die Mehrheit der von uns gehandelten Devisenpaare verbessern.

Natürlich hängt die Anzahl der gefilterten Handelsgeschäfte von den Parametern der Indikatoren ab. In dieser Studie verwenden wir gängige Parameterwerte, die eine ähnliche Anzahl von Handelsgeschäften filtern: einen exponentiellen gleitenden Durchschnitt mit einer Periodenlänge von 500 sowie eine Messvarianz von 10 und eine Prozessvarianz von 1 für den Kalman-Filter. Die Leser werden ermutigt, die Parameter so einzustellen, dass die besten Ergebnisse erzielt werden.

Zunächst testen wir das Ergebnis ohne Strategiefilter als Basiswert. Wir gehen davon aus, dass der EA mit Strategiefiltern im Durchschnitt besser abschneidet als die meisten der Basisergebnisse.

Das Ergebnis der am besten abschneidenden Devisenpaare sieht in etwa so aus:

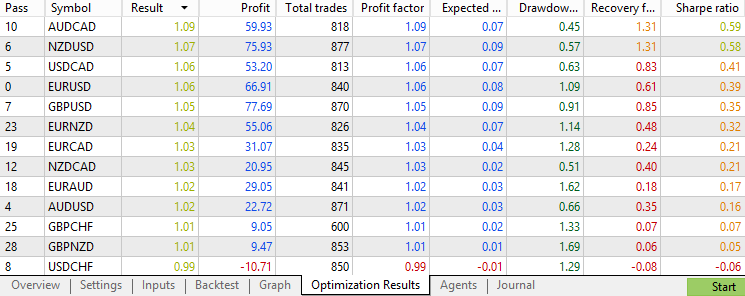
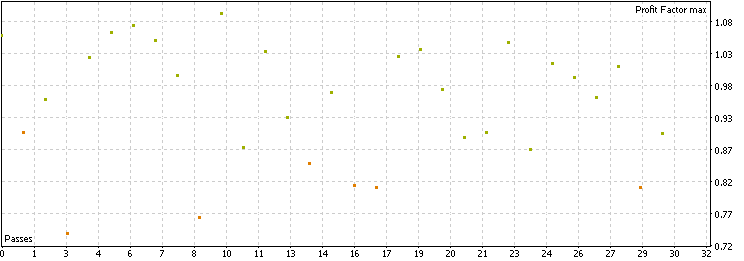
Wir sehen, dass die Strategie in den letzten 3 Jahren im Durchschnitt mehr als 800 Handelsgeschäfte für jedes Paar ausgeführt hat, was genügend Stichproben liefert, um die Schlussfolgerungen zu verallgemeinern. Die Verteilung liegt meist zwischen 0,8 und 1,1, was anständig ist, aber kein Paar überschreitet die Marken von 1,1 beim Gewinnfaktor oder 1 beim Sharpe Ratio. Insgesamt funktioniert die Rohstrategie bei vielen Devisenpaaren in den letzten Jahren, aber die Rentabilität ist nicht besonders beeindruckend. Behalten Sie dies im Hinterkopf, wenn wir sie mit der Leistung bei Anwendung von Filtern vergleichen.

Als Nächstes führen wir einen Backtest der Strategie mit dem Filter des gleitenden Durchschnitts durch. Hier sind die Ergebnisse:

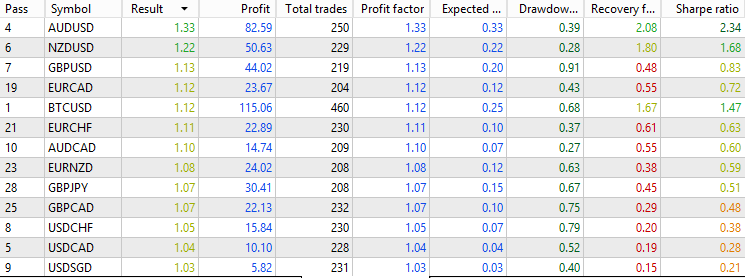
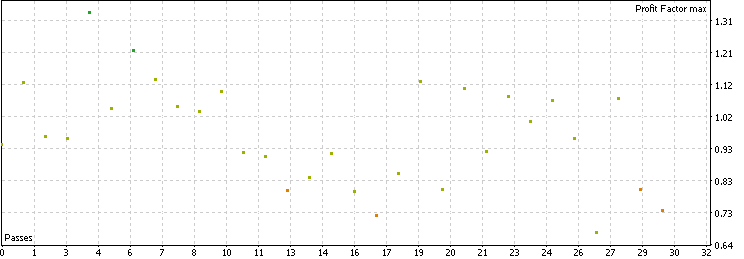
Wir sehen, dass wir durch die Verwendung des Filters für den gleitenden Durchschnitt etwa 70 % der ursprünglichen Abschlüsse herausgefiltert haben, sodass für jedes Paar etwa 250 Abschlüsse übrig bleiben. Darüber hinaus sind die gefilterten Handelsgeschäfte im Durchschnitt von höherer Qualität als die Basiswerte. Die meisten Devisenpaare bewegen sich zwischen einem Gewinnfaktor von 0,9 und 1,2, wobei das leistungsstärkste Paar einen Gewinnfaktor von 1,33 und eine Sharpe Ratio von 2,34 aufweist. Dies deutet darauf hin, dass die Verwendung des gleitenden Durchschnitts als Filter die Rentabilität dieser klassischen Rückkehr zur Mitte insgesamt verbessert hat.

Nun wollen wir uns dem Problem widmen und sehen, wie die Strategie mit dem Kalman-Filter abschneidet.

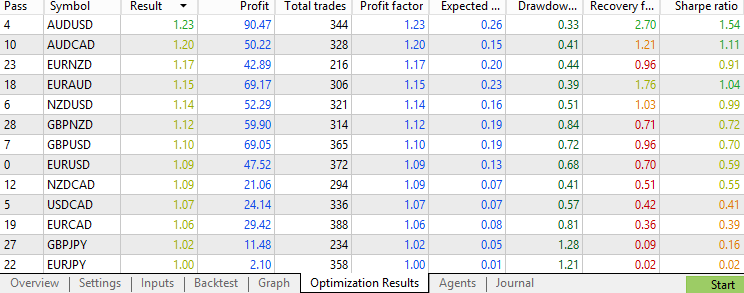
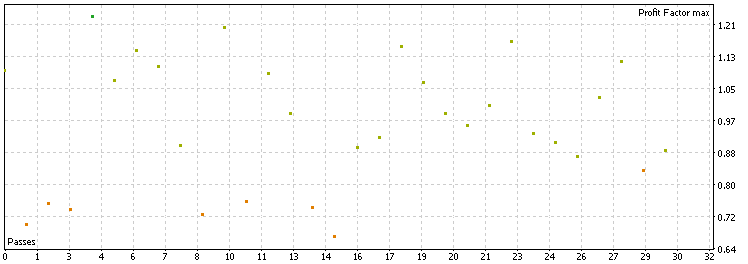
Durch den Kalman-Filter wurden etwa 60 % der ursprünglichen Handelsgeschäfte herausgefiltert, sodass für jedes Paar etwa 350 Handelsgeschäfte übrig blieben. Aus der Verteilung geht hervor, dass die Gewinnfaktoren meistens zwischen 0,85 und 1,2 liegen, was der Leistung des gleitenden Durchschnitts entspricht und besser ist als die Leistung der Basislinie. Betrachtet man darüber hinaus die Gesamtzahl der Devisenpaare mit einem Gewinnfaktor von 1,0+ und einem Gewinnfaktor von 1,2+, so kann man zu dem Schluss kommen, dass sowohl der gleitende Durchschnitt als auch der Kalman-Filter in Bezug auf die Verbesserung der durchschnittlichen Handelsqualität für diese Strategie ähnlich sind. Der Kalman-Filter ist dem gleitenden Durchschnitt in diesem Szenario nicht überlegen, was darauf hindeutet, dass Komplexität nicht immer zu einer besseren Leistung führt.

Wir haben bereits erwähnt, dass sich die Verwendung des Kalman-Filters in Bezug auf die Filterlogik leicht von der Verwendung des gleitenden Durchschnitts unterscheidet. In diesem Fall scheinen sie jedoch ähnlich gut zu funktionieren, was das Herausfiltern von schlechten Handelsgeschäften angeht. Um zu untersuchen, ob sie ähnliche Handelsgeschäfte filtern, werden wir die Unterschiede zwischen ihren gefilterten Handelsgeschäften analysieren, um festzustellen, ob die Wirkung des Kalman-Filters lediglich dieselbe ist wie die des EMA.

Als Referenz wählen wir das Devisenpaar AUDUSD, da es unter den beiden oben genannten Bedingungen die beste Performance erzielt hat.

Das Backtest-Ergebnis der Baseline:

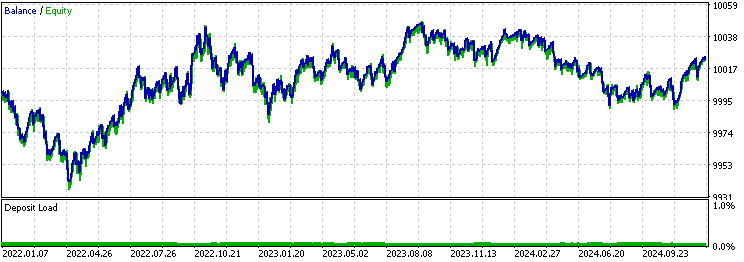
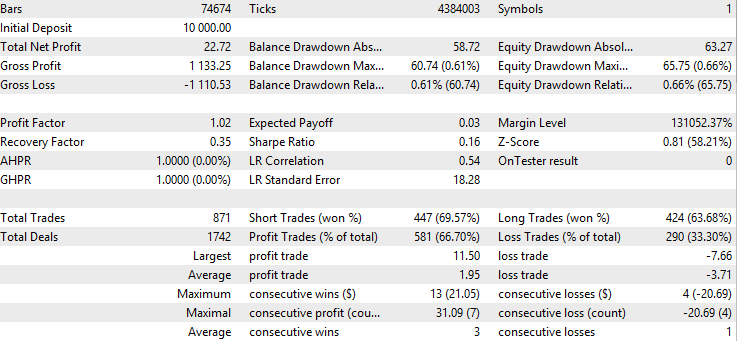
Das Backtest-Ergebnis des exponentiellen gleitenden Durchschnittsfilters:

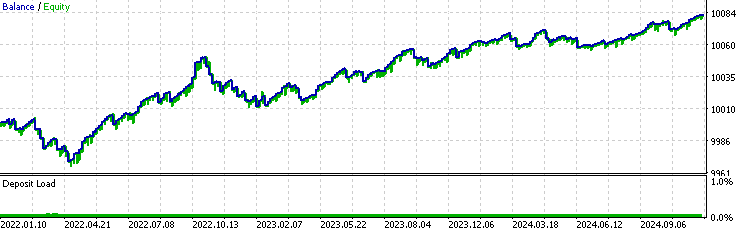
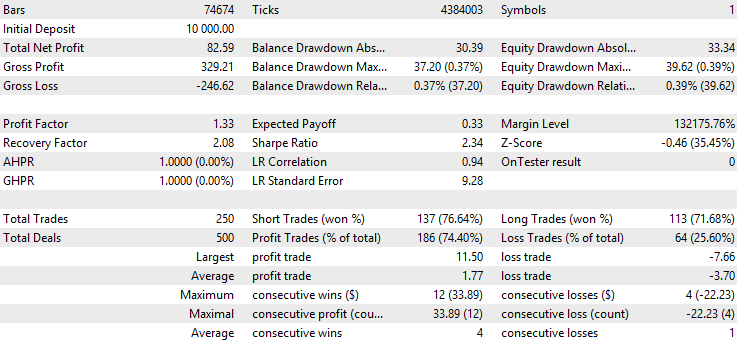
Das Ergebnis des Kalman-Filters:

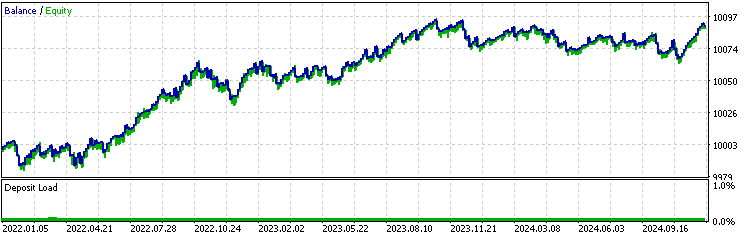
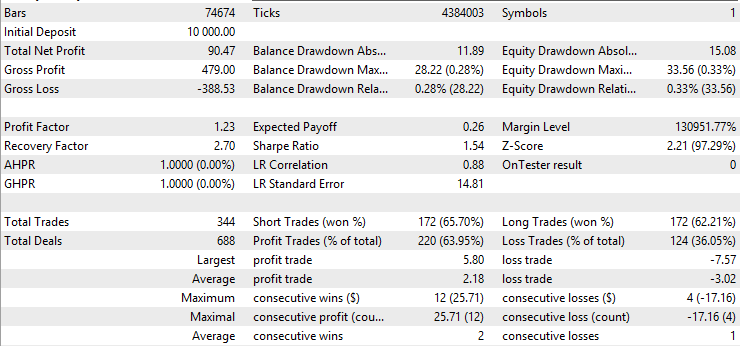
Zunächst ist festzustellen, dass die Gewinnrate der Version mit gleitendem Durchschnitt deutlich höher ist als die der Basisversion oder der Kalman-Version, während der durchschnittliche Gewinn niedriger und der durchschnittliche Verlust höher ist als bei den anderen Versionen. Dies deutet bereits darauf hin, dass die Version mit gleitendem Durchschnitt ganz andere Handelsgeschäfte tätigt als die Kalman-Version. Zur weiteren Untersuchung rufen wir den Excel-Bericht des Backtests auf, indem wir mit der rechten Maustaste auf die Seite mit den Backtestergebnissen klicken:

Für jeden Bericht notieren wir die Zeilennummer des Zeichens „Deals“:

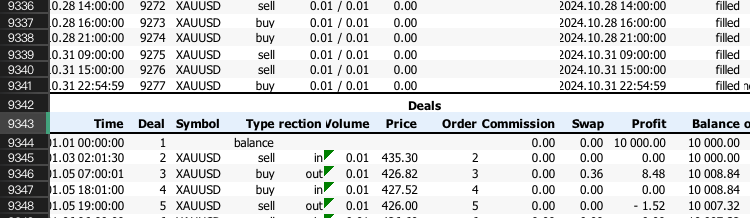
Als nächstes gehen wir zu Python oder Jupyter Notebook über. Wir kopieren und fügen den folgenden Code ein, ändern die Nummer von skiprow in die Zeilennummer des jeweiligen Excel-Berichts „Deals“ und sind fertig.

import pandas as pd
import matplotlib.pyplot as plt
from matplotlib_venn import venn3
df1 = pd.read_excel("baseline.xlsx", skiprows=1805)
df2 = pd.read_excel("ma.xlsx", skiprows =563 )
df3 = pd.read_excel("kalman.xlsx",skiprows = 751)
df1 = df1[['Time']][1:-1]
df1 = df1[df1.index % 2 == 0]  # Filter for rows with odd indices
df2 = df2[['Time']][1:-1]
df2 = df2[df2.index % 2 == 0]
df3 = df3[['Time']][1:-1]
df3 = df3[df3.index % 2 == 0]

# Convert "Time" columns to datetime
df1['Time'] = pd.to_datetime(df1['Time'])
df2['Time'] = pd.to_datetime(df2['Time'])
df3['Time'] = pd.to_datetime(df3['Time'])

# Find intersections
set1 = set(df1['Time'])
set2 = set(df2['Time'])
set3 = set(df3['Time'])

# Create the Venn diagram
venn_labels = {
    '100': len(set1 - set2 - set3),  # Only in df1
    '010': len(set2 - set1 - set3),  # Only in df2
    '001': len(set3 - set1 - set2),  # Only in df3
    '110': len(set1 & set2 - set3),  # In df1 and df2
    '011': len(set2 & set3 - set1),  # In df2 and df3
    '101': len(set1 & set3 - set2),  # In df1 and df3
    '111': len(set1 & set2 & set3)   # In all three
}

# Plot the Venn diagram
plt.figure(figsize=(8, 8))
venn3(subsets=venn_labels, set_labels=('Baseline', 'EMA', 'Kalman'))
plt.title("Venn Diagram of Time Overlap")
plt.show()

Die Logik dieses Codes besteht im Wesentlichen darin, dass wir die Positionsausgangszeiten in drei Datenrahmen für jede Version speichern, indem wir Zeilen überspringen und Zeilen mit geraden Indizes auswählen. Dann speichern wir jeden Datenrahmen in einer Menge und erhalten das Venn-Diagramm, indem wir vergleichen, ob sich die Zeiten überschneiden. Das Diagramm zeigt die Anzahl der Handelsgeschäfte in jeder Region, getrennt durch verschiedene Farben. Beachten Sie, dass selbst die Basislinie nicht alle Abschlüsse enthält, die die EMA- und Kalman-Versionen haben, weil wir die Strategie so eingestellt haben, dass sie immer nur einen Abschluss tätigt, was dazu führt, dass sie einige Abschlüsse verpasst, die die anderen Versionen haben.

Hier ist das Venn-Diagramm der Ausgabe:

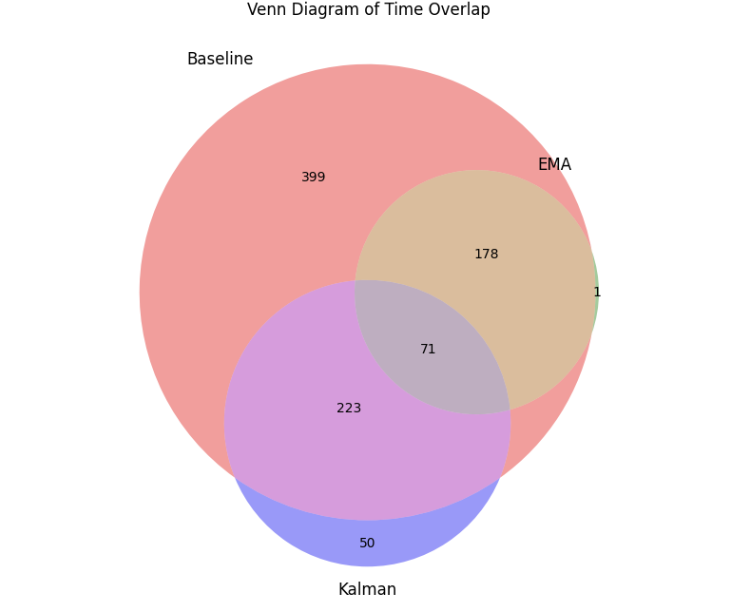
Betrachtet man den Bereich, in dem sich Kalman und MA überschneiden, so stellt man fest, dass von den Hunderten von Abschlüssen, die jede Version getätigt hat, nur 71 Abschlüsse identisch waren. Dies deutet darauf hin, dass die Filtereffekte dieser beiden Strategien sehr unterschiedlich sind, obwohl sie eine ähnliche Anzahl von Handelsgeschäften aus der ursprünglichen Strategie herausfiltern. Dies unterstreicht die Bedeutung der Untersuchung und Nutzung des Kalman-Filters, da er eine einzigartige Filteroption bietet, die sich von den üblichen Trendfiltern unterscheidet.

Schlussfolgerung

In diesem Artikel haben wir einen fortschrittlichen rekursiven Algorithmus für den algorithmischen Handel vorgestellt, den Kalman-Filter. Wir begannen damit, die Mechanismen und Implementierungen zu erklären und stellten Visualisierungen und Formeln zur Verfügung. Anschließend haben wir den gesamten Prozess der Entwicklung einer Forex-Mittelwertumkehrstrategie und der Implementierung des Kalman-Filters in MQL5 durchlaufen. Schließlich führten wir verschiedene statistische Analysen durch, darunter Markt-Scanning, Backtesting und Überschneidungsvergleiche, um seine Filterfähigkeit im Vergleich zum gleitenden Durchschnitt und zur Basislinie zu bewerten.

Im tatsächlichen Handel wird der Kalman-Filter von führenden quantitativen Handelsinstitutionen häufig eingesetzt, ist aber im Bereich des Einzelhandels noch weniger bekannt. Dieser Artikel soll der MQL5-Gemeinschaft Einblicke und eine praktische Umsetzung bieten, indem er einen Ansatz zur Bewertung der Filterfähigkeiten des Kalman-Filters anbietet, damit dieser besser in die zukünftige Strategieentwicklung integriert werden kann. Die Leser werden ermutigt, mit diesem Rahmenwerk selbst zu experimentieren und es in ihr eigenes Handelsarsenal einzubauen.

Datei-Tabelle

Datei Name	Dateiverwendung
Kalman visualizations.ipynb	Der Python-Code für die in diesem Artikel verwendeten Visualisierungen
MR-Kalman.mq5	Der Code des Expertenberaters