Neuronale Netze im Handel: Verwenden von Sprachmodellen für die Zeitreihenprognose

MetaTrader 5 — Handelssysteme | 26 Februar 2025, 09:17

Einführung

In dieser Artikelserie haben wir verschiedene Architekturansätze für die Zeitreihenmodellierung untersucht. Viele dieser Ansätze erzielen lobenswerte Ergebnisse. Es ist jedoch offensichtlich, dass sie die Vorteile komplexer Muster in Zeitreihen, wie etwa Saisonalität und Trend, nicht voll ausnutzen. Diese Komponenten sind grundlegende Unterscheidungsmerkmale von Zeitreihendaten. Folglich deuten neuere Studien darauf hin, dass auf Deep Learning basierende Architekturen möglicherweise nicht so robust sind wie bisher angenommen, da sogar flache neuronale Netzwerke oder lineare Modelle sie bei bestimmten Benchmarks übertreffen.

Mittlerweile wurden mit der Entstehung grundlegender Modelle in der Verarbeitung natürlicher Sprache (NLP) und der Computervision (CV) wichtige Meilensteine für das effektive Lernen von Repräsentationen erreicht. Das Vortraining grundlegender Modelle für Zeitreihen mit großen Datensätzen verbessert die Leistung bei nachfolgenden Aufgaben. Darüber hinaus ermöglichen große Sprachmodelle die Verwendung vorab trainierter Darstellungen, sodass die Modelle nicht von Grund auf neu trainiert werden müssen. Allerdings erfassen die vorhandenen grundlegenden Strukturen und Methoden in Sprachmodellen die Entwicklung zeitlicher Muster nicht vollständig, was für die Modellierung von Zeitreihen von entscheidender Bedeutung ist.

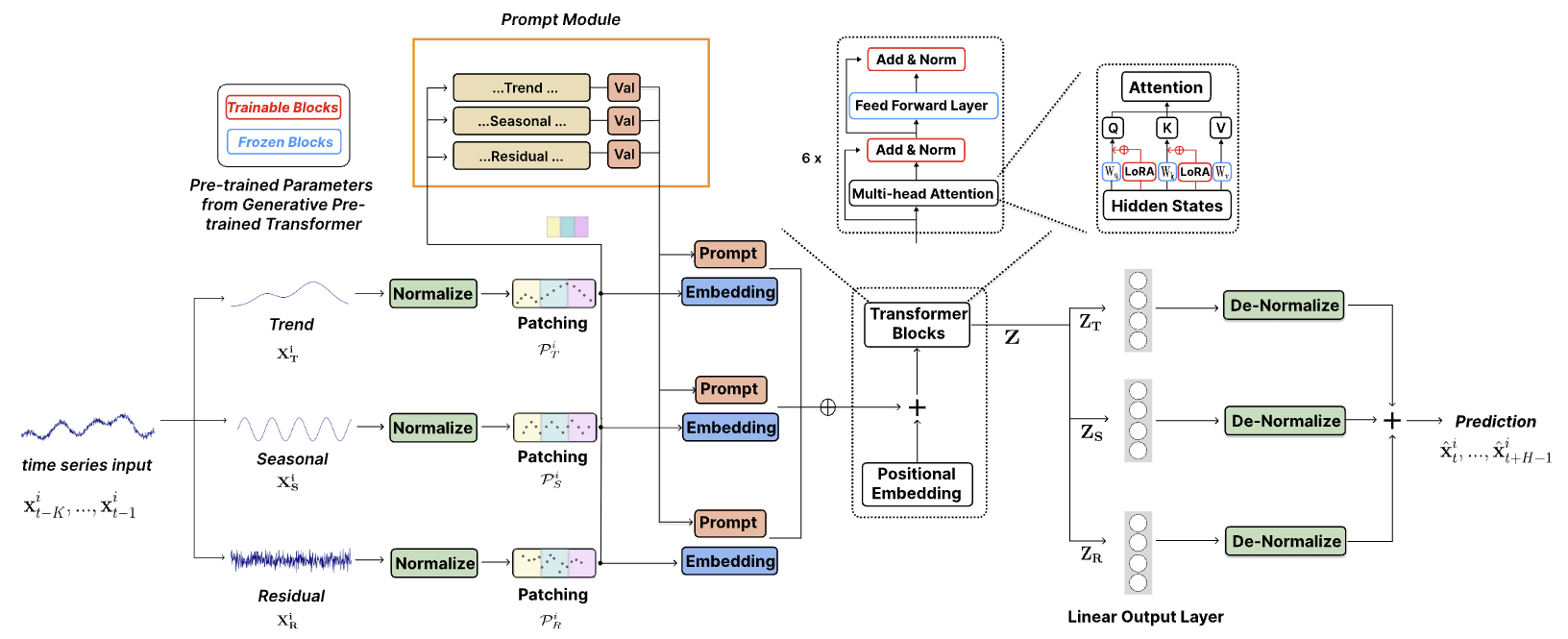
Die Autoren des Artikels „TEMPO: Prompt-based Generative Pre-trained Transformer for Time Series Forecasting“ wenden sich der kritische Herausforderung zu, große, vorab trainierte Modelle für die Zeitreihenprognose anzupassen. Sie schlagen TEMPO vor, ein umfassendes, auf GPT basierendes Modell, das für effektives Lernen der Zeitreihendarstellung entwickelt wurde. TEMPO besteht aus zwei wesentlichen Analysekomponenten: Die eine konzentriert sich auf die Modellierung spezifischer Zeitreihenmuster wie Trends und Saisonalität, die andere zielt darauf ab, mithilfe eines prompten Ansatzes allgemeinere Erkenntnisse aus intrinsischen Dateneigenschaften abzuleiten. Insbesondere zerlegt TEMPO zunächst die ursprünglichen multimodalen Zeitreihendaten in drei Komponenten: Trend, Saisonalität und Residuen. Jede Komponente wird dann in einen entsprechenden latenten Raum abgebildet, um die anfängliche Zeitreiheneinbettung für GPT zu erstellen.

Die Autoren führen eine formale Analyse durch, die den Zeitreihenbereich mit dem Frequenzbereich verknüpft, um die Notwendigkeit der Zerlegung solcher Komponenten für die Zeitreihenanalyse hervorzuheben. Sie zeigen auch theoretisch, dass der Aufmerksamkeitsmechanismus Schwierigkeiten hat, diese Zerlegung automatisch durchzuführen.

TEMPO verwendet Eingabeaufforderungen, die zeitliches Wissen über Trends und Saisonalität kodieren und so GPT effektiv für Prognoseaufgaben optimieren. Darüber hinaus werden Trend, Saisonalität und Residuen verwendet, um eine interpretierbare Struktur zum Verständnis der Interaktionen zwischen den ursprünglichen Komponenten bereitzustellen.

1. Der Algorithmus von TEMPO

In ihrer Arbeit verfolgen die Autoren von TEMPO einen hybriden Ansatz, der die Robustheit der statistischen Zeitreihenanalyse mit der Anpassungsfähigkeit datengetriebener Methoden kombiniert. Sie führen eine neuartige Integration der Saison- und Trendzerlegung in vortrainierte Sprachmodelle basierend auf der Architektur des Transformers ein. Diese Strategie nutzt die einzigartigen Vorteile sowohl statistischer als auch maschineller Lernmethoden und verbessert die Fähigkeit des Modells, Zeitreihendaten effizient zu verarbeiten.

Darüber hinaus führen sie einen halbweichen, auf Eingabeaufforderungen basierenden Ansatz ein, der die Anpassungsfähigkeit vorab trainierter Modelle für die Verarbeitung von Zeitreihen erhöht. Diese innovative Technik ermöglicht es Modellen, ihr umfangreiches vorab trainiertes Wissen mit den spezifischen Anforderungen der Zeitreihenanalyse zu integrieren.

Bei multimodalen Zeitreihendaten trägt die Zerlegung komplexer Rohdaten in aussagekräftige Komponenten wie Trends und Saisonalität zur Optimierung der Informationsextraktion bei.

Die Trendkomponente XT erfasst langfristige Muster in den Daten. Die saisonale Komponente XS fasst sich wiederholende, kurzfristige Zyklen zusammen, die nach dem Entfernen des Trends bewertet werden. Die Restkomponente XR stellt den verbleibenden Teil der Daten nach dem Extrahieren von Trend und Saisonalität dar.

In der Praxis empfiehlt es sich, für eine genauere Zerlegung möglichst viele Informationen zu nutzen. Um jedoch die Rechenleistung aufrechtzuerhalten, entscheiden sich die Autoren für eine lokale Zerlegung mit einem Fenster fester Größe anstelle einer globalen Zerlegung über den gesamten Datensatz. Es werden trainierbare Parameter eingeführt, um verschiedene Komponenten der lokalen Zerlegung zu schätzen und dieses Prinzip auf andere Modellkomponenten auszuweiten.

Experimentelle Ergebnisse zeigen, dass die Zerlegung den Prognoseprozess erheblich vereinfacht.

Die vorgeschlagene Zerlegung der Rohdaten ist für moderne, auf Transformer basierende Architekturen von entscheidender Bedeutung, da Aufmerksamkeitsmechanismen theoretisch nicht in der Lage sind, unidirektionale Trends und saisonale Signale automatisch voneinander zu trennen. Wenn Trend- und Saisonkomponenten nicht orthogonal sind, können sie mithilfe eines Satzes orthogonaler Basen nicht vollständig getrennt werden. Die Schicht der Selbstaufmerksamkeit verwandelt sich auf natürliche Weise in eine orthogonale Transformation, ähnlich der Hauptkomponentenanalyse. Daher wäre die direkte Betrachtung der Rohdaten von Zeitreihen für die Trennung nichtorthogonaler Trend- und Saisonkomponenten nicht effektiv.

Die Methode TEMPO wendet zunächst eine reversible Normalisierung auf jede globale Komponente an, um die Informationsübertragung zu erleichtern und durch Verteilungsverschiebungen verursachte Verluste zu minimieren.

Zusätzlich wird eine auf dem mittleren, quadratischen Fehler (MSE) basierende Rekonstruktionsverlustfunktion implementiert, um sicherzustellen, dass die lokalen Zerlegungskomponenten mit der im Trainingsdatensatz beobachteten globalen Zerlegung übereinstimmen.

Als Nächstes werden die Zeitreihendaten segmentiert und mit einer Positionskodierung versehen, um durch die Aggregation benachbarter Zeitschritte in Token lokale Semantik zu extrahieren. Dadurch wird der historische Horizont erheblich erweitert und die Redundanz reduziert.

Die resultierenden Zeitreihen-Token werden dann durch eine Einbettungsschicht geleitet. Diese erlernten Einbettungen ermöglichen es der Sprachmodellarchitektur, ihre Fähigkeiten effektiv auf eine neue sequentielle Modalität der Zeitreihendaten zu übertragen.

Eingabeaufforderungstechniken haben sich in verschiedenen Anwendungsbereichen als bemerkenswert wirksam erwiesen, indem sie in sorgfältig gestalteten Eingabeaufforderungen kodiertes Vorwissen anwenden. Dieser Erfolg ist auf Eingabeaufforderungen zurückzuführen, die eine Struktur bereitstellen, welche die Modellergebnisse mit den gewünschten Zielen in Einklang bringt. Dies verbessert die Genauigkeit, Konsistenz und Gesamtqualität des Inhalts. Im Bemühen, die in den verschiedenen Zeitreihenkomponenten enthaltenen umfangreichen semantischen Informationen auszunutzen, führten die Autoren eine abgeschwächte Eingabeaufforderungsstrategie ein. Dieser Ansatz generiert eindeutige Eingabeaufforderungen, die den einzelnen primären Komponenten der Zeitreihe entsprechen: Trend, Saisonalität und Residuen. Diese Eingabeaufforderungen werden mit ihren jeweiligen Rohdatenkomponenten kombiniert, wodurch ein fortgeschrittenerer Ansatz zur Sequenzmodellierung ermöglicht wird, der der Vielschichtigkeit von Zeitreihendaten Rechnung trägt.

Diese Struktur verknüpft jede Dateninstanz mit bestimmten Eingabeaufforderungen als induktive Verzerrungen und kodiert gemeinsam wichtige, prognosebezogene Informationen. Es ist zu beachten, dass der vorgeschlagene dynamische Rahmen ein hohes Maß an Anpassungsfähigkeit aufweist und so die Kompatibilität mit einer breiten Palette von Zeitreihenanalysen gewährleistet. Diese Anpassungsfähigkeit unterstreicht das Potenzial, Strategien zu entwickeln, die auf die Komplexität unterschiedlicher Zeitreihen-Datensätze reagieren.

Die Autoren von TEMPO verwenden ein decoderbasiertes Modell von GPT als grundlegende Struktur für das Lernen der Zeitreihendarstellung. Um zerlegte semantische Informationen effektiv zu nutzen, werden Eingabeaufforderungen und verschiedene Komponenten integriert und durch den Block von GPT geleitet.

Ein alternativer Ansatz besteht darin, separate GPT-Blöcke für verschiedene Arten von Zeitreihenkomponenten zu verwenden.

Die Gesamtprognose ergibt sich dann aus der Kombination der einzelnen Komponentenprognosen. Jede Komponente wird nach dem Durchlaufen von GPT über eine vollständig verbundene Schicht verarbeitet, um Vorhersagen zu generieren. Die endgültigen Prognosen werden durch Einbeziehung der entsprechenden, während der Normalisierung extrahierten statistischen Parameter in den ursprünglichen Datenraum zurückprojiziert. Durch Summieren der Vorhersagen der einzelnen Komponenten lässt sich die gesamte Zeitreihenkurve rekonstruieren.

Die Visualisierung von TEMPO von den Autoren ist unten verfügbar.

2. Implementierung in MQL5

Nachdem wir die theoretischen Aspekte von TEMPO besprochen haben, gehen wir zum praktischen Teil unseres Artikels über, in dem wir unsere Vision der vorgeschlagenen Ansätze mithilfe von MQL5 umsetzen.

Es ist wichtig zu beachten, dass wir leider keinen Zugriff auf ein vortrainiertes Sprachmodell haben. Aus diesem Grund können wir die Übertragbarkeit von Sprachmodelldarstellungen auf die Zeitreihenprognose nicht vollständig beurteilen. Wir können jedoch das vorgeschlagene Architektur-Framework replizieren und seine Wirksamkeit bei der Prognose von Finanzzeitreihen anhand realer historischer Daten beurteilen.

Bevor wir mit der Untersuchung des Codes fortfahren, untersuchen wir zunächst die bei unserer Implementierung getroffenen Architekturentscheidungen.

Eingehende Rohdaten werden in drei Komponenten zerlegt: Trend, Saisonalität und Residuen. Um den Trend zu extrahieren, verwendeten die Autoren der Methode die Berechnung des Durchschnittswerts der Eingabedaten mithilfe eines gleitenden Fensters. Dies ähnelt im Allgemeinen dem Standardindikator des gleitenden Durchschnitt. In unserer Implementierung entscheide ich mich für die zuvor besprochene Methode der stückweisen, linearen Darstellung (PLR). Meiner Meinung nach ist dies eine informativere Methode, mit der sich Trends unterschiedlicher Länge identifizieren lassen. Da PLR-Ergebnisse jedoch nicht direkt von der Originalreihe abgezogen werden können, sind zusätzliche algorithmische Verfeinerungen erforderlich, die wir während der Implementierung untersuchen werden.

Im Hinblick auf die Extraktion der Saisonalität ist ein Frequenzspektrumansatz eine natürliche Wahl. Da jedoch die diskrete Fourier-Transformation (DFT) die Zeitreihe im Frequenzbereich vollständig darstellt, rekonstruiert die inverse DFT (iDFT) die ursprüngliche Zeitreihe ohne Verzerrung. Um die saisonale Komponente von Rauschen und Ausreißern zu isolieren, müssen wir bestimmte Frequenzbänder ausschneiden. Daher stellt sich als Nächstes die Frage, welches Volumen und Frequenzliste zurückgesetzt werden soll. Auf diese Frage gibt es keine eindeutige Antwort. Wir haben bereits ähnliche Probleme bei der Zeitreihenprognose im Frequenzbereich diskutiert. Dieses Mal bin ich jedoch aus einem etwas anderen Blickwinkel an das Thema herangegangen. Für unsere Datenanalyse verwenden wir eine multimodale Zeitreihe, die sich auf ein Finanzinstrument bezieht. Und es ist durchaus zu erwarten, dass die Zyklen der einzelnen Komponenten miteinander übereinstimmen. Warum also nicht den Mechanismus der Selbstaufmerksamkeit nutzen, um konsistente Frequenzen in den Spektren einzelner einheitlicher Zeitreihen zu identifizieren? Wir erwarten, dass die angepassten Spektrumfrequenzen die saisonale Komponente hervorheben.

Auf diese Weise können wir die Originaldaten in die einzelnen Komponenten zerlegen, so wie TEMPO das macht. Die Funktionsweise des erstellten Modells wird teilweise erläutert. Um einheitliche Modelle in einzelne Segmente aufzuteilen und einzubetten, verfügen wir bereits über eine fertige Lösung. Dasselbe gilt für Architekturlösungen auf Basis eines Transformers. Wie sieht es mit Prompts bzw. Eingabeaufforderungen aus? Die Autoren der Methode schlagen die Verwendung von Eingabeaufforderungen vor, die GPT dazu bringen können, eine Sequenz im erwarteten Kontext zu generieren. Bei dieser Arbeit habe ich beschlossen, die Ausgabe von PLR als Eingabeaufforderungen zu verwenden.

Und die letzte globale Frage betrifft wahrscheinlich die Anzahl der verwendeten Aufmerksamkeitsmodelle: ein allgemeines Modell oder ein Modell pro Komponente. Ich habe mich für die Verwendung eines allgemeinen Modells entschieden, da damit der gesamte Datenverarbeitungsprozess gleichzeitig in parallelen Streams organisiert werden kann. Die Verwendung eines separaten Modells für jede Komponente würde hingegen dazu führen, dass diese nacheinander verarbeitet würden. Dies wiederum würde sowohl den Zeitaufwand für das Trainieren der Modelle als auch für die anschließende Entscheidungsfindung erhöhen.

Wir haben die wichtigsten Punkte des zu erstellenden Modells besprochen und können nun mit der praktischen Arbeit fortfahren.

2.1 Erweiterung des OpenCL-Programms

Beginnen wir unsere Arbeit mit der Erstellung neuer Kernel auf der Programmseite von OpenCL. Um die Haupttrends aus der multimodalen Zeitreihe der Originaldaten zu extrahieren, verwenden wir, wie oben erwähnt, die Methode der stückweise linearen Darstellung (PLR). Dabei wird jedes Segment durch drei Werte dargestellt: Steigung, Offset und Segmentgröße. Offensichtlich ist es bei einer solchen Darstellung der Zeitreihe recht schwierig, Trends aus den Originaldaten abzuleiten. Es ist jedoch möglich. Um diese Funktionsweise zu implementieren, erstellen wir einen Kernel CutTrendAndOther. Dieser Kernel erhält in den Parametern 4 Zeiger auf Datenpuffer. 2 davon enthalten die Eingangsdaten in Form eines Tensors der Eingangszeitreihe (Inputs) und des stückweise linearen Darstellungstensors (PLR). Wir werden die Ergebnisse der Operationen in zwei weiteren Puffern speichern:

trend – Trends in Form einer regelmäßigen Zeitreihe
other – der Werteunterschied zwischen den Originaldaten und der Trendlinie

__kernel void CutTrendAndOther(__global const float *inputs,
                               __global const float *plr,
                               __global float *trend,
                               __global float *other
                              )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

Wir planen, diesen Kernel in einem zweidimensionalen Aufgabenraum aufzurufen. Die erste Dimension stellt die Größe der Eingabedatensequenz dar und die zweite die Anzahl der analysierten Variablen (einheitliche Sequenzen). Im Kernel-Body identifizieren wir den aktuellen Thread in allen Dimensionen des Task-Raums.

Danach können wir die notwendigen Konstanten deklarieren.

//--- constants
   const int shift_in = i * variables + v;
   const int step_in = variables;
   const int shift_plr = v;
   const int step_plr = 3 * step_in;

Der nächste Schritt besteht darin, das Segment der stückweise linearen Darstellung zu finden, zu dem das aktuelle Element der Sequenz gehört. Dazu erstellen wir eine Schleife mit Iteration über Segmente.

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int dist = 0;
   do
     {
      pos++;
      prev_in += dist;
      dist = (int)fmax(plr[shift_plr + pos * step_plr + 2 * step_in] * lenth, 1);
     }
   while(!(prev_in <= i && (prev_in + dist) > i));

Basierend auf den Parametern des gefundenen Segments bestimmen wir den Wert der Trendlinie am aktuellen Punkt und ihre Abweichung vom Wert der ursprünglichen Zeitreihe.

//--- calc trend
   float sloat = plr[shift_plr + pos * step_plr];
   float intercept = plr[shift_plr + pos * step_plr + step_in];
   pos = i - prev_in;
   float trend_i = sloat * pos + intercept;
   float other_i = inputs[shift_in] - trend_i;

Jetzt müssen wir nur noch die Ausgabewerte in den entsprechenden Elementen der globalen Ergebnispuffer speichern.

//--- save result
   trend[shift_in] = trend_i;
   other[shift_in] = other_i;
  }

In ähnlicher Weise werden wir einen Kernel der Fehlergradientenverteilung durch die obigen Operationen für den Rückwärtsdurchgang CutTrendAndOtherGradient konstruieren. Dieser Kernel empfängt Zeiger auf ähnliche Datenpuffer mit Fehlergradienten in seinen Parametern.

__kernel void CutTrendAndOtherGradient(__global float *inputs_gr,
                                       __global const float *plr,
                                       __global float *plr_gr,
                                       __global const float *trend_gr,
                                       __global const float *other_gr
                                      )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

Hier verwenden wir denselben zweidimensionalen Aufgabenraum, in dem wir den aktuellen Thread identifizieren. Danach definieren wir die Werte der Konstanten.

//--- constants
   const int shift_in = i * variables + v;
   const int step_in = variables;
   const int shift_plr = v;
   const int step_plr = 3 * step_in;

Als Nächstes wiederholen wir den Algorithmus und suchen nach dem erforderlichen Segment.

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int dist = 0;
   do
     {
      pos++;
      prev_in += dist;
      dist = (int)fmax(plr[shift_plr + pos * step_plr + 2 * step_in] * lenth, 1);
     }
   while(!(prev_in <= i && (prev_in + dist) > i));

Aber dieses Mal berechnen wir die Fehlergradienten der Segmentparameter.

//--- get gradient
   float other_i_gr = other_gr[shift_in];
   float trend_i_gr = trend_gr[shift_in] - other_i_gr;
//--- calc plr gradient
   pos = i - prev_in;
   float sloat_gr = trend_i_gr * pos;
   float intercept_gr = trend_i_gr;

Und wir speichern die Ergebnisse im Datenpuffer.

//--- save result
   plr_gr[shift_plr + pos * step_plr] += sloat_gr;
   plr_gr[shift_plr + pos * step_plr + step_in] += intercept_gr;
   inputs_gr[shift_in] = other_i_gr;
  }

Beachten Sie, dass wir den Fehlergradienten nicht überschreiben, sondern an die vorhandenen Daten im PRP-Gradientenpuffer anhängen. Dies liegt daran, dass wir die PRP-Zeitreihenergebnisse in zwei Richtungen verwenden möchten:

Um Trends isolieren, wie im oben dargestellten Kernel implementiert.
Als Aufforderung zum Aufmerksamkeitsmodell, wie oben erwähnt.

Daher müssen wir den Fehlergradienten aus zwei Richtungen erfassen. Um die Verwendung eines zusätzlichen Puffers und die unnötige Operation der Summierung der Werte von zwei Puffern zu vermeiden, haben wir Summierungen in diesem Kernel implementiert.

Darüber hinaus haben wir die Kernel CutOneFromAnother und CutOneFromAnotherGradient erstellt, um die saisonale Komponente von anderen Daten zu trennen. Der Algorithmus dieser Kernel ist sehr einfach und besteht buchstäblich aus 2-3 Codezeilen. Ich denke, Sie werden keine Probleme haben, es selbst zu verstehen. Der vollständige Code für alle in diesem Artikel verwendeten Programme ist im Anhang enthalten.

Damit ist der Vorgang auf der Seite von OpenCL abgeschlossen. Als Nächstes können wir mit der Arbeit mit unserer Hauptbibliothek beginnen.

2.2 Erstellen einer Methodenklasse mit TEMPO

Auf der Seite des Hauptprogramms werden wir einen ziemlich komplexen und umfassenden Algorithmus der betrachteten Methode von TEMPO erstellen. Wie Sie vielleicht bemerkt haben, verfügt der vorgeschlagene Ansatz über eine komplexe und verzweigte Datenflussstruktur. Dies ist wahrscheinlich dann der Fall, wenn die Implementierung des gesamten Ansatzes im Rahmen einer Klasse die Effizienz der Nutzung der vorgeschlagenen Ansätze erheblich steigern wird.

Um die vorgeschlagenen Ansätze zu implementieren, erstellen wir die Klasse CNeuronTEMPOOCL, die die Hauptfunktionalität von der Basisklasse der vollständig verbundenen Schicht, CNeuronBaseOCL, ableitet. Unten sehen Sie die umfangreiche Struktur der neuen Klasse. Es enthält sowohl aus früheren Werken bereits bekannte als auch völlig neue Elemente. Mit der Funktionalität jedes Elements in der Struktur der neuen Klasse werden wir uns im Prozess der Implementierung ihrer Methoden vertraut machen.

class CNeuronTEMPOOCL   :  public CNeuronBaseOCL
  {
protected:
   //--- constants
   uint              iVariables;
   uint              iSequence;
   uint              iForecast;
   uint              iFFT;
   //--- Trend
   CNeuronPLROCL     cPLR;
   CNeuronBaseOCL    cTrend;
   //--- Seasons
   CNeuronBaseOCL    cInputSeasons;
   CNeuronTransposeOCL cTranspose[2];
   CBufferFloat      cInputFreqRe;
   CBufferFloat      cInputFreqIm;
   CNeuronBaseOCL    cInputFreqComplex;
   CNeuronBaseOCL    cNormFreqComplex;
   CBufferFloat      cMeans;
   CBufferFloat      cVariances;
   CNeuronComplexMLMHAttention cFreqAtteention;
   CNeuronBaseOCL    cUnNormFreqComplex;
   CBufferFloat      cOutputFreqRe;
   CBufferFloat      cOutputFreqIm;
   CNeuronBaseOCL    cOutputTimeSeriasRe;
   CBufferFloat      cOutputTimeSeriasIm;
   CBufferFloat      cZero;
   //--- Noise
   CNeuronBaseOCL    cResidual;
   //--- Forecast
   CNeuronBaseOCL    cConcatInput;
   CNeuronBatchNormOCL cNormalize;
   CNeuronPatching   cPatching;
   CNeuronBatchNormOCL cNormalizePLR;
   CNeuronPatching   cPatchingPLR;
   CNeuronPositionEncoder acPE[2];
   CNeuronMLCrossAttentionMLKV cAttention;
   CNeuronTransposeOCL  cTransposeAtt;
   CNeuronConvOCL    acForecast[2];
   CNeuronTransposeOCL  cTransposeFrc;
   CNeuronRevINDenormOCL cRevIn;
   CNeuronConvOCL    cSum;
   //--- Complex functions
   virtual bool      FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, 
                         CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false);
   virtual bool      ComplexNormalize(void);
   virtual bool      ComplexUnNormalize(void);
   virtual bool      ComplexNormalizeGradient(void);
   virtual bool      ComplexUnNormalizeGradient(void);
   //---
   bool              CutTrendAndOther(CBufferFloat *inputs);
   bool              CutTrendAndOtherGradient(CBufferFloat *inputs_gr);
   bool              CutOneFromAnother(void);
   bool              CutOneFromAnotherGradient(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   //---

public:
                     CNeuronTEMPOOCL(void)   {};
                    ~CNeuronTEMPOOCL(void)   {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint sequence, uint variables, uint forecast, uint heads, uint layers, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronTEMPOOCL;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual CBufferFloat   *getWeights(void)  override;
  };

Beachten Sie, dass trotz der großen Vielfalt verschachtelter Objekte diese alle statisch deklariert sind. Dadurch können wir den Konstruktor und Destruktor der Klasse leer lassen. Alle Vorgänge im Zusammenhang mit der Freigabe des Speichers nach dem Löschen eines Klassenobjekts werden vom System selbst ausgeführt.

Alle verschachtelten Objekte und Variablen werden in Init initialisiert. Wie üblich erhalten wir in den Methodenparametern die Hauptparameter, die es uns ermöglichen, die Architektur der erstellten Schicht eindeutig zu definieren. Die Parameter sind uns bereits bekannt:

sequence — die Größe der analysierten Sequenz der multimodalen Zeitreihe
variables — die Anzahl der analysierten Variablen (einheitliche Sequenzen)
forecast – Planungstiefe der Prognosewerte
heads — die Anzahl der Aufmerksamkeitsköpfe in den verwendeten Mechanismus der Selbstaufmerksamkeit
layers – die Anzahl der Schichten in den Aufmerksamkeitsblöcken.

bool CNeuronTEMPOOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                           uint sequence, uint variables, uint forecast, uint heads, uint layers, 
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
//--- base
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, 
                                                          optimization_type, batch))
      return false;

Im Rumpf der Methode zur Initialisierung abgeleiteter Objekte rufen wir wie üblich die gleichnamige Methode der übergeordneten Klasse auf. Neben der Initialisierung geerbter Objekte implementiert die Methode der übergeordneten Klasse die erforderliche Validierung der empfangenen Parameter.

Nach erfolgreicher Ausführung der Methodenoperationen der übergeordneten Klasse speichern wir die empfangenen Parameter in verschachtelten Variablen.

//--- constants
   iVariables = variables;
   iForecast = forecast;
   iSequence = MathMax(sequence, 1);

Als Nächstes definieren wir die Größe der Datenpuffer für Signalfrequenzzerlegungsoperationen.

//--- Calculate FFTsize
   uint size = iSequence;
   int power = int(MathLog(size) / M_LN2);
   if(MathPow(2, power) < size)
      power++;
   iFFT = uint(MathPow(2, power));

Um die Trends aus der analysierten Eingabesequenz zu isolieren, initialisieren wir ein stückweise lineares Zerlegungsobjekt der Sequenz.

//--- trend
   if(!cPLR.Init(0, 0, OpenCL, iVariables, iSequence, true, optimization, iBatch))
      return false;

Anschließend initialisieren wir das Objekt, um bestimmte Trends in Form einer regelmäßigen Zeitreihe zu schreiben.

   if(!cTrend.Init(0, 1, OpenCL, iSequence * iVariables, optimization, iBatch))
      return false;

Wir werden die Abweichung der Zeitreihe der Trends von den Anfangswerten in ein separates Objekt schreiben, das als Ausgangsdaten für den Auswahlblock der saisonalen Schwankungen dienen wird.

//--- seasons
   if(!cInputSeasons.Init(0, 2, OpenCL, iSequence * iVariables, optimization, iBatch))
      return false;

Dabei ist zu beachten, dass die erhaltenen Ausgangsdaten eine Folge multimodaler Daten darstellen, die einzelne Zeitschritte beschreiben. Um das Frequenzspektrum einer einheitlichen Zeitreihe zu extrahieren, müssen wir den Eingangstensor transponieren. Am Ausgang des Blocks führen wir die umgekehrte Operation durch. Um diese Funktionsweise zu implementieren, initialisieren wir zwei Datentranspositionsebenen.

   if(!cTranspose[0].Init(0, 3, OpenCL, iSequence, iVariables, optimization, iBatch))
      return false;
   if(!cTranspose[1].Init(0, 4, OpenCL, iVariables, iSequence, optimization, iBatch))
      return false;

Die Ergebnisse der Signalfrequenzzerlegung speichern wir in zwei Datenpuffern: einen für den Realteil des Signals und einen für den Imaginärteil.

   if(!cInputFreqRe.BufferInit(iFFT * iVariables, 0) || !cInputFreqRe.BufferCreate(OpenCL))
      return false;
   if(!cInputFreqIm.BufferInit(iFFT * iVariables, 0) || !cInputFreqIm.BufferCreate(OpenCL))
      return false;

Aber für den Aufmerksamkeitsblock im Frequenzbereich müssen wir zwei Datenpuffer zu einem Objekt zusammenfassen.

   if(!cInputFreqComplex.Init(0, 5, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

Vergessen Sie nicht, dass Modelle stabilere Ergebnisse zeigen, wenn mit normalisierten Daten gearbeitet wird. Erstellen wir also Objekte, um normalisierte Daten und extrahierte Parameter der ursprünglichen Verteilung zu schreiben.

   if(!cNormFreqComplex.Init(0, 6, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;
   if(!cMeans.BufferInit(iVariables, 0) || !cMeans.BufferCreate(OpenCL))
      return false;
   if(!cVariances.BufferInit(iVariables, 0) || !cVariances.BufferCreate(OpenCL))
      return false;

Jetzt haben wir die Initialisierung des Aufmerksamkeitsobjekts im Frequenzbereich erreicht. Ich möchte Sie daran erinnern, dass die Aufgabe dieser Funktion unserer Logik zufolge darin besteht, konsistente Frequenzmerkmale in multimodalen Daten zu ermitteln, die uns dabei helfen, saisonale Schwankungen in den Eingabedaten zu erkennen.

   if(!cFreqAtteention.Init(0, 7, OpenCL, iFFT, 32, heads, iVariables, layers, optimization, batch))
      return false;

In diesem Fall verwenden wir die Anzahl der Aufmerksamkeitsköpfe und die Anzahl der Ebenen im Aufmerksamkeitsblock entsprechend den Werten der externen Parameter.

Nachdem wir die wichtigsten Frequenzeigenschaften ermittelt haben, führen wir die inversen Operationen durch. Lassen Sie uns zunächst die Häufigkeiten auf ihre ursprüngliche Verteilung zurückführen.

   if(!cUnNormFreqComplex.Init(0, 8, OpenCL, iFFT * iVariables * 2, optimization, batch))
      return false;

Dann trennen wir den Real- und Imaginärteil des Signals in separate Datenpuffer

   if(!cOutputFreqRe.BufferInit(iFFT * iVariables, 0) || !cOutputFreqRe.BufferCreate(OpenCL))
      return false;
   if(!cOutputFreqIm.BufferInit(iFFT * iVariables, 0) || !cOutputFreqIm.BufferCreate(OpenCL))
      return false;

und transformieren Sie sie in den Zeitbereich.

   if(!cOutputTimeSeriasRe.Init(0, 9, OpenCL, iFFT * iVariables, optimization, iBatch))
      return false;
   if(!cOutputTimeSeriasIm.BufferInit(iFFT * iVariables, 0) || 
      !cOutputTimeSeriasIm.BufferCreate(OpenCL))
      return false;

Als Nächstes erstellen wir einen Hilfspuffer mit Nullwerten, der zum Ausfüllen leerer Werte verwendet wird.

   if(!cZero.BufferInit(iFFT * iVariables, 0) || !cZero.BufferCreate(OpenCL))
      return false;

Damit ist unsere Arbeit mit dem Block zur saisonalen Komponentenauswahl abgeschlossen. Isolieren wir die Signalunterschiede in einem separaten Objekt der dritten Signalkomponente.

//--- Noise
   if(!cResidual.Init(0, 10, OpenCL, iSequence * iVariables, optimization, iBatch))
      return false;

Nachdem wir das ursprüngliche Datensignal in drei Komponenten aufgeteilt haben, fahren wir mit der nächsten Stufe des TEMPO-Algorithmus fort – der Vorhersage nachfolgender Werte. Hier verketten wir zunächst die Daten der drei Komponenten zu einem einzigen Tensor.

//--- Forecast
   if(!cConcatInput.Init(0, 11, OpenCL, 3 * iSequence * iVariables, optimization, iBatch))
      return false;

Danach gleichen wir die Daten ab.

   if(!cNormalize.Init(0, 12, OpenCL, 3 * iSequence * iVariables, iBatch, optimization))
      return false;

Als Nächstes müssen wir die unitären Sequenzen segmentieren, von denen es jetzt dreimal mehr gibt, weil jede unitäre Sequenz in drei Komponenten zerlegt wurde.

   int window = MathMin(5, (int)iSequence - 1);
   int patches = (int)iSequence - window + 1;
   if(!cPatching.Init(0, 13, OpenCL, window, 1, 8, patches, 3 * iVariables, optimization, iBatch))
      return false;
   if(!acPE[0].Init(0, 14, OpenCL, patches, 3 * 8 * iVariables, optimization, iBatch))
      return false;

Wir werden den resultierenden Segmenten eine Positionscodierung hinzufügen.

Ähnliche Operationen werden für die stückweise lineare Darstellung der Eingabezeitreihen durchgeführt.

   int plr = cPLR.Neurons();
   if(!cNormalizePLR.Init(0, 15, OpenCL, plr, iBatch, optimization))
      return false;
   plr = MathMax(plr/(3 * (int)iVariables),1);
   if(!cPatchingPLR.Init(0, 16, OpenCL, 3, 3, 8, plr, iVariables, optimization, iBatch))
      return false;
   if(!acPE[1].Init(0, 17, OpenCL, plr, 8 * iVariables, optimization, iBatch))
      return false;

Wir initialisieren die Schicht der Kreuzaufmerksamkeit, die das in drei Komponenten zerlegte Signal im Kontext der stückweise linearen Darstellung der ursprünglichen Zeitreihe analysiert.

   if(!cAttention.Init(0, 18, OpenCL, 3 * 8 * iVariables, 3 * iVariables, MathMax(heads, 1), 
                       8 * iVariables, MathMax(heads / 2, 1), patches, plr, MathMax(layers, 1), 
                       2, optimization, iBatch))
      return false;

Nach der Verarbeitung fahren wir mit der Prognose nachfolgender Daten fort. Hier wird uns klar, dass wir, wie im Fall der Frequenzzerlegung, die Daten einheitlicher Sequenzen vorhersagen müssen. Dazu müssen wir zunächst die Daten transponieren.

   if(!cTransposeAtt.Init(0, 19, OpenCL, patches, 3 * 8 * iVariables, optimization, iBatch))
      return false;

Als Nächstes verwenden wir einen Block aus zwei aufeinanderfolgenden Faltungsschichten, die die Aufgabe der Datenvorhersage in einzelnen einheitlichen Sequenzen übernehmen. Die erste Schicht sagt unitäre Sequenzen für jedes eingebettete Element voraus.

   if(!acForecast[0].Init(0, 20, OpenCL, patches, patches, iForecast, 3 * 8 * iVariables, 
                                                                      optimization, iBatch))
      return false;
   acForecast[0].SetActivationFunction(LReLU);

Die zweite Methode fasst die Einbettungssequenzen zu einheitlichen Reihen der analysierten Komponenten der Originaldaten zusammen.

   if(!acForecast[1].Init(0, 21, OpenCL, 8 * iForecast, 8 * iForecast, iForecast, 3 * iVariables, 
                                                                            optimization, iBatch))
      return false;
   acForecast[1].SetActivationFunction(TANH);

Danach bringen wir den Tensor der vorhergesagten Werte auf die Dimension der erwarteten Ergebnisse zurück.

   if(!cTransposeFrc.Init(0, 22, OpenCL, 3 * iVariables, iForecast, optimization, iBatch))
      return false;

Die erhaltenen Werte projizieren wir in die ursprüngliche Verteilung der analysierten Komponenten. Dazu fügen wir statistische Parameter hinzu, die während der Datennormalisierung entfernt wurden.

   if(!cRevIn.Init(0, 23, OpenCL, 3 * iVariables * iForecast, 11, GetPointer(cNormalize)))
      return false;

Um den vorhergesagten Wert der Zielvariablen zu erhalten, müssen wir die vorhergesagten Werte der einzelnen Komponenten addieren. Ich habe beschlossen, die einfache Summationsoperation durch eine gewichtete Summe mit trainierbaren Parametern innerhalb der Faltungsschicht zu ersetzen.

   if(!cSum.Init(0, 24, OpenCL, 3, 3, 1, iVariables, iForecast, optimization, iBatch))
      return false;
   cSum.SetActivationFunction(None);

Um unnötiges Kopieren von Daten zu vermeiden, ersetzen wir Zeiger durch die entsprechenden Puffer.

   SetActivationFunction(None);
   SetOutput(cSum.getOutput(), true);
   SetGradient(cSum.getGradient(), true);
//---
   return true;
  }

Damit ist die Beschreibung der neuen Klasseninitialisierungsmethode abgeschlossen. Vergessen Sie nicht, die Arbeitsabläufe in jeder Phase zu überwachen. Am Ende der Methode geben wir den logischen Wert der Operationen an den Anrufer zurück.

Nachdem wir das Objekt initialisiert haben, fahren wir mit dem nächsten Schritt fort, dem Erstellen eines Vorwärtsdurchgangs-Algorithmus. Um den Vorwärtsdurchgang zu implementieren, habe ich eine Reihe von Methoden erstellt, um die Ausführung der oben beschriebenen Kernel in die Warteschlange zu stellen. Der Algorithmus solcher Methoden ist Ihnen bereits bekannt. Die neuen Methoden nutzen keine spezifischen Merkmale. Aus diesem Grund werde ich solche Methoden dem Selbststudium überlassen. Der vollständige Code dieser Klasse und aller ihrer Methoden finden Sie im Anhang. Fahren wir nun mit der Implementierung des Hauptteils des Algorithmus vom Vorwärtsdurchgang CNeuronTEMPOOCL::feedForward fort.

bool CNeuronTEMPOOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- trend
   if(!cPLR.FeedForward(NeuronOCL))
      return false;

In den Methodenparametern erhalten wir einen Zeiger auf das Objekt der vorherigen Ebene, das die Originaldaten übergibt. Wir übertragen diesen Zeiger auf die Vorwärts-Methode der verschachtelten Ebene, die Trends mithilfe der Methode der stückweise linearen Darstellung extrahiert.

Bitte beachten Sie, dass wir den empfangenen Zeiger zu diesem Zeitpunkt nicht validieren. Diese Validierung ist bereits in der von uns aufgerufenen verschachtelten Objektmethode implementiert. Die Einrichtung eines weiteren Kontrollpunktes wäre überflüssig.

Sobald die Trends identifiziert sind, ziehen wir ihre Auswirkungen von den Originaldaten ab.

   if(!CutTrendAndOther(NeuronOCL.getOutput()))
      return false;

Der nächste Schritt unserer Arbeit besteht darin, die saisonale Komponente zu extrahieren. Hier transponieren wir zunächst die nach Abzug der Trends erhaltenen Daten.

   if(!cTranspose[0].FeedForward(cInputSeasons.AsObject()))
      return false;

Als Nächstes verwenden wir die schnelle Fourier-Transformation, um das Frequenzspektrum des analysierten Signals zu erhalten.

   if(!FFT(cTranspose[0].getOutput(), NULL,GetPointer(cInputFreqRe),GetPointer(cInputFreqIm),false))
      return false;

Wir verketten die Real- und Imaginärteile der Frequenzcharakteristik zu einem einzigen Tensor

   if(!Concat(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), cInputFreqComplex.getOutput(),
                                                                           1, 1, iFFT * iVariables))
      return false;

und normalisieren die erhaltenen Werte.

   if(!ComplexNormalize())
      return false;

Anschließend wählen wir im Aufmerksamkeitsblock einen signifikanten Teil des Frequenzcharakteristikspektrums aus.

   if(!cFreqAtteention.FeedForward(cNormFreqComplex.AsObject()))
      return false;

Durch Ausführen der inversen Operationen erhalten wir die saisonale Komponente in Form einer Zeitreihe.

   if(!ComplexUnNormalize())
      return false;
   if(!DeConcat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
                cUnNormFreqComplex.getOutput(), 1, 1, iFFT * iVariables))
      return false;
   if(!FFT(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
           GetPointer(cInputFreqRe), GetPointer(cOutputTimeSeriasIm), true))
      return false;
   if(!DeConcat(cOutputTimeSeriasRe.getOutput(), cOutputTimeSeriasRe.getGradient(), 
                GetPointer(cInputFreqRe), iSequence, iFFT - iSequence, iVariables))
      return false;
   if(!cTranspose[1].FeedForward(cOutputTimeSeriasRe.AsObject()))
      return false;

Danach wählen wir den Wert der dritten Komponente aus.

//--- Noise
   if(!CutOneFromAnother())
      return false;

Nachdem wir die drei Komponenten aus der Zeitreihe extrahiert haben, verketten wir sie zu einem einzigen Tensor.

//--- Forecast
   if(!Concat(cTrend.getOutput(), cTranspose[1].getOutput(), cResidual.getOutput(),
              cConcatInput.getOutput(), 1, 1, 1, 3 * iSequence * iVariables))
      return false;

Beachten Sie, dass wir beim Verketten von Daten nacheinander jeweils ein Element jeder einzelnen Komponente übernehmen. Dadurch können wir Elemente unterschiedlicher Komponenten, die sich auf denselben Zeitschritt derselben unitären Reihe beziehen, nebeneinander platzieren. Diese Datensequenz ermöglicht es uns, eine Faltungsschicht zur gewichteten Summierung der vorhergesagten Werte einzelner Komponenten zu verwenden, um die Zielvorhersagesequenz am Schichtausgang zu erhalten.

Als Nächstes normalisieren wir die Werte des Tensors der verketteten Komponenten, wodurch wir die Werte der einzelnen Komponenten und der analysierten Variablen angleichen können.

   if(!cNormalize.FeedForward(cConcatInput.AsObject()))
      return false;

Wir teilen die normalisierten Daten in Segmente auf und erstellen Einbettungen für diese.

   if(!cPatching.FeedForward(cNormalize.AsObject()))
      return false;

Danach fügen wir eine Positionskodierung hinzu, um die Position jedes Elements im Tensor eindeutig zu identifizieren.

   if(!acPE[0].FeedForward(cPatching.AsObject()))
      return false;

In ähnlicher Weise bereiten wir die Daten für die stückweise lineare Darstellung der Zeitreihe auf. Zuerst normalisieren wir die Daten.

   if(!cNormalizePLR.FeedForward(cPLR.AsObject()))
      return false;

Dann teilen wir es in Segmente auf und fügen eine Positionskodierung hinzu.

   if(!cPatchingPLR.FeedForward(cPatchingPLR.AsObject()))
      return false;
   if(!acPE[1].FeedForward(cPatchingPLR.AsObject()))
      return false;

Nachdem wir nun die Komponentendarstellung und die Eingabeaufforderungen vorbereitet haben, können wir den Aufmerksamkeitsblock verwenden, der die Hauptmerkmale der Darstellung der analysierten Zeitreihe isolieren soll.

   if(!cAttention.FeedForward(acPE[0].AsObject(), acPE[1].getOutput()))
      return false;

Dann transponieren wir die Daten.

   if(!cTransposeAtt.FeedForward(cAttention.AsObject()))
      return false;

Anschließend werden zukünftige Werte mithilfe eines zweischichtigen MLP vorhergesagt, das durch zwei Faltungsschichten dargestellt wird.

   if(!acForecast[0].FeedForward(cTransposeAtt.AsObject()))
      return false;
   if(!acForecast[1].FeedForward(acForecast[0].AsObject()))
      return false;

Durch die Verwendung von Faltungsschichten können wir eine unabhängige Vorhersage von Sequenzen in Form einzelner Einheitssequenzen organisieren.

Wir setzen die Prognosedaten in ihre ursprüngliche Darstellung zurück.

   if(!cTransposeFrc.FeedForward(acForecast[1].AsObject()))
      return false;

Als Nächstes fügen wir die Parameter der statistischen Verteilung der Originaldaten hinzu, die bei der Normalisierung des Tensors mit den verketteten Komponenten entfernt wurden.

   if(!cRevIn.FeedForward(cTransposeFrc.AsObject()))
      return false;

Am Ende der Methode summieren wir die vorhergesagten Werte der einzelnen Komponenten, um die gewünschte Reihe zukünftiger Werte zu erhalten.

   if(!cSum.FeedForward(cRevIn.AsObject()))
      return false;
//---
   return true;
  }

Hier möchte ich Sie daran erinnern, dass wir durch das Ersetzen der Zeiger auf die Ergebnis- und Fehlergradientenpuffer das unnötige Kopieren von Daten aus dem Ergebnispuffer der Komponentensummierungsebene in den Ergebnispuffer unserer Ebene vermieden haben. Darüber hinaus können wir dadurch den umgekehrten Vorgang vermeiden – das Kopieren von Fehlergradienten beim Erstellen von Backpropagation-Methoden.

Wie Sie wissen, besteht der Backpropagation-Durchlauf in unserer Implementierung normalerweise aus zwei Methoden:

calcInputGradients, das den Fehlergradienten auf alle Elemente entsprechend ihrem Einfluss auf das Gesamtergebnis verteilt und
updateInputWeights, das die Modellparameter anpasst, um Fehler zu minimieren.

Wir führen zunächst Fehlergradientenverteilungsoperationen durch, um den Einfluss jedes Modellparameters auf das Gesamtergebnis zu bestimmen. Diese Operationen stellen die umgekehrte Reihenfolge des Datenflusses im Vorwärtsdurchgang dar.

bool CNeuronTEMPOOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;
//--- Devide to Trend, Seasons and Noise
   if(!cRevIn.calcHiddenGradients(cSum.AsObject()))
      return false;

Zunächst verteilen wir den erhaltenen Fehlergradienten zwischen den einzelnen Komponenten und passen ihn an die Datennormalisierungsparameter an.

//--- Forecast gradient
   if(!cTransposeFrc.calcHiddenGradients(cRevIn.AsObject()))
      return false;

Dann propagieren wir den Fehlergradienten durch MLP.

   if(!acForecast[1].calcHiddenGradients(cTransposeFrc.AsObject()))
      return false;
   if(acForecast[1].Activation() != None &&
      !DeActivation(acForecast[1].getOutput(), acForecast[1].getGradient(),
                    acForecast[1].getGradient(), acForecast[1].Activation())
     )
      return false;
   if(!acForecast[0].calcHiddenGradients(acForecast[1].AsObject()))
      return false;

Und leiten Sie es dann durch die Schicht der Kreuzaufmerksamkeit weiter.

//--- Attention gradient
   if(!cTransposeAtt.calcHiddenGradients(acForecast[0].AsObject()))
      return false;
   if(!cAttention.calcHiddenGradients(cTransposeAtt.AsObject()))
      return false;
   if(!acPE[0].calcHiddenGradients(cAttention.AsObject(), acPE[1].getOutput(), 
                                   acPE[1].getGradient(), (ENUM_ACTIVATION)acPE[1].Activation()))
      return false;

Der Kreuzaufmerksamkeits-Block im Vorwärtsdurchgang empfängt Daten von zwei Daten-Threads:

Verkettete Komponenten
Stückweise, lineare Darstellung der Originaldaten

Wir verteilen den Fehlergradienten sequentiell in beide Richtungen. Zunächst in Richtung PLR.

//--- Gradient to PLR
   if(!cPatchingPLR.calcHiddenGradients(acPE[1].AsObject()))
      return false;
   if(!cNormalizePLR.calcHiddenGradients(cPatchingPLR.AsObject()))
      return false;
   if(!cPLR.calcHiddenGradients(cNormalizePLR.AsObject()))
      return false;

Dann weiter zum Tensor der verketteten Komponenten.

//--- Gradient to Concatenate buffer of Trend, Season and Noise
   if(!cPatching.calcHiddenGradients(acPE[0].AsObject()))
      return false;
   if(!cNormalize.calcHiddenGradients(cPatching.AsObject()))
      return false;
   if(!cConcatInput.calcHiddenGradients(cNormalize.AsObject()))
      return false;

Als Nächstes verteilen wir den Fehlergradienten auf die einzelnen Komponentenpuffer.

//--- DeConcatenate
   if(!DeConcat(cTrend.getGradient(), cOutputTimeSeriasRe.getGradient(), cResidual.getGradient(),
                cConcatInput.getGradient(), 1, 1, 1, 3 * iSequence * iVariables))
      return false;

Bitte beachten Sie, dass beim Aufteilen des zusammengesetzten Tensors in einzelne Teile jede Komponente ihren Anteil am Fehlergradienten erhält. Es gibt jedoch einen weiteren Datenthread. Bei der Ermittlung des Restrauschanteils haben wir den saisonalen Anteil vom Gesamtwert abgezogen. Daher beeinflusst die saisonale Komponente die Rauschwerte und sollte einen Rauschfehlergradienten erhalten. Passen wir die Gradienten-Werte an.

//--- Seasons
   if(!CutOneFromAnotherGradient())
      return false;
   if(!SumAndNormilize(cOutputTimeSeriasRe.getGradient(), cTranspose[1].getGradient(), 
                       cTranspose[1].getGradient(), 1, false, 0, 0, 0, 1))
      return false;

Als Nächstes müssen wir den Fehlergradienten für die Zeitreihe der saisonalen Komponente vorbereiten. Bei der Bildung der saisonalen Komponente aus dem Frequenzspektrum mit Hilfe der Methode der inversen Fourier-Transformation erhalten wir den Real- und Imaginärteil der Zeitreihe. Den Fehlergradienten des Realteils ermitteln wir durch die aus dem Rauschen und dem Tensor der verknüpften Komponenten gewonnenen Werte. Die fehlenden Elemente ergänzen wir mit Nullwerten.

   if(!cOutputTimeSeriasRe.calcHiddenGradients(cTranspose[1].AsObject()))
      return false;
   if(!Concat(cOutputTimeSeriasRe.getGradient(), GetPointer(cZero), GetPointer(cInputFreqRe), 
                                                 iSequence, iFFT - iSequence, iVariables))
      return false;

Für den Imaginärteil erwarten wir Nullwerte. Daher schreiben wir die Werte des Imaginärteils mit umgekehrtem Vorzeichen in den Fehlergradienten.

   if(!SumAndNormilize(GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasIm),

                       GetPointer(cOutputTimeSeriasIm), 1, false, 0, 0, 0, -0.5f))
      return false;

Wir übersetzen die erhaltenen Fehlergradienten in den Frequenzbereich.

   if(!FFT(GetPointer(cInputFreqRe), GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputFreqRe),

           GetPointer(cOutputFreqIm), false))
      return false;

Und leiten Sie sie durch die Frequenzaufmerksamkeitsschicht an die Originaldaten weiter.

   if(!Concat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
              cUnNormFreqComplex.getGradient(), 1, 1, iFFT * iVariables))
      return false;
   if(!ComplexUnNormalizeGradient())
      return false;
   if(!cNormFreqComplex.calcHiddenGradients(cFreqAtteention.AsObject()))
      return false;
   if(!ComplexNormalizeGradient())
      return false;
   if(!DeConcat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
                cInputFreqComplex.getGradient(), 1, 1, iFFT * iVariables))
      return false;
   if(!FFT(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), 
           GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), true))
      return false;
   if(!DeConcat(cTranspose[0].getGradient(), GetPointer(cInputFreqIm), 
                GetPointer(cInputFreqRe), iSequence, iFFT - iSequence, iVariables))
      return false;
   if(!cInputSeasons.calcHiddenGradients(cTranspose[0].AsObject()))
      return false;

Dann addieren wir den Rauschfehlergradienten zum erhaltenen Gradienten der Originaldaten.

   if(!SumAndNormilize(cInputSeasons.getGradient(), cResidual.getGradient(),
                       cInputSeasons.getGradient(), 1, 1, false, 0, 0, 1))
      return false;

Jetzt müssen wir nur noch den Fehlergradienten durch die PLR-Schicht fortpflanzen und an die vorherige Schicht weitergeben.

//--- trend
   if(!CutTrendAndOtherGradient(NeuronOCL.getGradient()))
      return false;
//---  input gradient
   if(!NeuronOCL.calcHiddenGradients(cPLR.AsObject()))
      return false;
   if(!SumAndNormilize(NeuronOCL.getGradient(), cInputSeasons.getGradient(), 
                       NeuronOCL.getGradient(), 1, false, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Der Algorithmus der Methode zum Aktualisieren der Modellparameter ist ziemlich standardmäßig. Es ruft nur sequenziell die gleichnamigen Methoden verschachtelter Objekte auf, die die zu trainierenden Parameter enthalten. Aus diesem Grund werden wir uns jetzt nicht näher mit der Methode befassen. Sie können sie selbst analysieren. Gleiches gilt für Hilfsmethoden, die unserer neuen Klasse dienen. Den vollständigen Code der Klasse und alle ihre Methoden finden Sie im Anhang.

Schlussfolgerung

In diesem Artikel haben wir eine neue Methode zur komplexen Zeitreihenprognose, TEMPO, vorgestellt, die die Verwendung vortrainierter Sprachmodelle zur Prognose von Zeitreihen beinhaltet. Darüber hinaus schlugen die Autoren der Methode einen neuen Ansatz zur Zerlegung von Zeitreihen vor, der die Effizienz des Lernens der Darstellung der Originaldaten erhöht.

Im praktischen Teil dieses Artikels haben wir unsere Vision der vorgeschlagenen Ansätze mit MQL5 umgesetzt. Wir haben ziemlich viel Arbeit geleistet. Leider erlaubt es das Format des Artikels nicht, das gesamte Werk aufzunehmen. Daher werden die Ergebnisse der Modelloperation mit realen historischen Daten im nächsten Artikel vorgestellt.

Referenzen

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	Beispielsammlung EA
2	ResearchRealORL.mq5	Expert Advisor	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modelltraining EA
4	StudyEncoder.mq5	Expert Advisor	Trainings-EA des Encoders
5	Test.mq5	Expert Advisor	Trainings-EA für das Model
6	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
7	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
8	NeuroNet.cl	Code Base	Die Bibliothek des Programmcodes von OpenCL

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15451

Beigefügte Dateien |

ZIP herunterladen

MQL5.zip (2433.12 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

Entwicklung eines Replay-Systems (Teil 59): Eine neue Zukunft

Wenn wir die unterschiedlichen Ideen richtig verstehen, können wir mit weniger Aufwand mehr erreichen. In diesem Artikel sehen wir uns an, warum es notwendig ist, eine Vorlage zu konfigurieren, bevor der Dienst mit dem Chart interagieren kann. Und was wäre, wenn wir den Mauszeiger verbessern würden, damit wir mehr damit machen können?

Von der Grundstufe bis zur Mittelstufe: Variablen (III)

Heute schauen wir uns an, wie vordefinierte Variablen und Konstanten der Sprache MQL5 verwendet werden. Darüber hinaus werden wir einen weiteren speziellen Variablentyp analysieren: Funktionen. Zu wissen, wie man richtig mit diesen Variablen arbeitet, kann den Unterschied zwischen einer funktionierenden und einer nicht funktionierenden Anwendung ausmachen. Um zu verstehen, was hier vorgestellt wird, ist es notwendig, das Material zu verstehen, das in früheren Artikeln besprochen wurde.

Meistern Sie MQL5 vom Anfänger bis zum Profi (Teil IV): Über Arrays, Funktionen und globale Terminalvariablen

Der Artikel ist eine Fortsetzung der Serie für Einsteiger. Ers behandelt im Detail Datenarrays, die Interaktion von Daten und Funktionen sowie globale Terminalvariablen, die einen Datenaustausch zwischen verschiedenen MQL5-Programmen ermöglichen.

Neuronale Netze im Handel: Leichtgewichtige Modelle für die Zeitreihenprognose

Leichtgewichtige Modelle zur Zeitreihenprognose erzielen eine hohe Leistung mit einer minimalen Anzahl von Parametern. Dies wiederum reduziert den Rechenaufwand und beschleunigt die Entscheidungsfindung. Trotz ihrer Einfachheit erreichen solche Modelle eine mit komplexeren Modellen vergleichbare Prognosequalität.