Red neural en la práctica: Pseudo inversa (I)

Introducción

Hola a todos, y bienvenidos a otro artículo sobre redes neuronales.

En el artículo anterior "Red neural en la práctica: Función de línea recta", hablamos de cómo podríamos, usando ecuaciones algebraicas, determinar algunas de las informaciones que estábamos buscando. Esto con el fin de crear una ecuación, que en nuestro caso específico es una ecuación de línea recta. Ya que nuestro pequeño conjunto de datos puede ser expresado, de hecho, como una recta. Todo este material, relacionado con la explicación de cómo funcionan las redes neuronales, no es algo fácil de presentar sin conocer el nivel de comprensión matemática de cada lector.

Aunque muchos puedan imaginar que el proceso sería mucho más simple y directo, especialmente con la proliferación de bibliotecas en la web que te prometen que puedes desarrollar tu propia red neuronal, la realidad es que las cosas no son tan sencillas.

No quiero, en esta pequeña serie, crear falsas expectativas. No te diré que con poco conocimiento o casi ninguna experiencia lograrás construir algo realmente práctico que puedas utilizar para ganar dinero, utilizando redes neuronales o inteligencia artificial para operar en el mercado. Quien te diga eso, te estaría mintiendo.

Crear, incluso una red neuronal simple, es algo realmente desafiante en muchos casos. Aquí quiero mostrarte cómo puedes crear algo que te sirva de inspiración para estudiar mejor el tema. Este asunto de las redes neuronales ha sido estudiado durante décadas, y eso siendo modesto. Como mencioné antes, durante los tres artículos sobre inteligencia artificial que precedieron a estos sobre redes neuronales, el tema es mucho más complicado de lo que muchos intentan hacer ver.

El hecho de usar esta o aquella función no significará que tu red neuronal será mejor o peor, simplemente significará que estarás realizando los cálculos usando una función u otra. Esto aplica a lo que veremos en este artículo.

Lo que veremos en este artículo, en comparación con los tres primeros de la serie sobre redes neuronales, podría hacer que pienses en abandonar el estudio del tema. Pero también podría incentivarte a profundizar aún más. Aquí exploraremos cómo implementar, utilizando MQL5 puro, el cálculo de la pseudo inversa. Aunque no parezca tan aterrador, el código que veremos será considerablemente más complicado para los principiantes de lo que me gustaría presentar. Así que no te asustes con lo que verás. Tómate el tiempo para estudiar el código con calma. Sin prisa. Intenté simplificar el código tanto como fue posible. Por lo que no está diseñado para ser eficiente ni de rápida ejecución. Todo lo contrario, su objetivo es ser lo más didáctico posible. Sin embargo, debido a que usaremos factorización matricial, el código en sí es un poco más complejo de lo que muchos están acostumbrados a ver o programar.

Y sí, antes de que alguien lo mencione, sé que MQL5 tiene una función llamada PInv, que implementa precisamente lo que veremos aquí. También sé que MQL5 tiene operaciones para trabajar con matrices. Pero aquí no realizaremos los cálculos usando matrices tal como están definidas en MQL5. Vamos a usar arrays, que aunque similares, tienen una lógica ligeramente diferente en cuanto al acceso a los elementos presentes en la memoria.

Pseudo Inversa

Implementar este cálculo no es una de las tareas más complicadas. Siempre y cuando lo entiendas. Básicamente, debemos realizar algunas multiplicaciones entre otros pequeños pasos. Usando solo una única matriz. Al hacer esto, se generará una matriz que será el resultado de todas las factorizaciones internas de la pseudo inversa.

En este punto, debemos aclarar algo. La pseudo inversa puede ser factorizada de dos maneras: una en la que no se ignora ningún valor dentro de la matriz, y otra en la que se utiliza un valor límite mínimo para los elementos presentes en la matriz. Cuando ese límite mínimo no se alcanza, el valor de ese elemento en la matriz será igual a cero. No soy yo quien impone esta condición; son las reglas presentes en el modelo de cálculo utilizado por todos los programas que calculan la pseudo inversa. Cada uno de estos casos tiene un objetivo muy específico. Por lo tanto, lo que veremos aquí NO es, y repito: NO es, un cálculo definitivo para la pseudo inversa. Lo que haremos será un cálculo cuyo objetivo es generar resultados similares a los obtenidos por programas como MatLab, SciLab, entre otros que también implementan la pseudo inversa.

Dado que MQL5 también puede calcular la pseudo inversa, podrás comparar los resultados obtenidos con la aplicación que implementaremos con los mismos resultados obtenidos a través de la función de pseudo inversa de la biblioteca de MQL5. Esto con el fin de verificar si todo está correcto. Así, el objetivo de este artículo no es simplemente implementar el cálculo de la pseudo inversa, sino entender qué hay detrás del cálculo. Esto es importante, ya que comprender cómo funcionan los cálculos te permitirá saber por qué y cuándo usar un método u otro en tu red neuronal.

Entonces, comencemos haciendo lo siguiente: implementemos un código lo más simple posible para utilizar la pseudo inversa de la biblioteca de MQL5. Este es el primer paso. para asegurarnos de que el cálculo que crearemos después realmente funcione. Te pido, por favor, que no modifiques el código hasta que lo hayas probado. Si cambias algo antes de probarlo, podrías obtener resultados diferentes a los que se muestran aquí. Así que, mi amigo y entusiasta lector. primero prueba el código que estoy mostrando. Luego, y solo después, si lo deseas, modifícalo para intentar entender mejor lo que está ocurriendo. Pero, por favor, no hagas ningún cambio en el código antes de probar la versión original.

Muy bien, los códigos originales están disponibles en el anexo de este artículo. Entonces, veamos el primero de ellos. Se muestra íntegramente a continuación:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart()
05. {
06.     matrix M_A {{1, -100}, {1, -80}, {1, 30}, {1, 100}};
07. 
08.     Print("Moore–Penrose inverse of :");
09.     Print(M_A);
10.     Print("is :");
11.     Print(M_A.PInv());
12. }
13. //+------------------------------------------------------------------+

El resultado de su ejecución se muestra en la imagen de abajo:

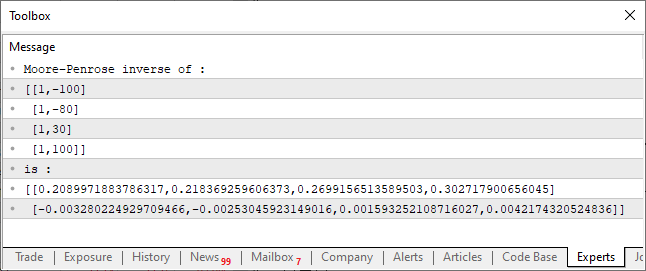
Este código supersimple que puedes ver arriba es capaz de calcular la matriz pseudo inversa. El resultado se nos muestra en la consola, como puedes observar en la imagen. Es así de sencillo. Sin embargo, presta atención a cómo está construido el código. Nota que es algo muy, pero muy específico de crear. Al usar matrix y vector, tienes a tu disposición toda una gama de operaciones posibles y perfectamente funcionales. Sin embargo, estas operaciones están incluidas en la biblioteca estándar de MQL5. así como también pueden estar incluidas en las bibliotecas estándar de otros lenguajes. dependiendo, claro, del tipo de lenguaje de programación del que estemos hablando.

No obstante, aunque esto sea muy útil, existen casos en los que necesitamos, o queremos, que el código se ejecute de una manera particular. Ya sea porque queremos optimizarlo de alguna forma, o simplemente porque no deseamos generar código que podría ejecutarse de otra manera. En fin, la razón no importa demasiado. Aunque muchos suelen decir que los programadores de C / C++ adoran intentar reinventar la rueda, este no es el caso aquí. En este artículo, quiero mostrarte, querido lector, qué está detrás de este complicado cálculo que observas. Ves el resultado, pero no tienes la menor idea de cómo se obtuvo. Y realizar cualquier tipo de estudio sin entender realmente por qué se obtuvo ese resultado, y no otro, no es realmente estudiar. Es solo una creencia. Es decir, lo ves y simplemente crees. Pero no sabes si es verdad o mentira, simplemente crees. Y los verdaderos programadores no creen ciegamente. Necesitan tocar, ver, probar y experimentar para creer realmente en lo que se está generando. Así que veamos cómo se logró el resultado que se muestra en la imagen. Para ello, pasemos a un nuevo tema.

Entendiendo el cálculo detrás de la pseudo inversa

Si ya estás satisfecho con solo ver los resultados, independientemente de cómo se logran, está bien. Este tema ya no te será de ninguna utilidad, y no vale la pena que pierdas tu tiempo leyéndolo. Pero si deseas entender cómo funciona el cálculo, prepárate. Aunque intentaré simplificar lo más posible, aún será necesario que prestes atención. Voy a evitar al máximo mostrar fórmulas complicadas, pero aun así es importante que estés atento, ya que el código que crearemos puede parecer mucho más confuso de lo que realmente es. Comencemos con lo siguiente: la pseudo inversa se calcula básicamente usando multiplicación y una matriz inversa.

Esta multiplicación es relativamente sencilla de realizar. Muchos utilizan algunos recursos que considero innecesarios para llevarla a cabo. En los artículos donde hablé sobre matrices, mostré un método para efectuar la multiplicación, pero ese método era para un escenario bastante específico. Aquí necesitamos un método un poco más genérico, porque será necesario hacer algunas cosas diferentes a lo visto en el artículo sobre matrices.

Para facilitar, veremos el código en pequeños fragmentos, cada uno explicando algo. Empezando con la multiplicación, que se puede ver en el fragmento justo abajo:

01. //+------------------------------------------------------------------+
02. void Generic_Matrix_A_x_B(const double &A[], const uint A_Row, const double &B[], const uint B_Line, double &R[], uint &R_Row)
03. {
04.     uint A_Line = (uint)(A.Size() / A_Row),
05.          B_Row  = (uint)(B.Size() / B_Line);
06. 
07.     if (A_Row != B_Line)
08.     {
09.         Print("Operation cannot be performed because the number of rows is different from that of columns...");
10.         B_Row = (uint)(1 / MathAbs(0));
11.     }
12.     if (!ArrayIsDynamic(R))
13.     {
14.         Print("Response array must be of the dynamic type...");
15.         B_Row = (uint)(1 / MathAbs(0));
16.     }
17.     ArrayResize(R, A_Line * (R_Row = B_Row));
18.     ZeroMemory(R);
19.     for (uint cp = 0, Ai = 0, Bi = 0; cp < R.Size(); cp++, Bi = ((++Bi) == B_Row ? 0 : Bi), Ai += (Bi == 0 ? A_Row : 0))
20.         for (uint c = 0; c < A_Row; c++)
21.             R[cp] += (A[Ai + c] * B[Bi + (c * B_Row)]);
22. }
23. //+------------------------------------------------------------------+

Al mirar este fragmento de código, ya podrías estar sintiéndote desorientado, o implorando el abrazo de tu madre. Quizá estés corriendo despavorido, huyendo a las colinas porque el fin del mundo se acerca. Algunos podrían arrodillarse y pedir perdón a DIOS por todos sus pecados. Pero, bromas aparte, este código es muy sencillo, aunque parezca algo de otro mundo o extremadamente complicado.

Quizá la razón por la que te parezca complicado es que está muy condensado, con muchas cosas aparentemente sucediendo al mismo tiempo. Pido disculpas a quienes estén empezando ahora, pero quienes han seguido mis artículos ya conocen mi forma de escribir el código, y puede que vean que este estilo es bastante común en mí. Bien, ahora entendamos qué está ocurriendo aquí. A diferencia del código mostrado antes, este es genérico, incluso tiene una prueba para verificar si podemos o no multiplicar dos matrices. Lo cual es bastante útil, aunque no sea muy amigable.

Muy bien, en la segunda línea tenemos la declaración del procedimiento. Debes tener cuidado al declarar y pasar los parámetros en los lugares correctos. Entonces, la matriz A se multiplicará por la matriz B, y el resultado se colocará en la matriz R. Necesitas indicar cuántas columnas tiene la matriz A y cuántas filas tiene la matriz B. El último argumento devolverá la cantidad de columnas en la matriz R. El motivo de devolver el número de columnas en la matriz R se explicará más adelante, así que por ahora no te preocupes por eso.

Bien. En las líneas cuatro y cinco, calculamos los valores restantes, para que no tengas que proporcionarlos manualmente. Luego, en la línea siete, hacemos una pequeña prueba cuyo objetivo es verificar si las matrices pueden multiplicarse. Por esto, el orden en que se pasan las matrices importa. No es como un código para cálculos escalares; en los cálculos matriciales debemos tener ciertos cuidados.

Ok, si la multiplicación no puede realizarse, en la línea nueve imprimiremos un mensaje en la consola de MetaTrader 5. Y justo después, en la línea diez, lanzaremos un error de RUN-TIME. Esto hará que la aplicación que esté intentando realizar la multiplicación de las matrices se cierre. Si ves este error en la consola, verifica si también aparece el mensaje de la línea nueve. Si eso ocurre, el error no está en el fragmento de código mostrado, sino en el punto donde este código está siendo llamado. Sé que no es nada amable, y mucho menos elegante, forzar un error de RUN-TIME para cerrar una aplicación, pero al hacerlo, evitamos que la aplicación nos muestre resultados incorrectos.

Ahora viene la parte que empieza a asustar a muchos: en la línea 17, asignamos memoria para almacenar todo el resultado que se generará. De esta forma, la matriz R debe ser de tipo dinámica en el autor de la llamada. No uses un array estático, porque si lo haces, la línea 12 detectará esto, y el código se cerrará con un error de RUN-TIME, con un mensaje en la línea 14 que indica la razón del cierre.

Un detalle sobre esta forma de generar el error es que, durante la ejecución, la aplicación intentará realizar una división por cero, lo que provocará que el procesador (¡la CPU misma!) dispare una interrupción interna. Esta interrupción hará que el sistema operativo tome medidas contra la aplicación que generó dicha interrupción, provocando su cierre. Incluso si el sistema operativo no hace nada, la CPU estará en modo de interrupción, lo que causará que, incluso en un sistema embebido dedicado a ejecutar la aplicación, se detenga.

Ahora quiero que prestes atención a lo siguiente: aquí estoy usando un truco para evitar que el compilador detecte que se va a generar un error de RUN-TIME. Si no lo hiciera de la manera que puedes ver en el código, el compilador impediría que el código fuera compilado. Incluso si la línea que generará el error de RUN-TIME rara vez se ejecutara en situaciones normales. Siempre que quieras forzar el final de la ejecución de un programa, puedes usar un truco similar. Siempre funciona. Aunque no es muy elegante hacer las cosas así, ya que el usuario podría irritarse con tu aplicación o contigo, que la programaste. Por lo tanto, úsalo con moderación.

En la línea 18 limpiamos completamente cualquier cosa que esté en la memoria asignada. Normalmente, algunos compiladores hacen esta limpieza por nosotros. Pero después de programar en MQL5 durante algún tiempo, noté que, naturalmente, no limpia la memoria asignada dinámicamente. Creo que esto se debe a que la memoria asignada dinámicamente en MetaTrader 5 está destinada a ser usada en buffers de indicadores. Y como esos buffers se actualizan conforme llegan los datos y se calculan, no tiene sentido limpiar la memoria. Además, esta limpieza consume tiempo, tiempo que podría aprovecharse mejor para otras tareas. Por lo tanto, depende de nosotros realizar esta limpieza y asegurarnos de que no estamos utilizando valores basura en ningún cálculo. Presta atención a esto en tus programas si estás usando memoria asignada dinámicamente y no se usa como buffers de indicadores personalizados.

Ok. Ahora viene la parte divertida del procedimiento: multiplicar la matriz A por la matriz B y colocar el resultado en la matriz R. Esto se hace en dos líneas. La línea 19 puede parecer muy complicada al principio, pero vamos a desglosarla con calma. La idea aquí es hacer que la multiplicación de dos matrices sea completamente dinámica y genérica. Es decir, no importa si una tiene más o menos filas o columnas. Si el procedimiento ha llegado hasta este punto, las matrices serán multiplicadas.

De la misma manera que el orden de las matrices afecta el resultado, aquí en la línea 19, el orden en el que ocurren las operaciones también influye en los resultados. Pero para no alargarme demasiado, voy a simplificar la explicación. Para entender lo que está sucediendo, lee el código tal como está escrito, es decir, de izquierda a derecha, término a término. Así es como el compilador lo procesa para construir el ejecutable. Entonces, aunque parezca confuso, en realidad no lo es. Solo está muy condensado, diferente de lo que la mayoría suele usar. De cualquier modo, la idea aquí es leer columna por columna de la matriz A y multiplicar el valor, leyendo fila por fila de la matriz B. Por esta razón, el orden de los factores influirá en el resultado. No necesitas preocuparte si la matriz B está organizada en forma de filas o columnas. Puede estar organizada de la misma manera que la matriz A, y aun así, este procedimiento de multiplicación se ejecutará con éxito.

Bien, la primera de las operaciones necesarias para obtener el valor de la pseudo inversa está lista. Ahora veamos el tipo de cálculo que necesitamos realizar para saber qué más debemos implementar. Tal vez lo que necesitamos implementar no sea una solución genérica, como en el caso de la multiplicación, sino algo más específico para ayudar a factorizar el valor de la pseudo inversa.

Ok, la fórmula para calcular la pseudo inversa se muestra justo a continuación.

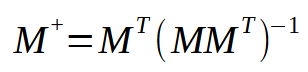
En esta fórmula, M representa la matriz utilizada. Observa que siempre es la misma. Sin embargo, al analizar esta fórmula, notamos que necesitamos realizar una multiplicación entre la matriz original y su transpuesta. Luego, tomamos el resultado y encontramos el valor de la matriz inversa. Finalmente, multiplicamos la matriz transpuesta por el resultado de la inversa. Parece sencillo, ¿verdad? Bueno, aquí es donde podemos crear algunos atajos. Claro que, para crear el atajo perfecto, tendríamos que modelar un procedimiento capaz de calcular únicamente la pseudo inversa. Pero generar dicho procedimiento, aunque no es una tarea muy complicada, haría que explicar su funcionamiento sea mucho más difícil. Para que tengas una idea de lo que estoy diciendo, haremos lo siguiente: uniré la multiplicación de la transpuesta y la matriz original en un solo procedimiento. Normalmente, cuando estudiamos esto en la universidad, nos piden hacerlo en dos bloques. Es decir, primero creamos una matriz transpuesta y luego usamos el procedimiento de multiplicación para obtener el resultado final. Sin embargo, podemos hacer un procedimiento que omita estos dos pasos y lo haga en un solo paso. Y aunque es algo muy fácil de implementar, verás que el código puede parecer complicado de entender.

Así que, ve en el fragmento a continuación cómo realizar la operación que aparece entre paréntesis en la imagen anterior.

01. //+------------------------------------------------------------------+
02. void Matrix_A_x_Transposed(const double &A[], const uint A_Row, double &R[], uint &R_Row)
03. {
04.     uint BL = (uint)(A.Size() / A_Row);
05.     if (!ArrayIsDynamic(R))
06.     {
07.         Print("Response array must be of the dynamic type...");
08.         BL = (uint)(1 / MathAbs(0));
09.     }
10.     ArrayResize(R, (uint) MathPow(R_Row = (uint)(A.Size() / A_Row), 2));
11.     ZeroMemory(R);
12.     for (uint cp = 0, Ai = 0, Bi = 0; cp < R.Size(); cp++, Bi = ((++Bi) == BL ? 0 : Bi), Ai += (Bi == 0 ? A_Row : 0))
13.         for (uint c = 0; c < A_Row; c++)
14.             R[cp] += (A[c + Ai] * A[c + (Bi * A_Row)]);
15. }
16. //+------------------------------------------------------------------+

Observa que este fragmento se parece mucho al fragmento anterior, salvo por el hecho de que la línea donde se obtiene el resultado es ligeramente diferente entre ambos. Aun así, este fragmento es capaz de realizar el cálculo necesario para multiplicar la matriz original por su transpuesta, ahorrándonos el trabajo de crear una matriz transpuesta. Este tipo de optimización es lo que podemos implementar. Claro, podríamos acumular en este mismo procedimiento aún más funciones, como generar la inversa de la matriz resultante o incluso realizar la multiplicación de la inversa con la transpuesta de la matriz original. Pero como podrás imaginar, cada uno de estos pasos agregaría más complejidad al procedimiento. No de manera global. Pero sí de forma localizada. Por eso, prefiero presentarlo poco a poco, para que puedas entender lo que está ocurriendo e incluso probar los conceptos si así lo deseas.

Pero como no quiero, ni voy, a reinventar la rueda —y ese no es el objetivo de este artículo—, no acumularemos todo en una sola función. Solo he mostrado este fragmento para que entiendas que no todo lo que aprendemos en la escuela se aplica tal cual en la práctica. Muchas veces, los procesos se optimizan para adaptarse a un problema específico. Y el hecho de optimizar algo hace que la ejecución sea mucho más rápida que en un proceso más generalizado.

Ahora hagamos lo siguiente: ya tenemos el cálculo de la multiplicación. Lo que necesitamos ahora es un cálculo que genere la inversa de la matriz resultante. Existen diversas maneras de programar esta inversa. Aunque las formas matemáticas de expresarla son pocas, los métodos de programación pueden variar considerablemente, haciendo que un algoritmo sea más rápido que otro. Sin embargo, lo que realmente nos interesa es obtener el resultado correcto, y cómo lo generemos no es tan relevante.

Para calcular la matriz inversa, prefiero usar un método específico que involucra el uso del determinante de la matriz. En este momento, es posible que prefieras usar un método distinto para encontrar el determinante, pero por costumbre, me gusta utilizar el método de Sarrus. Lo considero más sencillo de programar. El método de Sarrus, para quienes no lo conocen, calcula el determinante basándose en los valores de las diagonales. Programar esto es bastante interesante. En el fragmento a continuación, verás una propuesta de cómo hacerlo. Funciona para cualquier matriz, o mejor dicho, array, siempre y cuando sea cuadrado.

01. //+------------------------------------------------------------------+
02. double Determinant(const double &A[])
03. {
04. #define def_Diagonal(a, b)  {                                                                                                                       \
05.                 Tmp = 1;                                                                                                                            \
06.                 for (uint cp = a, cc = (a == 0 ? 0 : cp - 1), ct = 0; (a ? cp > 0 : cp < A_Row); cc = (a ? (--cp) - 1 : ++cp), ct = 0, Tmp = 1)     \
07.                 {                                                                                                                                   \
08.                     do {                                                                                                                            \
09.                         for (; (ct < A_Row); cc += b, ct++)                                                                                         \
10.                             if ((cc / A_Row) != ct) break; else Tmp *= A[cc];                                                                       \
11.                         cc = (a ? cc + A_Row : cc - A_Row);                                                                                         \
12.                     }while (ct < A_Row);                                                                                                            \
13.                     Result +=  (Tmp * (a ? -1 : 1));                                                                                                \
14.                 }                                                                                                                                   \
15.                             }
16. 
17.     uint A_Row, A_Size = A.Size();
18.     double Result, Tmp;
19. 
20.     if (A_Size == 1)
21.         return A[0];
22.     Tmp = MathSqrt(A_Size);
23.     A_Row = (uint)MathFloor(Tmp);
24.     if ((A_Row != (uint)MathCeil(Tmp)) || (!A_Size))
25.     {
26.         Print("The matrix needs to be square");
27.         A_Row = (uint)(1 / MathAbs(0));
28.     }
29.     if (A_Row == 2)
30.         return (A[0] * A[3]) - (A[1] * A[2]);
31.     Result = 0;
32. 
33.     def_Diagonal(0, A_Row + 1);
34.     def_Diagonal(A_Row, A_Row - 1);
35. 
36.     return Result;
37. 
38. #undef def_Diagonal
39. }
40. //+------------------------------------------------------------------+

Este hermoso fragmento que ves frente a ti, querido lector, es capaz de establecer el valor del determinante de una matriz. Aquí hacemos algo tan maravilloso que prácticamente no necesito describir mucho, ya que el código se explica por sí mismo.

Muy bien. Tenemos una macro definida en la línea cuatro. Esta macro es capaz de recorrer el array, o en nuestro caso, una matriz dentro del array, a lo largo de la diagonal. Así es. La matemática presente en este código te permite calcular el valor de las diagonales, una por una, tanto en el sentido de la diagonal principal como en el sentido de la diagonal secundaria, todo de manera elegante y eficiente. Ten en cuenta que lo único que necesitamos especificar al código es el array que contiene nuestra matriz, y el valor devuelto es el determinante de dicha matriz. Sin embargo, el método de Sarrus, tal como está implementado en este código, tiene una limitación: cuando la matriz es de dimensión 1x1, el determinante es la propia matriz, y esto se devuelve de inmediato, como puedes ver en la línea 21. Si la matriz está vacía o no es cuadrada, en la línea 27 lanzaremos un error de RUN-TIME, evitando que el código siga ejecutándose. Si la matriz es de 2x2, el cálculo de las diagonales no pasa por la macro, sino que se realiza antes, en la línea 30. Para cualquier otro caso, el cálculo del determinante pasa por la macro: primero, en la línea 33, hacemos el cálculo de la diagonal principal, y en la línea 34, el cálculo de la diagonal secundaria. Si no has logrado entender lo que está ocurriendo, consulta la figura a continuación, donde muestro un ejemplo de lo que está sucediendo. Esto es para quienes no conocen el método de Sarrus.

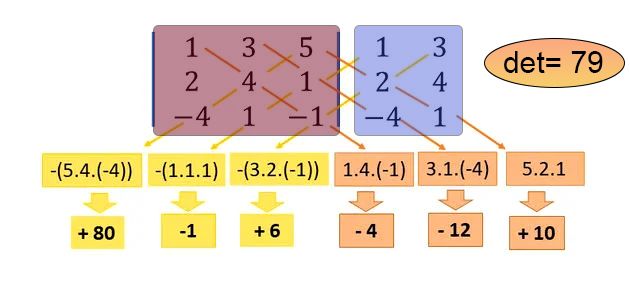
En esta figura, la región en rojo representa la matriz de la cual queremos calcular el determinante, mientras que la región en azul es una copia virtual de algunos de los elementos de la matriz. El código de la macro realiza exactamente este cálculo mostrado en la figura, devolviéndonos el determinante, que en el ejemplo es el valor 79.

Consideraciones finales

Bueno, querido lector, hemos llegado al final de otro artículo. Sin embargo, aún no hemos implementado todos los procedimientos necesarios para calcular el valor de la pseudo inversa. Esto lo completaremos en el próximo artículo. Donde veremos la aplicación que realmente llevará a cabo esta tarea. Aunque podrías decir que podemos utilizar el código del anexo de este artículo, el problema es que no nos da la libertad de usar cualquier tipo de estructura. Para utilizar la pseudo inversa (PInv), realmente necesitamos trabajar con un tipo de matriz. En lo que estoy mostrando como medio para explicar el cálculo, podemos usar cualquier tipo de modelado de datos. Solo es cuestión de hacer los ajustes necesarios para poder usar cualquier cosa.  Así que nos vemos en el próximo artículo.