神经网络实践：伪逆（I）

引言

我很高兴欢迎各位阅读这篇关于神经网络的新文章。

在之前的文章 《神经网络实践：直线函数》中，我们讨论了如何使用代数方程来确定我们正在寻找的部分信息。对于构建一个方程来说这是必要的，在我们这个特定情况下是直线的方程，因为我们的小数据集实际上可以用一条直线来表示。如果不了解每位读者的数学知识水平，就很难呈现所有与解释神经网络工作原理相关的材料。

尽管许多人可能认为这个过程会简单直接得多，尤其是考虑到互联网上有很多库声称你可以开发自己的神经网络，但现实并非如此简单。

我不想给大家带来错误的期望：我不会告诉你，仅凭很少的知识或经验，你就可以创建出真正实用的、可以用来通过神经网络或人工智能交易市场来赚钱的东西。如果有人这样告诉你，那他们肯定是在撒谎。

即使是创建最简单的神经网络，在许多情况下也是一项具有挑战性的任务。在这里，我想向你展示一些能够激励你更深入地探索这个主题的东西。神经网络至少是几十年来一直研究的主题。如前面三篇关于人工智能的文章所述，这个主题比许多人认为的要复杂得多。

使用特定的函数并不意味着我们的神经网络会更好或更差，它只是意味着我们将使用特定的函数进行计算。这与我们今天将在文章中看到的内容有关。

与神经网络系列的前三篇文章相比，在阅读了今天的文章之后，你可能会想要放弃。你不应该这样做。因为同一篇文章也可能会激励你更深入地研究这个主题。在这里，我们将探讨如何使用纯MQL5实现伪逆计算。虽然它看起来并不可怕，但今天的代码对于初学者来说将比我们希望的更加困难，所以不要害怕。请仔细、冷静地研究代码，不要急于求成。我尽量使代码尽可能简单。因此，它并不是为了高效快速地执行而设计的。相反，它力求尽可能具有教育意义。但是，由于我们将使用矩阵分解，代码本身比许多人习惯看到的或编写的要复杂一些。

在任何人提及之前，我知道MQL5有一个名为PInv的函数，它做的正是我们将在本文中看到的事情。我也知道MQL5有用于矩阵运算的函数。但是，在这里我们不会使用MQL5中定义的矩阵进行计算，而是将使用数组，尽管它们很相似，但访问存储在内存中的元素的逻辑略有不同。

伪逆

只要开发人员清楚一切，实现这一计算并不是最困难的任务之一。基本上，我们只需要使用一个矩阵执行一些乘法和其他简单运算。输出将是一个矩阵，它是伪逆所有内部分解的结果。

在这个阶段，我们需要澄清一些事情。伪逆可以以两种方式分解：在一种情况下，矩阵内的值不会被忽略，而在另一种情况下，将使用矩阵中存在的元素的最小极限值。如果未达到此最小极限，则矩阵中该元素的值将为零。这一条件不是我设定的，而是由所有计算伪逆的程序所使用的计算模型中的规则所规定的。这两种情况都有非常特定的用途。因此，我们在这里看到的是伪逆的非最终计算。我们将执行一个计算，其目的是获得与MatLab、SciLab等也实现伪逆的程序所获得的结果相似的结果。

由于MQL5也可以计算伪逆，我们可以将使用我们实现的应用程序获得的结果与使用MQL5库伪逆函数获得的结果进行比较。这是必要的，以便检查一切是否正确。因此，本文的目标不仅仅是实现伪逆计算，而是要理解其背后的原理。这很重要，因为了解计算原理将使你能够理解为什么以及在何时在我们的神经网络中使用特定方法。

让我们从实现使用MQL5库中伪逆的最简单代码开始。这是确保我们稍后创建的计算实际可行的第一步。请不要在检查之前更改代码。如果你在此之前更改了任何内容，你可能会得到与这里显示的不同的结果。所以，请先用我将向你展示的代码进行尝试。然后，并且只有在那时（如果你愿意），更改它以更好地了解发生了什么，但在测试原始版本之前，请不要对代码进行任何更改。

原始代码可在本文的附件中找到。让我们看看第一个。完整代码如下所示：

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart()
05. {
06.     matrix M_A {{1, -100}, {1, -80}, {1, 30}, {1, 100}};
07. 
08.     Print("Moore–Penrose inverse of :");
09.     Print(M_A);
10.     Print("is :");
11.     Print(M_A.PInv());
12. }
13. //+------------------------------------------------------------------+

代码执行的结果如下图所示：

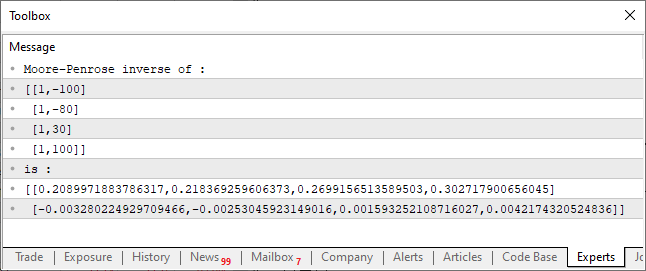
上面展示的代码非常简单，能够计算矩阵的伪逆。结果如图所示，显示在控制台上。一切都很简单。但是，请注意代码的结构，这是代码创建中一个非常特定的点。通过使用矩阵和向量，我们可以获得一系列可能且非常有用的操作。这些操作包含在MQL5标准库中，也可以包含在其他语言的标准库中。

虽然这非常有用，但有时我们需要或希望代码以特定方式执行。要么是因为我们想以某种方式优化它，要么仅仅是因为我们不想生成可以以其他方式执行的代码。最终，原因并不那么重要。尽管很多人说C/C++程序员喜欢重复造轮子，但我们并非如此。在本文中，我们将一起看看这些复杂计算背后的东西。你看到结果，但完全不知道它是如何实现的。任何没有理解结果确切来源的研究都不是真正的研究，它只是信仰。换句话说，你看到它并相信它，但你不知道它是否正确，你只能相信它。而真正的程序员不能盲目信任，他们需要触摸、观察、品味和体验才能真正相信自己所创造的东西。现在，让我们看看图中所示结果是如何实现的。为此，让我们进入一个新的话题。

理解伪逆背后的计算

如果你只满足于看到结果而不知道它们是如何实现的，那很好。这意味着这个话题对你不再有用，你不应该浪费时间阅读它。但如果你想了解这些计算是如何完成的，请做好准备。尽管我会尽量简化这个过程，但你仍然需要集中注意力。我会尽量避免使用复杂的公式，但你的注意力在这里仍然很重要，因为我们将要创建的代码可能看起来比实际要复杂得多。让我们从以下开始：伪逆基本上是通过矩阵乘法和求逆来计算的。

这种乘法很简单。很多人为此使用一些资源，但我个人认为这些是不必要的。在我们谈论矩阵的文章中，我们讨论了一种执行乘法的方法，但那种方法是为了一个相当特定的场景。在这里，我们需要一个稍微更通用的方法，因为我们将不得不做一些与我们之前在矩阵文章中所看到的不同的事情。

为了让事情更容易理解，我们将分小部分查看代码，每部分解释一些特定的东西。让我们从乘法开始，如下所示：

01. //+------------------------------------------------------------------+
02. void Generic_Matrix_A_x_B(const double &A[], const uint A_Row, const double &B[], const uint B_Line, double &R[], uint &R_Row)
03. {
04.     uint A_Line = (uint)(A.Size() / A_Row),
05.          B_Row  = (uint)(B.Size() / B_Line);
06. 
07.     if (A_Row != B_Line)
08.     {
09.         Print("Operation cannot be performed because the number of rows is different from that of columns...");
10.         B_Row = (uint)(1 / MathAbs(0));
11.     }
12.     if (!ArrayIsDynamic(R))
13.     {
14.         Print("Response array must be of the dynamic type...");
15.         B_Row = (uint)(1 / MathAbs(0));
16.     }
17.     ArrayResize(R, A_Line * (R_Row = B_Row));
18.     ZeroMemory(R);
19.     for (uint cp = 0, Ai = 0, Bi = 0; cp < R.Size(); cp++, Bi = ((++Bi) == B_Row ? 0 : Bi), Ai += (Bi == 0 ? A_Row : 0))
20.         for (uint c = 0; c < A_Row; c++)
21.             R[cp] += (A[Ai + c] * B[Bi + (c * B_Row)]);
22. }
23. //+------------------------------------------------------------------+

看着这段代码，你可能会感到困惑不已。有人可能会吓得好像世界末日即将来临。其他人可能会想向上天祈求原谅自己所有的罪过。但玩笑归玩笑，这段代码其实很简单，即使它看起来不同寻常或极其复杂。

你可能会觉得困难，因为它非常紧凑，似乎同时发生了很多事情。我向初学者道歉，但那些一直关注我的文章的人已经知道我写代码的风格了，你们会发现这是我的典型风格。现在我们来弄清楚这里发生了什么。与之前展示的代码不同，这段代码是通用的，它甚至有一个测试来检查我们是否能够相乘两个矩阵。这非常有用，尽管对我们来说不太方便。

在第二行，我们有过程声明。我们必须小心地在正确的位置声明和传递参数。然后矩阵A将乘以矩阵B，结果将放入矩阵R中。我们需要指定矩阵A有多少列和矩阵B有多少行。最后一个参数将返回矩阵R的列数。返回矩阵R的列数的原因稍后会解释，所以现在不用担心。

好的。在第四行和第五行，我们将计算剩余的值，这样我们就不必手动指定它们了。然后，在第七行，我们进行一个小测试，看看矩阵是否可以相乘，因此传递矩阵的顺序很重要。这与标量计算的代码不同之处在于：在矩阵计算中，我们必须非常小心。

如果乘法失败，那么在第九行，我们将在MetaTrader 5控制台输出一条消息。紧接着，在第十行，将抛出一个运行时错误，这将导致尝试进行矩阵乘法的应用程序关闭。如果控制台出现这样的错误，你需要检查第九行是否也出现了消息。如果发生这种情况，错误将不在所讨论的代码片段中，而是在调用此代码的位置。我知道在运行时错误发生时强制应用程序关闭并不优雅，更不用说美观了，但这样我们可以防止应用程序向我们显示错误的结果。

现在来到了让很多人害怕的部分：在第十七行，我们分配内存来存储整个输出。因此，矩阵R在调用者中必须具有动态形式。不要使用静态数组，因为第十二行会检测到这一点，并且代码将以运行时错误退出，第十四行的消息会指出退出的原因。

这种错误生成方法的一个细节是，当执行时，应用程序将尝试除以零，这将导致处理器触发内部中断。这个中断将导致操作系统对导致中断的应用程序采取行动，并强制其关闭。即使操作系统什么都不做，处理器也会进入中断模式，导致其终止，即使在为运行应用程序而设计的嵌入式系统中也是如此。

现在，要注意的是，我在这里使用了一个技巧来防止编译器检测到将生成运行时错误。如果我按照代码中所示之外的方式来做，编译器将无法编译代码，尽管导致运行时错误的行在正常情况下很少被执行。如果你需要强制终止一个程序，你可以使用类似的技术，它总是有效的。尽管这并不优雅，因为用户可能会对你的应用程序或编写它的你感到愤怒。所以请谨慎使用这种方法。

在第18行，我们完全清除了分配内存中的所有内容。通常，一些编译器会自己进行清理，但在使用MQL5编程一段时间后，我发现它并不会自动清理动态分配的内存。我认为这是因为MetaTrader 5中的动态分配内存主要用于指标缓冲区。由于这些缓冲区会随着数据的接收和计算而更新，因此没有必要清除内存。此外，这样的清理操作会花费大量时间，而这些时间可以用于其他任务。因此，我们必须手动进行清理，并确保在计算中不使用不必要的值。如果你在程序中使用动态分配的内存，并且它不是用作用户指标缓冲区，请务必注意这一点。

接下来，我们进入这个过程的最有趣部分：我们将矩阵A乘以矩阵B，并将结果放在矩阵R中。这将在两行代码中完成。第19行乍一看可能非常复杂，但让我们将其分解为几个部分。我们的想法是让两个矩阵的乘法完全动态且通用。也就是说，无论行或列是多是少，只要程序到达这一点，矩阵就会被相乘。

就像矩阵的顺序会影响结果一样，在第19行中，操作的顺序也会影响结果。为了避免冗长的解释，我将简化说明。为了理解发生了什么，让我们按照代码编写的顺序，即从左到右，逐项阅读。这是编译器处理以创建可执行文件的方式，所以虽然它可能看起来令人困惑，但实际上并非如此。代码非常简洁，与大多数人的使用习惯不同。无论如何，我们的想法是从矩阵A中逐列读取，并将其值与从矩阵B中逐行读取的值相乘。因此，系数的顺序会影响结果。你不需要担心矩阵B是如何组织的（按行还是按列），它可以与矩阵A以相同的方式组织，并且这种乘法过程仍然会成功。

现在，我们获得了伪逆值所需的第一个操作。接下来，让我们看看我们需要执行哪些计算，以便了解我们还需要实现什么。我们可能不需要像乘法那样的一般解决方案，而是需要更具体的东西来帮助确定伪逆的值。

以下是计算伪逆的公式：

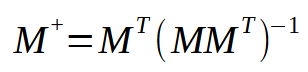
在这个公式中，M表示使用的矩阵。请注意，它始终相同。但是，当查看这个公式时，我们注意到需要在原始矩阵和其转置矩阵之间进行乘法运算。然后，我们取结果并找到逆矩阵的值。最后，我们将转置矩阵与逆的结果相乘。听起来很简单，不是吗？在这里，我们可以创建几个快捷方式。当然，为了创建一个完美的快捷方式，我们需要构建一个只能计算伪逆的过程。但是，创建这样的过程虽然不难，但会使解释其工作原理变得更加困难。为了更好地理解我在说什么，让我们做以下操作：我将把转置矩阵和原始矩阵的乘法放入一个过程中通常，当我们在大学学习这个问题时，我们会被要求分两步来做。也就是说，我们首先创建转置矩阵，然后使用乘法过程来获得最终结果。但是，我们可以创建一个过程，它不包括这两个步骤，而是在一步中完成它们。虽然这很容易实现，但你会发现代码可能难以理解。

让我们在下面的代码中看看如何执行上图中括号内所示的操作。

01. //+------------------------------------------------------------------+
02. void Matrix_A_x_Transposed(const double &A[], const uint A_Row, double &R[], uint &R_Row)
03. {
04.     uint BL = (uint)(A.Size() / A_Row);
05.     if (!ArrayIsDynamic(R))
06.     {
07.         Print("Response array must be of the dynamic type...");
08.         BL = (uint)(1 / MathAbs(0));
09.     }
10.     ArrayResize(R, (uint) MathPow(R_Row = (uint)(A.Size() / A_Row), 2));
11.     ZeroMemory(R);
12.     for (uint cp = 0, Ai = 0, Bi = 0; cp < R.Size(); cp++, Bi = ((++Bi) == BL ? 0 : Bi), Ai += (Bi == 0 ? A_Row : 0))
13.         for (uint c = 0; c < A_Row; c++)
14.             R[cp] += (A[c + Ai] * A[c + (Bi * A_Row)]);
15. }
16. //+------------------------------------------------------------------+

请注意，这段代码与之前的代码非常相似，只是产生结果的那一行代码在两个代码片段中略有不同。然而，这个代码片段能够执行必要的计算，将原始矩阵与其转置矩阵相乘，从而避免了创建转置矩阵。我们可以实现这种类型的优化。当然，在这个相同的过程中，我们还可以添加更多的功能，例如生成逆矩阵，甚至执行逆矩阵与输入矩阵转置的乘法。但是，正如你所能想象的那样，这些步骤虽然不会全局增加复杂性，但会局部增加复杂性。这就是为什么我要一点一点地向你介绍，以便你能理解正在发生的事情，甚至如果你愿意的话，还可以尝试这些概念。

但是，由于我不想重复造轮子，我们不会将所有内容都累积到一个函数中。我展示这部分内容只是为了让你理解，我们在学校学到的东西并不都会在实践中应用。通常，过程会被优化以解决特定的问题。而且，优化某些内容可以让你比使用更通用的过程更快地完成工作。

接下来我们将做以下事情：我们已经有了乘法计算。接下来，我们需要一个计算来生成结果矩阵的逆矩阵。编程实现逆矩阵的方法有很多种。尽管数学上表示逆矩阵的方法很少，但编程方法可能会有很大差异，使得一种算法比另一种更快。然而，我们真正关心的是得到正确的结果，而生成结果的方式并不是那么重要。

为了计算矩阵的逆，我更喜欢使用一种特殊的方法，该方法涉及使用矩阵的行列式。在这一点上，你可以使用另一种方法来找到行列式，但出于习惯，我更喜欢使用萨鲁斯（Sarrus）方法。我认为这样编程更容易。对于那些不熟悉这种方法的人，我会解释一下：萨鲁斯（Sarrus）方法基于对角线的值来计算行列式。编程实现这一点是非常有趣的。在下面的代码片段中，你会看到一个关于如何实现这一点的建议。它适用于任何矩阵，或者说数组，只要它是方形的。

01. //+------------------------------------------------------------------+
02. double Determinant(const double &A[])
03. {
04. #define def_Diagonal(a, b)  {                                                                                                                       \
05.                 Tmp = 1;                                                                                                                            \
06.                 for (uint cp = a, cc = (a == 0 ? 0 : cp - 1), ct = 0; (a ? cp > 0 : cp < A_Row); cc = (a ? (--cp) - 1 : ++cp), ct = 0, Tmp = 1)     \
07.                 {                                                                                                                                   \
08.                     do {                                                                                                                            \
09.                         for (; (ct < A_Row); cc += b, ct++)                                                                                         \
10.                             if ((cc / A_Row) != ct) break; else Tmp *= A[cc];                                                                       \
11.                         cc = (a ? cc + A_Row : cc - A_Row);                                                                                         \
12.                     }while (ct < A_Row);                                                                                                            \
13.                     Result +=  (Tmp * (a ? -1 : 1));                                                                                                \
14.                 }                                                                                                                                   \
15.                             }
16. 
17.     uint A_Row, A_Size = A.Size();
18.     double Result, Tmp;
19. 
20.     if (A_Size == 1)
21.         return A[0];
22.     Tmp = MathSqrt(A_Size);
23.     A_Row = (uint)MathFloor(Tmp);
24.     if ((A_Row != (uint)MathCeil(Tmp)) || (!A_Size))
25.     {
26.         Print("The matrix needs to be square");
27.         A_Row = (uint)(1 / MathAbs(0));
28.     }
29.     if (A_Row == 2)
30.         return (A[0] * A[3]) - (A[1] * A[2]);
31.     Result = 0;
32. 
33.     def_Diagonal(0, A_Row + 1);
34.     def_Diagonal(A_Row, A_Row - 1);
35. 
36.     return Result;
37. 
38. #undef def_Diagonal
39. }
40. //+------------------------------------------------------------------+

这段精美的代码片段，正如您所见，成功地计算出了矩阵的行列式值。在这里，我们所做的事情如此出色，以至于代码甚至不需要任何解释。

第四行定义了一个宏。这个宏能够遍历数组（在我们的情况下是数组中的数组）的对角线。这正是它的工作原理。这段代码背后的数学原理允许您以优雅且高效的方式逐个计算主对角线和副对角线的值。请注意，在代码中我们只需要指定包含矩阵的数组。返回的值就是该矩阵的行列式。然而，在这段代码中实现的萨鲁斯方法有一个限制：如果矩阵是1x1的，行列式就是矩阵本身，并且会立即返回，如第21行所示。如果数组为空或不是方形的，我们将在第27行抛出一个运行时错误，以防止代码进一步执行。如果矩阵大小是2x2，那么对角线的计算不会通过宏进行，而是在宏之前的第30行进行。对于任何其他情况，行列式的计算都是通过宏完成的：首先，在第33行计算主对角线，然后在第34行计算副对角线。如果您不明白发生了什么，请查看下面的图片，我在其中清晰地展示了所有内容。这是为那些不熟悉萨鲁斯（SARRUS）方法的人准备的。

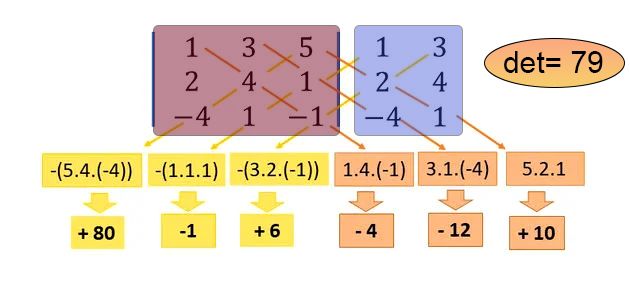
在这张图片中，红色区域表示我们想要计算行列式的矩阵，蓝色区域是矩阵某些元素的虚拟副本。宏代码执行了图中所示的确切计算，并返回行列式，在这个例子中是79。

后记

好了，亲爱的读者，我们已经到了另一篇文章的结尾。然而，我们还没有实现计算伪逆值所需的所有程序。我们将在下一篇文章中讨论这个问题，在那里我们将看到一个执行此任务的应用程序。虽然可以说我们可以使用本文附录中提供的代码，但问题是它并没有给我们使用任何类型的结构的自由。要使用伪逆（PInv），我们实际上需要处理矩阵类型。在我作为计算说明所展示的那个中，我们可以使用任何数据建模。我们只需要做出必要的更改，以便能够使用任何东西。所以，与您下一篇文章相会。