Neuronales Netz in der Praxis: Geradenfunktion

Einführung

Ich freue mich sehr, Sie alle begrüßen zu dürfen und lade Sie ein, einen neuen Artikel über neuronale Netze zu lesen.

Im vorherigen Artikel „Neuronales Netzwerk in der Praxis: Kleinste Quadrate“ haben wir uns angesehen, wie wir in sehr einfachen Fällen eine Gleichung finden können, die den von uns verwendeten Datensatz am besten beschreibt. Die Gleichung, die in diesem System gebildet wurde, war sehr einfach, sie verwendete nur eine Variable. Wir haben bereits gezeigt, wie man die Berechnung durchführt, also kommen wir hier direkt zur Sache. Dies liegt daran, dass die Mathematik, die zur Erstellung einer Gleichung auf der Grundlage der in der Datenbank verfügbaren Werte verwendet wird, erhebliche Kenntnisse in analytischer Mathematik und algebraischer Berechnung erfordert. Darüber hinaus muss man natürlich wissen, welche Art von Daten sich in der verwendeten Datenbank befinden.

Da dieser Artikel einen breiten Bildungsauftrag hat, möchte ich es meinen Lesern nicht schwer machen. Wenn Sie wirklich daran interessiert sind, sich in die Berechnungen zu vertiefen, empfehle ich Ihnen, die Materialien zu diesem Thema zu studieren. Wie bereits erwähnt, müssen Sie vor allem analytische Mathematik und algebraische Berechnungen studieren. Um diesen Prozess weniger theoretisch und langwierig zu gestalten, schlage ich vor, dass Sie mit dem Studium der Spieltheorie beginnen. Dort können Sie sich auf unterhaltsamere Weise mit Berechnungen und Analysen vertraut machen, ohne die monotone Wiederholung von endlosen Berechnungen.

Im Internet gibt es viele Materialien zu diesem Thema, die gut erklärt und leicht zu verstehen sind. Wenn es Ihnen aber nur darum geht, sich den Code anzuschauen, können Sie das gerne tun, denn ich werde in diesem Artikel nicht auf den mathematischen Teil eingehen. Die mathematische Frage ist ziemlich tiefgründig und erfordert das Verständnis aller Details und viel Zeit. Die meisten Leser werden an diesen Aspekten nicht interessiert sein.

Daher werden wir in diesem Artikel nur einen kurzen Blick auf einige Methoden werfen, um eine Funktion zu erhalten, die unsere Daten in der Datenbank darstellen könnte. Ich werde nicht im Detail darauf eingehen, wie man Statistiken und Wahrscheinlichkeitsstudien zur Interpretation der Ergebnisse verwendet. Überlassen wir das denjenigen, die sich wirklich mit der mathematischen Seite der Angelegenheit befassen wollen. Die Erforschung dieser Fragen wird entscheidend sein für das Verständnis dessen, was bei der Untersuchung neuronaler Netze eine Rolle spielt. Hier werden wir dieses Thema in aller Ruhe besprechen.

Erstellen einer Gleichung in allgemeiner Form

Lassen Sie uns zunächst einige Berechnungen anstellen. (Schon wieder?!). Beruhigen Sie sich, liebe Leserin, lieber Leser, Sie müssen sich keine Sorgen darüber machen, was wir tun werden. Diesmal verspreche ich, freundlicher zu sein. Heute werden wir anders handeln. Unser Ziel ist es, ein System zu schaffen, das allgemeinere Geradengleichungen erzeugen kann. Und damit Sie nicht völlig verblüfft sind über die Entwicklung der Formeln, die wir verwenden werden, werden wir nicht auf die mathematische Entwicklung hinter den Gleichungen eingehen. Dies ist nicht notwendig, da wir im vorherigen Artikel gezeigt haben, wie eine mathematische Gleichung auf der Grundlage einiger grundlegender Ideen und Prinzipien entwickelt werden kann. Wir werden hier nur versuchen zu verstehen, was diese Gleichungen eigentlich bedeuten. Natürlich werden wir versuchen, alles so zugänglich wie möglich zu machen. Auch wenn sie auf den ersten Blick verwirrend erscheinen mögen, werde ich Sie nicht verwirren. Lesen Sie den Artikel ohne Eile. Sehen Sie sich an, wie das Ganze abläuft, denn hier werde ich verschiedene mathematische Studien zusammenfassen, um Ihnen zu zeigen, wie wir ein neuronales Netz dazu bringen können, Wissen auf der Grundlage von Informationen aus einer Datenbank zu lernen.

Doch bevor wir beginnen, möchte ich eines klarstellen: Was wir hier sehen werden, gilt für ein neuronales Netz, das keine neuen Informationen in seine Datenbank aufnimmt. Das heißt, die Datenbank ist bereits vollständig erstellt, und wir wollen nur, dass sie eine Gleichung generiert, die das, was bereits in der Datenbank steht, am besten darstellt. Erst später können wir mit Hilfe anderer Mechanismen die Wahrscheinlichkeit herausfiltern, dass neue Informationen mit dem, was bereits in der Datenbank vorhanden ist, in Verbindung stehen oder nicht. Solche Mechanismen fallen in der Regel in den Bereich der künstlichen Intelligenz. Aber das ist ein Thema für eine andere Diskussion.

Kehren wir nun zu unserem Codebeispiel zurück. In diesem Beispiel haben wir bereits zwei Datensätze, die auf einer zweidimensionalen Ebene aufgetragen werden können. Das heißt, es werden nur X- und Y-Koordinaten verwendet. Nach einer ruhigen Analyse der Situation können wir feststellen, dass die gewünschte Gleichung relativ einfach zu konstruieren ist, da unsere Daten mit einer gewissen Annäherung an eine wahrscheinliche gerade Linie ausgedrückt werden können. Manchmal ist dies nicht der Fall, da die Gleichung eine Kurve oder eine trigonometrische Funktion sein kann. Aber lassen Sie uns einen Schritt nach dem anderen machen. Zunächst müssen wir uns mit einfacheren Fällen befassen. Machen wir uns zunächst Folgendes klar: Die Gleichung, die wir erhalten möchten, hat das unten dargestellte Format.

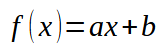
Dabei stellt der Wert der Konstante < a > die Steigung dar. Die Konstante < b > ist der Schnittpunkt. Wenn < b > Null ist, ist auch die Wurzel der Funktion Null. Im vorigen Artikel haben wir uns angesehen, wie man diesen Koeffizienten berechnet, wenn < b > gleich Null ist. Am Ende desselben Artikels haben wir auch gesehen, wie man beide Werte anpasst, um die Konstanten der Gleichung anzunähern und so die oben gezeigte lineare Funktion zu konstruieren. Erinnern wir uns noch einmal daran, dass sich die Wurzel der Funktion ändert, wenn wir den Wert der Konstante < b > ändern. Dies zu verstehen ist wichtig, um das System mit Hilfe von Polynomen zu lösen. Wir werden hier jedoch eine Methode verwenden, die aus dem vorherigen Artikel übernommen wurde.

Ich denke, es ist klar, dass der Versuch, diese Werte durch Versuch und Irrtum zu finden, in der Programmierung als Brute-Force-Verfahren bekannt ist, bei dem alle möglichen Werte ausprobiert werden (und das ist bei weitem nicht der beste Weg). Das ist zwar möglich, aber in den meisten Fällen ist die Bearbeitungszeit sehr lang. In Fällen wie dem unseren wird es einfach viel Zeit und Mühe kosten, aber es ist durchaus machbar. Wenn jedoch die Anzahl der Variablen erheblich ansteigt, wird dieses Verfahren unpraktisch, egal ob man es manuell oder mit roher Gewalt durchführt.

Aber selbst wenn wir uns für „brute force“ (rohe Gewalt) entscheiden, habe ich im vorigen Artikel gezeigt, wie man die Steigung berechnen kann, wenn die Konstante < b > gleich Null ist. Diese Methode ermöglichte es, den Winkelkoeffizienten relativ einfach und schnell zu ermitteln, unabhängig von der Datenmenge in der Datenbank. Die einzige Vorgabe war, dass die resultierende Gleichung eine gerade Linie sein musste. Wenn jedoch die Konstante < b > ungleich Null ist, dann funktioniert diese Berechnung nicht mehr. Dies gibt uns nur eine grobe Vorstellung davon, in welche Richtung wir uns bewegen müssen. Wir werden uns das später ansehen. Vorerst werden wir versuchen, uns an bekannten Funktionen zu orientieren, wie zum Beispiel an der Funktion, die wir uns zu Beginn dieses Themas angesehen haben.

Lassen Sie uns nun über den allgemeinen Fall der Lösung nachdenken. Denken Sie daran, dass Sie die Art des Polynoms kennen müssen, das Sie verwenden. Ohne dieses Wissen kann die Suche nach der Gleichung, die die Daten am besten darstellt, selbst in den einfachsten Fällen sehr zeitaufwändig sein. Denken Sie also daran: Alles, was wir als Nächstes sehen, basiert auf diesem Vorwissen.

Verallgemeinern wir die Methode der kleinsten Quadrate auf jeden Fall. Dazu müssen Sie den Typ des verwendeten Polynoms kennen. Wir beginnen mit einem einfachen Beispiel, das eine gerade Linie erzeugt. Dieses Polynom kann mit Hilfe des unten stehenden Ausdrucks verallgemeinert werden.

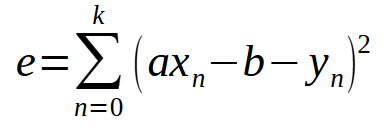
Moment, ist das nicht die gleiche Formel wie im vorherigen Artikel? Das ist es! Im Grunde ist es dasselbe, aber jetzt wird die Variable < b > in die Formel aufgenommen, weil wir nicht mehr davon ausgehen, dass sie Null ist. Wenn wir diese Summe erweitern, kommen wir zu einem ähnlichen Ergebnis wie im vorherigen Artikel. Zum besseren Verständnis müssen wir jedoch bei der Verallgemeinerung dieser Berechnung die Ableitung nach den beiden Variablen < a > und < b > berücksichtigen. Daraus ergibt sich die unten stehende Definition.

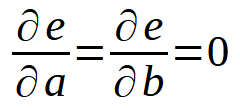
Mit anderen Worten: Es ist alles so wie im vorherigen Artikel. Dieses Prinzip ist jedoch nicht auf die Gleichung einer Geraden beschränkt. Wir können in beiden Fällen den gleichen Ansatz verwenden. Nehmen wir zum Beispiel an, ein Datensatz lässt sich am besten als Parabel ausdrücken oder darstellen. In diesem Fall müssen wir uns überlegen, wie wir eine quadratische Gleichung anhand der Daten in unserer Datenbank finden können. Die letzten beiden Definitionen werden in die folgenden umgewandelt.

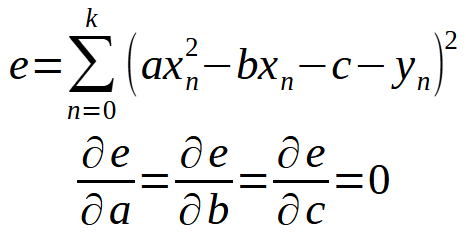
Wir müssen also einen neuen Begriff entwickeln, um eine Gleichung zu erzeugen, die in diesem Fall eine quadratische Gleichung sein wird. Das heißt, wir müssen die Konstanten finden, damit eine quadratische Gleichung alles anzeigen kann, was in der Datenbank steht. Kehren wir jedoch zu unserem Fall zurück, bei dem wir die Geradengleichung verwenden, und setzen wir die Berechnung unter der Annahme fort, dass < b > ungleich Null ist, so erhalten wir zunächst die folgende Gleichung.

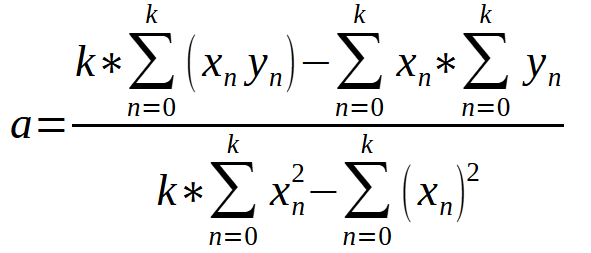
Mit dieser Gleichung können wir den Wert von < a > auf der Grundlage der in unserer Datenbank enthaltenen Daten berechnen.

Nachdem wir den Wert der Konstante < a > ermittelt haben, können wir die nachstehende Gleichung verwenden, um die Konstante < b > zu bestimmen.

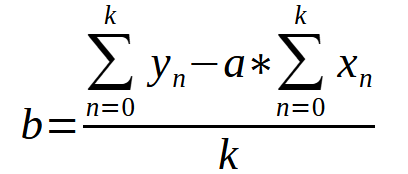
In beiden Fällen ist der Wert < k > die Anzahl der Punkte im Diagramm. Wenn man sich nur die Gleichungen ansieht, könnte man vielleicht verwirrt sein und denken, dass es sich um etwas Kompliziertes handelt. Oder Sie wissen nicht, wie Sie diese Ausdrücke mit einer Programmiersprache in Code umwandeln können. Dies würde es ermöglichen, die Werte von Konstanten zu ermitteln, ohne dies manuell tun zu müssen. Genau das haben wir im vorigen Artikel getan. Wir werden dieses mathematische Format in ein Format einer Programmiersprache übersetzen, in diesem Fall MQL5, aber Sie könnten jede andere Sprache verwenden und die Ergebnisse wären die gleichen. Unten sehen Sie, wie diese Gleichungen in unserem MQL5-Code aussehen werden.

28. //+------------------------------------------------------------------+
29. void Func_01(void)
30. {
31.     int A[]={
32.                   -100, -150,
33.                    -80,  -50,
34.                     30,   80,
35.                    100,  120
36.             };
37. 
38.     int vx, vy;
39.     uint k;
40.     double ly, err, dx, dy, dxy, dx2, a, b;
41.     string s0 = "";
42. 
43.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
44.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
45. 
46.     err = dx = dy = dxy = dx2 = 0;
47.     k = 0;    
48.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++, k++)
49.     {
50.         vx = A[c1++];
51.         vy = A[c1++];
52.         dx += vx;
53.         dy += vy;
54.         dxy += (vx * vy);
55.         dx2 += MathPow(vx, 2);
56.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
57.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle))) - global.Const_B;
58.         s0 += StringFormat("%.4f || ", MathAbs(ly));
59.         canvas.LineVertical(global.x + vx, global.y - vy, global.y + (int)(ly - vy), ColorToARGB(clrPurple));
60.         err += MathPow(ly, 2);
61.     }
62.     a = ((k * dxy) - (dx * dy)) / ((k * dx2) - MathPow(dx, 2));
63.     b = (dy - (a * dx)) / k;
64.     PlotText(3, StringFormat("Error: %.8f", err));
65.     PlotText(4, s0);
66.     PlotText(5, StringFormat("f(x) = %.4fx %c %.4f", a, (b < 0 ? '-' : '+'), MathAbs(b)));
67. }
68. //+------------------------------------------------------------------+

Lassen Sie uns herausfinden, was in diesem Fragment vor sich geht. In den Zeilen 46 und 47 initialisieren wir alle Variablen auf Null. Der Grund dafür ist, dass wir explizit zeigen wollen, dass sie bei Null beginnen, obwohl wir diese Deklaration auch weglassen könnten, da der Compiler Variablen normalerweise implizit auf Null initialisiert. In Zeile 52 berechnen wir die Summe aller X-Werte und in Zeile 53 die Summe der Y-Werte. In Zeile 54 wird die Summe des Produkts aus den Werten X und Y berechnet. Und schließlich wird in Zeile 55 die Summe der Quadrate der X-Werte berechnet.

Alle diese Berechnungen werden in den Formeln verwendet, die wir uns bereits angesehen haben. Mit anderen Worten: Die Berechnungen sind viel einfacher, als es scheint. Alle oben genannten Berechnungen werden in den Formeln verwendet, die wir zuvor betrachtet haben. Diesmal ist es also viel einfacher.

Nun müssen wir die Werte der Konstanten berechnen, die in der Gleichung einer Geraden verwendet werden. Hierfür verwenden wir die Zeile 62, in der wir den Steigungswert berechnen, und die Zeile 63, in der wir den Achsenabschnitt finden. Haben Sie bemerkt, wie einfach es ist, eine mathematische Formel in eine Berechnung zu verwandeln, die unser Programm ausführen kann? Es gibt Leute, die behaupten, Mathematik zu verstehen, aber sie können sie nicht in Programmiersprache übersetzen. Meiner Meinung nach machen sich diese Leute etwas vor, denn eine mathematische Formel in Code zu schreiben ist genauso einfach wie sie zu lesen. Wenn wir die Formel nicht verstehen, können wir einem Computer, der nur ein riesiger Taschenrechner ist, natürlich nicht erklären, wie er die Berechnung durchführen soll.

Nun zeichnen wir die resultierende Gleichung auf. Dies geschieht in Zeile 66. Auf diese Weise können wir manuell feststellen, ob die berechneten Werte für den gegebenen Datensatz am besten geeignet sind. Im folgenden GIF sehen Sie das Ergebnis der Ausführung unseres Programms mit den in Matrix A in Zeile 31 angegebenen Werten.

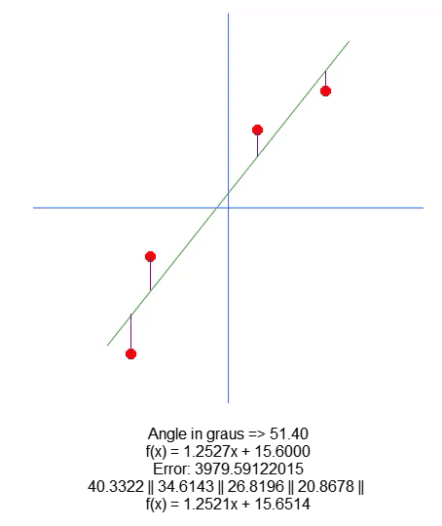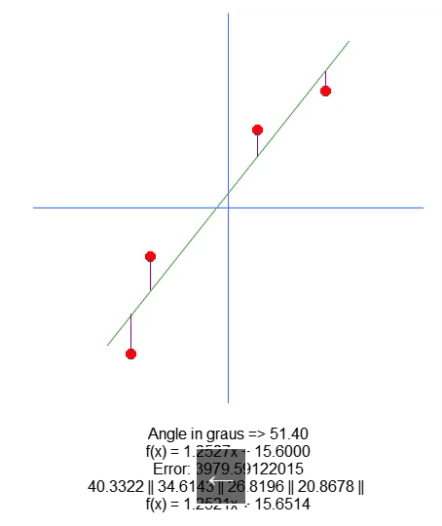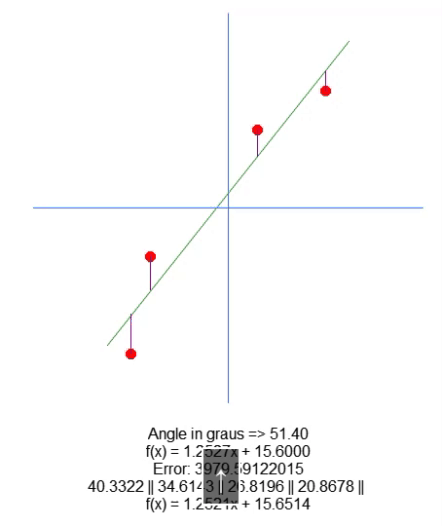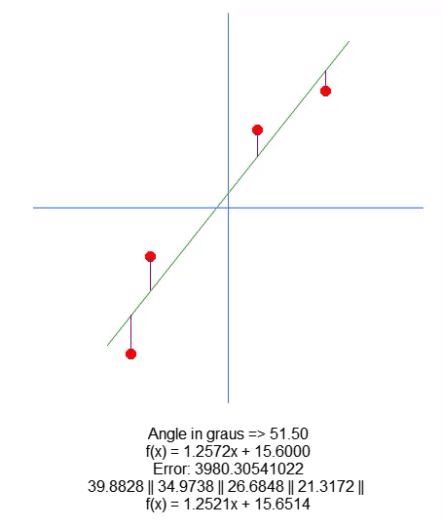
Beobachten Sie, wie sich die Fehlerwerte ändern, wenn wir versuchen, den idealen Punkt zu finden. Vergleichen Sie die Gleichung einer Geraden, die als Ideal dargestellt ist, mit der Gleichung der Linie, die wir mit Hilfe der Pfeile zu zeichnen versuchen. Wir erhalten keine sehr genaue Einstellung, aber wir haben einen Wert, der dem Ideal sehr nahe kommt. Dies zu verstehen ist wichtig, weil wir uns bald mit derselben Eigenschaft befassen werden, allerdings auf eine andere Art und Weise.

Jetzt fragen Sie sich vielleicht: Gibt es eine Möglichkeit, dem berechneten Wert näher zu kommen? Ja, liebe Leserin, lieber Leser, es gibt sie. Dazu müssen Sie lediglich einen Wert im Programm ändern, wie im folgenden Code gezeigt.

void NewAngle(const char direct, const char updow, const double step = 0.1)

Der zu ändernde Wert ist das Schritt-Argument. Hier verwenden wir einen Schritt von 0,1, wie Sie im Code sehen können, aber Sie können einen kleineren oder größeren Wert verwenden. Wenn Sie einen kleineren Wert verwenden, braucht das Programm länger, um die berechneten Werte zu erreichen, aber die Fehlergenauigkeit ist aufgrund der geringeren Abweichung höher. Denken Sie daran, dass das eine mehr Gewicht hat als das andere: Es gibt keine 100 % perfekte Lösung, aber es gibt einen idealen Ausgleichspunkt.

Sobald wir einen Code haben, der die Geradengleichung berechnen kann, können wir die Werte in der Matrix A beliebig ändern, um beliebige Bedingungen oder eine Wissensbasis zu schaffen. Möglicherweise müssen Sie nur die Art der von Ihnen verwendeten Variablen ändern. Hier verwenden wir Ganzzahlen, aber wenn Sie fließende Datentypen wie Double oder Float verwenden möchten, ändern Sie einfach den Typ, die Berechnung ändert sich nicht. Dies ist notwendig, um die Gleichung der Geraden zu erhalten. Wenn die Daten in der Datenbank jedoch am besten durch eine quadratische Gleichung dargestellt werden, müssen wir die Berechnungen ändern, um das beste Konstantensystem für unsere Datenbank zu finden, wie oben beschrieben. Es kommt auf den jeweiligen Kontext an; es gibt keine 100%ig wirksame Lösung für alle möglichen und denkbaren Fälle.

Aber man könnte meinen, dass dies die einzige Möglichkeit ist, die Gleichung einer Geraden zu berechnen. Wenn Sie genau so gedacht haben, dann ist Ihr Wissen noch unzureichend. Um einen anderen Weg zu zeigen, wie man dieselben Werte erhält, die wir in diesem Thema betrachtet haben, werden wir einen neuen Abschnitt untersuchen und die Konzepte entsprechend aufteilen. Dieser Abschnitt ist eine Einführung in das, was wir im nächsten Artikel sehen werden.

Pseudoinverse

Bis jetzt schien alles sehr kompliziert und schwer in Code umzusetzen zu sein. Das liegt daran, dass jede geforderte Änderung ordnungsgemäß in den generierten Code implementiert werden muss. Es gibt jedoch eine schönere Art, Code für diese Situation zu schreiben, in der sich die Variablen ständig ändern. Zumindest glaube ich das. Wenn es darum geht, Code zu schreiben, bei dem sich die Anzahl der Variablen häufig ändert, ziehe ich es vor, von Skalar- zu Matrixberechnungen überzugehen. Mit Matrixoperationen können wir alle Faktoren berücksichtigen, ohne viele Zeitvariablen erstellen zu müssen. Ich weiß, dass viele von Ihnen das Schreiben von Code für die Matrixfaktorisierung sehr schwierig finden und oft Bibliotheken verwenden, die diese Faktorisierung durchführen, ohne zu verstehen, wie sie funktioniert. Das kann dazu führen, dass Sie von diesen Bibliotheken abhängig werden, weil Sie nicht verstehen, wie die Berechnungen durchgeführt werden.

Vor einiger Zeit habe ich zwei Artikel zur Einführung in die Matrixfaktorisierung geschrieben. In diesen Artikeln haben wir uns die grundlegendsten Elemente angesehen, die wir kennen sollten, um Code zu erstellen, der Matrixfaktorisierungsoperationen durchführt. Viele Probleme lassen sich einfacher und schneller lösen, wenn Sie Matrizen für Berechnungen verwenden.

Artikel: „Matrixfaktorisierung: Die Grundlagen“ und „Matrixfaktorisierung: Ein praktikables Modell“. Wenn Sie mehr über dieses Thema erfahren möchten, empfehle ich Ihnen, die Artikel zu lesen und in der Praxis zu testen. Natürlich decken sie nur die Grundlagen ab, aber wenn Sie deren Inhalt verstehen, können Sie nachvollziehen, was wir in diesem Abschnitt tun werden.

Hier werden wir Matrizen verwenden, um die im vorherigen Thema ermittelten Werte zu ermitteln. Um zu verstehen, was wir tun werden, müssen wir wissen, wie Matrizen addiert werden. Ich meine nicht das Programmieren, denn das Programmieren dieser Berechnungen ist der einfache Teil. Ich meine damit, dass Sie zumindest Grundkenntnisse in der Durchführung von Berechnungen mit Matrizen haben sollten. Ich werde nicht im Detail darauf eingehen, wie diese Berechnungen durchzuführen sind, da ich davon ausgehe, dass Sie über einige Kenntnisse auf diesem Gebiet verfügen. Sie müssen kein Experte sein. Die Kenntnis der Grundlagen wird für das, was wir tun werden, ausreichen.

Kehren wir nun zu der Frage zurück, wie man die Gleichung einer Geraden findet, wenn wir eine Datenbank haben und den Inhalt der Datenbank als mathematische Gleichung speichern wollen. Auf den ersten Blick scheint es sehr schwierig zu sein, so als ob nur ein Genie dies schaffen könnte. Aber nein, wir werden das Gleiche tun wie im vorherigen Thema. Nur ein bisschen anders.

Fangen wir mit dem Anfang an. Die Fehlergleichung ist in der nachstehenden Abbildung dargestellt.

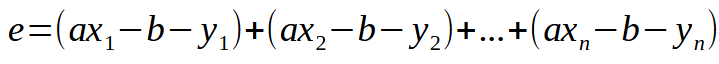
Dies ist die skalare Form der Gleichung. Wir können die gleiche Gleichung jedoch auch in Matrixform schreiben, wie unten gezeigt.

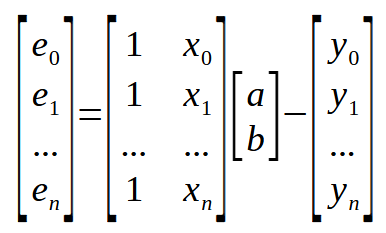
Diese Matrizendarstellung ist genau das, was in der vorherigen Abbildung zu sehen ist, ohne irgendwelche Zusätze. Aber wir können diese Matrixdarstellung noch weiter vereinfachen. Wir gehen dabei wie folgt vor:

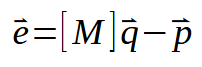
Ich weiß, diese Darstellung mag sehr kompliziert erscheinen. Dennoch stellt sie genau das dar, was eine skalare Berechnung tun würde. Diese kompaktere Form der Matrixfaktorisierung ermöglicht es uns jedoch, die Berechnungen besser zu verstehen, da wir weniger Elemente in die Formel schreiben müssen. Hier geben wir an, dass der Vektor < e > gleich der Matrix < M > ist, die die x-Werte enthält, multipliziert mit dem Vektor < q >, der die gesuchten Konstanten enthält. Dazu gehören der Winkelkoeffizient und der Schnittpunkt. Dann subtrahieren wir den Vektor < p >, der die Werte der Matrix mit den y-Werten darstellt.

Jetzt möchte ich Sie an Folgendes erinnern: Wir suchen die Ableitung der Konstanten <a> und <b> nach dem Fehler, die wir leicht berechnen können. Jetzt haben wir die Lage der Punkte, die wir für die Berechnung verwenden werden. Wenn wir sie also in Form einer Matrix darstellen, erhalten wir Folgendes.

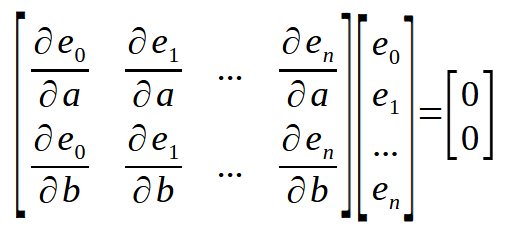
Hier noch ein kleines Detail:

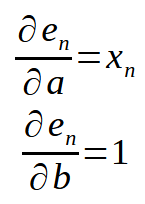
Wenn wir uns daran erinnern, dass < n > in unserem Code den Array-Index darstellt, kann die obige Gleichung wie folgt umgeschrieben werden.

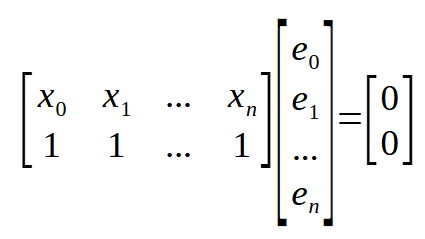
Okay, jetzt haben wir etwas wirklich Interessantes. Wenn Sie sich die obigen Matrizen ansehen, können Sie sehen, dass wir hier das gleiche Ergebnis zeigen. Sie kommt auch an anderen Stellen vor, nur ist diese Matrix transponiert, was die Formel noch kompakter macht. Sehen Sie sich das folgende Bild an.

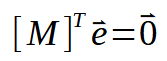
Der nächste Schritt besteht darin, einige Ersetzungen in den bereits vorhandenen Daten vorzunehmen. Daraus ergibt sich die folgende Formulierung.

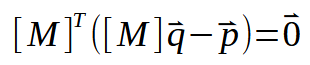
Lassen Sie uns nun die oben dargestellte Berechnung oder Formel (Sie können sie nennen, wie Sie wollen) entwickeln. Dies führt uns zu folgendem Ergebnis:

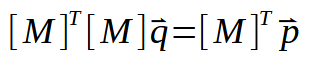
Wenn wir nun die transponierte Matrix invertieren, erhalten wir etwas wie dieses:

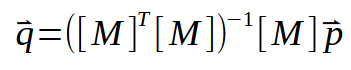
Dieses Ergebnis ist eigentlich eine sehr schöne und interessante Faktorisierung, so besonders, dass die Person, die es geschaffen hat, eigentlich den Nobelpreis für Mathematik im Jahr 2020 verdient hätte. Diese Formulierung ist nach ihren Schöpfern als Moore-Penrose-Pseudoinverse bekannt. Sie liefert uns genau das, was wir suchen, nämlich die Werte für den Winkelkoeffizienten und den Achsenabschnitt. Und beide werden innerhalb des Vektors < q > liegen. Diese Art der Berechnung kann in einer Vielzahl verschiedener Programme durchgeführt werden, von denen viele ausschließlich für die Arbeit mit Berechnungen konzipiert sind. Mit SCILab können Sie zum Beispiel das folgende Programm verwenden. Sie berechnet die Werte für die Steigung und den Schnittpunkt.

clc;
clear;
clf;

x=[-100; -80; 30; 100];
y=[-150; -50; 80; 120];

A = [ones(x), x];

plot(x, y, 'ro');
zoom_rect([-150, -180, 180, 180]);
xgrid;

x = pinv(A) * y;
b = x(1);
a = x(2);

x =[-120:1:120];
y = a * x + b;

plot(x, y, 'b-');

Das Ergebnis der Ausführung ist unten zu sehen:

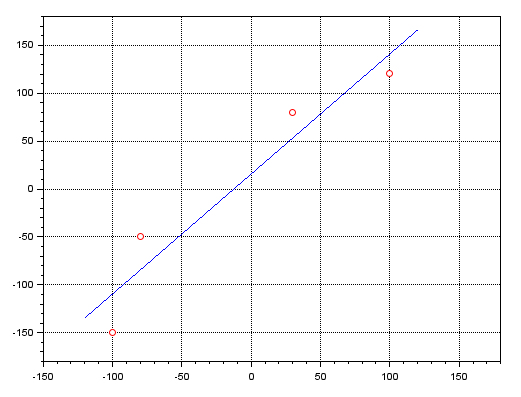
Die roten Punkte zeigen die Lage der gleichen Punkte wie im Programm MQL5. Die blaue Linie zeigt das Ergebnis der Geradengleichung, die mit Hilfe der Pseudoinverse ermittelt wurde. Das Gleiche kann mit MATLAB und anderen Programmen wie Excel gemacht werden. Dies erklärt sich durch die große Nützlichkeit dieser Pseudoinverse in verschiedenen Bereichen.

Um Ihnen eine Vorstellung davon zu geben, wie interessant diese Pseudoinverse ist, können wir die verwendeten Vektoren sowie die Matrizen der Gleichung leicht verändern. Sie können Polynome jeglicher Art lösen, und zwar recht effektiv.

Abschließende Überlegungen

Da die Pseudoinverse eine Faktorisierung ist, die mit Hilfe von Matrizen durchgeführt werden muss, werde ich in diesem Artikel nicht zeigen, wie das Programm zur Ermittlung der Konstanten < a > und < b > aussehen würde. Das liegt daran, dass wir bestimmte Erklärungen berücksichtigen müssen, damit Sie wirklich verstehen, was vor sich geht. Es geht nicht nur darum, den Code selbst zu präsentieren. Matrixoperationen erfordern aufgrund der Besonderheiten ihrer Verarbeitung wesentlich mehr Aufmerksamkeit. Bei manueller Durchführung sind die Vorgänge relativ einfach. Dies im Code zu tun, ist jedoch eine ganz andere Geschichte. Selbst in den Artikeln, in denen wir über die Verwendung der Faktorisierung in Matrizen sprechen, ist das, was sie dort tun, nicht allgemein, sondern sehr spezifisch. Für unsere Zwecke benötigen wir jedoch einen allgemeineren Code. Andernfalls wird die Pseudoinverse nicht korrekt berechnet.