
Neuronale Netze leicht gemacht (Teil 50): Soft Actor-Critic (Modelloptimierung)
Einführung
Wir fahren fort mit der Untersuchung des Algorithmus Soft Actor Critic. Im vorherigen Artikel haben wir den Algorithmus implementiert, konnten aber kein profitables Modell trainieren. Heute werden wir uns mit möglichen Lösungen befassen. Eine ähnliche Frage wurde bereits in dem Artikel „Modell der Prokrastination, Gründe und Lösungen“ aufgeworfen. Ich schlage vor, unser Wissen in diesem Bereich zu erweitern und neue Ansätze am Beispiel unseres Soft Actor-Critic-Modells zu prüfen.
1. Optimierung der Modelle
Bevor wir direkt zur Optimierung des von uns erstellten Modells übergehen, möchte ich Sie daran erinnern, dass Soft Actor-Critic ein Verstärkungslernalgorithmus für stochastische Modelle in einem kontinuierlichen Aktionsraum ist. Das Hauptmerkmal dieser Methode ist die Einführung einer Entropiekomponente in die Belohnungsfunktion.
Durch die Verwendung einer stochastischen Actors-Politik ist das Modell flexibler und in der Lage, Probleme in komplexen Umgebungen zu lösen, in denen einige Handlungen ungewiss sind oder keine klaren Regeln festgelegt werden können. Diese Strategie ist oft robuster, wenn es um Daten geht, die viel Rauschen enthalten, da sie die probabilistische Komponente berücksichtigt und nicht an klare Regeln gebunden ist.
Die Hinzufügung einer Entropiekomponente fördert die Erkundung der Umgebung und erhöht die Belohnung für Aktionen mit geringer Wahrscheinlichkeit. Das Gleichgewicht zwischen Erkundung und Ausbeutung wird durch das Temperaturverhältnis bestimmt.
In mathematischer Form kann die Soft Actor-Critic-Methode durch die folgende Gleichung dargestellt werden
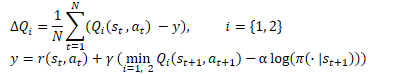
1.1 Hinzufügen von Stochastik zur Politik des Actors
In unserer Implementierung haben wir aufgrund der Komplexität der OpenCL-Implementierung auf die Verwendung der stochastischen Actor-Politik verzichtet. Ähnlich wie bei TD3 haben wir sie durch einen zufälligen Versatz der ausgewählten Aktion in einigen ihrer Umgebungen ersetzt. Dieser Ansatz ist einfacher zu implementieren und ermöglicht es dem Modell, die Umgebung zu erkunden. Aber es hat auch seine Nachteile.
Das erste, was auffällt, ist die fehlende Verbindung zwischen der abgetasteten Aktion und der vom Modell gelernten Verteilung. In einigen Fällen, wenn die gelernte Verteilung breiter ist als das Stichprobengebiet, wird das Untersuchungsgebiet dadurch komprimiert. Das bedeutet, dass die Modellpolitik höchstwahrscheinlich nicht optimal ist, sondern von einem zufällig gewählten Startpunkt des Lernens abhängt. Bei der Initialisierung eines neuen Modells füllen wir es schließlich mit Zufallsgewichten.
In anderen Fällen kann es vorkommen, dass die gesampelte Aktion außerhalb der gelernten Verteilung liegt. Dies erweitert den Umfang der Forschung, steht aber im Widerspruch zur Entropiekomponente der Belohnungsfunktion. Aus der Sicht des Modells hat eine Handlung außerhalb der gelernten Verteilung die Wahrscheinlichkeit Null. Dank der Entropiekomponente erhält sie unabhängig von ihrem Wert die maximale Belohnung.
Während des Trainings versucht das Modell, eine gewinnbringende Strategie zu finden, und erhöht die Wahrscheinlichkeit von Aktionen mit maximaler Belohnung. Gleichzeitig sinkt die Wahrscheinlichkeit, dass weniger rentable und unrentable Maßnahmen durchgeführt werden. Bei der einfachen Stichprobe, die wir zuvor verwendet haben, wird dieser Faktor nicht berücksichtigt. Es wird uns jede Aktion aus dem Stichprobengebiet mit gleicher Wahrscheinlichkeit liefern. Die geringe Wahrscheinlichkeit unrentabler Aktionen erzeugt eine hohe Entropiekomponente. Dies verzerrt den wahren Wert von Handlungen, neutralisiert zuvor gesammelte Erfahrungen und führt zur Konstruktion einer falschen Actors-Politik.
Hier gibt es nur eine Lösung - ein stochastisches Modell des Actors zu erstellen und Aktionen aus der gelernten Verteilung zu entnehmen.
Wir haben bereits über das Fehlen eines Pseudozufallszahlengenerators auf der OpenCL-Kontextseite gesprochen, daher werden wir den Generator auf der Seite des Hauptprogramms verwenden.
Dabei ist zu beachten, dass die gelernte Verteilung nur auf der OpenCL-Seite verfügbar ist. Sie ist in den internen Objekten unseres Modells enthalten. Um den Sampling-Prozess zu organisieren, müssen wir daher eine Datenübertragung zwischen dem Hauptprogramm und dem OpenCL-Kontext implementieren. Dies hängt nicht davon ab, wo das Verfahren durchgeführt wird.
Wenn wir den Prozess auf der Seite des Hauptprogramms organisieren, müssen wir die Verteilung laden. Dazu gehören 2 Puffer: Wahrscheinlichkeiten und entsprechende Funktionswerte.
Wenn wir einen Prozess auf der OpenCL-Kontextseite arrangieren, müssen wir einen Puffer mit Zufallswerten übergeben. Sie wird später verwendet, um eine separate Aktion auszuwählen.
Hier sollte noch ein weiterer Punkt berücksichtigt werden - der Verbraucher der erhaltenen Werte. Während des Betriebs werden wir die gesampelten Werte verwenden, um Aktionen durchzuführen, d.h. auf der Seite des Hauptprogramms. Aber während des Trainings werden wir sie auf den Kritiker (Critic) auf der OpenCL-Seite des Kontexts übertragen. Wie wir wissen, stellt die Modellschulung die strengsten Anforderungen, um die Zeit für die Durchführung von Operationen zu reduzieren. In Anbetracht dessen erscheint die Entscheidung, nur einen Puffer mit Zufallswerten in den OpenCL-Kontext zu übertragen und dort den weiteren Sampling-Prozess zu organisieren, recht logisch.
Die Entscheidung ist gefallen, jetzt geht es an die Umsetzung. Zunächst wird der SAC_AlphaLogProbs-Kernel des OpenCL-Programms geändert. Durch unsere Änderungen wird der Algorithmus des angegebenen Kerns sogar in gewissem Maße vereinfacht.
Wir fügen einen Puffer mit Zufallswerten in die externen Parameter des Kernels ein. Wir erwarten, dass wir eine Reihe von Zufallswerten im Bereich [0, 1] erhalten, um die Probenahme in diesem Puffer zu organisieren.
__kernel void SAC_AlphaLogProbs(__global float *outputs, __global float *quantiles, __global float *probs, __global float *alphas, __global float *log_probs, __global float *random, const int count_quants, const int activation ) { const int i = get_global_id(0); int shift = i * count_quants; float prob = 0; float value = 0; float sum = 0; float rnd = random[i];
Um eine Aktion auszuwählen, führen wir eine Schleife durch, in der wir die Wahrscheinlichkeiten aller Quantile der zu analysierenden Aktion aufzählen und ihre kumulative Summe berechnen. Im Hauptteil der Schleife wird gleichzeitig mit der Berechnung der kumulativen Summe auch deren aktueller Wert mit dem resultierenden Zufallswert verglichen. Sobald er diesen Wert überschreitet, wird das aktuelle Quantil als ausgewählte Aktion verwendet und die Ausführung der Schleifeniterationen unterbrochen.
for(int r = 0; r < count_quants; r++) { prob = probs[shift + r]; sum += prob; if(sum >= rnd || r == (count_quants - 1)) { value = quantiles[shift + r]; break; } }
Jetzt brauchen wir nicht mehr nach dem nächstgelegenen Paar von Quantilen zu suchen, wie wir es vorher getan haben. Wir haben ein ausgewähltes Quantil mit einer bekannten Wahrscheinlichkeit. Wir müssen nur noch den resultierenden Wert aktivieren und den Wert der Entropiekomponente berechnen.
switch(activation) { case 0: outputs[i] = tanh(value); break; case 1: outputs[i] = 1 / (1 + exp(-value)); break; case 2: if(value < 0) outputs[i] = value * 0.01f; else outputs[i] = value; break; default: outputs[i] = value; break; } log_probs[i] = -alphas[i] * log(prob); }
Nachdem wir Änderungen am Kernel vorgenommen haben, werden wir den Code des Hauptprogramms ergänzen. Zunächst werden wir Änderungen an der Klasse CNeuronSoftActorCritic vornehmen. Hier fügen wir einen Puffer für Zufallswerte hinzu. Seine Initialisierung erfolgt in der Init-Methode, ähnlich wie beim Puffer cLogProbs. Ich will mich nicht damit aufhalten. Es muss nicht gespeichert werden, da es bei jedem direkten Durchgang neu gefüllt wird. Daher nehmen wir keine Anpassungen an den Dateiverarbeitungsmethoden vor.
class CNeuronSoftActorCritic : public CNeuronFQF { protected: .......... .......... CBufferFloat cRandomize; .......... .......... };
Wenden wir uns nun der Vorwärtsdurchgangsmethode CNeuronSoftActorCritic::feedForward zu. Hier wird nach einem direkten Durchlauf durch die Elternklasse und die innere Schicht cAlphas eine Schleife nach der Anzahl der Aktionen angeordnet und der Puffer cRandomize mit Zufallswerten gefüllt.
bool CNeuronSoftActorCritic::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!CNeuronFQF::feedForward(NeuronOCL)) return false; if(!cAlphas.FeedForward(GetPointer(cQuantile0), cQuantile2.getOutput())) return false; //--- int actions = cRandomize.Total(); for(int i = 0; i < actions; i++) { float probability = (float)MathRand() / 32767.0f; cRandomize.Update(i, probability); } if(!cRandomize.BufferWrite()) return false;
Die Daten des gefüllten Puffers werden an den Kontextspeicher OpenCL übergeben.
Als Nächstes wird der Kernel in die Ausführungswarteschlange gestellt. Hier müssen wir die dem Kernel hinzugefügten Parameter übertragen.
uint global_work_offset[1] = {0}; uint global_work_size[1] = {Neurons()}; if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_alphas, cAlphas.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_log_probs, cLogProbs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_outputs, getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_probs, cSoftMax.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_quantiles, cQuantile2.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_random, cRandomize.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_SAC_AlphaLogProbs, def_k_sac_alp_count_quants, (int)(cSoftMax.Neurons() / global_work_size[0]))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_SAC_AlphaLogProbs, def_k_sac_alp_activation, (int)activation)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_SAC_AlphaLogProbs, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
So haben wir die Stochastizität der Handlungswahl während der Vorwärtsdurchgang unseres Akteurs implementiert. Es gibt jedoch eine Nuance in Bezug auf den umgekehrten Abschnitt. Der Punkt ist, dass der Rückwärtsdurchlauf den Fehlergradienten auf jedes Entscheidungselement entsprechend seinem Beitrag verteilen sollte. Zuvor wurde ein direkter Durchgang der Elternklasse verwendet, und der Fehlergradient war ähnlich verteilt. Jetzt haben wir in der letzten Phase der Aktionsauswahl Anpassungen vorgenommen. Folglich sollte sich dies auch in der Verteilung des Fehlergradienten widerspiegeln.
Die Erzeugung von Zufallswerten liegt außerhalb des Rahmens unseres Modells, und wir werden keinen Gradienten auf sie verteilen. Aber wir sollten die Verteilung des Fehlergradienten nur für die ausgewählte Aktion festlegen. Schließlich hatte keiner der anderen Werte einen Einfluss auf die Handlung des Akteurs. Daher ist ihr Fehlergradient „0“.
Anders als bei der direkten Übergabe können wir der Funktionalität keine neue Methode hinzufügen, da der Aufruf der Methode der übergeordneten Klasse die gespeicherten Farbverläufe überschreiben würde. Daher müssen wir die Methode zur Verteilung der Fehlergradienten auf die Elemente unserer neuronalen Schicht völlig neu definieren.
Wie immer beginnen wir mit der Erstellung des Kernels SAC_OutputGradient. Die Struktur der Kernel-Parameter wird Sie an den FQF_OutputGradient-Kernel der übergeordneten Klasse erinnern. Wir haben sie als Grundlage genommen und 1 Puffer und 2 Konstanten hinzugefügt:
- output — Puffer der Vorwärtsdurchgangs-Ergebnisse
- count_quants — Anzahl der Quantile für jede Aktion
- activation — angewandte Aktivierungsfunktion.
__kernel void SAC_OutputGradient(__global float* quantiles, __global float* delta_taus, __global float* output_gr, __global float* quantiles_gr, __global float* taus_gr, __global float* output, const int count_quants, const int activation ) { size_t action = get_global_id(0); int shift = action * count_quants;
Wir werden den Kernel in einem eindimensionalen Aufgabenraum entsprechend der Anzahl der Aktionen starten.
Im Kernelkörper identifizieren wir sofort die zu analysierende Aktion des Akteurs und bestimmen den Offset in den Datenpuffern.
Als Nächstes führen wir eine Schleife durch, in der wir den Durchschnittswert jedes Quantils und die perfekte Aktion aus dem Ergebnispuffer unserer Schicht vergleichen. Es ist jedoch zu beachten, dass die durchschnittlichen Quantilwerte im Originalwert gespeichert werden und die ausgewählte Aktion im Ergebnispuffer den Wert nach der Aktivierungsfunktion enthält. Bevor wir die Werte vergleichen, müssen wir daher eine Aktivierungsfunktion auf den Mittelwert jedes Quantils anwenden.
for(int i = 0; i < count_quants; i++) { float quant = quantiles[shift + i]; switch(activation) { case 0: quant = tanh(quant); break; case 1: quant = 1 / (1 + exp(-quant)); break; case 2: if(quant < 0) quant = quant * 0.01f; break; } if(output[i] == quant) { float gradient = output_gr[action]; quantiles_gr[shift + i] = gradient * delta_taus[shift + i]; taus_gr[shift + i] = gradient * quant; } else { quantiles_gr[shift + i] = 0; taus_gr[shift + i] = 0; } } }
Es sei darauf hingewiesen, dass wir theoretisch die inverse Funktion einmal ausführen und den Wert des Ergebnispuffers vor der Aktivierungsfunktion bestimmen könnten. Aufgrund des Fehlers in der Genauigkeit der Berechnungen werden wir jedoch höchstwahrscheinlich einen Wert erhalten, der zwar nahe am Originalwert liegt, sich aber von diesem unterscheidet. Wir werden gezwungen sein, einen Vergleich mit einer Art von Toleranz anzustellen. Dies wiederum erschwert den Vergleich und verringert die Genauigkeit.
Wenn ein Quantil übereinstimmt, verteilen wir den Fehlergradienten auf den Mittelwert des Quantils und seine Wahrscheinlichkeit. Für die übrigen Quantile und ihre Wahrscheinlichkeiten setzen wir den Gradienten auf „0“.
Nach Abschluss der Schleifenwiederholungen wird der Kernel heruntergefahren.
Wie oben erwähnt, müssen wir auf der Seite des Hauptprogramms die Fehlergradientenverteilungsmethode calcInputGradients komplett neu definieren. Die Methode wurde von der ähnlichen Methode der Elternklasse kopiert. Die Änderungen betrafen nur den über dem Kernel beschriebenen Warteschlangenblock. Daher werde ich jetzt nicht näher auf seine Beschreibung eingehen. Sie finden sie in der beigefügten Datei „..\NeuroNet_DNG\NeuroNet.mqh“.
1.2 Anpassung des Prozesses der Aktualisierung der Zielmodelle
Sie haben vielleicht bemerkt, dass ich in meinen Modellen die Methode Adam bevorzuge, um die Gewichtungsverhältnisse zu aktualisieren. In diesem Zusammenhang kam die Idee auf, diese Methode in die sanfte Aktualisierung der Zielmodelle der Kritiker einzubringen.
Wie Sie sich vielleicht erinnern, ermöglicht der Algorithmus Soft Actor Critic eine sanfte Aktualisierung der Zielmodelle unter Verwendung eines konstanten Verhältnisses im Bereich (0, 1}. Wenn das Verhältnis gleich „1“ ist, werden die Parameter einfach kopiert. „0“ wird nicht angewendet, da das Zielmodell in diesem Fall nicht aktualisiert wird.
Die Verwendung der Adam-Methode ermöglicht es dem Modell, die Verhältnisse für jeden einzelnen trainierten Parameter unabhängig anzupassen. Dies ermöglicht eine schnelle Aktualisierung von Parametern, die in eine Richtung verschoben sind, was bedeutet, dass sich das Zielmodell schneller von den Anfangswerten zur ersten Annäherung verschiebt. Gleichzeitig ermöglicht es die adaptive Methode, die Kopiergeschwindigkeit für multidirektionale Schwingungen zu verringern, wodurch das Rauschen in den Werten der Zielmodelle reduziert wird.
Es sollte jedoch darauf geachtet werden, dass das Risiko besteht, dass die Modelle in der Anfangsphase der Ausbildung unausgewogen werden. Erhebliche Unterschiede in der Geschwindigkeit des Kopierens einzelner Parameter können zu unerwarteten und unvorhersehbaren Ergebnissen führen.
Nachdem ich alle Vor- und Nachteile abgewogen hatte, beschloss ich, die Wirksamkeit dieses Ansatzes in der Praxis zu testen.
Wir führen den Prozess der Modelloptimierung auf der OpenCL-Kontextseite durch. Die aktuellen Werte aller trainierten Modellparameter werden im Kontextspeicher gespeichert. Es ist ganz logisch, dass es für uns profitabler ist, diese Parameter zwischen den trainierten und den Zielmodellen auf der OpenCL-Seite zu übertragen. Dieser Ansatz hat mehrere Vorteile:
- es entfällt das Laden der aktuellen Parameter des trainierten Modells aus dem Kontext in den Hauptspeicher und das anschließende Kopieren der neuen Parameter der Zielmodelle in den Kontextspeicher;
- es können wir mehrere Parameter gleichzeitig in parallelen Datenströmen übertragen.
Erstellen wir den SoftUpdateAdam-Kernel zur Datenübertragung. In den Kernel-Parametern werden Zeiger auf 4 Datenpuffer und 3 von der Methode bereitgestellte Parameter übergeben.
__kernel void SoftUpdateAdam(__global float *target, __global const float *source, __global float *matrix_m, __global float *matrix_v, const float tau, const float b1, const float b2 ) { const int i = get_global_id(0); float m, v, weight;
Wir planen, den Kernel sequentiell für jede neuronale Schicht im eindimensionalen Aufgabenraum entsprechend der Anzahl der aktualisierten Parameter der aktuellen Modellschicht zu starten. Bei dieser Option dient die im Kernelkörper definierte Thread-ID gleichzeitig als Zeiger auf den zu analysierenden Parameter und den Offset in den Datenpuffern.
Hier deklarieren wir auch lokale Variablen, um Zwischendaten zu speichern, und schreiben die Originaldaten aus den globalen Puffern in diese Variablen.
m = matrix_m[i]; v = matrix_v[i]; weight=target[i];
Die Adam-Methode wurde entwickelt, um die Modellparameter in Richtung des Anti-Gradienten zu aktualisieren. In unserem Fall ist der Fehlergradient die Abweichung der Parameter des Zielmodells von dem trainierten Modell. Da wir den Wert der Parameter in Richtung des Anti-Gradienten anpassen, definieren wir die Abweichung als die Differenz zwischen dem Parameter des trainierten Modells und dem entsprechenden Parameter des trainierten Modells.
float g = source[i] - weight; m = b1 * m + (1 - b1) * g; v = b2 * v + (1 - b2) * pow(g, 2);
Außerdem bestimmen wir sofort den exponentiellen Durchschnitt des Fehlergradienten seines quadratischen Wertes.
Als Nächstes bestimmen wir den erforderlichen Parameter-Offset und speichern das entsprechende Element im globalen Datenpuffer.
float delta = tau * m / (v != 0.0f ? sqrt(v) : 1.0f); if(delta * g > 0) target[i] = clamp(weight + delta, -MAX_WEIGHT, MAX_WEIGHT);
Am Ende der Kerneloperationen speichern wir die Durchschnittswerte des Fehlergradienten und seines Quadrats in globalen Datenpuffern. Wir werden sie in den folgenden Iterationen der Aktualisierung der Parameter benötigen.
matrix_m[i] = m; matrix_v[i] = v; }
Nachdem wir den Kernel erstellt haben, müssen wir den Prozess seines Aufrufs auf der Seite des Hauptprogramms organisieren. Hier haben wir 2 Möglichkeiten:
- das Erstellen einer neuen Methode
- die Aktualisierung einer zuvor erstellten Methode.
In diesem Artikel schlage ich das Erstellen einer neuen Methode vor, die wir auf der Ebene der Basisklasse der neuronalen Schicht CNeuronBaseOCL::WeightsUpdateAdam erstellen werden. In den Methodenparametern übergeben wir einen Zeiger auf die neuronale Schicht des trainierten Modells und den Aktualisierungskoeffizienten, ähnlich wie bei der zuvor erstellten Soft Update des Zielmodells. Wir werden die Hyperparameter der Adam-Methode verwenden, um die Standardmodelle zu aktualisieren.
bool CNeuronBaseOCL::WeightsUpdateAdam(CNeuronBaseOCL *source, float tau) { if(!OpenCL || !source) return false; if(Type() != source.Type()) return false; if(!Weights || Weights.Total() == 0) return true; if(!source.Weights || Weights.Total() != source.Weights.Total()) return false;
Der Block von Steuerelementen wird im Körper der Methode implementiert. Hier prüfen wir die Relevanz von Zeigern auf die verwendeten Objekte. Wir überprüfen auch die Übereinstimmung zwischen dem Typ der aktuellen neuronalen Schicht und dem resultierenden Zeiger.
Nach erfolgreicher Übergabe des Kontrollblocks übergeben wir Parameter an den Kernel und stellen ihn in die Ausführungswarteschlange.
Bitte beachten Sie, dass die Adam-Methode die Erstellung von zwei zusätzlichen Datenpuffern erfordert. Wir erinnern uns aber daran, dass wir in jedem Modell ähnliche Puffer anlegen, um die trainierbaren Parameter des Modells zu aktualisieren. In diesem Fall handelt es sich um das Zielmodell, bei dem die Parameter aktualisiert werden. Seine Optimierung erfolgt durch die periodische Übertragung von Daten des trainierten Modells. Mit anderen Worten: Wir haben ein Modell mit eingeschränkter Funktionalität. Gleichzeitig haben wir keine separaten Objekttypen für die Zielmodelle erstellt, sondern bereits erstellte Objekte für voll funktionsfähige Modelle verwendet und alle erforderlichen Objekte und Puffer erstellt. Dies kann als ineffiziente Nutzung von Speicherressourcen angesehen werden. Wir haben uns aber bewusst für diesen Schritt entschieden, um die Modelle zu vereinheitlichen. Jetzt haben wir Puffer für Zielmodelle erstellt und nicht verwendet. Wir werden sie verwenden, um die Parameter zu aktualisieren.
uint global_work_offset[1] = {0}; uint global_work_size[1] = {Weights.Total()}; ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdateAdam, def_k_sua_target, getWeightsIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdateAdam, def_k_sua_source, source.getWeightsIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdateAdam, def_k_sua_matrix_m, getFirstMomentumIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdateAdam, def_k_sua_matrix_v, getSecondMomentumIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_SoftUpdateAdam, def_k_sua_tau, (float)tau)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_SoftUpdateAdam, def_k_sua_b1, (float)b1)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_SoftUpdateAdam, def_k_sua_b2, (float)b2)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_SoftUpdateAdam, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
Vergessen Sie nicht, die Korrektheit der Vorgänge in jeder Phase zu kontrollieren. Beenden Sie die Methode nach erfolgreichem Abschluss aller Iterationen.
Nachdem wir eine Methode erstellt haben, müssen wir ihren Aufruf durchdenken und organisieren. Ich wollte einen Ansatz finden, der den Aufruf so einfach wie möglich macht, mit einer minimalen Anzahl von Änderungen an der Gesamtstruktur der Modelle. Ich habe den Eindruck, dass ich einen Kompromiss gefunden habe. Ich habe keinen separaten Zweig für den Aufruf einer Methode aus einem externen Programm durch die Dispatcher-Klasse des Modells und das dynamische Array der neuronalen Schichten erstellt. Stattdessen habe ich in der zuvor erstellten Methode Soft Update CNeuronBaseOCL::WeightsUpdate eine Prüfung für die Methode zur Aktualisierung der trainierten Modellparameter eingerichtet, die vom Nutzer bei der Beschreibung der Modellarchitektur für jede neuronale Schicht angegeben wird. Wenn der Nutzer die Adam-Methode zur Aktualisierung der Modellparameter angegeben hat, leiten wir den Arbeitsablauf einfach zur Ausführung unserer neuen Methode um. Für andere Methoden der Parameteraktualisierung verwenden wir das klassische Soft-Update.
bool CNeuronBaseOCL::WeightsUpdate(CNeuronBaseOCL *source, float tau) { if(optimization == ADAM) return WeightsUpdateAdam(source, tau); //--- ........ ........ }
Dieser Ansatz garantiert unter anderem, dass wir über die notwendigen Datenpuffer verfügen.
1.3 Änderungen an der Quelldatenstruktur vornehmen
Ich habe auch auf die Struktur der Quelldaten berücksichtigt. Wie Sie wissen, besteht die Beschreibung der einzelnen historischen Datenbalken aus 12 Elementen:
- Differenz zwischen Eröffnungs- und Schlusskurs
- Differenz zwischen Eröffnungs- und Höchstpreisen
- Unterschied zwischen Eröffnungs- und Mindestpreisen
- Stunde der Kerze
- Wochentag
- Monat
- 5 Indikatorparameter.
State.Add((float)Rates[b].close - open); State.Add((float)Rates[b].high - open); State.Add((float)Rates[b].low - open); State.Add((float)Rates[b].tick_volume / 1000.0f); State.Add((float)sTime.hour); State.Add((float)sTime.day_of_week); State.Add((float)sTime.mon); State.Add(rsi); State.Add(cci); State.Add(atr); State.Add(macd); State.Add(sign);
In diesem Datensatz wurde meine Aufmerksamkeit auf die Zeitstempel gelenkt. Die Bewertung der Zeitkomponente ist von großem Wert für das Verständnis der Saisonalität und des unterschiedlichen Verhaltens von Währungen in verschiedenen Phasen. Aber wie wichtig ist ihre Vorkommen für jede Kerze? Ich persönlich bin der Meinung, dass ein Satz von Zeitstempeln ausreicht, um eine umfassende „Momentaufnahme“ der aktuellen Marktlage zu erstellen. Bisher waren wir bei der Verwendung eines Puffers von Quelldaten gezwungen, diese Daten zu wiederholen, um die Struktur der Beschreibung jeder Kerze zu erhalten. Wenn unsere Modelle nun über 2 Quellen von Ausgangsdaten verfügen, können wir Zeitstempel in den Puffer für die Beschreibung des Kontostands eingeben. Hier belassen wir es bei historischen Daten einer Momentaufnahme der Marktsituation. Auf diese Weise reduzieren wir das Gesamtvolumen der analysierten Daten, ohne dass die Informationskapazität verloren geht. Dadurch verringern wir die Anzahl der durchgeführten Operationen und erhöhen gleichzeitig die Leistung unseres Modells.
Außerdem haben wir die Darstellung von Zeitstempeln für unser Modell geändert. Ich möchte Sie daran erinnern, dass wir relative Parameter verwenden, um den Zustand des Kontos zu beschreiben. Dies ermöglicht es uns, sie in eine vergleichbare und teilweise normalisierte Form zu bringen. Wir möchten eine normalisierte Ansicht der Zeitstempel haben. Gleichzeitig ist es wichtig, Informationen über die Saisonalität der Prozesse zu erhalten. In solchen Fällen verwendet man häufig die Sinus- und Kosinusfunktionen. Die Graphen dieser Funktionen sind kontinuierlich und zyklisch. Die Länge des Funktionszyklus ist bekannt und gleich 2π.
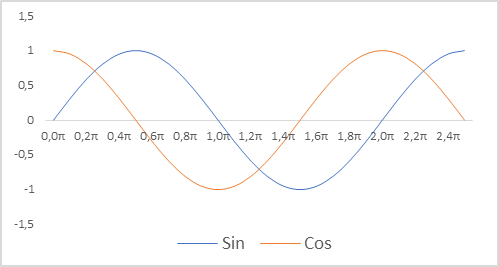
Um den Zeitstempel zu normalisieren und die zyklische Natur zu berücksichtigen, müssen wir das tun:
- Wir dividieren die aktuelle Zeit durch die Periodengröße.
- Wir multiplizieren den resultierenden Wert mit der Konstante „2π“.
- Wir berechnen den Funktionswert (sin oder cos).
- Wir fügen den resultierenden Wert zum Puffer hinzu.
Bei meiner Implementierung habe ich die Zeiträume Jahr, Monat, Woche und Tag verwendet.
double x = (double)Rates[0].time / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
Vergessen Sie auch nicht, die Größenkonstanten für die Beschreibung einer Kerze und den Kontostand zu ändern. Ihre Werte werden sich in der Architektur unseres Modells widerspiegeln, und die Größen der Felder dienen als Puffer für die Beschreibung der Trajektorien der gesammelten Erfahrungen.
#define BarDescr 9 //Elements for 1 bar description #define AccountDescr 12 //Account description
Es sei darauf hingewiesen, dass die Aufbereitung der Quelldaten und insbesondere die Normalisierung der Zeitstempel nichts mit dem Aufbau des Modells selbst und seiner Architektur zu tun hat. Sie wird auf der Seite eines externen Programms durchgeführt. Die Qualität der Quelldatenaufbereitung wirkt sich jedoch stark auf den Modellbildungsprozess und das Ergebnis aus.
2. Modellhafte Ausbildung
Nachdem Sie konstruktive Änderungen am Modell vorgenommen haben, ist es an der Zeit, zur Ausbildung überzugehen. In der ersten Phase verwenden wir den EA „..\SoftActorCritic\Research.mq5“, um mit der Umgebung zu interagieren und Daten für den Trainingssatz zu sammeln.
Im angegebenen EA nehmen wir die oben beschriebenen Änderungen vor, um Zeitstempel aus dem Umgebungszustandspuffer in den Kontostandspuffer zu übertragen.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- ......... ......... //--- float atr = 0; for(int b = 0; b < (int)HistoryBars; b++) { float open = (float)Rates[b].open; float rsi = (float)RSI.Main(b); float cci = (float)CCI.Main(b); atr = (float)ATR.Main(b); float macd = (float)MACD.Main(b); float sign = (float)MACD.Signal(b); if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE) continue; //--- int shift = b * BarDescr; sState.state[shift] = (float)(Rates[b].close - open); sState.state[shift + 1] = (float)(Rates[b].high - open); sState.state[shift + 2] = (float)(Rates[b].low - open); sState.state[shift + 3] = (float)(Rates[b].tick_volume / 1000.0f); sState.state[shift + 4] = rsi; sState.state[shift + 5] = cci; sState.state[shift + 6] = atr; sState.state[shift + 7] = macd; sState.state[shift + 8] = sign; } State.AssignArray(sState.state); //--- ........ ........ //--- Account.Clear(); Account.Add((float)((sState.account[0] - PrevBalance) / PrevBalance)); Account.Add((float)(sState.account[1] / PrevBalance)); Account.Add((float)((sState.account[1] - PrevEquity) / PrevEquity)); Account.Add(sState.account[2]); Account.Add(sState.account[3]); Account.Add((float)(sState.account[4] / PrevBalance)); Account.Add((float)(sState.account[5] / PrevBalance)); Account.Add((float)(sState.account[6] / PrevBalance)); double x = (double)Rates[0].time / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); //--- if(Account.GetIndex() >= 0) if(!Account.BufferWrite()) return;
Darüber hinaus habe ich beschlossen, die Absicherungsgeschäfte aufzugeben. Ein Handelsgeschäft wird nur für die Differenz der Mengen in Richtung des größeren eröffnet. Zu diesem Zweck überprüfen wir die prognostizierten Transaktionsvolumina und reduzieren deren Umfang.
........ ........ //--- vector<float> temp; Actor.getResults(temp); float delta = MathAbs(ActorResult - temp).Sum(); ActorResult = temp; //--- if(temp[0] >= temp[3]) { temp[0] -= temp[3]; temp[3] = 0; } else { temp[3] -= temp[0]; temp[0] = 0; }
Außerdem habe ich auf die Belohnung geachtet. Bei der Bildung des Hauptteils der Belohnung haben wir die relative Veränderung des Kontosaldos verwendet. Sein Wert ist sehr gering und liegt deutlich unter 1. Gleichzeitig schwankte der Wert der Entropiekomponente der Belohnung in der ersten Trainingsphase im Bereich von 8-12. Es ist offensichtlich, dass die Entropiekomponente unvergleichlich groß ist. Um diese Wertlücke zu kompensieren, habe ich sie durch den Restbetrag geteilt, so wie es auch mit der Veränderung bei der Bildung des Zielteils der Belohnung gemacht wird. Außerdem habe ich zusätzlich das Reduktionsverhältnis LogProbMultiplier eingeführt.
........ ........ //--- float reward = Account[0]; if((buy_value + sell_value) == 0) reward -= (float)(atr / PrevBalance); for(ulong i = 0; i < temp.Size(); i++) sState.action[i] = temp[i]; if(Actor.GetLogProbs(temp)) reward += LogProbMultiplier * temp.Sum() / (float)PrevBalance; if(!Base.Add(sState, reward)) ExpertRemove(); }
Nachdem ich diese Änderungen vorgenommen hatte, begann ich mit der ersten Phase der Sammlung von Trainingsdaten. Zu diesem Zweck habe ich historische Daten zu EURUSD H1 verwendet. Die Datenerhebung wurde im Strategietester für die ersten 5 Monate des Jahres 2023 im Modus der vollständigen Aufzählung der Parameter durchgeführt. Das Startkapital beträgt 10.000 USD. In dieser Phase habe ich eine Stichprobendatenbank mit 200 Durchläufen zusammengestellt, die uns mehr als 0,5 Millionen Datensätze „Zustand“→„Aktion"“→„Neuer Zustand“→„Belohnung“ über den angegebenen Zeitraum liefert.
Wie Sie sich vielleicht erinnern, haben wir in diesem Stadium noch kein vortrainiertes Modell. Bei jedem Durchlauf erzeugt der EA ein neues Modell und füllt es mit Zufallsparametern. Während des Durchgangs durch die Geschichte wird kein Modelltraining durchgeführt. Wir erhalten also 200 völlig zufällige und unabhängige Durchgänge. Keiner von ihnen wies einen Gewinn aus.
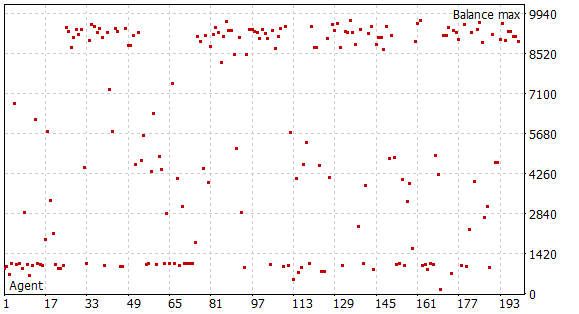
Der eigentliche Prozess des Trainings des Modells ist in der EA „..\SoftActorCritic\Study.mq5“ organisiert. Auch hier haben wir einige punktuelle Änderungen vorgenommen.
Zunächst haben wir den Prozess der Erstellung des Vektors zur Beschreibung des Kontostandes dahingehend geändert, dass wir Zeitstempel hinzugefügt haben, ähnlich wie bei dem oben beschriebenen Ansatz in der Umweltforschung EA.
Darüber hinaus haben wir die Bildung der Zielbelohnung in Bezug auf die Entropiekomponente angepasst. Der Ansatz sollte in allen drei EAs derselbe sein.
void Train(void) { ......... ......... //--- for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { ......... ......... Account.Clear(); Account.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i + 1].account[2]); Account.Add(Buffer[tr].States[i + 1].account[3]); Account.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance); double x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); //--- ......... ......... //--- TargetCritic1.getResults(Result); float reward = Result[0]; TargetCritic2.getResults(Result); reward = Buffer[tr].Revards[i] + DiscFactor * (MathMin(reward, Result[0]) - Buffer[tr].Revards[i + 1] + LogProbMultiplier * log_prob.Sum() / (float)PrevBalance);
Wir haben dann das Training von Actor (Akteur) und Critic (Kritiker) getrennt. Wie zuvor wechseln wir Critic1 und Critic2 in den geraden und ungeraden Trainingsiterationen ab. Wenn wir nun einen Actor trainieren, deaktivieren wir die Trainingsfunktion des verwendeten Critic. Er gibt nur den Fehlergradienten an Actor weiter. In diesem Fall werden die kritischen Parameter nicht aktualisiert. Unser Ziel ist es also, einen objektiven Kritiker für die Belohnungen der realen Umgebung zu trainieren.
........ ........ //--- if((iter % 2) == 0) { if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) || !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } Critic1.getResults(Result); Actor.GetLogProbs(log_prob); Result.Update(0, reward); Critic1.TrainMode(false); if(!Critic1.backProp(Result, GetPointer(Actor)) || !Critic1.AlphasGradient(GetPointer(Actor)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Critic1.TrainMode(true); break; } Critic1.TrainMode(true);
Darüber hinaus schließen wir beim Training eines Kritikers die Entropiekomponente von der Zielbelohnung aus, da wir einen objektiven Kritiker benötigen, während die Funktion der Entropiekomponente darin besteht, den Actor zur Erkundung der Umgebung anzuregen.
Result.Update(0, reward - LogProbMultiplier * log_prob.Sum() / (float)PrevBalance); if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } //--- Update Target Nets TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau); }
Nach der Aktualisierung der kritischen Parameter aktualisieren wir das Zielmodell von nur einem Kritiker. Ansonsten bleibt der EA-Code unverändert, und Sie können ihn im Anhang sehen.
Nachdem wir die Änderungen vorgenommen haben, beginnen wir das Modelltraining mit einem Zyklus von 100.000 Iterationen (Standardparameter). In diesem Stadium werden die Modelle Actor und 2 Critics gebildet. Auch ihre Erstausbildung wird durchgeführt.
Sie sollten von der ersten Runde des Modelltrainings keine signifikanten Ergebnisse erwarten. Hierfür gibt es eine Reihe von Gründen. Die vollständige Anzahl der Iterationen deckt nur 1/5 unserer Beispielbasis ab. Sie kann nicht als vollständig bezeichnet werden. Es gibt keine einzige gewinnbringende Passage darin, die das Modell lernen könnte.
Nach Abschluss der ersten Phase des Modelltrainings habe ich die zuvor gesammelte Beispieldatenbank gelöscht. Meine Logik ist hier ziemlich einfach. Diese Datenbank enthält unabhängige Zufallsdurchläufe. Die Belohnungen enthalten die unbekannte Entropiekomponente. Ich gehe davon aus, dass bei einem untrainierten Modell alle Aktionen gleich wahrscheinlich sind. In jedem Fall sind sie aber nicht mit der Wahrscheinlichkeitsverteilung unseres Modells vergleichbar. Daher löschen wir die zuvor gesammelte Datenbank mit Beispielen und erstellen eine neue.
Gleichzeitig wiederholen wir den Prozess des Sammelns einer Trainingsstichprobe und führen die Optimierung des Umweltforschungs-EA mit einer vollständigen Parametersuche erneut durch. Nur dieses Mal verschieben wir den Wert der Agenten, die iteriert werden. Dieser einfache Trick ist notwendig, um das Laden von Daten aus dem vorherigen Optimierungscache zu vermeiden.
Der Hauptunterschied zwischen der neuen Beispielbasis besteht darin, dass unser vorab trainiertes Modell während der Umwelterkundung verwendet wurde. Die Vielfalt der Handlungen des Agenten ist auf die Stochastizität der Politik des Akteurs zurückzuführen. Und alle abgeschlossenen Aktionen liegen innerhalb der gelernten Wahrscheinlichkeitsverteilung unseres Modells. In dieser Phase sammeln wir zum letzten Mal alle Ausweise unserer Agenten ein.
Nach dem Sammeln einer neuen Beispieldatenbank führen wir das Modelltraining EA „..\SoftActorCritic\Study.mq5“ erneut durch. Dieses Mal erhöhen wir die Anzahl der Trainingsiterationen auf 500.000.
Nach Abschluss des zweiten Zyklus des Trainingsprozesses wenden wir uns dem EA „..\SoftActorCritic\Test.mq5“ zu, um das trainierte Modell zu testen. Wir nehmen Änderungen daran vor, ähnlich wie bei der Umweltforschung EA. Sie finden sie in der Anlage.
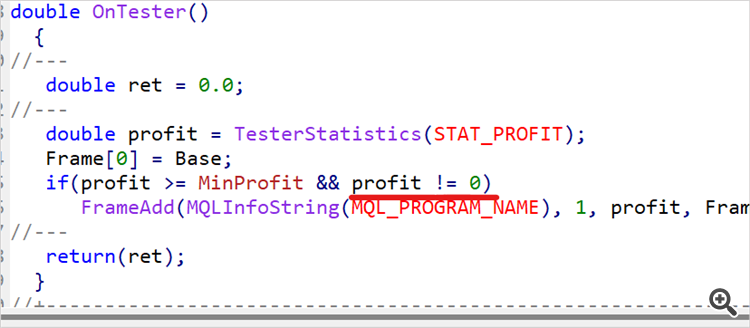
Der Wechsel zur Test-EA bedeutet nicht das Ende des Trainings. Wir lassen den EA mehrmals auf historischen Daten aus dem Trainingszeitraum laufen. In meinem Fall sind das die ersten 5 Monate des Jahres 2023. Ich habe 10 Durchgänge durchgeführt und das ungefähre obere 1/4 oder 1/5 der erzielten Gewinnspanne ermittelt. Kehren wir zum Code des Umweltforschungs-EA zurück und führen eine Beschränkung für die Mindestrentabilität der in der Beispieldatenbank gespeicherten Durchgänge ein.
input double MinProfit = 10;
double OnTester() { //--- double ret = 0.0; //--- double profit = TesterStatistics(STAT_PROFIT); Frame[0] = Base; if(profit >= MinProfit && profit != 0) FrameAdd(MQLInfoString(MQL_PROGRAM_NAME), 1, profit, Frame); //--- return(ret); }
Daher bemühen wir uns, nur die besten Passagen auszuwählen und unseren Actor darauf zu trainieren, die optimale Strategie zu verwenden.
Wir haben den Mindestrentabilitätsindikator bewusst in die externen Parameter aufgenommen, da wir die Messlatte beim Training des Modells schrittweise anheben werden.
Nach den Änderungen setzen wir das zuvor ermittelte Mindestrentabilitätsniveau fest und führen weitere 100 Durchläufe im Optimierungsmodus des Strategietesters mit Trainingsdaten durch.
Wir wiederholen den Prozess der Modellschulung so lange, bis die gewünschten Ergebnisse erzielt werden oder die Obergrenze der Modellfähigkeiten erreicht ist (der nächste Schulungszyklus ändert nichts an der Rentabilität). Dies kann auch bei einzelnen Durchläufen der EA-Prüfung festgestellt werden. In diesem Fall werden trotz der Stochastizität der Politik des Akteurs mehrere perfekte Durchläufe zu fast identischen Ergebnissen führen. Dies ist ein Beweis dafür, dass das Modell die Wahrscheinlichkeit individueller Handlungen in den relevanten Zuständen maximiert hat. Wir erhalten den Effekt einer deterministischen Strategie. Dieses Ergebnis ist nicht immer ein Nachteil. Eine stabile und deterministische Strategie kann bei einigen Aufgaben vorzuziehen sein, insbesondere wenn deterministische Aktionen zu guten Ergebnissen führen.
3. Test
Nach etwa 15 Iterationen, in denen ich die Beispieldatenbank aktualisierte, das Modell trainierte, mit der Trainingsstichprobe testete, die Mindestprofitabilitätsgrenze anhob und die Beispieldatenbank regelmäßig auffüllte, konnte ich ein Modell entwickeln, das auf dem Trainingsbereich der historischen Daten durchgängig Profit erzielt.
In der nächsten Phase werden die Fähigkeiten des trainierten Modells außerhalb des Trainingssatzes an neuen Daten getestet. Ich habe die Leistung des trainierten Modells anhand historischer Daten für Juni 2023 getestet. Wie Sie sehen können, ist dies der Monat nach der Trainingszeit.
Während des Testzeitraums tätigte das Modell nur vier Käufe. Nur einer von ihnen war rentabel. Dies ist wahrscheinlich nicht das Ergebnis, das wir erwartet haben. Aber sehen Sie sich die Saldenkurve an. 3 Verlustgeschäfte führten zu einem Gesamtverlust von 300 USD bei einem Startguthaben von 10.000 USD. Gleichzeitig führte ein profitables Geschäft zu einem Gewinn von mehr als 2000 USD. Daraus ergibt sich für den Monat ein Gewinn von 17,5 %. Der Gewinnfaktor - 6,77, der Erholungsfaktor - 1,32 und der Drawdown - 1,65%.
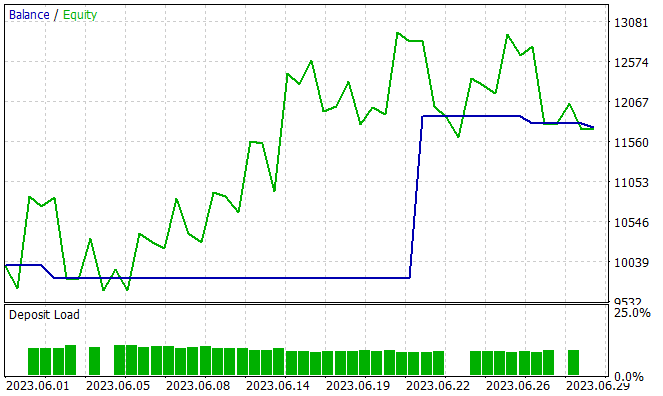
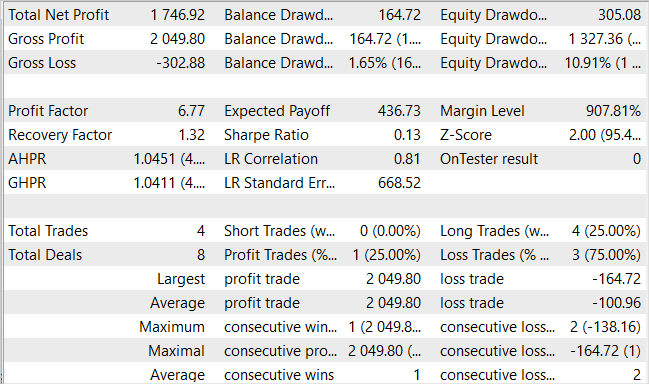
Die geringe Anzahl von Geschäften und ihre Einseitigkeit sind verwirrend. Aber was ist wichtiger? Die Anzahl der Handelsgeschäfte und deren Vielfalt oder die endgültige Veränderung des Saldos?
Schlussfolgerung
In diesem Artikel haben wir unsere Arbeit an der Entwicklung des Algorithmus Soft Actor Critic fortgesetzt. Die Ergänzungen halfen uns, die gewinnbringende Strategie des Akteurs zu trainieren. Es ist schwer zu sagen, wie optimal das resultierende Modell ist. Alles ist relativ.
Die in diesem Artikel vorgeschlagenen Ansätze ermöglichten es, die Rentabilität unseres Modells zu erhöhen, aber sie sind nicht die einzigen und erschöpfenden. Im Forumsthread zum vorigen Artikel hat der Nutzer JimReaper beispielsweise seine Modellarchitektur vorgeschlagen. Auch dies ist eine durchaus realisierbare Option. Ich persönlich habe es noch nicht getestet, aber ich gebe zu, dass es möglich ist, mit der vorgeschlagenen oder einer anderen Architektur einen Gewinn zu erzielen. Es ist sehr wahrscheinlich, dass die Hinzufügung neuer Daten für die Analyse des Modells dessen Effizienz verbessern wird. Ich ermutige immer zur Erkundung und zu neuen Forschungen. Bei der Entwicklung und Optimierung von Modellen im Bereich des verstärkenden Lernens (wie auch in anderen Bereichen des maschinellen Lernens) sind das Erforschen und Experimentieren mit verschiedenen Architekturen, Hyperparametern und neuen Daten Schlüsselelemente, die zur Modelloptimierung und -verbesserung führen können.
Links
- Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor
- Soft Actor-Critic Algorithms and Applications
- Neuronale Netze leicht gemacht (Teil 49): Soft Actor-Critic
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Beispielsammlung EA |
| 2 | Study.mq5 | Expert Advisor | Trainings-EA des Agenten |
| 3 | Test.mq5 | Expert Advisor | Test-EA des Modells |
| 4 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 5 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 6 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/12998
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Theoretisch ist das möglich, aber es hängt alles von den Ressourcen ab. Wir sprechen zum Beispiel von einer TP-Größe von 1000 Punkten. Im Konzept eines kontinuierlichen Aktionsraums sind das 1000 Varianten. Selbst wenn wir in 10er-Schritten vorgehen, sind das 100 Varianten. Lassen Sie die gleiche Anzahl von SLs oder sogar die Hälfte von ihnen (50 Varianten). Fügen Sie mindestens 5 Varianten des Handelsvolumens hinzu und wir erhalten 100 * 50 * 5 = 25000 Varianten. Multiplizieren Sie mit 2 (Kauf / Verkauf) - 50 000 Varianten für eine Kerze. Multiplizieren Sie mit der Länge der Trajektorie und Sie erhalten die Anzahl der Trajektorien, um den gesamten möglichen Raum abzudecken.
Beim schrittweisen Lernen werden Trajektorien in der unmittelbaren Umgebung der Aktionen des aktuellen Akteurs ausgewählt. So grenzen wir das Untersuchungsgebiet ein. Und wir untersuchen nicht alle möglichen Varianten, sondern nur einen kleinen Bereich mit der Suche nach Varianten zur Verbesserung der aktuellen Strategie. Nach einem kleinen "Tuning" der aktuellen Strategie sammeln wir neue Daten in dem Bereich, in den uns diese Verbesserungen geführt haben, und bestimmen den weiteren Bewegungsvektor.
Dies kann an die Suche nach einem Ausweg in einem unbekannten Labyrinth erinnern. Oder an den Weg eines Touristen, der die Straße entlang läuft und Passanten nach dem Weg fragt.
Aha. Ich danke Ihnen.
Mir ist aufgefallen, dass bei der Sammlung Research.mqh die Ergebnisse irgendwie in Gruppen mit einem sehr engen Gleichgewicht in der Gruppe gebildet werden. Und es scheint, als ob es in Research.mqh einen gewissen Fortschritt gibt (positive Gruppen von Ergebnissen begannen häufiger zu erscheinen oder so). Aber bei Test.mqh scheint es überhaupt keinen Fortschritt zu geben. Es gibt eine gewisse Zufälligkeit und im Allgemeinen endet ein Durchgang häufiger mit einem Minus. Manchmal geht es nach oben und dann nach unten, und manchmal geht es direkt nach unten und bleibt dann stehen. Er scheint auch das Volumen der Eingabe am Ende zu erhöhen. Manchmal handelt er nicht im Minus, sondern nur um die Null herum. Mir ist auch aufgefallen, dass er die Anzahl der Trades ändert - seit 5 Monaten eröffnet er 150 Trades, und jemand eröffnet 500 (ungefähr). Ist das alles normal, was beobachte ich da?
Aha, ich verstehe. Ich danke Ihnen.
Mir ist aufgefallen, dass bei der Sammlung von Research.mqh die Ergebnisse irgendwie in Gruppen mit einem sehr engen Endsaldo in der Gruppe gebildet werden. Und es scheint , als ob es in Research.mqh einige Fortschritte gibt (positive Gruppen von Ergebnissen begannen häufiger zu erscheinen oder so). Aber bei Test.mqh scheint es überhaupt keinen Fortschritt zu geben. Es gibt eine gewisse Zufälligkeit und im Allgemeinen endet ein Durchgang häufiger mit einem Minus. Manchmal geht es nach oben und dann nach unten, und manchmal geht es direkt nach unten und bleibt dann stehen. Er scheint auch das Volumen der Eingabe am Ende zu erhöhen. Manchmal handelt er nicht im Minus, sondern nur um die Null herum. Mir ist auch aufgefallen, dass er die Anzahl der Trades ändert - seit 5 Monaten eröffnet er 150 Trades, und jemand eröffnet 500 (ungefähr). Ist das alles normal, was beobachte ich da?
Die Zufälligkeit ist ein Ergebnis der Stochastik des Akteurs. Je mehr Sie lernen, desto weniger wird sie auftreten. Sie wird vielleicht nicht ganz verschwinden, aber die Ergebnisse werden ähnlich sein.
Die Datenbank mit den Beispielen wird nicht durch Durchläufe ohne Abschlüsse "verstopft". Research.mq5 hat eine Prüfung und speichert solche Durchgänge nicht. Aber es ist gut, dass ein solcher Durchgang von Test.mq5 gespeichert wird . Es gibt eine Strafe für das Fehlen von Deals bei der Generierung des Rewards. Und es sollte dem Modell helfen, aus einer solchen Situation herauszukommen.
Dmitriy Ich habe mehr als 90 Zyklen (Training-Test-Sammlung von Datenbank) gemacht und ich habe immer noch das Modell gibt zufällig. Ich kann sagen, dass von 10 Läufen von Test.mqh 7 Abflüsse 2-3 auf 0 und 1-2 mal für etwa 4-5 Zyklen gibt es einen Lauf im Plus. Sie in dem Artikel angegeben, dass Sie ein positives Ergebnis für 15 Zyklen bekam. Ich verstehe, dass es eine Menge von Zufälligkeiten im System, aber ich verstehe nicht, warum ein solcher Unterschied? Nun, ich verstehe, wenn mein Modell nach 30 Zyklen ein positives Ergebnis liefert, sagen wir 50, dann sind es schon 90 und man kann keinen großen Fortschritt sehen.....
Sind Sie sicher, dass Sie denselben Code gepostet haben, den Sie selbst trainiert haben? Vielleicht haben Sie etwas für Tests korrigiert und versehentlich vergessen und die falsche Version gepostet.....?
Und wenn zum Beispiel der Trainingskoeffizient um eine Stufe erhöht wird, lernt er dann nicht schneller?
Ich verstehe etwas nicht......