MetaTrader 5 / 交易系统
English Русский Español Deutsch 日本語 Português
preview
神经网络变得轻松（第五十部分）：软性扮演者-评价者（模型优化）

神经网络变得轻松（第五十部分）：软性扮演者-评价者（模型优化）

MetaTrader 5 — 交易系统 |
631 18
Dmitriy Gizlyk
Dmitriy Gizlyk

概述

我们继续研究软性扮演者-评论者算法。在上一篇文章中，我们实现了该算法，但未能训练出一个可盈利的模型。今天，我们将研究可能的解决方案。在“模型拖延症，原因和解决方案”一文中已经提过类似的问题。我建议扩展我们在这一领域的知识，并以我们的软性扮演者-评论者模型为例研究新方式。


1. 模型优化

在我们转到直接优化我们构建的模型之前，我要提醒您，软性扮演者-评论者是一种在连续动作空间中随机模型的强化学习算法。这种方法的主要特点是在奖励函数中引入了熵分量。

使用随机扮演者策略可令模型更加灵活，并且能够解决复杂环境中的问题，在这些环境中，某些操作可能不确定或无法定义明确的规则。在处理包含大量噪声的数据时，该策略往往更健壮，因为它考虑到概率分量，并且不受明确规则的约束。

添加熵分量可以鼓励对环境的探索，从而增加低概率动作的奖励。探索和开发之间的平衡由温度比率支配。

在数学形式中，软性扮演者-评论者方法可表述为以下等式。

SAC 数学表述

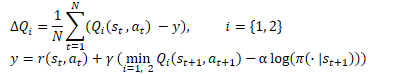
1.1向扮演者政策里增添随机性

在我们的实现中，由于利用 OpenCL 实现的复杂性，我们放弃了使用随机扮演者政策。类似于 TD3，我们将其替换为某些环境中所选动作的随机偏移量。这种方式更易于实现，并允许模型探索环境。但它也有其缺点。

引起注意的第一件事是采样动作与模型学习的分布之间缺乏联系。在某些情况下，当学习的分布比采样区域宽时，这会压缩研究区域。这意味着模型政策很可能不是最优的，而是取决于随机选择的学习起点。毕竟，在初始化新模型时，我们用随机权重填充它。

在其它情况下，采样动作也许会落在学习分布外围。这扩大了研究界域，但与奖励函数的熵分量相冲突。从模型的观点，学习分布之外的动作其概率为零。多亏熵分量，无论其价值如何，它都会收到最大奖励。

在训练过程中，该模型努力寻找可盈利策略，并提升具有最大回报的行动的可能性。同时，减少了利润较低和无利可图的行动的可能性。我们之前使用的简单采样没有考虑到这个因素。来自采样区域的任何动作，它都为我们提供相等的概率。无利可图动作的低概率会产生高熵分量。这扭曲了动作的真正价值，抵消了以前积累的经验，并导致构建出不正确的扮演者政策。

此处仅有一个解决方案 — 构建扮演者的随机模型，并从所学习分布中抽取动作。

我们已经讨论过 OpenCL 关联环境端缺少伪随机数生成器，因此我们将在主程序端使用生成器。

同时，我们记得所学习分布仅在 OpenCL 端可用。它包含在我们模型的内部对象之中。因此，为了安排采样过程，我们必须在主程序和 OpenCL 关联环境之间实现数据传输。这并不依赖于安排流程的所在。

在主程序端组织进程时，我们需要加载分布。这涉及 2 个缓冲区：概率和相应的函数值。

在 OpenCL 关联环境端安排进程时，我们必须传递随机值的缓冲区。稍后将要用它来选择单独的动作。

于此还应该考虑一点 — 所获值的消费者。在操作期间，我们将使用采样值来执行动作，即在主程序端。但在训练期间，我们会将它们传输给 OpenCL 关联环境端的评论者。众所周知，模型训练对减少执行操作的时间提出了最严格的要求。考虑到这一点，决定仅将一个随机值缓冲区传输到 OpenCL 关联环境，并在那里安排进一步的采样过程似乎非常合乎逻辑。

决策已然做出，我们开始实现。首先，我们修改 OpenCL 程序的 SAC_AlphaLogProbs 内核。我们的改动甚至会在一定程度上简化特定内核的算法。

我们在内核的外部参数中添加一个随机值的缓冲区。我们期望收到一组 [0,1] 范围内的随机值，安排在该缓冲区中的采样过程。

__kernel void SAC_AlphaLogProbs(__global float *outputs,
                                __global float *quantiles,
                                __global float *probs,
                                __global float *alphas,
                                __global float *log_probs,
                                __global float *random,
                                const int count_quants,
                                const int activation
                               )
  {
   const int i = get_global_id(0);
   int shift = i * count_quants;
   float prob = 0;
   float value = 0;
   float sum = 0;
   float rnd = random[i];

为了选择一个动作，我们安排了一个循环，枚举所分析动作的所有分位数的概率，并计算它们的累积总和。在循环主体中，在计算累积总和的同时，我们还用结果随机值检查其当前值。超过该值的第一时间，我们就会用当前分位数作为选定动作，并中断循环迭代的执行。

   for(int r = 0; r < count_quants; r++)
     {
      prob = probs[shift + r];
      sum += prob;
      if(sum >= rnd || r == (count_quants - 1))
        {
         value = quantiles[shift + r];
         break;
        }
     }

现在我们不需要再像以前那样寻找最接近的分位数配对。我们有一个已知概率的选定分位数。我们所要做的全部就是激活结果值，并计算熵分量的值。

   switch(activation)
     {
      case 0:
         outputs[i] = tanh(value);
         break;
      case 1:
         outputs[i] = 1 / (1 + exp(-value));
         break;
      case 2:
         if(value < 0)
            outputs[i] = value * 0.01f;
         else
            outputs[i] = value;
         break;
      default:
         outputs[i] = value;
         break;
     }
   log_probs[i] = -alphas[i] * log(prob);
  }

对内核进行修改后，我们将补充主程序的代码。我们将首先对 CNeuronSoftActorCritic 类进行修改。在此，我们为随机值添加一个缓冲区。它的初始化发生在 Init 方法当中，类似于 cLogProbs 缓冲区。我就不多说了。无需保存它，因为每次直接验算都会重新填充它。因此，我们不会对文件处理方法进行任何调整。

class CNeuronSoftActorCritic  :  public CNeuronFQF
  {
protected:
..........
..........
   CBufferFloat         cRandomize;
..........
..........
  };

我们转向前向验算方法 CNeuronSoftActorCritic::feedForward。在此，通过父类和内部 cAlpha 层直接验算之后，我们按动作数量安排一个循环，并用随机值填充 cRandomize 缓冲区。

bool CNeuronSoftActorCritic::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!CNeuronFQF::feedForward(NeuronOCL))
      return false;
   if(!cAlphas.FeedForward(GetPointer(cQuantile0), cQuantile2.getOutput()))
      return false;
//---
   int actions = cRandomize.Total();
   for(int i = 0; i < actions; i++)
     {
      float probability = (float)MathRand() / 32767.0f;
      cRandomize.Update(i, probability);
     }
   if(!cRandomize.BufferWrite())
      return false;

填充缓冲区的数据将传递到 OpenCL 关联环境内存。

接下来，我们实现将内核放入执行队列。在此，我们需要加上把参数传输到内核。

   uint global_work_offset[1] = {0};
   uint global_work_size[1] = {Neurons()};
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_alphas, cAlphas.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_log_probs, cLogProbs.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_outputs, getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_probs, cSoftMax.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_quantiles, 
                                                                            cQuantile2.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SAC_AlphaLogProbs, def_k_sac_alp_random, cRandomize.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_SAC_AlphaLogProbs, def_k_sac_alp_count_quants, 
                                                        (int)(cSoftMax.Neurons() / global_work_size[0])))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_SAC_AlphaLogProbs, def_k_sac_alp_activation, (int)activation))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.Execute(def_k_SAC_AlphaLogProbs, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

因此，我们已经在扮演者的前向验算中实现了动作选择的随机性。但要留意反向验算有一处细微差别。要点是，向后验算应根据其贡献将误差梯度分布在每个决策元素。以前，我们调用父类的直接验，误差梯度的分布类似。现在，我们已经在动作选择的最后阶段进行了调整。故此，这也应反映在误差梯度的分布上。

生成随机值超出了我们模型的范畴，我们不会依据它们分布梯度。但是我们应该只为所选动作安排误差梯度的分布。毕竟，其它值都没有对执行的扮演者动作产生影响。因此，它们的误差梯度为 “0”。

与直接验算不同，我们不能向功能添加新方法，因为调用父类方法将覆盖我们保存的梯度。因此，我们必须彻底重新定义通过神经层元素分布误差梯度的方法。

如常，我们从创建 SAC_OutputGradient 内核开始。内核参数的结构会令您回想起父类的 FQF_OutputGradient 内核。我们以它为基础，添加了 1 个缓冲区和 2 个常量：

  • output — 前向验算结果的缓冲区
  • count_quants — 每个动作的分位数
  • activation — 所应用的激活函数。

__kernel void SAC_OutputGradient(__global float* quantiles,
                                 __global float* delta_taus,
                                 __global float* output_gr,
                                 __global float* quantiles_gr,
                                 __global float* taus_gr,
                                 __global float* output,
                                 const int count_quants,
                                 const int activation
                                )
  {
   size_t action = get_global_id(0);
   int shift = action * count_quants;

我们将根据动作的数量在一维任务空间中启动内核。

在内核主体中，我们立即识别正在分析的扮演者操作，并判定其在数据缓冲区中的偏移量。

接下来，我们安排一个循环，在循环中，我们将取每个分位数的平均值和来自层结果缓冲区中的完美动作进行比较。不过，我们应该记住，平均分位数值存储在原始值当中，结果缓冲区中的选定动作包含激活函数之后的值。因此，在比较数值之前，我们需要针对每个分位数的平均值应用激活函数。

   for(int i = 0; i < count_quants; i++)
     {
      float quant = quantiles[shift + i];
      switch(activation)
        {
         case 0:
            quant = tanh(quant);
            break;
         case 1:
            quant = 1 / (1 + exp(-quant));
            break;
         case 2:
            if(quant < 0)
               quant = quant * 0.01f;
            break;
        }
      if(output[i] == quant)
        {
         float gradient = output_gr[action];
         quantiles_gr[shift + i] = gradient * delta_taus[shift + i];
         taus_gr[shift + i] = gradient * quant;
        }
      else
        {
         quantiles_gr[shift + i] = 0;
         taus_gr[shift + i] = 0;
        }
     }
  }

需要注意的是，理论上我们可以执行一次逆函数，并在激活函数之前检测结果缓冲区的值。不过，由于计算的精度误差，我们很可能会得到一个接近、但与原始值不同的值。我们将被迫按某种容错进行对比。这反过来又会令比较复杂化，并降低准确性。

当分位数匹配时，我们将误差梯度分布到分位数的平均值及其概率。对于剩余的分位数及其概率，我们将梯度设置为 “0”。

循环迭代完成后，我们关停内核。

如上所述，在主程序这端，我们要何地重新定义误差梯度分布方法 calcInputGradients。该方法是从类似的父类方法复制而来的。这些修改仅影响内核上方描述的队列模块。因此，我现在不会详述它。在附件 “..\NeuroNet_DNG\NeuroNet.mqh“ 里可以找到它。

1.2调整目标模型的更新过程

您也许已经注意到，我更喜欢在我的模型中使用 Adam 方法来更新权重比。有关于此，冒出了将这种方法引入评论者目标模型的软性更新的想法。

您也许还记得，软性扮演者-评论者算法采用 (0,1} 范围内的恒定比率提供目标模型的软性更新。如果比率等于 “1”，则只需复制参数即可。不会应用 “0”，因为在这种情况下不会更新目标模型。

使用 Adam 方法允许模型独立调整每个单独训练参数的比率。这样可以快速更新往一个方向偏移的参数，这意味着目标模型将从初始值更快地偏移到第一个近似值。同时，自适应方法可以降低多向振荡的复制速度，从而降低目标模型值的噪声。

不过，应当注意模型在训练初始阶段变得不平衡的风险。复制单个参数的速度存在显著差异，会导致意外和不可预测的结果。

在评估了所有利弊之后，我决定在实践中测试这种方式的有效性。

我们在 OpenCL 关联环端执行模型优化过程。所有经过训练的模型参数的当前值都存储在关联环境内存之中。十分合乎逻辑的是，在 OpenCL 端，已训练模型和目标模型之间传输这些参数对我们来说更有好处。这种方式具有多项优点：

  • 我们剔除了从关联环境加载训练模型的当前参数到主内存，以及随后将目标模型的新参数复制到关联环境内存的过程；
  • 我们可以在并行数据流中并发传输若干个参数。

我们创建 SoftUpdateAdam 内核来传输数据。在内核参数中，我们将传递由该方法提供的指向 4 个数据缓冲区的指针和 3 个参数。

__kernel void SoftUpdateAdam(__global float *target,
                             __global const float *source,
                             __global float *matrix_m,
                             __global float *matrix_v,
                             const float tau,
                             const float b1,
                             const float b2
                            )
  {
   const int i = get_global_id(0);
   float m, v, weight;

我们计划根据当前模型层更新的参数数量，在一维任务空间中依次启动每个神经层的内核。在此选项中，内核主体中定义的线程 ID 同时当作指向正在分析的参数，及其在数据缓冲区中的偏移量。

在此，我们还声明局部变量来存储中间数据，并将全局缓冲区中的原始数据写入其中。

   m = matrix_m[i];
   v = matrix_v[i];
   weight=target[i];

开发 Adam 方法是为了往反梯度更新模型参数。在我们的例子中，误差梯度将是目标模型的参数与训练模型的参数的偏差。由于我们把参数值往反梯度调整，因此我们将偏差定义为训练模型的参数与训练模型相应参数之间的差值。

   float g = source[i] - weight;
   m = b1 * m + (1 - b1) * g;
   v = b2 * v + (1 - b2) * pow(g, 2);

此外，我们立即判定其二次值的误差梯度的指数平均值。

接下来，我们检测所需参数的偏移量，并将其相应的元素存储在全局数据缓冲区之中。

   float delta = tau * m / (v != 0.0f ? sqrt(v) : 1.0f);
   if(delta * g > 0)
      target[i] = clamp(weight + delta, -MAX_WEIGHT, MAX_WEIGHT);

在内核操作结束时，我们将误差梯度及其平方的平均值保存到全局数据缓冲区之中。在更新参数的后续迭代中，我们会需要它们。

   matrix_m[i] = m;
   matrix_v[i] = v;
  }

内核创建之后，我们必须在主程序的一端安排调用它的过程。此处，我们有 2 个选项：

  • 创建新方法
  • 更新以前创建的方法。

在本文中，我建议创建一个新方法，我们将在 CNeuronBaseOCL::WeightsUpdateAdam 神经层的基类层面创建该方法。在方法参数中，我们将传递指向训练模型神经层的指针和更新系数，类似于之前创建的目标模型的软更新方法。我们将用指定 Adam 方法的超参数来更新默认模型。

bool CNeuronBaseOCL::WeightsUpdateAdam(CNeuronBaseOCL *source, float tau)
  {
   if(!OpenCL || !source)
      return false;
   if(Type() != source.Type())
      return false;
   if(!Weights || Weights.Total() == 0)
      return true;
   if(!source.Weights || Weights.Total() != source.Weights.Total())
      return false;

控件模块将在方法主体中实现。在此，我们检查指针与正在使用的对象的相关性。我们还要检查当前神经层的类型与生成的指针之间的对应关系。

成功通过控制模块后，我们将参数传输到内核，并放入执行队列之中。

请注意，Adam 方法需要创建两个额外的数据缓冲区。但要记住，我们在每个模型中创建了类似的缓冲区，来更新模型的可训练参数。在本例中，我们正在与目标模型打交道，在其中参数会被更新。它的优化是通过定期从训练模型传输数据来运作的。换言之，我们所拥有的模型功能有限。同时，我们没有为目标模型创建单独的对象类型，而是将先前创建的那个当作全功能模型，并创建所有必要的对象和缓冲区。这可看出是内存资源的低效使用。但我们有意识地迈出了这一步，以便统一模型。现在我们已有创建好的，且未使用的目标模型缓冲区。我们将用它们来更新参数。

   uint global_work_offset[1] = {0};
   uint global_work_size[1] = {Weights.Total()};
   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdateAdam, def_k_sua_target, getWeightsIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdateAdam, def_k_sua_source, source.getWeightsIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdateAdam, def_k_sua_matrix_m, getFirstMomentumIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdateAdam, def_k_sua_matrix_v, getSecondMomentumIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_SoftUpdateAdam, def_k_sua_tau, (float)tau))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_SoftUpdateAdam, def_k_sua_b1, (float)b1))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_SoftUpdateAdam, def_k_sua_b2, (float)b2))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.Execute(def_k_SoftUpdateAdam, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

不要忘记在每个阶段监控操作的正确性。所有迭代成功完成后该方法结束。

创建方法后，我们需要仔细思考，并安排它的调用。我想找到一种方式，能尽可能简单地调用它，同时针对模型的整体结构修改最少。在我看来，我已找到了一个折衷方案。我没有创建一个单独的分支，来通过模型的调度程序类和神经层的动态数组从外部程序调用方法。代之，我去之前创建的 CNeuronBaseOCL::WeightsUpdate 软更新方法，并针对更新训练模型参数的方法设置一处检查，该参数由用户在描述模型架构时为每个神经层指定。如果用户指定了 Adam 方法来更新模型参数，我们只需重定向工作流即可执行新方法。对于其它参数更新方法，我们使用经典的软更新。

bool CNeuronBaseOCL::WeightsUpdate(CNeuronBaseOCL *source, float tau)
  {
   if(optimization == ADAM)
      return WeightsUpdateAdam(source, tau);
//---
........
........
  }

无关它事，该方式保证了我们得到必要的数据缓冲区。

1.3修改源数据结构

我还关注到源数据结构。如您所知，每个历史数据柱线的定义由 12 个元素组成：

  • 开盘价和收盘价之间的差值
  • 开盘价和最高价之间的差值
  • 开盘价和最低价之间的差值
  • 蜡烛时钟
  • 工作日
  • 月份
  • 5 个指标参数。

      State.Add((float)Rates[b].close - open);
      State.Add((float)Rates[b].high - open);
      State.Add((float)Rates[b].low - open);
      State.Add((float)Rates[b].tick_volume / 1000.0f);
      State.Add((float)sTime.hour);
      State.Add((float)sTime.day_of_week);
      State.Add((float)sTime.mon);
      State.Add(rsi);
      State.Add(cci);
      State.Add(atr);
      State.Add(macd);
      State.Add(sign);

在这个数据集中，我的注意力被时间戳所吸引。评估时间分量对于理解季节性，和货币在不同时段的不同行为具有重要价值。但是，它们的存在对每根蜡烛有多重要？我个人观点是，一组时间戳足以形成市场当前状态的整体“快照”。以前，当使用一个源数据缓冲区时，我们被迫重复这些数据，以便保留每根蜡烛的定义结构。现在，当我们的模型有 2 个初始数据源时，我们可以将时间戳放入帐户状态定义缓冲区当中。在此，我们只留下市场状况历史数据的快照。以这种方式，我们可以在不损失信息容量的情况下减少所分析数据的总量。由此，我们减少了需执行操作的数量，同时提高了模型的性能。

此外，我们还修改了模型的时间戳表示。我要提醒您，我们使用相对参数来描述帐户的状态。这令我们能够将它们转换为可比较、且部分常规化的形式。我们希望有一个常规化的时间戳视图。同时，保留有关过程的季节性信息也很重要。在这种情况下，人们常会冒出使用正弦和余弦函数的想法。这些函数的图形是连续且周期性的。函数的周期长度是已知的，等于 2π。


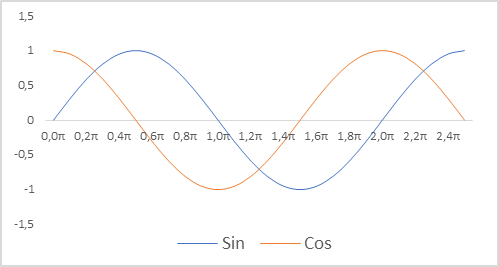
为了规范化时间戳，并考虑到周期性，我们需要：

  1. 将当前时间除以周期大小
  2. 将结果值乘以 “2π” 常数
  3. 计算函数值（sin 或 cos）
  4. 将结果值添加到缓冲区

在我的实现中，我使用了年、月、周和日的周期。

   double x = (double)Rates[0].time / (double)(D'2024.01.01' - D'2023.01.01');
   Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
   x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_MN1);
   Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
   x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_W1);
   Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
   x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_D1);
   Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));

另外，不要忘记更改一根蜡烛定义和账户状态的大小常量。它们的值将反映在我们模型的架构，和定义累积经验轨迹的缓冲区数组的大小。

#define                    BarDescr        9            //Elements for 1 bar description
#define                    AccountDescr   12            //Account description

值得注意的是，源数据的准备，特别是时间戳的常规化，与模型本身的构造及其架构无关。它是在外部程序的一端运作的。但源数据准备的品质对模型训练过程和结果有很大影响。


2. 模型训练

在针对模型进行建设性改造工作之后，是时候转入训练了。在第一阶段，我们使用 “..\SoftActorCritic\Research.mq5“ EA 与环境交互，并将数据收集到训练集。

在指定的 EA 中，我们进行上述更改，将时间戳从环境状态缓冲区传输到帐户状态缓冲区。

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
.........
.........
//---
   float atr = 0;
   for(int b = 0; b < (int)HistoryBars; b++)
     {
      float open = (float)Rates[b].open;
      float rsi = (float)RSI.Main(b);
      float cci = (float)CCI.Main(b);
      atr = (float)ATR.Main(b);
      float macd = (float)MACD.Main(b);
      float sign = (float)MACD.Signal(b);
      if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
         continue;
      //---
      int shift = b * BarDescr;
      sState.state[shift] = (float)(Rates[b].close - open);
      sState.state[shift + 1] = (float)(Rates[b].high - open);
      sState.state[shift + 2] = (float)(Rates[b].low - open);
      sState.state[shift + 3] = (float)(Rates[b].tick_volume / 1000.0f);
      sState.state[shift + 4] = rsi;
      sState.state[shift + 5] = cci;
      sState.state[shift + 6] = atr;
      sState.state[shift + 7] = macd;
      sState.state[shift + 8] = sign;
     }
   State.AssignArray(sState.state);
//---
........
........
//---
   Account.Clear();
   Account.Add((float)((sState.account[0] - PrevBalance) / PrevBalance));
   Account.Add((float)(sState.account[1] / PrevBalance));
   Account.Add((float)((sState.account[1] - PrevEquity) / PrevEquity));
   Account.Add(sState.account[2]);
   Account.Add(sState.account[3]);
   Account.Add((float)(sState.account[4] / PrevBalance));
   Account.Add((float)(sState.account[5] / PrevBalance));
   Account.Add((float)(sState.account[6] / PrevBalance));
   double x = (double)Rates[0].time / (double)(D'2024.01.01' - D'2023.01.01');
   Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
   x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_MN1);
   Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
   x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_W1);
   Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
   x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_D1);
   Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
//---
   if(Account.GetIndex() >= 0)
      if(!Account.BufferWrite())
         return;

此外，我决定放弃对冲操作。仅针对交易量差异较大的方向开放成交。为此，我们检查业务的预测交易量，并降低其交易量。

........
........
//---
   vector<float> temp;
   Actor.getResults(temp);
   float delta = MathAbs(ActorResult - temp).Sum();
   ActorResult = temp;
//---
   if(temp[0] >= temp[3])
     {
      temp[0] -= temp[3];
      temp[3] = 0;
     }
   else
     {
      temp[3] -= temp[0];
      temp[0] = 0;
     }

此外，我还关注了产生的奖励。在形成奖励的主体时，我们用的是账户余额的相对变化。其值稀薄，明显低于 1。同时，初始训练阶段奖励的熵分量值在 8-12 的范围内波动。很明显，熵分量的大小无比巨大。为了弥补这种数值上的豁口，我将其除以余额，就像在形成奖励的目标部分时它的变化一样。此外，我还引入了 LogProbMultiplier 约简率。

........
........
//---
   float reward = Account[0];
   if((buy_value + sell_value) == 0)
      reward -= (float)(atr / PrevBalance);
   for(ulong i = 0; i < temp.Size(); i++)
      sState.action[i] = temp[i];
   if(Actor.GetLogProbs(temp))
      reward += LogProbMultiplier * temp.Sum() / (float)PrevBalance;
   if(!Base.Add(sState, reward))
      ExpertRemove();
  }

进行这些修改后，我开始了收集训练数据的第一阶段。为此，我使用了 EURUSD H1 的历史数据。在策略测试器中，以全参数枚举模式收集了 2023 年前 5 个月的数据。启动资金为 10,000 美元。在这个阶段，我收集了一个包含 200 次验算的样本数据库，它为我们提供了覆盖指定时间间隔内超过 50 万个 “状态”→“动作”→“新状态”→“奖励” 数据集。

您也许还记得，我们现阶段没有预训练模型。每次验算时，EA 都会生成一个新模型，并用随机参数填充它。在贯穿历史的验算期间，不进行模型训练。因此，我们得到 200 个完全随机和独立的验算。它们都没有展现出盈利。

第一个数据集合

训练模型的实际过程组织在 “..\SoftActorCritic\Study.mq5“ EA。我们还在此进行了一些现场编辑。

首先，我们修改了生成帐户状态描述向量的过程，添加了时间戳项，类似于上述环境研究 EA 中讲述的方式。

此外，我们还根据熵分量调整了目标奖励的形成。在所有三个 EA 中，方式应该是相同的。

void Train(void)
  {
.........
.........
//---
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
.........
.........
      Account.Clear();
      Account.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance);
      Account.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance);
      Account.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity);
      Account.Add(Buffer[tr].States[i + 1].account[2]);
      Account.Add(Buffer[tr].States[i + 1].account[3]);
      Account.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance);
      Account.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance);
      Account.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance);
      double x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01');
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1);
      Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1);
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1);
      Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      //---
.........
.........
      //---
      TargetCritic1.getResults(Result);
      float reward = Result[0];
      TargetCritic2.getResults(Result);
      reward = Buffer[tr].Revards[i] + DiscFactor * (MathMin(reward, Result[0]) - Buffer[tr].Revards[i + 1] + 
                                                     LogProbMultiplier * log_prob.Sum() / (float)PrevBalance);

然后，我们将扮演者和评论者的训练分开。如前，我们在偶数和奇数训练迭代中交替使用 Critic1 和 Critic2。但现在，在训练扮演者时，我们禁用了正在使用的评论者训练功能。它只将误差梯度传递给扮演者。在这种情况下，不会更新评论者参数。因此，我们的目标是依据真实环境奖励训练一名客观的评论者。

........
........
      //---
      if((iter % 2) == 0)
        {
         if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) ||
            !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         Critic1.getResults(Result);
         Actor.GetLogProbs(log_prob);
         Result.Update(0, reward);
         Critic1.TrainMode(false);
         if(!Critic1.backProp(Result, GetPointer(Actor)) ||
            !Critic1.AlphasGradient(GetPointer(Actor)) ||
            !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer) ||
            !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Critic1.TrainMode(true);
            break;
           }
         Critic1.TrainMode(true);

此外，在训练评论者时，我们从目标奖励中排除了熵分量，因为我们需要一名客观的评论者，而熵分量的功能是刺激行动者探索环境。

         Result.Update(0, reward - LogProbMultiplier * log_prob.Sum() / (float)PrevBalance);
         if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         //--- Update Target Nets
         TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau);
        }

更新评论者参数后，我们只更新一个评论者的目标模型。否则，EA 代码保持不变，您可以在附件中查看。

进行修改后，我们开始模型训练过程，循环迭代 100,000 次（默认参数）。在这个阶段，形成了扮演者和 2 个评论者模型。还运作了它们的初步训练。


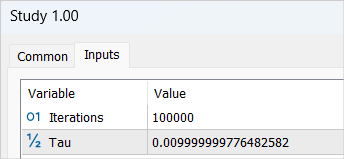
您不应期望从第一轮模型训练中获得显著结果。造成这种情况的原因有很多。完成的迭代次数仅覆盖了我们样本库的 1/5。它不能称为完整。其中没有一次模型可学习的可盈利验算。

完成模型训练的第一阶段后，我删除了之前收集的样本数据库。此处，我的逻辑很简单。该数据库包含随机独立验算。奖励包含未知熵分量。我假设在未经训练的模型中，所有动作的可能性都相同。但无论如何，它们都无法与我们模型的概率分布进行比较。因此，我们删除了以前收集的呀昂本数据库，并创建一个新数据库。

同时，我们重复收集训练样本的过程，并依据完整的参数搜索，重新运行环境研究 EA 的优化。只是这一次，我们偏移了正在迭代的代理者的值。这个简单的技巧对于避免从以前的优化缓存加载数据是必要的。


新样本库之间的主要区别在于，我们的预训练模型是在环境探索期间所用的。代理者行动的多样性是由于代理者政策的随机性。所有完成的动作都位于我们模型的学习概率分布当中。在此阶段，我们将收集所有代理者最后一次的验算。

在收集了新的样本数据库后，我们重新运行 “..\SoftActorCritic\Study.mq5“ 模型训练 EA。这一次，我们将训练迭代次数增加到 500,000 次。

完成第二轮训练过程后，我们转向 “..\SoftActorCritic\Test.mq5“ EA，测试训练后的模型。我们正在对它进行类似于环境研究 EA 的修改。您可以在附件中找到它们。

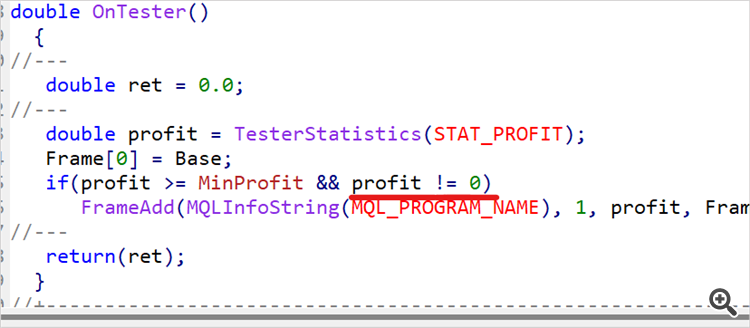
切换到测试 EA 并不意味着培训结束。我们依据辣子训练期间的历史数据运行若干次 EA。在我的例子中，这是 2023 年的前 5 个月。我运作了 10 次验算，并判定了所获得盈利范围的近似上限 1/4 或 1/5。我们回到环境研究 EA 的代码，并限制把验算的最小盈利保存到样本数据库。

input double               MinProfit   =  10;
double OnTester()
  {
//---
   double ret = 0.0;
//---
   double profit = TesterStatistics(STAT_PROFIT);
   Frame[0] = Base;
   if(profit >= MinProfit && profit != 0)
      FrameAdd(MQLInfoString(MQL_PROGRAM_NAME), 1, profit, Frame);
//---
   return(ret);
  }

因此，我们只努力选择最好的验算，并训练我们的扮演者使用基于它们的最优策略。

我们特意在外部参数中包含了最小盈利能力指标，因为我们将在训练模型时逐渐提高标准。

进行修改后，我们设置先前测定的最小盈利能力水平，并在策略测试器优化模式下对训练数据再执行 100 次验算。

我们重复模型训练过程的迭代，直到获得所需的结果，或达到模型能力的上限（下一轮训练周期不会改变盈利能力）。在执行测试 EA 的单次验算时，也可以注意到这一点。在这种情况下，尽管扮演者的政策是随机的，但几次完美的验算将产生几乎相同的结果。这证明该模型最大限度地提高了相关状态中独立动作的概率。我们得到了确定性策略的效果。这种结果并不总是一个缺点。在某些任务中，稳定和确定性的策略也许更可取，特别是如果确定性动作导致良好的结果。 


3. 测试

经过大约 15 次迭代，包括更新样本数据库、训练模型、测试训练样本、提高最低盈利能力标准、和定期补充样本数据库，我能够得到一个模型，其在历史数据的训练范围内始终如一地产生利润。

下一阶段是在测试训练集之外的新数据上训练模型的能力。我在 2023 年 6 月的历史数据上测试了训练模型的性能。如您所见，这是训练区间之后的一个月。

在测试期间，该模型只进行了四次多头交易。其中只有一次是盈利的。这大概不是我们预期的结果。但是看看余额图形。3 笔亏损交易导致总共损失 300 美元，而开始余额为 10,000 美元。同时，一笔盈利交易导致利润超过 2000 美元。结果就是，我们本月的盈利为 17.5%。盈利因子 — 6.77，恢复因子 — 1.32，余额回撤 — 1.65%。

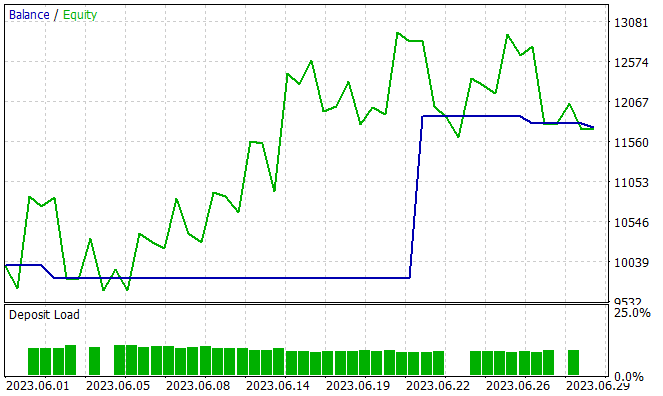
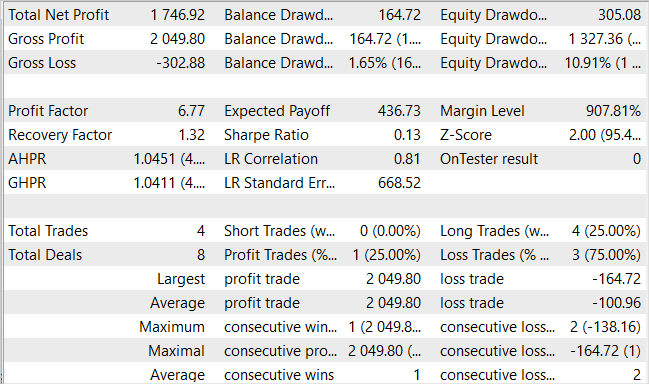
测试已训练模型

测试已训练模型

交易数量少，而且是单向的，令人困惑。但更重要的是什么？交易的数量，其种类，或余额的最终变化？


结束语

在本文中，我们继续构建软性扮演者-评论者算法的工作。这些新增内容帮助我们训练了扮演者的盈利策略。很难说成果模型有多优秀。一切都是相对的。

文章中提出的方式令我们提高模型的盈利能力成为可能，但它们并不是唯一、及尽善尽美的。例如，在上一篇文章的论坛帖子中，用户 JimReaper 提出了他的模型架构。这也是一个完全可行的选择。就个人而言，我还没有测试过它，但我完全承认使用建议的架构、或其它架构获利的可能性。添加新数据以供模型分析极可能有助于提高其效率。我总是鼓励探索和新研究。在强化学习中开发和优化模型时（如机器学习的其它领域），探索和试验不同的架构、超参数和新数据是可以优化和改进模型的关键要素。


链接


本文中用到的程序

# 名称 类型 说明
1 Research.mq5 智能交易系统 样本收集 EA
2 Study.mq5  智能交易系统 代理者训练 EA
3 Test.mq5 智能交易系统 模型测试 EA
4 Trajectory.mqh 类库 系统状态定义结构
5 NeuroNet.mqh 类库 用于创建神经网络的类库
6 NeuroNet.cl 代码库 OpenCL 程序代码库

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/12998

附加的文件 |
下载ZIP
MQL5.zip (1721.81 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

该作者的其他文章

最近评论 | 前往讨论 (18)
Viktor Kudriavtsev
Viktor Kudriavtsev | 28 7月 2023 在 16:14
Dmitriy Gizlyk #:

理论上是可行的，但这完全取决于资源。例如，我们正在讨论 1000 个点的 TP 大小。在连续行动空间的概念中，这就是 1000 个变量。即使我们以 10 为增量，也有 100 种变体。再加上同样数量的 SL，甚至一半（50 个变量）。再加上至少 5 个交易量变量，我们就得到 100 * 50 * 5 = 25000 个变量。乘以 2（买入/卖出） - 一根蜡烛的变体数为 50 000。再乘以轨迹的长度，就得到了完全覆盖所有可能空间的轨迹数量。

在逐步学习过程中，我们会对当前行为者行动附近的轨迹进行采样。这样，我们就缩小了研究范围。而且，我们研究的并不是所有可能的变体，而只是一小块区域，通过寻找变体来改进当前策略。在对当前策略进行小幅 "调整 "后，我们会在这些改进所涉及的区域收集新数据，并确定下一步的运动矢量。

这可能会让人联想到在未知的迷宫中寻找出路。或者是游客走在街上向路人问路的路径。

我明白了。谢谢。

我现在注意到，当你进行Research.mqh 收集时，结果会以某种方式形成一组，组内的最终平衡非常接近。而且，Research.mqh 似乎取得了一些进展（积极的结果组开始更频繁地出现，或者其他什么原因）。但 Test.mqh 似乎没有任何进展。它有一定的随机性，一般来说，更经常以负数结束一次通过。有时先上升后下降，有时直接下降然后停滞。他似乎还增加了最后的进场量。有时，他的交易量不是负数，而是在零附近。我还注意到他改变了交易次数--有 5 个月他开了 150 笔交易，有人开了 500 笔（大约）。这一切正常吗？

Dmitriy Gizlyk
Dmitriy Gizlyk | 28 7月 2023 在 17:59
Viktor Kudriavtsev #:

我明白了谢谢。

我注意到，当我进行Research.mqh 收集时，结果会以某种方式形成一组，组内的最终平衡非常接近。而且，Research.mqh 似乎取得了一些进展（积极的结果组开始更频繁地出现或其他）。但 Test.mqh 似乎没有任何进展。它有一定的随机性，一般来说，更经常以负数结束一次通过。有时先上升后下降，有时直接下降然后停滞。他似乎还会在最后增加进场量。有时，他的交易量不是负数，而是在零附近。我还注意到他改变了交易次数--有 5 个月他开了 150 笔交易，有人开了 500 笔（大约）。这一切正常吗？

随机性是 Actor 随机性的结果。随着学习的深入，随机性会越来越小。它可能不会完全消失，但结果会很接近。

Viktor Kudriavtsev
Viktor Kudriavtsev | 28 7月 2023 在 19:55
德米特里 我的 neuronka 现在发生了一些变化 - 它开始奇怪地打开交易（在一根蜡烛上打开，在下一根蜡烛上关闭），而且由于某种原因，余额和净值没有变化。它只是在图表上画了 一条直线。余额的变化结果为 0。此外，这种情况在Test.mqh 和Research.mqh 上都会发生。现在整个基数都充满了这样的通证。这正常吗？我该怎么办--继续教学，或者我有个想法，暂时把基础和训练好的模型从一个文件夹移到另一个文件夹，用随机模型创建一个新的基础，然后把模型带回来继续教学。以某种方式让它们脱离直线。
Dmitriy Gizlyk
Dmitriy Gizlyk | 28 7月 2023 在 20:52
Viktor Kudriavtsev 上画了 一条直线。余额的变化结果为 0。此外，这种情况在Test.mqh 和Research.mqh 上都会发生。现在整个基数都充满了这样的通证。这正常吗？我该怎么办--继续教学，或者我有个想法，暂时把基础和训练好的模型从一个文件夹移到另一个文件夹，用随机模型创建一个新的基础，然后把模型带回来继续教学。以某种方式让它们脱离直线。

没有交易的传递不会 "堵塞 "示例数据库。Research.mq5有一个检查机制，不会保存这样的通行证。不过，Test.mq5 会保存这样的传票，这是好事。在生成奖励时，没有交易会受到惩罚。这将有助于模型摆脱这种情况。

Viktor Kudriavtsev
Viktor Kudriavtsev | 30 7月 2023 在 16:51

Dmitriy 我已经做了 90 多个循环（数据库的训练-测试-收集），模型仍然是随机的。我可以说，在 Test.mqh 的 10 次运行中，7 次排水 2-3 次为 0，1-2 次为大约 4-5 个周期，有一次运行在加号中。您在文章中指出，您在 15 个周期中得到了一个积极的结果。我知道系统中存在很大的随机性，但我不明白为什么会出现这样的差异？好吧，我明白如果我的模型在 30 个周期后给出了正结果，比方说 50 个周期，那么现在已经是 90 个周期了，你看不到什么进展.....。

你确定你发布的是你自己训练的代码吗？也许你在测试时修正了一些东西，但不小心忘记了，所以发布了错误的版本.....？

举例来说，如果把训练系数提高一个等级，学习速度不是会更快吗？

我有些不明白......。

从外汇市场的季节性获益 从外汇市场的季节性获益
我们都熟悉季节性的概念，例如，我们都习惯于冬季新鲜蔬菜价格的上涨或严重霜冻期间燃料价格的上涨，但很少有人知道外汇市场也存在类似的模式。
暴力方式搜素形态（第 V 部分）：全新视角 暴力方式搜素形态（第 V 部分）：全新视角
在这篇文章中，我将展示一种完全不同的方式进行算法交易，我经历了很长一段时间后才最终遇到它。当然，这一切所作所为全靠我的暴力程序，其经历了许多更改，令其能够并发解决若干问题。尽管如此，这篇文章明面上仍然比较笼统和尽可能简单，这就是为什么它也适合那些对暴力一无所知的人。
开发回放系统 — 市场模拟（第 21 部分）：外汇（II） 开发回放系统 — 市场模拟（第 21 部分）：外汇（II）
我们将继续构建一个在外汇市场工作的系统。为了解决这个问题，我们必须在加载以前的柱线之前首先声明加载跳价。这解决了问题，但同时迫使用户遵循配置文件中的某些结构，就个人而言，这对我来说没有多大意义。原因是，通过设计一个负责分析和执行配置文件中内容的程序，我们可以允许用户按任何顺序声明他需要的元素。
时间序列挖掘的数据标签（第3部分）：使用标签数据的示例 时间序列挖掘的数据标签（第3部分）：使用标签数据的示例
本系列文章介绍了几种时间序列标记方法，这些方法可以创建符合大多数人工智能模型的数据，而根据需要进行有针对性的数据标记可以使训练后的人工智能模型更符合预期设计，提高我们模型的准确性，甚至帮助模型实现质的飞跃！