Das Preisbewegungsmodell und seine wichtigsten Aspekte. (Teil 3): Berechnung der optimalen Parameter des Börsenhandels

Einführung

In den vorangegangenen Artikeln (Teil 1 und Teil 2) habe ich die grundlegenden Prinzipien und latenten Mechanismen für die Preisdynamik dargestellt, was rein theoretischer Natur war und sogar über den Rahmen dessen hinausging, was beobachtet wurde (was jedoch die Grundlage dafür war). In diesem und den folgenden Artikeln werde ich versuchen, den Grundstein für eine neue technische Disziplin zu legen (in der viele Berechnungen bewertenden Charakter haben werden), die es den Nutzern ermöglicht, aus der beobachteten Preisdynamik praktisch nützliche Schlussfolgerungen zu ziehen und sie direkt beim Handel anzuwenden. In diesem Artikel werde ich über technische Ansätze und Algorithmen sprechen, die im Allgemeinen in der Lage sind, nachhaltige Gewinne zu erzielen, sowie über probabilistische Berechnungen der optimalen Take-Profit- und Stop-Loss-Werte, die es ermöglichen würden, den maximalen Durchschnittsgewinn zu erzielen.

1. Modell.

Im vorangegangenen Artikel (Teil 2) habe ich die Gleichung (II.3) für den Preiswahrscheinlichkeitsstrom aufgestellt (der Kürze halber wird die Gleichung (N) des Artikels Teil R von nun an als (R.N) nummeriert, wobei R eine römische Zahl ist). Ein solcher Wahrscheinlichkeitsfluss in reduzierter oder beobachteter Form drückt sich in Wahrscheinlichkeiten für eine „Aufwärts-“ und „Abwärtsbewegung“ des Preises aus, oder, genauer gesagt, er erzeugt solche Wahrscheinlichkeiten. Lassen Sie uns den Ansatz für die praktische Bewertung solcher Wahrscheinlichkeiten formulieren.

 

Bei der diskreten Zeitdarstellung (auf der Grundlage des Balkenkonzepts) bewegt sich der Kurs in diskreten Schritten, wenn das Segment (Open, Close, High oder Low) als Serie dargestellt wird (die Nummerierungsreihenfolge ist hier so, dass nachfolgende Balken höhere Nummern haben als die vorherigen). Auf großen Skalen oder im Falle von ziemlich großen , erlaubt uns dies, die Wahrscheinlichkeiten solcher Preissprünge zu diskutieren, die für die Aufwärtskursbewegungswahrscheinlichkeit als , mit - Anzahl der Setmitglieder, oder für die Abwärtswahrscheinlichkeit , mit - Anzahl der Mitglieder, bewertet werden.  Gleichzeitig ist es möglich, die Langlebigkeit des durchschnittlichen Sprungs zu berechnen 

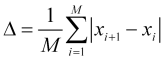                                                                                                    (1.1)

des Preises . In der Praxis kann man feststellen, dass ein chaotisch laufender Preis für den Zeitraum von seinem aktuellen Durchschnitt (definiert durch solche Wahrscheinlichkeiten) aufgrund eines Random Walk abweicht. Die Abweichung liegt in der Größenordnung von

              , (1.2)

(dies wird durch den Indikator Casual Channel bestätigt, dessen Kanallinien oder Abweichungen (1.2) vom gleitenden Durchschnitt der Periode sind).

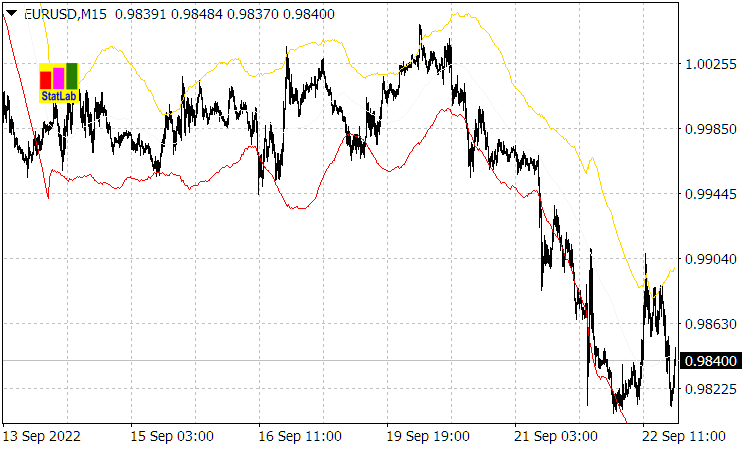
Abb. 1. Der Indikator Casual Channel

Offensichtlich ist die charakteristische Zeit der zufälligen Preisabweichung durch in der Größenordnung von , wobei eine temporäre Balkenlänge des entsprechenden Zeitrahmens ist.  Wir würden die gleiche Abweichung (1.2) des Preises vom Durchschnitt sehen, wenn sich der Preis zufällig um ähnliche Sprünge bewegen würde, die genau entsprechen.

 

In der hier vorgenommenen Modellvereinfachung gehen wir daher davon aus, dass sich der Preis in ähnlichen Sprüngen bewegt, mit den Wahrscheinlichkeiten ihrer Richtungen von und . 

 

Die mit den oben beschriebenen Methoden berechneten Sprünge sowie die Wahrscheinlichkeiten waren bereits für das vorangegangene Intervall als Ganzes, d.h. als Durchschnittswerte für den Wertebereich, relevant und nicht für die aktuellen Kursbewegungen, die unter dem Einfluss verschiedener Sprünge und vor allem den Wahrscheinlichkeiten und gebildet werden, die noch zu prognostizieren sind.

 

Wie ich bereits in Teil 2 festgestellt habe, sind die Methoden der konventionellen Statistik und ihr mathematischer Apparat nicht geeignet ist und zu großen Fehhlern führt, wenn die Preisdynamik aus Überlagerungen von Wahrscheinlichkeitswellen gebildet wird. Die Analyse, die auf der Verwendung von Beobachtungsdaten und den entsprechenden probabilistischen und statistischen Berechnungen beruht, hat daher nur Näherungscharakter.

2. Praktische Bestimmung der früheren Operationswahrscheinlichkeiten und der normalisierten Preisgeschwindigkeit. Das Prinzip der Verwendung dieser Parameter zur Berechnung der zukünftigen Preisverteilung.

Die durchschnittliche Geschwindigkeit der Kursbewegung über das Mittelungsintervall ist gleich

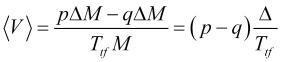                                                                                  (2.1)

und zeigt die Änderungsrate des gleitenden Durchschnitts (wobei ein Balkenindex ist) mit dem entsprechenden Mittelungszeitraum und nicht irgendeine Art von Geschwindigkeitsschwankungen. Daher ist die Durchschnittsgeschwindigkeit eine praktisch berechenbare Größe

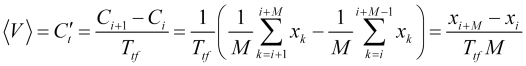               .         (2.2)

Wenn wir (2.1) mit (2.2) gleichsetzen, erhalten wir einen empirisch bestimmbaren Parameter

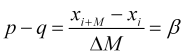              ,                                                                                            (2.3)

Nennen wir dies eine normalisierte Preisgeschwindigkeit , da , während leicht zu demonstrieren ist, dass . . Aus (1.1) folgt zum Beispiel die Ungleichung

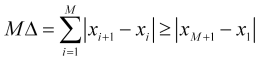             ,                                                                            (2.4)

was zusammen mit (2.3) zu führt. Wir können auch annehmen, und da die Wahrscheinlichkeit ist, folgt . Wir verwenden (2.3) und , um die Wahrscheinlichkeiten zu ermitteln: 

                 und ,                                                                        (2.5)

sowie ein weiterer Ausdruck für die normierte Geschwindigkeit:

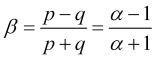                ,                                                                                    (2.6)                               

wobei der Parameter:

               .                                                                   (2.7)

Für weitere Berechnungen benötigen wir auch den Parameter:  

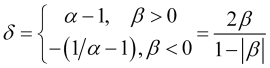               ,                                                            (2.8)

durch die die normierte Geschwindigkeit selbst wie folgt ausgedrückt wird:

              .                                                                                            (2.9)

 

Die für das Preisintervall berechneten (2.5) Sprungwahrscheinlichkeiten sind die Durchschnittswerte für das Intervall und tragen zur Bildung des Endpreises bei. Wenn wir also diese durchschnittlichen Wahrscheinlichkeiten kennen (zum aktuellen Zeitpunkt , wenn der Preis bekannt ist), können wir den Preis in der Zukunft vorhersagen, oder, genauer gesagt, die Wahrscheinlichkeitsverteilung des Preises. Vergleicht man die Preischarts von und die normalisierte Geschwindigkeit von (aus der und berechnet werden), kann man ihre starke Ähnlichkeit (durch die Übereinstimmung der Standorte ihrer Scheitelpunkte) feststellen, was zeigt, dass es diese Geschwindigkeit (genauer gesagt, die ihr entsprechenden Wahrscheinlichkeiten) war, die den aktuellen Preis von bildete.

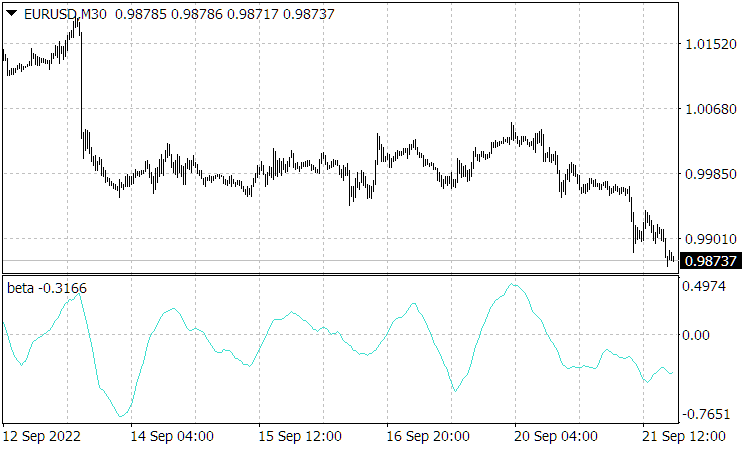
Abb. 2. Die Abbildung zeigt das normalisierte Geschwindigkeitsdiagramm.

 

Aus (2.3) ergibt sich nämlich . Dies bedeutet, dass der Preis aus dem Preis durch die Reihe der zukünftigen Geschwindigkeiten oder deren Mittelwerte durch das Intervall gebildet wird:

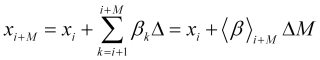  ,                         (2.10)                                                              

wobei die normierte Durchschnittsgeschwindigkeit über das künftige Intervall, die in der Grafik an dem Punkt 

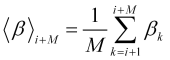            ,                                                    (2.11)

während die Mittelwerte des Wahrscheinlichkeitsintervalls und durch Einsetzen von in die Gleichungen (2.5) gefunden werden (wenn in (2.10) das Mitglied um herum liegt, haben wir natürlich die Graphen, die und ähneln). Nachdem wir hinreichend glatte Funktionen auf Balken vorausgesagt haben, berechnen wir die notwendigen Wahrscheinlichkeiten und , die es uns erlauben, (zum Zeitpunkt ) die Wahrscheinlichkeitsverteilung des zukünftigen Preises und seine für den Handel notwendigen Parameter (Richtung der Positionseröffnung und Position der Stop-Order) zu berechnen.

 

Das Wesen der hier verwendeten normalisierten Geschwindigkeitsprognose ist wie folgt. Die temporäre Funktion der normierten Geschwindigkeit schwankt im Bereich von in der Nähe ihres mathematischen Erwartungswerts gleich Null (oder des kleinen Werts , der die Geschwindigkeit des globalen Trends anzeigt, wenn er das gesamte betrachtete Gebiet umfasst). In diesem Fall wird z. B. die einfachste statistische Vorhersage, die auf der bedingten mathematischen Erwartung in Form von beruht, die Vorhersagefunktion gemäß näher an Null oder bringen. Mit anderen Worten, wenn die Autokorrelationsfunktion des entsprechenden Prozesses abnimmt, wird die Anzahl der durch eine Bedingung wie eröffneten Positionen stark reduziert und das Spiel noch unrentabler als ein Spiel mit einer trivialen Prognose auf der Grundlage des letzten Wertes . Andererseits lässt sich die Preisdynamik durch oszillierende Prozesse gut modellieren und vorhersagen. Die Idee dahinter wurde bereits in früheren Artikeln erläutert. In diesem Stadium der Theorieentwicklung wurde die Vorhersage der Funktion (die einen oszillierenden Charakter hat) auf auf der Grundlage der Fourier-Extrapolation vorgenommen, die auf der Basis empirischer historischer Daten berechnet wurde, da die Verwendung der in früheren Artikeln vorgeschlagenen Wavelet-Extrapolation in diesem Fall noch keine spürbaren Vorteile gebracht hat.

3. Trend Qualität. Bewertung des Ausmaßes aktueller und zukünftiger Trends, angemessener Arbeitshorizont.

Dauert der Trend länger als die Mittelungszeit , so liegt der natürliche Preisanstieg während der Mittelungszeit (gemäß (2.1) und (2.3)) in der Größenordnung von

               .                                    (3.1)

Inkrementelle Unsicherheit 

               ,                                                                                                (3.2)

dann die gesamte Bandbreite der Preisbewegung (siehe Abb. 1), wenn er sich von einem Rand des Indikatorkanals Casual Channel zu einem anderen bewegt und dabei im Durchschnitt mit der auf normierten Geschwindigkeit driftet, wird geschätzt als

                 ,                                                               (3.3)

wobei

                 .                                                                                 (3.4)         

Wenn wir dem Trend folgen, dann ist es wünschenswert, dass der Wert der Verschiebung (3.1) deutlich größer bleibt als die Unsicherheit (3.2) dieser Verschiebung

               ,                                                                (3.5)

daraus und aus (2.6) und (2.9) ergibt sich ein niedrigerer Schätzwert für die erforderliche Mittelungszeit

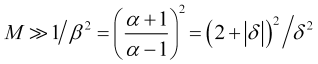              ,                                                   (3.6)

wenn sie erfüllt ist, wird gemäß (3.4) die Mittelungszeit (in Balken) wie folgt berechnet 

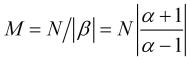              .                                                                                  (3.7)

Wenn der Anstieg des Unsicherheitspreises nicht vernachlässigt werden kann, dann wird die Mittelungszeit als positive Wurzel der quadratischen Gleichung (3.4) betrachtet

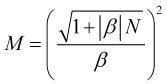               .                                                                                        (3.7.1)

 

Definieren wir die Trendqualität

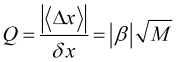               ,                                                                                        (3.8)

als das Verhältnis seines natürlichen Zuwachses zu seiner Unsicherheit oder seinem Rauschen. Es liegt auf der Hand, dass eine stabile und profitable Trendfolgestrategie eine hohe Qualität erfordert. Aber der Indikator Quality Trend, der die Qualität berechnet (Abb. 3), erreicht bestenfalls den Wert von mehreren Einheiten einer Währung. Selbst wenn man einen hochwertigen Trend identifiziert hat, ist es nicht möglich zu bestimmen, wann er zu Ende geht, da das Auftreten starker externer Ereignisse, die die Eigendynamik des Marktes stören und den Trend beenden oder sogar umkehren können, nicht vorhersehbar ist. Daher kann eine gewinnbringende Strategie kann nur auf Gewinnmitnahmen bei relativ kleinen Schwankungen in Trendrichtung beruhen.

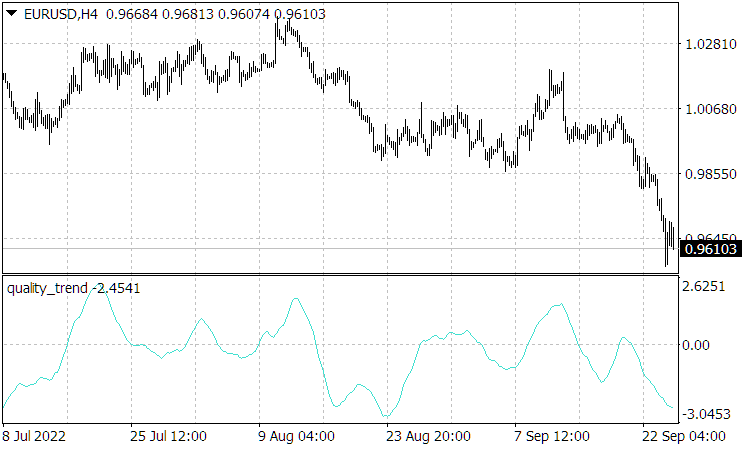
Abb. 3. Der Indikator Quality Trend, bei dem der Kursanstieg nicht modulo genommen wird, d.h. das Vorzeichen des Indikators gibt die Richtung des Trends an.

Es ist zu beachten, dass die Messwerte des Indikators Quality Trend, die proportional zur normalisierten Geschwindigkeit sind, wie das Verhältnis (2.10) zeigt, in den Positionen ihrer Spitzen dem Kursverlauf ähneln und dementsprechend die Messwerte des Quality Trend nicht hinterherhinken. Darüber hinaus können die Indikatorwerte die Kursbewegungen übertreffen (was sie oft tun), da die entsprechende Geschwindigkeit einer Kursbewegung (Anstieg bei einem Aufwärtstrend oder Rückgang bei einem Abwärtstrend) noch vor dem Trendwechsel abnimmt. Ein solches Vorhersageverhalten dieses Indikators tritt jedoch nur auf, wenn keine starken Einflüsse auf den Markt vorhanden sind, die seine eigene Bewegung stören. Nach solchen Einflüssen werden die Werte des Quality Trend während ihrer Entspannungszeit zu „normalen“ verzögerten Werten, wobei die Verzögerung durch die Mittelungszeit bestimmt wird.

 

Analysieren wir das Verhalten der Funktion und bewerten wir das mögliche Ausmaß der Trends, vorausgesetzt, es gibt keine starken Einflüsse Dritter auf den Markt. Mit abnehmender Durchschnittsperiode können die berechneten Werte der normierten Geschwindigkeit ansteigen (schließlich ändern sich ihre „Augenblickswerte“ in einem sich ständig verändernden Markt mit einer größeren Amplitude als die Durchschnittswerte, und je größer die Mittelwertbildung ist, desto geringer sind solche Schwankungen), d.h. im Verhältnis der Qualitätsfaktoren werden die Glieder, für die gilt und umgekehrt , multipliziert, was es der Funktion ermöglicht, Maxima auszubilden. In einem sehr kleinen Intervall, in dem die wahren Wahrscheinlichkeiten der Sprünge und konstant sind, werden die statistisch berechneten Werte und über diesen kurzen Mittelungszeitraum jedoch höchstwahrscheinlich stark von den wahren Wahrscheinlichkeiten abweichen, da mit der Verringerung des Unsicherheitszeitraums die und der darauf berechneten Wahrscheinlichkeiten steigen. Für den Mittelungszeitraum , der die Berechnung von mehr oder weniger zuverlässigen Wahrscheinlichkeiten ermöglicht, sollten daher die Verhältnisse des Typs erfüllt sein, was seinen Mindestwert bestimmt. Andernfalls, wenn (obwohl dies ein umfassenderer Fall ist als der Fall großer Schwankungen der momentanen normierten Geschwindigkeit in kleinen Mittelungsintervallen, da ein solches Verhältnis auch in großen Intervallen mit einer schnellen Änderung der wahren Wahrscheinlichkeit auftreten kann ), können statistisch berechnete Wahrscheinlichkeitswerte nicht verwendet werden. Es ist zu beachten, dass bei starken Schwankungen der normalisierten Geschwindigkeit auch die darauf basierende Funktion in der Nähe ihres Maximums stark schwankt, sodass das zur Analyse der Marktsituation verwendete Maximum so gewählt werden sollte, dass es sich gleichmäßig ausbildet, was, wie aus dem oben Gesagten folgt, mit ausreichend großen Mittelungszeiträumen erreicht wird. Wenn die Bedingung erfüllt ist, die in der weiteren Theorie als erfüllt angenommen wird, können die geschätzten Wahrscheinlichkeiten und mit den handelnden Wahrscheinlichkeiten und identifiziert werden, die wir dann auch als und schreiben werden.

 

Gerade in den Bereichen, in denen die Wahrscheinlichkeiten und konstant sind, bildet sich ein stabiler Trend, während der Rückgang der vorherrschenden Wahrscheinlichkeit (d.h. ) die Wachstumsrate des Zuwachses verringert und vielleicht sogar (wenn das umgekehrte Verhältnis erreicht wird) den Trend umkehrt, was auch zu einem Rückgang des berechneten Qualitätsfaktors führt. Im Gegenteil, der hohe Qualitätsfaktor und sein Wachstum deuten nicht nur auf ein starkes Vorherrschen der vorherrschenden Wahrscheinlichkeit über hin, sondern auch auf ihre Beständigkeit und sogar Zunahme. Je höher also die Trendqualität (3.8) ist, desto größer ist die Wahrscheinlichkeit, dass er dort, d. h. über das gesamte Intervall , vorhanden ist, während der niedrige Qualitätswert eine Abflachung anzeigt. Es ist auch klar, dass der Qualitätsfaktor stark abnimmt, wenn man den Mittelungszeitraum vergrößert, der nicht nur einen Trend (mit der Länge ), sondern auch eine Seitwärtsbewegung und darüber hinaus einen Abschnitt der Preisgeschichte mit einem gegenläufigen Trend abdeckt; daher wird die Länge des Trends durch den Spitzenqualitätsfaktor bestimmt.

 

Erhöht man die Periodenlänge , sodass man damit einen unidirektionalen Trend einer größeren Skala abdeckt, als die Skala eines kleineren Trendabschnitts mit der Länge von , so steigt im Gegenteil die Trendqualität, da aufgrund der Ähnlichkeit der Charts in verschiedenen Zeitrahmen (sofern ) die Skala der normalisierten Geschwindigkeiten in (3.8) mit einer Erhöhung von nahezu unverändert bleibt, während zunimmt. Darüber hinaus (dies erfordert bereits die Korrektur der Wertberechnung , die in der Qualitätsgleichung (3.8) auftaucht) wird die Kontaminierung durch Rauschen des Trends durch große und kleine chaotische Preissprünge stark verstärkt, die über die statistische Verteilung hinausgehen, die durch „Standard“-Sprünge (entsprechend dem betrachteten Modell) mit den Wahrscheinlichkeiten und gebildet wird. Solche nicht standardisierten Sprünge sind für alle Skalen gleich und erzeugen ein „zusätzliches“ Rauschen zum Trend, sodass das Gewicht dieses zusätzlichen Rauschens mit zunehmender Skala, auf der der Trend ermittelt wird, abnimmt. All dies hat zur Folge, dass die Funktion dazu verwendet werden kann, im Falle eines globalen unidirektionalen Trends eine Reihe von Qualitätsspitzen zu definieren, die mit einer Zunahme von oder einer Vergrößerung des Umfangs der identifizierten Trendbereiche zunehmen werden.

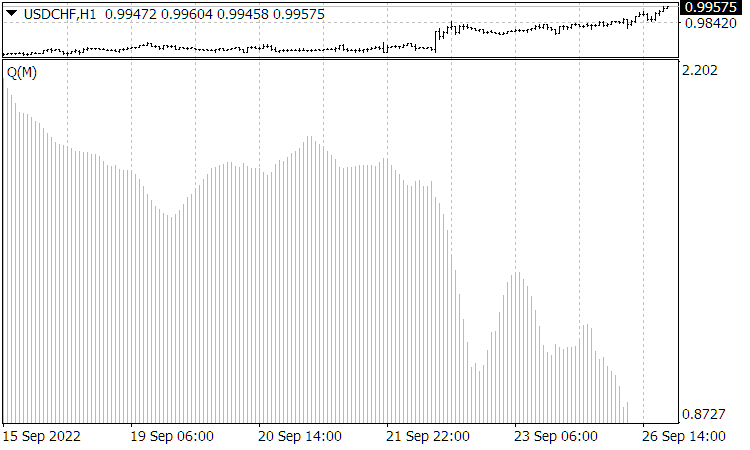
Abb. 4. Die aktuelle Funktion . Die X-Achse zeigt hier den Mittelungszeitraum für den Qualitätstrend von 10 bis 160 an und nicht die Zeit.

  

Schließlich basiert das Spiel nicht auf einer bereits gebildeten Historie, sondern in Echtzeit ist die Kenntnis einer Reihe von Prognosen erforderlich, die auf dem Satz von normalisierten Geschwindigkeitsprognosewerten basieren. Um die mögliche Länge eines neu entstehenden Trends zu beurteilen, müssen wir daher das gesamte Spektrum der Mittelungszeiträume durchgehen und eine Reihe von Maxima der Prognosegüte ermitteln, wenn die Vorhersage um Balken vom aktuellen Balken aus weitergeht, d. h. berechnet

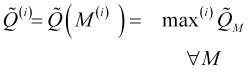               ,                                                                 (3.9)                 

wobei eine Identifizierungsfunktion des ten Maximums ist. In diesem Fall müssen wir auch den maximalen Spitzenwert festlegen

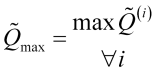                 ,                                                                                    (3.10) 

und der entsprechende Punkt auf der Mittelwertskala.  

 

Es liegt auf der Hand, dass bei kleineren Mittelungsintervallen bis zum maximalen Peak der Prognosequalität, sofern in diesen Intervallen die Qualität auch signifikant ist und monoton oder in einer Folge von steigenden (auch auf einem wachsenden Rückstand basierenden) Peaks wächst, ein entsprechender unidirektionaler Trend (mit Rollbacks nach jedem Peak der Qualität) zu beobachten ist. Nach der maximalen Spitze der Qualität, wenn sie auf der Skala der entsprechenden Mittelung zu fallen beginnt, gibt es eine Verlangsamung des Trends, die bald zu einer Umkehr führen kann. Letzteres ist am wahrscheinlichsten, wenn der Spitzenwert in dem Sinne sehr signifikant ist, dass der Qualitätsfaktor für das betrachtete Börseninstrument selten Werte über erreicht. In jedem Fall wird sich der Aufwärtstrend bis zur Marke fortsetzen, vor deren Erreichen wir die gemäß diesem Trend eröffnete Position schließen müssen.   

 

Versuchen wir nun, die Länge der für den Handel vielversprechenden Trendsegmente abzuschätzen, die nicht unbedingt der vorhergesagten Länge des Trends entsprechen muss. Erstens, aufgrund der geringen Zuverlässigkeit der Arbeit der prädiktiven Mathematik selbst (was für alle ihre Arten gilt, auch für verschiedene Frequenz- und andere Extrapolatoren, einschließlich neuronaler Netze und ARIMA usw.), sollte der Gewinn auf relativ kleine Segmente des identifizierten, zukünftigen Trends genommen werden, ist ein beginnenden Trend wahrscheinlicher. Wie aus dem vorangegangenen Absatz hervorgeht, sollte daher die Ungleichung unbedingt erfüllt sein. Zweitens verwendet das vorgestellte Modell Schätzungen der zukünftigen Wahrscheinlichkeitswerte und , sowie die durchschnittlichen Sprünge werden als konstant angenommen, da es Prognosen gibt, die funktionieren, wenn sich der Markt durch Trägheit und nach seinen eigenen Gesetzen entwickelt. Wie jedoch im ersten Artikel (Teil 1) gezeigt wurde, beginnt das Intervall der vorhersehbaren Marktentwicklung mit dem letzten starken externen Ereignis und dauert bis zum Auftreten des nächsten solchen Ereignisses. Daher gibt es den adäquate Arbeitshorizont des gesamten mathematischen Apparats, der hier entwickelt wird, wobei die Menge gleich der Anzahl der Balken zwischen dem aktuellen Balken und dem zukünftigen Balken des Eintretens eines starken äußeren Ereignisses ist. Wenn wir versuchen, einen solchen mathematischen Apparat (der äußerst wichtig ist) über einen bestimmten Horizont hinaus zu verwenden, wird dies zu Fehlern in seiner Funktionsweise und unvermeidlichen Verlusten führen. Um den möglichen Horizont für den angemessenen Betrieb eines solchen mathematischen Apparats zu bestimmen, muss man sich auf eine Fundamentalanalyse oder Expertenforschung stützen, die die Stärke des Einflusses aller gegenwärtigen und zukünftigen politischen und wirtschaftlichen Ereignisse auf den Zustand des Marktes bewertet. Daher wird die Länge des prognostizierten Trendabschnitts, der für den Handel vielversprechend ist, von oben durch das Verhältnis

              ,                                                                        (3.11)   

und von unten nach oben auf der Grundlage des zuvor festgelegten Verhältnisses zwischen der Geringfügigkeit der Wahrscheinlichkeitsunsicherheit (Fluktuationen) und der Wahrscheinlichkeit selbst geschätzt werden sollte

               ,                                                                                     (3.12)

der ebenfalls aus dem vorausberechneten Qualitätsfaktorkurvenverlauf ermittelt wird und den Bereichen entspricht, in denen sich dieser Verlauf recht gleichmäßig verändert. Die erwartete natürliche Preisänderung in diesem Abschnitt des Trends ist

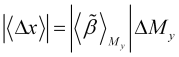               ,                                                                                    (3.13)

was der Größenordnung des mit einer reinen Trendfolgestrategie erzielten Gewinns entspricht.

 

Drittens sollte die Auswahl der Längen des Trendsegments auch auf den unten dargestellten Berechnungen basieren, die es im Wesentlichen ermöglichen, das Intervall Werte festzulegen, in dem es möglich ist, unter gegebenen Marktbedingungen einen durchschnittlichen statistischen Gewinn zu erzielen, d.h. . Hinzu kommt, dass die Händler den Zeitrahmen selbst wählen und die tatsächliche Qualität (und nicht die des Modells, berechnet nach Formel (3.8)) mit einer Verringerung des Zeitrahmens aufgrund des Preisrauschens in allen Zeitrahmen durch die Sprünge des Nicht-Modells (in allen Zeitrahmen identisch) abnimmt. Daher haben die Händler die Wahl zwischen Optionen mit hoher Trendqualität, aber einer langen Wartezeit bis zum Gewinn, was bei großen Zeitrahmen der Fall ist, oder einer schnellen Gewinnerzielung bei Trends geringerer Qualität (und dementsprechend größeren Risiken), was für kleine Zeitrahmen typisch ist.

4. Probabilistische Berechnung der Take-Profit- und Stop-Loss-Werte, die bei konstanten Betriebswahrscheinlichkeiten einen maximalen Gewinn ergeben, und deren Darstellung.

Formulieren der Aufgabe. 

Der Preis bewegt sich in Sprüngen in der vertikalen Dimension von der Nullmarke aus. Die Wahrscheinlichkeit eines Preissprungs nach oben ist und die eines Preissprungs nach unten , bzw. . Natürlich gibt es hier vorausgesagte Durchschnittswerte und , was aber jetzt nicht wichtig ist. Oben befindet sich der Take-Profit im Abstand von „a“, unten der Stop-Loss im Abstand von „c“ von der Nullmarke (in den Koordinatenachsen ). Finden Sie die Parameter des Börsenspiels, die einen maximalen Gewinn garantieren.

 

Lösung.

              Der Preis kann bis zum Punkt mit der Koordinate „n“ oder von unten vom Punkt „n-1“ oder von oben vom Punkt „n+1“ gehen. Die Wahrscheinlichkeit, den Preis am Punkt „n“ zu finden, ist also gleich 

               .                                                                                     (4.1)

Aus (4.1) ergibt sich die Gleichung der endlichen Differenzen 

                                                                                (4.2)

 

Ausbaufähige Sprünge. 

              Betrachten wir zunächst den Fall von gleichwertigen Sprüngen . Hier ergibt sich aus (4.2) folgendes

              ,                                           (4.3)

wobei eine Konstante ist, aus der sich ergibt

               .                                                                                                 (4.4)

              Die Wahrscheinlichkeit, dass der Kurs zum Zeitpunkt des Beginns seiner Bewegung bei Null liegt, ist also , 

               .                                                                                                      (4.5)

              Nehmen wir an, dass der Stop-Loss „c“ zusammen mit dem Take-Profit „a“ das Merkmal (hier geschätzt (3.4) in durchschnittlichen Preissprüngen ) Preisbereich der Bewegung über den Zeitraum seiner Mittelung (und Bewegung) der Konstanz der Wahrscheinlichkeiten und zugrunde liegt. Die Wahrscheinlichkeit, dass der Kurs bereits den Stop-Loss-Punkt erreicht, an dem einen Take-Profit von Null erreicht, ist . Setzt man (4.5) ein, erhält man

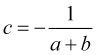                                                                                                                       (4.6)

zusammen mit (4.5) ergibt sich daraus die Wahrscheinlichkeit, einen Take-Profit zu erzielen, der gleich ist

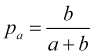                                                                                                                        (4.7)

während die Wahrscheinlichkeit, dass ein Stop-Loss ausgelöst wird

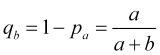               .                                                                                         (4.8)

Bei gleich wahrscheinlichen Preissprüngen in verschiedene Richtungen ist daher der durchschnittliche Gewinn bei der Anzahl der Sprünge

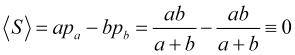                                                                          (4.9)

immer Null ist (der Spread macht ihn natürlich negativ), unabhängig von der Position des Take-Profits und des Stop-Loss, die beliebig sein können. 

 

Es besteht die Tendenz, sich in Richtung Take-Profit zu bewegen.

 

Wenn wir (oder, genauer gesagt, ) nehmen und alle Gleichungen (4.2) multiplizieren, erhalten wir

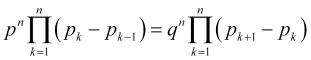               ,                                                      (4.10)

Wenn man die identischen Faktoren in (4.10) reduziert, die Notation (2.7) verwendet und berücksichtigt, dass , erhält man 

                .                                                                                 (4.11)

Stellen wir als Summe der Differenzen benachbarter Terme der Wahrscheinlichkeitsreihe dar, wobei wir weitere Beziehungen (4.11) und die Gleichung für die Summierung der geometrischen Progression verwenden

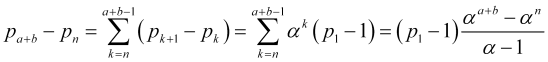 ,             (4.12)

, daher

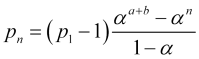                                                                                                   (4.13)

, daher

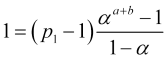              ,                                                                                           (4.14)

Dividiert man (4.13) durch (4.14), so erhält man die Wahrscheinlichkeit, Take-Profit „а“ zu erzielen               

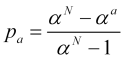              .                                                                                                      (4.15)

Die Wahrscheinlichkeit, dass Stop-Loss ausgelöst wird, ist demnach gleich . Dann ist der durchschnittliche Gewinn einer Position bei Preissprüngen gleich

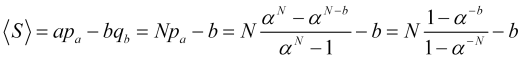              ,         (4.16)

die in der Darstellung (4.16) eine Funktion des Stop-Loss-Wertes „c“ ist, der in dieser Darstellung einfach eine Anzahl von Sprüngen ist, aber in Wirklichkeit gibt es einen Wert von . Der Gewinn ist . Es ist klar, dass der durchschnittliche Gewinn (4.16) steigt, wenn die Wahrscheinlichkeit einer Kursbewegung in Richtung einer offenen Position zunimmt. Wenn den Wert von annimmt, d.h. ist eine wachsende Funktion von .

 

Finden wir das Maximum des durchschnittlichen statistischen Gewinns (4.16) in Abhängigkeit von den gegebenen Werten von N und . Um dies zu erreichen, setzen wir seine Ableitung mit Null gleich

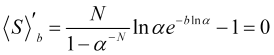                ,                                                            (4.17)

von wo aus wir den Wert des gewünschten Stop-Loss in Kurssprünge finden 

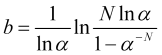              ,                                                                                        (4.18)

 

da der Logarithmus von positiv ist und . Dementsprechend sollte der Logarithmus 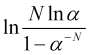positiv sein. Diese Bedingung ist erfüllt, wenn

               ,                                                                                              (4.19)

oder   

      ,                                                      (4.20)                                                                                      

wobei . Die Ungleichung (4.20) ist für jedes streng erfüllt, da der Exponent oberhalb der Geraden verläuft und diese nur bei berührt. 

Die zweite Ableitung der Funktion (4.16)

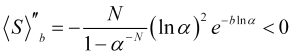                                                                            (4.21)

ist unter diesen Bedingungen immer negativ, d.h. die Krümmung der Funktion ist nach unten gerichtet und wir haben das Maximum bei (4.18). Die Funktion (4.16) bei N=100 und ist in Abb. 5 dargestellt. 

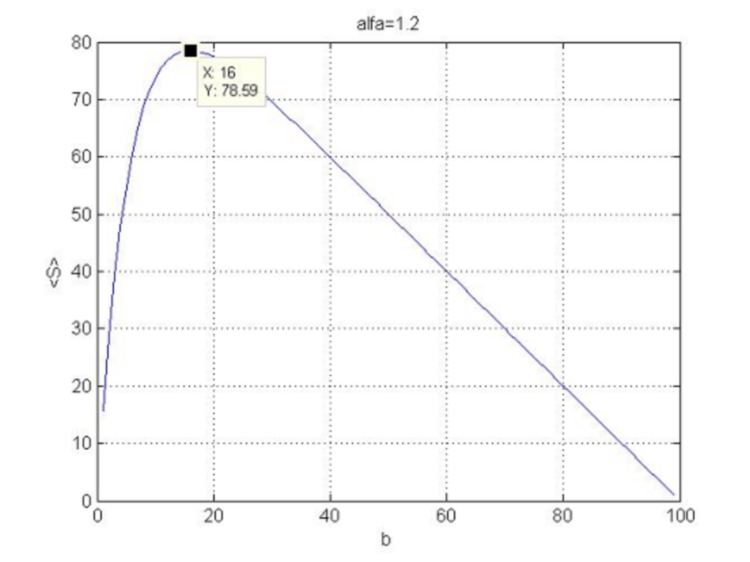
Abb. 5. Die Abhängigkeit der Gewinnfunktion vom Stop-Loss.

Damit der durchschnittliche Gewinn positiv ist, muss das Verhältnis deutlich über eins liegen. Tatsächlich, wenn , wobei und wir den zweiten Term der Expansion vernachlässigen können, sodass nur der erste Term übrig bleibt, dann ist der durchschnittliche Gewinn pro Handel 

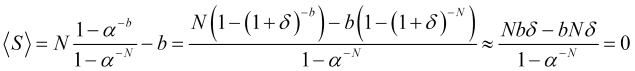    (4.22)

gleich Null (wie im Falle gleicher Wahrscheinlichkeiten für entgegengesetzte Sprünge). Wenn der zweite Term der Expansion nicht vernachlässigt werden kann, ergibt sich unter Berücksichtigung der Tatsache, dass die Anzahl der Sprünge groß genug ist oder

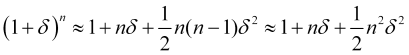               ,                               (4.23)

was einen positiven Wert für den durchschnittlichen Gewinn ergibt (4.16)

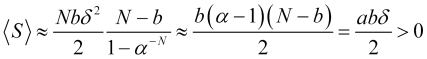               ,                          (4.24)

da , (und somit ).

              Der ungefähre durchschnittliche Gewinn (4.24) in Bezug auf das Argument ist eine umgekehrte quadratische Parabel, deren Maximum bei erreicht wird (das ist die Gleichheit von Stop-Loss und Take-Profit), wenn .

 

Dies ist ein sehr wichtiger Punkt. In der oben dargestellten Theorie wurde der Durchschnittsgewinn nur auf der Grundlage von Durchschnittspreisen berechnet, die in der Tat stark schwanken und die entsprechenden Durchschnittsverschiebungen im Bereich ihrer Schwankungen sogar weit übersteigen können. Die Stopp-Aufträge (Take-Profit und Stop-Loss) werden jedoch nicht an den Durchschnittspreisen, sondern genau an den Rändern der Schwankungsbreite geschlossen. Damit der vorgestellte mathematische Apparat (auf der Grundlage von Durchschnittswerten) funktioniert, sollte der Stop-Loss daher deutlich über die Preisunsicherheit hinausgehen (sodass sich seine Schwankungsauslösung kaum von der Modellauslösung in Bezug auf den Durchschnitt unterscheidet und diese Schwankungen vernachlässigt werden können), d.h. gemäß (1.2), 

                .                                                                                                         (4.25)

In diesem Fall ergibt sich aus (4.25) unter Verwendung der (3.7.1)-Ausdrücke für die Mittelungszeit die Funktion, für die folgende Ungleichung erfüllt sein sollte

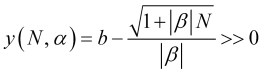               ,                                                                 (4.26)

das ein Kriterium für die Geringfügigkeit von Preisschwankungen ist, wobei sich aus dem Verhältnis (2.6) ergibt. Setzt man in (4.26) den Stop-Loss (4.18) ein, so erhält man den Funktionsgraphen (Abb. 6), der deutlich macht, dass eine solche Funktion nicht viel größer als Null ist, sondern im Gegenteil grundsätzlich negativ ist, d.h. das Verhältnis (4.25) ist niemals mit dem optimalen Stop-Loss (4.18) erfüllt.

 

MATLAB-Code

>> [N,a]=meshgrid([3:200],[1.01:0.01:3]);
>> b=log(N.*log(a)./(1-a.^(-N)))./log(a);
>> beta=(a-1)./(a+1);
>> s=(N.*beta+1).^(1/2)./beta;
>> y=b-s;
>> plot3(N,a,y)
>> grid on

   

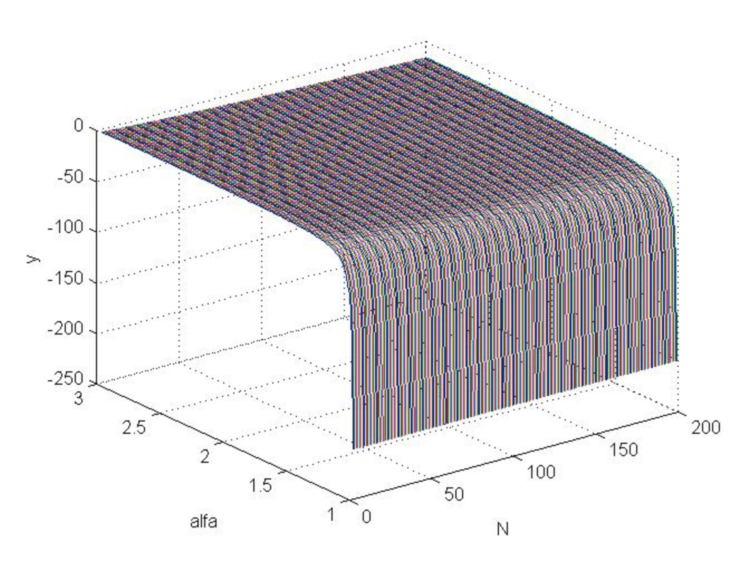
Abb. 6: Diagramm der Funktion „y“ bei Änderung von Alpha von 1 auf 3 und Änderung von N von 3 auf 200.

 

 

So führt die Verwendung der oben berechneten Stop-Order-Werte zu durchschnittlichen statistischen Verlusten, da sich die Kursschwankungen als wesentlich größer erweisen als der optimale Wert im Modell der durchschnittlichen Stop-Loss-Bewegung.

               .                                                                                                              (4.27)

Das bedeutet, dass wir die Größe des Stop-Losses selbst ändern müssen, anstatt nach dem Mittelungszeitraum zu suchen, der den optimalen Stop-Loss (4.18) relativ klein macht (4.25) (da diese Aufgabe keine Lösung hat). Dies wird sich natürlich auch auf den Gewinn auswirken.

 

Der optimale Take-Profit für das Modell der durchschnittlichen Preisbewegung fällt mit dem Punkt des prognostizierten gleitenden Durchschnittspreises zusammen, der sich Balken vor dem aktuellen Balken befindet. Wenn wir jedoch starke Kursabweichungen vom Durchschnitt berücksichtigen, bei denen Stop-Orders geschlossen werden, dann (wie in der Grafik des Indikators Casual Channel in Abb. 1 zu sehen) sollte ein solcher optimaler Take-Profit um einen Betrag reduziert werden, der größer ist als die durchschnittliche Abweichung

             ,                                                                                                  (4.28)

wobei das Verhältnis für schwache Trends (mit fast keinem Gewinn) etwas größer als 1 und für starke Trends ungefähr sein sollte, wobei es sich hier genau um den Parameter handelt, dessen genauer Wert durch Optimierung gesucht werden sollte, und der Stop-Loss um denselben Betrag erhöht werden sollte, d. h. 

               .                                                                                                  (4.29)

Dann wird ein Stop-Loss, als ein Wert, der vom Durchschnittswert der möglichen Preisabweichung (für zukünftige Balken) gegenüber einer offenen Position durch getrennt ist, viel seltener mit einer geringeren Wahrscheinlichkeit als ausgelöst, während ein Take-Profit häufiger mit einer größeren Wahrscheinlichkeit als ausgelöst wird. Für den maximalen Gewinn ergibt sich somit die Schätzung

               , (4.30)

wobei ein Wert aus (4.16) ist, oder unter Berücksichtigung von (3.7.1)

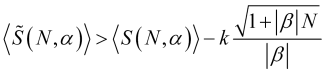                                                                    (4.31)

deren Funktion (im Falle des optimalen b aus (4.18)) konstruiert werden kann, sodass wir in der Lage sind, die N Wert zu finden, der ihn maximiert, sowie die Mittelungszeit. 

 

MATLAB-Code für k=3

>> [N,a]=meshgrid([3:200],[1.01:0.01:3]);
>> b=log(N.*log(a)./(1-a.^(-N)))./log(a);
>> beta=(a-1)./(a+1);
>> s=(N.*beta+1).^(1/2)./beta;
>> s0=N.*(1-a.^(-b))./(1-a.^(-N))-b;
>> Profit=s0-3*s;
>> plot3(N , a, Profit)
>> grid on 

 

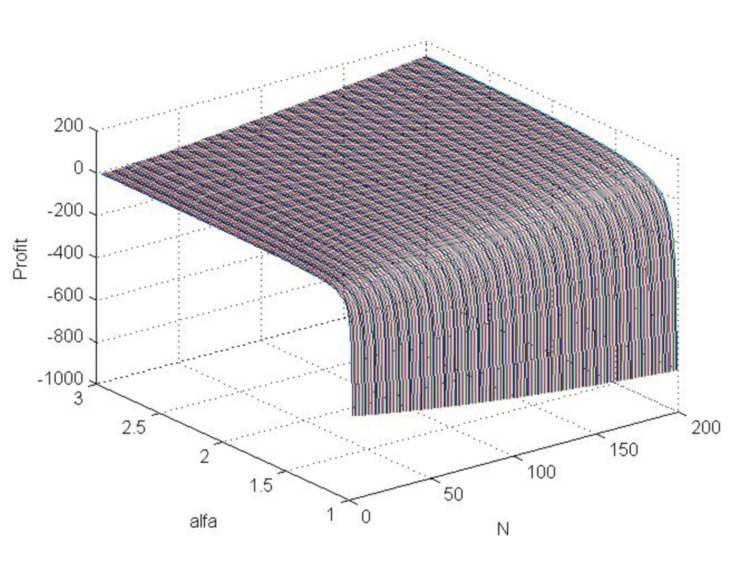
Abb. 7. Das Diagramm der Gewinnfunktiun (in Modellpreissprüngen), wenn sich Alpha von 1 auf 3 und N von 3 auf 200 ändert.

Die Grafik zeigt, dass der Gewinn mit einem positiven mathematischen Erwartungswert generell möglich ist und mit zunehmendem Alpha und N. 

 

Um den vielversprechendsten Mittelungszeitraum zu finden, müssen wir eine prädiktive Qualitätsfaktor-Funktion konstruieren. Aus diesem Grund wurde das Skript CalculateScientificTradePeriod entwickelt. Wir müssen die vielversprechendste Periode durch die Maximalstelle definieren, wo , wenn dieses Maximum reibungslos erreicht wird (das (3.12)-Verhältnis erfüllt ist) und nicht weiter liegt als der angemessene Arbeitshorizont. Liefert der so gefundene Wert einen positiven (sowie mindestens einige Spreads übersteigenden) Gewinnwert (4.31) und eine ausreichend hohe Gewinnwahrscheinlichkeit (4.15), die das Intervall festlegt, so sollte die Handelsentscheidung hierauf basieren. Um den optimalen (den durchschnittlichen Gewinn maximierenden) Take-Profit und Stop-Loss zu berechnen sowie die weitere Kursentwicklung zu bestimmen, habe ich den Indikator ScientificTrade entwickelt, dessen Algorithmen auf der gesamten oben dargestellten Theorie beruhen.

Beachten Sie, dass der Algorithmus des Skripts CalculateScientificTradePeriod sehr ressourcenintensiv ist. Daher verwenden wir das Skript und nicht den Indikator, der diesen Algorithmus bei jedem Tick ausführen und den Computer einfrieren würde. Der Indikator FindScientificTradePeriod wird verwendet, um die vom Skript berechneten Daten anzuzeigen.  

 

 

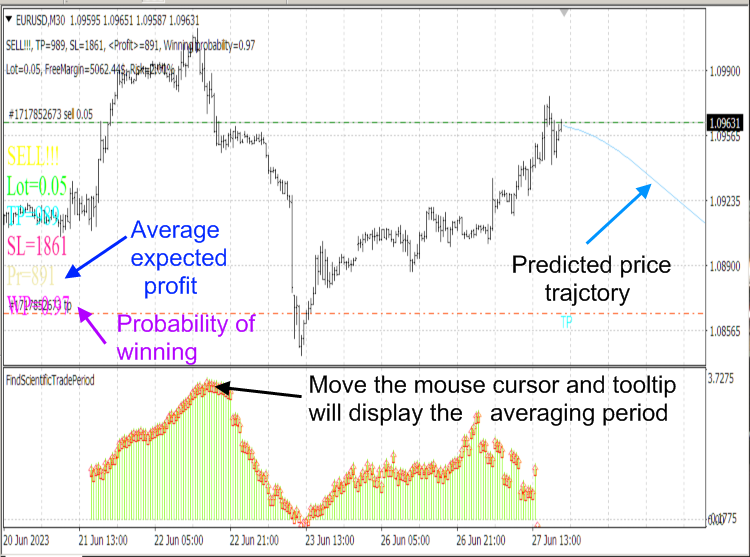
Abb. 8. Die Indikatoren ScientificTrade und FindScientificTradePeriod. 

 

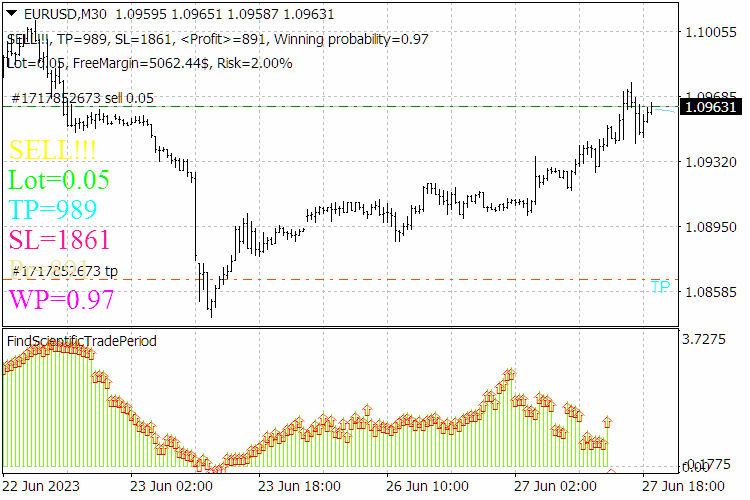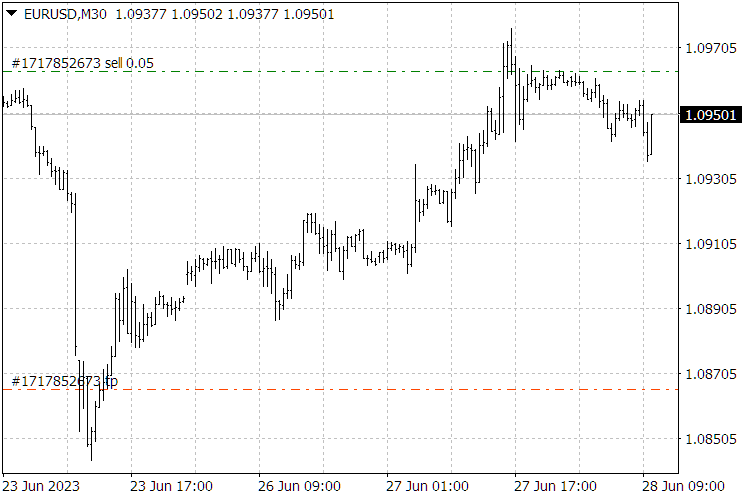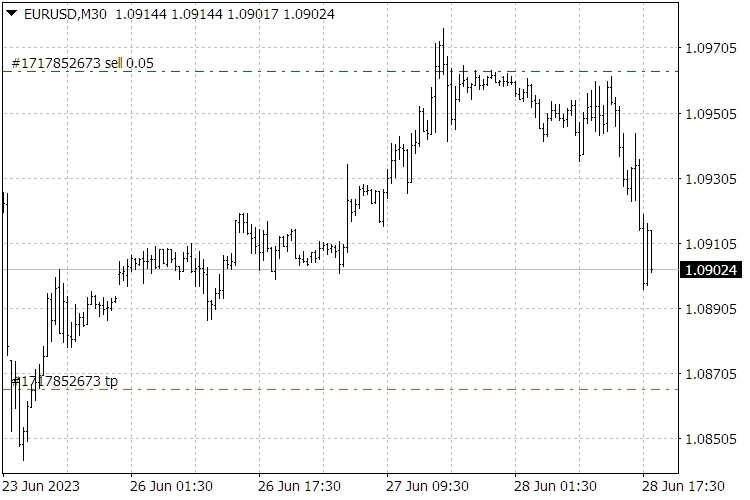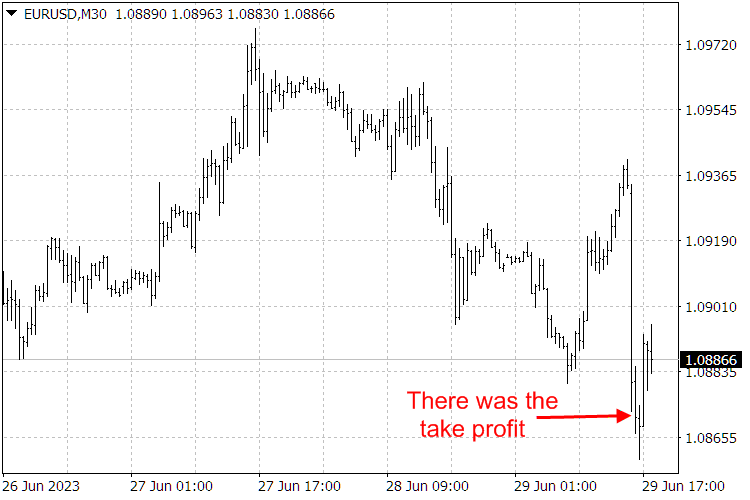
Abb. 9. Ergebnisse des ScientificTrade-Indikators. 

5. Unbehebbarer Fehler der angewandten Berechnungen im Rahmen des mathematischen Apparats selbst. Der Ansatz zur Identifizierung von Momenten natürlich auftretender Kurserholungen und -umkehrungen.

Wie bereits erwähnt, basieren die vom Indikator ScientificTrade vorhergesagten und vom Stop-Loss- und Take-Profit-Location-Indikator berechneten Trends auf den Prognosewerten von und , die sich aufgrund der Unzuverlässigkeit des Prognoseapparats selbst (im Fourier-Extrapolator-Indikator) als fehlerhaft erweisen können. Daher können sich solche Prognosen innerhalb eines angemessenen Zeitraums als falsch erweisen. angemessenen Arbeitshorizont des oben vorgestellten mathematischen Apparats als falsch erweisen.

Um zumindest einen Teil der Fälle falscher mathematischer Prognosen auszuschließen, sollten die vom Indikator ScientificTrade berechneten Trends in dem für ihn mit dem Skript CalculateScientificTradePeriod definierten Intervall mit den von maßgeblichen Experten aus der Fundamentalanalyse für dieses Intervall abgegebenen Prognosetrends übereinstimmen. Es ist klar, dass, wenn sowohl ScientificTrade als auch die Experten dieselbe Fehlprognose abgeben (was wir nicht wissen können), auch Verluste unvermeidlich sind. Nach meinen subjektiven Beobachtungen machen Experten eher Fehler als der Indikator ScientificTrade in Kombination mit dem Skript CalculateScientificTradePeriod, was meiner Meinung nach darauf zurückzuführen ist, dass die inneren Gesetze der Marktentwicklung einen stärkeren Einfluss haben als die meisten äußeren Ereignisse, die Veränderungen in Trends verursachen, die Experten nicht bestimmen können. Darüber hinaus treten solche Marktumschwünge aus internen Gründen oft vor dem Einsetzen starker externer Ereignisse auf, aber auch häufiger als diese. Auf die entsprechenden Mechanismen wird weiter unten eingegangen.        

Um das Wesen des obigen Problems zum Ausdruck zu bringen, ist zunächst festzustellen, dass sich der Preis nicht immer in gleichmäßigen Sprüngen bewegt, selbst wenn sich der Markt nach seinen eigenen Gesetzen entwickelt (wenn der Preis nicht durch starke äußere Ereignisse beeinflusst wird). Dieses Konzept ist ein vereinfachtes Modell, das es uns ermöglicht, zumindest etwas zu verstehen und Berechnungen im Marktchaos anzustellen. In der Realität kommt es gelegentlich zu kurzfristigen (über den Rahmen der klassischen Statistik hinausgehenden) starken Bewegungen des Preises, die den durchschnittlichen statischen Trends zuwiderlaufen, nach denen er langsam (mit großen Schwankungen) in eine bestimmte Richtung driftet. Wenn solche starken Bewegungen nicht durch äußere Einflüsse auf den Markt verursacht werden, sondern ihren Ursprung in dessen inneren Prozessen haben, dann richten sie sich in der Regel gegen statistische Trends. Daher reißen solche starken Bewegungen die Verluststopps nach unten und führen bei den meisten Kleinanlegern zu maximalen Verlusten.

In der Tat (wenn man das gezielte Absenken von Stop-Losses durch Anbieter von Handelsdienstleistungen und Kursen ausklammert) wirkt hier das Prinzip von Le Chatelier in Verbindung mit dem dialektischen Gesetz des Übergangs von Quantität in Qualität. Bei Erreichen eines bestimmten (auch vom Markt abhängigen) Wachstumsniveaus (oder Rückgangs) eines bestimmten Marktinstruments kommt es zu einem starken Qualitätssprung, der gemäß dem Prinzip von Le Chatelier (dessen Wirkung sich auf jedes komplexe System im Gleichgewicht erstreckt, einschließlich der Wirtschaft, die sich die meiste Zeit über enge Quasi-Gleichgewichtszustände entwickelt) dazu neigt, sich dem Wachstum der oben genannten Menge zu widersetzen und sie (sprunghaft) stark zu senken. Da der Markt als System mit seiner monotonen Entwicklung allmählich enge Quasi-Gleichgewichtszustände durchläuft, reagiert das Prinzip von Le Chatelier nicht auf seine kleinen Veränderungen, sondern wirkt abrupt, wenn sich in einem bestimmten System bereits große quantitative Veränderungen anhäufen. Aus der Sicht des Marktwellenmodells (Teil 1) lassen sich solche Sprünge durch die fortschreitende Annäherung (oder Gleichheit) der Phasen von Teilwahrscheinlichkeitswellen des entsprechenden Marktinstruments erklären.

Theoretisch lässt sich der Ansatz eines natürlichen Preissprungs anhand der Kennzahl (II.17) ermitteln. In der Praxis ist es jedoch viel einfacher, einen bevorstehenden Sprung anhand der vorausberechneten Qualitätsfaktorkurve zu erkennen. Insbesondere, wenn der prognostizierte Qualitätsfaktor zu einem zukünftigen Zeitpunkt (um Balken vom aktuellen Balken entfernt) einen bestimmten kritischen Wert für ein bestimmtes Marktinstrument auf dem entsprechenden Zeitrahmen , d.h. (wenn wir die aktuelle und nicht die prognostizierte Situation betrachten, dann einfach ), überschreitet oder sich diesem nähert, dann ist zu diesem Zeitpunkt eine Änderung des globalen Trends möglich.

Im Allgemeinen werden natürliche Preissprünge (jeglicher Art, sowohl global als auch klein) auf der Ebene der Wahrscheinlichkeitsamplituden ihrer Verteilung durch antisymmetrische Wavelets beschrieben (Teil 1, Verhältnis (I.17)), wenn nach der Realisierung der Nähe und Gleichheit der Phasen aller partiellen Preiswellen, aus denen sich ihre gesamte Wahrscheinlichkeitsamplitude zusammensetzt, die Phase der letzteren aufgrund der Antisymmetrie der entsprechenden Wavelets invertiert wird, was zu einer starken Veränderung der tatsächlichen Wahrscheinlichkeiten und führt, die sich dann grundlegend von den prognostizierten Wahrscheinlichkeiten und unterscheiden. Es liegt auf der Hand, dass solche kritischen Situationen, in denen Qualitätssprünge aufgrund der Eigengesetzlichkeit des Marktes auftreten, vom Handel ausgeschlossen werden sollten. Diese Antisymmetrie der partiellen Preiswellen gewährleistet ihre Ähnlichkeit mit Fermionen, was den ständigen Wunsch nach einer Änderung des Preisniveaus und ihre signifikante Breite (die als Ergebnis von Preisschwankungen interpretiert wird) bestimmt. Daher ist es richtiger, die Entwicklung der Marktinstrumente nicht durch gewöhnliche Statistiken, sondern durch Fermi-Dirac-Statistiken zu beschreiben.  

Aufgrund des beschriebenen Effekts der Preiswelleninversion (Teil 1) in der intensivsten Phase ihrer Bewegung (dem maximalen Modul der Amplitude ihrer Wahrscheinlichkeit) ist es auch witzig zu bemerken, dass, wie es scheint, die optimalsten Handelsparameter auf der Grundlage des höchsten Qualitätsfaktors auch den maximalen Gewinn gewährleisten sollten. Diese Handelsparameter, die von den meisten Händlern (intuitiv oder mathematisch) auf der Grundlage gewohnheitsmäßiger Vorstellungen (charakteristisch für alles, was im physikalischen Makrokosmos beobachtet wird) über die Monotonie von Prozessen und ihre Trägheit identifiziert werden, verursachen jedoch in Wirklichkeit maximale Verluste.

Damit bewahrheitet sich auch hier das alltägliche „Gesetz“: Geld erzeugt Geld, das zum größten Teil in Banken gelagert wird, sodass der Markt den kleinen Händlern das Geld aus der Tasche zieht. Schließlich entwickelt sich der Markt aus den oben genannten Gründen plötzlich (und zwar regelmäßig) entgegen den Trends, die von der Mehrheit der Händler, die gegen sie spielen, vorhergesagt wurden. Dieser Prozess hat keine menschliche „böse“ Absicht. Der Markt hat keine konstante Trägheit (die von kleinen Händlern ausgenutzt wird, um für eine gewisse Zeit Gewinne zu erzielen), die für physikalische Makroprozesse charakteristisch ist, und in bestimmten Momenten (die für Experten und Händler, die nicht mit der entsprechenden Theorie ausgestattet sind, nicht vorhersehbar sind) kehrt er leicht die Phasen aller einzelnen partiellen Preiswellen um, die von verschiedenen Marktteilnehmern unter dem Einfluss seiner inneren Gesetze ausgesendet werden, die auf seiner emergenten Ebene wirken (und den Einfluss selbst starker externer Ereignisse übertreffen). 

Insgesamt wird der Markt vom Chaos beherrscht. Deshalb muss jede Marktordnung, wenn sie maximal erkannt wird, verletzt werden, was als ein ziemlich gut beobachtetes Gesetz des Marktes angesehen werden kann. Es ist unmöglich, einen stabilen Gewinn zu erzielen, ohne ihn zu kennen.

Schlussfolgerung

Der Artikel stellt meinen technischen Ansatz zur Entwicklung einer profitablen Handelsstrategie vor. Dieser Ansatz zeigt, dass der Markt den Händlern eine extrem enge Reihe von Bedingungen für die Eröffnung und Schließung von Positionen lässt, die ihnen ein Spiel mit einem positiven erwarteten Gewinn ermöglichen könnten. Diese Menge ist mit klassischen Methoden nicht identifizierbar. Aber ein Spiel mit einer positiven Gewinnerwartung ist immer noch möglich, was bis zu einem gewissen Grad durch meine persönliche Verwendung des Indikators ScientificTrade bestätigt wird, der auf diesem technischen Ansatz und der Verwendung der Fourier-Extrapolation für die Vorhersage basiert (obwohl die Statistik bisher bei weitem nicht ausreichend ist). Natürlich muss dieser Indikator noch verbessert werden. Derzeit besteht der größte Nachteil darin, dass ein unzureichend genauer mathematischer Vorhersageapparat verwendet wird.