文章中的这段话引起了我的注意。尽管这篇文章写得非常好,并详细介绍了它是如何设计和思考的。在这段话中,你对这一主题的理解存在微妙之处。也许你有偏见,因为每个人都坚持说神经网络的某些事情。但你的文章写得很好,也解释了其中的细节。我决定预测一下我将来要展示的东西。这方面的文章已经写好了,但首先我想解释一下如何构建 Replay / Simulator,现在只剩下几篇文章就可以完成出版了。请注意以下几点:激活函数不是 用来在方程中产生非线性的。相反,它们是一种过滤器,目的是减少正在构建的网络中的层数或感知器数量。这加快了数据向特定方向收敛的过程。在这个过程中,我们可以对知识进行分类或保留。最终,我们会得到这样或那样的结果,但绝不会两者兼得。
在我的文章https://www.mql5.com/zh/articles/13745 中,我以 相对简单的方式演示了这一点。虽然在那里,我才刚刚开始解释如何理解神经网络。不过,既然你的文章写得很好,而且你也付出了很多努力,那我就给你一个提示吧。取一些看似随机的数据,去掉感知器的激活函数。然后,开始尝试收敛。你会发现效果并不好。但是,如果你开始增加层数和/或更多感知器,收敛情况就会随着时间的推移开始改善。这将帮助你更好地理解为什么需要激活函数。😁👍

- www.mql5.com
文章中的这段话引起了我的注意。虽然文章写得很好,详细介绍了设计和思考的过程。在这段话中,你对主题的理解有微妙之处。也许你有偏见,因为每个人都坚持说神经网络的某些事情。但你的文章写得很好,而且你解释了细节。我决定预测一下我将来要展示的内容。这方面的文章已经写好了,但首先我想解释一下如何建立一个重放/模拟器,现在只剩下几篇文章来完成出版了。请注意以下几点:激活函数不是 用来在方程中创建非线性的。相反,它们是一种滤波器,目的是减少正在构建的网络中的层数或感知器数量。这可以加快数据向特定方向收敛的过程。在这个过程中,我们可以以分类或知识保留为目标。我们最终会得到其中一种结果,但绝不会同时 得到两种 结果。
自动翻译可能不是很准确,但突出显示是不正确的。正是非线性提高了网络的计算能力,它不仅加快了收敛过程(你自己在另一句话中也是这么说的),而且从根本上允许你解决那些不引入非线性就无法解决的问题(无论你添加了多少层)。此外,如果没有非线性,任何(同步)神经网络都可以 "折叠 "成一个等效的单层网络。
我想,我想说的话和我实际用文字表述的内容之间存在误解。
这次我会尽量说得清楚一些。 明确 当我们要对事物进行分类时,比如图像、物体、数字、声音,简而言之,就是对概率进行分类。我们需要限制神经网络中的数值,使其在给定的范围内。这个范围通常在-1 和 1 之间,但也可以在 0 和 1 之间,这取决于我们希望神经网络接触到的输入信息的速度、命中率和处理方式,以及它如何更好地指导自己的学习,以创建对事物的分类。 在这种情况下,我们确实需要 激活函数。正是为了将值保持在这个范围内。最终,我们将有办法根据输入为某一事物的概率生成数值。这是事实,我不否认。因此,我们经常需要对输入数据进行规范化或标准化处理。
然而,神经网络不仅用于对事物进行分类,还可以而且也在用于保留知识。在这种情况下,激活函数在很多情况下都应被摒弃。细节:在某些情况下,我们需要限制一些东西。但这些都是非常特殊的情况。这是因为这些函数会妨碍网络实现其目的。这正是为了保留知识。事实上,我部分同意斯坦尼斯拉夫-科罗特基 的观点,即在这些情况下,如果我们不使用激活函数,网络就可以被折叠成相当于单层的东西。但是,当这种情况发生时,这只是几种情况中的一种,因为在有些情况下,一个包含多个变量的多项式不足以表示或保留知识。在这种情况下,我们需要使用额外的层,这样才能真正复制结果。或者可以生成新的多项式。在没有适当演示的情况下,这样解释有点令人困惑。但这是可行的。
最大的问题是,由于现在什么都流行,在过去的十多年里,如果没记错的话,它一直与人工智能和神经网络联系在一起。尽管这项业务在最近五年才真正兴起。很多人完全不知道它们到底是什么。也不知道它们究竟是如何工作的。这是因为我看到的每个人都在使用现成的框架。这根本无助于理解神经网络的工作原理。它们只是一个多变量方程。它们在学术界已经被研究了几十年。即使它们走出学术界,也从未大张旗鼓地宣布过。在初始阶段和很长一段时间内 没有使用激活函数.但这些网络(当时甚至还不叫神经网络)的目的是不同的。然而,因为有三个人想从中获利,所以在我看来,他们的宣传方式有些错误。至少在我看来,正确的做法应该是对它们进行适当的解释。恰恰是这样,才不会给这么多人的思想造成混乱。不过这样也好,他们三个人赚了大钱,而人们却比从搬运车上掉下来的狗还迷茫。无论如何,我不想打击你写新文章的积极性,安德烈-迪克,但我确实希望你能继续学习,努力深入研究这个问题。我看到您尝试使用纯 MQL5 来创建系统。顺便说一句,这非常好。这引起了我的注意,让我意识到你的文章写得很好,也很有计划性。我只是想提请您注意这一点,并让您多思考一下。事实上,这个话题非常有趣,有很多东西很少有人知道。但你还是去研究了。
Debates em alto nível, são sempre interessantes, pois nos faz crescer e pensar fora da caixa. Brigas não nos leva a nada, e só nos faz perder tempo. 👍

- 2025.01.21
- MetaQuotes
- www.mql5.com
任何激活函数都可以使用,甚至余弦函数也可以,其结果与常用激活函数相同。 建议使用 relu(偏置为 0.1(不建议与 随机行走初始化一起使用 )),因为它简单(计数速度快),学习效果更好:这些区块很容易优化,因为它们与线性区块非常相似。唯一 不同的是,线性整流区块在 其定义域 的一半范围内 输出 0。 因此,线性整流 区块 的导数 在该区块处于活动状态的任何地方都很大。不仅梯度大,而且 一致。整流运算的二阶导数在任何地方都为 0,而 一阶导数在任何地方都为 1。这意味着梯度的方向 比 激活函数受 二阶效应影响时 更有助于学习 ...在初始化仿射变换参数时,建议给b的所有元素赋一个 小的正值,例如 0.1.这样, 对于大多数训练示例, 线性修正块 很可能 在 初始时刻 处于激活状态, 导数也将不同于零。
与分线性方程块 不同的是,正余弦方程块 在 其定义域的大部分范围 内 都接近于 渐近线 -- 当 z 趋于 无穷大 时 接近于 高值 ,而 当 z趋于负无穷大时 接近 于 低值。它们仅在 零点附近 具有较高的灵敏度。由于西格码块的饱和度,梯度 学习会受到严重影响。因此, 现在不建议在前向传播网络 中 使用它们 作为隐藏块 ...如果必须使用西格玛激活函数,最好使用 双曲正切 而不是对数西格玛 。 从 tanh(0) = 0 而 σ(0) = 1/2 的意义上讲, 它更接近于 同一函数。由于 tanh 类似于 零邻域的同一函数 ,因此训练深度神经网络 类似于训练线性模型, 前提是网络激活信号可以保持在较低水平。在这种情况下,使用激活函数 tanh 的网络训练 就得到了简化。
对于 lstm,我们需要使用 sigmoid 或 arctangent(建议将遗忘风口的偏移量设为 1):西格玛激活函数仍在使用,但不适用于前馈 网络 。 递归网络、许多概率模型和 一些自动编码器都有一些额外的要求,这些要求排除了 使用片断线性激活函数的 可能性 ,因此 尽管存在饱和问题,西格码块还是更适合使用。
线性激活和参数缩减:如果网络的每一层都只包含 线性变换,那么 整个 网络 将是线性的。不过,某些层 也可能是 纯线性的 ,这也没有问题。假设一个 神经网络 的某一层 有 n 个 输入和 p 个 输出。可以用两层来代替,一层是权重矩阵 U, 另一层 是权重矩阵 V。 如果 U 产生 q个 输出,那么 U 和 V 加起来只包含 (n + p)q 个 参数, 而 W 则 包含 np 个 参数。对于较小的 q , 节省的参数可能非常可观。代价是一个限制 --线性变换必须 具有较低的秩,但这种低秩链接通常就足够了。因此, 线性隐藏块是减少网络参数数量的有效方法。
Relu更适合深度网络:尽管整流 在 早期模型 中 很受欢迎 ,但 在二十世纪八十年代,它几乎被sigmoid普遍取代,因为它 更适合 非常小的神经网络。
但它在一般情况下效果更好:对于小型数据集 ,使用整流非线性比学习 隐层权重更为重要 。随机权重足以通过网络 传播有用的线性整流信息 ,从而训练分类输出层将不同的特征向量映射到类别标识符上。 如果有更多的数据,学习过程就会开始提取大量 有用的知识,从而超越随机选择的参数... 与 激活函数具有曲率或双向饱和特征的深度网络相比,整流线性 网络的学习要容易得多 ...
我想,我想说的话和我实际用文字表述的内容之间存在误解。
这次我会尽量说得清楚一点。 进行分类时 当我们要对图像、物体、形状、声音等事物进行分类时,简而言之,就是对概率进行分类。我们需要对神经网络中的值进行限制,使其在给定的范围内。通常这个范围在-1 和 1 之间,但也可以在 0 和 1 之间,这取决于我们希望神经网络学习的输入信息的处理速度、速率和方式,以及神经网络如何以最佳方式引导其学习,以创建事物分类。 在这种情况下,我们需要 激活函数。它的作用是将数值保持在该范围内。最终,我们将根据输入为二者之一的概率来生成数值。这是事实,我并不否认。因此,我们经常需要对输入数据进行归一化或标准化处理。
然而,神经网络不仅可用于分类,也可用于知识保留。在这种情况下,激活函数在很多情况下都应被摒弃。细节:在某些情况下,我们需要限制一些东西。但这些都是非常特殊的情况。问题的关键在于,这些功能会妨碍网络实现其目的。And that is to preserve knowledge.事实上,我部分同意斯坦尼斯拉夫-科罗茨基(Stanislav Korotsky )的观点,即在这种情况下,如果不使用激活函数,网络可以简化为单层。但是,当这种情况发生时,它只是几种情况中的一种,因为在有些情况下,一个包含多个变量的多项式不足以表示或存储知识。在这种情况下,我们必须使用额外的层,以便能够实际复制结果。或者,也可以生成新的层。在没有适当演示的情况下,这样解释有点令人困惑。但这是可行的。
最大的问题是,由于现在什么都流行,在过去 10 年左右的时间里,如果我没记错的话,人们一直在谈论人工智能和神经网络。尽管这项业务在过去五年中才真正蓬勃发展起来。很多人完全不知道这些东西到底是什么。以及它们究竟是如何工作的。这是因为我看到的每个人都在使用现成的框架。这根本无助于理解神经网络的工作原理。它只是一个有几个变量的等式。几十年来,学术界一直在研究神经网络。即使它们走出了学术界,也从未如此隆重地宣布过。最初,在很长一段时间里 激活函数并没有.但这些网络(当时甚至还不叫神经网络)的目的是不同的。然而,因为有三个人想利用它们,所以它们被炒得沸沸扬扬,我认为这有些不妥。至少在我看来,正确的做法应该是正确解释其本质。这样才不会让很多人产生混淆。不过没关系,他们三人赚了不少钱,人们比从垃圾车上掉下来的狗还迷茫。总之,我不想打击你写更多文章的积极性,安德鲁-迪克,但我希望你能继续学习,努力钻研这个课题。我看到你尝试使用纯 MQL5 创建一个系统。顺便说一句,这非常好。这引起了我的注意,我意识到你的文章写得很好,也很有计划性。我只是想提请您注意这一点,并让您多思考一下。这个话题其实非常有趣,知道的人并不多。但你却把它拿出来研究了一番。
是的,非线性是激活 phs 的一种间接影响。它们的初衷是将目标定义从一个领域转换到另一个领域,例如,用于分类任务。"非线性 "可以通过不同的方式实现,例如通过增加特征数量或转换特征,或者通过转换特征的核来实现。
最简单的例子就是逻辑回归,尽管最后的激活函数仍是线性的。
但在多层网络中,非线性是由于具有激活函数的层数而产生的,这仅仅是核类型转换的结果。历史背景:
你说得对, 逻辑 回归和早期神经网络的基本概念要早于 现代深度神经网络。
让我们看看时间顺序:
-
逻辑函数 是在 19 世纪开发的。将其用作分类统计模型(逻辑回归)在 20 世纪中期(大约20 世纪 40-50 年代)开始流行。
-
第一个带有激活函数的神经元数学模型(McCulloch 和 Pitts 模型)出现于1943 年。它使用了一个简单的阈值函数。
-
感知器是一种单层神经网络,由弗兰克-罗森布拉特(Frank Rosenblatt)于1958 年 开发。它使用阈值激活函数,只能解决线性可分离问题。
-
1986年,Rumelhart、Hinton和Williams推广了反向传播 算法,深度学习 和多层网络才有了突破性进展。
正是该算法使多层神经网络的训练变得切实可行,并表明它不仅需要阈值,还需要可微分的非线性激活函数(如 sigmoid 和后来的 ReLU)。
结论
历史证明
-
首先,有一些模型(逻辑回归、感知器)本质上是单层模型。
-
在这些模型中,激活函数实际上是对所需领域的转换(从线性和到二元类或概率),因为整个模型仍然是线性的。
-
后来,随着多层网络的出现,激活函数出现了一个新的、从根本上说更为重要的作用--将非线性引入隐层,从而使网络能够学习。
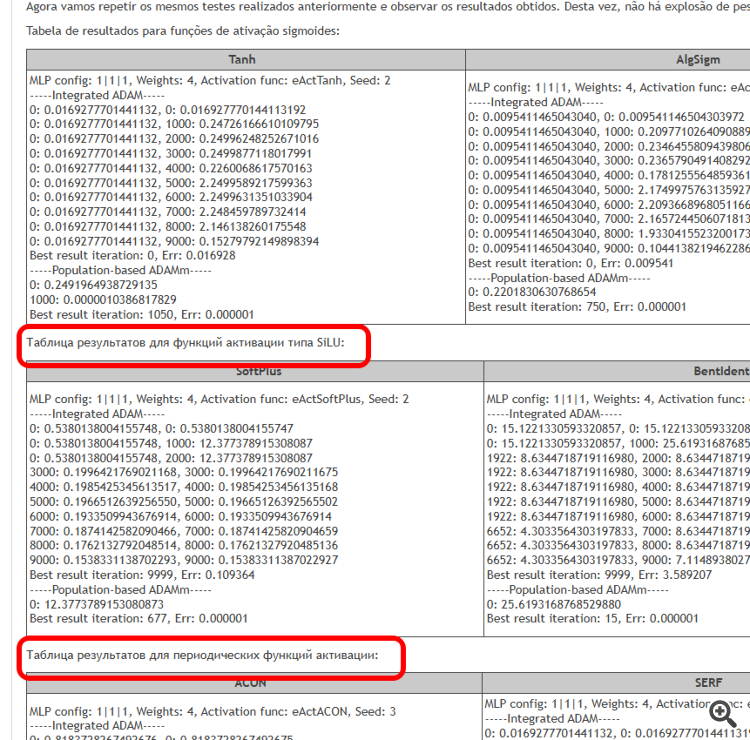
新文章 在训练中激活神经元的函数:快速收敛的关键?已发布:
想象一条有许多支流的河流。在正常状态下,水自由流动,形成复杂的洋流和漩涡模式。但如果我们开始建造一套船闸和水坝系统会怎么样呢?我们将能够控制水流,将其引向正确的方向,并调节水流的力量。神经网络中的激活函数扮演着类似的角色:它决定哪些信号可以通过,哪些信号需要延迟或衰减。没有它,神经网络将只是一组线性变换。
激活函数为神经网络的操作增加了动态性,使其能够捕捉数据中的细微差别。例如,在人脸识别任务中,激活函数帮助网络注意到微小的细节,如眉毛的弧度或下巴的形状。正确选择激活函数会影响神经网络在各种任务上的表现。一些函数更适合训练的早期阶段,提供清晰且易于理解的信号。其他函数则允许网络在高级阶段捕捉更微妙的模式,而还有一些函数则负责筛选掉不必要的部分,只留下最重要的部分。
如果我们不了解激活函数的特性,就可能会遇到问题。神经网络可能会在简单任务上“磕磕绊绊”,或者“忽略”重要的细节。激活函数的主要目的是为神经网络引入非线性,并归一化输出值。
本文旨在识别当使用不同的激活函数,及其在最小化误差时,对神经网络精确遍历样本点(插值)影响的相关问题。我们还将弄清楚激活函数是否真的影响收敛速度,或者这仅仅是所用优化算法的特性。作为参考算法,我们将使用改进的种群 ADAMm,它利用了随机性元素,并与 MLP 内置的 ADAM(经典用法)进行测试比较。后者凭直觉应该具有优势,因为它通过激活函数的导数,可以直接访问适应度函数表面的梯度。与此同时,种群随机 ADAMm 无法访问导数,并且对优化问题的表象一无所知。让我们看看结果如何,并得出一些结论。
作者:Andrey Dik