Практическое использование нейросетей Кохонена в алгоритмическом трейдинге (Часть I): Инструментарий

Тема нейронных сетей Кохонена уже поднималась на сайте mql5.com в рамках нескольких статей, например, Использование самоорганизующихся карт Кохонена в трейдинге и Еще раз о картах Кохонена. В них читатели познакомились с общими принципами построениях нейронных сетей данного типа и визуального анализа экономических показателей рынков с помощью карт.

Однако применение сети Кохонена именно для алгоритмического трейдинга на практике ограничилось лишь одним подходом — всё тем же визуальным анализом топологических карт, построенных для результатов оптимизации советника. В этом случае субъективное мнение, а точнее — видение, человека и его способность делать правильные выводы из картинки оказывается, пожалуй, определяющим фактором, отодвигая на второй план способности сети по представлению данных в разрезе прикладных категорий.

Иными словами, возможности нейросетевых алгоритмов были использованы не в полной мере, без автоматического извлечения знаний и поддержки принятия решений конкретными рекомендациями. В данной статье мы рассмотрим задачу определения оптимальных наборов параметров роботов в более формализованном виде. Кроме того, мы применим сеть Кохонена для прогнозирования экономических рядов. Но прежде чем приступить к этим прикладным задачам, необходимо провести ревизию имеющихся исходных кодов, исправить кое-какие ошибки и внести усовершенствования.

Для тех, кто не знаком с терминами сеть, слой, нейрон (узел), связь, вес, скорость обучения, радиус обучения и других, относящихся к сетям Кохонена, — настоятельно рекомендуется предварительно ознакомиться с указанными статьями. Далее нам потребуется углубиться в данную тему, и повторение базовых понятий существенно удлинило бы материал.

Работа над ошибками

Мы будем отталкиваться от классов CSOM и CSOMNode, опубликованных в первой статье из вышеупомянутых, с некоторой оглядкой на дополнения во второй статье. Основные фрагменты кода в них практически идентичны и наследуют общие проблемы.

Прежде всего, следует отметить, что по каким-то причинам нейроны в данных классах индексируются (идентифицируются и задаются параметрами конструкторов) по пиксельным координатам. Это не особо логично и в некоторых местах усложняет расчеты и отладку. В частности, при таком подходе презентационные настройки влияют на расчетную часть. Только представьте: имеется два полностью аналогичных экземпляра сетей с одинаковыми размерами решетки и они обучаются на одинаковом наборе данных при одинаковых настройках и инициализации генератора случайных чисел, однако результаты получаются разными только потому, что картинки одной сети крупнее, чем другой. Это — ошибка.

Мы перейдем к индексации нейронов по номерам: у каждого нейрона в массиве m_node (класс CSOM) будут координаты x и y, соответствующие номерам колонки и ряда в выходном слое сети Кохонена. Каждый нейрон будет инициализироваться с помощью метода CSOMNode::InitNode(x, y) вместо CSOMNode::InitNode(x1, y1, x2, y2). Когда мы перейдем к визуализации, координаты нейрона будут оставаться неизменными при изменении размеров карты в пикселях.

В унаследованных исходных кодах не используется нормализация входных данных, однако она очень важна для случаев, когда разные компоненты (признаки) входных векторов имеют разный диапазон значений. А это именно так и в результатах оптимизации советников, и при сведении воедино показателей различных индикаторов. Что касается результатов оптимизации, то в них величины с общей прибылью, исчисляемые в десятках тысяч, соседствуют, например, с долями единицы коэффициента Шарпа или однозначными величинами фактора восстановления.

Обучать сеть Кохонена на таких "разномасштабных" данных нельзя, так как сеть фактически будет учитывать только большие компоненты и практически игнорировать малые. Это можно наглядно увидеть на следующем изображении, полученном с помощью программы, которую мы поэтапно рассмотрим в рамках данной статьи и приложим в конце. В программе имеется возможность генерировать случайные входные вектора, в которых три компоненты определены соответственно в диапазонах [0, 1000], [0, 1] и [-1, +1]. Специальный входной параметр UseNormalization позволяет включать и отключать нормализацию.

Посмотрим на финальную структуру сети Кохонена в трех плоскостях, соответствующих трем размерностям векторов.  Сначала результат обучения сети без нормализации.

Результат обучения сети Кохонена без нормализации входных данных

А теперь — с нормализацией.

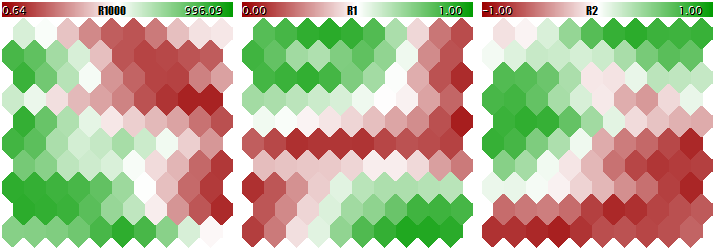
Результат обучения сети Кохонена с нормализацией входных данных

Степень подстройки весов нейронов пропорциональна цветовому градиенту. Очевидно, что в отсутствии нормализации сеть обучилась топологическому разделению (классификации) только в первой плоскости, а вторая и третья компоненты заполнены мелким шумом. Таким образом, аналитические возможности сети реализовались лишь на одну треть. При включении нормализации пространственная структура заметна во всех трех плоскостях.

Способов нормализации известно много, но наиболее популярным, пожалуй, является вычитание из каждой компоненты среднего значения всей выборки и деление на стандартное отклонение (сигма, квадратный корень из дисперсии). Это приводит среднее преобразованных данных к нулю, а стандартное отклонение к единице.

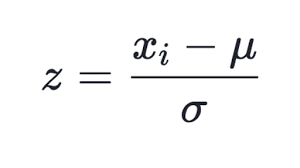 (1)

Этот способ используется в обновленном классе CSOM, в методе Normalize. Разумеется, предварительно необходимо рассчитать среднее и сигму по каждой компоненте входного набора данных, что делается в методе InitNormalization (см. далее).

Канонические формулы расчета среднего и стандартного отклонения подразумевают двухпроходный алгоритм: сперва ищется среднее, а затем с его помощью вычисляется сигма.

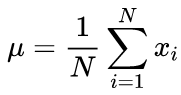                             (2)

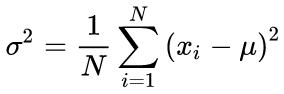     (3)

В нашем исходном коде используется однопроходный алгоритм, основанный на формуле:

 (4)

Разумеется, нормализация на входе требует обратной операции — денормализации — на выходе, то есть при переводе выходных значений сети в диапазон реальных величин. Этим занимается метод CSOM::Denormalize.

Поскольку нормализованные величины ложатся симметрично в окрестность нуля, изменим принцип инициализации весов нейронов перед обучением — вместо диапазона [0, 1] теперь это диапазон [-1, +1] (см. метод CSOMNode::InitNode). Это повысит эффективность обучения сети.

Еще один аспект, требующий корректировки, — подсчет итераций обучения. В исходных классах под итерацией понимается предъявление сети каждого отдельного входного вектора. В связи с этим количество итераций требуется корректировать исходя из и согласуясь с размером обучающей выборки. Напомним, что принцип обучения и обобщения информации сетью Кохонена предполагает, что каждый образец предъявляется сети достаточно большое количество раз. Например, если в выборке 100 записей, то для прохода по каждой из них в среднем по 100 раз потребуется задать число итераций, равное 10000. Однако если выборка составляет 1000 записей, то число итераций должно стать 100000. Более удобным и традиционным способом считается задание числа, так называемых, эпох обучения — циклов, в течение каждого из которых на вход сети в случайном порядке подаются все образцы. Это количество будет задаваться в параметре EpochNumber. Благодаря его введению длительность обучения параметрически отвязывается от размера набора данных.

Это тем более важно, что общий входной набор данных может, при необходимости, делиться на 2 составляющих: непосредственно обучающую выборку и так называемую валидационную. Последняя применяется для отслеживания качества обучения сети. Дело в том, что адаптация сети под входные данные в процессе обучения имеет "оборотную сторону медали": сеть начинает подстраиваться под особенности конкретных образцов и тем самым теряет способность обобщения и адекватной работы на неизвестных данных (отличных от тех, что были использованы для обучения). А ведь смысл обучения, как правило, в том, чтобы выявленные с помощью сети особенности были применимы в будущем.

В рассматриваемой программе за включение валидации отвечает входной параметр ValidationSetPercent. По умолчанию он равен 0, и все данные используются для обучения. Если там указать, например, 10, то только 90% образцов используется для обучения, а на оставшихся 10% на каждой итерации (эпохе) рассчитывается относительная нормализованная среднеквадратическая ошибка (Normalized Mean Squared Error), и обучение останавливается в тот момент, когда ошибка начинает расти.

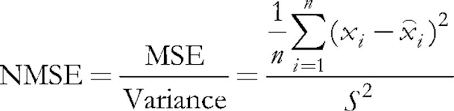 (5)

Нормализация заключается в делении среднеквадратической ошибки на дисперсию самих данных, в результате чего показатель всегда меньше 1. При рассмотрении каждого вектора отдельно данная среднеквадратическая ошибка, по сути, представляет ошибку квантизации, поскольку она основывается на разнице между его компонентами и весами соответствующих синапсов нейрона, дающего наилучшее приближение этого вектора среди всех нейронов. Напомним, что такой выигравший нейрон называется в сетях Кохонена - BMU (best matching unit) или BMN (best matching node) — в классе CSOM за его поиск отвечает метод GetBestMatchingNode и его аналоги.

При включенной валидации количество итераций будет больше, чем заданное в параметре EpochNumber. В связи с особенностями архитектуры сети Кохонена, валидация может производиться только после того, как сеть пройдет фазу самоорганизации на EpochNumber эпохах. По завершению этой фазы скорость обучения и область обучения уменьшаются настолько, что начинается уже тонкая подстройка весов и наступает фаза сходимости. Здесь как раз и используется "ранняя остановка" обучения с помощью валидационного набора.

Использовать или нет валидацию — зависит от конкретики задачи. Кроме всего, валидационный набор можно использовать для подбора размера сети. В рамках данной статьи мы не будем заниматься данным вопросом, а воспользуемся известным эмпирическим правилом, связывающим размер сети с количеством обучающих данных:

N ~ 5 * sqrt(M)          (6)

где N — количество нейронов в сети, M — количество входных векторов. Для сети Кохонена с квадратным выходным слоем получим размер:

S = sqrt(5 * sqrt(M))  (7)

где S — количество нейронов по вертикали и по горизонтали. Эту величину будем вводить в параметры CellsX и CellsY.

Последняя проблема, которую необходимо исправить в оригинальных исходных кодах, касается обработки гексагональной сетки. Как известно, карты Кохонена обычно строятся с использованием прямоугольного или гексагонального размещения ячеек (нейронов), и оба режима изначально реализованы в исходных кодах. Однако гексагональная сетка только отображается в виде сот, однако считается полностью так же, как прямоугольная. Чтобы понять, в чем здесь ошибка, рассмотрим следующую иллюстрацию.

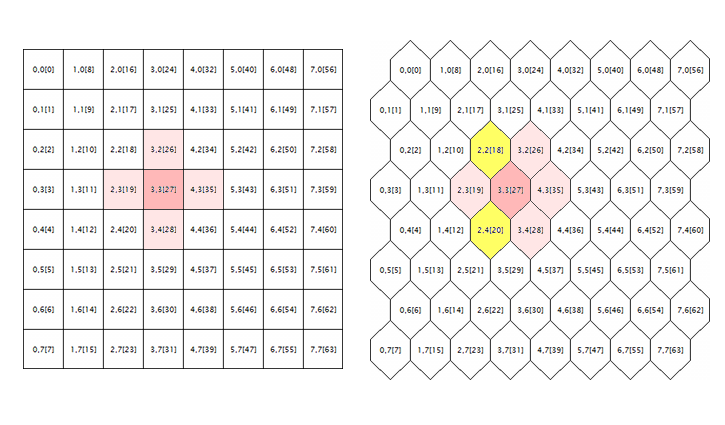
Геометрия окрестности нейрона в прямоугольной и гексагональной решетках

Здесь изображено логическое окружение произвольного нейрона (в данном случае с координатами 3;3) для сеток обеих геометрий. Радиус окружения равен 1. В квадратной сетке у нейрона 4 непосредственных соседа, а в гексагональной - 6. Реализация сотообразного вида достигается смещением каждой второй строки ячеек на половину ячейки в сторону. Однако их внутренние координаты от этого не меняются, и с точки зрения алгоритма окружение нейрона в гексагональной сетке выглядит прежним образом — оно помечено розовым.

Это, очевидно, неверно и должно быть исправлено, путем включения нейронов, подсвеченных желтым.

Строго говоря, алгоритм считает окружение не только по прилегающим соседям, а как выпуклую убывающую радиальную функцию, зависящую от расстояния между координатами ячеек. Иными словами, соседство является не бинарным свойством нейрона (либо сосед, либо нет), а непрерывной величиной, рассчитываемой по формуле Гауссиана:

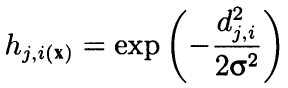 (8)

Здесь dji - расстояние между нейронами j и i (имеется в виду сквозная нумерация, а не координаты x и y); сигма — эффективная ширина окрестности или радиус обучения, который постепенно уменьшается в процессе обучения. В начале обучения окрестность охватывает симметричным "колоколом" гораздо большее пространство, нежели непосредственно прилегающие нейроны.

Поскольку данная формула зависит от расстояния, она также искажает окрестность, если координаты не откорректированы соответствующим образом. Поэтому следующие строчки оригинального исходного кода из метода CSOM::Train:

      for(int i = 0; i < total_nodes; i++)
      {
         double DistToNodeSqr = (m_som_nodes[winningnode].X() - m_som_nodes[i].X()) * (m_som_nodes[winningnode].X() - m_som_nodes[i].X())
                              + (m_som_nodes[winningnode].Y() - m_som_nodes[i].Y()) * (m_som_nodes[winningnode].Y() - m_som_nodes[i].Y());

были дополнены:

      bool odd = ((winningnode % m_ycells) % 2) == 1;
      for(int i = 0; i < total_nodes; i++)
      {
        bool odd_i = ((i % m_ycells) % 2) == 1;
        double shiftx = 0;

        if(m_hexCells && odd != odd_i)
        {
          if(odd && !odd_i)
          {
            shiftx = +0.5;
          }
          else // vice versa (!odd && odd_i)
          {
            shiftx = -0.5;
          }
        }
        double DistToNodeSqr = (m_node[winningnode].GetX() - (m_node[i].GetX() + shiftx)) * (m_node[winningnode].GetX() - (m_node[i].GetX() + shiftx))
                             + (m_node[winningnode].GetY() - m_node[i].GetY()) * (m_node[winningnode].GetY() - m_node[i].GetY());

Направление поправки shiftx зависит от соотношения свойств четности и нечетности рядов, где находятся два нейрона, между которыми рассчитывается расстояние. Если нейроны в одинаково выровненных рядах, то поправки нет. Если выигравший нейрон в нечетном ряду, то четные ряды относительно него выглядят сдвинутыми вправо на половину ячейки, поэтому shiftx равен +0.5. Если выигравший нейрон в четном ряду, то нечетные ряды кажутся сдвинутыми относительно него на пол-ячейки влево, поэтому shiftx равен -0.5.

Теперь особенно важно обратить внимание на следующие оригинальные строки:

        if(DistToNodeSqr < WS)
        {
          double influence = MathExp(-DistToNodeSqr / (2 * WS));
          m_node[i].AdjustWeights(data, learning_rate, influence);
        }

Данный условный оператор фактически обеспечивает некоторое ускорение расчетов за счет отбрасывания нейронов вне окрестности одной сигмы. Однако с точки зрения качества обучения Гауссиан является идеальной формой и подобное вмешательство неоправданно. Если уж и производить отбрасывание слишком далеких нейронов, то по трем сигмам, а не по одной. Это тем более критично после того, как мы поправили расчет гексагональной решетки, поскольку расстояние между смежными нейронами, расположенными в соседних рядах, равно sqrt(1*1 + 0.5*0.5) = 1.118, то есть больше единицы. В прилагаемых исходных кодах этот условный оператор закомментирован. Если возникнет реальная необходимость ускорить расчеты, используйте вариант:

        if(DistToNodeSqr < 9 * WS)

Внимание! В связи с указанным нюансом в различии расстояний между соседними нейронами в зависимости от их ряда (однорядные имеют дистанцию 1, а со смежными рядами - 1.118), текущая реализация по-прежнему не идеальна и предполагает дальнейшую корректировку для достижения полной анизотропности.

Визуализация

Несмотря на то, что сети Кохонена ассоциируются, в первую очередь, с видимой графической картой, их топология и алгоритмы обучения могут прекрасно работать без пользовательского интерфейса. В частности, задачи прогнозирования или сжатия информации не требуют обязательного визуального анализа, да и классификация образов может выдавать результат в виде числа — номера класса или вероятности события. В связи с этим функционал сетей Кохонена был разделен между двумя классами. В классе CSOM осталась лишь вычислительная часть, загрузка и сохранение данных, загрузка и сохранение сетей. А в дополнение к нему был создан производный класс CSOMDisplay, куда вынесена вся графика. Это, на мой взгляд, более простая и логичная иерархия, чем предложенная в статье 2. В дальнейшем для задачи выбора оптимальных параметров эксперта будем использовать CSOMDisplay, а для прогнозирования — CSOM.

Обратите внимание, что признак типа решетки — прямоугольная или гексагональная — относится к базовому классу, поскольку влияет на расчет расстояний. Наравне с количеством узлов по вертикали и горизонтали, а также размерностью входного пространства данных, тип решетки составляет архитектуру сети и сохраняется в файл. При загрузке сети из файла, все эти параметры считываются именно оттуда, а не из настроек программы. Прочие настройки, которые влияют лишь на визуальное представление — такие как размер карт в пикселях, отображение границ между ячейками, вывод надписей, — в файл сети не сохраняются и могут меняться многократно, произвольно для единожды обученной сети.

Стоит отметить, что ни один из обновленных классов не предоставляет пользовательского графического интерфейса с элементами управления — все настройки задаются через входные параметры MQL-программ. Вместе с тем, класс CSOMDisplay все же реализует некоторые полезные возможности.

Напомним, что в прежних вариантах примеров работы с сетями Кохонена был входной параметр MaxPictures, и он оставлен в новой реализации. Он передается как maxpict в метод CSOMDisplay::Init и задает количество карт (плоскостей) сети, выводимых на графике в одном ряду. Оперируя данным параметром вместе с унифицированным размером изображений в ImageW и ImageH, можно подобрать вариант, когда все карты умещаются на экране. Однако, когда карт много (например, если требуется проанализировать много настроек советника) их размер приходится существенно уменьшать, что неудобно. Для подобных случаев с помощью MaxPictures можно активизировать новый режим, установив параметр в 0.

В этом режиме изображения карт формируются на графике не в виде объектов OBJ_BITMAP_LABEL с привязкой к пиксельным координатам, а в виде объектов OBJ_BITMAP с привязкой к временной шкале. Размер таких карт может быть увеличен вплоть до всей высоты графика, а пролистывать их можно с помощью привычной горизонтальной прокрутки — перетаскивая мышью, колесиком или с клавиатуры. Количество карт более не ограничено размером экрана, однако нужно убедиться в наличии достаточного количества баров.

Увеличение размера карт позволяет изучить их более подробно, тем более что класс CSOMDisplay опционально выводит внутри ячеек различную информацию, такую как значение веса синапса соответствующей плоскости, количество попаданий векторов обучающего набора, среднее и дисперсию значений соответствующего признака всех векторов, попавших в ячейку. Данная информация по умолчанию не выводится, но она всегда доступна во всплывающих подсказках, которые появляются, если задержать мышь над той или иной ячейкой. Также в подсказках выводится название текущей плоскости и координаты нейрона.

Кроме того, по двойному щелчку на любом нейроне, он подсвечивается инверсным цветом в текущей карте, а также сразу во всех остальных картах. Это позволяет наглядно сравнить активность нейрона сразу по всем признакам.

Ну и наконец, следует отметить, что вся графика переведена на стандартный класс CCanvas. Это избавляет код от внешних зависимостей, но имеет и один побочный эффект: координаты Y отсчитываются теперь сверху вниз, а не снизу вверх, как было ранее. В результате этого легенда карт с названием компонент и диапазонами их значений выводится над картами, а не под, однако это изменение кажется не принципиальным.

Усовершенствования

Прежде чем мы сможем приступить к прикладным задачам, требуется еще несколько усовершенствовать нейросетевые классы. В дополнение к стандартным картам, представляющим веса синапсов в 2D-пространствах конкретных признаков, подготовим расчет и отображение нескольких служебных карт, которые являются стандартом de-facto для сетей Кохонена. Забегая вперед, скажем, что многие из них потребуются нам на стадии прикладных экспериментов.

Определим индексы дополнительных размерностей - всего их будет 5.

#define EXTRA_DIMENSIONS 5
#define DIM_HITCOUNT (m_dimension + 0)
#define DIM_UMATRIX  (m_dimension + 1)
#define DIM_NODEMSE  (m_dimension + 2) // quantization errors per node: average variance (square of standard deviation)
#define DIM_CLUSTERS (m_dimension + 3)
#define DIM_OUTPUT   (m_dimension + 4)

U-Matrix

Прежде всего, для оценки топологии, возникшей в процессе обучения внутри сети, рассчитаем унифицированную матрицу расстояний — U-matrix. Для каждого нейрона в сети данная матрица содержит среднее расстояние между этим нейроном и его непосредственными соседями. Поскольку сеть Кохонена отображает многомерное пространство признаков в двумерное пространство карты, в этом двумерном пространстве возникают складки. Иными словами, несмотря на свойство сети Кохонена сохранять порядок, присущий исходному пространству, это недостижимо в равной степени на всей 2D-плоскости, и кое-где географическая близость нейронов становится обманчивой. Для определения таких мест и используется U-matrix. На ней места, где существует большая разница между весами нейрона и весами его соседей, выглядят как "горы", а места, где нейроны сильно похожи — как "низины".

Для расчета расстояния между нейроном и вектором признаков имеется метод CSOMNode::CalculateDistance. Мы создадим для него метод-двойник, который будет принимать вместо вектора (массива double) указатель на другой нейрон.

double CSOMNode::CalculateDistance(const CSOMNode *other) const
{
  double vector[];
  other.GetCodeVector(vector);
  return CalculateDistance(vector);
}

Здесь метод GetCodeVector получает массив с весами другого нейрона и тут же отправляет его для расчета расстояния привычным способом.

Для получения унифицированного расстояния нейрона необходимо рассчитать расстояние со всеми соседними нейронами и усреднить. Поскольку обход соседних нейронов является общей задачей для нескольких операций над решеткой сети, создадим базовый класс для обхода, а затем в его наследниках реализуем конкретные алгоритмы, включая и суммирование расстояний.

#define NBH_SQUARE_SIZE    4
#define NBH_HEXAGONAL_SIZE 6

template<typename T>
class Neighbourhood
{
  protected:
    int neighbours[];
    int nbhsize;
    bool hex;
    int m_ycells;

  public:
    Neighbourhood(const bool _hex, const int ysize)
    {
      hex = _hex;
      m_ycells = ysize;

      if(hex)
      {
        nbhsize = NBH_HEXAGONAL_SIZE;
        ArrayResize(neighbours, NBH_HEXAGONAL_SIZE);
        neighbours[0] = -1; // up (visually)
        neighbours[1] = +1; // down (visually)
        neighbours[2] = -m_ycells; // left
        neighbours[3] = +m_ycells; // right
        /* template, applied dynamically in the loop below
        // odd row
        neighbours[4] = -m_ycells - 1; // left-up
        neighbours[5] = -m_ycells + 1; // left-down
        // even row
        neighbours[4] = +m_ycells - 1; // right-up
        neighbours[5] = +m_ycells + 1; // right-down
        */
      }
      else
      {
        nbhsize = NBH_SQUARE_SIZE;
        ArrayResize(neighbours, NBH_SQUARE_SIZE);
        neighbours[0] = -1; // up (visually)
        neighbours[1] = +1; // down (visually)
        neighbours[2] = -m_ycells; // left
        neighbours[3] = +m_ycells; // right
      }
    
    }
    ~Neighbourhood()
    {
      ArrayResize(neighbours, 0);
    }

    T loop(const int ind, const CSOMNode &p_node[])
    {
      int nodes = ArraySize(p_node);
      int j = ind % m_ycells;
      
      if(hex)
      {
        int oddy = ((j % 2) == 1) ? -1 : +1;
        neighbours[4] = oddy * m_ycells - 1;
        neighbours[5] = oddy * m_ycells + 1;
      }
      
      reset();

      for(int k = 0; k < nbhsize; k++)
      {
        if(ind + neighbours[k] >= 0 && ind + neighbours[k] < nodes)
        {
          // skip wrapping edges
          if(j == 0) // upper row
          {
            if(k == 0 || k == 4) continue;
          }
          else if(j == m_ycells - 1) // bottom row
          {
            if(k == 1 || k == 5) continue;
          }
          
          iterate(p_node[ind], p_node[ind + neighbours[k]]);
        }
      }
      
      return getResult();
    }
    
    virtual void reset() = 0;
    virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) = 0;
    virtual T getResult() const = 0;
};

В зависимости от типа решетки, передаваемой в конструктор, число соседей nbhsize берется равным 4 и 6. Приращения номеров соседних нейронов относительно текущего нейрона хранит массив neighbours. Например, в квадратной решетке сосед сверху получается вычитанием единицы, а сосед снизу — прибавлением единицы к номеру нейрона. Соседи слева и справа имеют номера, отличающиеся на высоту столбца решетки, поэтому в конструктор передается эта величина как ysize.

Непосредственно обход соседей осуществляет метод loop. Класс Neighbourhood не имеет у себя массива нейронов, и потому он передается как параметр в метод loop.

Данный метод в цикле проходит по массиву neighbours и дополнительно проверят, чтобы с учетом приращения номер соседа не вышел за пределы решетки. Для всех валидных номеров вызывается абстрактный метод iterate, куда передаются ссылки на текущий нейрон и один из нейронов окружения.

Перед циклом вызывается абстрактный метод reset, а после цикла — абстрактный метод getResult. Набор трех абстрактных методов позволяет в классах-наследниках подготовить и осуществить перебор соседей, а также сформировать результат. Концепция построения метода loop соответствует известному ООП паттерну проектирования — шаблонный метод. Здесь следует отличать термин "шаблонный" в собственном названии паттерна, от языковой конструкции шаблонов, которая также используется в классе Neighbourhood, поскольку он является шаблонным (параметризуется неким переменным типом T). В частности, сам метод loop и метод getResult возвращают значение типа T.

На основе класса Neighbourhood напишем класс для расчета U-matrix.

class UMatrixNeighbourhood: public Neighbourhood<double>
{
  private:
    int n;
    double d;
    
  public:
    UMatrixNeighbourhood(const bool _hex, const int ysize): Neighbourhood(_hex, ysize)
    {
    }
    
    virtual void reset() override
    {
      n = 0;
      d = 0.0;
    }
    
    virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) override
    {
      d += node1.CalculateDistance(&node2);
      n++;
    }
    
    virtual double getResult() const override
    {
      return d / n;
    }
};

Рабочим типом является double. Благодаря базовому классу, вычисления расстояния достаточно прозрачны.

Обсчет расстояний для всей карты выполним в методе CSOM::CalculateDistances.

void CSOM::CalculateDistances()
{
  UMatrixNeighbourhood umnh(m_hexCells, m_ycells);
  
  for(int i = 0; i < m_xcells * m_ycells; i++)
  {
    double d = umnh.loop(i, m_node);
    
    if(d > m_max[DIM_UMATRIX])
    {
      m_max[DIM_UMATRIX] = d;
    }
    
    m_node[i].SetDistance(d);
  }
}

Значение унифицированного расстояния сохраняется в объекте нейрона. Позднее, при выводе всех плоскостей, мы сможем обозначить величины расстояний стандартным способом с помощью цветовой палитры, включив дополнительное измерение DIM_UMATRIX в расчет. Для правильного масштабирования палитры мы в этом методе сохраняем максимальное значение расстояния в соответствующем элементе массива m_max (все принципы визуализации остались неизменными с прежних реализаций).

Количество попаданий и ошибка квантизации

Следующая дополнительная размерность будет собирать статистику по количеству попаданий обучающих векторов в конкретные нейроны. Иными словами, это плотность заселения нейронов прикладными данными. Чем она больше у конкретного нейрона, тем более статистически обоснованными являются его весовые коэффициенты. В сети могут встречаться нейроны с малым и даже нулевым покрытием данными. Если их много, это может свидетельствовать о проблемах в выборе размера сети или перекручивании топологии в 2D-проекции многомерного пространства. Подсчет попаданий образцов в конкретный нейрон выполняет метод:

void CSOMNode::RegisterPatternHit(const double &vector[])
{
  m_hitCount++;
  double e = 0;
  for(int i = 0; i < m_dimension; i++) 
  {
    m_sum[i] += vector[i];
    m_sumP2[i] += vector[i] * vector[i];
    e += (m_weights[i] - vector[i]) * (m_weights[i] - vector[i]);
  }
  m_mse += e / m_dimension;
}

Собственно подсчет делается в первой строке m_hitCount++, где увеличивается внутренний счетчик. Остальной код выполняет другую полезную работу, о которой пойдет речь ниже.

Вызов метода RegisterPatternHit будем делать после завершения обучения, из класса CSOM, где создадим специальный метод статистической обработки каждого вектора.

double CSOM::AddPatternStats(const double &data[])
{
  static double vector[];
  ArrayCopy(vector, data);
  
  int ind = GetBestMatchingIndex(vector);
  
  m_node[ind].RegisterPatternHit(vector);

  double code[];
  m_node[ind].GetCodeVector(code);
  Denormalize(code);
  
  double mse = 0;
  
  for(int i = 0; i < m_dimension; i++)
  {
    mse += (data[i] - code[i]) * (data[i] - code[i]);
  }
  
  mse /= m_dimension;
  
  return mse;
}

В качестве отступления заметим, что метод GetBestMatchingIndex (использованный здесь) как и некоторые другие из группы GetBestMatchingXYZ методов, производит внутри себя нормализацию поступающих данных, в связи с чем необходимо передавать в него копию вектора (иначе была бы открыта возможность неявной модификации исходных данных в вызывающем коде).

Кроме регистрации попадания данный метод подсчитывает ошибку квантизации для текущего нейрона и переданного вектора. Для этого у выигравшего нейрона запрашивается его, так называемый, кодовый вектор (code vector) — массив весов синапсов, и считается сумма квадратов покомпонентных разностей между весами и входным вектором.

Непосредственно AddPatternStats вызывается из другого метода CSOM::CalculateStats, который просто организует цикл по всем входным данным.

double CSOM::CalculateStats(const bool complete = true)
{
  double data[];
  ArrayResize(data, m_dimension);
  double trainedMSE = 0.0;
  
  for(int i = complete ? 0 : m_validationOffset; i < m_nSet; i++)
  {
    ArrayCopy(data, m_set, 0, m_dimension * i, m_dimension);
    trainedMSE += AddPatternStats(data, complete);
  }
  
  double nmse = trainedMSE / m_dataMSE;
  if(complete) Print("Overall NMSE=", nmse);

  return nmse;
}

Этот метод суммирует все ошибки квантизации и соотносит их с дисперсией входных данных в m_dataMSE — это и есть расчет NMSE, о котором шла речь выше в контексте валидации и остановки обучения. В данном методе упоминается переменная m_validationOffset, которая задается при создании объекта CSOM на основе того, используется ли деление входного множества данных на обучающий и валидационный поднабор.

Как нетрудно догадаться, метод CalculateStats вызывается на каждой эпохе внутри метода Train (если уже наступила фаза сходимости), и по возвращаемому значению можно судить, стала ли увеличиваться общая ошибка сети, т.е. не пора ли останавливаться.

Расчет дисперсии m_dataMSE делается заблаговременно с помощью метода:

void CSOM::CalculateDataMSE()
{
  double data[];

  m_dataMSE = 0.0;
  
  for(int i = m_validationOffset; i < m_nSet; i++)
  {
    ArrayCopy(data, m_set, 0, m_dimension * i, m_dimension);

    double mse = 0;
    for(int k = 0; k < m_dimension; k++)
    {
      mse += (data[k] - m_mean[k]) * (data[k] - m_mean[k]);
    }
    
    mse /= m_dimension;
    m_dataMSE += mse;
  }
}

Значение средней величины m_mean для каждой компоненты мы получаем еще на стадии нормализации данных.

void CSOM::InitNormalization(const bool normalization = true)
{
  ArrayResize(m_max, m_dimension + EXTRA_DIMENSIONS);
  ArrayResize(m_min, m_dimension + EXTRA_DIMENSIONS);
  ArrayInitialize(m_max, 0);
  ArrayInitialize(m_min, 0);
  ArrayResize(m_mean, m_dimension);
  ArrayResize(m_sigma, m_dimension);

  for(int j = 0; j < m_dimension; j++)
  {
    double maxv = -DBL_MAX;
    double minv = +DBL_MAX;
    
    if(normalization)
    {
      m_mean[j] = 0;
      m_sigma[j] = 0;
    }
    
    for(int i = 0; i < m_nSet; i++)
    {
      double v = m_set[m_dimension * i + j];
      if(v > maxv) maxv = v;
      if(v < minv) minv = v;
      if(normalization)
      {
        m_mean[j] += v;
        m_sigma[j] += v * v;
      }
    }
    
    m_max[j] = maxv;
    m_min[j] = minv;
    
    if(normalization && m_nSet > 0)
    {
      m_mean[j] /= m_nSet;
      m_sigma[j] = MathSqrt(m_sigma[j] / m_nSet - m_mean[j] * m_mean[j]);
    }
    else
    {
      m_mean[j] = 0;
      m_sigma[j] = 1;
    }
  }
}

Возвращаясь к дополнительным плоскостям, отметим, что после проведенных расчетов в CSOMNode::RegisterPatternHit каждый нейрон способен вернуть соответствующую статистику с помощью методов:

int CSOMNode::GetHitsCount() const
{
  return m_hitCount;
}

double CSOMNode::GetHitsMean(const int plane) const
{
  if(m_hitCount == 0) return 0;
  return m_sum[plane] / m_hitCount;
}

double CSOMNode::GetHitsDeviation(const int plane) const
{
  if(m_hitCount == 0) return 0;
  double z = m_sumP2[plane] / m_hitCount - m_sum[plane] / m_hitCount * m_sum[plane] / m_hitCount;
  if(z < 0) return 0;
  return MathSqrt(z);
}

double CSOMNode::GetMSE() const
{
  if(m_hitCount == 0) return 0;
  return m_mse / m_hitCount;
}

Таким образом, мы получаем данные для заполнения двух плоскостей — с количеством отображений входных векторов по нейронам и с ошибкой квантизации.

Реакция сети

Следующей дополнительной плоскостью будет карта выхода или реакции сети на конкретный образец. Не стоит забывать, что после подачи сигнала на сеть помимо выигравшего нейрона активируются и все остальные - в большей или меньшей степени. Возможность сравнить размах активных областей отклика может помочь в определении устойчивости решения, которое предлагает сеть.

Расчет реакции сети предельно прост. В классе CSOMNode напишем метод:

double CSOMNode::CalculateOutput(const double &vector[])
{
  m_output = CalculateDistance(vector);
  return m_output;
}

И в классе сети вызовем его для каждого нейрона.

void CSOM::CalculateOutput(const double &vector[], const bool normalize = false)
{
  double temp[];
  ArrayCopy(temp, vector);
  if(normalize) Normalize(temp);
  m_min[DIM_OUTPUT] = DBL_MAX;
  m_max[DIM_OUTPUT] = -DBL_MAX;
  for(int i = 0; i < ArraySize(m_node); i++)
  {
    double x = m_node[i].CalculateOutput(temp);
    if(x < m_min[DIM_OUTPUT]) m_min[DIM_OUTPUT] = x;
    if(x > m_max[DIM_OUTPUT]) m_max[DIM_OUTPUT] = x;
  }
}

Если тестовый вектор не предоставлен программе, реакция рассчитывается по-умолчанию — для нулевого вектора.

Кластеризация

Наконец, последней из рассматриваемых, но, пожалуй, самой важной плоскостью будет карта кластеров. Упорядочить исходные данные на двумерной карте — это только полдела, истинная цель анализа — в выявлении особенностей и категоризации по понятным с прикладной точки зрения классам. Когда размерность пространства признаков относительно мала, мы можем достаточно легко различить области с требуемыми характеристиками по цветным пятнам на конкретных плоскостях, причем пятна эти обычно обособлены. Но по мере расширения структуры входных данных картина усложняется, и вместо перекрестного анализа десятка карт с различными показателями удобнее иметь одну карту с готовым разделением на участки, требующие внимания.

Результатом кластеризации будет не только разметка карты на области со схожими характеристиками, но и определение центров кластеров. А их уже можно рассматривать как наиболее представительные (в статистическом смысле) образцы соответствующих классов. И здесь мы плавно подбираемся к задаче выбора оптимальных параметров эксперта. Но сперва нужно реализовать кластеризацию.

K-Means

Методов кластеризации существует великое множество. Наиболее простой вариант для MQL5: воспользоваться версией ALGLIB, входящей в состав стандартной библиотеки. Достаточно включить заголовочный файл:

#include <Math/Alglib/dataanalysis.mqh>

и написать примерно такой метод:

void CSOM::Clusterize(const int clusterNumber)
{
  int count = m_xcells * m_ycells;
  CMatrixDouble xy(count, m_dimension);
  int info;
  CMatrixDouble clusters;
  int membership[];
  double weights[];
  
  for(int i = 0; i < count; i++)
  {
    m_node[i].GetCodeVector(weights);
    xy[i] = weights;
  }

  CKMeans::KMeansGenerate(xy, count, m_dimension, clusterNumber, KMEANS_RETRY_NUMBER, info, clusters, membership);
  Print("KMeans result: ", info);
  if(info == 1) // ok
  {
    for(int i = 0; i < m_xcells * m_ycells; i++)
    {
      m_node[i].SetCluster(membership[i]);
    }
    
    ArrayResize(m_clusters, clusterNumber * m_dimension);
    for(int j = 0; j < clusterNumber; j++)
    {
      for(int i = 0; i < m_dimension; i++)
      {
        m_clusters[j * m_dimension + i] = clusters[i][j];
      }
    }
  }
}

Он выполняет кластеризацию с помощью алгоритма K-Means. К сожалению, насколько мне известно, это единственный алгоритм кластеризации в версии ALGLIB на MQL5, хотя последняя версия оригинальной библиотеки предоставляет и другие, в частности, агломеративную иерархическую кластеризацию.

"К сожалению" — потому что алгоритм K-Means является наиболее "прямолинейным", в некотором смысле: его суть сводится к поиску центров заданного числа сфероидов (в пространстве признаков), покрывающих точки выборки наиболее экономичным способом (минимум суммы квадратов расстояний от точек до центров кластеров). Проблема в том, что из-за своей фиксированной формы сфероиды имеют специфические ограничения на разделимость нелинейных кластеров. В принципе, K-Means является частным случаем алгоритма Expectation Maximization, который оперирует эллипсоидами разной ориентации и формы, и потому был бы предпочтительнее. Однако даже при его применении остается вероятность застревания в локальном минимуме (поскольку оба алгоритма используют только выпуклые формы и случайное начальное расположение центров кластеров). Кроме того, к  минусам можно отнести и то, что требуется заранее указать количество кластеров.

Но все же, рассмотрим, как организована кластеризация с помощью K-Means в ALGLIB. Всю основную работу выполняет метод CKMeans::KMeansGenerate. В него мы передаем массив с исходными данными в специальном объектном формате (CMatrixDouble xy), число векторов count, размерность пространства признаков m_dimension и желаемое количество кластеров clusterNumber (его приходится задавать в параметрах MQL программы). Следующий входной параметр — KMEANS_RETRY_NUMBER — количество повторов, которые алгоритм сделает с различными, случайно выбранными, начальными центрами в попытке избежать локального решения. В нашем случае это — макрос, равный 10. В качестве результата работы функции мы получим код выполнения info (различные значения говорят об успехе или ошибке), объектный массив CMatrixDouble clusters с координатами кластеров, а также массив принадлежности входных данных кластерам — membership.

Мы сохраняем центры кластеров в массив m_clusters, чтобы пометить их на карте, а также раскрашиваем каждый нейрон цветом согласно принадлежности кластеру:

m_node[i].SetCluster(membership[i]);

При работе с ALGLIB имейте в виду, что она использует свой собственный генератор случайных чисел, учитывающий внутреннее состояние специального статического объекта. Поэтому даже явная инициализации стандартного генератора через MathSrand не сбрасывает его состояние. Это особенно критично для экспертов, так как в них глобальные объекты не пересоздаются при смене настроек. В результате, с ALGLIB могут возникнуть трудности с воспроизводимостью результатов расчетов, если не обнулять CMath::m_state в OnInit.

Учитывая озвученные минусы K-Means, желательно иметь запасной вариант кластеризации. Одно альтернативное решение лежит на поверхности.

Альтернатива

Давайте еще раз обратим внимание на карты Кохонена, и в особенности на дополнительные размерности, которые мы ввели. Особый интерес вызывает U-Matrix. Эта плоскость показывает области наиболее близких нейронов — близких не только в топологическом смысле 2D-карты, но и близких в пространстве признаков. Как мы помним, похожие нейроны формируют в U-Matrix своего рода "низины". Они являются прекрасными кандидатами на то, чтобы стать кластерами.

Преобразовать карту унифицированных расстояний в кластеры можно, например, следующим образом.

Скопируем информацию о всех нейронах в массив и отсортируем его по величине У-расстояния (CSOMNode::GetDistance()) по возрастанию.

В цикле по массиву будем проверять для очередного нейрона, не принадлежат ли соседние нейроны к какому-либо кластеру.

• Если нет, создаем новый кластер и относим к нему текущий нейрон. Заметьте, что кластеры будут создаваться, начиная с нулевого индекса, что соответствует самому "важному" кластеру, поскольку он соответствует минимальному У-расстоянию, и далее в порядке уменьшения ценности. Каждый следующий кластер будет менее компактным в смысле У-расстояний.
• Если среди соседних нейронов уже есть помеченные каким-либо кластером, выберем из них старший, т.е. с минимальным индексом, и отнесем текущий нейрон к нему.

Всё просто. Но не следует ли рассмотреть и плотность заселения нейронов? Ведь У-расстояние имеет разную подкрепленность для нейронов с различным числом попаданий. Иными словами, при равном У-расстоянии у двух нейронов — тот из них, в который было отображено больше образцов, должен иметь преимущество перед нейроном с меньшим числом.

Тогда достаточно в описанном алгоритме изменить начальную сортировку массива в порядке значений формулы CSOMNode::GetDistance() / sqrt(CSOMNode::GetHitsCount()). Я добавил квадратный корень, чтобы при большом населении его влияние сглаживалось, а вот малое должно "штрафоваться" сильнее.

Но если уж мы используем две служебные плоскости, может быть имеет смысл проанализировать и третью — с ошибкой квантизации? Действительно, чем больше ошибка квантизации в конкретном нейроне, тем меньше мы должны доверять сведениям о малом У-расстоянии в нем, и наоборот.

Если мы вспомним, как выглядит функция с ошибкой квантизации:

double CSOMNode::GetMSE() const
{
  if(m_hitCount == 0) return 0;
  return m_mse / m_hitCount;
}

то, легко заметим, что в ней уже используется счетчик попаданий m_hitCount (только в знаменателе), поэтому предыдущую формулу для сортировки массива нейронов можно переписать как CSOMNode::GetDistance() * MathSqrt(CSOMNode::.GetMSE()) — и в ней будут учтены все три дополнительных показателя, которыми мы снабдили свою реализацию сети Кохонена.

Мы почти готовы представить альтернативный алгоритм кластеризации в окончательном виде, но осталась одна мелочь. Внутри цикла по массиву нейронов нам необходимо просматривать окрестность текущего нейрона на предмет наличия соседних кластеров. Чуть раньше мы реализовали для местного обзора шаблонный класс Neighbourhood. Теперь создадим его наследник, специализирующийся на поиске кластеров.

class ClusterNeighbourhood: public Neighbourhood<int>
{
  private:
    int cluster;

  public:
    ClusterNeighbourhood(const bool _hex, const int ysize): Neighbourhood(_hex, ysize)
    {
    }
    
    virtual void reset() override
    {
      cluster = -1;
    }
    
    virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) override
    {
      int x = node2.GetCluster();
      if(x > -1)
      {
        if(cluster != -1) cluster = MathMin(cluster, x);
        else cluster = x;
      }
    }
    
    virtual int getResult() const override
    {
      return cluster;
    }
};

Класс хранит в себе номер потенциального кластера cluster (номер — целого типа, потому параметризуем шаблон типом int). Изначально эта переменная инициализируется в -1 в методе reset — то есть кластера нет. Затем, по мере того, как родительский класс вызывает из своего метода loop нашу новую реализацию iterate, мы получаем номер кластера каждого соседнего нейрона, сравниваем его с cluster и сохраняем минимальное значение. Оно же, или -1, если кластеров не было найдено, возвращается методом getResult.

В качестве усовершенствования предлагается отслеживать "высоту хребтов" между нейронами (т.е. значение node1.CalculateDistance(&node2)) и осуществлять "перетекание" номера кластера из одного нейрона в другой только в том случае, если "высота" меньше той, что была. Окончательный вариант реализации представлен в исходном коде.

Наконец, мы можем реализовать альтернативную кластеризацию.

void CSOM::Clusterize()
{
  double array[][2];
  int n = m_xcells * m_ycells;
  ArrayResize(array, n);
  for(int i = 0; i < n; i++)
  {
    if(m_node[i].GetHitsCount() > 0)
    {
      array[i][0] = m_node[i].GetDistance() * MathSqrt(m_node[i].GetMSE());
    }
    else
    {
      array[i][0] = DBL_MAX;
    }
    array[i][1] = i;
    m_node[i].SetCluster(-1);
  }
  ArraySort(array);
  
  ClusterNeighbourhood clnh(m_hexCells, m_ycells);

  int count = 0; // number of clusters
  ArrayResize(m_clusters, 0);
  
  for(int i = 0; i < n; i++)
  {
    // skip if already assigned
    if(m_node[(int)array[i][1]].GetCluster() > -1) continue;
    
    // check if current node is adjusent to any existing cluster
    int r = clnh.loop((int)array[i][1], m_node);
    if(r > -1) // a neighbour belongs to a cluster already
    {
      m_node[(int)array[i][1]].SetCluster(r);
    }
    else // we need new cluster
    {
      ArrayResize(m_clusters, (count + 1) * m_dimension);
      
      double vector[];
      m_node[(int)array[i][1]].GetCodeVector(vector);
      ArrayCopy(m_clusters, vector, count * m_dimension, 0, m_dimension);
      
      m_node[(int)array[i][1]].SetCluster(count++);
    }
  }
}

Алгоритм практически полностью следует словесному псевдокоду, описанному ранее: заполняем двумерный массив (в первой размерности — значение из формулы, во второй — индекс нейрона), сортируем, в цикле обходим все нейроны и для каждого — анализируем окрестность.

Качество кластеризации, конечно, следует оценить на практике, и я заранее допускаю наличие топологических проблем. Однако, учитывая то, что у большинства классических способов кластеризации проблемы также имеются, а по простоте они уступают предложенному, новое решение выглядит привлекательно.

К преимуществам данной реализации я бы отнес то, что кластеры упорядочены по важности (в том же самом K-Means кластеры равноценны), их форма — произвольная, и количество не нужно задавать заранее. Следует отметить, что последний плюс имеет и обратную сторону — количество кластеров может быть достаточно большим. Вместе с тем, упорядоченность кластеров по степени похожести содержимого и минимальной ошибке позволяет рассматривать на практике лишь 5-10 первых кластеров, и все остальные "оставлять за кадром".

Поскольку я не обнаружил в открытых источниках похожего метода кластеризации, предлагаю называть его кластеризацией Короткого (или более длинно, но скромно — кластеризацией короткого пути) на основе U-Matrix и ошибки квантизации (QE).

Забегая вперед, скажу, что после многочисленных тестов было на практике подтверждено, что центры кластеров, найденные алгоритмом K-Means, дают худшие результаты, чем альтернативная кластеризация (по крайней мере в задаче анализа результатов оптимизации). В связи с этим далее по тексту будет везде подразумеваться и применяться только она.

Тестирование

Настала пора переходить от теории к практике и проверить работу сети на деле. Создадим простой, универсальный эксперт с возможностями демонстрации основного функционала. Назовем его SOM-Explorer.

Включим заголовочные файлы с классами, рассмотренными выше. Определим входные параметры.

Группа — Network Structure and Data Settings

• DataFileName — имя текстового файла с данными для обучения или тестирования; класс CSOM поддерживает формат csv, но в самом эксперте чуть позже добавим чтение set-файлов, поскольку "на кону" анализ оптимизационных настроек других экспертов; когда файл с входными данными указан, его имя используется также для сохранения сети после обучения, но с другим расширением (см. ниже); расширение csv можно указывать или нет; имя может включать папку внутри MQL5/Files;
  
  
• NetFileName — имя двоичного файла собственного формата с расширением som; класс CSOM умеет сохранять и читать сети в/из таких файлов; если у кого-то возникнет необходимость изменить структуру хранимых данных, поменяйте номер версии в сигнатуре, которая пишется в начале файла; если NetFileName пустой, эксперт работает в режиме обучения, а если сеть указана — то в режиме тестирования (отображение входных данных в готовую сеть); расширение som можно указывать или нет; имя может включать папку внутри MQL5/Files;
  
  
• если оба параметра DataFileName и NetFileName пусты, эксперт будет генерировать демонстрационный набор случайных 3D-данных и проводить обучение на нем;
  
  
• при корректном имени сети в NetFileName в параметре DataFileName можно указать имя несуществующего файла, например, просто символ '?', в результате чего эксперт сгенерирует случайных образец тестовых данных для той области определения, которая сохранена в файле сети (обратите внимание, эта информация требуется обученной сети для правильной нормализации неизвестных данных в рабочем режиме; подача на вход сети величин из другой области определения не приведет, конечно, к выходу из строя, но результаты окажутся недостоверными; например, сложно рассчитывать на адекватную работу сети, если ей будет передано отрицательное значение просадки или количества сделок);
  
  
• CellsX — размер решетки по горизонтали (количество нейронов), по-умолчанию 10;
  
  
• CellsY — размер решетки по вертикали (количество нейронов), по-умолчанию 10;
  
  
• HexagonalCell — признак использования гексагональной решетки, по-умолчанию — true; переключите в false для прямоугольной решетки;
  
  
• UseNormalization — включение/отключение нормализации входных данных, по-умолчанию — true, и рекомендуется не выключать;
  
  
• EpochNumber — количество эпох обучения, по-умолчанию — 100;
  
  
• ValidationSetPercent — размер валидационной выборки в процентах от общего числа входных данных, по-умолчанию — 0, т.е. валидация отключена; рекомендуемые значения в случае использования — в районе 10;
  
  
• ClusterNumber — количество кластеров, по-умолчанию — 1, что означает нашу адаптивную кластеризацию; значение 0 отключает кластеризацию; значение больше 0 запускает кластеризацию методом K-Means; кластеризация выполняется непосредственно после обучения, кластеры сохраняются в файл сети;

Группа - Visualization

• ImageW — размер каждой карты (плоскости) в пикселях по горизонтали, по-умолчанию — 500;
  
  
• ImageH — размер каждой карты (плоскости) в пикселях по вертикали, по-умолчанию — 500;
  
  
• MaxPictures — количество карт в одном ряду, по умолчанию — 0, что означает режим вывода карт в один сплошной ряд с возможностью прокрутки (допустимы крупные изображения); если MaxPictures больше 0, то весь набор плоскостей выводится в несколько рядов, в каждом из которых MaxPictures карт (удобно для осмотра сразу всех карт в мелком масштабе);
  
  
• ShowBorders — включение/отключение отрисовки границ между нейронами, по-умолчанию — false;
  
  
• ShowTitles — включение/отключения вывода текстов с характеристиками нейронов, по-умолчанию — true;
  
  
• ColorScheme — выбор одной из 4-х цветовых схем, по-умолчанию — Blue_Green_Red (самая разноцветная);
  
  
• ShowProgress — включение/отключение динамического обновления изображений сети во время обучения; производится 1 раз в секунду, по-умолчанию — true;

Группа - Options

• RandomSeed — целое число для инициализации генератора случайных чисел, по-умолчанию — 0;
• SaveImages — опция сохранения изображений сети после отработки; может использоваться и после обучения, и после тестового запуска; по-умолчанию — false;

Это лишь основные настройки. Часть других специфических параметров мы будем добавлять по ходу решения задач.

Внимание! Эксперт изменяет настройки текущего чарта — откройте новый чарт, выделенный только для работы с этим экспертом.

Всю работу в эксперте будет выполнять объект класса CSOMDisplay.

CSOMDisplay KohonenMap;

Во время инициализации не забываем включить обработку событий перемещения мыши — они используются классом для вывода всплывающих подсказок и прокрутки.

void OnInit()
{
  ChartSetInteger(0, CHART_EVENT_MOUSE_MOVE, true);
  EventSetMillisecondTimer(1);
}

void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
{
  KohonenMap.OnChartEvent(id, lparam, dparam, sparam);
}

Нейросетевые алгоритмы (обучение или тест) запускаются в эксперте один раз — по таймеру, и таймер затем отключается.

void OnTimer()
{
  EventKillTimer();
  
  MathSrand(RandomSeed);
  
  bool hasOneTestPattern = false;
  
  if(NetFileName != "")
  {
    if(!KohonenMap.Load(NetFileName)) return;
    KohonenMap.DisplayInit(ImageW, ImageH, MaxPictures, ColorScheme, ShowBorders, ShowTitles);

    Comment("Map ", NetFileName, " is loaded; size: ", KohonenMap.GetWidth(), "*", KohonenMap.GetHeight(), "; features: ", KohonenMap.GetFeatureCount());

Если указан готовый файл с сетью, загружаем его и подготавливаем дисплей в соответствии с визуальными настройками.

    if(DataFileName != "")
    {
      if(!KohonenMap.LoadPatterns(DataFileName))
      {
        Print("Data loading error, file: ", DataFileName);

        // generate a random test vector
        int n = KohonenMap.GetFeatureCount();
        double min, max;
        double v[];
        ArrayResize(v, n);
        for(int i = 0; i < n; i++)
        {
          KohonenMap.GetFeatureBounds(i, min, max);
          v[i] = (max - min) * rand() / 32767 + min;
        }
        KohonenMap.AddPattern(v, "RANDOM");
        Print("Random Input:");
        ArrayPrint(v);
        double y[];
        CSOMNode *node = KohonenMap.GetBestMatchingFeatures(v, y);
        Print("Matched Node Output (", node.GetX(), ",", node.GetY(), "); Hits:", node.GetHitsCount(), "; Error:", node.GetMSE(),"; Cluster N", node.GetCluster(), ":");
        ArrayPrint(y);
        KohonenMap.CalculateOutput(v, true);
        hasOneTestPattern = true;
      }
    }

Если указан файл с тестовыми данными, пытаемся его загрузить. Если это не удалось, выводим сообщение в лог и генерируем случайный тестовый образец данных v. Количество признаков (размерность векторов) и их допустимые диапазоны определяются с помощью методов GetFeatureCount и GetFeatureBounds. Далее вызовом AddPattern образец добавляется в рабочий набор данных под именем "RANDOM".

Данный метод подойдет для формирования обучающих выборок из источников данных неподдерживаемых форматов, например, из баз данных, а также для заполнения непосредственно из индикаторов. В принципе, в этом конкретном случае добавление образца в рабочий набор нужно только для последующей визуализации на карте (показано чуть ниже), а для определения наиболее подходящего нейрона в сети достаточно одного вызова — GetBestMatchingFeatures. Этот метод из числа нескольких доступных GetBestMatchingXYZ методов позволяет получить соответствующие значения признаков выигравшего нейрона в массив y. Наконец, с помощью CalculateOutput отображаем реакцию сети на тестовый образец в дополнительной плоскости.

Идем далее по коду эксперта.

  }
  else // a net file is not provided, so training is assumed
  {
    if(DataFileName == "")
    {
      // generate 3-d demo vectors with unscaled values {[0,+1000], [0,+1], [-1,+1]}
      // feed them to the net to compare results with and without normalization
      // NB. titles should be valid filenames for BMP
      string titles[] = {"R1000", "R1", "R2"};
      KohonenMap.AssignFeatureTitles(titles);
      double x[3];
      for(int i = 0; i < 1000; i++)
      {
        x[0] = 1000.0 * rand() / 32767;
        x[1] = 1.0 * rand() / 32767;
        x[2] = -2.0 * rand() / 32767 + 1.0;
        KohonenMap.AddPattern(x, StringFormat("%f %f %f", x[0], x[1], x[2]));
      }
    }

Если обученная сеть не задана, предполагаем режим обучения. Проверяем, есть ли входные данные. Если нет — генерируем случайный набор трехмерных векторов, в котором первая компонента лежит в диапазоне [0,+1000], вторая - [0,+1], и третья - [-1,+1]. Названия компонент передаются в сеть с помощью AssignFeatureTitles, сами данные — с помощью уже известной AddPattern.

    else // a data file is provided
    {
      if(!KohonenMap.LoadPatterns(DataFileName))
      {
        Print("Data loading error, file: ", DataFileName);
        return;
      }
    }

Если входные данные поступают из файла, загружаем его. В случае возникновения ошибки завершаем работу, т.к. нет ни сети, ни данных.

Далее выполняем непосредственно обучение и кластеризацию.

    KohonenMap.Init(CellsX, CellsY, ImageW, ImageH, MaxPictures, ColorScheme, HexagonalCell, ShowBorders, ShowTitles);
    
    if(ValidationSetPercent > 0 && ValidationSetPercent < 50)
    {
      KohonenMap.SetValidationSection((int)(KohonenMap.GetDataCount() * (1.0 - ValidationSetPercent / 100.0)));
    }

    KohonenMap.Train(EpochNumber, UseNormalization, ShowProgress);

    if(ClusterNumber > 1)
    {
      KohonenMap.Clusterize(ClusterNumber);
    }
    else
    {
      KohonenMap.Clusterize();
    }
  }

Если анализ конкретного тестового образца не был задан (в частности, сразу после обучения), по-умолчанию формируем реакцию сети на вектор с нулями.

  if(!hasOneTestPattern)
  {
    double vector[];
    ArrayResize(vector, KohonenMap.GetFeatureCount());
    ArrayInitialize(vector, 0);
    KohonenMap.CalculateOutput(vector);
  }

Далее отрисуем все карты во внутренних буферах графических ресурсов — сперва цветовая подложка:

  KohonenMap.Render(); // draw maps into internal BMP buffers

и затем — надписи:

  if(hasOneTestPattern)
    KohonenMap.ShowAllPatterns();
  else
    KohonenMap.ShowAllNodes(); // draw labels in cells in BMP buffers

Пометим кластеры:

  if(ClusterNumber != 0)
  {
    KohonenMap.ShowClusters(); // mark clusters
  }

Выведем буфера на график и опционально сохраним изображения в файлы:

  KohonenMap.ShowBMP(SaveImages); // display files as bitmap images on chart, optionally save into files

Файлы складываются в отдельную папку с тем же именем, что и файл сети (если указан) или файл с данными (если указан). Если файл с данными не был указан, и сеть обучалась на случайных сгенерированных данных, имя для som-файла и папки с картинками формируется из префикса SOM и текущих даты и времени.

Наконец, сохраним обученную сеть в файл. Если имя сети уже было задано в NetFileName, значит эксперт работал в режиме тестирования и сохранять сеть снова не нужно.

  if(NetFileName == "")
  {
    KohonenMap.Save(KohonenMap.GetID());
  }
}

Попробуем запустить эксперт с генерацией тестовых случайных данных. Со всеми установками по умолчанию кроме уменьшенных размеров изображений, чтобы все плоскости попали на "скриншот" - ImageW = 230, ImageH = 230, MaxPictures = 3, - получим такую картину:

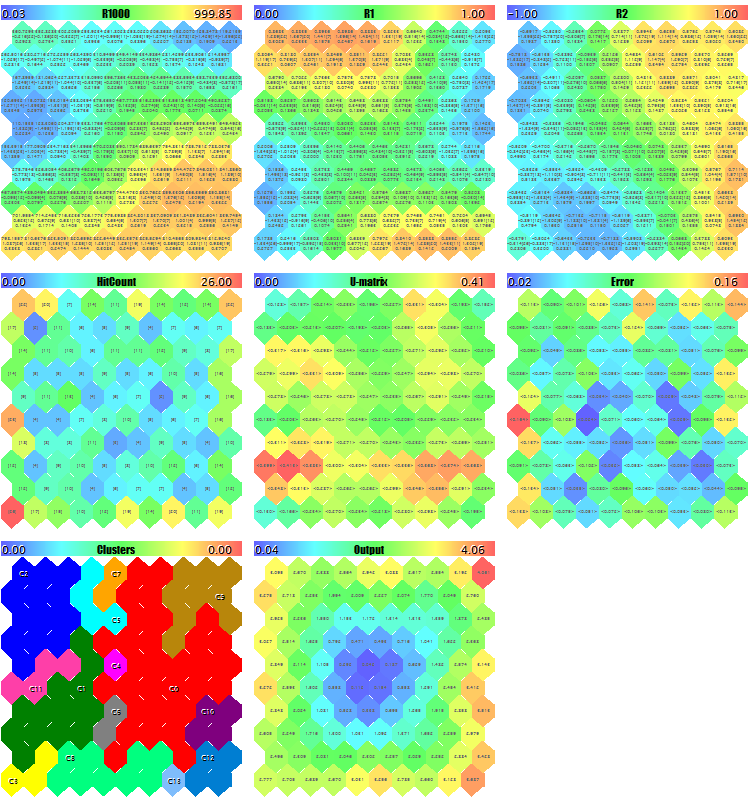
Пример карт Кохонена для случайных 3D-векторов

Здесь в каждом нейроне отображена служебная информация (можно просмотреть подробно по наведению курсора мыши) и расставлены метки найденных кластеров.

В лог в процессе выводится примерно такая информация (информация по кластерам ограничена пятью — можно изменить в исходном коде):

Pass 0 from 1000 0%
Pass 78 from 1000 7%
Pass 157 from 1000 15%
Pass 232 from 1000 23%
Pass 310 from 1000 31%
Pass 389 from 1000 38%
Pass 468 from 1000 46%
Pass 550 from 1000 55%
Pass 631 from 1000 63%
Pass 710 from 1000 71%
Pass 790 from 1000 79%
Pass 870 from 1000 87%
Pass 951 from 1000 95%
Overall NMSE=0.09420336270396877
Training completed at pass 1000, NMSE=0.09420336270396877
Clusters [14]:
"R1000" "R1"    "R2"   
N0
754.83131   0.36778   0.25369
N1
341.39665   0.41402  -0.26702
N2
360.72925   0.86826  -0.69173
N3
798.15569   0.17846  -0.37911
N4
470.30648   0.52326   0.06442
Map file SOM-20181205-134437.som saved

Если теперь указать имя созданного файла SOM-20181205-134437.som с сетью в параметре NetFileName, а в параметре DataFileName — '?', то получим результат тестового прогона для случайного образца не из обучающего набора. Для того чтобы лучше рассмотреть карты установим размеры покрупнее и MaxPictures в 0. 

Карты Кохонена для двух первых компонент случайных 3D-векторов

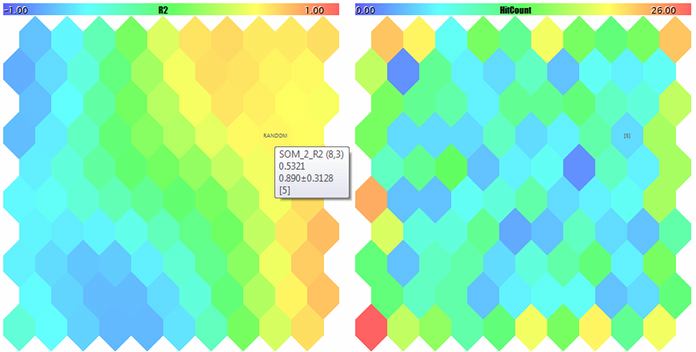
Карта Кохонена для третьей компоненты случайных 3D-векторов и счетчик попаданий

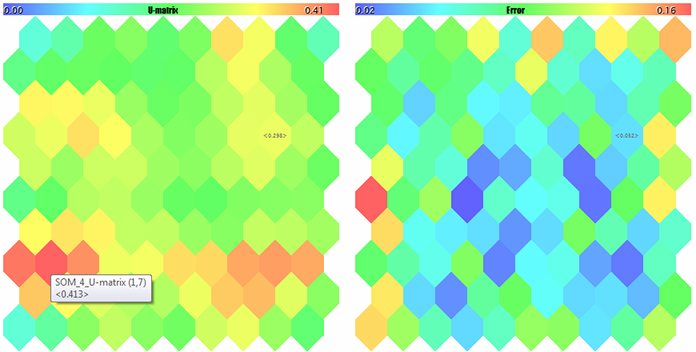
U-Matrix и ошибки квантизации

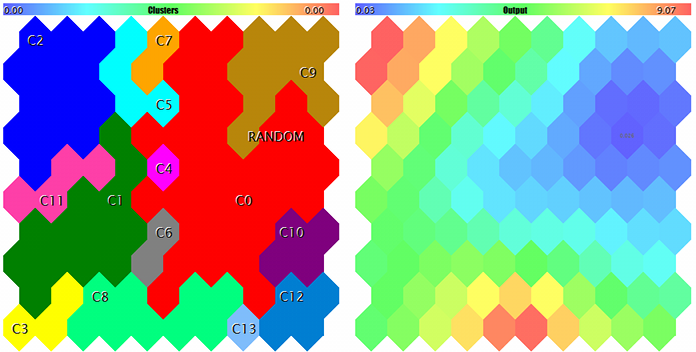
Кластеры и реакция сети Кохонена на тестовый образец

Образец помечен меткой RANDOM. Подсказки по нейронам всплывают по наведению мыши. В лог выводится примерно следующее:

FileOpen error ?.csv : 5004
Data loading error, file: ?
Random Input:
457.17510   0.29727   0.57621
Matched Node Output (8,3); Hits:5; Error:0.05246704285146882; Cluster N0:
497.20453   0.28675   0.53213

Итак, инструментарий для работы с сетью Кохонена готов. Можно приступать к прикладным задачам. И мы вплотную займемся этим в рамках второй статьи.

Заключение

Открытые реализации нейронных сетей Кохонена доступны пользователям MetaTrader уже несколько лет. Мы исправили в них некоторые ошибки, дополнили полезными инструментами и протестировали работу с помощью специального демонстрационного эксперта. Исходные коды позволяют применять классы для собственных задач, примеры этого мы рассмотрим далее — продолжение следует.