Вычисление математических выражений (Часть 2). Парсеры Пратта и сортировочной станции

В этой статье мы продолжаем изучать различные методы парсинга математических выражений и их реализацию на языке MQL. В первой части были рассмотрены парсеры рекурсивного спуска. Их главное достоинство — интуитивно понятное устройство, напрямую связанное с конкретной грамматикой выражений. Но если речь заходит об эффективности и технологичности, то существуют и другие типы парсеров, на которые стоит обратить внимание.

Парсеры с использованием старшинства операторов

Следующей разновидностью парсеров, которые мы рассмотрим, являются парсеры с использованием старшинства (precedence) операторов. Они характеризуются более компактной реализацией за счет того, что методы классов создаются не на основе правил грамматики (как мы видели, в этом случае каждое правило преобразуется в свой метод), а в более обобщенном виде, учитывающем лишь старшинство операторов.

Старшинство (или приоритет) операций в неявном виде уже присутствовало в EBNF-описании грамматики: её правила разворачиваются от операций с меньшим приоритетом к операциям с большим приоритетом, вплоть до терминальных сущностей — констант и переменных. Так происходит потому, что старшинство определяет, в какой последовательности должны выполняться операции в отсутствии явной группировки с помощью скобок. Например, старшинство операции умножения выше, чем у сложения. Но унарный минус приоритетнее умножения. Чем ближе элемент синтаксического дерева в корню (выражения целиком), тем позже он будет вычислен.

Для реализации парсеров нам потребуется две таблицы с числовыми значениями, соответствующими приоритету каждой операции. Чем выше значение, тем выше приоритет.

Таблиц — две, потому что унарные и бинарные операции будут логически разнесены в алгоритмах. А если более строго, то речь идет не только об операциях, но в более общем смысле о символах, которые могут встречаться в выражениях в виде префиксов и инфиксов (более подробно о типах операторов в Википедии).

Как можно понять из названия, префикс — это символ, предваряющий операнд (например, '!' в выражение "!var"), а инфикс — символ, стоящий между операндами (например, '+' в выражении "a + b"). Существуют еще и постфиксы (например, пара '+' в операторе инкремента, который есть и в MQL — "i++"), но они в наших выражениях не используются и потому остаются за кадром.

В качестве префиксов, помимо унарных операций '!', '-', '+', могут выступать открывающая круглая скобка '(' — признак начала группы, буква или подчеркивание — признак начала идентификатора, а также цифра или точка '.' — признак начала числовой константы.

Опишем таблицы в классе ExpressionPrecedence, от которого затем будут унаследованы конкретные классы парсеров на базе приоритетов. Все эти парсеры будут работать на основе Promise.

  class ExpressionPrecedence: public AbstractExpressionProcessor<Promise *>
  {
    protected:
      static uchar prefixes[128];
      static uchar infixes[128];
      
      static ExpressionPrecedence epinit;
      
      static void initPrecedence()
      {
        // grouping
        prefixes['('] = 9;
  
        // unary
        prefixes['+'] = 9;
        prefixes['-'] = 9;
        prefixes['!'] = 9;
        
        // identifiers
        prefixes['_'] = 9;
        for(uchar c = 'a'; c <= 'z'; c++)
        {
          prefixes[c] = 9;
        }
        
        // numbers
        prefixes['.'] = 9;
        for(uchar c = '0'; c <= '9'; c++)
        {
          prefixes[c] = 9;
        }
        
        // operators
        // infixes['('] = 9; // parenthesis is not used here as 'function call' operator
        infixes['*'] = 8;
        infixes['/'] = 8;
        infixes['%'] = 8;
        infixes['+'] = 7;
        infixes['-'] = 7;
        infixes['>'] = 6;
        infixes['<'] = 6;
        infixes['='] = 5;
        infixes['!'] = 5;
        infixes['&'] = 4;
        infixes['|'] = 4;
        infixes['?'] = 3;
        infixes[':'] = 2;
        infixes[','] = 1; // arg list delimiter
      }
  
      ExpressionPrecedence(const bool init)
      {
        initPrecedence();
      }
  
    public:
      ExpressionPrecedence(const string vars = NULL): AbstractExpressionProcessor(vars) {}
      ExpressionPrecedence(VariableTable &vt): AbstractExpressionProcessor(vt) {}
  };
  
  static uchar ExpressionPrecedence::prefixes[128] = {0};
  static uchar ExpressionPrecedence::infixes[128] = {0};
  static ExpressionPrecedence ExpressionPrecedence::epinit(true);

Таблицы приоритетов выполнены "экономным" способом — с помощью разреженных массивов размером 128 элементов (этого достаточно, потому что символы с кодами из других диапазонов не поддерживаются). В ячейках, соответствующих кодам символов, указаны их приоритеты. Таким образом, приоритет легко получить путем прямой адресации по коду токена.

В классах наследниках также потребуется два новых вспомогательных метода для проверки символов, идущих следом во входной строке: _lookAhead просто возвращает следующий токен (как бы заглядывая на шаг вперед), а _matchNext — считывает его, если он совпадает с ожидаемым, или выдает ошибку в противном случае.

  class ExpressionPrecedence: public AbstractExpressionProcessor<Promise *>
  {
    protected:
      ...
      ushort _lookAhead()
      {
        int i = 1;
        while(_index + i < _length && isspace(_expression[_index + i])) i++;
        if(_index + i < _length)
        {
          return _expression[_index + i];
        }
        return 0;
      }
      
      void _matchNext(ushort c, string message, string context = NULL)
      {
        if(_lookAhead() == c)
        {
          _nextToken();
        }
        else if(!_failed) // prevent chained errors
        {
          error(message, context);
        }
      }
      ...
  };

Первым парсером на основе старшинства операций, который мы изучим, будет парсер Пратта.

Парсер Пратта (ExpressionPratt)

Парсер Пратта является нисходящим, как и парсер рекурсивного спуска. Это означает, что в нем тоже будут рекурсивные вызовы неких методов, анализирующих отдельные конструкции в выражении, но этих методов будет значительно меньше.

Конструкторы и основной публичный метод evaluate выглядят знакомо.

  class ExpressionPratt: public ExpressionPrecedence
  {
    public:
      ExpressionPratt(const string vars = NULL): ExpressionPrecedence(vars) { helper = new ExpressionHelperPromise(&this); }
      ExpressionPratt(VariableTable &vt): ExpressionPrecedence(vt) { helper = new ExpressionHelperPromise(&this); }
  
      virtual Promise *evaluate(const string expression) override
      {
        Promise::environment(&this);
        AbstractExpressionProcessor<Promise *>::evaluate(expression);
        if(_length > 0)
        {
          return parseExpression();
        }
        return NULL;
      }

Новый метод parseExpression — это сердце алгоритма Пратта. Он стартует с установки текущего приоритета равным по умолчанию 0, что означает возможность прочитать любой символ.

      virtual Promise *parseExpression(const int precedence = 0)
      {
        if(_failed) return NULL; // cut off subexpressions in case of errors
      
        _nextToken();
        if(prefixes[(uchar)_token] == 0)
        {
          this.error("Can't parse " + ShortToString(_token), __FUNCTION__);
          return NULL;
        }
        
        Promise *left = _parsePrefix();
        
        while((precedence < infixes[_token]) && !_failed)
        {
          left = _parseInfix(left, infixes[(uchar)_token]);
        }
        
        return left;
      }

Суть метода проста: начинаем разбор выражения с чтения следующего символа, который обязан быть префиксом (иначе ошибка), и передаем управление методу _parsePrefix, умеющему читать любую префиксную конструкцию целиком. После этого, пока приоритет следующего символа выше, чем текущий приоритет, передаем управление методу _parseInfix, умеющему читать любую инфиксную конструкцию целиком. Таким образом, весь парсер состоит всего из 3-х методов. В некотором смысле парсер Пратта представляет выражение, как иерархию префиксных и инфиксных конструкций.

Обратите внимание, что если текущий символ _token отсутствует в таблице инфиксов, его приоритет будет равен нулю и цикл while перестанет (или не начнет вовсе) выполняться.

Хитрость метода _parseInfix заключается в том, что текущий объект Promise (left) передается внутрь в первом параметре и станет частью подвыражения, а допустимый минимальный приоритет операций, которые разрешается считывать методу, устанавливается во втором параметре, как приоритет текущего инфиксного токена. Метод вернет новый объект Promise для всего подвыражения, причем он сохраняется в той же переменной (и прежняя ссылка на Promise будет тем или иным образом доступна по ссылочным полям из нового объекта).

Рассмотрим, как устроены методы _parsePrefix и _parseInfix.

Логично, что _parsePrefix ожидает текущий токен из числа разрешенных префиксов и обрабатывает их с помощью switch. В случае открывающей скобки '(' вызывается уже знакомый метод parseExpression, чтобы считать вложенное выражение. Параметр приоритета опущен, что означает парсинг с самого низкого нулевого приоритета (ведь в скобках по сути находится отдельное выражение). В случае '!' используется объект helper, чтобы получить логическое отрицание, от идущего следом фрагмента, а читает его опять же метод parseExpression, но на этот раз внутрь передается приоритет текущего токена. Это означает, что фрагмент, подлежащий отрицанию, закончится перед первым символом с более низким приоритетом, чем у '!'. Например, если в выражении написано "!a*b", то parseExpression остановится после чтения имени переменной 'a', потому что приоритет умножения '*' ниже, чем отрицания '!'. Унарные '+' и '-' обрабатываются похожим образом, но здесь обходимся без объекта helper. Для '+' достаточно просто прочитать подвыражение в parseExpression, а для '-' вызываем для полученного результата переопределенный оператор "минус" (напомним, что результаты представляют собой объекты Promise).

Все прочие символы метод _parsePrefix сортирует по принадлежности к категории isalpha. Подразумевается, что буква — это начало идентификатора, а цифра или точка — начало числа. Во всех прочих случаях метод вернет NULL.

      Promise *_parsePrefix()
      {
        Promise *result = NULL;
        switch(_token)
        {
          case '(':
            result = parseExpression();
            _match(')', ") expected!", __FUNCTION__);
            break;
          case '!':
            result = helper._negate(parseExpression(prefixes[_token]));
            break;
          case '+':
            result = parseExpression(prefixes[_token]);
            break;
          case '-':
            result = -parseExpression(prefixes[_token]);
            break;
          default:
            if(isalpha(_token))
            {
              string variable;
            
              while(isalnum(_token))
              {
                variable += ShortToString(_token);
                _nextToken();
              }
              
              if(_token == '(')
              {
                const string name = variable;
                const int index = _functionTable.index(name);
                if(index == -1)
                {
                  error("Function undefined: " + name, __FUNCTION__);
                  return NULL;
                }
                
                const int arity = _functionTable[index].arity();
                if(arity > 0 && _lookAhead() == ')')
                {
                  error("Missing arguments for " + name + ", " + (string)arity + " required!", __FUNCTION__);
                  return NULL;
                }
                
                Promise *params[];
                ArrayResize(params, arity);
                for(int i = 0; i < arity; i++)
                {
                  params[i] = parseExpression(infixes[',']);
                  if(i < arity - 1)
                  {
                    if(_token != ',')
                    {
                      _match(',', ", expected (param-list)!", __FUNCTION__);
                      break;
                    }
                  }
                }
              
                _match(')', ") expected after " + (string)arity + " arguments!", __FUNCTION__);
                
                result = helper._call(index, params);
              }
              else
              {
                return helper._variable(variable); // get index and if not found - optionally reserve the name with nan
              }
            }
            else // digits are implied, must be a number 
            {
              string number;
              if(_readNumber(number))
              {
                return helper._literal(number);
              }
            }
        }
        return result;
      }

Идентификатор, за которым следует скобка '(', воспринимается как вызов функции. Для него опционально парсится список аргументов (согласно арности функции), разделенных запятыми. Каждый аргумент получается за счет вызова parseExpression с приоритетом запятой ','. Объект Promise для функции генерируется с помощью helper._call(). Если скобки после идентификатора нет, создается объект Promise для переменной helper._variable().

Когда первый токен не является буквой, метод _parsePrefix пытается прочитать число с помощью _readNumber и создает для него Promise вызовом helper._literal().

Метод _parseInfix ожидает, что текущий токен будет одним из разрешенных инфиксов, причем в первом параметре он получает левый операнд, уже прочитанный в объект Promise *left. Во втором параметре указан минимальный приоритет токенов, которые подлежат разбору — как только встретится нечто с более низким приоритетом, подвыражение закончилось. Задача _parseInfix вызвать parseExpression с приоритетом precedence, чтобы прочитать правый операнд, после чего можно создать объект Promise для бинарной операции, соответствующей инфиксу.

      Promise *_parseInfix(Promise *left, const int precedence = 0)
      {
        Promise *result = NULL;
        const ushort _previous = _token;
        switch(_previous)
        {
          case '*':
          case '/':
          case '%':
          case '+':
          case '-':
            result = new Promise((uchar)_previous, left, parseExpression(precedence));
            break;
          case '>':
          case '<':
            if(_lookAhead() == '=')
            {
              _nextToken();
              result = new Promise((uchar)(_previous == '<' ? '{' : '}'), left, parseExpression(precedence));
            }
            else
            {
              result = new Promise((uchar)_previous, left, parseExpression(precedence));
            }
            break;
          case '=':
          case '!':
            _matchNext('=', "= expected after " + ShortToString(_previous), __FUNCTION__);
            result = helper._isEqual(left, parseExpression(precedence), _previous == '=');
            break;
          case '&':
          case '|':
            _matchNext(_previous, ShortToString(_previous) + " expected after " + ShortToString(_previous), __FUNCTION__);
            result = new Promise((uchar)_previous, left, parseExpression(precedence));
            break;
          case '?':
            {
              Promise *truly = parseExpression(infixes[':']);
              if(_token != ':')
              {
                _match(':', ": expected", __FUNCTION__);
              }
              else
              {
                Promise *falsy = parseExpression(infixes[':']);
                if(truly != NULL && falsy != NULL)
                {
                  result = helper._ternary(left, truly, falsy);
                }
              }
            }
          case ':':
          case ',': // just skip
            break;
          default:
            error("Can't process infix token " + ShortToString(_previous));
          
        }
        return result;
      }

Важно, что текущий инфиксный токен в начале метода запоминается в переменной _previous. Это сделано потому, что вызов parseExpression в случае успеха сдвигает позицию в строке на какой-то другой токен, на произвольное количество символов правее.

Итак, мы рассмотрели всего 3 метода с довольно прозрачной структурой, но это и есть весь парсер Пратта целиком.

Его применение аналогично парсеру ExpressionCompiler: создаем объект ExpressionPratt, задаем таблицу переменных, запускаем метод evaluate для строки с выражением и получаем на выходе Promise с синтаксическим деревом, которое можно вычислить с помощью resolve().

Использование синтаксического дерева, конечно, не единственный способ отложенного вычисления выражений. Следующий тип парсера, который мы собираемся рассмотреть, обходится вовсе без дерева и записывает алгоритм вычисления в так называемый байт-код. Поэтому сперва необходимо познакомиться с этой технологией.

Генерация байт-кода

Байт-код — это последовательность команд, описывающих в "быстром" двоичном представлении весь алгоритм расчетов. Создание байт-кода напоминает настоящую компиляцию программы, но результат содержит не инструкции процессора, а переменные или структуры прикладного языка, управляющие неким классом-вычислителем. В нашем случае единицей исполнения будет такая структура ByteCode.

  struct ByteCode
  {
      uchar code;
      double value;
      int index;
  
      ByteCode(): code(0), value(0.0), index(-1) {}
      ByteCode(const uchar c): code(c), value(0.0), index(-1) {}
      ByteCode(const double d): code('n'), value(d), index(-1) {}
      ByteCode(const uchar c, const int i): code(c), value(0.0), index(i) {}
      
      string toString() const
      {
        return StringFormat("%s %f %d", CharToString(code), value, index);
      }
  };

Её поля повторяют поля объектов Promise, но не все, а лишь минимальный набор, необходимый для "поточных" вычислений. Поточными они являются в том смысле, что в процессе работы команды будут считываться и выполняться последовательно слева направо, без переходов по каким-либо иерархическим структурам.

Поле code содержит суть команды (значение соответствует кодам Promise), поле value — число (константу), поле index — номер переменной или функции в таблицах, соответственно, переменных или функций.

Одним из способов записи вычислительных инструкций является обратная польская нотация (Reverse Polish Notation), известная также как постфиксная. Суть её в том, что сперва записываются операнды, а затем код операции. Например, привычная нам инфиксная запись "a + b" становится в постфиксной "a b +", а более сложный случай "a + b * sqrt(c)" превращается в "a b c 'sqrt' * +".

RPN хороша для байт-кода, потому что по ней легко реализовать вычисления с помощью стека. Когда программа "видит" во входном потоке символов число или ссылку на переменную, она кладет это значение в стек. Если во входном потоке встречается оператор или функция, программа достает из стека нужное количество значений, выполняет над ними указанную операцию и кладет результат снова в стек. По окончании процесса результат вычисления выражения останется единственным числом в стеке.

Поскольку RPN описывает в альтернативном виде те же выражения, для которых мы строим синтаксические деревья, эти два представления можно конвертировать одно в другое. Попробуем сгенерировать байт-код на основе дерева Promise. Для этого добавим в класс Promise метод exportToByteCode.

  class Promise
  {
    ...
    public:
      void exportToByteCode(ByteCode &codes[])
      {
        if(left) left.exportToByteCode(codes);
        const int truly = ArraySize(codes);
        
        if(code == '?')
        {
          ArrayResize(codes, truly + 1);
          codes[truly].code = code;
        }
        
        if(right) right.exportToByteCode(codes);
        const int falsy = ArraySize(codes);
        if(last) last.exportToByteCode(codes);
        const int n = ArraySize(codes);
        
        if(code != '?')
        {
          ArrayResize(codes, n + 1);
          codes[n].code = code;
          codes[n].value = value;
          codes[n].index = index;
        }
        else // (code == '?')
        {
          codes[truly].index = falsy; // jump over true branch
          codes[truly].value = n;     // jump over both branches
        }
      }
      ...
  };

Метод получает в качестве параметра массив структур ByteCode, в который он должен сохранить содержимое текущего объекта Promise. Сперва анализируются все подчиненные узлы, для чего метод рекурсивно вызывается для указателей left, right, last, если они не нулевые. И только после этого, когда все части (операнды) сохранены, в байт-код записываются свойства самого объекта Promise.

Поскольку в грамматике выражений имеется условный оператор, метод дополнительно запоминает размер массива байт-кодов в точках, где начинается истинная и ложная ветвь инструкций, а также конец условного выражения. Это позволяет записать в структуру байт-кода условного оператора смещения в массиве, куда следует перескочить в процессе вычислений, если условие будет истинным или ложным. Ветвь инструкций для истинного условия начинается сразу после байт-кода '?', и после их выполнения нужно перейти по смещению в поле value. Ветвь инструкций для ложного условия начинается по смещению в поле index, сразу поле "истинных" инструкций.

Обратите внимание, что когда мы вычисляем выражение в режиме интерпретации или по синтаксическому дереву, обе ветви условного оператора рассчитываются до того, как одно из их значений будет выбрано в зависимости от условия, то есть одна из ветвей считается вхолостую. В случае байт-кода мы перескакиваем вычисления ненужной ветви.

Чтобы перевести все дерево выражения в байт-код, нужно вызвать exportToByteCode для корневого объекта, полученного как результат evaluate. Например, для парсера Пратта:

    ExpressionPratt e(vars);
    Promise *p = e.evaluate(expr);
  
    ByteCode codes[];
    p.exportToByteCode(codes);
  
    for(int i = 0; i < ArraySize(codes); i++)
    {
      Print(i, "] ", codes[i].toString());
    }

Теперь осталось написать функцию, которая выполняла бы вычисления на базе байт-кода. Разместим её также в классе Promise, потому что в байт-кодах используются индексы переменных и функций, а Promise по умолчанию имеет ссылки на эти таблицы.

  #define STACK_SIZE 100
  
  // stack imitation
  #define push(S,V,N) S[N++] = V
  #define pop(S,N) S[--N]
  #define top(S,N) S[N-1]
  
  class Promise
  {
    ...
    public:
      static double execute(const ByteCode &codes[], VariableTable *vt = NULL, FunctionTable *ft = NULL)
      {
        if(vt) variableTable = vt;
        if(ft) functionTable = ft;
  
        double stack[]; int ssize = 0; ArrayResize(stack, STACK_SIZE);
        int jumps[]; int jsize = 0; ArrayResize(jumps, STACK_SIZE / 2);
        const int n = ArraySize(codes);
        for(int i = 0; i < n; i++)
        {
          if(jsize && top(jumps, jsize) == i)
          {
            --jsize; // fast "pop & drop"
            i = pop(jumps, jsize);
            continue;

          }
          switch(codes[i].code)
          {
            case 'n': push(stack, codes[i].value, ssize); break;
            case 'v': push(stack, variableTable[codes[i].index], ssize); break;
            case 'f':
              {
                IFunctor *ptr = functionTable[codes[i].index];
                double params[]; ArrayResize(params, ptr.arity()); int psize = 0;
                for(int j = 0; j < ptr.arity(); j++)
                {
                  push(params, pop(stack, ssize), psize);
                }
                ArrayReverse(params);
                push(stack, ptr.execute(params), ssize);
              }
              break;
            case '+': push(stack, pop(stack, ssize) + pop(stack, ssize), ssize); break;
            case '-': push(stack, -pop(stack, ssize) + pop(stack, ssize), ssize); break;
            case '*': push(stack, pop(stack, ssize) * pop(stack, ssize), ssize); break;
            case '/': push(stack, Promise::safeDivide(1, pop(stack, ssize)) * pop(stack, ssize), ssize); break;
            case '%':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, fmod(first, second), ssize);
              }
              break;
            case '!': push(stack, (double)(!pop(stack, ssize)), ssize); break;
            case '~': push(stack, (double)(-pop(stack, ssize)), ssize); break;
            case '<':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first < second), ssize);
              }
              break;
            case '>':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first > second), ssize);
              }
              break;
            case '{':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first <= second), ssize);
              }
              break;
            case '}':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first >= second), ssize);
              }
              break;
            case '&': push(stack, (double)(pop(stack, ssize) && pop(stack, ssize)), ssize); break;
            case '|':
              {
                const double second = pop(stack, ssize);
                const double first = pop(stack, ssize);
                push(stack, (double)(first || second), ssize); // order is important
              }
              break;
            case '`': push(stack, _precision < fabs(pop(stack, ssize) - pop(stack, ssize)), ssize); break;
            case '=': push(stack, _precision > fabs(pop(stack, ssize) - pop(stack, ssize)), ssize); break;
            case '?':
              {
                const double first = pop(stack, ssize);
                if(first) // true
                {
                  push(jumps, (int)codes[i].value, jsize); // to where the entire if ends
                  push(jumps, codes[i].index, jsize);      // we jump from where true ends
                }
                else // false
                {
                  i = codes[i].index - 1; // -1 is needed because of forthcoming ++
                }
              }
              break;
            default:
              Print("Unknown byte code ", CharToString(codes[i].code));
          }
        }
        return pop(stack, ssize);
      }
      ...
  };

Работа со стеком организована с помощью макросов на массиве stack, в котором заранее выделяется предопределенное количество элементов STACK_SIZE. Это сделано для ускорения за счет исключения вызовов ArrayResize при выполнении операций push и pop. STACK_SIZE равный 100 кажется достаточным для большинства реальных однострочных выражений. В противном случае будет переполнение стека.

Для контроля выполнения условных операторов, которые могут быть вложенными, приходится использовать дополнительный стек jumps.

Все операции уже знакомы нам по рассмотренным выше кодам Promise и парсера Пратта. Единственное отличие — повсеместное использование стека как источника операндов и места сохранения промежуточного результата. Выполнение всего байт-кода происходит в цикле, за единственный вызов метода, без рекурсии.

Имея данный функционал, мы уже можем вычислять выражения по байт-коду, полученному путем экспорта синтаксических деревьев от парсера Пратта или ExpressionCompiler.

    ExpressionPratt e(vars);
    Promise *p = e.evaluate(expr);
  
    ByteCode codes[];
    p.exportToByteCode(codes);
    double r = Promise::execute(codes);

Чуть позже, при тестировании всех парсеров, мы сравним быстродействие вычислений по дереву и байт-коду.

Но основная цель введения байт-кодов была в том, чтобы сделать возможной реализацию другого типа парсеров — парсера "сортировочной станции".

Парсер сортировочной станции (ExpressionShuntingYard)

Парсер сортировочной станции (Shunting Yard) обязан своим названием способу, которым он разделяет поток входных токенов на те, которые можно сразу пропустить на выход, и те, которые следует поместить в специальный стек, откуда токены извлекаются по особым правилам сочетания приоритетов токенов (того, что в стеке, и того, что идет следующим во входном потоке). Парсер преобразует входное выражение в обратную польскую нотацию RPN. Для нас это удобно тем, что можно сразу генерировать байт-код, минуя синтаксическое дерево. Как видно из общего описания, способ сортировки базируется на старшинстве операторов, поэтому данный парсер родственен парсеру Пратта и будет реализован как класс-наследник ExpressionPrecedence.

Данный парсер относится к классу восходящих (bottom-up).

Алгоритм, в общих чертах, следующий (здесь опущены нюансы с правой ассоциативностью, т.к. её у нас нет, а также усложнения, связанные с тернарным условным оператором):

  В цикле читаем очередной токен из выражения (пока оно не закончилось)
    если токен -- унарная операция, сохраняем её на стеке
    если это число, записываем его в байт-код
    если это переменная, записываем её индекс в байт-код
    если это индентификатор функции, сохраняем её индекс на стеке
    если токен -- инфиксный оператор
      пока на вершине стека не '(' и ((приоритет оператора на вершине стека >= приоритету текущего оператора) или на вершине функция)
        перенести вершину стека в выходной байт-код
      сохранить оператор на стеке
    если токен '(', сохранить его на стеке
    если токен ')'
      пока на вершине стека не '('
        перенести вершину стека в выходной байт-код
      если на вершине стека '(', вынуть и выкинуть
  если в стеке остались токены, последовательно переносим их в выходной байт-код

Очевидно, что реализация данного парсера потребует лишь одного единственного метода.

Ниже класс ExpressionShuntingYard представлен целиком. Главный публичный метод convertToByteCode запускает парсинг, который осуществляется в exportToByteCode. Поскольку наши выражения поддерживают условные операторы, для разбора их подвыражений используется рекурсивный вызов exportToByteCode.

  class ExpressionShuntingYard: public ExpressionPrecedence
  {
    public:
      ExpressionShuntingYard(const string vars = NULL): ExpressionPrecedence(vars) { }
      ExpressionShuntingYard(VariableTable &vt): ExpressionPrecedence(vt) { }
  
      bool convertToByteCode(const string expression, ByteCode &codes[])
      {
        Promise::environment(&this);
        AbstractExpressionProcessor<Promise *>::evaluate(expression);
        if(_length > 0)
        {
          exportToByteCode(codes);
        }
        return !_failed;
      }
  
    protected:
      template<typename T>
      static void _push(T &stack[], T &value)
      {
        const int n = ArraySize(stack);
        ArrayResize(stack, n + 1, STACK_SIZE);
        stack[n] = value;
      }
  
      void exportToByteCode(ByteCode &output[])
      {
        ByteCode stack[];
        int ssize = 0;
        string number;
        uchar c;
        
        ArrayResize(stack, STACK_SIZE);
        
        const int previous = ArraySize(output);
        
        while(_nextToken() && !_failed)
        {
          if(_token == '+' || _token == '-' || _token == '!')
          {
            if(_token == '-')
            {
              _push(output, ByteCode(-1.0));
              push(stack, ByteCode('*'), ssize);
            }
            else if(_token == '!')
            {
              push(stack, ByteCode('!'), ssize);
            }
            continue;
          }
          
          number = "";
          if(_readNumber(number)) // if a number was read, _token has changed
          {
            _push(output, ByteCode(StringToDouble(number)));
          }
          
          if(isalpha(_token))
          {
            string variable;
            while(isalnum(_token))
            {
              variable += ShortToString(_token);
              _nextToken();
            }
            if(_token == '(')
            {
              push(stack, ByteCode('f', _functionTable.index(variable)), ssize);
            }
            else // variable name
            {
              int index = -1;
              if(CheckPointer(_variableTable) != POINTER_INVALID)
              {
                index = _variableTable.index(variable);
                if(index == -1)
                {
                  if(_variableTable.adhocAllocation())
                  {
                    index = _variableTable.add(variable, nan);
                    _push(output, ByteCode('v', index));
                    error("Unknown variable is NaN: " + variable, __FUNCTION__, true);
                  }
                  else
                  {
                    error("Unknown variable : " + variable, __FUNCTION__);
                  }
                }
                else
                {
                  _push(output, ByteCode('v', index));
                }
              }
            }
          }
          
          if(infixes[_token] > 0) // operator, including least significant '?'
          {
            while(ssize > 0 && isTop2Pop(top(stack, ssize).code))
            {
              _push(output, pop(stack, ssize));
            }
            
            if(_token == '?' || _token == ':')
            {
              if(_token == '?')
              {
                const int start = ArraySize(output);
                _push(output, ByteCode((uchar)_token));
                exportToByteCode(output); // subexpression truly, _token has changed
                if(_token != ':')
                {
                  error("Colon expected, given: " + ShortToString(_token), __FUNCTION__);
                  break;
                }
                output[start].index = ArraySize(output);
                exportToByteCode(output); // subexpression falsy, _token has changed
                output[start].value = ArraySize(output);
                if(_token == ':')
                {
                  break;
                }
              }
              else
              {
                break;
              }
            }
            else
            {
              if(_token == '>' || _token == '<')
              {
                if(_lookAhead() == '=')
                {
                  push(stack, ByteCode((uchar)(_token == '<' ? '{' : '}')), ssize);
                  _nextToken();
                }
                else
                {
                  push(stack, ByteCode((uchar)_token), ssize);
                }
              }
              else if(_token == '=' || _token == '!')
              {
                if(_lookAhead() == '=')
                {
                  push(stack, ByteCode((uchar)(_token == '!' ? '`' : '=')), ssize);
                  _nextToken();
                }
              }
              else if(_token == '&' || _token == '|')
              {
                _matchNext(_token, ShortToString(_token) + " expected after " + ShortToString(_token), __FUNCTION__);
                push(stack, ByteCode((uchar)_token), ssize);
              }
              else if(_token != ',')
              {
                push(stack, ByteCode((uchar)_token), ssize);
              }
            }
          }
          
          if(_token == '(')
          {
            push(stack, ByteCode('('), ssize);
          }
          else if(_token == ')')
          {
            while(ssize > 0 && (c = top(stack, ssize).code) != '(')
            {
              _push(output, pop(stack, ssize));
            }
            if(c == '(') // must be true unless it's a subexpression (then 'c' can be 0)
            {
              ByteCode disable_warning = pop(stack, ssize);
            }
            else
            {
              if(previous == 0)
              {
                error("Closing parenthesis is missing", __FUNCTION__);
              }
              return;
            }
          }
        }
        
        while(ssize > 0)
        {
          _push(output, pop(stack, ssize));
        }
      }
      
      bool isTop2Pop(const uchar c)
      {
        return (c == 'f' || infixes[c] >= infixes[_token]) && c != '(' && c != ':';
      }
  };

Использование сортировочного парсера отличается от предыдущих типов. Для него исключается шаг получения дерева с помощью вызова evaluate. Вместо этого метод convertToByteCode сразу возвращает байт-код для переданного выражения.

  ExpressionShuntingYard sh;
  sh.variableTable().adhocAllocation(true);
  
  ByteCode codes[];
  bool success = sh.convertToByteCode("x + y", codes);
  if(success)
  {
    sh.variableTable().assign("x=10;y=20");
    double r = Promise::execute(codes);
  }

На этом обзор различных типов парсеров закончен. Диаграмма классов выглядит так.

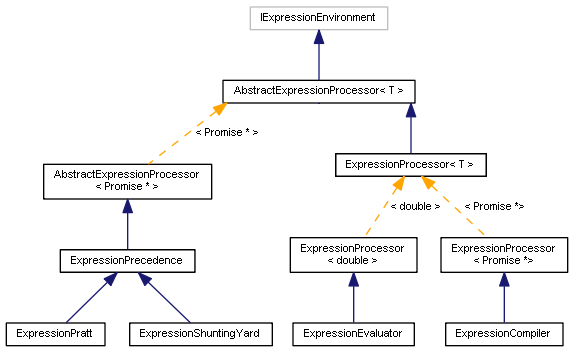
Диаграмма классов парсеров

Для тестирования и сравнения различных парсеров мы позже создадим тестовый скрипт.

Чтобы приблизить задачу к прикладной области трейдинга добавим последний штрих — покажем, как можно дополнить список встроенных функций техническими индикаторами.

Встраивание индикаторов в выражения в качестве функций

При расчете выражений трейдеру может потребоваться специфическая информация, такая как размер баланса, количество позиций, показания индикаторов и прочее. Всё это можно сделать доступным внутри выражений путем расширения перечня встроенных функций. Чтобы продемонстрировать данный подход, добавим в набор функций индикатор скользящего среднего.

Механизм встраивания индикатора в выражения опирается на рассмотренные ранее функторы и потому реализуется в виде класса, производного от AbstractFunc. Напомним, что все экземпляры классов семейства AbstractFunc автоматически регистрируются в AbstractFuncStorage и становятся доступны в таблице функций.

  class IndicatorFunc: public AbstractFunc
  {
    public:
      IndicatorFunc(const string n, const int a = 1): AbstractFunc(n, a)
      {
        // the single argument is the bar number,
        // two arguments are bar number and buffer index
      }
      static IndicatorFunc *create(const string name);
  };

Особенностью индикаторов в MetaTrader 5 является то, что они требуют двух этапов для применения: сперва индикатор нужно создать (получить его дескриптор) и только потом запрашивать у него данные. В контексте обработки выражений первый этап следует выполнять в процессе разбора, а второй — во время вычисления. Поскольку создание индикатора требует указания всех параметров, они должны быть зашиты в имени, а не передаваться в параметрах функции. Например, если бы мы создали функцию "iMA" с параметрами (период, метод, тип_цены), то на стадии парсинга получили бы только её имя, а определение параметров было бы отложено до стадии исполнения, когда создавать индикатор уже поздно (т.к. пора уже читать из него данные).

В связи с этим было принято решение зарезервировать за индикатором скользящего среднего целый набор имен, составленных по следующему правилу: метод_цена_период. Здесь метод — одно из значащих слов перечисления ENUM_MA_METHOD (SMA, EMA, SMMA, LWMA), цена — один из типов цены перечисления ENUM_APPLIED_PRICE (CLOSE, OPEN, HIGH, LOW, MEDIAN, TYPICAL, WEIGHTED), период — целое число. Таким образом, использование функции "SMA_OPEN_10" должно создать простую скользящую по ценам открытия периодом 10.

Арность функции индикатора равна по умолчанию 1. В единственном параметре передается номер бара. Если арность установить равной 2, то во втором параметре предполагается указывать номер буфера. Для скользящей средней он нам не понадобится.

Создание экземпляров индикаторов с параметрами, соответствующими запрошенным именам, поручено классу MAIndicatorFunc.

  class MAIndicatorFunc: public IndicatorFunc
  {
    protected:
      const int handle;
      
    public:
      MAIndicatorFunc(const string n, const int h): IndicatorFunc(n), handle(h) {}
      
      ~MAIndicatorFunc()
      {
        IndicatorRelease(handle);
      }
      
      static MAIndicatorFunc *create(const string name) // SMA_OPEN_10(0)
      {
        string parts[];
        if(StringSplit(name, '_', parts) != 3) return NULL;
        
        ENUM_MA_METHOD m = -1;
        ENUM_APPLIED_PRICE t = -1;
        
        static string methods[] = {"SMA", "EMA", "SMMA", "LWMA"};
        for(int i = 0; i < ArraySize(methods); i++)
        {
          if(parts[0] == methods[i])
          {
            m = (ENUM_MA_METHOD)i;
            break;
          }
        }
  
        static string types[] = {"NULL", "CLOSE", "OPEN", "HIGH", "LOW", "MEDIAN", "TYPICAL", "WEIGHTED"};
        for(int i = 1; i < ArraySize(types); i++)
        {
          if(parts[1] == types[i])
          {
            t = (ENUM_APPLIED_PRICE)i;
            break;
          }
        }
        
        if(m == -1 || t == -1) return NULL;
        
        int h = iMA(_Symbol, _Period, (int)StringToInteger(parts[2]), 0, m, t);
        if(h == INVALID_HANDLE) return NULL;
        
        return new MAIndicatorFunc(name, h);
      }
      
      double execute(const double &params[]) override
      {
        const int bar = (int)params[0];
        double result[1] = {0};
        if(CopyBuffer(handle, 0, bar, 1, result) != 1)
        {
          Print("CopyBuffer error: ", GetLastError());
        }
        return result[0];
      }
  };

Фабричный метод create парсит переданное ему имя, выделяет из него параметры и создает индикатор с дескриптором handle. Получение значения индикатора происходит в стандартном методе функторов — execute.

Поскольку в перспективе в функции могут быть добавлены и другие индикаторы, в классе IndicatorFunc предусмотрена единая точка входа для запросов любых индикаторов — метод create. Пока в нем находится лишь переадресация на вызов MAIndicatorFunc::create().

  static IndicatorFunc *IndicatorFunc::create(const string name)
  {
    // TODO: support more indicator types, dispatch calls based on the name
    return MAIndicatorFunc::create(name);
  }

Данный метод необходимо вызывать из таблицы функций, поэтому дополним класс FunctionTable.

  class FunctionTable: public Table<IFunctor *>
  {
    public:
      ...
      #ifdef INDICATOR_FUNCTORS
      virtual int index(const string name) override
      {
        int i = _table.getIndex(name);
        if(i == -1)
        {
          i = _table.getSize();
          IFunctor *f = IndicatorFunc::create(name);
          if(f)
          {
            Table<IFunctor *>::add(name, f);
            return i;
          }
          return -1;
        }
        return i;
      }
      #endif
  };

Новая версия метода index пытается найти подходящий индикатор, если переданное имя не найдено в списке встроенных 25 функций. Для подключения этого дополнительного функционала требуется определить макро INDICATOR_FUNCTORS.

При включенной опции мы сможем вычислять, например, такое выражение: "EMA_OPEN_10(0)/EMA_OPEN_21(0)".

На практике параметры вызываемых индикаторов часто выносятся в настройки. Это означает, что они должны неким образом динамически встраиваться в строку с выражением. Для упрощения этой задачи класс AbstractExpressionProcessor поддерживает специальную опцию препроцессинга выражения. Мы опустили этот нюанс для краткости изложения. Включением препроцессинга управляет второй, необязательный параметр метода evaluate (по умолчанию он равен false — препроцессинг отключен).

Принцип работы этой опции следующий. В выражении можно в фигурных скобках указать имя переменной, которое будет заменено на значение переменной перед разбором. Например, если выражение равно "EMA_TYPICAL_{Period}(0)" и в таблице переменных имеется переменная Period со значением 11, то анализироваться будет выражение "EMA_TYPICAL_11(0)".

Для тестирования функций-индикаторов мы позже создадим эксперт, торговые сигналы которого будут формироваться на основе рассчитываемых выражений, включая и скользящую среднюю.

Но прежде нужно удостовериться, что сами парсеры работают правильно.

Тестовый скрипт (ExpresSParserS)

Тестовый скрипт ExpresSParserS.mq5 включает набор функциональных тестов и измерение скорости вычислений для 4-х типов парсеров, а также демонстрацию различных режимов, вывод синтаксического дерева и байт-кода в лог, использование индикаторов в качестве встроенных функций.

Среди функциональных тестов есть как правильные выражения, так и заведомо ошибочные (незадекларированные переменные, деление на ноль на стадии вычисления и т.д.). Правильность теста определяется по соответствию фактического и ожидаемого результатов, то есть ошибки тоже могут быть "правильными". Вот, например, как выглядит лог тестирования парсера Пратта.

  Running 19 tests on ExpressionPratt* …
  1 passed, ok: a > b ? b > c ? 1 : 2 : 3 = 3.0; expected = 3.0
  2 passed, ok: 2 > 3 ? 2 : 3 > 4 ? 3 : 4 = 4.0; expected = 4.0
  3 passed, ok: 4 > 3 ? 2 > 4 ? 2 : 4 : 3 = 4.0; expected = 4.0
  4 passed, ok: (a + b) * sqrt(c) = 8.944271909999159; expected = 8.944271909999159
  5 passed, ok: (b == c) > (a != 1.5) = 0.0; expected = 0.0
  6 passed, ok: (b == c) >= (a != 1.5) = 1.0; expected = 1.0
  7 passed, ok: (a > b) || sqrt(c) = 1.0; expected = 1.0
  8 passed, ok: (!1 != !(b - c/2)) = 1.0; expected = 1.0
  9 passed, ok: -1 * c == -sqrt(-c * -c) = 1.0; expected = 1.0
  10 passed, ok: pow(2, 5) % 5 = 2.0; expected = 2.0
  11 passed, ok: min(max(a,b),c) = 2.5; expected = 2.5
  12 passed, ok: atan(sin(0.5)/cos(0.5)) = 0.5; expected = 0.5
  13 passed, ok: .2 * .3 + .1 = 0.16; expected = 0.16
  14 passed, ok: (a == b) + (b == c) = 0.0; expected = 0.0
  15 passed, ok: -(a + b) * !!sqrt(c) = -4.0; expected = -4.0
  16 passed, ok: sin ( max ( 2 * 1.5, 3 ) / 3 * 3.14159265359 ) = -2.068231111547469e-13; expected = 0.0
  lookUpVariable error: Variable is undefined: _1c @ 7: 1 / _1c^
  17 passed, er: 1 / _1c = nan; expected = nan
  safeDivide error: Error : Division by 0! @ 15: 1 / (2 * b - c)^
  18 passed, er: 1 / (2 * b - c) = inf; expected = inf
  19 passed, ok: sqrt(b-c) = -nan(ind); expected = -nan(ind)
  19 tests passed of 19
  17 for correct expressions, 2 for invalid expressions

Здесь видно, что все 19 тестов прошли успешно, при этом два раза были получены ожидаемые ошибки.

Замер скорости проводится только для многократных вычислений в цикле. В случае интерпретатора это включает этап разбора выражения, т.к. он делается при каждом расчете, а для всех прочих типов парсеров этап разбора "вынесен за скобки". Однократный разбор выражения требует примерно равного времени у всех методов. Вот один из результатов замеров 10000 циклов (микросекунды).

  >>> Performance tests (timing per method)
  Evaluation: 104572
  Compilation: 25011
  Pratt bytecode: 23738
  Pratt: 24967
  ShuntingYard: 23147

Как и предполагалось, предварительно "откомпилированные" выражения рассчитываются в несколько раз быстрее интерпретируемых. Также можно сделать вывод, что наиболее быстрыми являются расчеты на основе байт-кода, причем тип парсера для получения байт-кода не играет особой роли — можно использовать и Пратта, и сортировку. Выбор одного из парсеров можно делать как на основе субъективной оценки понятности алгоритма, так и легкости адаптации под свои задачи, такие как расширение синтаксиса или интеграция с существующими наработками.

Использование выражений для настройки сигналов эксперта (ExprBot)

Выражения могут использоваться в роботах для генерации торговых сигналов. Это дает бОльшую гибкость, чем просто изменение параметров. За счет расширяемого списка функций, возможности практически не отличаются от того, что позволяет MQL, но всё это не нужно компилировать. Кроме того, внутри готовых функторов легко спрятать рутинные операции. Таким образом, программист обеспечивает для пользователя баланс между гибкостью и сложностью настройки продукта.

У нас имеется в распоряжении набор индикаторов скользящих средних, поэтому построим торговую систему на них (хотя ничто не мешает встроить в выражения также и временнЫе функции, управление рисками, тиковые цены и прочее).

Для демонстрации принципа создадим простой эксперт ExprBot. Во входных переменных SignalBuy и SignalSell будут вводиться выражения с условиями совершения, соответственно, сделок покупок и продаж. Для стратегии на пересечении двух МА можно предложить следующие формулы.

  #define INDICATOR_FUNCTORS
  #include <ExpresSParserS/ExpressionCompiler.mqh>
  
  input string SignalBuy = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) > 1 + Threshold";
  input string SignalSell = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) < 1 - Threshold";
  input string Variables = "Threshold=0.01";
  input int Fast = 10;
  input int Slow = 21;

Порог задан как константа просто для демонстрации ввода произвольных переменных. Параметры с периодами усреднения Fast и Slow предназначены для подставки в выражения до их разбора, как фрагмент имени индикатора.

Поскольку сигналов два, инстанцируем два парсера рекурсивного спуска. В принципе, можно было взять и один, но потенциально в двух выражениях могут различаться таблицы переменных, и тогда нужно было бы переключать этот контекст перед каждым вычислением.

  ExpressionCompiler ecb(Variables), ecs(Variables);
  Promise *p1, *p2;

В обработчике OnInit сохраним параметры в таблицах переменных и построим синтаксические деревья.

  int OnInit()
  {
    ecb.variableTable().set("Fast", Fast);
    ecb.variableTable().set("Slow", Slow);
    p1 = ecb.evaluate(SignalBuy, true);
    if(!ecb.success())
    {
      Print("Syntax error in Buy signal:");
      p1.print();
      return INIT_FAILED;
    }
    ecs.variableTable().set("Fast", Fast);
    ecs.variableTable().set("Slow", Slow);
    p2 = ecs.evaluate(SignalSell, true);
    if(!ecs.success())
    {
      Print("Syntax error in Sell signal:");
      p2.print();
      return INIT_FAILED;
    }
    
    return INIT_SUCCEEDED;
  }

Стратегия умещается в небольшом обработчике OnTick (вспомогательные функции здесь опущены; также требуется подключить библиотеку MT4Orders).

  #define _Ask SymbolInfoDouble(_Symbol, SYMBOL_ASK)
  #define _Bid SymbolInfoDouble(_Symbol, SYMBOL_BID)
  
  void OnTick()
  {
    if(!isNewBar()) return;
    
    bool buy = p1.resolve();
    bool sell = p2.resolve();
    
    if(buy && sell)
    {
      buy = false;
      sell = false;
    }
    
    if(buy)
    {
      OrdersCloseAll(_Symbol, OP_SELL);
      if(OrdersTotalByType(_Symbol, OP_BUY) == 0)
      {
        OrderSend(_Symbol, OP_BUY, Lot, _Ask, 100, 0, 0);
      }
    }
    else if(sell)
    {
      OrdersCloseAll(_Symbol, OP_BUY);
      if(OrdersTotalByType(_Symbol, OP_SELL) == 0)
      {
        OrderSend(_Symbol, OP_SELL, Lot, _Bid, 100, 0, 0);
      }
    }
    else
    {
      OrdersCloseAll();
    }
  }

Оба выражения рассчитываются по "обязательствам" p1 и p2. Результат — два флага buy и sell, которые инициируют открытие или закрытие позиции в соответствующих направлениях. MQL-код гарантирует, что одновременно может быть открыта лишь одна позиция, и если сигналы противоречат друг другу (такое возможно, если поменять выражения на нечто более сложное, чем переворотная система, или по ошибке задать порог отрицательным), то любая существующая позиция закрывается. Условия же для сигналов могут редактироваться как угодно в пределах того, что заложено в функциях парсеров.

Если запустить эксперт в тестере, получим, скорее всего, отчет с показателями ниже среднего, но важно другое — торговля ведется, и управляют ею парсеры. Они не дают готовых прибыльных систем, но дополнительный инструмент для их поиска.

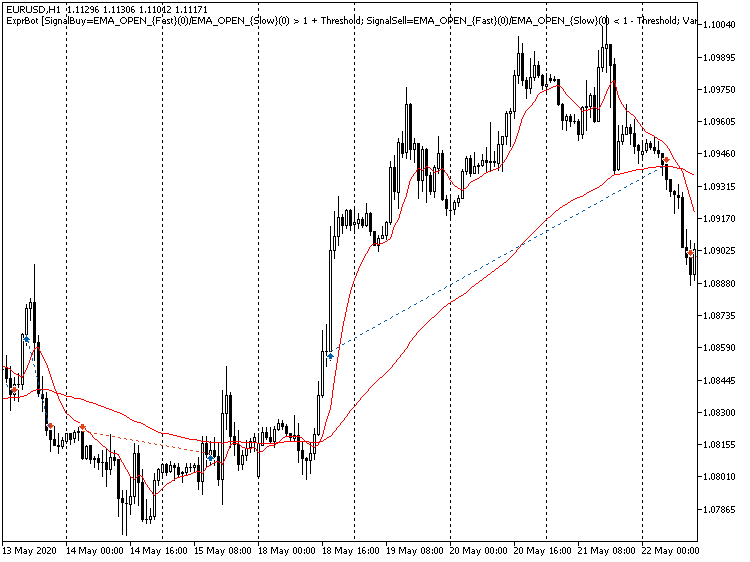
Пример торговли по сигналам, вычисленным по выражениям

Заключение

В данной статье (в двух частях) мы рассмотрели 4 вида парсеров, сравнили их возможности и реализовали классы, готовые для встраивания в программы на языке MQL. Во всех парсерах использовалась одна и та же грамматика с наиболее востребованными математическими операциями и 25 функциями. При необходимости грамматику можно расширить за счет пополнения перечня поддерживаемых операторов, добавления новых встроенных функций прикладного плана (индикаторы, цены, статистические показатели торговли) и синтаксических конструкций (в частности, массивов и функций их обработки).

Технология позволяет более гибко подходить к разделению настроек и неизменяемого кода MQL. Возможность кастомизации алгоритмов за счет редактирования выражений во входных параметрах представляется для конечных пользователей более простой, чем необходимость изучать азы программирования на MQL, чтобы даже при наличии исходных кодов локализовать требуемый фрагмент, отредактировать его с соблюдением всех условностей и разобраться с потенциальными ошибками компиляции. С точки зрения авторов MQL-программ поддержка парсинга и вычисления выражений сулит и другие плюсы, в частности, она способна при должной проработке трансформироваться в концепцию "скрипта поверх MQL", что дает возможность избавиться от библиотек и версионности компилятора MQL.