Вычисление математических выражений (Часть 1). Парсеры рекурсивного спуска

При автоматизации торговых задач иногда требуется обеспечить гибкость вычислительных алгоритмов на стадии их выполнения. Так, например, для тонкой настройки программ, распространяемых в закрытом (откомпилированном) виде, можно организовать подбор вида целевой функции из широкого набора возможных комбинаций. В частности, при оптимизации эксперта или быстрой оценке прототипа индикатора. Тогда в диалоге свойств пользователю доступно изменение не только параметров, но и расчетной формулы. В этих случаях требуется вычислить арифметическое выражение по его текстовому представлению без изменения MQL-кода программы.

Для решения этой задачи применяются парсеры различных типов, позволяющие выполнять интерпретацию формул на лету, их "компиляцию" в синтаксическое дерево, генерацию так называемого байт-кода (последовательности вычислительных инструкций), и его последующее исполнение для расчета результата. В данной статье мы рассмотрим несколько типов парсеров и способов вычисления выражений.

Постановка задачи

Под арифметическим выражением будем понимать однострочную последовательность элементов данных и операторов, описывающих действия над ними. Элементами данных у нас будут числа и именованные переменные. Значения переменных можно будет назначать и менять извне, то есть не в выражении, а с помощью специальных атрибутов парсера. Иными словами, оператор присваивания ('=') для сохранения промежуточных результатов не предусмотрен. Список поддерживаемых операторов в порядке их приоритета в вычислениях таков:

• !, - , + — унарное логическое отрицание, минус и плюс
• () — группировка с помощью скобок
• *, /, % — умножение, деление и деление по модулю
• +, - — сложение и вычитание
• >, <, >=, <= — сравнение больше-меньше
• ==, != — сравнение равно-не равно
• &&, || — логическое И и ИЛИ (внимание, приоритет одинаков, нужны скобки)
• ?: — тернарный условный оператор, позволяющий ветвить вычисления по условиям

Кроме того, разрешим использовать в выражениях стандартные математические функции MQL, всего их — 25. Среди них, в частности, имеется и функция pow для возведения в степень. По этой причине в списке операторов отсутствует оператор возведения в степень ('^'). Кроме того, оператор '^' позволяет возводить только в целую степень, а функция таких ограничений не имеет. Есть и еще один нюанс, отличающий оператор '^' от остальных рассмотренных.

Дело в том, что среди свойств операторов есть такое, как ассоциативность — направление выполнения последовательности операторов с одинаковым приоритетом (в частности, однотипных) — либо начиная слева, либо начиная справа. В принципе, существуют и других виды ассоциативности, но они нам в контексте текущей задачи не встретятся.

Вот пример того, как ассоциативность могла бы влиять на результат вычисления.

1 - 2 - 3

В данном выражении отсутствует явное указание очередности выполнения двух вычитаний с помощью скобок. Поскольку оператор '-' имеет левую ассоциативность, сперва вычитаем 2 из 1, а затем 3 из промежуточной -1, получая -4, что эквивалентно:

((1 - 2) - 3)

Если бы, чисто гипотетически, оператор '-' имел правую ассоциативность, операции выполнялись бы в обратном порядке:

(1 - (2 - 3))

и мы получили бы 2. К счастью, оператор '-' все же левоассоциативный.

Таким образом, левая или правая ассоциативность влияет на правила разбора выражений при парсинге и тем самым усложняет алгоритм. Среди перечисленных бинарных операторов все имеют левую ассоциативность, и только '^' - правую.

Например, выражение:

3 ^ 2 ^ 5

означает, что сначала 2 возводится в степень 5, а затем 3 - в степень 32.

Для упрощения имеет смысл вообще избавиться от оператора возведения в степень (в пользу функции pow) и реализовывать алгоритмы только с учетом левой ассоциативности. Унарные операторы всегда правоассоциативны и потому обрабатываются единообразно.

Все числа в наших выражениях (как записанные в виде констант, так и переменных) будут вещественного типа. Для их сравнения на равенство зададим величину допуска. В логических выражениях числа используются по простому принципу: ноль — false, не ноль — true.

Побитовые операторы не предусмотрены. Массивы не поддерживаются.

Вот несколько примеров выражений:

• "1 + 2 * 3" — вычисления по старшинству операций
• "(1 + 2) * 3" — группировка с помощью скобок
• "(a + b) * c" — использование переменных
• "(a + b) * sqrt(1 / c)" — использование функции
• "a > 0 && a != b ? a : c" — вычисления по логическим условиям

Переменные идентифицируются по имени, составленному по привычным правилам идентификаторов MQL: они могут состоять из букв, цифр или подчеркивания, и не могут начинаться с цифры. Имена переменных не должны совпадать с именами встроенных функций.

Анализ входной строки будем производить посимвольно. Общие проверки на принадлежность символов к набору букв или цифр, обработку ошибок, установку переменных и таблицы встроенных функций (расширяемой по необходимости) определим в базовом классе, от которого унаследуем все типы парсеров.

Рассмотрим последовательно все классы парсеров. В статьях они представлены с некоторыми упрощениями. Полные исходные коды прилагаются.

Базовый класс парсеров (шаблон AbstractExpressionProcessor)

Данный класс является шаблоном, поскольку результатом анализа выражения может быть не только скалярное значение, но и дерево узлов (объектов специального класса), описывающее синтаксис выражения. О том, как это делается и зачем нужно, мы узнаем чуть позже.

Объект класса хранит, прежде всего, само выражение (_expression), его длину (_length), текущую позицию курсора в процессе чтения строки (_index) и текущий символ (_token). Также зарезервированы переменные для признака ошибки в выражении (_failed) и точность сравнения величин (_precision).

  template<typename T>
  class AbstractExpressionProcessor
  {
    protected:
      string _expression;
      int _index;
      int _length;
      ushort _token;
  
      bool _failed;
      double _precision;

Для хранения переменных и ссылок на функции заведены соответствующие таблицы, однако с их классами VariableTable и FunctionTable мы познакомимся позднее.

      VariableTable *_variableTable;
      FunctionTable _functionTable;

Сейчас достаточно лишь знать, что таблицы представляют собой карты с парами "ключ=значение", где ключ — строка с именем переменной или функции, а значение — либо величина double в случае переменной, либо объект функтора в случае функции.

Таблица переменных описана ссылкой, потому что в выражении может не быть переменных. А вот минимальный набор встроенных функций в парсере присутствует всегда (и может быть расширен пользователем), в связи с чем таблица функций представлена готовым объектом.

Заполнение таблицы встроенных функций осуществляется в методе:

      virtual void registerFunctions();

Далее описываются функции, выполняющие подзадачи, общие для различных парсеров, такие как переход на следующий символ, проверку символа на соответствие ожидаемому (с выдачей ошибки при несоответствии), последовательное чтение цифр, удовлетворяющих формату записи чисел, а также несколько статических вспомогательных методов классификации символов.

      bool _nextToken();
      void _match(ushort c, string message, string context = NULL);
      bool _readNumber(string &number);
      virtual void error(string message, string context = NULL, const bool warning = false);
      
      static bool isspace(ushort c);
      static bool isalpha(ushort c);
      static bool isalnum(ushort c);
      static bool isdigit(ushort c);

Все эти функции определены в данном базовом классе, в частности:

  template<typename T>
  bool AbstractExpressionProcessor::_nextToken()
  {
    _index++;
    while(_index < _length && isspace(_expression[_index])) _index++;
    if(_index < _length)
    {
      _token = _expression[_index];
      return true;
    }
    else
    {
      _token = 0;
    }
    return false;
  }
  
  template<typename T>
  void AbstractExpressionProcessor::_match(ushort c, string message, string context = NULL)
  {
    if(_token == c)
    {
      _nextToken();
    }
    else if(!_failed) // prevent chained errors
    {
      error(message, context);
    }
  }
  
  template<typename T>
  bool AbstractExpressionProcessor::_readNumber(string &number)
  {
    bool point = false;
    while(isdigit(_token) || _token == '.')
    {
      if(_token == '.' && point)
      {
        error("Too many floating points", __FUNCTION__);
        return false;
      }
      number += ShortToString(_token);
      if(_token == '.') point = true;
      _nextToken();
    }
    return StringLen(number) > 0;
  }

При парсинге числа научная запись с экспонентой не поддерживается.

Кроме них в классе декларируется основной метод evaluate, который будет переопределен в наследниках. Здесь он только инициализирует переменные.

    public:
      virtual T evaluate(const string expression)
      {
        _expression = expression;
        _length = StringLen(_expression);
        _index = -1;
        _failed = false;
        return NULL;
      }

Это главный метод класса, получающий на входе строку с выражением, а на выходе выдающий результат её обработки: конкретное значение, если выполнялось вычисление, или синтаксическое дерево, если выполнялся анализ.

Публичный интерфейс класса содержит также конструкторы, в которые можно при необходимости передать переменные вместе с их значениями (как в виде строки вида "name1=value1;name2=value2;...", так и готового объекта VariableTable), методы установки допуска для сравнения чисел, получения признака успеха парсинга (отсутствие синтаксических ошибок) и доступа к таблицам переменных и функций.

    public:
      AbstractExpressionProcessor(const string vars = NULL);
      AbstractExpressionProcessor(VariableTable &vt);
  
      bool success() { return !_failed; };
      void setPrecision(const double p) { _precision = p; };
      double getPrecision(void) const { return _precision; };
      virtual VariableTable *variableTable();
      virtual FunctionTable *functionTable();
  };

Обратите внимание, что даже при отсутствии синтаксических ошибок вычисление выражения может закончиться ошибкой (например, делением на 0, корнем из отрицательного числа и т.д.). Для контроля подобных ситуаций следует проверять, что результат действительно является числом с помощью функции MathIsValidNumber. Наши парсеры должны уметь генерировать соответствующие величины разных типов NaN (Not A Number), а не "падать" во время выполнения.

Самым простым для освоения является парсер рекурсивного спуска. С него мы и начнем.

Парсер рекурсивного спуска (шаблон ExpressionProcessor)

Парсер рекурсивного спуска представляет собой набор функций, вызываемых рекурсивно друг из друга по правилам, описывающим отдельные операции. Если свести синтаксис нескольких наиболее употребительных операций в грамматику в нотации расширенной BNF (Extended Backus–Naur Form), то выражение можно представить следующим образом (каждая строка — отдельное правило):

  Expr    -> Sum
  Sum     -> Product { ('+' | '-') Product }
  Product -> Value { ('*' | '/') Value }
  Value   -> [0-9]+ | '(' Expr ')'

На естественном языке эти правила эквиваленты примерно следующему. Выражение начинает анализироваться с операции с наименьшим приоритетом — в данном примере это суммирование/вычитание. Сумма (Sum) — это два операнда Product, разделенных знаками '+' или '-', но сама операция и второй операнд опциональны. Произведение (Product) — это два операнда Value, разделенных знаками '*' или '/', но опять же операция и второй операнд могут отсутствовать. Величина (Value) — это либо число, состоящее из цифр, либо вложенное выражение, заключенное в пару круглых скобок.

Например, выражение "10" (просто число) будет развернуто в такую последовательность правил:

  Expr -> Sum -> Product -> Value -> 10

А выражение "1 + 2 * 3" приведет к более сложной конструкции:

  Expr -> Sum -> Product -> Value -> 1
              |  '+'
              -> Product -> Value -> 2
                         |  '*'
                         -> Value -> 3

Как нетрудно заметить, алгоритм предполагает просмотр грамматики с подбором соответствий между входным потоком символов и правилами операций, причем просмотр осуществляется от главного правила (всего выражения целиком) к более мелким компонентам (вплоть до отдельных чисел). Парсер рекурсивного спуска относится к классу нисходящих (top-down).

В нашем парсере будет поддерживаться больше операций (см. список приведенный в первом разделе), и для каждой из них в производном классе ExpressionProcessor зарезервирован свой метод.

  template<typename T>
  class ExpressionProcessor: public AbstractExpressionProcessor<T>
  {
    public:
      ExpressionProcessor(const string vars = NULL);
      ExpressionProcessor(VariableTable &vt);
      T evaluate(const string expression) override
      {
        AbstractExpressionProcessor<T>::evaluate(expression);
        if(_length > 0)
        {
          _nextToken();
          return _parse();
        }
        return NULL;
      }
      
    protected:
      T _parse();
      T _if();        // ?:
      T _logic();     // && ||
      T _eq();        // == !=
      T _compare();   // ><>=<=
      T _expr();      // +-
      T _term();      // */%
      T _unary();     // !-+
      T _factor();    // ()
      T _identifier();
      T _number();
      T _function(const string &name);
  };

Примерный вид EBNF-грамматики выражений служит инструкцией по написанию кода методов.

  expression -> if
  if         -> logic { '?' if ':' if }
  logic      -> eq { ('&&' | '||' ) eq }
  eq         -> compare { ('==' | '!=' ) compare }
  compare    -> expr { ('>' | '<' | '>=' | '<=') expr }
  expr       -> term  { ('+' | '-') term }
  term       -> unary { ('*' | '/' | '%') unary }
  unary      -> { ('!' | '-' | '+') } unary | factor
  factor     -> '(' if ')' | number | identifier
  identifier -> function | variable
  variable   -> name
  function   -> name '(' { arglist } ')'
  name       -> char { char | digit }*
  arglist    -> if { ',' if } 

Точкой начала спуска является метод _parse — он вызван из публичного метода evaluate. С учетом приоритетов операторов метод _parse передает управление самому "младшему" — _if. После разбора всего выражения текущий символ должен быть нулем (признак конца строки).

  template<typename T>
  T ExpressionProcessor::_parse(void)
  {
    T result = _if();
    if(_token != '\0')
    {
      error("Tokens after end of expression.", __FUNCTION__);
    }
    return result;
  }

Тернарный условный оператор состоит из трех подвыражений: логического условия, и двух вариантов расчетов — для истинного и ложного условия. Логическое условие — это следующий уровень грамматики: метод _logic. А варианты расчета могут в свою очередь является тернарными условными операторами, в связи с чем мы рекурсивно вызываем _if. Между условием и истинным вариантом должен стоять знак '?'. Если его нет, то это не тернарный оператор, и алгоритм вернет значение из _logic как есть. Если знак '?' есть, то мы дополнительно проверяем, чтобы между истинным и ложным вариантами находился символ ':'. Когда все компоненты в наличии, проверяем условие и возвращаем первое или второе значение, в зависимости от истинности.

  template<typename T>
  T ExpressionProcessor::_if()
  {
    T result = _logic();
    if(_token == '?')
    {
      _nextToken();
      T truly = _if();
      if(_token == ':')
      {
        _nextToken();
        T falsy = _if();
        return result ? truly : falsy; // NB: to be refined
      }
      else
      {
        error("Incomplete ternary if-condition", __FUNCTION__);
      }
    }
    return result;
  }

Операции логического И или ИЛИ представлены методом _logic. В нем мы ожидаем появления последовательных символов "&&" или "||" между операндами, представляющими собой сравнение (метод _eq). Если логической операции нет, результат возвращается напрямую из метода _eq. Если же она есть, мы её вычисляем. Благодаря циклу while парсер может выполнять подряд несколько логических сложений или умножений, например "a > 0 && b > 0 && c > 0".

  template<typename T>
  T ExpressionProcessor::_logic()
  {
    T result = _eq();
    while(_token == '&' || _token == '|')
    {
      ushort previous = _token;
      _nextToken();
      if(previous == '&' && _token == '&')
      {
        _nextToken();
        result = _eq() && result;
      }
      else
      if(previous == '|' && _token == '|')
      {
        _nextToken();
        result = _eq() || result;
      }
      else
      {
        error("Unexpected tokens " + ShortToString(previous) + " and " + ShortToString(_token), __FUNCTION__);
      }
    }
    return result;
  }

Обратите внимание, что приоритеты у "&&" и "||" в данной реализации равны, и потому при последовательной записи разных операций требуется указывать желаемый порядок с помощью скобок.

Операции сравнения ('==', '!=') обрабатываются похожим образом в методе _eq.

  template<typename T>
  T ExpressionProcessor::_eq() 
  {
    T result = _compare();
    if(_token == '!' || _token == '=')
    {
      const bool equality = _token == '=';
      _nextToken();
      if(_token == '=')
      {
        _nextToken();
        const bool equal = fabs(result - _compare()) <= _precision; // NB: to be refined
        return equality ? equal : !equal;
      }
      else
      {
        error("Unexpected token " + ShortToString(_token), __FUNCTION__);
      }
    }
    return result;
  }

Пропустим для краткости некоторые методы в статье, а желающие могут с ними ознакомиться в прилагаемых исходных кодах.

В методе _factor мы добираемся фактически до операндов. Это может быть подвыражение внутри круглых скобок — для него рекурсивно вызывается _if, либо идентификатор, либо число (константа, литерал).

  template<typename T>
  T ExpressionProcessor::_factor()
  {
    T result;
    
    if(_token == '(')
    {
      _nextToken();
      result = _if();
      _match(')', ") expected!", __FUNCTION__);
    }
    else if(isalpha(_token))
    {
      result = _identifier();
    }
    else
    {
      result = _number();
    }
    
    return result;
  }

Идентификатор может означать имя переменной или функции, если после имени идет открывающая скобка. Этим анализом занимается метод _identifier. В случае функции специальный метод _function находит в таблице функций _functionTable соответствующий объект, парсит список параметров (причем каждый из них может быть самостоятельным выражением и получается за счет рекурсивного вызова _if) и затем передает управлению объекту-функтору.

  template<typename T>
  T ExpressionProcessor::_identifier()
  {
    string variable;
  
    while(isalnum(_token))
    {
      variable += ShortToString(_token);
      _nextToken();
    }
    
    if(_token == '(')
    {
      _nextToken();
      return _function(variable);
    }
    
    return _variableTable.get(variable); // NB: to be refined
  }

Метод _number просто преобразует прочитанную последовательность цифр в число с помощью StringToDouble (вспомогательная функция _readNumber была приведена выше).

  template<typename T>
  T ExpressionProcessor::_number()
  {
    string number;
    
    if(!_readNumber(number))
    {
      error("Number expected", __FUNCTION__);
    }
    return StringToDouble(number); // NB: to be refined
  }

Вот и весь парсер рекурсивного спуска. Он почти готов к работе. "Почти" — потому что класс является шаблонным и требует специализации конкретным типом. Для вычисления выражения на основе переменных числового типа достаточно сделать специализацию для double, примерно так:

  class ExpressionEvaluator: public ExpressionProcessor<double>
  {
    public:
      ExpressionEvaluator(const string vars = NULL): ExpressionProcessor(vars) { }
      ExpressionEvaluator(VariableTable &vt): ExpressionProcessor(vt) { }
  };

Но на практике дела обстоят несколько сложнее. Рассмотренный алгоритм вычисляет выражение в процессе разбора. Это режим интерпретатора — самый простой, но и самый медленный. Представим себе, что необходимо вычислять одну и ту же формулу на каждом тике, для меняющихся значений переменных (например, цен или объемов). Для ускорения вычислений желательно разделить этапы разбора и выполнения операций. Тогда можно выполнить парсинг лишь один раз, сохранить структуру выражения в некоем промежуточном представлении, оптимизированном для вычислений, и затем выполнять быстрый пересчет по этому представлению.

Для этой цели все промежуточные результаты, которые получаются в рассмотренных методах и передаются по цепочке рекурсивных вызовов вплоть до возврата окончательного значения из публичного метода evaluate, должны быть заменены на объекты, хранящие в себе описание операторов и операндов конкретного фрагмента выражения (вместе со всеми их взаимосвязями). На основе этого описания можно произвести расчет выражения отложенным образом. Подобные объекты называются Promise (обязательства).

Отложенные вычисления (Promise)

Класс Promise описывает отдельную сущность из состава выражения: операнд или операцию вместе со ссылками на операнды. Например, если в выражении встретилось имя переменной, то в методе _identifier отрабатывает строка:

    return _variableTable.get(variable); // NB: to be refined

Она возвращает текущее значение переменной из таблицы по её имени. Это значение типа double, что подходит для случая, когда парсер специализирован типом double и выполняет вычисления на лету. Однако, если требуется отложить вычисления, то вместо значения переменной следует создать объект Promise и сохранить в нем имя переменной. В будущем, когда значение переменной, вероятно, поменяется в таблице, мы должны иметь возможность запросить её новое значение у объекта Promise, и он точно также по имени найдет её значение. Таким образом, становится понятно, что текущая строка кода, помеченная комментарием "NB: to be refined", не подходит для общего случая шаблона ExpressionProcessor и должна быть на что-то заменена. Таких строк в ExpressionProcessor на самом деле несколько, и мы скоро найдем для них единообразное решение, но прежде разберемся с классом Promise.

Для описания произвольного операнда или операции в классе Promise есть несколько полей.

  class Promise
  {
    protected:
      uchar code;
      double value;
      string name;
      int index;
      Promise *left;
      Promise *right;
      Promise *last;
      
    public:
      Promise(const uchar token, Promise *l = NULL, Promise *r = NULL, Promise *v = NULL):
        code(token), left(l), right(r), last(v), value(0), name(NULL), index(-1)
      {
      }
      Promise(const double v): // value (const)
        code('n'), left(NULL), right(NULL), last(NULL), value(v), name(NULL), index(-1)
      {
      }
      Promise(const string n, const int idx = -1): // name of variable
        code('v'), left(NULL), right(NULL), last(NULL), value(0), name(n), index(idx)
      {
      }
      Promise(const int f, Promise *&params[]): // index of function
        code('f'), left(NULL), right(NULL), last(NULL), value(0), name(NULL)
      {
        index = f;
        if(ArraySize(params) > 0) left = params[0];
        if(ArraySize(params) > 1) right = params[1];
        if(ArraySize(params) > 2) last = params[2];
        // more params not supported
      }

Поле code хранит признак типа элемента: 'n' — число, 'v' — переменная, 'f' — функция, а все прочие символы рассматриваются как операции из числа допустимых (например, '+', '-', '*', '/', '%', и т.д.). В случае числа, его значение хранится в поле value. В случае переменной, её имя хранится в поле name. Для быстрого многократного доступа к переменным Promise будет пытаться после первого вызова закэшировать номер переменной в поле index и далее извлекать её из таблицы по индексу, а не имени. Функции всегда идентифицируются по номеру в поле index, т.к. в отличие от переменных, таблица Функций изначально заполнена встроенными функциями, а таблица переменных может быть в момент анализа выражения еще пуста.

Ссылки left, right и last опциональны и могут хранить операнды. Например, для чисел или переменных все три ссылки равны NULL. Для унарных операций используется только ссылка left, для бинарных операций — ссылки left и right, а все три ссылки задействованы только в тернарном условном операторе: там left содержит условие, right — выражение для истинного условия и last — для ложного условия. Также ссылки хранят объекты-параметры функций (текущая реализация парсера ограничивает число параметров функций тремя).

Поскольку объекты Promise участвуют в вычислениях, мы переопределим в них все основные операторы. Вот, например, как обрабатываются операции сложения и вычитания с "обязательствами".

      Promise *operator+(Promise *r)
      {
        return new Promise('+', &this, r);
      }
      Promise *operator-(Promise *r)
      {
        return new Promise('-', &this, r);
      }

Текущий объект (&this), т.е. тот, что стоит в выражении слева от операции, и соседний объект (r), который стоит справа от операции, передаются в конструктор нового объекта Promise, создаваемого с кодом соответствующей операции.

Прочие операции обрабатываются аналогичным образом. В результате, всё выражение отображается в дерево объектов класса Promise, причем корневой элемент представляет выражение целиком. Для получения актуального значения любого объекта "обязательства", в том числе и выражения целиком, предусмотрен метод resolve.

      double resolve()
      {
        switch(code)
        {
          case 'n': return value;        // number constant
          case 'v': value = _variable(); // variable name
                    return value;
          case 'f': value = _execute();  // function index
                    return value;
          default:  value = _calc();
                    return value;
        }
        return 0;
      };

Здесь видно, как значение числовой константы возвращается из поля value, а для переменных, функций и операций реализованы вспомогательные методы.

      static void environment(AbstractExpressionProcessor<Promise *> *e)
      {
        variableTable = e.variableTable();
        functionTable = e.functionTable();
      }
      
    protected:
      static VariableTable *variableTable;
      static FunctionTable *functionTable;
  
      double _variable()
      {
        double result = 0;
        if(index == -1)
        {
          index = variableTable.index(name);
          if(index == -1)
          {
            return nan; // error: Variable undefined
          }
          result = variableTable[index];
        }
        else
        {
          result = variableTable[index];
        }
        return result;
      }
      
      double _execute()
      {
        double params[];
        if(left)
        {
          ArrayResize(params, 1);
          params[0] = left.resolve();
          if(right)
          {
            ArrayResize(params, 2);
            params[1] = right.resolve();
            if(last)
            {
              ArrayResize(params, 3);
              params[2] = last.resolve();
            }
          }
        }
        IFunctor *ptr = functionTable[index]; // TBD: functors
        if(ptr == NULL)
        {
          return nan; // error: Function index out of bound 
        }
        return ptr.execute(params);
      }
      
      double _calc()
      {
        double first = 0, second = 0, third = 0;
        if(left)
        {
          first = left.resolve();
          if(right)
          {
            second = right.resolve();
            if(last)
            {
              third = last.resolve();
            }
          }
        }
        
        switch(code)
        {
          case '+': return first + second;
          case '-': return first - second;
          case '*': return first * second;
          case '/': return safeDivide(first, second);
          case '%': return fmod(first, second);
          case '!': return !first;
          case '~': return -first;
          case '<': return first < second;
          case '>': return first > second;
          case '{': return first <= second;
          case '}': return first >= second;
          case '&': return first && second;
          case '|': return first || second;
          case '`': return _precision < fabs(first - second); // first != second;
          case '=': return _precision > fabs(first - second); // first == second;
          case '?': return first ? second : third;
        }
        return nan; // error: Unknown operator
      }

Обработка ошибок здесь опущена, в случае их возникновения возвращается специальное значение nan ("не число", генерация вынесена в отдельный заголовочный файл NaNs.mqh, с ним можно ознакомиться самостоятельно). Обратите внимание, что выполнение операций предваряется рекурсивным вызовом resolve у всех нижележащих в иерархии объектов по ссылкам. Таким образом, вызов resolve у выражения инициирует последовательное вычисление всех связанных "обязательств" и последующую передачу "наверх" результатов вычислений, уже в виде чисел double. В конце они "схлопываются" в окончательное значение выражения.

Имея класс Promise, мы можем использовать его для специализации парсера рекурсивного спуска, возвращающего в качестве результата обработки дерево подобных объектов, то есть фактически синтаксическое дерево выражения.

Во всех методах шаблонного класса ExpressionProcessor, где возвращается некое T, оно теперь должно быть равно (Promise *). В частности, в методе _identifier, где мы обратили внимание на строку

    return _variableTable.get(variable); // NB: to be refined

необходимо каким-то образом обеспечить, чтобы вместо double можно было создать и вернуть новый объект Promise, указывающий на переменную с именем variable.

Для решения этой задачи следовало бы "обернуть" действие по возврату значения типа T для переменной в отдельный виртуальный метод, который в производных классах ExpressionProcessor<double> и ExpressionProcessor<Promise *> выполнил бы требуемые разные манипуляции. Но тут возникает небольшая проблема.

Класс ExpressionHelper

Мы планируем реализовать несколько классов парсеров, и все они будут унаследованы от AbstractExpressionProcessor. Но методы, характерные для рекурсивного спуска, потребуются не во всех из них, причем в разных ветвях иерархии наследования. Можно было бы их переопределить пустыми там, где они не нужны, но это не очень красиво с точки зрения ООП. Если бы MQL поддерживал в том или ином виде множественное наследование, мы могли бы использовать специальный типаж (trait) — дополнительный набор методов, который можно было бы включить в класс парсера по необходимости. Поскольку такой возможности нет, мы оформим все соответствующие методы как отдельный шаблонный класс и создадим его экземпляр только внутри тех парсеров, где он востребован.

  template<typename T>
  class ExpressionHelper
  {
    protected:
      VariableTable *_variableTable;
      FunctionTable *_functionTable;
  
    public:
      ExpressionHelper(AbstractExpressionProcessor<T> *owner): _variableTable(owner.variableTable()), _functionTable(owner.functionTable()) { }
  
      virtual T _variable(const string &name) = 0;
      virtual T _literal(const string &number) = 0;
      virtual T _negate(T result) = 0;
      virtual T _call(const int index, T &args[]) = 0;
      virtual T _ternary(T condition, T truly, T falsy) = 0;
      virtual T _isEqual(T result, T next, const bool equality) = 0;
  };

Здесь собраны все действия, которые по-разному обрабатываются при немедленных и отложенных вычислениях. В частности, метод _variable отвечает за доступ к переменным, на чем мы акцентировали внимание ранее. _literal получает значение константы, _negate выполняет логическое отрицание, _call — вызов функции, _ternary — условный оператор, а _isEqual предназначен для сравнения величин. Все прочие случаи вычислений обрабатываются для double и Promise одинаковыми синтаксическими конструкциями за счет переопределения операторов в классе Promise.

Может позникнуть вопрос, почему оператор логического отрицания '!' не был переопределен в Promise и вместо него потребовался метод _negate. Дело в том, что оператор '!' применяется только для объектов, но не указателей. Иными словами, имея переменную типа Promise *p, мы не можем привычно написать !p в надежде, что сработает переопределенный оператор. Вместо этого требуется предварительно разыменовать указатель: !*p. А такая запись становится неверной для других типов, в частности для T=double.

Вот как методы ExpressionHelper могут быть реализованы для чисел double.

  class ExpressionHelperDouble: public ExpressionHelper<double>
  {
    public:
      ExpressionHelperDouble(AbstractExpressionProcessor<T> *owner): ExpressionHelper(owner) { }
  
      virtual double _variable(const string &name) override
      {
        if(!_variableTable.exists(name))
        {
          return nan;
        }
        return _variableTable.get(name);
      }
      virtual double _literal(const string &number) override
      {
        return StringToDouble(number);
      }
      virtual double _call(const int index, double &params[]) override
      {
        return _functionTable[index].execute(params);
      }
      virtual double _isEqual(double result, double next, const bool equality) override
      {
        const bool equal = fabs(result - next) <= _precision;
        return equality ? equal : !equal;
      }
      virtual double _negate(double result) override
      {
        return !result;
      }
      virtual double _ternary(double condition, double truly, double falsy) override
      {
        return condition ? truly : falsy;
      }
  };

А вот как они же реализуются для Promise.

  class ExpressionHelperPromise: public ExpressionHelper<Promise *>
  {
    public:
      ExpressionHelperPromise(AbstractExpressionProcessor<T> *owner): ExpressionHelper(owner) { }
  
      virtual Promise *_negate(Promise *result) override
      {
        return new Promise('!', result);
      }
      virtual Promise *_call(const int index, Promise *&params[]) override
      {
        return new Promise(index, params);
      }
      virtual Promise *_ternary(Promise *condition, Promise *truly, Promise *falsy) override
      {
        return new Promise('?', condition, truly, falsy);
      }
      virtual Promise *_variable(const string &name) override
      {
        if(CheckPointer(_variableTable) != POINTER_INVALID)
        {
          int index = _variableTable.index(name);
          if(index == -1)
          {
            return new Promise(nan); // error: Variable is undefined
          }
          return new Promise(name, index);
        }
        return new Promise(name);
      }
      virtual Promise *_literal(const string &number) override
      {
        return new Promise(StringToDouble(number));
      }
      virtual Promise *_isEqual(Promise *result, Promise *next, const bool equality) override
      {
        return new Promise((uchar)(equality ? '=' : '`'), result, next);
      }
  };

Теперь мы можем добавить в AbstractExpressionProcessor поле helper:

    protected:
      ExpressionHelper<T> *helper;
      
    public:  
      ~AbstractExpressionProcessor()
      {
        if(CheckPointer(helper) == POINTER_DYNAMIC) delete helper;
      }

и пересмотреть реализацию методов ExpressionProcessor, в которых были строки, помеченные "NB" — все они должны делегировать операции объекту helper. Например, так:

  template<typename T>
  T ExpressionProcessor::_eq()
  {
    T result = _compare();
    if(_token == '!' || _token == '=')
    {
      const bool equality = _token == '=';
      _nextToken();
      if(_token == '=')
      {
        _nextToken();
        return helper._isEqual(result, _compare(), equality); // OK
      }
    }
    return result;
  }
  
  template<typename T>
  T ExpressionProcessor::_identifier()
  {
    string variable;
    while(isalnum(_token))
    {
      variable += ShortToString(_token);
      _nextToken();
    }
    ...
    return helper._variable(variable); // OK
  }
  
  template<typename T>
  T ExpressionProcessor::_number()
  {
    string number;
    if(!_readNumber(number))
    {
      error("Number expected", __FUNCTION__);
    }
    return helper._literal(number); // OK
  }

С помощью представленных классов мы наконец можем собрать первый парсер, выполняющий вычисления в процессе разбора выражений — ExpressionEvaluator.

  class ExpressionEvaluator: public ExpressionProcessor<double>
  {
    public:
      ExpressionEvaluator(const string vars = NULL): ExpressionProcessor(vars) { helper = new ExpressionHelperDouble(&this); }
      ExpressionEvaluator(VariableTable &vt): ExpressionProcessor(vt) { helper = new ExpressionHelperDouble(&this); }
  };

И тут же у нас получается второй парсер для отложенных вычислений — ExpressionCompiler.

  class ExpressionCompiler: public ExpressionProcessor<Promise *>
  {
    public:
      ExpressionCompiler(const string vars = NULL): ExpressionProcessor(vars) { helper = new ExpressionHelperPromise(&this); }
      ExpressionCompiler(VariableTable &vt): ExpressionProcessor(vt) { helper = new ExpressionHelperPromise(&this); }
      
      virtual Promise *evaluate(const string expression) override
      {
        Promise::environment(&this);
        return ExpressionProcessor<Promise *>::evaluate(expression);
      }
  };

Основные отличия заключаются лишь в объектах в поле helper и предварительном вызове Promise::environment для передачи таблиц переменных и функций внутрь Promise.

Для того чтобы получить полностью рабочий парсер остается лишь разобраться с таблицами переменных и функций.

Таблицы переменных и функций

Обе таблицы представляют собой шаблонные классы карт, состоящих из пар "ключ=значение", где ключ — строковый идентификатор, а значение — некая величина типа T. Их реализацию можно найти в файле VariableTable.mqh. Базовый класс описывает все востребованные операции с картами: добавление элементов, изменение значений и их извлечение по имени или по индексу.

  template<typename T>
  class Table
  {
    public:
      virtual T operator[](const int index) const;
      virtual int index(const string variableName);
      virtual T get(const string variableName) const;
      virtual int add(const string variableName, T value);
      virtual void update(const int index, T value);
      ...
  };

В случае переменных тип T — это double.

  class VariableTable: public Table<double>
  {
    public:
      VariableTable(const string pairs = NULL)
      {
        if(pairs != NULL) assign(pairs);
      }
      
      void assign(const string pairs);
  };

С помощью метода assign переменные можно добавлять в таблицу не только по одной, но сразу списком, как строку вида "имя1=значение1;имя2=значение2;...".

Для функций нам потребуется создать специальный интерфейс-функтор, содержащий код для вычисления функций.

  interface IFunctor
  {
    string name(void) const;
    int arity(void) const;
    double execute(const double &params[]);
  };

Каждая функция имеет имя и свойство, описывающее количество аргументов (арность). Вычисление функции выполняется методом execute, в который передаются аргументы. Все встроенные математические функции MQL нужно будет обернуть в этот интерфейс и затем добавить соответствующие объекты в таблицу (по одному или массивом):

  class FunctionTable: public Table<IFunctor *>
  {
    public:
      void add(IFunctor *f)
      {
        Table<IFunctor *>::add(f.name(), f);
      }
      void add(IFunctor *&f[])
      {
        for(int i = 0; i < ArraySize(f); i++)
        {
          add(f[i]);
        }
      }
  };

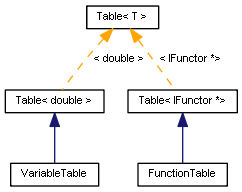
Диаграмма классов таблиц переменных и функций

Для хранения всех функторов определен класс-хранилище.

  class AbstractFuncStorage
  {
    protected:
      IFunctor *funcs[];
      int total;
      
    public:
      ~AbstractFuncStorage()
      {
        for(int i = 0; i < total; i++)
        {
          CLEAR(funcs[i]);
        }
      }
      void add(IFunctor *f)
      {
        ArrayResize(funcs, total + 1);
        funcs[total++] = f;
      }
      void fill(FunctionTable &table)
      {
        table.add(funcs);
      }
  };

Метод fill позволяет заполнить переданную в него таблицу встроенными функциями из хранилища (массива funcs). Для того чтобы все создаваемые функторы автоматически попадали в хранилище, мы делаем его статический экземпляр внутри базового класса функций AbstractFunc и пополняем ссылками на this из конструктора.

  class AbstractFunc: public IFunctor
  {
    private:
      const string _name;
      const int _arity;
      static AbstractFuncStorage storage;
  
    public:
      AbstractFunc(const string n, const int a): _name(n), _arity(a)
      {
        storage.add(&this);
      }
      string name(void) const override
      {
        return _name;
      }
      int arity(void) const override
      {
        return _arity;
      }
      static void fill(FunctionTable &table)
      {
        storage.fill(table);
      }
  };
  
  static AbstractFuncStorage AbstractFunc::storage;

Разумеется, конструктор принимает входные параметры, позволяющие установить имя и арность функции.

Для декларации функций специфической арности введен промежуточный шаблонный класс FuncN, в котором арность задается размером переданного типа (поскольку арность функций у нас пока не превышает 3, а типов с нулевым размером не существует, используется запись sizeof(T) % 4 — таким образом, размер 4 даст арность 0).

  template<typename T>
  class FuncN: public AbstractFunc
  {
    public:
      FuncN(const string n): AbstractFunc(n, sizeof(T) % 4) {}
  };

Сами типы с размерами от 0 до 3 генерируются с помощью макросов.

  struct arity0 { char x[4]; };
  
  #define _ARITY(N)   struct arity##N { char x[N]; };
  
  _ARITY(1);
  _ARITY(2);
  _ARITY(3);

Также для автоматизации генерации описания функций нам потребуются списки аргументов.

  #define PARAMS0 
  #define PARAMS1 params[0]
  #define PARAMS2 params[0],params[1]
  #define PARAMS3 params[0],params[1],params[2]

Теперь мы можем определить макрос для функтора на базе класса FuncN<T>.

  #define FUNCTOR(CLAZZ,NAME,ARITY) \
  class Func_##CLAZZ: public FuncN<arity##ARITY> \
  { \
    public: \
      Func_##CLAZZ(): FuncN(NAME) {} \
      double execute(const double &params[]) override \
      { \
        return CLAZZ(PARAMS##ARITY); \
      } \
  }; \
  Func_##CLAZZ __##CLAZZ;

И вот, наконец, список поддерживаемых функций с именами и количеством аргументов.

  FUNCTOR(fabs, "abs", 1);
  FUNCTOR(acos, "acos", 1);
  FUNCTOR(acosh, "acosh", 1);
  FUNCTOR(asin, "asin", 1);
  FUNCTOR(asinh, "asinh", 1);
  FUNCTOR(atan, "atan", 1);
  FUNCTOR(atanh, "atanh", 1);
  FUNCTOR(ceil, "ceil", 1);
  FUNCTOR(cos, "cos", 1);
  FUNCTOR(cosh, "cosh", 1);
  FUNCTOR(exp, "exp", 1);
  FUNCTOR(floor, "floor", 1);
  FUNCTOR(log, "log", 1);
  FUNCTOR(log10, "log10", 1);
  FUNCTOR(fmax, "max", 2);
  FUNCTOR(fmin, "min", 2);
  FUNCTOR(fmod, "mod", 2);
  FUNCTOR(pow, "pow", 2);
  FUNCTOR(rand, "rand", 0);
  FUNCTOR(round, "round", 1);
  FUNCTOR(sin, "sin", 1);
  FUNCTOR(sinh, "sinh", 1);
  FUNCTOR(sqrt, "sqrt", 1);
  FUNCTOR(tan, "tan", 1);
  FUNCTOR(tanh, "tanh", 1);

Диаграмма классов функторов в обобщенном виде выглядит следующим образом.

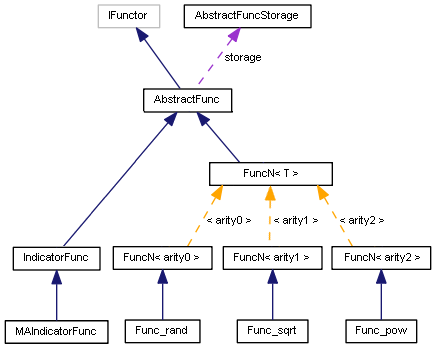
Диаграмма классов функторов

Здесь показаны не все функции, а лишь по одной каждой арности. Также здесь присутствуют некоторые классы, которые мы рассмотрим позднее.

С учетом функций все готово для эксплуатации двух парсеров рекурсивного спуска. Один умеет вычислять выражения в режиме интерпретации, а другой — по его синтаксическому дереву.

Вычисление выражений на лету (ExpressionEvaluator)

Способ вычисления выражения интерпретатором соответствует следующей схеме: создаем экземпляр ExpressionEvaluator, при необходимости передаем в него переменные и вызываем метод evaluate со строкой, содержащей требуемое выражение.

  ExpressionEvaluator ee("a=-10");
  double result = ee.evaluate("1 + sqrt(a)"); // -nan(ind)
  bool success = ee.success();                // true

С помощью метода success можно проверить синтаксическую правильность выражения, но она не гарантирует, что в процессе вычислений не произойдет ошибка. В приведенном выше примере извлечение корня из отрицательной переменной приведет к возврату результата NaN. Так что рекомендуется всегда проверять результат с помощью функции MathIsValidNumber.

После того как мы разработаем другие типы парсеров, мы напишем тесты, в которых продемонстрируем приемы работы более подробно.

"Компиляция" выражений в синтаксическое дерево и вычисление по дереву (ExpressionCompiler)

Вычисление выражения с помощью построения синтаксического дерева выполняется по следующей схеме: создаем экземпляр ExpressionCompiler, при необходимости передаем в него начальные переменные и вызываем метод evaluate со строкой, содержащей требуемое выражение. В результате мы получим ссылку на объект Promise, для которого требуется вызвать resolve, чтобы вычислить выражение и получить число. Это выглядит более громоздко, но работает значительно быстрее, когда нужно произвести многократное вычисление для разных значений переменных.

  double a[10] = {...}, b[10] = {...}, c[10] = {...};
  
  VariableTable vt;
  ExpressionCompiler с(vt);
  vt.adhocAllocation(true);
  const string expr = "(a + b) * sqrt(c)";
  Promise *p = c.evaluate(expr);
  
  for(int i = 0; i < 10; i++)
  {
    vt.set("a", a[i]);
    vt.set("b", b[i]);
    vt.set("c", c[i]);
    Print(p.resolve());
  }

В данном примере изначально создается пустая таблица переменных, в которую внутри цикла записываются меняющиеся значения для переменных a, b, c. Использованные здесь метод adhocAllocation, который мы опустили при изучении классов таблиц, взводит флаг, предписывающий парсеру принимать и резервировать в таблице любые имена переменных на стадии анализа и генерации дерева. Любая такая неявная переменная получает значение nan, поэтому вызывающий код должен позаботиться, чтобы установить для них реальные значения перед вычислением "обязательства".

Если в приведенном примере не вызвать vt.adhocAllocation(true) перед c.evaluate, то все переменные, встреченные в выражении, будут генерировать ошибки, т.к. по умолчанию предполагается, что переменные должны быть описаны заранее, а таблица пуста. Наличие ошибок можно проверить в коде с помощью вызова c.success() после c.evaluate(). Ошибки также выводятся в лог.

Как и в случае с интерпретатором, метод evaluate в любом случае вернет некий результат. Так, если переменные не были известны на стадии разбора, в дереве для них будут созданы узлы со значением nan. Вычисления по такому дереву не имеют смысла, так как также дадут nan. Но наличие дерева позволяет понять, в чем проблема. В классе Promise имеется вспомогательный метод для печати дерева — print.

Заключение

В данной статье мы познакомились с основами парсинга математических выражений и создали два парсера на MQL, готовых к работе. Небольшой тестовый скрипт приложен к этой первой части и позволяет самостоятельно начать использовать технологию в своих программах. Мы продолжим изучение других типов парсеров во второй части, сравним их быстродействие, и приведем примеры применения для решения задач трейдера.