Die praktische Verwendung eines neuronalen Kohonen-Netzes im algorithmischen Handel. Teil I: Werkzeug

Das Thema der neuronalen Kohonen-Netze wurde in einigen Artikeln auf der Website mql5.com angesprochen, wie z.B. Verwendung von selbstorganisierenden Karten (Kohonenkarten) in MetaTrader 5 und Selbst-organisierende Feature Maps (Kohonen Maps) - Wiederaufgreifen des Themas. Sie führten die Leser in die allgemeinen Prinzipien des Aufbaus solcher neuronaler Netze ein und analysierten anhand solcher Netze visuell die wirtschaftlichen Zahlen der Märkte.

Praktisch gesehen wurde die Nutzung von Kohonen-Netzen nur für den algorithmischen Handel auf einen einzigen Ansatz beschränkt, nämlich die gleiche visuelle Analyse von Topologiekarten, die für die Ergebnisse der EA-Optimierung erstellt wurden. In diesem Fall ist die subjektive Meinung bzw. die Vision einer Person und ihre Fähigkeit, aus dem Bild korrekte Schlussfolgerungen zu ziehen, möglicherweise der entscheidende Faktor, der die Fähigkeit des Netzwerks, Daten im Kontext der angewandten Kategorien darzustellen, in den Hintergrund stellt.

Mit anderen Worten, die Eigenschaften neuronaler Netzwerkalgorithmen wurden nicht vollständig genutzt, d.h. sie wurden verwendet, ohne automatisch Wissen zu extrahieren oder die Entscheidungsfindung mit spezifischen Empfehlungen zu unterstützen. In diesem Papier betrachten wir das Problem, die optimalen Parametersätze der Roboter in einer formalisierteren Weise zu definieren. Darüber hinaus werden wir das Kohonen-Netz nutzen, um Wirtschaftsbereiche vorherzusagen. Bevor wir jedoch mit diesen angewandten Problemen fortfahren, sollten wir die bestehenden Quellcodes überarbeiten, etwas korrigieren und einige Verbesserungen vornehmen.

Es wird dringend empfohlen, die obigen Artikel zuerst zu lesen, wenn Sie mit den Begriffen wie "Netzwerk", "Schicht", "Neuron" ("Knoten"), "Link", "Gewicht", "Lernrate", "Lernbereich" und anderen Begriffen im Zusammenhang mit Kohonen-Netzen nicht vertraut sind. Als Nächstes müssen wir uns mit diesem Thema beschäftigen, und die Wiederholung grundlegender Konzepte würde das Material erheblich verlängern.

Fehlerkorrekturen

Wir werden die Klassen CSOM und CSOMNode aufrufen, die im ersten der oben genannten Artikel veröffentlicht wurden, mit Blick auf die Ergänzungen im zweiten. Die Fragmente des Schlüsselcodes in ihnen sind praktisch identisch und erben die gleichen Probleme.

Zunächst ist zu beachten, dass aus irgendeinem Grund Neuronen in den obigen Klassen durch Pixelkoordinaten indiziert, d.h. identifiziert und mit Konstruktorparametern definiert werden. Dies ist nicht sehr logisch und erschwert Berechnungen und Debugging an einigen Stellen. Insbesondere bei diesem Ansatz wirken sich die Einstellungen der Darstellung auf die Kalkulation aus. Stellen Sie sich vor: Es gibt zwei völlig ähnliche Netzwerke mit den gleich großen Gittern, und sie lernen mit dem gleichen Datensatz und mit den gleichen Einstellungen und der gleichen Initialisierung des Zufallsdatengenerators. Die Ergebnisse sind jedoch unterschiedlich, nur weil die Bilder eines Netzwerks größer sind als die eines anderen. Das ist ein Fehler.

Wir werden zur Indizierung der Neuronen durch Zahlen übergehen: Jedes Neuron wird in Array m_node (Klasse CSOM) die Koordinaten x und y haben, die den Spalten- bzw. Zeilennummern in der Ausgabeschicht des Kohonen-Netzwerks entsprechen. Jedes Neuron wird mit der CSOMNode::InitNode(x, y) Methode anstelle der CSOMNode::InitNode(x1, y1, x2, y2) Methode initialisiert. Wenn wir zur Visualisierung übergehen, bleiben die Neuronenkoordinaten beim Ändern der Kartengröße in Pixel unverändert.

In vererbten Quellcodes wird keine Normalisierung der Eingangsdaten verwendet. Dies ist jedoch sehr wichtig, wenn verschiedene Komponenten (Merkmale) von Eingangsvektoren unterschiedliche Wertebereiche haben. Und das ist der Fall bei den Optimierungsergebnissen der EAs und bei der Zusammenführung der Daten verschiedener Indikatoren. Was die Optimierungsergebnisse betrifft, so können wir dort sehen, dass die Werte mit den Gesamtprofiten von Dutzenden von Tausenden von Menschen mit kleinen Werten, wie z.B. den Bruchteilen der Sharp Ratio oder den einstelligen Werten des Restitutionsfaktors, zusammenpassen.

Sie sollten ein Kohonen-Netzwerk nicht mit solch unterschiedlichen Daten trainieren, da das Netzwerk praktisch nur die größeren Komponenten berücksichtigen und die kleineren ignorieren würde. Sie können dies in der folgenden Abbildung sehen, die mit dem Programm erhalten wurde, das wir in diesem Artikel schrittweise betrachten und am Ende anhängen werden. Das Programm ermöglicht das Erzeugen von zufälligen Eingangsvektoren, bei denen drei Komponenten in den Bereichen[0, 1000],[0, 1] und[-1, +1] definiert sind. Eine speziellee Eingabeparameter, UseNormalization, ermöglicht das Aktivieren/Deaktivieren der Normalisierung.

Lassen Sie uns einen Blick auf die endgültige Struktur des Kohonen-Netzwerks in drei Schichten werfen, die für die drei Dimensionen der Vektoren relevant sind. Erstens, das Netzwerk-Lernergebnis ohne Normalisierung.

Kohonen Netzwerk-Lernergebnis ohne Normalisierung der Eingänge

Jetzt - mit der Normalisierung.

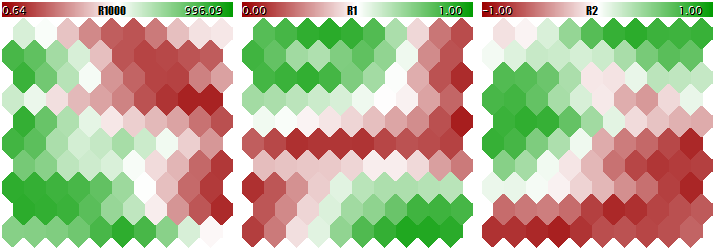
Kohonen Netzwerk-Lernergebnis mit einer Normalisierung der Eingänge

Der Grad der Anpassung der Neuronengewichte ist proportional zum Farbverlauf. Offensichtlich hat das Netzwerk ohne Normalisierungsbedingungen die topologische Partitionierung (Klassifizierung) nur in der ersten Schicht gelernt, während die zweite und die dritte Komponente mit geringem Rauschen gefüllt sind. Das heißt, die analytischen Fähigkeiten des Netzwerks wurden nur zu einem Drittel realisiert. Bei aktivierter Normalisierung ist die räumliche Anordnung in allen drei Schichten sichtbar.

Viele Möglichkeiten der Normalisierung sind bekannt, aber die beliebteste ist vielleicht die Subtraktion des Mittelwerts der gesamten Auswahl von jeder Komponente, gefolgt von der Division durch die Standardabweichung (Sigma oder Quadratwurzel der Varianz). Dadurch wird der Mittelwert der transformierten Daten auf Null und die Standardabweichung auf Einheit gesetzt.

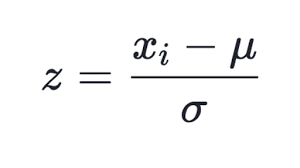 (1)

Diese Technik wird in der aktualisierten Klasse von CSOM, in der Methode Normalize, verwendet. Es ist klar, dass Sie zunächst die Mittelwerte und Sigma für jede Komponente des Eingangsdatensatzes berechnen sollten, was in der Methode InitNormalization (siehe unten) geschieht.

Kanonische Formeln zur Berechnung der Mittelwerte und der Standardabweichung Mittelwert unter Verwendung eines Zwei-Durchlaufs-Algorithmus: Der Mittelwert sollte zuerst gefunden werden, dann wird er zur Berechnung des Sigmas verwendet.

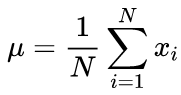                             (2)

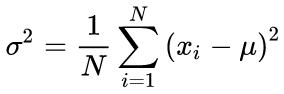     (3)

In unserem Quellcode verwenden wir einen Ein-Durchlaufs-Algorithmus auf Basis der folgenden Formel:

 (4)

Offensichtlich erfordert die Normalisierung der Eingänge einen entgegengesetzten Vorgang - die Denormalisierung - der Ergebnisse, d.h. die Transformation der Ergebniswerte des Netzwerks zurück zu Realwerte. Dies geschieht mit der Methode CSOM::Denormalize.

Da die normierten Werte in der Nähe von Null symmetrisch fallen, werden wir das Initialisierungsprinzip der Neuronengewichte vor Beginn des Trainierens des Netzwerks ändern - anstelle von Bereich[0, 1] ist es jetzt Bereich[-1, +1] (siehe Methode CSOMNode::InitNode). Dies wird die Effizienz des Lernens des Netzwerks steigern.

Ein weiterer zu korrigierender Aspekt ist die Zählung der Lerniterationen. In Quellklassen versteht man unter Iteration die Angabe jedes einzelnen Eingangsvektors für das Netzwerk. Daher sollte die Anzahl der Wiederholungen basierend auf und in Übereinstimmung mit der Größe der Lernauswahl korrigiert werden. Erinnern wir uns, dass das Lern- und Informationsfusionsprinzip des Kohonen-Netzes davon ausgeht, dass jede Auswahl dem Netzwerk mehrmals präsentiert wird. Wenn beispielsweise 100 Datensätze in einer Stichprobe vorhanden sind, müssen durchschnittlich alle Datensätze 100 Mal durchlaufen werden, um eine Anzahl der Iterationen von 10.000 zu erreichen. Wenn die Stichprobe jedoch 1000 Datensätze enthält, sollte die Anzahl der Iterationen 100.000 betragen. Die Zyklen der sogenannten 'Lern-Epochen', in denen alle Proben zufällig dem Eingang des Netzwerks zugeführt werden. Diese Anzahl wird im Parameter EpochNumber eingestellt. Dank der Einführung hängt die Lerndauer parametrisch nicht mehr von der Größe des Datensatzes ab.

Dies ist umso wichtiger, als der gesamte Eingangssatz in 2 Komponenten aufgeteilt werden kann: Die Auswahl, die zum Lernen verwendet wird, und die sogenannte validierende Auswahl. Letztere wird verwendet, um die Lernqualität des Netzwerks zu kontrollieren. Es geht darum, dass die Anpassung des Netzwerks an die Eingänge während des Lernens eine "Kehrseite" hat: Das Netzwerk beginnt sich an die Eigenschaften bestimmter Proben anzupassen und verliert dadurch seine Fähigkeit, unbekannte Daten (außer denen, die für den Unterricht verwendet werden) zu verallgemeinern und angemessen zu bearbeiten. Schließlich besteht die Idee des Lernens in der Regel in der Fähigkeit der über das Netzwerk erfassten Merkmale, in Zukunft angewendet zu werden.

Im betrachteten Programm ist der Eingabeparameter ValidationSetPercent für die Freigabe der Validierung verantwortlich. Standardmäßig ist er gleich 0, und alle Daten werden zum Lernen verwendet. Wenn wir dort beispielsweise 10 angeben, dann werden nur 90% der Stichproben zum Lernen verwendet, während für die restlichen 10% der normalisierte mittlere quadratische Fehler bei jeder Iteration (Epoche) berechnet wird und der Lernprozess zu dem Zeitpunkt endet, zu dem der Fehler zu wachsen beginnt.

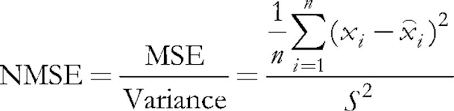 (5)

Die Normalisierung besteht darin, den mittleren quadratischen Fehler durch die Verteilung der Daten selbst zu dividieren, was dazu führt, dass der Index immer unter 1 liegt. Wenn man jeden Vektor einzeln betrachtet, ist dieser mittlere quadratische Fehler in der Tat ein Quantisierungsfehler, da er auf der Differenz zwischen seinen Komponenten und den Gewichten der relevanten neuronalen Synapsen basiert und die beste Annäherung dieses Vektors unter allen Neuronen ergibt. Wir sollten uns daran erinnern, dass dieses gewinnende Neuron in Kohonen-Netzwerken BMU (best matching unit) oder BMN (best matching node) genannt wird - in der Klasse CSOM sind die GetBestMatchingNode Methode und ähnliche Techniken für die Suche verantwortlich.

Wenn die Validierung aktiviert ist, übersteigt die Anzahl der Iterationen die im Parameter EpochNumber angegebene Anzahl. Aufgrund der besonderen Merkmale der Kohonen-Netzwerkarchitektur kann die Validierung erst durchgeführt werden, nachdem das Netzwerk die Selbstorganisationsphase mit der Anzahl der EpochNumber Epochen durchlaufen hat. Nach Abschluss dieser Phase verringern sich Lernrate und Umfang so stark, dass die Feinabstimmung der Gewichte beginnt und dann die Konvergenzphase beginnt. Hier wird der "frühe Stopp" des Lernens mit Hilfe des Validierungssatzes angewendet.

Ob die Validierung verwendet wird oder nicht, hängt von der Spezifität des Problems ab. Außerdem kann das Validierungsset verwendet werden, um die Netzwerkgröße anzupassen. Für die Zwecke dieses Artikels werden wir uns nicht mit dieser Angelegenheit befassen. Wir verwenden nur die bekannte empirische Regel, die die Netzwerkgröße mit der Umfang der Lerndaten in Beziehung setzt:

N ~ 5 * sqrt(M) (6)

wobei N die Anzahl der Neuronen innerhalb des Netzwerks und M die Anzahl der Eingangsvektoren ist. Für ein Kohonen-Netzwerk mit der quadratischen Output-Schicht erhalten wir die Größe:

S = sqrt(5 * sqrt(M))) (7)

wobei S die Anzahl der Neuronen vertikal und horizontal ist. Wir werden diesen Wert in die Parameter CellsX und CellsY einführen.

Das letzte Problem, das in den ursprünglichen Quellcodes korrigiert wurde, betrifft die Verarbeitung des hexagonalen Gitters. Kohonen-Karten sind bekannt dafür, dass sie aus der rechteckigen oder hexagonalen Anordnung von Zellen (Neuronen) aufgebaut werden, und beide Modi werden zunächst in den Quellcodes realisiert. Das hexagonale Gitter wird jedoch nur als hexagonale Zelle dargestellt, aber vollständig als rechteckige Zelle berechnet. Um hier zur Ursache des Fehlers zu gelangen, lassen Sie uns die folgende Abbildung betrachten.

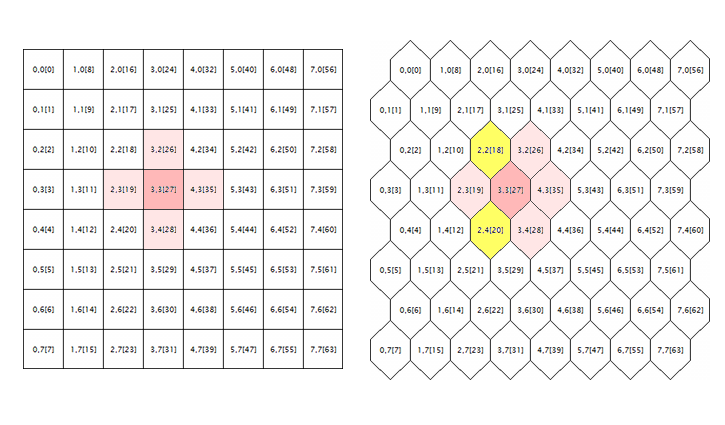
Geometrie der neuronalen Nachbarschaft in einem rechteckigen und einem hexagonalen Gitter

Die logische Umgebung eines zufälligen Neurons ist hier (mit den Koordinaten von 3;3, in diesem Fall) für die Gitter beider Geometrien dargestellt. Der Radius des Umkreises ist 1. Im quadratischen Gitter hat das Neuron 4 direkte Nachbarn, während es im hexagonalen Gitter 6 Nachbarn hat. Die Realisierung des Mosaikbildes wird erreicht, indem jede abwechselnde Zellreihe um eine halbe Zelle verschoben wird. Dadurch ändern sich jedoch die internen Koordinaten nicht, und algorithmisch erscheint das im hexagonalen Gitter umgebende Neuron wie bisher - es ist rosa markiert.

Offensichtlich ist dies falsch und sollte durch die Hinzunahme der gelb markierten Neuronen korrigiert werden.

Formal berechnet der Algorithmus die Umgebung sowohl unter Verwendung der benachbarten Nachbarn als auch als konvex abnehmende Radialfunktion in Abhängigkeit vom Abstand zwischen den Koordinaten der Zellen. Mit anderen Worten, Nachbarschaft ist keine binäre Eigenschaft eines Neurons (entweder ein Nachbar oder nicht), sondern eine kontinuierliche Größe, die nach der gaußschen Formel berechnet wird:

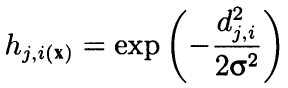 (8)

Hier ist dji der Abstand zwischen den Neuronen j und i (fortlaufende Nummerierung ist gemeint, nicht die Koordinaten x und y); und Sigma ist die effiziente Breite der Nachbarschaft oder der Lernradius, der sich beim Lernen allmählich verringert. Zu Beginn des Lernens bedeckt die Nachbarschaft mit einer symmetrischen "Glocke" einen viel größeren Raum als die unmittelbar benachbarten Neuronen.

Da diese Formel von Entfernungen abhängt, stellt sie auch die Nachbarschaft falsch dar, wenn die Koordinaten nicht richtig korrigiert wurden. Daher verwenden wir die folgenden Quellcode-Zeilen aus der Methode CSOM::Train:

      for(int i = 0; i < total_nodes; i++)
      {
         double DistToNodeSqr = (m_som_nodes[winningnode].X() - m_som_nodes[i].X()) * (m_som_nodes[winningnode].X() - m_som_nodes[i].X())
                              + (m_som_nodes[winningnode].Y() - m_som_nodes[i].Y()) * (m_som_nodes[winningnode].Y() - m_som_nodes[i].Y());

ergänzt:

      bool odd = ((winningnode % m_ycells) % 2) == 1;
      for(int i = 0; i < total_nodes; i++)
      {
        bool odd_i = ((i % m_ycells) % 2) == 1;
        double shiftx = 0;

        if(m_hexCells && odd != odd_i)
        {
          if(odd && !odd_i)
          {
            shiftx = +0.5;
          }
          else // vice versa (!odd && odd_i)
          {
            shiftx = -0.5;
          }
        }
        double DistToNodeSqr = (m_node[winningnode].GetX() - (m_node[i].GetX() + shiftx)) * (m_node[winningnode].GetX() - (m_node[i].GetX() + shiftx))
                             + (m_node[winningnode].GetY() - m_node[i].GetY()) * (m_node[winningnode].GetY() - m_node[i].GetY());

Die Korrekturrichtung "shiftx" hängt vom Verhältnis der Eigenschaften ab, ob es eine gerade oder ungerade Zeile ist, in denen sich zwei Neuronen befinden, zwischen denen der Abstand berechnet wird. Wenn sich die Neuronen in gleichmäßig nivellierten Reihen befinden, gibt es keine Korrektur. Wenn sich das gewinnende Neuron in einer ungeraden Reihe befindet, dann erscheinen die geraden Reihen um eine Halbzelle nach rechts verschoben, so dass shiftx gleich +0,5 ist. Wenn sich das gewinnende Neuron in einer geraden Reihe befindet, dann erscheinen die ungeraden Reihen um eine Halbzelle weiter links davon verschoben, daher ist shiftx gleich -0,5.

Nun ist es besonders wichtig, auf die folgenden Originalzeilen zu achten:

        if(DistToNodeSqr < WS)
        {
          double influence = MathExp(-DistToNodeSqr / (2 * WS));
          m_node[i].AdjustWeights(data, learning_rate, influence);
        }

Tatsächlich sorgt dieser bedingte Operator für eine gewisse Beschleunigung der Berechnungen, da er die Neuronen außerhalb der Nachbarschaft von einem Sigma vernachlässigt. In Bezug auf die Lernqualität ist die Gaußsche Formel jedoch ideal, und ein solcher Eingriff ist unangemessen. Wenn die zu weit entfernten Neuronen vernachlässigt werden sollen, dann für drei Sigma, nicht nur für eines. Noch kritischer ist es, nachdem wir die Berechnungen des hexagonalen Gitters korrigiert haben, dass der Abstand zwischen den benachbarten Neuronen in benachbarten Reihen gleich sqrt(1*1 + 0,5*0,5) = 1,118, also über 1 ist. In den beigefügten Quellcodes wird dieser bedingte Operator kommentiert. Wenn Sie Ihre Berechnungen wirklich beschleunigen müssen, verwenden Sie die Option:

        if(DistToNodeSqr < 9 * WS)

Achtung! Aufgrund der oben genannten Nuancen in der Differenz der Abstände zwischen benachbarten Neuronen in Abhängigkeit von ihrer Reihe (einreihige Neuronen haben einen Abstand von 1, während diejenigen mit benachbarten Reihen den von 1.118 haben), ist die aktuelle Realisierung immer noch nicht ideal und schlägt eine weitere Korrektur vor, um eine vollständige Richtungsabhängigkeit zu erreichen.

Visualisierung

Obwohl Kohonen-Netzwerke in erster Linie mit einer sichtbaren grafischen Karte verbunden sind, können ihre Topologie und Lernalgorithmen ohne jegliche Benutzeroberfläche perfekt funktionieren. Insbesondere die Probleme der Vorhersage oder Verdichtung der Informationen erfordern keine notwendige visuelle Analyse, und die Klassifizierung der Bilder kann ein Ergebnis als Zahl, i, liefern. Insbesondere erfordern die Probleme der Vorhersage oder Verdichtung der Informationen keine notwendige visuelle Analyse, h. die Zahl einer Klasse oder die einer Wahrscheinlichkeit eines Ereignisses. Daher wurde die Funktionalität der Kohonen-Netzwerke auf zwei Klassen aufgeteilt. In der Klasse CSOM sind nur noch Berechnungen, das Laden und Speichern von Daten sowie das Laden und Speichern von Netzwerken übrig geblieben. Zusätzlich wurde die abgeleitete Klasse von CSOMDisplay erstellt, in der alle Grafiken platziert wurden. Meiner Meinung nach ist dies eine einfachere und logischere Hierarchie als die in Artikel 2 vorgeschlagene. In Zukunft werden wir CSOMDisplay zur Lösung des Problems der Wahl der optimalen EA-Parameter einsetzen, während CSOM für die Prognose verwendet wird.

Es ist zu beachten, dass das Merkmal Gittertyp, d. h., ob er rechteckig oder hexagonal ist, zur Grundklasse gehört, da das die Berechnung von Abständen beeinflusst. Zusammen mit der Anzahl der Knoten in vertikaler und horizontaler Richtung sowie den Abmessungen des Dateneingaberaums ist der Gittertyp Teil der Architektur und sollte in der Datei gespeichert werden. Beim Herunterladen des Netzwerks aus einer Datei werden alle diese Parameter von dort gelesen, nicht von den Programmeinstellungen. Andere Einstellungen, die nur die visuelle Darstellung betreffen, wie z.B. Kartengrößen in Pixeln, Anzeige der Zellbegrenzungen oder Anzeige der Bildunterschriften, werden nicht in der Netzwerkdatei gespeichert und können für das einmal eingelernte Netzwerk wiederholt und zufällig geändert werden.

Es ist zu beachten, dass keine der aktualisierten Klassen über eine grafische Nutzeroberfläche mit Steuerelementen verfügt - alle Einstellungen werden über die Eingänge von MQL-Programmen festgelegt. Gleichzeitig realisiert die Klasse CSOMDisplay noch einige nützliche Funktionen.

Erinnern Sie sich daran, dass in den vorhergehenden Beispielen, wie man mit Kohonen-Netzwerken arbeitet, ein Eingabeparameter namens MaxPictures vorhanden war. Es bleibt in der neuen Version bestehen. Es wird als maxpict an die Methode CSOMDisplay::Init übergeben und legt die Anzahl der innerhalb einer Zeile im Diagramm angezeigten Netzwerkkarten (Schichten) fest. Wenn wir diesen Parameter zusammen mit den vereinheitlichten Bildgrößen in ImageW und ImageH verwenden, können wir eine Option finden, bei der alle Karten auf den Bildschirm passen. Wenn es jedoch viele Karten gibt, z.B. wenn Sie viele Einstellungen eines EA analysieren müssen, erfordern deren Größen eine deutliche Reduzierung, was unangenehm ist. In solchen Fällen können Sie mit MaxPictures einen neuen Modus aktivieren und den Parameter auf 0 setzen.

In diesem Modus werden Kartenbilder auf dem Chart nicht als Objekte OBJ_BITMAP_LABEL mit Pixelkoordinaten, sondern als Objekte OBJ_BITMAP mit einer Zeitskala erzeugt. Die Größe solcher Karten kann bis zur vollen Höhe des Charts vergrößert werden, und Sie können sie mit einer herkömmlichen horizontalen Bildlaufleiste scrollen, indem Sie sie mit der Maus oder dem Rad oder mit der Tastatur ziehen. Die Anzahl der Karten ist nicht mehr auf die Bildschirmgröße beschränkt. Sie sollten jedoch darauf achten, dass die Anzahl der Bars ausreicht.

Mit zunehmender Kartengröße sehen wir mehr Details, insbesondere, da die Klasse CSOMDisplay optional verschiedene Informationen innerhalb der Zellen anzeigt, wie z.B. die Synapsengewichtswerte der jeweiligen Schicht, die Anzahl der Treffer der Vektoren des Lernsets, den Mittelwert und die Streuung der relevanten Merkmalswerte aller Vektoren, die die Zelle getroffen haben. Diese Informationen werden standardmäßig nicht angezeigt, sind aber immer in Popup-Tooltipps verfügbar, die angezeigt werden, wenn Sie den Mauszeiger über die eine oder andere Zelle halten. Der Name der aktuellen Schicht und die Neuronenkoordinaten werden auch in den Popup-Tooltipps angezeigt.

Außerdem markiert ein Doppelklick auf ein beliebiges Neuron dieses Neuron in invertierter Farbe in der aktuellen Karte und in allen anderen Karten gleichzeitig. Dies ermöglicht es uns, die Neuronenaktivitäten aller Merkmale gleichzeitig visuell zu vergleichen.

Und schließlich ist zu beachten, dass die gesamte Grafik in die Standardklasse CCanvas verschoben wurde. Dadurch wird der Code von externen Abhängigkeiten befreit, hat aber auch einen Nebeneffekt: Die Y-Koordinaten werden nun von oben nach unten gezählt, nicht wie bisher von unten nach oben. Daraus ergibt sich die Anzeige der Kartenlegenden mit den Komponentennamen und den Bereichen ihrer Werte über und nicht unter den Karten. Diese Veränderung scheint jedoch nicht kritisch zu sein.

Verbesserungen

Bevor wir uns den angewandten Problemen nähern können, ist es notwendig, einige Verbesserungen an den Klassen neuronaler Netze vorzunehmen. Zusätzlich zu den Standardkarten, die die Synapsengewichte in den 2D-Räumen bestimmter Merkmale darstellen, werden wir die Berechnungen und Darstellungen einiger Servicekarten vorbereiten, die de facto ein Standard für Kohonen-Netze sind. Mit Blick auf die Zukunft werden wir sagen, dass wir viele von ihnen im Stadium der angewandten Experimente benötigen werden.

Definieren wir die Indizes der zusätzlichen Dimensionen, es werden insgesamt 5 davon sein.

#define EXTRA_DIMENSIONS 5
#define DIM_HITCOUNT (m_dimension + 0)
#define DIM_UMATRIX  (m_dimension + 1)
#define DIM_NODEMSE  (m_dimension + 2) // Quantisierungsfehler je Knoten: durchschnittliche Varianz (Quadrat der Standardabweichung)
#define DIM_CLUSTERS (m_dimension + 3)
#define DIM_OUTPUT   (m_dimension + 4)

U-Matrix

Zuerst werden wir die U-Matrix berechnen, eine vereinheitlichte Matrix von Entfernungen, um die Topologie zu bewerten, die im Lernprozess innerhalb des Netzwerks entsteht. Für jedes Neuron im Netzwerk enthält diese Matrix den durchschnittlichen Abstand zwischen diesem Neuron und seinen unmittelbaren Nachbarn. Seit Kohonen zeigt das Netzwerk einen mehrdimensionalen Raum von Merkmalen als zweidimensionale Karte. In diesem zweidimensionalen Raum treten Faltungen auf. Mit anderen Worten, trotz der Eigenschaft des Kohonen-Netzwerks, die dem Ausgangsraum innewohnende Anordnung beizubehalten, ist sie über den gesamten 2D-Raum gleichermaßen unerreichbar, und die geografische Nähe von Neuronen wird illusorisch. Es ist genau die U-Matrix, die verwendet wird, um solche Bereiche zu erkennen. In ihm erscheinen die Bereiche, in denen es einen großen Unterschied zwischen Neuronengewichten und den Gewichten seiner Nachbarn gibt, als "Berge", während die Bereiche, in denen Neuronen sehr ähnlich sind, wie "Täler" aussehen.

Um den Abstand zwischen dem Neuron und dem Merkmalsvektor zu berechnen, gibt es die Methode CSOMNode::CalculateDistance. Wir werden dafür eine entgegengesetzte Methode erstellen, die den Zeiger auf ein anderes Neuron anstelle des Vektors (Array 'double') bringt.

double CSOMNode::CalculateDistance(const CSOMNode *other) const
{
  double vector[];
  other.GetCodeVector(vector);
  return CalculateDistance(vector);
}

Hier holt die Methode GetCodeVector das Array der Gewichte eines anderen Neurons und sendet es sofort zur Berechnung der Entfernung in der üblichen Weise.

Um die einheitliche Neuronen-Distanz zu erhalten, ist es notwendig, die Entfernungen zu allen benachbarten Neuronen zu berechnen und zu mitteln. Da die Durchquerung der benachbarten Neuronen eine gemeinsame Aufgabe für mehrere Operationen mit dem Netzwerkgitter ist, werden wir eine Basisklasse für die Durchquerung erstellen und dann einzelne Algorithmen in ihren Nachkommen implementieren, einschließlich der Summierung der Entfernungen.

#define NBH_SQUARE_SIZE    4
#define NBH_HEXAGONAL_SIZE 6

template<typename T>
class Neighbourhood
{
  protected:
    int neighbours[];
    int nbhsize;
    bool hex;
    int m_ycells;

  public:
    Neighbourhood(const bool _hex, const int ysize)
    {
      hex = _hex;
      m_ycells = ysize;

      if(hex)
      {
        nbhsize = NBH_HEXAGONAL_SIZE;
        ArrayResize(neighbours, NBH_HEXAGONAL_SIZE);
        neighbours[0] = -1; // aufwärts (visuell)
        neighbours[1] = +1; // abwärts (visuell)
        neighbours[2] = -m_ycells; // links
        neighbours[3] = +m_ycells; // rechts
        /* Template, dynamisch in der unteren Schleife verwendet
        // ungerade Reihe
        neighbours[4] = -m_ycells - 1; // links-aufwärts
        neighbours[5] = -m_ycells + 1; // links-abwärts
        // gerade Reihe
        neighbours[4] = +m_ycells - 1; // rechts-aufwärts
        neighbours[5] = +m_ycells + 1; // rechts-abwärts
        */
      }
      else
      {
        nbhsize = NBH_SQUARE_SIZE;
        ArrayResize(neighbours, NBH_SQUARE_SIZE);
        neighbours[0] = -1; // aufwärts (visuell)
        neighbours[1] = +1; // abwärts (visuell)
        neighbours[2] = -m_ycells; // links
        neighbours[3] = +m_ycells; // rechts
      }
    
    }
    ~Neighbourhood()
    {
      ArrayResize(neighbours, 0);
    }

    T loop(const int ind, const CSOMNode &p_node[])
    {
      int nodes = ArraySize(p_node);
      int j = ind % m_ycells;
      
      if(hex)
      {
        int oddy = ((j % 2) == 1) ? -1 : +1;
        neighbours[4] = oddy * m_ycells - 1;
        neighbours[5] = oddy * m_ycells + 1;
      }
      
      reset();

      for(int k = 0; k < nbhsize; k++)
      {
        if(ind + neighbours[k] >= 0 && ind + neighbours[k] < nodes)
        {
          // Randkanten auslassen
          if(j == 0) // obere Reihe
          {
            if(k == 0 || k == 4) continue;
          }
          else if(j == m_ycells - 1) // untere Reihe
          {
            if(k == 1 || k == 5) continue;
          }
          
          iterate(p_node[ind], p_node[ind + neighbours[k]]);
        }
      }
      
      return getResult();
    }
    
    virtual void reset() = 0;
    virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) = 0;
    virtual T getResult() const = 0;
};

Abhängig von der Art des an den Konstruktor übergebenen Gitters wird die Anzahl der Nachbarn, nbhsize, als gleich 4 oder 6 angenommen. Erhöhungen der Anzahl der benachbarten Neuronen, bezogen auf das aktuelle Neuron, werden durch das Array 'neighbours' gespeichert. So wird beispielsweise in einem quadratischen Gitter der obere Nachbar durch Abzug einer Einheit von dem unteren Nachbarn durch Hinzufügen einer Einheit zur Neuronenzahl erhalten. Linke und rechte Nachbarn haben Zahlen, die sich durch die Höhe der Rasterspalte unterscheiden, so dass dieser Wert als ysize an den Konstruktor übergeben wird.

Die eigentliche Traversierung der Nachbarn erfolgt über die Methode 'loop'. Die Klasse Neighbourhood enthält kein Array von Neuronen, daher wird sie als Parameter an die Methode 'loop' übergeben.

Diese Methode in der Schleife geht über das Array 'neighbours' und überprüft zusätzlich, ob die Nummer des Nachbarn unter Berücksichtigung der Schrittweite nicht über das Raster hinausgeht. Für alle gültigen Zahlen wird die abstrakte Methode 'iterate' aufgerufen, bei der die Verbindungen zum aktuellen Neuron und zu einem der umgebenden Neuronen übergeben werden.

Die abstrakte Methode 'reset' wird vor der Schleife aufgerufen, und die abstrakte Methode 'getResult' wird nach der Schleife aufgerufen. Diese drei abstrakten Methoden ermöglichen es, in den Nachkommenklassen das Aufzählen von Nachbarn vorzubereiten und durchzuführen und das Ergebnis zu erzeugen. Das Konzept der Methodenkonstruktion 'loop' entspricht dem bekannten OOP-Design-Muster - Template Method. Hier sollten wir den Begriff 'template' im eigenen Namen des Musters vom Sprachmuster der Vorlagen unterscheiden, das auch in der Klassenumgebung verwendet wird, da es sich um eine Vorlage handelt, d. h., es wird durch einen bestimmten Variablentyp T parametrisiert. Insbesondere die Methode 'loop' selbst und die Methode 'getResult' liefern den Wert des Typs T.

Basierend auf der Klasse Nachbarschaft werden wir eine Klasse schreiben, um die U-Matrix zu berechnen.

class UMatrixNeighbourhood: public Neighbourhood<double>
{
  private:
    int n;
    double d;
    
  public:
    UMatrixNeighbourhood(const bool _hex, const int ysize): Neighbourhood(_hex, ysize)
    {
    }
    
    virtual void reset() override
    {
      n = 0;
      d = 0.0;
    }
    
    virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) override
    {
      d += node1.CalculateDistance(&node2);
      n++;
    }
    
    virtual double getResult() const override
    {
      return d / n;
    }
};

Der BerechnungstTyp ist double. Durch die Basisklasse sind die Entfernungsberechnungen recht transparent.

Wir werden die Entfernungen für die gesamte Karte in der Methode CSOM::CalculateDistances berechnen.

void CSOM::CalculateDistances()
{
  UMatrixNeighbourhood umnh(m_hexCells, m_ycells);
  
  for(int i = 0; i < m_xcells * m_ycells; i++)
  {
    double d = umnh.loop(i, m_node);
    
    if(d > m_max[DIM_UMATRIX])
    {
      m_max[DIM_UMATRIX] = d;
    }
    
    m_node[i].SetDistance(d);
  }
}

Der Wert der vereinheitlichten Entfernung wird im Objekt des Neurons gespeichert. Später, bei der Darstellung aller Schichten, werden wir in der Lage sein, die Abstandswerte standardmäßig über eine Farbpalette zu definieren, nachdem wir eine zusätzliche Dimension, DIM_UMATRIX, in die Berechnung einbezogen haben. Um die Palette korrekt zu skalieren, speichern wir in dieser Methode den höchsten Wert der Entfernung innerhalb des relevanten Elements des Arrays m_max (alle Realisierungsprinzipien bleiben unverändert gegenüber den vorherigen Realisierungen).

Anzahl der Treffer und Quantisierungsfehler

Die nächste zusätzliche Dimension wird Statistiken über die Anzahl der Treffer der Lernvektoren in bestimmten Neuronen sammeln. Mit anderen Worten, es ist die Dichte der Population der Neuronen mit angewandten Daten. Je höher er in einem bestimmten Neuron ist, desto statistisch sinnvoller sind seine Gewichtungsfaktoren. Im Netzwerk können Neuronen mit geringer oder gar keiner Datenabdeckung auftreten. Es gibt viele von ihnen, es kann für die Probleme bei der Auswahl der Netzwerkgröße oder für die Verdrehung der Topologie in der 2D-Projektion des multidimensionalen Raumes sprechen. Treffer der Proben in ein bestimmtes Neuron werden mit folgendem Verfahren berechnet:

void CSOMNode::RegisterPatternHit(const double &vector[])
{
  m_hitCount++;
  double e = 0;
  for(int i = 0; i < m_dimension; i++) 
  {
    m_sum[i] += vector[i];
    m_sumP2[i] += vector[i] * vector[i];
    e += (m_weights[i] - vector[i]) * (m_weights[i] - vector[i]);
  }
  m_mse += e / m_dimension;
}

Das Zählen selbst wird in der ersten Zeile von m_hitCount++ durchgeführt, wo der interne Zähler erhöht wird. Der verbleibende Code führt andere nützliche Arbeiten aus, die im Folgenden erläutert werden.

Wir werden die Methode RegisterPatternHit nach Abschluss des Lernens aus der Klasse CSOM aufrufen, wo wir eine spezielle Methode zur statistischen Verarbeitung jedes Vektors erstellen werden.

double CSOM::AddPatternStats(const double &data[])
{
  static double vector[];
  ArrayCopy(vector, data);
  
  int ind = GetBestMatchingIndex(vector);
  
  m_node[ind].RegisterPatternHit(vector);

  double code[];
  m_node[ind].GetCodeVector(code);
  Denormalize(code);
  
  double mse = 0;
  
  for(int i = 0; i < m_dimension; i++)
  {
    mse += (data[i] - code[i]) * (data[i] - code[i]);
  }
  
  mse /= m_dimension;
  
  return mse;
}

Als Exkurs ist anzumerken, dass die hier verwendete Methode GetBestMatchingIndex, wie auch einige andere aus der Gruppe der Methoden GetBestMatchingXYZ, die eingehenden Daten in sich selbst normalisiert, weshalb es notwendig ist, ihr eine Kopie des Vektors zu übergeben. Andernfalls wäre eine unscharfe Modifikation der Quelldaten in einem Aufrufcode möglich.

Neben dem Zählen der Treffer berechnet dieses Verfahren auch den Quantisierungsfehler für das aktuelle Neuron und den übergebenen Vektor. Zu diesem Zweck wird aus dem Gewinnneuron der sogenannte Code-Vektor aufgerufen, d. h., das Array der Synapsengewichte und die Summe der Quadrate der komponentenweisen Unterschiede zwischen den Gewichten und dem Eingangsvektor berechnet wird.

Was AddPatternStatsm betrifft, so wird es sofort von einer anderen Methode aufgerufen, CSOM::CalculateStats, wo nur die Schleife für alle Eingänge angeordnet werden.

double CSOM::CalculateStats(const bool complete = true)
{
  double data[];
  ArrayResize(data, m_dimension);
  double trainedMSE = 0.0;
  
  for(int i = complete ? 0 : m_validationOffset; i < m_nSet; i++)
  {
    ArrayCopy(data, m_set, 0, m_dimension * i, m_dimension);
    trainedMSE += AddPatternStats(data, complete);
  }
  
  double nmse = trainedMSE / m_dataMSE;
  if(complete) Print("Overall NMSE=", nmse);

  return nmse;
}

Diese Methode fasst alle Quantisierungsfehler zusammen und vergleicht sie mit der Streuung der Eingangsdaten in m_dataMSE - genau das sind die oben beschriebenen NMSE-Berechnungen im Rahmen von Validierung und Lernstopp. Diese Methode erwähnt die Variable m_validationOffset, die beim Erstellen des Objekts CSOM angegeben wurde, je nachdem, ob sie die Division des Eingangsdatensatzes durch die lernenden und validierenden Teilmengen verwendet.

Sie haben es erraten, die Methode CalculateStats wird in jeder Epoche innerhalb der Methode von Train aufgerufen (wenn die Konvergenzphase bereits begonnen hat), und wir können anhand des zurückgegebenen Wertes beurteilen, ob der gesamte Netzwerkfehler begonnen hat, sich zu erhöhen, d. h., ob es an der Zeit ist, aufzuhören.

Die Streuung von m_dataMSE wird vorher mit der Methode berechnet:

void CSOM::CalculateDataMSE()
{
  double data[];

  m_dataMSE = 0.0;
  
  for(int i = m_validationOffset; i < m_nSet; i++)
  {
    ArrayCopy(data, m_set, 0, m_dimension * i, m_dimension);

    double mse = 0;
    for(int k = 0; k < m_dimension; k++)
    {
      mse += (data[k] - m_mean[k]) * (data[k] - m_mean[k]);
    }
    
    mse /= m_dimension;
    m_dataMSE += mse;
  }
}

Wie erhalten bereits den Durchschnittswert, k_mean, für jede Komponente in der Phase der Datennormalisierung.

void CSOM::InitNormalization(const bool normalization = true)
{
  ArrayResize(m_max, m_dimension + EXTRA_DIMENSIONS);
  ArrayResize(m_min, m_dimension + EXTRA_DIMENSIONS);
  ArrayInitialize(m_max, 0);
  ArrayInitialize(m_min, 0);
  ArrayResize(m_mean, m_dimension);
  ArrayResize(m_sigma, m_dimension);

  for(int j = 0; j < m_dimension; j++)
  {
    double maxv = -DBL_MAX;
    double minv = +DBL_MAX;
    
    if(normalization)
    {
      m_mean[j] = 0;
      m_sigma[j] = 0;
    }
    
    for(int i = 0; i < m_nSet; i++)
    {
      double v = m_set[m_dimension * i + j];
      if(v > maxv) maxv = v;
      if(v < minv) minv = v;
      if(normalization)
      {
        m_mean[j] += v;
        m_sigma[j] += v * v;
      }
    }
    
    m_max[j] = maxv;
    m_min[j] = minv;
    
    if(normalization && m_nSet > 0)
    {
      m_mean[j] /= m_nSet;
      m_sigma[j] = MathSqrt(m_sigma[j] / m_nSet - m_mean[j] * m_mean[j]);
    }
    else
    {
      m_mean[j] = 0;
      m_sigma[j] = 1;
    }
  }
}

Was zusätzliche Schichten betrifft, so ist zu beachten, dass jedes Neuron, nachdem es in CSOMNode::RegisterPatternHit berechnet worden war, in der Lage ist, die relevanten Statistiken mit den folgenden Methoden zu berechnen:

int CSOMNode::GetHitsCount() const
{
  return m_hitCount;
}

double CSOMNode::GetHitsMean(const int plane) const
{
  if(m_hitCount == 0) return 0;
  return m_sum[plane] / m_hitCount;
}

double CSOMNode::GetHitsDeviation(const int plane) const
{
  if(m_hitCount == 0) return 0;
  double z = m_sumP2[plane] / m_hitCount - m_sum[plane] / m_hitCount * m_sum[plane] / m_hitCount;
  if(z < 0) return 0;
  return MathSqrt(z);
}

double CSOMNode::GetMSE() const
{
  if(m_hitCount == 0) return 0;
  return m_mse / m_hitCount;
}

So erhalten wir die Daten, um zwei Schichten zu füllen - mit der Anzahl der Anzeigen der Eingangsvektoren durch Neuronen und mit dem Quantisierungsfehler.

Netzwerkreaktion

Die nächste zusätzliche Schicht wird die Karte mit den Erträgen und die Netzwerkreaktion auf eine bestimmte Probe sein. Es sei daran erinnert, dass bei der Einspeisung eines Signals in das Netzwerk zusammen mit dem gewinnenden Neuron alle anderen Neuronen stärker und in geringerem Maße aktiviert werden. Die Möglichkeit, die aktive Response-Exkursion zu vergleichen, kann dazu beitragen, die Stabilität der vom Netzwerk vorgeschlagenen Lösung zu definieren.

Die Berechnung der Netzwerkreaktion ist denkbar einfach. In der Klasse CSOMNode schreiben wir die folgende Methode:

double CSOMNode::CalculateOutput(const double &vector[])
{
  m_output = CalculateDistance(vector);
  return m_output;
}

Und wir werden sie für jedes Neuron in der Klasse des Netzwerkes aufrufen.

void CSOM::CalculateOutput(const double &vector[], const bool normalize = false)
{
  double temp[];
  ArrayCopy(temp, vector);
  if(normalize) Normalize(temp);
  m_min[DIM_OUTPUT] = DBL_MAX;
  m_max[DIM_OUTPUT] = -DBL_MAX;
  for(int i = 0; i < ArraySize(m_node); i++)
  {
    double x = m_node[i].CalculateOutput(temp);
    if(x < m_min[DIM_OUTPUT]) m_min[DIM_OUTPUT] = x;
    if(x > m_max[DIM_OUTPUT]) m_max[DIM_OUTPUT] = x;
  }
}

Wenn der Testvektor dem Programm nicht zur Verfügung gestellt wird, wird die Antwort standardmäßig berechnet, d.h. für den Nullvektor.

Clusterbildung

Schließlich wird die letzte der betrachteten Schichten, aber wahrscheinlich die wichtigste, die Cluster-Karte sein. Die Anordnung der Eingabedaten auf einer zweidimensionalen Karte ist nur die halbe Miete. Der eigentliche Zweck der Analyse besteht darin, die Merkmale zu erkennen und sie in Klassen einzuteilen, die in Bezug auf die Anwendung leicht verständlich sind. Bei relativ kleinen Abmessungen des Merkmalsraumes können wir die Bereiche mit den erforderlichen Merkmalen recht einfach durch farbige Punkte auf einzelnen Schichten unterscheiden, die in der Regel isoliert sind. Mit der Erweiterung der Eingangsdatenstruktur wird das Bild jedoch komplizierter, und anstatt ein Dutzend Karten mit verschiedenen Indizes zu analysieren, ist es viel bequemer, eine Karte in Bereiche aufzuteilen, die Aufmerksamkeit erfordern.

Die Clusterbildung führt dazu, dass sowohl die Karte nach Gebieten mit ähnlichen Merkmalen markiert als auch die Zentren der Cluster identifiziert werden. Dann können wir sie als die repräsentativsten betrachten, was die Statistiken und die Stichproben der relevanten Klassen betrifft. Hier nähern wir uns schrittweise der Aufgabe, die optimalen EA-Parameter auszuwählen. Wir sollten jedoch eine Clusterbildung implementieren.

K-Means

Es gibt sehr viele Clusteralgorithmen. Die einfachste Option für MQL5 ist die Verwendung der Version von ALGLIB, die in der Standardbibliothek enthalten ist. Es genügt, eine Header-Datei einzubinden:

#include <Math/Alglib/dataanalysis.mqh>

und eine Methode wie diese zu schreiben:

void CSOM::Clusterize(const int clusterNumber)
{
  int count = m_xcells * m_ycells;
  CMatrixDouble xy(count, m_dimension);
  int info;
  CMatrixDouble clusters;
  int membership[];
  double weights[];
  
  for(int i = 0; i < count; i++)
  {
    m_node[i].GetCodeVector(weights);
    xy[i] = weights;
  }

  CKMeans::KMeansGenerate(xy, count, m_dimension, clusterNumber, KMEANS_RETRY_NUMBER, info, clusters, membership);
  Print("KMeans result: ", info);
  if(info == 1) // ok
  {
    for(int i = 0; i < m_xcells * m_ycells; i++)
    {
      m_node[i].SetCluster(membership[i]);
    }
    
    ArrayResize(m_clusters, clusterNumber * m_dimension);
    for(int j = 0; j < clusterNumber; j++)
    {
      for(int i = 0; i < m_dimension; i++)
      {
        m_clusters[j * m_dimension + i] = clusters[i][j];
      }
    }
  }
}

Das führt die Clusterisierung mit dem Algorithmus K-Means durch. Leider ist es, soweit ich weiß, der einzige Clustering-Algorithmus in der ALGLIB-Version in MQL5, obwohl die neueste Version der Originalbibliothek andere bietet, wie z.B. Agglomerative Hierarchische Clusteranalyse.

"Leider", denn der Algorithmus K-Means ist bis zu einem gewissen Grad der "linearste": Seine Essenz reduziert sich auf die Suche nach den Zentren einer bestimmten Anzahl von Sphäroiden im Raum von Merkmalen, die die Probenpunkte auf die effizienteste Weise abdecken, nämlich das Minimum der Summe der Quadrate der Abstände zu den Punkten von den Clusterzentren. Es geht darum, dass die Sphäroide aufgrund ihrer festen Form einige spezifische Einschränkungen in Bezug auf die Trennbarkeit nichtlinearer Cluster aufweisen. Im Prinzip ist K-Means ein Sonderfall des Algorithmus Expectation-Maximization, der Ellipsoide unterschiedlicher Ausrichtung und Form betreibt und daher besser wäre. Allerdings besteht auch bei seiner Verwendung eine Wahrscheinlichkeit, im lokalen Minimum zu bleiben, da beide Algorithmen konvexe Formen und nur eine zufällige Anordnung der Clusterzentren verwenden. Nachteilig könnte auch die Tatsache sein, dass die Anzahl der Cluster vorher festgelegt werden muss.

Betrachten wir jedoch, wie die Clusterbildung mit K-Means in ALGLIB durchgeführt ist. Die Hauptoperation wird mit der Methode CKMeans::KMeansGenerate durchgeführt. Wir übergeben ihm ein Array mit Quelldaten in einem speziellen objektbasierten Format (CMatrixDouble xy), Anzahl der Vektoren (count), Dimensionen des Merkmalsraums (m_dimension) und der gewünschten Anzahl von Clustern (clusterNumber), letzteres ist in den Parametern des MQL-Programms anzugeben. Der nächste Parameter, KMEANS_RETRY_NUMBER, ist die Anzahl der Iterationen, die der Algorithmus mit verschiedenen, zufällig ausgewählten Anfangszentren durchführen muss, um die lokale Lösung zu vermeiden. In unserem Fall ist es ein Makro, das gleich 10 ist. Als Ergebnis der Funktionsoperation erhalten wir den Ausführungscode namens 'info' (verschiedene Werte deuten auf Erfolg oder einen Fehler hin), das objektbasierte Array namens CMatrixDouble Cluster mit Clusterkoordinaten und das Array der Eingänge sind die Mitglieder der Cluster (Mitgliedschaft).

Wir speichern die Clusterzentren im Array m_clusters, um sie auf der Karte zu markieren, und wir färben jedes Neuron mit einer Farbe, die für seine Zugehörigkeit zum Cluster relevant ist:

m_node[i].SetCluster(membership[i]);

Wenn Sie mit ALGLIB arbeiten, beachten Sie bitte, dass ein eigener Zufallszahlengenerator verwendet wird, der den internen Status des speziellen statischen Objekts berücksichtigt. Daher setzt auch eine offensichtliche Initialisierung des Standardgenerators durch MathSrand seinen Status nicht zurück. Dies ist besonders kritisch für EAs, da in ihnen beim Ändern der Einstellungen keine globalen Objekte neu generiert werden. Infolgedessen kann sich die Reproduzierbarkeit von Berechnungsergebnissen mit ALGLIB als schwierig erweisen, wenn CMath::m_state in OnInit nicht auf Null gesetzt wird.

In Anbetracht der oben genannten Nachteile von K-Means ist es wünschenswert, eine alternative Methode zur Clusterbildung zu haben. Eine alternative Lösung ist offensichtlich.

Alternative

Lassen Sie uns unser Augenmerk auf die Kohonen-Karten richten, insbesondere auf die zusätzlichen Dimensionen, die wir eingeführt haben. Von besonderem Interesse ist die U-Matrix. Diese Schicht zeigt die Bereiche der nächstgelegenen Neuronen, d.h. sie sind sowohl in Bezug auf die 2D-Karten-Topologie als auch in Bezug auf den Merkmalsraum nahe beieinander. Wie wir uns erinnern können, ähnliche Neuronen für eine Art "Täler" in U-Matrix. Sie sind großartige Kandidaten, um zu Clustern zu werden.

Wir können die Karte der vereinheitlichten Entfernungen beispielsweise auf folgende Weise in Cluster umwandeln.

Wir kopieren die Informationen über alle Neuronen in ein Array und sortieren es aufsteigend nach dem Wert der U-Distanz (CSOMNode::GetDistance()).

Für ein bestimmtes Neuron werden wir in der Schleife Array für Array prüfen, ob die benachbarten Neuronen zu einem Cluster gehören.

• Wenn nicht, erstellen wir einen neuen Cluster und weisen ihm das aktuelle Neuron zu. Beachten Sie, dass die Cluster erstellt werden, beginnend mit dem Nullindex, der dem wichtigsten" Cluster entspricht, da er dem minimalen U-Abstand entspricht, und dann weiter in der Reihenfolge der absteigenden Bedeutung. In Bezug auf die U-Abstände wird jeder nachfolgende Cluster weniger kompakt sein.
• Wenn es unter den benachbarten Neuronen welche gibt, die mit einem Cluster markiert sind, werden wir unter ihnen das höchste auswählen, nämlich das, das den niedrigsten Index aufweist, und weisen das aktuelle Neuron diesem Cluster zu.

Das ist einfach. Sollten nicht auch die Populationsdichte der Neuronen berücksichtigt werden? Schließlich wurde die U-Entfernung für Neuronen mit unterschiedlicher Trefferzahl unterschiedlich unterstützt. Mit anderen Worten, wenn zwei Neuronen den gleichen U-Abstand haben, muss das eine von ihnen, zu dem mehr Proben angezeigt wurden, den Vorteil haben gegenüber denen mit einer geringeren Zahl.

Dann genügt es, die anfängliche Array-Sortierung im beschriebenen Algorithmus in der Reihenfolge der Werte in der Formel CSOMNode::GetDistance() / sqrt(CSOMNode::GetHitsCount()) zu ändern. Ich habe die Quadratwurzel hinzugefügt, um ihre Wirkung im Falle einer großen Population zu glätten, während die kleinere Population strenger "bestraft" werden sollte.

Wenn wir jedoch zwei Wartungsebenen verwenden, dann wäre es vielleicht sinnvoll, die dritte zu analysieren, nämlich die mit dem Quantisierungsfehler? Je größer der Quantisierungsfehler in einem bestimmten Neuron ist, desto weniger sollten wir auf die Informationen über den kleinen U-Abstand in ihm vertrauen und umgekehrt.

Wenn wir uns erinnern, wie die Funktion mit einem Quantisierungsfehler aussieht:

double CSOMNode::GetMSE() const
{
  if(m_hitCount == 0) return 0;
  return m_mse / m_hitCount;
}

dann werden wir leicht feststellen, dass der Zähler m_hitCount der Treffer darin verwendet wird (nur im Nenner). Daher können wir die vorhergehende Formel zum Sortieren des Neuronenarrays als CSOMNode::GetDistance() * MathSqrt(CSOMNode::.GetMSE()) umschreiben - und dann werden alle drei zusätzlichen Indizes darin berücksichtigt, die wir zu unserer Kohonen-Netzwerkrealisierung hinzugefügt haben.

Wir sind fast bereit, den alternativen Algorithmus zur Clusterbildung in seiner endgültigen Form vorzustellen, aber eine Kleinigkeit ist geblieben. Innerhalb der Schleife durch das Neuronen-Array sollten wir die Nachbarschaft des aktuellen Neurons auf das Vorhandensein benachbarter Cluster überprüfen. Etwas früher haben wir die Template-Klasse, Neighbourhood, für den lokalen Überblick implementiert. Jetzt werden wir ihren Nachkommen erschaffen, die sich auf die Suche nach Clustern konzentriert.

class ClusterNeighbourhood: public Neighbourhood<int>
{
  private:
    int cluster;

  public:
    ClusterNeighbourhood(const bool _hex, const int ysize): Neighbourhood(_hex, ysize)
    {
    }
    
    virtual void reset() override
    {
      cluster = -1;
    }
    
    virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) override
    {
      int x = node2.GetCluster();
      if(x > -1)
      {
        if(cluster != -1) cluster = MathMin(cluster, x);
        else cluster = x;
      }
    }
    
    virtual int getResult() const override
    {
      return cluster;
    }
};

Die Klasse enthält die Anzahl der potentiellen Cluster (die Anzahl ist eine ganze Zahl, daher parametrisieren wir das Template mit dem Typ int). Zunächst wird diese Variable innerhalb der Reset-Methode mit -1 initialisiert, d. h., es gibt keinen Cluster. Dann, wenn die übergeordnete Klasse von ihrer Schleifenmethode aus unsere neue Realisierung "iterieren" aufruft, erhalten wir die Cluster-Nummer jedes benachbarten Neurons, vergleichen sie mit dem Cluster und speichern den Minimalwert. Dasselbe, oder -1, dann wenn keine Cluster gefunden wurden, wird von der Methode getResult zurückgegeben.

Als Verbesserung schlagen wir vor, die "Berghöhe" zwischen Neuronen zu verfolgen, d. h., den Wert von node1.CalculateDistance(&node2)), und die Cluster-Nummer "fließend" von einem Neuron zum anderen auszuführen, nur wenn die "Höhe" niedriger ist als vorher. Die endgültig realisierte Version wird im Quellcode dargestellt.

Schließlich können wir die alternative Clusterbildung implementieren.

void CSOM::Clusterize()
{
  double array[][2];
  int n = m_xcells * m_ycells;
  ArrayResize(array, n);
  for(int i = 0; i < n; i++)
  {
    if(m_node[i].GetHitsCount() > 0)
    {
      array[i][0] = m_node[i].GetDistance() * MathSqrt(m_node[i].GetMSE());
    }
    else
    {
      array[i][0] = DBL_MAX;
    }
    array[i][1] = i;
    m_node[i].SetCluster(-1);
  }
  ArraySort(array);
  
  ClusterNeighbourhood clnh(m_hexCells, m_ycells);

  int count = 0; // Anzahl der Cluster
  ArrayResize(m_clusters, 0);
  
  for(int i = 0; i < n; i++)
  {
    // Auslassen, wenn bereits zugewiesen
    if(m_node[(int)array[i][1]].GetCluster() > -1) continue;
    
    // Prüfen, ob der aktuelle Knoten benachbart zu einem existierenden Cluster ist.
    int r = clnh.loop((int)array[i][1], m_node);
    if(r > -1) // ein Nachbar gehört bereits zu einem Cluster
    {
      m_node[(int)array[i][1]].SetCluster(r);
    }
    else // wir benötigen einen neuen Cluster
    {
      ArrayResize(m_clusters, (count + 1) * m_dimension);
      
      double vector[];
      m_node[(int)array[i][1]].GetCodeVector(vector);
      ArrayCopy(m_clusters, vector, count * m_dimension, 0, m_dimension);
      
      m_node[(int)array[i][1]].SetCluster(count++);
    }
  }
}

Der Algorithmus folgt praktisch vollständig dem oben beschriebenen verbalen Pseudocode: Wir füllen das zweidimensionale Array (der Wert aus der Formel in der ersten Dimension und der Neuronenindex in der zweiten), sortieren, besuchen alle Neuronen in der Schleife und analysieren die Nachbarschaft für jeden von ihnen.

Die Qualität der Clusterbildung sollte natürlich in der Praxis bewertet werden, und ich setze das Vorhandensein von topologischen Fragen voraus. In Anbetracht der Tatsache, dass die meisten der klassischen Methoden zur Clusterbildung auch Probleme haben und der vorgeschlagenen unterlegen sind, sieht die neue Lösung jedoch attraktiv aus.

Zu den Vorteilen dieser Erkenntnis gehört die Tatsache, dass Cluster nach ihrer Wichtigkeit geordnet sind (in den oben genannten K-Mitteln sind Cluster gleich), ihre Form zufällig ist und die Anzahl nicht vordefiniert werden muss. Es ist zu beachten, dass die letzte eine Kehrseite hat, nämlich die Anzahl der Cluster kann ziemlich groß sein. Die Anordnung der Cluster nach inhaltlichem Ähnlichkeitsgrad und minimalem Fehler ermöglicht es dabei, praktisch nur die ersten 5-10 Cluster zu betrachten und die anderen "hinter den Kulissen" zu lassen.

Da ich keine ähnliche Methode der Clusterbildung in Open Source gefunden habe, schlage ich vor, sie Korotky clusterization zu nennen, oder länger, aber anständig - verkürzte Clusterbildung, basierend auf U-Matrix und Quantisierungsfehler (QE).

Vorgreifend, sollte ich sagen, dass, nach vielen Tests, die Cluster-Zentren, die durch Algorithmus K-Mittel gefunden wurden, schlechtere Ergebnisse lieferten, als die alternative Clusterbildung (zumindest in das Problem der Analyse der Optimierung Ergebnisse). Es wird also nur diese Methode der Clusterbildung gemeint sein und im Folgenden angewendet.

Tests

Es ist an der Zeit, von der Theorie in die Praxis zu wechseln und zu testen, wie das Netzwerk funktioniert. Lassen Sie uns einen einfachen, universellen Expert Advisor mit den Möglichkeiten zur Demonstration der Grundfunktionalität erstellen. Wir werden ihn den SOM-Explorer nennen.

Lassen Sie uns Header-Dateien mit den oben genannten Klassen einbinden. Definieren der Eingabeparameter.

Gruppe — Netzwerkstruktur und Dateneinstellungen

• DataFileName - der Name einer Textdatei mit den Daten zum Lernen oder Testen; die Klasse CSOM unterstützt das Format csv, aber wir werden die Leseset-Dateien im EA selbst etwas später hinzufügen, da die Analyse der Optimierungseinstellungen anderer EAs "auf dem Spiel steht"; wo die Datei mit den Eingängen angegeben wird, wird ihr Name auch verwendet, um das Netzwerk nach dem Unterrichten zu speichern, aber mit einer anderen Erweiterung (siehe unten); Sie können die csv-Erweiterung angeben oder nicht; und der Name kann einen Ordner innerhalb von MQL5/Files beinhalten;
  
  
• NetFileName - der Name einer Binärdatei mit der Erweiterung som; die Klasse CSOM ist in der Lage, die Netzwerke in/aus solchen Dateien zu speichern und zu lesen; wenn jemand die Struktur der zu speichernden Daten ändern muss, dann ändern Sie die Versionsnummer in der Signatur, die am Anfang der Datei geschrieben wird; wenn NetFileName leer ist, arbeitet das EA im Lernmodus, während, wenn das Netzwerk angegeben ist, dann im Testmodus, d. h., Anzeigen der Eingaben im fertigen Netzwerk; Sie können die Erweiterung som angeben oder nicht; und der Name kann einen Ordner innerhalb von MQL5/Files beinhalten;
  
  
• Wenn sowohl DataFileName als auch NetFileName leer sind, erzeugt das EA einen Demonstrationssatz von zufälligen 3D-Daten und führt einen Lernvorgang darin durch;
  
  
• Wenn der Netzwerkname in NetFileName korrekt ist, können Sie in DataFileName den Namen einer nicht existierenden Datei angeben, z.B. nur einen Namen mit dem Zeichen '?', das dazu führt, dass das EA eine Zufallsstichprobe von Testdaten für den Definitionsbereich erzeugt, der in der Netzwerkdatei gespeichert ist (beachten Sie, dass diese Informationen notwendig sind, damit das eingelernte Netzwerk die unbekannten Daten im Betriebsmodus korrekt normalisieren kann; die Einspeisung der Netzwerkeingabe mit den Werten aus einem anderen Definitionsbereich führt natürlich nicht zu einem Fallout, aber die Ergebnisse sind unzuverlässig; z.B. ist es schwierig zu erwarten, dass das Netzwerk ordnungsgemäß funktioniert, wenn ihm ein negativer Wert des Drawdown oder der Anzahl der Deals zur Verfügung gestellt wird.
  
  
• CellsX - horizontale Größe des Gitters (Anzahl der Neuronen), standardmäßig 10;
  
  
• CellsY - vertikale Größe des Gitters (Anzahl der Neuronen), standardmäßig 10;
  
  
• HexagonalCell - die Funktion für die Verwendung eines hexagonalen Gitters, ist standardmäßig 'true'; für ein rechteckiges Gitter wechseln Sie zu 'false';
  
  
• UseNormalization - Aktivieren/Deaktivieren der Normalisierung der Eingänge; sie ist standardmäßig 'true' und es wird empfohlen, sie nicht zu deaktivieren;
  
  
• EpochNumber - die Anzahl der Lernepochen; standardmäßig 100;
  
  
• ValidationSetPercent - die Größe der Validierungsauswahl in Prozent der Gesamtzahl der Eingänge; sie ist standardmäßig 0, d. h., die Validierung ist deaktiviert; im Falle ihrer Verwendung liegt der empfohlene Wert bei etwa 10;
  
  
• ClusterNumber - die Anzahl der Cluster; sie ist standardmäßig 1, d.h. es ist unsere adaptive Clusterbildung; der Wert 0 deaktiviert die Clusterbildung; Werte über 0 starten die Clusterbildung mit der K-Means-Methode; die Clusterbildung wird unmittelbar nach dem Lernen durchgeführt; und die Cluster werden in der Netzwerkdatei gespeichert;

Gruppe - Visualisierung

• ImageW — die horizontale Größe jeder Karte (Schicht) in Pixeln, standardmäßig 500;
  
  
• ImageH — die vertikale Größe jeder Karte (Schicht) in Pixeln, standardmäßig 500;
  
  
• MaxPictures — die Anzahl der Karten in einer Reihe; standardmäßig ist es 0, d.h. der Modus der Darstellung der Karten in einer fortlaufenden Reihe mit der Scroll-Option (große Bilder sind erlaubt); wenn MaxPictures über 0 liegt, wird der gesamte Satz von Schichten in mehreren Reihen angezeigt, in denen sich jeweils die MaxPictures der Karten befinden (es ist praktisch, alle Karten zusammen in kleinem Maßstab anzuzeigen);
  
  
• ShowBorders — Aktivieren/Deaktivieren des Zeichnens der Grenzen zwischen Neuronen; es ist standardmäßig 'false';
  
  
• ShowTitles — Aktiviert/deaktiviert die Anzeige der Texte mit Neuronenmerkmalen, sie ist standardmäßig 'true';
  
  
• Farbschema — Auswahl eines von 4 Farbschemata; standardmäßig ist es Blau_Grün_Rot (das farbenfroheste);
  
  
• ShowProgress — Aktivieren/Deaktivieren der dynamischen Aktualisierung der Netzwerkbilder während des Lernens; es wird 1 Mal pro Sekunde durchgeführt; es ist standardmäßig 'true';

Gruppe - Optionen

• RandomSeed — eine ganze Zahl zur Initialisierung des Zufallszahlengenerators; sie ist standardmäßig 0;
• SaveImages — die Option, die Netzwerkbilder nach Abschluss zu speichern; sie können auch nach dem Lernen und nach dem ersten Start verwendet werden; sie sind standardmäßig 'false';

Dies sind nur die Grundeinstellungen. Während wir die Probleme weiter lösen, werden wir einige weitere spezifische Parameter hinzufügen.

Hinweis! Das EA ändert die Einstellungen des aktuellen Diagramms — öffnet ein neues Diagramm, das nur für die Arbeit mit diesem EA bestimmt ist.

CSOMDisplay Klassenobjekt führt die gesamte Arbeit im EA aus.

CSOMDisplay KohonenMap;

Vergessen Sie bei der Initialisierung nicht, die Verarbeitung von Mausbewegungsereignissen zu aktivieren — die Klasse verwendet sie zur Anzeige von Popup-Tooltipps und zum Scrollen.

void OnInit()
{
  ChartSetInteger(0, CHART_EVENT_MOUSE_MOVE, true);
  EventSetMillisecondTimer(1);
}

void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
{
  KohonenMap.OnChartEvent(id, lparam, dparam, sparam);
}

Neuronale Netzwerkalgorithmen (Lernen oder Testen) sollen im EA nur einmal gestartet werden — durch den Timer, der dann deaktiviert wird.

void OnTimer()
{
  EventKillTimer();
  
  MathSrand(RandomSeed);
  
  bool hasOneTestPattern = false;
  
  if(NetFileName != "")
  {
    if(!KohonenMap.Load(NetFileName)) return;
    KohonenMap.DisplayInit(ImageW, ImageH, MaxPictures, ColorScheme, ShowBorders, ShowTitles);

    Comment("Map ", NetFileName, " is loaded; size: ", KohonenMap.GetWidth(), "*", KohonenMap.GetHeight(), "; features: ", KohonenMap.GetFeatureCount());

Wenn eine fertige Datei mit dem Netzwerk angegeben wird, laden wir diese und bereiten die Anzeige entsprechend den visuellen Einstellungen vor.

    if(DataFileName != "")
    {
      if(!KohonenMap.LoadPatterns(DataFileName))
      {
        Print("Data loading error, file: ", DataFileName);

        // Erzeugen eines zufälligen Testvektors
        int n = KohonenMap.GetFeatureCount();
        double min, max;
        double v[];
        ArrayResize(v, n);
        for(int i = 0; i < n; i++)
        {
          KohonenMap.GetFeatureBounds(i, min, max);
          v[i] = (max - min) * rand() / 32767 + min;
        }
        KohonenMap.AddPattern(v, "RANDOM");
        Print("Random Input:");
        ArrayPrint(v);
        double y[];
        CSOMNode *node = KohonenMap.GetBestMatchingFeatures(v, y);
        Print("Matched Node Output (", node.GetX(), ",", node.GetY(), "); Hits:", node.GetHitsCount(), "; Error:", node.GetMSE(),"; Cluster N", node.GetCluster(), ":");
        ArrayPrint(y);
        KohonenMap.CalculateOutput(v, true);
        hasOneTestPattern = true;
      }
    }

Wenn eine Datei mit Testdetails angegeben wird, versuchen wir, sie zu laden. Wenn es fehlschlägt, wird eine Meldung im Protokoll angezeigt und eine zufällige Stichprobe, v, von Daten für den Test erstellt. Die Anzahl der Eigenschaften (die Dimension der Vektoren) und deren zulässige Bereiche werden mit den Methoden GetFeatureCount und GetFeatureBounds bestimmt. Anschließend wird das Beispiel durch Aufrufen von AddPattern der Arbeitsdatei "RANDOM" hinzugefügt.

Dieses Verfahren eignet sich, um Lehrselektionen aus Datenquellen mit nicht unterstützten Formaten, wie z.B. Datenbanken, zu bilden und diese direkt aus Indikatoren zu füllen. Im Prinzip ist in diesem speziellen Fall das Hinzufügen eines Samples zu einem Working Set nur notwendig, um es anschließend auf der Karte zu visualisieren (siehe unten), während nur ein Aufruf, GetBestMatchingFeatures, ausreicht, um das am besten geeignete Neuron im Netzwerk zu finden. Diese Methode aus mehreren verfügbaren Methoden GetBestMatchingXYZ ermöglicht es uns, die relevanten Werte der Merkmale des gewinnenden Neurons in Array y zu erhalten. Schließlich zeigen wir mit CalculateOutput die Netzwerkreaktion auf den Teststreifen in einer zusätzlichen Schicht an.

Wir fahren mit dem EA-Code fort.

  }
  else // die Datei mit einem Netz wurde nicht übergeben, daher wird ein Training angenommen
  {
    if(DataFileName == "")
    {
      // Erzeugen eines 3-D Vektors mit unskalierten Werten {[0,+1000], [0,+1], [-1,+1]}
      // Einspeisen ins Netz für den Vergleich der Ergebnisse mit und ohne Normalisierung
      // NB. Titel sollten gültige Dateinamen für BMP sein
      string titles[] = {"R1000", "R1", "R2"};
      KohonenMap.AssignFeatureTitles(titles);
      double x[3];
      for(int i = 0; i < 1000; i++)
      {
        x[0] = 1000.0 * rand() / 32767;
        x[1] = 1.0 * rand() / 32767;
        x[2] = -2.0 * rand() / 32767 + 1.0;
        KohonenMap.AddPattern(x, StringFormat("%f %f %f", x[0], x[1], x[2]));
      }
    }

Wenn das trainierte Netzwerk nicht angegeben ist, gehen wir vom Lernmodus aus. Wir überprüfen, ob es Eingänge gibt. Wenn nicht, erzeugen wir eine zufällige Menge dreidimensionaler Vektoren, bei denen die erste Komponente im Bereich von[0,+1000], die zweite Komponente im Bereich von[0,+1] und die dritte im Bereich von[-1,+1] liegt. Die Namen der Komponenten werden über AssignFeatureTitles an das Netzwerk übergeben, und die Daten — über AddPattern bereits bekannt.

    else // eine Datendatei wurde übergeben
    {
      if(!KohonenMap.LoadPatterns(DataFileName))
      {
        Print("Data loading error, file: ", DataFileName);
        return;
      }
    }

Wenn die Eingänge aus einer Datei kommen, laden wir diese Datei. Im Fehlerfall wird die Arbeit beendet, da es kein Netzwerk oder keine Daten gibt.

Darüber hinaus führen wir das Lernen und die Clusterbildung durch.

    KohonenMap.Init(CellsX, CellsY, ImageW, ImageH, MaxPictures, ColorScheme, HexagonalCell, ShowBorders, ShowTitles);
    
    if(ValidationSetPercent > 0 && ValidationSetPercent < 50)
    {
      KohonenMap.SetValidationSection((int)(KohonenMap.GetDataCount() * (1.0 - ValidationSetPercent / 100.0)));
    }

    KohonenMap.Train(EpochNumber, UseNormalization, ShowProgress);

    if(ClusterNumber > 1)
    {
      KohonenMap.Clusterize(ClusterNumber);
    }
    else
    {
      KohonenMap.Clusterize();
    }
  }

Wenn die Analyse einer einzelnen Testprobe nicht spezifiziert ist (insbesondere unmittelbar nach dem Lernen), bilden wir standardmäßig die Netzwerkantwort auf den Vektor mit Nullen.

  if(!hasOneTestPattern)
  {
    double vector[];
    ArrayResize(vector, KohonenMap.GetFeatureCount());
    ArrayInitialize(vector, 0);
    KohonenMap.CalculateOutput(vector);
  }

Dann zeichnen wir alle Karten im internen Puffer der grafischen Quellen —zuerst den farbigen Hintergrund:

  KohonenMap.Render(); // draw maps into internal BMP buffers

und dann die Bildtexte:

  if(hasOneTestPattern)
    KohonenMap.ShowAllPatterns();
  else
    KohonenMap.ShowAllNodes(); // draw labels in cells in BMP buffers

Markieren der Cluster:

  if(ClusterNumber != 0)
  {
    KohonenMap.ShowClusters(); // Markieren der Cluster
  }

Anzeigen der Puffer auf dem Chart und, gegebenenfalls, sichern der Bilder in Dateien:

  KohonenMap.ShowBMP(SaveImages); // Dateien als Bitmap-Bilder im Chart anzeigen, optional in Dateien speichern

Die Dateien werden in einem separaten Ordner mit dem gleichen Namen wie die Netzwerkdatei, falls vorhanden, oder die Datei mit Daten, falls vorhanden, abgelegt. Wenn die Datendatei nicht angegeben wurde und das Netzwerk auf zufällig generierten Daten gelernt hat, wird der Name der som-Datei und der Ordner, die die Bilder enthalten, mit dem SOM-Präfix und dem aktuellen Datum und der aktuellen Uhrzeit gebildet.

Speichern Sie schließlich das eingelernte Netzwerk in einer Datei. Wenn der Netzwerkname bereits in NetFileName angegeben wurde, bedeutet dies, dass das EA im Testmodus gearbeitet hat, so dass wir das Netzwerk nicht erneut speichern müssen.

  if(NetFileName == "")
  {
    KohonenMap.Save(KohonenMap.GetID());
  }
}

Wir werden versuchen, den EA mit der Generierung zufälliger Testdaten zu starten. Mit allen Standardeinstellungen, mit Ausnahme der Bildabstufungen, die verwendet werden, um sicherzustellen, dass alle Schichten auf den Screenshot gelangen, ImageW = 230, ImageH = 230, MaxPictures = 3, erhalten wir das folgende Bild:

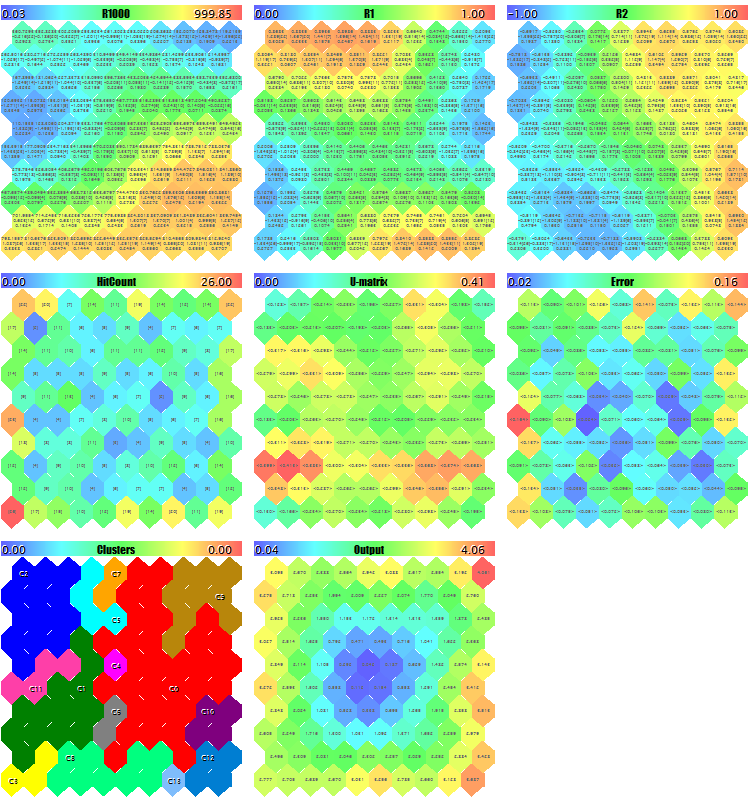
Beispiel einer Kohonen-Karten für zufällige 3D-Vektoren

Hier werden in jedem Neuron die Servicedaten angezeigt (die Details sehen Sie mit dem Mauszeiger) und die gefundenen Cluster werden markiert.

Dabei werden folgende Informationen (Clusterinformationen sind auf fünf begrenzt, im Quellcode können Sie das ändern) im Protokoll angezeigt:

Pass 0 from 1000 0%
Pass 78 from 1000 7%
Pass 157 from 1000 15%
Pass 232 from 1000 23%
Pass 310 from 1000 31%
Pass 389 from 1000 38%
Pass 468 from 1000 46%
Pass 550 from 1000 55%
Pass 631 from 1000 63%
Pass 710 from 1000 71%
Pass 790 from 1000 79%
Pass 870 from 1000 87%
Pass 951 from 1000 95%
Overall NMSE=0.09420336270396877
Training completed at pass 1000, NMSE=0.09420336270396877
Clusters [14]:
"R1000" "R1"    "R2"   
N0
754.83131   0.36778   0.25369
N1
341.39665   0.41402  -0.26702
N2
360.72925   0.86826  -0.69173
N3
798.15569   0.17846  -0.37911
N4
470.30648   0.52326   0.06442
Map file SOM-20181205-134437.som saved

Wenn Sie nun den Namen der erstellten Datei SOM-20181205-134437.som mit dem Netzwerk im Parameter NetFileName und im Parameter DataFileName '?' angeben, erhalten wir das Ergebnis des Testlaufs für die Zufallsstichprobe nicht aus dem Trainingssatz. Um die Karten besser anzeigen zu können, vergrößern wir die Abmessungen und setzen MaxPictures auf 0. 

Die Kohonen-Karten für die ersten beiden Komponenten zufälliger 3D-Vektoren

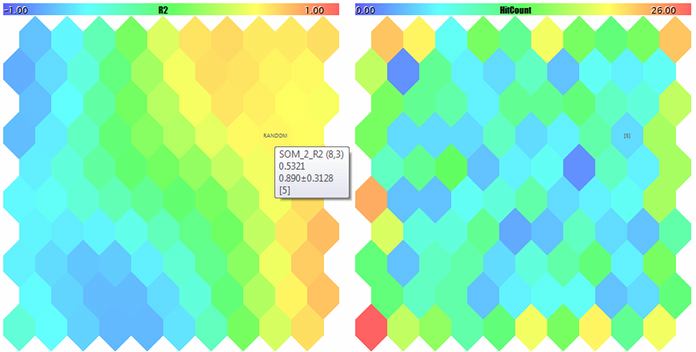
Die Kohonen-Karten für die dritte Komponente zufälliger 3D-Vektoren der Treffer

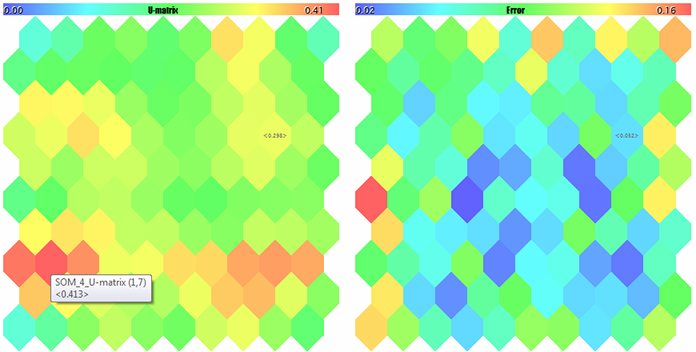
U-Matrix und Quantifizierung der Fehler

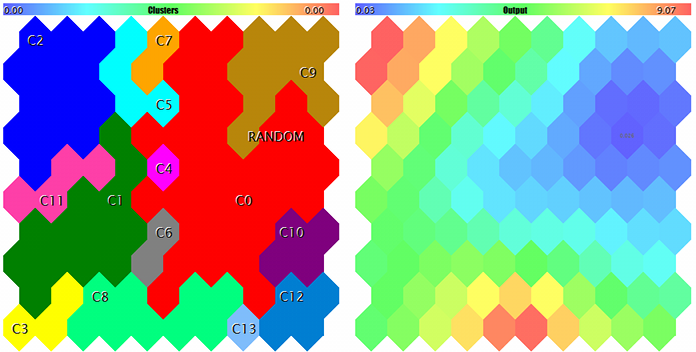
Cluster und Kohonen-Netzwerk Reaktion der besten Probe

Die Probe ist mit RANDOM gekennzeichnet. Die Tooltips zu Neuronen erscheinen, wenn Sie mit dem Mauszeiger darauf zeigen. Im Protokoll wird etwa Folgendes angezeigt:

FileOpen error ?.csv : 5004
Data loading error, file: ?
Random Input:
457.17510   0.29727   0.57621
Matched Node Output (8,3); Hits:5; Error:0.05246704285146882; Cluster N0:
497.20453   0.28675   0.53213

Damit sind die Werkzeuge für die Arbeit mit dem Kohonen-Netzwerk fertiggestellt. Wir können zu den zu lösenden Problemen übergehen. Wir werden das in unserem zweiten Artikel angehen.

Schlussfolgerungen

Den Nutzern des MetaTraders stehen seit mehreren Jahren die offenen neuronalen Netzwerke von Kohonen zur Verfügung. Wir haben einige Fehler korrigiert, mit nützlichen Tools ergänzt und die Arbeit mit einem speziellen EA zu Demonstrationszwecken getestet. Mit den Quellcodes können Sie Klassen für Ihre eigenen Aufgaben verwenden, Beispiele hierfür werden weiter erörtert — wird fortgesetzt.