Uso Prático das Redes Neurais de Kohonen na Negociação Algorítmica. Parte I. Ferramentas

O tema das redes neurais de Kohonen foi abordado em alguns artigos no site mql5.com, como Usar Mapas Auto-Organizáveis (Mapas de Kohonen) no MetaTrader 5 e Mais uma vez vamos falar sobre Mapas de Kohonen. Eles introduziram os leitores aos princípios gerais de construção de redes neurais desse tipo e analisaram visualmente os números econômicos dos mercados usando esses mapas.

No entanto, em termos práticos, o uso das redes de Kohonen apenas para negociação algorítmica foi confinado com apenas uma abordagem, ou seja, a mesma análise visual de mapas de topologia construídos para os resultados da otimização do EA. Nesse caso, o juízo de valor de alguém, ou melhor, a visão e a capacidade de tirar conclusões razoáveis de algo revelam-se, talvez, o fator crucial, deixando de lado as propriedades da rede em relação a representação dos dados em termos de práticos.

Em outras palavras, os recursos dos algoritmos das redes neurais não foram utilizados ao máximo, ou seja, foram utilizados sem a extração automática de conhecimento ou suporte à tomada de decisão com recomendações específicas. Neste artigo, nós vamos consideramos o problema de definir os conjuntos ótimos dos parâmetros dos robôs de uma maneira mais formalizada. Além disso, nós vamos aplicar a rede de Kohonen à previsão de intervalos econômicos. No entanto, antes de prosseguir para esses problemas aplicados, nós devemos revisar os códigos-fonte existentes, consertar algo e fazer algumas melhorias.

É altamente recomendado ler primeiro os artigos acima, se você não estiver familiarizado com termos como 'rede', 'camada', 'neurônio' ('nó'), 'aresta', 'peso', 'taxa de aprendizado', 'faixa de aprendizagem' e outras noções relacionadas com as redes de Kohonen. Então nós teremos que nos saturar neste assunto, assim, relembrar as noções básicas prolongaria significativamente esta publicação.

Corrigindo os Erros

Nós vamos invocar as classes CSOM e CSOMNode publicadas no primeiro dos artigos acima, de olho nas adições ao último. Os fragmentos de código-chave neles são praticamente idênticos e herdam os mesmos problemas.

Em primeiro lugar, deve-se notar que, por alguma razão, os neurônios nas classes acima são indexados, ou seja, identificados e definidos com parâmetros construtivos, por coordenadas de pixel. Isso não é muito lógico e complica os cálculos e a depuração em alguns pontos. Particularmente, sob essa abordagem, as configurações de apresentação afetam os cálculos. Apenas imagine: Existem duas redes completamente similares com as redes de tamanho idêntico, e elas estão aprendendo usando o mesmo conjunto de dados e tendo as mesmas configurações e inicialização do gerador de dados aleatórios. Entretanto, os resultados obtidos são diferentes, apenas porque as imagens de uma rede são maiores que as da outra. Isto é um erro.

Nós vamos indexar os neurônios por números: Cada neurônio terá no array m_node as coordenadas x e y (classe CSOM), correspondentes aos números da coluna e linha, respectivamente, na camada de saída da rede de Kohonen. Cada neurônio será inicializado usando o método CSOMNode::InitNode(x, y) em vez do método CSOMNode::InitNode(x1, y1, x2, y2). Quando nós vamos para a visualização, as coordenadas dos neurônios permanecerão inalteradas ao alterar o tamanho do mapa em pixels.

Nos códigos-fonte herdados, nenhuma normalização de dados de entrada é usada. No entanto, ele é muito importante no caso de diferentes componentes (características) de vetores de entrada terem diferentes faixas de valores. E esse é o caso nos resultados de otimização dos EAs e no agrupamento dos dados de diferentes indicadores. Quanto aos resultados de otimização, nós podemos ver que os valores que têm o lucro total de dezenas de milhares são atrelados a valores pequenos, como as frações do Sharp ratio ou os valores de um dígito do fator de restituição.

Você não deve ensinar uma rede de Kohonen usando dados de escala tão diferente, já que a rede consideraria praticamente apenas os componentes maiores e ignoraria os menores. Você pode ver isso na imagem obtida abaixo usando o programa que vamos considerar de uma maneira passo a passo dentro deste artigo e anexá-lo no final. O programa permite gerar vetores de entrada aleatórios, nos quais três componentes são definidos dentro dos intervalos de [0, 1000], [0, 1] e [-1, +1], respectivamente. Uma entrada especial, UseNormalization, permite ativar/desativar a normalização.

Vamos dar uma olhada na estrutura final da rede de Kohonen em três planos relevantes para as três dimensões dos vetores. Primeiro, o resultado da aprendizagem da rede sem normalização.

Resultado da aprendizagem da rede de Kohonen sem a normalização das entradas

Agora, o mesmo acontece com a normalização.

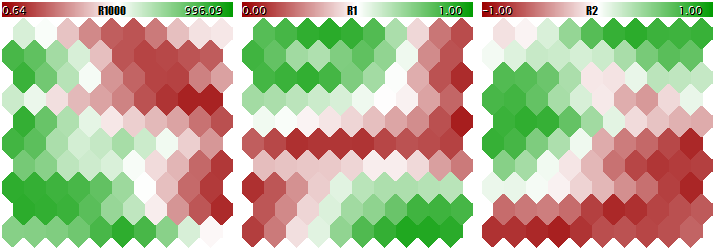
Resultado da aprendizagem da rede de Kohonen com a normalização das entradas

O grau de adaptação do peso do neurônio é proporcional ao gradiente da cor. Obviamente, em condições de não normalização, a rede aprendeu o particionamento topológico (classificação) apenas no primeiro plano, enquanto o segundo e o terceiro componentes estão cheios de ruídos menores. Ou seja, as capacidades analíticas da rede foram realizadas tão pouco quanto a um terço delas. Com a normalização ativada, o arranjo espacial é visível em todos os três planos.

Muitas formas de normalização são conhecidas, mas a mais popular é, talvez, subtrair o valor médio de toda a seleção de cada componente, seguido da divisão pelo desvio padrão, ou seja, sigma ou a raiz quadrada da média. Isso define o valor médio dos dados transformados para zero e o desvio padrão para a unidade.

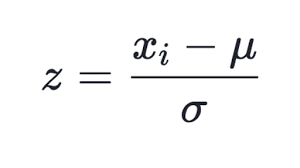 (1)

Essa técnica é usada na classe atualizada do CSOM, no método Normalize. É claro que você deve primeiro calcular os valores médios e sigmas para cada componente do conjunto de dados de entrada, o que é feito no método InitNormalization (veja abaixo).

As fórmulas canônicas para calcular os valores médios e o desvio padrão médio usando um algoritmo de duas etapas: O valor médio deve ser encontrado em primeiro lugar, e depois ele é usado no cálculo do sigma.

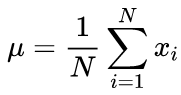                             (2)

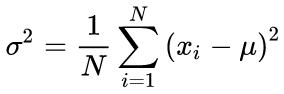     (3)

Em nosso código-fonte, nós usamos um algoritmo de execução única baseada na fórmula abaixo:

 (4)

Obviamente, a normalização na entrada requer uma operação oposta — desnormalização — na saída, ou seja, na transformação dos valores de saída da rede para o intervalo de valores reais. isso é feito pelo método CSOM::Denormalize.

Como os valores normalizados caem simetricamente na vizinhança do zero, nós vamos alterar o princípio de inicialização dos pesos dos neurônios antes de começar a ensinar a rede — em vez do intervalo [0, 1], agora é o intervalo [-1, +1] (veja o método CSOMNode::InitNode). Isso aumentará a eficiência do aprendizado da rede.

Outro aspecto a ser corrigido é contar as iterações do aprendizado. Nas classes fonte, a iteração deve ser entendida como a especificação de cada vetor de entrada individual para a rede. Portanto, o número de iterações deve ser corrigido com base nele e de acordo com o tamanho da seleção do aprendizado. Lembre-se de que o princípio de fusão de aprendizado e informação da rede de Kohonen pressupõe que cada amostra seja especificada para a rede várias vezes. Por exemplo, se houver 100 entradas na seleção, o número de iterações igual a 10000 terá que ser especificado 100 vezes cada, em média. No entanto, se a seleção fizer 1000 entradas, o número de iterações deverá se tornar 100000. Um método mais conveniente e convencional é definir o número da chamada "épocas de aprendizado", ou seja, ciclos dentro de cada um dos quais todas as amostras são alimentadas aleatoriamente na entrada da rede. Esse número será definido no parâmetro EpochNumber. Devido à sua introdução, a duração da aprendizagem é separada parametricamente do tamanho do conjunto de dados.

Isso é ainda mais importante, já que o conjunto total de entradas pode ser dividido em dois componentes: A seleção de aprendizado e a chamada seleção de validação. Este último é usado para rastrear a qualidade da aprendizagem da rede. A questão é que adaptar a rede às entradas durante o aprendizado tem um "efeito reverso": A rede começa a se adaptar às características específicas das amostras e, ao fazê-lo, ela perde sua capacidade de generalização e de trabalhar adequadamente em dados nunca vistos antes (dados que não foram utilizados na aprendizagem). Afinal, a ideia de aprender, como regra, consiste em utilizar a rede para aplicações futuras de acordo com as características detectadas na aprendizagem.

No programa em consideração, o parâmetro de entrada ValidationSetPercent é responsável por ativar a validação. Por padrão, ele é igual a 0 e todos os dados são usados para aprendizado. Se nós especificarmos, digamos, 10 lá, então apenas 90% das amostras são usadas para aprendizado, enquanto que para os 10% restantes o Erro Quadrado Médio Normalizado é calculado em cada iteração (época), e o processo de aprendizado interrompe no momento em que o erro começa a crescer.

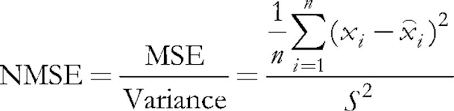 (5)

A normalização consiste em dividir o erro quadrático médio pela dispersão dos dados em si, o que resulta em que o índice está sempre abaixo de 1. Ao considerar cada vetor separadamente, esse erro médio quadrático é, na verdade, um erro de quantização, pois é baseado na diferença entre seus componentes e os pesos das sinapses neurais relevantes, dando a melhor aproximação desse vetor entre todos os neurônios. Nós devemos lembrar que este neurônio vencedor é chamado de BMU (melhor unidade de correspondência) ou BMN (melhor nó correspondente) nas redes de Kohonen — na classe CSOM, o método GetBestMatchingNode e técnicas similares são responsáveis por buscá-lo.

Com a validação ativada, o número de iterações excederá a quantidade especificada no parâmetro EpochNumber. Devido às características especiais da arquitetura de rede de Kohonen, a validação só pode ser realizada depois que a rede tiver passado a fase de auto-organização nas épocas EpochNumber. Após a conclusão dessa fase, a taxa de aprendizado e o escopo reduzem-se de forma tão significativa que o ajuste fino dos pesos começa e, então, a fase de convergência começa. É aqui que a "interrupção precoce" da aprendizagem é aplicada usando o conjunto de validação.

Se utilizado a validação ou não, dependendo da especificidade do problema. Além disso, o conjunto de validação pode ser usado para corresponder ao tamanho da rede. Para o propósito deste artigo, nós não vamos entrar neste assunto. Nós estamos apenas usando a conhecida regra empírica relacionando o tamanho da rede com o número de dados para aprendizagem:

N ~ 5 * sqrt(M)          (6)

onde N é o número de neurônios dentro da rede e M é o número de vetores de entrada. Para uma rede de Kohonen com a camada de saída quadrada, nós obtemos o tamanho:

S = sqrt(5 * sqrt(M))  (7)

onde S é o número de neurônios vertical e horizontal. Nós vamos introduzir este valor nos parâmetros CellsX e CellsY.

A última questão a ser corrigida nos códigos-fonte originais está relacionada ao processamento da grade hexagonal. Mapas de Kohonen são conhecidos por serem construídos usando a colocação retangular ou hexagonal de células (neurônios), e ambos os modos são inicialmente realizados nos códigos fonte. No entanto, a grade hexagonal é apenas exibida como células hexagonais, mas é calculada completamente como uma retangular. Para chegar à raiz do erro, nós vamos considerar a seguinte ilustração.

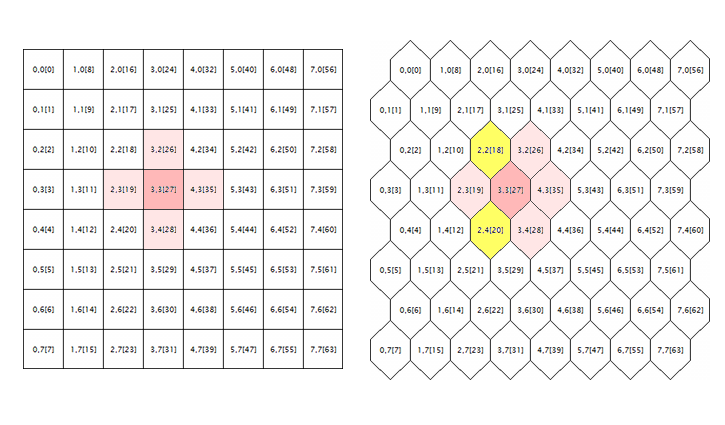
Geometria da vizinhança de neurônios em uma grade retangular e hexagonal

A lógica ao redor de um neurônio aleatório é mostrada aqui (com as coordenadas de 3;3, neste caso) para as grades de ambas as geometrias. Raio da redondeza é 1. Na grade quadrada, o neurônio tem 4 vizinhos diretos, enquanto ele tem 6 na grade hexagonal. A realização da aparência da tesselação é obtida trocando cada sequência de células por uma meia célula. No entanto, isso não altera suas coordenadas internas e, em termos do algoritmo, o neurônio ao redor da grade hexagonal aparece como antes — ele é marcado em rosa.

Aparentemente, isso está errado e deve ser corrigido pela inclusão de neurônios destacados em amarelo.

Formalmente, o algoritmo calcula o seu arredor usando os vizinhos adjacentes e como uma função radial decrescente convexa dependendo da distância entre as coordenadas das células. Em outras palavras, a vizinhança não é uma propriedade binária de um neurônio (seja um vizinho ou não), mas uma quantidade contínua calculada pela fórmula gaussiana:

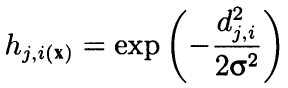 (8)

Aqui, dji é a distância entre os neurônios j e i (significando a numeração contínua e não as coordenadas x e y); e sigma é a largura eficiente da vizinhança ou o raio de aprendizado que reduz gradualmente durante o aprendizado. No início da aprendizagem, a vizinhança cobre com um "sino" simétrico um espaço muito maior do que os neurônios imediatamente adjacentes.

Como essa fórmula depende de distâncias, ela também representa erroneamente a vizinhança, as coordenadas não foram corrigidas corretamente. Portanto, segue as linhas do código-fonte do método CSOM::Train:

      for(int i = 0; i < total_nodes; i++)
      {
         double DistToNodeSqr = (m_som_nodes[winningnode].X() - m_som_nodes[i].X()) * (m_som_nodes[winningnode].X() - m_som_nodes[i].X())
                              + (m_som_nodes[winningnode].Y() - m_som_nodes[i].Y()) * (m_som_nodes[winningnode].Y() - m_som_nodes[i].Y());

foram complementados:

      bool odd = ((winningnode % m_ycells) % 2) == 1;
      for(int i = 0; i < total_nodes; i++)
      {
        bool odd_i = ((i % m_ycells) % 2) == 1;
        double shiftx = 0;

        if(m_hexCells && odd != odd_i)
        {
          if(odd && !odd_i)
          {
            shiftx = +0.5;
          }
          else // vice versa (!odd && odd_i)
          {
            shiftx = -0.5;
          }
        }
        double DistToNodeSqr = (m_node[winningnode].GetX() - (m_node[i].GetX() + shiftx)) * (m_node[winningnode].GetX() - (m_node[i].GetX() + shiftx))
                             + (m_node[winningnode].GetY() - m_node[i].GetY()) * (m_node[winningnode].GetY() - m_node[i].GetY());

A direção da correção 'shiftx' depende da taxa das propriedades de ser par ou ímpar das linhas onde há dois neurônios, entre os quais a distância é calculada. Se os neurônios estão em linhas igualmente niveladas, então não há correção. Se o neurônio vencedor estiver em uma linha ímpar, as linhas pares aparecerão deslocadas por uma meia célula para a direita, portanto, shiftx é igual a +0.5. Se o neurônio vencedor estiver em uma linha par, as linhas ímpares aparecerão deslocadas por uma meia célula à esquerda dele, portanto, shiftx é igual a -0.5.

Agora, ele é especialmente importante prestar atenção às seguintes sequências originais:

        if(DistToNodeSqr < WS)
        {
          double influence = MathExp(-DistToNodeSqr / (2 * WS));
          m_node[i].AdjustWeights(data, learning_rate, influence);
        }

Na verdade, esse operador condicional garante alguma aceleração nos cálculos devido a negligência dos neurônios além da vizinhança por um sigma. No entanto, em termos de qualidade de aprendizagem, a fórmula gaussiana é ideal, e tal intervenção não é razoável. Se os neurônios longe demais devem ser negligenciados, então por três sigmas, não apenas um. É ainda mais crítico, após termos corrigido os cálculos da grade hexagonal, já que a distância entre os neurônios adjacentes localizados nas fileiras vizinhas é igual a sqrt(1*1 + 0.5*0.5) = 1.118, ou seja, acima de 1. Nos códigos-fonte anexados, este operador condicional é comentado. Se você realmente precisa acelerar seus cálculos, use a opção:

        if(DistToNodeSqr < 9 * WS)

Atenção! Devido à nuance acima na diferença de distâncias entre neurônios vizinhos dependendo de sua linha (os de linha única têm uma distância igual a 1, enquanto aqueles que possuem linhas adjacentes têm 1.118), a realização atual ainda é não ideal e sugere mais corrigindo para alcançar a anisotropia completa.

Visualização

Apesar das redes de Kohonen serem associadas principalmente a um mapa gráfico visível, sua topologia e algoritmos de aprendizado podem funcionar perfeitamente sem qualquer interface de usuário. Particularmente, os problemas de prever ou compactar a informação não requerem nenhuma análise visual necessária, e a classificação das imagens pode fornecer um resultado como um número, ou seja, o número de uma classe ou de uma probabilidade de um evento. Portanto, a funcionalidade das redes de Kohonen foi dividida entre duas classes. Na classe CSOM, apenas cálculos, carregamento e armazenamento de dados, e o carregamento e armazenamento das redes permaneceram. Além disso, a classe derivada de CSOMDisplay foi criada, onde todos os gráficos foram colocados. Na minha opinião, esta é uma hierarquia mais simples e mais lógica do que a proposta no artigo 2. No futuro, nós vamos usar a CSOMDisplay para resolver o problema de escolher os parâmetros ideais do EA, enquanto a CSOM será usada para previsão.

Deve-se notar que o recurso do tipo grade, ou seja, se for retangular ou hexagonal, ele pertence à classe básica, pois afeta os cálculos das distâncias. Juntamente com o número de nós nas direções vertical e horizontal, bem como com as dimensões do espaço de entrada de dados, o tipo de grade é uma parte da arquitetura e deve ser salvo no arquivo. Ao baixar a rede do arquivo, todos esses parâmetros são lidos a partir daí, não das configurações do programa. Outras configurações que afetam apenas a representação visual, como tamanhos do mapa em pixels, exibição dos limites da célula ou exibição das legendas, não são salvas no arquivo de rede e podem ser alteradas repetidamente e aleatoriamente para a rede, depois de ensinadas.

Deve-se notar que nenhuma das classes atualizadas não representam uma interface gráfica de usuário com controles — todas as configurações são especificadas através dos parâmetros de entrada do programa em MQL. Ao mesmo tempo, a classe CSOMDisplay ainda realiza alguns recursos úteis.

Lembre-se de que, nas amostras anteriores de como trabalhar com as redes de Kohonen, havia uma entrada chamada MaxPictures. Ele persiste na nova realização. Ele é passado como maxpict para o método CSOMDisplay::Init e define o número dos mapas da rede (planos) exibidos em uma linha no gráfico. Operando este parâmetro junto com os tamanhos de imagem unificados em ImageW e ImageH, nós podemos encontrar uma opção onde todos os mapas se encaixam na tela. No entanto, quando há muitos mapas, como quando você precisa analisar muitas configurações de um EA, seus tamanhos exigem uma redução significativa, o que é inconveniente. Nesses casos, você pode ativar um novo modo usando MaxPictures, configurando o parâmetro como 0.

Nesse modo, as imagens do mapa são geradas no gráfico não como objetos OBJ_BITMAP_LABEL alinhados com coordenadas de pixel, mas como objetos OBJ_BITMAP alinhados com a escala de tempo. Tamanhos de tais mapas podem ser aumentados até a altura total do gráfico, e você pode rolá-los usando uma barra de rolagem horizontal comum, arrastando-os com o mouse ou a roda, ou usando o teclado. O número de mapas não está limitado ao tamanho da tela. No entanto, você deve se certificar de que o número de barras seja suficiente.

O aumento dos tamanhos do mapa nos permite estudá-los em mais detalhes, especialmente a classe CSOMDisplay que exibe opcionalmente várias informações dentro das células, como os valores de peso da sinapse do plano relevante, número de acessos dos vetores do conjuntos de aprendizagem, o valor médio e a dispersão dos valores relevantes de todos os vetores que atingiram a célula. Essas informações não são exibidas por padrão, mas estão sempre disponíveis como dicas pop-up exibidas se você mantiver o cursor do mouse sobre uma célula ou outra. O nome do plano atual e as coordenadas do neurônio também são mostrados nas dicas pop-up.

Além disso, um clique duplo em qualquer neurônio destacará esse neurônio na cor invertida no mapa atual e em todos os outros mapas simultaneamente. Isso nos permite comparar visualmente as atividades dos neurônios por todos os recursos simultaneamente.

E, finalmente, deve-se notar que os gráficos inteiros foram movidos para a classe padrão CCanvas. Isso libera o código de dependências externas, mas também tem um efeito colateral: as coordenadas Y agora são contadas de maneira descendente, não de baixo para cima como era anteriormente. Isso resulta na exibição das legendas do mapa com os nomes dos componentes e os intervalos de seus valores acima dos mapas, não abaixo deles. No entanto, essa mudança não parece ser crítica.

Melhorias

Antes de nos aproximarmos dos problemas aplicados, é necessário fazer algumas melhorias nas classes da rede neural. Além dos mapas padrão representando os pesos de sinapse nos espaços 2D de características específicas, nós prepararemos os cálculos e exibições de alguns mapas de serviço que são um padrão de fato para as redes de Kohonen. Olhando adiante, nós diremos que precisaremos de muitos deles no estágio de experimentos aplicados.

Vamos definir os índices de dimensões adicionais, haverá 5 deles no total.

#define EXTRA_DIMENSIONS 5
#define DIM_HITCOUNT (m_dimension + 0)
#define DIM_UMATRIX  (m_dimension + 1)
#define DIM_NODEMSE  (m_dimension + 2) // erros de quantização por nó: variância média (o quadrado do desvio padrão)
#define DIM_CLUSTERS (m_dimension + 3)
#define DIM_OUTPUT   (m_dimension + 4)

U-Matrix

Primeiramente, nós vamos calcular a U-matrix, uma matriz unificada de distâncias, para avaliar a topologia gerada no processo de aprendizagem dentro da rede. Para cada neurônio na rede, essa matriz contém a distância média entre esse neurônio e seus vizinhos imediatos. Já que a rede de Kohonen exibe um espaço multidimensional de recursos no espaço bidimensional do mapa. Dobras ocorrem neste espaço bidimensional. Em outras palavras, apesar da propriedade da rede de Kohonen de manter o arranjo inerente ao espaço inicial, ele é igualmente inatingível em todo o espaço 2D, e a proximidade geográfica dos neurônios torna-se ilusória. É exatamente por isso que a U-matrix é usada para detectar essas áreas. Nele, as áreas onde há uma grande diferença entre os pesos dos neurônios e os pesos de seus vizinhos aparecem como "picos", enquanto as áreas onde os neurônios são muito semelhantes aos "fundos".

Para calcular a distância entre o neurônio e o vetor de características, existe o método CSOMNode::CalculateDistance. Nós vamos criar para ele um método de contrapartida que levará o ponteiro para outro neurônio ao invés do vetor (array 'double').

double CSOMNode::CalculateDistance(const CSOMNode *other) const
{
  double vector[];
  other.GetCodeVector(vector);
  return CalculateDistance(vector);
}

Aqui, o método GetCodeVector obtém o array dos pesos de outro neurônio e o envia imediatamente para calcular a distância de maneira comum.

Para obter a distância do neurônio unificado, é necessário calcular as distâncias de todos os neurônios vizinhos e medi-los. Como a travessia dos neurônios vizinhos é uma tarefa comum para várias operações com a rede, nós criaremos uma classe base para a travessia e, em seguida, implementaremos os algoritmos em seus descendentes, incluindo a soma das distâncias.

#define NBH_SQUARE_SIZE    4
#define NBH_HEXAGONAL_SIZE 6

template<typename T>
class Neighbourhood
{
  protected:
    int neighbours[];
    int nbhsize;
    bool hex;
    int m_ycells;

  public:
    Neighbourhood(const bool _hex, const int ysize)
    {
      hex = _hex;
      m_ycells = ysize;

      if(hex)
      {
        nbhsize = NBH_HEXAGONAL_SIZE;
        ArrayResize(neighbours, NBH_HEXAGONAL_SIZE);
        neighbours[0] = -1; // cima (visualmente)
        neighbours[1] = +1; // abaixo (visualmente)
        neighbours[2] = -m_ycells; // esquerda
        neighbours[3] = +m_ycells; // direita
        /* template, aplicado dinamicamente no loop abaixo
        // linha ímpar
        neighbours[4] = -m_ycells - 1; // esquerda-cima
        neighbours[5] = -m_ycells + 1; // esquerda-abaixo
        // linha par
        neighbours[4] = +m_ycells - 1; // direita-cima
        neighbours[5] = +m_ycells + 1; // direita-abaixo
        */
      }
      else
      {
        nbhsize = NBH_SQUARE_SIZE;
        ArrayResize(neighbours, NBH_SQUARE_SIZE);
        neighbours[0] = -1; // cima (visualmente)
        neighbours[1] = +1; // abaixo (visualmente)
        neighbours[2] = -m_ycells; // esquerda
        neighbours[3] = +m_ycells; // direita
      }
    
    }
    ~Neighbourhood()
    {
      ArrayResize(neighbours, 0);
    }

    T loop(const int ind, const CSOMNode &p_node[])
    {
      int nodes = ArraySize(p_node);
      int j = ind % m_ycells;
      
      if(hex)
      {
        int oddy = ((j % 2) == 1) ? -1 : +1;
        neighbours[4] = oddy * m_ycells - 1;
        neighbours[5] = oddy * m_ycells + 1;
      }
      
      reset();

      for(int k = 0; k < nbhsize; k++)
      {
        if(ind + neighbours[k] >= 0 && ind + neighbours[k] < nodes)
        {
          // pula arestas de quebra
          if(j == 0) // linha superior
          {
            if(k == 0 || k == 4) continue;
          }
          else if(j == m_ycells - 1) // linha inferior
          {
            if(k == 1 || k == 5) continue;
          }
          
          iterate(p_node[ind], p_node[ind + neighbours[k]]);
        }
      }
      
      return getResult();
    }
    
    virtual void reset() = 0;
    virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) = 0;
    virtual T getResult() const = 0;
};

Dependendo do tipo de grade passada para o construtor, o número de vizinhos, nbhsize, é considerado igual a 4 e 6. Incrementos dos números de neurônios vizinhos, como relacionados ao neurônio atual, são armazenados pelo array 'neighbours'. Por exemplo, em uma grade quadrada, o vizinho superior é obtido deduzindo uma unidade dele e o vizinho inferior adicionando uma unidade ao número do neurônio. Os vizinhos esquerdo e direito têm números que diferem pela altura da coluna da grade, portanto, esse valor é passado para o construtor como ysize.

A travessia real dos vizinhos é realizada pelo método 'loop'. A classe Neighborhood não inclui nenhum array de neurônios, então ele é passado como um parâmetro para o método 'loop'.

Esse método no loop passa pelo array 'neighbours e, além disso, verifica se o número do vizinho não vai além da grade, considerando o incremento. Para todos os números válidos, o método abstrato 'iterate' é chamado onde as ligações para o neurônio atual e para um dos neurônios circundantes são passadas.

O método abstrato 'reset' é chamado antes do loop, e o método abstrato getResult é chamado após o loop. Um conjunto de três métodos abstratos permite preparar e executar nas classes descendentes a enumeração de vizinhos e gerar o resultado. O conceito de construção do método 'loop' corresponde ao padrão de projeto POO — Método Template. Aqui, nós devemos distinguir o termo 'template' no próprio nome do padrão do padrão de linguagem dos modelos, que também é usado na classe Neighbourhood, já que ele é um template, ou seja, ele é parametrizado por uma determinada variável tipo T. Particularmente, o próprio método 'loop' e o método getResult retornam o valor do tipo T.

Com base na classe Neighbourhood, nós escreveremos uma classe para calcular a U-matrix.

class UMatrixNeighbourhood: public Neighbourhood<double>
{
  private:
    int n;
    double d;
    
  public:
    UMatrixNeighbourhood(const bool _hex, const int ysize): Neighbourhood(_hex, ysize)
    {
    }
    
    virtual void reset() override
    {
      n = 0;
      d = 0.0;
    }
    
    virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) override
    {
      d += node1.CalculateDistance(&node2);
      n++;
    }
    
    virtual double getResult() const override
    {
      return d / n;
    }
};

O tipo do trabalho é double. Através da classe básica, os cálculos da distância são bastante transparentes.

Nós vamos calcular as distâncias para todo o mapa no método CSOM::CalculateDistances.

void CSOM::CalculateDistances()
{
  UMatrixNeighbourhood umnh(m_hexCells, m_ycells);
  
  for(int i = 0; i < m_xcells * m_ycells; i++)
  {
    double d = umnh.loop(i, m_node);
    
    if(d > m_max[DIM_UMATRIX])
    {
      m_max[DIM_UMATRIX] = d;
    }
    
    m_node[i].SetDistance(d);
  }
}

O valor da distância unificada é salvo no objeto do neurônio. Posteriormente, ao exibir todos os planos, nós poderemos definir os valores da distância de maneira padrão usando uma paleta de cores, incluindo nos cálculos uma dimensão adicional, DIM_UMATRIX. Para escalar a paleta corretamente, nós salvamos neste método o maior valor da distância dentro do elemento relevante do array m_max (todos os princípios de realização permanecem inalterados das realizações anteriores).

Número de ocorrências e erro de quantização

A próxima dimensão adicional coletará estatísticas do número de ocorrências de vetores de aprendizado em neurônios específicos. Em outras palavras, é a densidade de preencher os neurônios com dados aplicados. Quanto mais alto ele estiver em um neurônio específico, mais razoáveis estatisticamente serão seus fatores de ponderação. Na rede, os neurônios com cobertura de dados menor ou mesmo zero podem ocorrer. Existem muitos deles, ele pode falar pelos problemas na seleção do tamanho da rede ou pela distorção da topologia na projeção 2D do espaço multidimensional. As ocorrências das amostras em um determinado neurônio são calculados pelo método:

void CSOMNode::RegisterPatternHit(const double &vector[])
{
  m_hitCount++;
  double e = 0;
  for(int i = 0; i < m_dimension; i++) 
  {
    m_sum[i] += vector[i];
    m_sumP2[i] += vector[i] * vector[i];
    e += (m_weights[i] - vector[i]) * (m_weights[i] - vector[i]);
  }
  m_mse += e / m_dimension;
}

A contagem em si é executada na primeira linha de m_hitCount++, onde o contador interno é aumentado. O código restante executa outro trabalho útil a ser discutido abaixo.

Nós chamaremos o método RegisterPatternHit após o término do aprendizado da classe CSOM, onde vamos criar um método especial de processamento estatístico para cada vetor.

double CSOM::AddPatternStats(const double &data[])
{
  static double vector[];
  ArrayCopy(vector, data);
  
  int ind = GetBestMatchingIndex(vector);
  
  m_node[ind].RegisterPatternHit(vector);

  double code[];
  m_node[ind].GetCodeVector(code);
  Denormalize(code);
  
  double mse = 0;
  
  for(int i = 0; i < m_dimension; i++)
  {
    mse += (data[i] - code[i]) * (data[i] - code[i]);
  }
  
  mse /= m_dimension;
  
  return mse;
}

Como uma digressão, deve-se notar que o método GetBestMatchingIndex usado aqui, bem como alguns outros do grupo de métodos GetBestMatchingXYZ, normaliza os dados de entrada dentro de si mesmo, razão pela qual é necessário passar para ele uma cópia do vetor. Caso contrário, a modificação difusa dos dados de origem seria possível em um código de chamada.

Juntamente com a recodificação da ocorrência, esse método também calcula o erro de quantização para o neurônio atual e para o vetor passado. Para este propósito, do neurônio vencedor, o chamado vetor de código é chamado, ou seja o conjunto de pesos de sinapse e a soma dos quadrados das diferenças dos componentes entre os pesos e o vetor de entrada são calculados.

Quanto ao AddPatternStatsm, ele é chamado imediatamente de outro método, CSOM::CalculateStats, que apenas organiza o loop para todas as entradas.

double CSOM::CalculateStats(const bool complete = true)
{
  double data[];
  ArrayResize(data, m_dimension);
  double trainedMSE = 0.0;
  
  for(int i = complete ? 0 : m_validationOffset; i < m_nSet; i++)
  {
    ArrayCopy(data, m_set, 0, m_dimension * i, m_dimension);
    trainedMSE += AddPatternStats(data, complete);
  }
  
  double nmse = trainedMSE / m_dataMSE;
  if(complete) Print("Overall NMSE=", nmse);

  return nmse;
}

Este método resume todos os erros de quantização e compara-os com a dispersão de dados de entrada em m_dataMSE — isto é exatamente os cálculos NMSE descritos acima dentro do contexto de validação e interrupção de aprendizagem. Esse método menciona a variável m_validationOffset especificada na criação do objeto CSOM com base no fato de ele usar a divisão do conjunto de dados de entrada pelos subconjuntos de aprendizado e validação.

Você adivinhou, o método CalculateStats é chamado em cada época dentro do método Train (se a fase de convergência já foi iniciada), e podemos julgar pelo valor retornado se o erro geral de rede começou a aumentar, ou seja se é hora de parar.

A dispersão de m_dataMSE é calculada antecipadamente, usando o método:

void CSOM::CalculateDataMSE()
{
  double data[];

  m_dataMSE = 0.0;
  
  for(int i = m_validationOffset; i < m_nSet; i++)
  {
    ArrayCopy(data, m_set, 0, m_dimension * i, m_dimension);

    double mse = 0;
    for(int k = 0; k < m_dimension; k++)
    {
      mse += (data[k] - m_mean[k]) * (data[k] - m_mean[k]);
    }
    
    mse /= m_dimension;
    m_dataMSE += mse;
  }
}

Nós obtemos o valor da média, m_mean, para cada componente no estágio de normalização de dados.

void CSOM::InitNormalization(const bool normalization = true)
{
  ArrayResize(m_max, m_dimension + EXTRA_DIMENSIONS);
  ArrayResize(m_min, m_dimension + EXTRA_DIMENSIONS);
  ArrayInitialize(m_max, 0);
  ArrayInitialize(m_min, 0);
  ArrayResize(m_mean, m_dimension);
  ArrayResize(m_sigma, m_dimension);

  for(int j = 0; j < m_dimension; j++)
  {
    double maxv = -DBL_MAX;
    double minv = +DBL_MAX;
    
    if(normalization)
    {
      m_mean[j] = 0;
      m_sigma[j] = 0;
    }
    
    for(int i = 0; i < m_nSet; i++)
    {
      double v = m_set[m_dimension * i + j];
      if(v > maxv) maxv = v;
      if(v < minv) minv = v;
      if(normalization)
      {
        m_mean[j] += v;
        m_sigma[j] += v * v;
      }
    }
    
    m_max[j] = maxv;
    m_min[j] = minv;
    
    if(normalization && m_nSet > 0)
    {
      m_mean[j] /= m_nSet;
      m_sigma[j] = MathSqrt(m_sigma[j] / m_nSet - m_mean[j] * m_mean[j]);
    }
    else
    {
      m_mean[j] = 0;
      m_sigma[j] = 1;
    }
  }
}

Voltando para os planos adicionais, deve-se notar que, após ter calculado em CSOMNode::RegisterPatternHit, cada neurônio é capaz de retornar as estatísticas relevantes usando os métodos:

int CSOMNode::GetHitsCount() const
{
  return m_hitCount;
}

double CSOMNode::GetHitsMean(const int plane) const
{
  if(m_hitCount == 0) return 0;
  return m_sum[plane] / m_hitCount;
}

double CSOMNode::GetHitsDeviation(const int plane) const
{
  if(m_hitCount == 0) return 0;
  double z = m_sumP2[plane] / m_hitCount - m_sum[plane] / m_hitCount * m_sum[plane] / m_hitCount;
  if(z < 0) return 0;
  return MathSqrt(z);
}

double CSOMNode::GetMSE() const
{
  if(m_hitCount == 0) return 0;
  return m_mse / m_hitCount;
}

Assim, nós obtemos os dados para preencher dois planos — com o número de exibições de vetores de entrada por neurônios e com o erro de quantização.

Resposta da rede

O próximo plano adicional será o mapa de produção e a resposta da rede para uma amostra específica. Deve ser lembrado que, ao alimentar um sinal para a rede, juntamente com o neurônio vencedor, todos os outros neurônios são ativados em menor escala. A possibilidade de comparar a excursão da resposta ativa pode auxiliar na definição da estabilidade da solução proposta pela rede.

Os cálculos de resposta de rede são maximamente simples. Na classe CSOMNode, nós vamos escrever o método de:

double CSOMNode::CalculateOutput(const double &vector[])
{
  m_output = CalculateDistance(vector);
  return m_output;
}

E nós vamos chamá-lo para cada neurônio na classe network.

void CSOM::CalculateOutput(const double &vector[], const bool normalize = false)
{
  double temp[];
  ArrayCopy(temp, vector);
  if(normalize) Normalize(temp);
  m_min[DIM_OUTPUT] = DBL_MAX;
  m_max[DIM_OUTPUT] = -DBL_MAX;
  for(int i = 0; i < ArraySize(m_node); i++)
  {
    double x = m_node[i].CalculateOutput(temp);
    if(x < m_min[DIM_OUTPUT]) m_min[DIM_OUTPUT] = x;
    if(x > m_max[DIM_OUTPUT]) m_max[DIM_OUTPUT] = x;
  }
}

Se o vetor de teste não for fornecido ao programa, a resposta é calculada por padrão, ou seja, para o vetor zero.

Clusterização

Finalmente, o último dos planos considerados, mas provavelmente o mais importante, será o mapa de cluster. Organizar os dados de entrada em um mapa bidimensional é apenas metade da batalha. O propósito real da análise é detectar os recursos e classificá-los em classes fáceis de entender em termos de aplicação. Onde as dimensões do espaço de características são relativamente pequenas, nós podemos facilmente distinguir as áreas que possuem as características requeridas por pontos coloridos em planos individuais, sendo esses pontos geralmente isolados. No entanto, com a expansão da estrutura de dados de entrada, a imagem se torna mais complicada e, em vez de analisar uma dúzia de mapas com diferentes índices, é muito mais conveniente ter um mapa dividido em áreas que reivindicam atenção.

A clusterização resultará em marcar o mapa por áreas com características semelhantes e identificar os centros dos clusters. Então, nós podemos considerá-los como os mais representativos, em termos estatísticos, de amostras de classes relevantes. Aqui, nós estamos gradualmente nos aproximando da tarefa de selecionar os parâmetros ótimos do EA. No entanto, nós devemos implementar a clusterização.

K-Means

Existem muitos métodos de clusterização. A opção mais simples para o MQL5 é usar a versão do ALGLIB, incluída na biblioteca padrão. É suficiente incluir apenas um arquivo de cabeçalho:

#include <Math/Alglib/dataanalysis.mqh>

e escrever um método como este:

void CSOM::Clusterize(const int clusterNumber)
{
  int count = m_xcells * m_ycells;
  CMatrixDouble xy(count, m_dimension);
  int info;
  CMatrixDouble clusters;
  int membership[];
  double weights[];
  
  for(int i = 0; i < count; i++)
  {
    m_node[i].GetCodeVector(weights);
    xy[i] = weights;
  }

  CKMeans::KMeansGenerate(xy, count, m_dimension, clusterNumber, KMEANS_RETRY_NUMBER, info, clusters, membership);
  Print("KMeans result: ", info);
  if(info == 1) // ok
  {
    for(int i = 0; i < m_xcells * m_ycells; i++)
    {
      m_node[i].SetCluster(membership[i]);
    }
    
    ArrayResize(m_clusters, clusterNumber * m_dimension);
    for(int j = 0; j < clusterNumber; j++)
    {
      for(int i = 0; i < m_dimension; i++)
      {
        m_clusters[j * m_dimension + i] = clusters[i][j];
      }
    }
  }
}

Ele realiza a clusterização usando o algoritmo K-Means. Infelizmente, até onde eu sei, ele é o único algoritmo de clusterização na versão ALGLIB da MQL5, embora a versão mais recente da biblioteca original forneça outras, como clusterização por hierárquica aglomerativa.

"Infelizmente", porque o algoritmo K-Means é o mais "direto" em certa medida: sua essência reduz à procura dos centros de um determinado número de esferoides no espaço de características, que cobrem os pontos de amostragem de maneira mais eficiente, ou seja, o mínimo da soma dos quadrados das distâncias para os pontos dos centros do cluster. A questão é que, devido às suas formas fixas, os esferoides possuem algumas limitações específicas quanto à separabilidade dos clusters não lineares. A princípio, o K-Means é um caso especial do algoritmo de Maximização de Expectativas que opera elipsoides de diferentes orientações e formas e, portanto, ele seria mais preferível. No entanto, mesmo quando usado, há uma probabilidade de persistir no mínimo local, uma vez que ambos os algoritmos usam formas convexas e um arranjo aleatório apenas nos centros do cluster. As desvantagens também podem incluir o fato de que o número de clusters deve ser especificado antecipadamente.

No entanto, vamos considerar como a clusterização é organizada usando o K-Means no ALGLIB. A operação principal é executada pelo método CKMeans::KMeansGenerate. Nós passamos para ele um array com os dados de origem em um formato especial baseado em objeto (CMatrixDouble xy), número de vetores (contagem), dimensões do espaço de características (m_dimension) e o número desejado de clusters (clusterNumber), o último a ser especificado nos parâmetros do programa em MQL. A próxima entrada, KMEANS_RETRY_NUMBER, é o número de iterações a serem feitas pelo algoritmo com diferentes centros iniciais selecionados aleatoriamente, tentando evitar a solução local. No nosso caso, é uma macro que é igual a 10. Como resultado da operação da função, nós obteremos o código de execução chamado 'info' (valores diferentes sugerem sucesso ou um erro), o array baseado em objetos chamado CMatrixDouble clusters com coordenadas de clusters, e o array das entradas sendo membros dos clusters (associação).

Nós salvamos os centros do cluster no array m_clusters para marcá-los no mapa, e nós também colorimos cada neurônio com uma cor relevante para sua associação no cluster:

m_node[i].SetCluster(membership[i]);

Ao trabalhar com o ALGLIB, tenha em mente que ele usa seu próprio gerador de números aleatórios que considera o status interno do objeto estático especial. Portanto, mesmo uma inicialização óbvia do gerador padrão através do MathSrand não redefine seu status. Isso é especialmente crítico para os EAs, pois os objetos globais não são gerados novamente ao alterar as configurações. Como resultado, a reprodutibilidade dos resultados do cálculo pode se tornar difícil com o ALGLIB, se o CMath::m_state não for zerado na OnInit.

Considerando as desvantagens acima do K-Means, é desejável ter um método alternativo de clusterização. Uma solução alternativa é fácil de ver.

Alternativa

Vamos voltar nossa atenção para os mapas de Kohonen, particularmente as dimensões adicionais que nós introduzimos. A U-Matrix é de particular interesse. Este plano mostra as áreas dos neurônios mais próximos, ou seja, eles estão próximos tanto em termos de topologia de mapa 2D quanto em termos do espaço de característica. Como nós podemos lembrar, os neurônios semelhantes para um tipo de "fundos" em U-Matrix. Eles são ótimos candidatos para se tornarem clusters.

Nós podemos transformar o mapa de distâncias unificadas em clusters, por exemplo, da seguinte maneira.

Copiar as informações sobre todos os neurônios em um array e classificá-lo de acordo com o valor da U-distance (CSOMNode::GetDistance()).

Para um dado neurônio, nós verificaremos o loop pelo array, se os neurônios vizinhos pertencem a um cluster.

• Se não, nós criamos um novo cluster e atribuímos o neurônio atual a ele. Observe que os clusters serão criados, começando com o índice zero, que corresponde ao cluster "mais importante", pois ele corresponde à distância mínima U-distance e, depois, na ordem decrescente de importância. Em termos de distâncias U (U-distance) cada cluster sucessivo será menos compacto.
• Se entre os neurônios vizinhos houver aqueles marcados com um cluster, nós selecionaremos entre eles o mais alto, ou seja, o que tem o índice mais baixo e atribui o neurônio atual a esse cluster.

Ele é simples. A densidade populacional dos neurônios também não deveriam ser considerados? Afinal, a U-distance tem sido suportada de maneira diferente para os neurônios com diferentes números de acertos. Em outras palavras, se dois neurônios têm a mesma distância U, um deles, para o qual mais amostras foram exibidas, deve ter a vantagem do neurônio ter um número menor.

Em seguida, é suficiente alterar a classificação inicial do array no algoritmo descrito na ordem dos valores na fórmula CSOMNode::GetDistance() / sqrt(CSOMNode::GetHitsCount()). Eu adicionei a raiz quadrada para suavizar o seu efeito no caso de uma grande população, enquanto a população menor deve ser "punida" de maneira mais rigorosa.

No entanto, se nós estamos usando dois planos de serviço, então seria razoável analisar o terceiro, ou seja, com o erro de quantização? De fato, quanto maior o erro de quantização em um neurônio específico, menos nós devemos confiar na informação da pequena U-distance, e vice-versa.

Se nos lembrarmos de como a função com um erro de quantização aparece:

double CSOMNode::GetMSE() const
{
  if(m_hitCount == 0) return 0;
  return m_mse / m_hitCount;
}

então, nós observaremos facilmente que o contador m_hitCount de ocorrências é usado nele (somente no denominador). Portanto, nós podemos reescrever a fórmula anterior para classificar o array de neurônios como CSOMNode::GetDistance() * MathSqrt(CSOMNode::.GetMSE()) — e, em seguida, todos os três índices adicionais serão considerados nele, na qual nós adicionamos à nossa realização da rede Kohonen.

Nós estamos quase prontos para apresentar o algoritmo alternativo de clusterização em sua forma final, mas uma coisa menor permaneceu. Dentro do loop pela matriz de neurônios, nós devemos verificar a vizinhança do neurônio atual para a presença de clusters vizinhos. Um pouco antes, nós implementamos a classe de modelo, Neighborhood, para a negligencia local. Agora, nós vamos criar seu descendente com foco na busca de clusters.

class ClusterNeighbourhood: public Neighbourhood<int>
{
  private:
    int cluster;

  public:
    ClusterNeighbourhood(const bool _hex, const int ysize): Neighbourhood(_hex, ysize)
    {
    }
    
    virtual void reset() override
    {
      cluster = -1;
    }
    
    virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) override
    {
      int x = node2.GetCluster();
      if(x > -1)
      {
        if(cluster != -1) cluster = MathMin(cluster, x);
        else cluster = x;
      }
    }
    
    virtual int getResult() const override
    {
      return cluster;
    }
};

A classe contém o número de cluster em potencial (o número é um número inteiro, portanto, parametrizamos o modelo com o tipo int). Inicialmente, esta variável é inicializada em -1 dentro do método de reset, ou seja, não há cluster. Então, com a classe pai chamando de seu método loop nossa nova realização 'iterate', nós obtemos o número do cluster de cada neurônio vizinho, comparamos com o cluster e salvamos o valor mínimo. O mesmo, ou -1, se nenhum cluster foi encontrado, é retornado pelo método de getResult.

Como uma melhoria, nos propomos o monitoramento da "altura do pico" entre os neurônios, ou seja, o valor de node1.CalculateDistance(& node2), e para executar o número de cluster "fluindo" de um neurônio para outro, somente se a "altura" for menor do que era antes. a versão da realização final é apresentada no código-fonte.

Finalmente, nós podemos implementar a clusterização alternativa.

void CSOM::Clusterize()
{
  double array[][2];
  int n = m_xcells * m_ycells;
  ArrayResize(array, n);
  for(int i = 0; i < n; i++)
  {
    if(m_node[i].GetHitsCount() > 0)
    {
      array[i][0] = m_node[i].GetDistance() * MathSqrt(m_node[i].GetMSE());
    }
    else
    {
      array[i][0] = DBL_MAX;
    }
    array[i][1] = i;
    m_node[i].SetCluster(-1);
  }
  ArraySort(array);
  
  ClusterNeighbourhood clnh(m_hexCells, m_ycells);

  int count = 0; // número de clusters
  ArrayResize(m_clusters, 0);
  
  for(int i = 0; i < n; i++)
  {
    // pula se já estiver atribuído
    if(m_node[(int)array[i][1]].GetCluster() > -1) continue;
    
    // verifica se o nó atual é adjacente a qualquer cluster existente
    int r = clnh.loop((int)array[i][1], m_node);
    if(r > -1) // um vizinho pertence a um cluster já existente
    {
      m_node[(int)array[i][1]].SetCluster(r);
    }
    else // precisamos de um novo cluster
    {
      ArrayResize(m_clusters, (count + 1) * m_dimension);
      
      double vector[];
      m_node[(int)array[i][1]].GetCodeVector(vector);
      ArrayCopy(m_clusters, vector, count * m_dimension, 0, m_dimension);
      
      m_node[(int)array[i][1]].SetCluster(count++);
    }
  }
}

O algoritmo segue praticamente todo o pseudocódigo verbal descrito acima: Nós preenchemos o arranjo bidimensional (o valor da fórmula na primeira dimensão, e o índice do neurônio na segunda), classificamos, visitamos todos os neurônios no loop e analisamos a vizinhança para cada um deles.

A qualidade da clusterização deve, obviamente, ser avaliada na prática, e eu pressuponho a presença de questões topológicas. No entanto, considerando que a maioria dos métodos clássicos de clusterização também tem problemas e são inferiores em facilidade ao proposto, a nova solução parece atraente.

Entre as vantagens dessa realização, eu mencionaria o fato de que os clusters são organizados por sua importância (no K-Means acima mencionado, os clusters são iguais), sua forma é aleatória e o número não precisa ser pré-definido. Deve-se notar que o último tem um lado reverso, ou seja, o número de clusters pode ser bem grande. Ao mesmo tempo, o arranjo de clusters pelo grau de similaridade de conteúdo e erro mínimo permite praticamente considerar apenas os primeiros 5-10 clusters e deixar os outros "nos bastidores".

Como eu não encontrei nenhum método de clusterização semelhante em nenhuma fonte aberta, eu propus denominá-lo de clusterização de Korotky, ou mais longo, porém, descente — short-path clusterization, baseada em U-Matrix e erro de quantização (QE).

Indo adiante, devo dizer que, após muitos testes, ficou praticamente fortalecido que os centros de cluster encontrados pelo algoritmo K-Means forneceram resultados piores do que a clusterização alternativa (pelo menos no problema de analisar os resultados de otimização). Assim, apenas esse método de clusterização será entendido e aplicado a seguir.

Testando

É hora de passar da teoria para a prática e testar como a rede funciona. Vamos criar um Expert Advisor simples e universal com as opções de demonstrar a funcionalidade básica. Nós vamos nomeá-lo de SOM-Explorer.

Vamos incluir arquivos de cabeçalho com as classes acima. Definir as entradas.

Grupo — Estrutura da Rede e Configurações dos Dados

• DataFileName — o nome de um arquivo de texto com os dados para aprendizado ou teste; A classe CSOM suporta formato csv, mas adicionaremos um pouco mais tarde arquivos de configuração de leitura no próprio EA, já que a análise de otimização de configurações de outros EAs está "em risco"; onde o arquivo contendo entradas é especificado, seu nome também é usado para salvar a rede depois de ter aprendido, mas com outra extensão (veja abaixo); você pode indicar ou não a extensão csv; e o nome pode incluir uma pasta dentro de MQL5/Files;
  
  
• NetFileName — o nome de um arquivo binário de seu próprio formato com extensão som; classe CSOM é capaz de salvar e ler as redes dentro/de tais arquivos; se alguém precisar alterar a estrutura dos dados a serem armazenados, então altere o número da versão na assinatura que está escrita no início do arquivo; se NetFileName estiver vazio, o EA funcionará no modo de aprendizado, enquanto se a rede estiver especificada, então no modo de teste, ou seja, exibindo as entradas na rede pronta; você pode indicar ou não a extensão som; e o nome pode incluir uma pasta dentro de MQL5/Files;
  
  
• se DataFileName e NetFileName estiverem vazios, o EA gerará um conjunto de demonstração de dados 3D aleatórios e executará o aprendizado sobre ele;
  
  
• se o nome da rede em NetFileName estiver correto, você pode indicar em DataFileName o nome de um arquivo não existente, como apenas o caractere '?', que leva ao EA gerando uma amostra aleatória de dados de teste para o intervalo de definições que é salvo no arquivo da rede, observe que essas informações são necessárias para que a rede ensinada normalize corretamente os dados desconhecidos no modo de operação; alimentar a entrada da rede com os valores de outro intervalo de definições não levará, naturalmente, a um fallout, mas os resultados não serão confiáveis, por exemplo, é difícil esperar que a rede funcione corretamente, se um valor negativo de rebaixamento ou do número de negócios é fornecido a ele.
  
  
• CellsX — tamanho horizontal da grade (número de neurônios), 10 por padrão;
  
  
• CellsY — tamanho vertical da grade (número de neurônios), 10 por padrão;
  
  
• HexagonalCell — o recurso de usar uma grade hexagonal, é 'true' por padrão; para uma grade retangular, mude para 'false';
  
  
• UseNormalization — habilita/desabilita a normalização de entradas; é "true" por padrão, e é recomendado não desativá-lo;
  
  
• EpochNumber — o número de épocas de aprendizado; 100 por padrão;
  
  
• ValidationSetPercent — o tamanho da seleção de validação em porcentagem do número total de entradas; é 0 por padrão, ou seja, a validação está desativada; no caso de usá-lo, o valor recomendado é de cerca de 10;
  
  
• ClusterNumber — o número de clusters; é 1 por padrão, o que significa nossa clusterização adaptativa; o valor 0 desabilita a clusterização; valores acima de 0 iniciam a clusterização usando o método K-Means; a clusterização é realizada imediatamente após o aprendizado; e os clusters são salvos no arquivo da rede;

Grupo - Visualização

• ImageW — o tamanho horizontal de cada mapa (plano) em pixels, 500 por padrão;
  
  
• ImageH — o tamanho vertical de cada mapa (plano) em pixels, 500 por padrão;
  
  
• MaxPictures — o número de mapas em uma linha; é 0 por padrão, significando o modo de exibição dos mapas em uma linha contínua com a opção de rolagem (imagens grandes são permitidas); se MaxPictures estiver acima de 0, o conjunto inteiro de planos será exibido em várias linhas, em cada uma das quais as MaxPictures dos mapas estão localizadas (é conveniente visualizar todos os mapas juntos em uma pequena escala);
  
  
• ShowBorders — habilita/desabilita o desenho das bordas entre os neurônios; é 'false' por padrão;
  
  
• ShowTitles — habilita/desabilita a exibição dos textos com características do neurônio, é 'true' por padrão;
  
  
• ColorScheme — seleciona um dos quatro esquemas de cores; sendo Blue_Green_Red (o mais colorido) por padrão;
  
  
• ShowProgress — habilita/desabilita a atualização dinâmica das imagens da rede durante o aprendizado; é realizado 1 vez por segundo; é 'true' por padrão;

Grupo - Opções

• RandomSeed — um inteiro para inicializar o gerador de números aleatórios; é 0 por padrão;
• SaveImages — a opção de salvar as imagens da rede após a conclusão; ele também pode ser usado depois de aprender e depois do primeiro lançamento; é 'false' por padrão;

Estas são apenas configurações básicas. À medida que nós continuamos resolvendo os problemas, nós vamos adicionar alguns outros parâmetros específicos.

Nota! O EA altera as configurações do gráfico atual — abra um novo gráfico dedicado para trabalhar somente com este EA.

O objeto da classe CSOMDisplay executará todo o trabalho do EA.

CSOMDisplay KohonenMap;

Durante a inicialização, não se esqueça de ativar o processamento de eventos de movimento do mouse — a classe os usa para exibir as dicas pop-up e para rolagem.

void OnInit()
{
  ChartSetInteger(0, CHART_EVENT_MOUSE_MOVE, true);
  EventSetMillisecondTimer(1);
}

void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
{
  KohonenMap.OnChartEvent(id, lparam, dparam, sparam);
}

Os algoritmos de redes neurais (aprendizado ou teste) devem ser lançados no EA apenas uma vez — pelo timer e, em seguida, o timer é desativado.

void OnTimer()
{
  EventKillTimer();
  
  MathSrand(RandomSeed);
  
  bool hasOneTestPattern = false;
  
  if(NetFileName != "")
  {
    if(!KohonenMap.Load(NetFileName)) return;
    KohonenMap.DisplayInit(ImageW, ImageH, MaxPictures, ColorScheme, ShowBorders, ShowTitles);

    Comment("Map ", NetFileName, " is loaded; size: ", KohonenMap.GetWidth(), "*", KohonenMap.GetHeight(), "; features: ", KohonenMap.GetFeatureCount());

Se um arquivo pronto com a rede for especificado, nós o carregaremos e prepararemos a exibição de acordo com as configurações visuais.

    if(DataFileName != "")
    {
      if(!KohonenMap.LoadPatterns(DataFileName))
      {
        Print("Data loading error, file: ", DataFileName);

        // gera um vetor de teste aleatório
        int n = KohonenMap.GetFeatureCount();
        double min, max;
        double v[];
        ArrayResize(v, n);
        for(int i = 0; i < n; i++)
        {
          KohonenMap.GetFeatureBounds(i, min, max);
          v[i] = (max - min) * rand() / 32767 + min;
        }
        KohonenMap.AddPattern(v, "RANDOM");
        Print("Random Input:");
        ArrayPrint(v);
        double y[];
        CSOMNode *node = KohonenMap.GetBestMatchingFeatures(v, y);
        Print("Matched Node Output (", node.GetX(), ",", node.GetY(), "); Hits:", node.GetHitsCount(), "; Error:", node.GetMSE(),"; Cluster N", node.GetCluster(), ":");
        ArrayPrint(y);
        KohonenMap.CalculateOutput(v, true);
        hasOneTestPattern = true;
      }
    }

Se um arquivo com os detalhes do teste for especificado, nós tentamos carregá-lo. Se ele não funcionar, exiba uma mensagem no log e gere uma amostra de dados de teste aleatória, v. O número de recursos (dimensões de vetores) e seus intervalos permitidos devem ser definidos usando os métodos GetFeatureCount e GetFeatureBounds. Em seguida, pela chamada de AddPattern, o exemplo é adicionado ao conjunto de dados de trabalho sob o nome de RANDOM.

Esse método seria adequado para formar seleções de aprendizado de fontes de dados com formatos não suportados, como bancos de dados, e para preenchê-los diretamente dos indicadores. Em princípio, neste caso específico, adicionar uma amostra a um conjunto de trabalho é necessário apenas para visualizá-las subsequentemente no mapa (mostrado abaixo), enquanto apenas uma chamada, GetBestMatchingFeatures, é suficiente para encontrar o neurônio mais adequado na rede. Este método entre vários métodos GetBestMatchingXYZ disponíveis nos permite obter os valores relevantes dos recursos do neurônio vencedor no array y. Finalmente, usando CalculateOutput, nós exibimos a resposta da rede para a amostra de teste em um plano adicional.

Nós continuamos seguindo o código do EA.

  }
  else // um arquivo de rede não é fornecido, então o treinamento é assumido
  {
    if(DataFileName == "")
    {
      // gera vetores de demonstração 3-d com valores sem escala {[0,+1000], [0,+1], [-1,+1]}
      // alimenta-os à rede para comparar resultados com e sem normalização
      // NB. os títulos devem ser nomes de arquivos válidos para BMP
      string titles[] = {"R1000", "R1", "R2"};
      KohonenMap.AssignFeatureTitles(titles);
      double x[3];
      for(int i = 0; i < 1000; i++)
      {
        x[0] = 1000.0 * rand() / 32767;
        x[1] = 1.0 * rand() / 32767;
        x[2] = -2.0 * rand() / 32767 + 1.0;
        KohonenMap.AddPattern(x, StringFormat("%f %f %f", x[0], x[1], x[2]));
      }
    }

Se a rede ensinada não for especificada, nós assumimos o modo de aprendizagem. Verifique se há alguma entrada. Se não, nós geramos um conjunto aleatório de vetores tridimensionais, no qual o primeiro componente está dentro do intervalo de [0,+1000], o segundo está dentro de [0,+1], e o terceiro está dentro de [-1,+1]. Os nomes dos componentes são passados para a rede usando AssignFeatureTitles e os dados — usando o já conhecido AddPattern.

    else // um arquivo de dados é fornecido
    {
      if(!KohonenMap.LoadPatterns(DataFileName))
      {
        Print("Data loading error, file: ", DataFileName);
        return;
      }
    }

Se as entradas vierem de um arquivo, carregue este arquivo. Em caso de erro, termine o trabalho, pois não há rede ou dados.

Além disso, nós realizamos a aprendizagem e a clusterização.

    KohonenMap.Init(CellsX, CellsY, ImageW, ImageH, MaxPictures, ColorScheme, HexagonalCell, ShowBorders, ShowTitles);
    
    if(ValidationSetPercent > 0 && ValidationSetPercent < 50)
    {
      KohonenMap.SetValidationSection((int)(KohonenMap.GetDataCount() * (1.0 - ValidationSetPercent / 100.0)));
    }

    KohonenMap.Train(EpochNumber, UseNormalization, ShowProgress);

    if(ClusterNumber > 1)
    {
      KohonenMap.Clusterize(ClusterNumber);
    }
    else
    {
      KohonenMap.Clusterize();
    }
  }

Se a análise de uma amostra de teste individual não foi especificada (particularmente, imediatamente após o aprendizado), nós formamos a resposta da rede para o vetor com zeros por padrão.

  if(!hasOneTestPattern)
  {
    double vector[];
    ArrayResize(vector, KohonenMap.GetFeatureCount());
    ArrayInitialize(vector, 0);
    KohonenMap.CalculateOutput(vector);
  }

Em seguida, nós desenhamos todos os mapas nos buffers internos de recursos gráficos — a cor por trás primeiro:

  KohonenMap.Render(); // desenha mapas em buffers BMP internos

e depois, legendas:

  if(hasOneTestPattern)
    KohonenMap.ShowAllPatterns();
  else
    KohonenMap.ShowAllNodes(); // desenha rótulos em células em buffers BMP

Marcando os clusters:

  if(ClusterNumber != 0)
  {
    KohonenMap.ShowClusters(); // marca clusters
  }

Mostra os buffers no gráfico e, opcionalmente, salva as imagens em arquivos:

  KohonenMap.ShowBMP(SaveImages); // exibe arquivos como imagens de bitmap no gráfico, opcionalmente, salva em arquivos

Os arquivos são colocados em uma pasta separada com o mesmo nome do arquivo de rede, se fornecido, ou o arquivo com dados, se fornecidos. Se o arquivo de dados não tiver sido especificado e a rede tiver aprendido em dados gerados aleatoriamente, o nome do arquivo som e as pastas que contêm as imagens serão formadas usando o prefixo SOM junto com a data e hora atuais.

Finalmente, salva a rede aprendida em um arquivo. Se o nome da rede já foi especificado no NetFileName, isso significa que o EA trabalhou no modo de teste, portanto, não precisamos salvar a rede novamente.

  if(NetFileName == "")
  {
    KohonenMap.Save(KohonenMap.GetID());
  }
}

Vamos tentar iniciar o EA gerando os dados aleatórios de teste. Com todas as configurações padrão, além das escalas de imagem usadas para garantir que todos os planos entrem na captura de tela, ImageW = 230, ImageH = 230, MaxPictures = 3, nós obtemos a seguinte imagem:

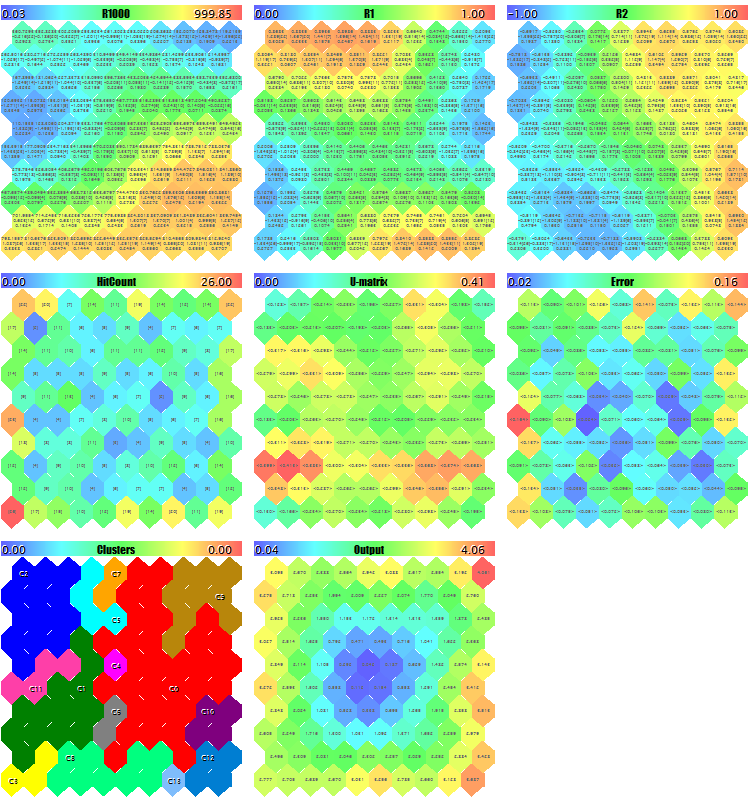
Exemplos de mapas de Kohonen para vetores 3D aleatórios

Aqui, os dados do serviço são exibidos em cada neurônio (você pode ver os detalhes apontando o cursor do mouse) e os clusters encontrados são marcados.

Nesse processo, as seguintes informações (informações de cluster são limitadas por cinco; você pode alterá-lo no código-fonte) são exibidas no log:

Pass 0 from 1000 0%
Pass 78 from 1000 7%
Pass 157 from 1000 15%
Pass 232 from 1000 23%
Pass 310 from 1000 31%
Pass 389 from 1000 38%
Pass 468 from 1000 46%
Pass 550 from 1000 55%
Pass 631 from 1000 63%
Pass 710 from 1000 71%
Pass 790 from 1000 79%
Pass 870 from 1000 87%
Pass 951 from 1000 95%
Overall NMSE=0.09420336270396877
Training completed at pass 1000, NMSE=0.09420336270396877
Clusters [14]:
"R1000" "R1"    "R2"   
N0
754.83131   0.36778   0.25369
N1
341.39665   0.41402  -0.26702
N2
360.72925   0.86826  -0.69173
N3
798.15569   0.17846  -0.37911
N4
470.30648   0.52326   0.06442
Map file SOM-20181205-134437.som saved

Se agora nós especificamos o nome do arquivo criado SOM-20181205-134437.som com a rede no parâmetro NetFileName e '?' no parâmetro DataFileName, nós obteremos o resultado de uma execução de teste para uma amostra aleatória que não seja do conjunto de aprendizado. Para ver melhor os mapas, deixe-os maiores e ajuste MaxPictures para 0. 

Mapas de Kohonen para os dois primeiros componentes de vetores 3D aleatórios

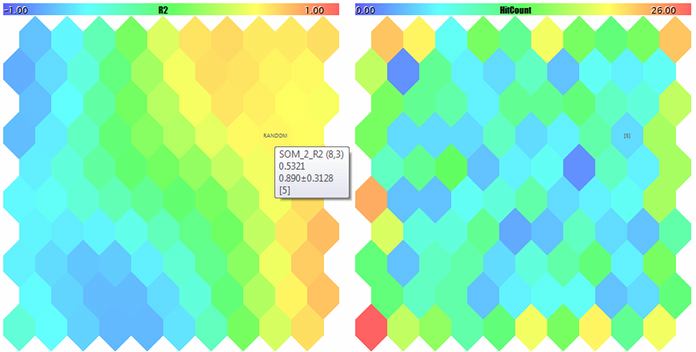
Um mapa de Kohonen para o terceiro componente de vetores 3D aleatórios e o contador de ocorrências

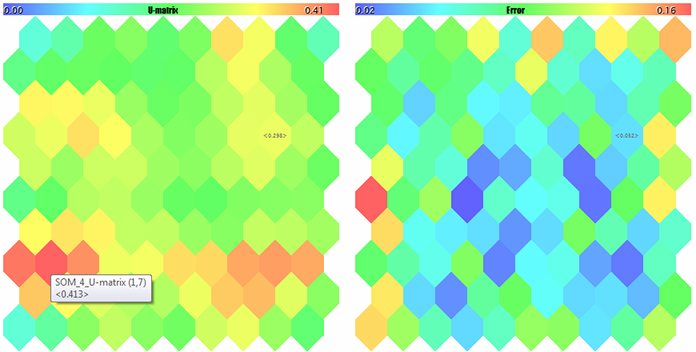
U-Matrix e erros de quantização

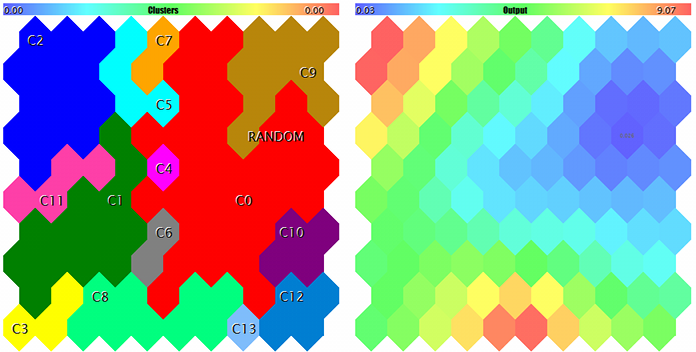
Clusters e a resposta da rede de Kohonen para a amostra de teste

A amostra está marcada com RANDOM. As dicas sobre os neurônios aparecem quando apontadas pelo cursor do mouse. Algo como o seguinte é exibido no log:

FileOpen error ?.csv : 5004
Data loading error, file: ?
Random Input:
457.17510   0.29727   0.57621
Matched Node Output (8,3); Hits:5; Error:0.05246704285146882; Cluster N0:
497.20453   0.28675   0.53213

Assim, as ferramentas para trabalhar com a rede de Kohonen estão prontas. Nós podemos ir para problemas aplicados. Nós vamos lidar com isso em nosso segundo artigo.

Conclusões

As realizações abertas das redes neurais de Kohonen já estão disponíveis para os usuários da MetaTrader há alguns anos. Nós corrigimos alguns erros neles, complementamos com ferramentas úteis e testamos sua operação usando um EA de demonstração especial. Códigos-fonte permitem que você aplique as classes para suas próprias tarefas; nós vamos considerar os exemplos relevantes mais adiante — continua.