アルゴリズムトレードにおける Kohonen ニューラルネットワークの実用的利用 パートI ツール

Kohonen ニューラルネットワークの主題は、 MetaTrader5 の自己組織化関数マップ (Kohonen map)と自己組織化関数マップ (Kohonen マップ) を使用するなど、mql5.com ウェブサイトの記事で、再考されてきました。 このタイプのニューラルネットワークを構築し、そのようなマップを使用して相場のマーケット数を視覚的に分析する一般的な原則を紹介しました。

しかし、実際には、アルゴリズムトレードのためだけに Kohonen ネットワークを使用することは、EA最適化の結果に構築されたトポロジマップの視覚的な分析という1つのアプローチのみに限定されます。 この場合、価値判断、あるいは画像から妥当な結論を引き出すというビジョンと能力は、おそらく重要な要素であり、データの表現に関するネットワーク特性を傍系することになります。

言い換えると、ニューラルネットワークアルゴリズムの特徴は完全には使用されておらず、すなわち、知識を自動的に抽出したり、特定の推奨事項を用いて意思決定を支援したりすることなく使用されました。 本稿では, ロボットのパラメータの最適な集合を, より形式化された方法で定義する問題について考察します。 さらに、Kohonen ネットワークを適用して経済範囲を予測します。 ただし、適用された問題に進む前に、既存のソースコードを修正し、解決し、改善を行う必要があります。

「ネットワーク」、「レイヤー」、「ニューロン」 (「ノード」)、「リンク」、「重み」、「学習率」、「学習範囲」、および Kohonen ネットワークに関連するその他の概念などの用語に精通していない場合は、上記の記事を最初に読むことを強くお勧めします。 その後、この問題を煮詰める必要がありますので、基本的な概念をおさらいすると、この記事が大幅に長くなってしまいます。

エラーの修正

上記の記事の前者で公開されているクラス CSOM と CSOMNode を呼び出して、後者への追加に目を向けていきます。 中のキーコードフラグメントは実質的に同一であり、同じ問題を継承します。

まず第一に、何らかの理由で、上記のクラスのニューロンは、インデックス化されていることに留意すべきで、すなわち、ピクセル座標によって、コンストラクタパラメータで識別され、定義します。 これはあまりロジカルではなく、デバッグが複雑になります。 特にこの方法では、プレゼンテーション設定は計算に影響します。 想像してみてください: 同じサイズのラティスを持つ2つの完全に類似したネットワークがあり、同じデータセットを使用して同じ設定とランダムデータジェネレーターの初期化を行うことを学習します。 しかし、1つのネットワークの画像が別のものよりも大きいため、得られる結果は異なります。 これは誤りです。

数字によってニューロンをインデックス化します: 各ニューロンは、Kohonen ネットワークの出力層で、それぞれ列と行番号に対応する配列 m_node (クラス CSOM) 座標 x と y になります。 各ニューロンは、CSOMNode:: InitNode (x1、y1、x2、y2) メソッドの代わりに、CSOMNode:: InitNode (x、y) メソッドを使用して初期化されます。 視覚化に進むと、ピクセル単位でマップサイズを変更しても、ニューロン座標は変更されません。

継承されたソースコードでは、インプットデータの正規化は行われません。 ただし、インプットベクトルの異なるコンポーネント (フィーチャ) の値の範囲が異なる場合は、重要です。 そして、EAの最適化結果と異なるインジケータのデータをプーリングする場合です。 最適化の結果については、数十千の総利益を持つ値は、シャープレシオの分数や反発係数の1桁の値など、小さな値であることがわかります。

このような異なるスケールのデータを使用して Kohonen ネットワークをやるべきではありません。ネットワークは実質的に大きなコンポーネントのみを考慮し、小さいものを無視します。 この記事内のステップワイズ方法で検討しようとしているプログラムを使用して取得し、最後にここに添付し、以下の画像で見ることができます。 このプログラムでは、3つの成分がそれぞれ [0, 1000]、[0, 1]、[-1, + 1] の範囲内で定義されているランダムなインプットベクトルを生成することができます。 特殊なインプット UseNormalization により、正規化を有効/無効にすることができます。

ベクトルの3次元に関連する3つの面で Kohonen ネットワークの最終的な構造を見てみましょう。第1に、正規化を伴わないネットワーク学習結果です。

インプットを正規化しないKohonenネットワーク学習結果

正規化と同じです。

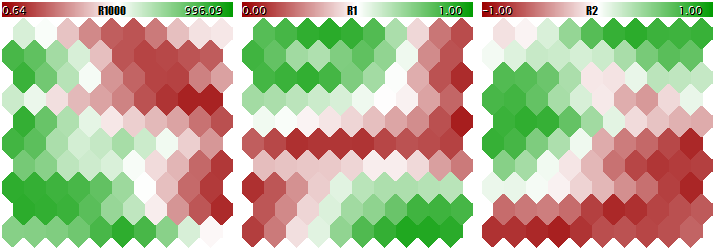
インプットを正規化した Kohonen ネットワーク学習結果

ニューロンの加重の適応の度合いは、色のグラデーションに比例します。 明らかに、正規化されていない条件では、ネットワークは最初の平面でのみトポロジカルパーティショニング (分類) を学習しており、第2および第3のコンポーネントはマイナーノイズで埋められます。 つまり、ネットワークの分析能力は、3分の1までしか実現していません。 正規化を有効にすると、空間配置が3つのすべての平面に表示されます。

正規化の多くの方法が知られていますが、最も一般的なものは、おそらく、各成分から選択全体の平均値を減算し、続いて、標準偏差、すなわち、σまたは２乗平均平方根で割ることです。 変換されたデータの平均値をゼロに、標準偏差を unity に設定します。

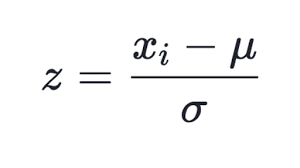 (1)

この手法は、メソッドの正規化で、CSOM の更新されたクラスで使用します。 最初に、メソッド InitNormalization (下記参照) で行われるインプットデータセットの各コンポーネントの平均値とシグマを計算する必要があることは明らかです。

実行アルゴリズムを使用して平均値と標準偏差平均を計算するための正規式: 平均値が最初に検出され、次にσの計算に使用します。

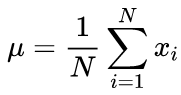                             (2)

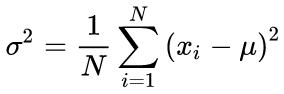     (3)

ソースコードでは、次の式に基づいて1回だけ実行されるアルゴリズムを使用します。

 (4)

明らかに、インプットの正規化では、逆の操作 (非正規化—終了)、つまり、ネットワークの出力値を実際の値の範囲に変換する必要があります。 これは、メソッドCSOM::Denormalizeによって行われます。

正規化された値がゼロの近傍で対称になるので、ネットワークを教えるために開始する前に、ニューロンの加重の初期化原理を変更します-範囲 [0, 1] ではなく、現在は範囲 [-1, + 1] になります (CSOMNode::InitNode 参照)。 これより、ネットワーク学習の効率が向上します。

修正するもう1つの側面は、学習の反復をカウントすることです。 ソースクラスでは、反復は、ネットワークの個々のインプットベクトルを指定することを意味すると理解されます。 したがって、繰り返しの数は、ティーチング選択のサイズに基づいて、そして応じて修正されるべきです。 Kohonen ネットワーク学習と情報融合の原則は、各サンプルがネットワークに対してかなりの回数指定されていると仮定していることを思い出してください。 たとえば、選択範囲に100のインプットがある場合、1万に等しいする反復の数は、各100回を平均して指定する必要があります。 ただし、選択によって1000のインプットが作成された場合、反復の数は10万になる必要があります。 より便利な従来の方法は、いわゆる「学習エポック」の数を定義する、すなわち、すべてのサンプルがランダムにネットワークインプットに供給されるそれぞれの中のサイクルです。 この番号は、パラメータ EpochNumber で設定されます。 これを導入することにより、学習期間はデータセットのサイズからパラメトリックに切り離されます。

合計インプットセットが2つのコンポーネント (学習する選択と、いわゆる検証選択) に分けることができるため、さらに重要です。 後者は、ネットワーク学習の品質を追跡するために使用します。 問題は、学習中にインプットにネットワークを適応させるということです "フリップ側": ネットワークは特定のサンプルの特性に適応し始め、そうすることで、未知のデータを一般化して適切に動作する能力を失います (使用されているもの以外教育に)。 結局のところ、学習のアイデアは、原則として、将来的に適用されるネットワークを使用して検出された特性の能力に含まれています。

検討中のプログラムでは、インプットパラメータ ValidationSetPercent が妥当性検査を使用可能にする役割があります。 デフォルトでは0に等しく、すべてのデータが学習に使用します。 たとえば、10を指定した場合、学習にはサンプルの 90% のみが使用され、残りの 10% では正規化平均２乗誤差が各繰り返し (エポック) で計算され、学習プロセスはエラーの増加が始まる時点でストップします。

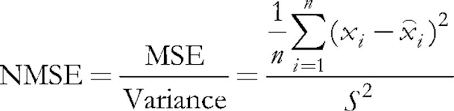 (5)

正規化は、平均２乗誤差をデータ自体の分散によって除算することで構成され、その結果、インデックスは常に1未満になります。 各ベクトルを別々に検討する場合、この２乗誤差は、実際には、量子化誤差であり、その成分と関連する神経シナプスの加重との差に基づいているので、すべての中でこのベクトルの最良の近似値を与えるニューロンです。 このウィニングニューロンは、Kohonen ネットワークでは BMU (ベストマッチングユニット) または BMN (ベストマッチングノード) と呼ばれ、クラス CSOM では GetBestMatchingNode メソッドと同様の手法で検索を行う必要があります。

検証を有効にすると、繰り返し回数はパラメータ EpochNumber で指定された数を超えます。 Kohonen ネットワークアーキテクチャの特別な特徴により、検証は、ネットワークが EpochNumber エポックで自己組織化フェーズを通過した後にのみ実行できます。 このフェーズが完了すると、学習率とスコープが大幅に減少し、加重の微調整が開始されてから収束フェーズが開始されます。 ここでは、学習の「早期ストップ」が検証セットを使用して適用されます。

検証を使用するかどうかは、問題の特異性によって異なります。 また、検証セットを使用してネットワークサイズを一致させることもできます。 この記事では、この問題に入るつもりはありません。 教育データの数にネットワークサイズに関連するよく知られているエンピリックルールを使用しています:

N ~ 5 * sqrt(M)          (6)

ここで、N はネットワーク内のニューロンの数であり、M はインプットベクトルの数です。 正方形の出力層を持つ Kohonen ネットワークの場合は、サイズを取得します。

S = sqrt(5 * sqrt(M))  (7)

ここで、S は、垂直方向および水平方向のニューロンの数です。 この値をパラメータ CellsX および CellsY に導入します。

元のソースコードで修正される直近の問題は、六角形のグリッドの処理に関連します。 Kohonen マップは、セル (ニューロン) の長方形または六角形の配置を使用して構築されることが知られており、両方のモードは、最初にソースコードで実現されています。 しかし、六角形のグリッドは、六角形のセルとして表示されますが、長方形のものとして完全に計算されます。 ここでエラーのルートを取得するには、次の図を考えてみましょう。

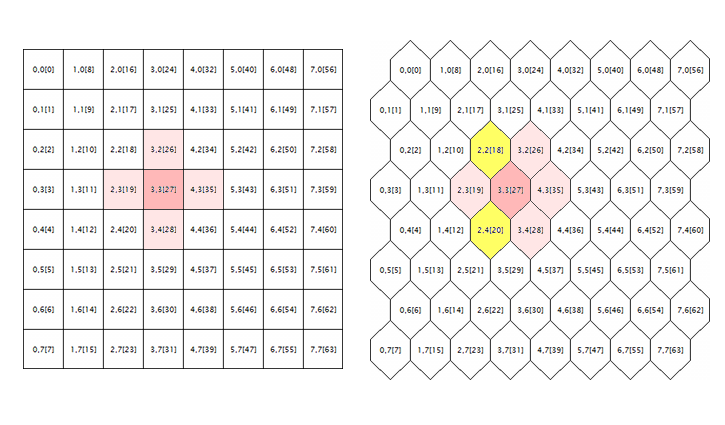
長方形と六角形のグリッドにおけるニューロン近傍の幾何学

ランダムニューロンの周囲の論理は、両方のジオメトリのグリッドにここに表示されています (この場合は3;3の座標があります)。 周囲半径は1です。 正方形のグリッドでは、ニューロンは4つの直接の近傍を持っていますが、六角形のグリッドには6つあります。 テッセレーションの外観の実現は、セルのすべての代替文字列を半セルだけずらして行うことによって実現されます。 しかし、内部座標を変更せず、アルゴリズムの観点から、六角形のグリッドの周囲のニューロンは、ピンク色でマークされています。

どうやら、これは間違っており、黄色で強調表示されたニューロンをインクルードすることによって修正する必要があります。.

公式には、アルゴリズムは、隣接する近傍を使用して、セルの座標間の距離に応じて、凸減少ラジアル関数として周囲の両方を計算します。 言い換えると、近傍はニューロン (近傍かどうか) のバイナリプロパティではなく、ガウス式によって計算された連続量です。

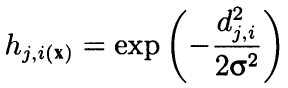 (8)

ここで、djiは、ニューロン j と i の間の距離である (連続ナンバリングは、座標 x および y ではない)。シグマは、学習中に徐々に減少する近傍または学習半径の効率的な幅です。 学習の開始時に、近傍は、隣接するニューロンよりもはるかに大きな空間を対称的な「ベル」で覆います。

この式は距離に依存しているので、また、近傍をダマシる、座標が適切に修正されていません。 したがって、メソッド CSOM::Train から次のソースコード文字列になります。

      for(int i = 0; i < total_nodes; i++)
      {
         double DistToNodeSqr = (m_som_nodes[winningnode].X() - m_som_nodes[i].X()) * (m_som_nodes[winningnode].X() - m_som_nodes[i].X())
                              + (m_som_nodes[winningnode].Y() - m_som_nodes[i].Y()) * (m_som_nodes[winningnode].Y() - m_som_nodes[i].Y());

補完されています:

      bool odd = ((winningnode % m_ycells) % 2) == 1;
      for(int i = 0; i < total_nodes; i++)
      {
        bool odd_i = ((i % m_ycells) % 2) == 1;
        double shiftx = 0;

        if(m_hexCells && odd != odd_i)
        {
          if(odd && !odd_i)
          {
            shiftx = +0.5;
          }
          else // vice versa (!odd && odd_i)
          {
            shiftx = -0.5;
          }
        }
        double DistToNodeSqr = (m_node[winningnode].GetX() - (m_node[i].GetX() + shiftx)) * (m_node[winningnode].GetX() - (m_node[i].GetX() + shiftx))
                             + (m_node[winningnode].GetY() - m_node[i].GetY()) * (m_node[winningnode].GetY() - m_node[i].GetY());

補正 ' shiftx ' の方向は、距離が計算される2つのニューロンがある行の偶数または奇数のプロパティの比率によって異なります。 ニューロンが均等に平準化された行にある場合は、補正はありません。 ウィニングニューロンが奇数行にある場合、偶数行はから右に半分のセルによってシフトとして表示されるため、shiftx は + 0.5 です。 ウィニングニューロンが偶数行にある場合、奇数行は左側のハーフセルによってシフトされているように見え、したがって、shiftx は-0.5 です。

ここでは、次の元の文字列に注意を払うことが特に重要です。

        if(DistToNodeSqr < WS)
        {
          double influence = MathExp(-DIstToNodeSqr / (2 * WS));
          m_node[i].AdjustWeights(data, learning_rate, influence);
        }

実際には、この条件演算子は、1シグマの近傍を越えてニューロンを無視することによる計算の加速を保証します。 しかし、学習品質の面では、ガウス式は理想的であり、そのような介入は不合理です。 あまりにも遠くのニューロンを無視する必要がある場合、１シグマではなく 3シグマです。 隣接する行に位置する近接ニューロン間の距離は sqrt (1 * 0.5 * 0.5) = 1.118、つまり1以上であるため、六角形グリッドの計算を修正した後はさらに重要になります。 アタッチされたソースコードでは、この条件演算子にコメントがあります。 本当に計算を加速する必要がある場合は、オプションを使用します。

        if(DistToNodeSqr < 9 * WS)

注意! 隣接するニューロン間の距離の差における上記のニュアンス上、 (単一行は、1の距離を持っています。隣り合う行を持つものは1.118 です)、 現在はまだ理想的ではなく、さらに完全な異方性を達成するために補正します。

可視化

Kohonen ネットワークは、主に可視のグラフィッベアップに関連付けられているにも関わらず、そのトポロジと学習アルゴリズムは、任意のユーザーインターフェイスなしで完全に動作することができます。 特に、情報の予測や圧縮の問題は、必要な視覚的分析を必要とせず、画像の分類によって結果を数値として提供することができます。 すなわち、クラスの数またはイベントの確率です。 したがって、Kohonen ネットワークの機能は、2つのクラス間で分割されました。 クラス CSOM では、計算、データの読み込みと格納、およびネットワークの読み込みと格納のみが残りました。 加えて、CSOMDisplay の派生クラスが作成され、すべてのグラフィックスが配置されました。 私の意見では、第２の記事で提案された方法よりもシンプルで論理的な階層だと思います。 将来的には、最適なEAパラメータを選択する問題を解決するために CSOMDisplay を使用し、CSOM は予測に使用する予定です。

なお、グリッド型であることに注意すべきです。 すなわち、長方形または六角形であるかどうか、距離の計算に影響を与えるので、基本的なクラスに属します。 データインプットスペースの寸法と同様に、垂直方向および水平向きのノード数とともに、グリッドタイプはアーキテクチャの一部であり、ファイルに保存する必要があります。 ファイルからネットワークをダウンロードする場合は、プログラムの設定からではなく、すべてのパラメータがそこから読み込まれます。 ピクセル単位でのマップサイズ、セルの境界線の表示、キャプション表示など、視覚的な表現にのみ影響を与えるその他の設定は、ネットワークファイルに保存されず、一度教えられたネットワークに繰り返し、ランダムに変更することができます。

更新されたクラスは、コントロールを使用したグラフィカルユーザーインターフェイスではなく、すべての設定が MQL プログラムのインプットによって指定されることに注意してください。 同時に、クラス CSOMDisplay はまだ便利な特徴を実現します。

Kohonen ネットワークの操作方法の前のサンプルでは、MaxPictures という名前のインプットがあったことを思い出してください。 これは新しい実現になります。 メソッド CSOMDisplay::Init に maxpict として渡され、チャートの1行に表示されるネットワーベアップ (プレーン) の数を設定します。 ImageW と ImageH で統一された画像サイズと一緒にこのパラメータを操作すると、すべてのマップが画面に収まるオプションを見つけることができます。 ただし、EAの多くの設定を分析する必要がある場合など、多くのマップがある場合、そのサイズには大幅な削減が必要ですが、これは不便です。 このような場合は、MaxPictures を使用して新しいモードをアクティブにし、パラメータを0に設定します。

このモードでは、マップイメージは、ピクセル座標で OBJ_BITMAP_LABEL に配置されたオブジェクトとしてではなく、タイムスケールに合わせて OBJ_BITMAP オブジェクトとしてチャート上に生成されます。 このようなマップのサイズは、チャートの最大の高さまで増やすことができ、マウスまたはホイールでドラッグするか、キーボードを使用して、共通の水平スクロール足を使用してスクロールできます。 マップの数は、もはや画面サイズに制限されていません。 ただし、足の数が十分であることを確認する必要があります。

マップサイズを増やすことで、特にクラス CSOMDisplay は、必要に応じて、関連する平面のシナプス加重値、ティーチングセットベクトルのヒット数、平均値など、セル内のさまざまな情報を表示することができます。 この情報はデフォルトでは表示されませんが、マウスカーソルを1つのセルまたは別のポジションに置いた場合に表示されるポップアップヒントで常に使用できます。 現在の平面の名前とニューロン座標もポップアップヒントに表示されます。

さらに、任意のニューロンをダブルクリックすると、現在のマップと他のすべてのマップの反転色でそのニューロンが同時に強調表示されます。 これより、すべての関数が同時にニューロンアクティビティを視覚的に比較することができます。

最後に、グラフィック全体が標準クラスの CCanvas に移動されていることに注意してください。 外部依存関係からコードをインプットしますが、副作用もあります: Y 座標は、以前のようにボトムアップではなく、トップダウン方式でカウントされるようになりました。 これより、マップの凡例は、コンポーネント名と値の範囲ではなく、マップの上に表示されます。 ただし、この変更は重要ではないようです。

改良点

適用された問題にアプローチする前に、ニューラルネットワーククラスの改善を行う必要があります。 特定の特徴の2d 空間におけるシナプスの加重を表す標準マップに加えて、Kohonen ネットワークのデファクトスタンダードであるサービスマップの計算と表示を準備します。 今後は、応用実験の段階で多くのものが必要になると思います。

追加の次元のインデックスを定義してみましょう、合計で5つあります。

#define EXTRA_DIMENSIONS 5
#define DIM_HITCOUNT (m_dimension + 0)
#define DIM_UMATRIX  (m_dimension + 1)
#define DIM_NODEMSE  (m_dimension + 2) //ノードごとの量子化誤差: 平均分散 (標準偏差の２乗)
#define DIM_CLUSTERS (m_dimension + 3)
#define DIM_OUTPUT   (m_dimension + 4)

U-Matrix

まず、ネットワーク内の学習過程で生成されたトポロジを評価するために、距離の統一行列である U 行列を計算します。 ネットワーク内の各ニューロンについて、この行列には、このニューロンとその直下の近傍の平均距離が含まれます。 Kohonen network では、フィーチャの多次元空間がマップの2次元空間に表示されるためです。 この2次元空間では折り目が発生します。 言い換えると、初期空間に内在する配置を維持するという Kohonen ネットワークの特性それにも関わらず、2d 空間全体にわたって均等に達成不可能なされ、ニューロンの地理的近接は錯覚になります。 このような領域を検出するために使用するのは、まさに U マトリクスです。 その中で、ニューロンの加重とその近傍の加重との間に大きな差がある領域は "天井 " として表示され、ニューロンが似ている領域は "低地" として見えます。

ニューロンと特徴ベクトルの間の距離を計算するために、メソッド CSOMNode:: CalculateDistance があります。 ベクトル (配列 ' double ') ではなく、別のニューロンへのポインタを取る対応するメソッドを作成します。

double CSOMNode::CalculateDistance(const CSOMNode *other) const
{
  double vector[];
  other.GetCodeVector(vector);
  return CalculateDistance(vector);
}

ここでは、メソッド GetCodeVector は、別のニューロンの加重の配列を取得し、共通の方法で距離を計算するためにすぐに送信します。

統合ニューロンの距離を取得するには, すべての隣接するニューロンへの距離を計算し、平均する必要があります。. 隣接ニューロンの走査は、ネットワークグリッドを用いた操作に共通のタスクであるため、トラバースの基底クラスを作成し、その子孫に個々のアルゴリズムを実装します (距離の合計を含む)。

#define NBH_SQUARE_SIZE    4
#define NBH_HEXAGONAL_SIZE 6

template<typename T>
class Neighbourhood
{
  protected:
    int neighbours[];
    int nbhsize;
    bool hex;
    int m_ycells;

  public:
    Neighbourhood(const bool _hex, const int ysize)
    {
      hex = _hex;
      m_ycells = ysize;

      if(hex)
      {
        nbhsize = NBH_HEXAGONAL_SIZE;
        ArrayResize(neighbours, NBH_HEXAGONAL_SIZE);
        neighbours[0] = -1; // up (visually)
        neighbours[1] = +1; // down (visually)
        neighbours[2] = -m_ycells; //左
        neighbours[3] = +m_ycells; //右
        /* テンプレートは、以下のループに動的に適用されます
        //奇数行
        neighbours[4] = -m_ycells - 1; // left-up
        neighbours[5] = -m_ycells + 1; // left-down
        //偶数行
        neighbours[4] = +m_ycells - 1; // right-up
        neighbours[5] = +m_ycells + 1; // right-down
        */
      }
      else
      {
        nbhsize = NBH_SQUARE_SIZE;
        ArrayResize(neighbours, NBH_SQUARE_SIZE);
        neighbours[0] = -1; // up (visually)
        neighbours[1] = +1; // down (visually)
        neighbours[2] = -m_ycells; //左
        neighbours[3] = +m_ycells; //右
      }
    
    }
    ~Neighbourhood()
    {
      ArrayResize(neighbours, 0);
    }

    T loop(const int ind, const CSOMNode &p_node[])
    {
      int nodes = ArraySize(p_node);
      int j = ind % m_ycells;
      
      if(hex)
      {
        int oddy = ((j % 2) == 1) ? -1 : +1;
        neighbours[4] = oddy * m_ycells - 1;
        neighbours[5] = oddy * m_ycells + 1;
      }
      
      reset();

      for(int k = 0; k < nbhsize; k++)
      {
        if(ind + neighbours[k] >= 0 && ind + neighbours[k] < nodes)
        {
          //エッジの折り返しをスキップ
          if(j == 0) //上の行
          {
            if(k == 0 || k == 4) continue;
          }
          else if(j == m_ycells - 1) // bottom row
          {
            if(k == 1 || k == 5) continue;
          }
          
          iterate(p_node[ind], p_node[ind + neighbours[k]]);
        }
      }
      
      return getResult();
    }
    
    virtual void reset() = 0;
    virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) = 0;
    virtual T getResult() const = 0;
};

コンストラクタに渡されるグリッドの種類に応じて、近傍の数、nbhsize、4と6に等しいと見なされます。 隣接ニューロンの数のインクリメントは、現在のニューロンに関連して、配列 ' 近傍' によって格納されます。 たとえば、正方形のグリッドでは、上位の近傍は、ニューロン番号に unity を追加することによって、下の近傍からの一致を差し引くことによって得られます。 左と右の近傍には、グリッド列の高さによって異なる数値があるため、この値は ysize としてコンストラクタに渡されます。

ネイバーの実際のトラバースは、メソッド ' loop ' によって実行されます。 クラス近傍にはニューロンの配列が含まれていないため、メソッド ' loop ' にパラメータとして渡されます。

ループ内のこのメソッドは、配列 ' 近傍 ' を横切って、さらに増加を考慮して、隣接ルータの数がグリッドを超えないことをチェックします。 すべての有効な数値について、現在のニューロンと周囲のニューロンの1つへのリンクが渡されるところで、抽象メソッド ' 繰り返し ' が呼び出されます。

ループの前に抽象メソッド ' reset ' が呼び出され、ループの後に抽象メソッド getResult が呼び出されます。 3つの抽象メソッドのセットを使用すると、子孫クラスで近傍ノードの列挙を準備して実行し、結果を生成できます。 ' loop ' メソッド構築の概念は、既知の OOP 設計パターン— Template Method に対応します。 ここでは、テンプレート1であるため、クラス近傍でも使用されているテンプレートの言語パターンから、パターンの独自の名前で「テンプレート」の用語を区別する必要があります。 すなわち、特定の変数型 t によってパラメータ化されます。特に、' loop ' メソッド自体とメソッド getResult は、t 型の値を返します。

クラス近傍に基づいて、U 行列を計算するクラスを記述します。

class UMatrixNeighbourhood: public Neighbourhood<double>
{
  private:
    int n;
    double d;
    
  public:
    UMatrixNeighbourhood(const bool _hex, const int ysize): Neighbourhood(_hex, ysize)
    {
    }
    
    virtual void reset() override
    {
      n = 0;
      d = 0.0;
    }
    
    virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) override
    {
      d += node1.CalculateDistance(&node2);
      n++;
    }
    
    virtual double getResult() const override
    {
      return d / n;
    }
};

タスクタイプはダブルです。 基本的なクラスを通して、距離の計算は透明です。

メソッド CSOM:: CalculateDistances でマップ全体の距離を計算します。

void CSOM::CalculateDistances()
{
  UMatrixNeighbourhood umnh(m_hexCells, m_ycells);
  
  for(int i = 0; i < m_xcells * m_ycells; i++)
  {
    double d = umnh.loop(i, m_node);
    
    if(d > m_max[DIM_UMATRIX])
    {
      m_max[DIM_UMATRIX] = d;
    }
    
    m_node[i].SetDistance(d);
  }
}

統合距離の値は、ニューロンのオブジェクトに保存されます。 後で、すべての平面を表示するとき、追加の寸法、DIM_UMATRIXが計算に含まれているカラーパレットを使用して、標準的な方法で距離値を定義することができるようになります。 パレットを正しくスケーリングするために、このメソッドでは、配列 m_max の関連要素内の距離の高値を保存します (すべての実現原則は以前の実現から変更されません)。

ヒット数と量子化エラー

次の追加の次元は、特定のニューロンにおける学習ベクトルのヒット数の統計を収集します。 言い換えると、適用されたデータのニューロンに移入する密度でもあります。 特定のニューロンの方が高いほど、その加重係数は統計的に妥当です。 このネットワークでは、マイナーまたはゼロのデータカバレッジを持つニューロンが発生する可能性があります。 ネットワークサイズを選択するか、多次元空間の2d 投影でトポロジをねじる問題にすることができます。 特定のニューロンへのサンプルのヒットは、次のメソッドによって計算されます。

void CSOMNode::RegisterPatternHit(const double &vector[])
{
  m_hitCount++;
  double e = 0;
  for(int i = 0; i < m_dimension; i++) 
  {
    m_sum[i] += vector[i];
    m_sumP2[i] += vector[i] * vector[i];
    e += (m_weights[i] - vector[i]) * (m_weights[i] - vector[i]);
  }
  m_mse += e / m_dimension;
}

カウント自体は、内部カウンタが増加する m_hitCount + + の最初の文字列で実行されます。 残りのコードは、以下で説明する他の有用なタスクを実行します。

クラス CSOM から学習の完了時にメソッド RegisterPatternHit を呼び出し、各ベクトルの統計処理の特別な方法を作成します。

double CSOM::AddPatternStats(const double &data[])
{
  static double vector[];
  ArrayCopy(vector, data);
  
  int ind = GetBestMatchingIndex(vector);
  
  m_node[ind].RegisterPatternHit(vector);

  double code[];
  m_node[ind].GetCodeVector(code);
  Denormalize(code);
  
  double mse = 0;
  
  for(int i = 0; i < m_dimension; i++)
  {
    mse += (data[i] - code[i]) * (data[i] - code[i]);
  }
  
  mse /= m_dimension;
  
  return mse;
}

脱線として、ここで使用するメソッド GetBestMatchingIndex は、GetBestMatchingXYZ のメソッドのグループから他のものと同様に、自身の内部の受信データを正規化し、ベクトルのコピーを渡すことが必要であることに留意すべきです。 そうしないと、呼び出し元のコードでソースデータのあいまいな変更が可能になります。

このメソッドは、ヒットの再コーディングと共に、現在のニューロンと渡されたベクトルの量子化誤差も計算します。 このために、ウィニングニューロンから、いわゆるコードベクトルが呼び出されます。 すなわち、シナプスの加重の配列、および加重とインプットベクトルの間の成分的な差の平方和が計算されます。

AddPatternStatsm は、他のメソッドである CSOM:: CalculateStats からすぐに呼び出され、すべてのインプットに対してループを配置するだけです。

double CSOM::CalculateStats(const bool complete = true)
{
  double data[];
  ArrayResize(data, m_dimension);
  double trainedMSE = 0.0;
  
  for(int i = complete ? 0 : m_validationOffset;< m_nSet; i++) m_nset;=""></ m_nSet; i++)>
  {
    ArrayCopy(data, m_set, 0, m_dimension * i, m_dimension);
    trainedMSE += AddPatternStats(data, complete);
  }
  
  double nmse = trainedMSE / m_dataMSE;
  if(complete) Print("Overall NMSE=", nmse);

  return nmse;
}

このメソッドは、すべての量子化エラーを合計し、m_dataMSE のインプットデータ分散と比較します。検証と学習ストップの文脈の中で説明されているまさに強化の計算です。 このメソッドは、学習および検証のサブセットによってインプットデータセットを分割するかどうかに基づいて、オブジェクト CSOM の作成で指定された変数 m_validationOffset について言及します。

これを推測し、メソッド CalculateStats は、(収束フェーズがすでに開始されている場合)、Trainメソッドの中で各エポックで呼ばれる、全体的なネットワークエラーが増加し始めているかどうかを返す値によって判断することができます。 すなわち、ストップする時間であるかどうか判断できます。

m_dataMSE の分散は、以下の方法を使用して、事前に計算されます。

void CSOM::CalculateDataMSE()
{
  double data[];

  m_dataMSE = 0.0;
  
  for(int i = m_validationOffset; i < m_nSet; i++)
  {
    ArrayCopy(data, m_set, 0, m_dimension * i, m_dimension);

    double mse = 0;
    for(int k = 0; k < m_dimension; k++)
    {
      mse += (data[k] - m_mean[k]) * (data[k] - m_mean[k]);
    }
    
    mse /= m_dimension;
    m_dataMSE += mse;
  }
}

データ正規化段階では、各成分の平均値 m_mean を取得します。

void CSOM::InitNormalization(const bool normalization = true)
{
  ArrayResize(m_max, m_dimension + EXTRA_DIMENSIONS);
  ArrayResize(m_min, m_dimension + EXTRA_DIMENSIONS);
  ArrayInitialize(m_max, 0);
  ArrayInitialize(m_min, 0);
  ArrayResize(m_mean, m_dimension);
  ArrayResize(m_sigma, m_dimension);

  for(int j = 0; j < m_dimension; j++)
  {
    double maxv = -DBL_MAX;
    double minv = +DBL_MAX;
    
    if(normalization)
    {
      m_mean[j] = 0;
      m_sigma[j] = 0;
    }
    
    for(int i = 0; i < m_nSet; i++)
    {
      double v = m_set[m_dimension * i + j];
      if(v > maxv) maxv = v;
      if(v < minv) minv = v;
      if(normalization)
      {
        m_mean[j] += v;
        m_sigma[j] += v * v;
      }
    }
    
    m_max[j] = maxv;
    m_min[j] = minv;
    
    if(normalization && m_nSet > 0)
    {
      m_mean[j] /= m_nSet;
      m_sigma[j] = MathSqrt(m_sigma[j] / m_nSet - m_mean[j] * m_mean[j]);
    }
    else
    {
      m_mean[j] = 0;
      m_sigma[j] = 1;
    }
  }
}

追加の平面に回すと、CSOMNode:: RegisterPatternHit で計算したときに、各ニューロンは次のメソッドを使用して関連する統計情報を返すことができることに注意してください。

int CSOMNode::GetHitsCount() const
{
  return m_hitCount;
}

double CSOMNode::GetHitsMean(const int plane) const
{
  if(m_hitCount == 0) return 0;
  return m_sum[plane] / m_hitCount;
}

double CSOMNode::GetHitsDeviation(const int plane) const
{
  if(m_hitCount == 0) return 0;
  double z = m_sumP2[plane] / m_hitCount - m_sum[plane] / m_hitCount * m_sum[plane] / m_hitCount;
  if(z < 0) return 0;
  return MathSqrt(z);
}

double CSOMNode::GetMSE() const
{
  if(m_hitCount == 0) return 0;
  return m_mse / m_hitCount;
}

このように、ニューロンによるインプットベクトルの表示数と量子化誤差によって、2つの平面を埋めるためのデータを取得します。

ネットワーク応答

次に追加される平面は、特定のサンプルに対する利回りマップとネットワーク応答になります。 これをリコールする必要があります。ネットワークにシグナルを供給するとき、ウィニングニューロンと一緒に、他のすべてのニューロンは、より少ない程度に活性化されます。 アクティブな応答のエクスカーションを比較する可能性は、ネットワークによって提案されたソリューションの安定性を定義するのに役立ちます。

ネットワーク応答の計算は最大限に簡単です。 クラス CSOMNode では、次のメソッドを記述します。

double CSOMNode::CalculateOutput(const double &vector[])
{
  m_output = CalculateDistance(vector);
  return m_output;
}

そして、ネットワーククラス内の各ニューロンに呼び出します。

void CSOM::CalculateOutput(const double &vector[], const bool normalize = false)
{
  double temp[];
  ArrayCopy(temp, vector);
  if(normalize) Normalize(temp);
  m_min[DIM_OUTPUT] = DBL_MAX;
  m_max[DIM_OUTPUT] = -DBL_MAX;
  for(int i = 0; i < ArraySize(m_node); i++)
  {
    double x = m_node[i].CalculateOutput(temp);
    if(x < m_min[DIM_OUTPUT]) m_min[DIM_OUTPUT] = x;
    if(x > m_max[DIM_OUTPUT]) m_max[DIM_OUTPUT] = x;
  }
}

テストベクトルがプログラムに提供されていない場合、応答はデフォルトで、すなわちゼロベクトルに対して計算されます。

クラスタ化

最後に、考慮される平面の最後、しかし、おそらく最も重要なものは、クラスターマップになります。 2次元マップ上のインプットデータの配置は、全体の半分にすぎません。 分析の本当の目的は、関数を検出し、アプリケーションの観点から理解しやすいクラスに分類することです。 特徴空間の寸法が比較的小さい場合、個々の平面上の色付きの斑点によって必要な特性を持つ領域を容易に区別することができ、スポットは通常孤立します。 しかし、インプットデータ構造の拡大に伴い、画像はより複雑になり、異なるインデックスを持つダースのマップをクロス分析する代わりに、1つのマップを注意を要する領域に分割する方がはるかに便利です。

インタラクションは、類似した特性を持つエリアによってマップをマーキングし、クラスターの中心を識別することになります。 その後、統計の観点から、関連するクラスのサンプルとして、最も代表的なものと見なすことができます。 ここで、最適なEAパラメータを選択するタスクに徐々に近づいています。 ただし、クラスタを実装する必要があります。

K-Means

多くのクラスタメソッドがあります。 MQL5 の最も簡単なオプションは、標準ライブラリに含まれているバージョンの ALGLIB を使用することです。 これは、ヘッダーファイルをインクルードするだけで十分です。

#include <Math/Alglib/dataanalysis.mqh>

次のようなメソッドを記述します。

void CSOM::Clusterize(const int clusterNumber)
{
  int count = m_xcells * m_ycells;
  CMatrixDouble xy(count, m_dimension);
  int info;
  CMatrixDouble clusters;
  int membership[];
  double weights[];
  
  for(int i = 0; i < count; i++)
  {
    m_node[i].GetCodeVector(weights);
    xy[i] = weights;
  }

  CKMeans::KMeansGenerate(xy, count, m_dimension, clusterNumber, KMEANS_RETRY_NUMBER, info, clusters, membership);
  Print("KMeans result: ", info);
  if(info == 1) // ok
  {
    for(int i = 0; i < m_xcells * m_ycells; i++)
    {
      m_node[i].SetCluster(membership[i]);
    }
    
    ArrayResize(m_clusters, clusterNumber * m_dimension);
    for(int j = 0; j < clusterNumber; j++)
    {
      for(int i = 0; i < m_dimension; i++)
      {
        m_clusters[j * m_dimension + i] = clusters[i][j];
      }
    }
  }
}

アルゴリズム K-Means を使用してインタラクションを実行します。 残念ながら、私の知る限りでは、元のライブラリの最新バージョンは、凝集型階層クラスタリングなどの他のものを提供していますが、MQL5 の ALGLIB バージョンでは一つしかありません。

"残念なことに、アルゴリズムの K-平均は、 " 直線 "であるため、その本質は、最も効率的な方法でサンプリングポイントをカバーする地物の空間内のスフェロイドの所与の数の中心を検索するために減少します。 すなわち、クラスター中心からのポイントまでの距離の平方和の最小値です。 問題は、固定された形態に、スフェロイドが非線形クラスターの分離性に関して特定の制限を有することです。 原則として、K 平均法は、異なる向きおよび形態の楕円体を操作するアルゴリズム期待値最大化の特殊なケースです。 しかし、これを使用している場合でも、両方のアルゴリズムが凸型を使用し、クラスタの中心のみをランダムに配置するため、局所的な最小値に固執する確率があります。 デメリットには、事前にクラスタの数を指定する必要があるという事実もあります。

しかし、インタラクションが ALGLIB で K-平均を用いてどのように配置されるかを考えてみましょう。 主な操作は、メソッド CKMeans:: KMeansGenerate によって実行されます。 特別なオブジェクトベースのフォーマット (CMatrixDouble xy)、ベクトルの数 (数)、特徴空間 (m_dimension) の次元、および希望のクラスタ数 (clusterNumber) のソースデータを持つ配列を渡し、後者は、MQL プログラムのパラメータです。 次のインプット KMEANS_RETRY_NUMBER は、ランダムに選択された異なる初期の中心を持つアルゴリズムによって行われる繰り返しの数であり、ローカルの解を回避します。 今回では、10に等しいマクロです。 関数操作の結果として、「info」という名前の実行コード (成功またはエラーを示す異なる値)、クラスター座標を持つ CMatrixDouble クラスターという名前のオブジェクトベースの配列、およびメンバであるインプットの配列を取得します。

マップ上でマークするために、配列 m_clusters にクラスターの中心を保存し、また、クラスター内のそのメンバシップに関連する色で各ニューロンを色付けします。

m_node[i].SetCluster(membership[i]);

ALGLIB を使用する場合は、特殊な静的オブジェクトの内部ステータスを考慮する独自の乱数ジェネレーターを使用することに注意してください。 したがって、MathSrand を通じて標準ジェネレーターを初期化しても、その状態はリセットされません。 設定を変更するときにグローバルオブジェクトが再生成されないため、EAにとって特に重要です。 結果として、CMath:: m_state が OnInit でゼロにリセットされない場合、計算結果の再現性が ALGLIB で困難になることがあります。

K −手段の上記の欠点を考慮すると、代替インタラクション法を有することが望ましいです。 1つの代替ソリューションは明白です。

代替法

Kohonen マップ、特に導入している追加の次元に注意を向けます。 U マトリックスは特に興味深いものです。 この平面は、最も近いニューロンの領域を示しています。すなわち, 2d マップトポロジの観点から、特徴空間の点で、両方の点で近いです。 記憶しているように、U 行列の一種の「低地」のようなニューロンです。 クラスターになるための偉大な候補者です。

たとえば、次の方法で、統一された距離のマップをクラスターに変換できます。

すべてのニューロンの情報を配列にコピーし、U 距離 (CSOMNode:: GetDistance) の値で昇順に並べ替えます。

特定のニューロンについては、隣接するニューロンがクラスターに属しているかどうかにかかわらず、配列によってループをチェックします。

• そうでない場合は、新しいクラスターを作成し、現在のニューロンを割り当てます。 クラスターは、最小の U 距離と一致し、さらに重要度が降順であるため、最も "重要 " クラスターに対応するゼロインデックスから開始されることに注意してください。 U-距離に関しては、連続した各クラスタはより少ないコンパクトになります。
• 隣接するニューロンの中にクラスターでマークされたものがある場合、中から最も高いものを選択します。 すなわち、最も低いインデックスを持つもので、現在のニューロンをそのクラスターに割り当てます。

これは簡単です。 密度を移入するニューロンも考慮すべきではありません? 結局のところ、U-距離は異なるヒット数を持つニューロンに対して異なる方法でサポートされています。 換言すれば、2つのニューロンが同じ U-距離を有する場合、うちの1つは、より多くのサンプルが表示されている、より低い数を有するニューロンの利点を有していなければなりません。

次に、式 CSOMNode の値のオーダーで記述されたアルゴリズムの初期配列ソートを変更するだけで十分です。CSOMNode::GetDistance() / sqrt(CSOMNode::GetHitsCount()) 大きな場合には、その影響を滑らかにするために平方根を追加しました。

ただし、2つのサービスプレーンを使用している場合は、3番目を分析するのが妥当かもしれません。 量子化誤差はあるでしょうか。 実際、量子化誤差が特定のニューロンにおいて大きいほど、小さい U 距離の情報を信頼すべきであり、その逆も同様です。

量子化エラーの関数がどのように表示されるか:

double CSOMNode::GetMSE() const
{
  if(m_hitCount == 0) return 0;
  return m_mse / m_hitCount;
}

その後、ヒットの m_hitCount カウンタが使用されていることに注意してください (分母のみ)。 したがって、ニューロンの配列を CSOMNode としてソートするための前の式を書き直すことができます:: GetDistance() * MathSqrt (CSOMNode::。GetMSE()) —その後、3つの追加インデックスがすべて考慮されますが、 Kohonen ネットワークの実現に追加されました。

最終的な形で代替インタラクションアルゴリズムを提示するほぼ準備ができていますが、1つマイナーなものが残っています。 ニューロン配列によるループ内では、隣接するクラスターの存在について現在のニューロンの近傍をチェックする必要があります。 少し前に、ローカルの見落とすためのテンプレートクラス、近傍を実装しました。 次に、クラスタの検索に焦点を当てた子孫を作成します。

class ClusterNeighbourhood: public Neighbourhood<int>
{
  private:
    int cluster;

  public:
    ClusterNeighbourhood (const bool _hex、 const int ysize): 近傍 (_hex、ysize)
    {
    }
    
    virtual void reset() override
    {
      cluster = -1;
    }
    
    virtual void iterate(const CSOMNode &node1, const CSOMNode &node2) override
    {
      int x = node2.GetCluster();
      if(x > -1)
      {
        if(cluster != -1) cluster = MathMin(cluster, x);
        else cluster = x;
      }
    }
    
    virtual int getResult() const override
    {
      return cluster;
    }
};

このクラスには、潜在的なクラスターの数が含まれています (数値は整数であるため、int 型でテンプレートをパラーメータします)。 初期状態では、この変数は reset メソッド内で-1 で初期化されます。 すなわち、クラスタはありません。 次に、親クラスのループメソッドからの呼び出しで、新しい実現 ' 繰り返し '、各隣接ニューロンのクラスター番号を取得し、クラスターと比較し、最小値を保存します。 同じ、または-1 (クラスターが見つからない場合) は、getResult のメソッドによって返されます。

改善として、ニューロン間の「天井高さ」を追跡することを提案します。 すなわち、ノード a の値。CalculateDistance (& node 2)) を実行して、「高さ」が以前よりも低い場合にのみ、1つのニューロンから別のものに「流れる」クラスタ番号を行います。 最終的な実現バージョンは、ソースコードに示されています。

最後に、代替インタラクションを実装することができます。

void CSOM::Clusterize()
{
  double array[][2];
  int n = m_xcells * m_ycells;
  ArrayResize(array, n);
  for(int i = 0; i < n; i++)
  {
    if(m_node[i].GetHitsCount() > 0)
    {
      array[i][0] = m_node[i].GetDistance() * MathSqrt(m_node[i].GetMSE());
    }
    else
    {
      array[i][0] = DBL_MAX;
    }
    array[i][1] = i;
    m_node[i].SetCluster(-1);
  }
  ArraySort(array);
  
  ClusterNeighbourhood clnh(m_hexCells, m_ycells);

  int count = 0; //クラスターの数
  ArrayResize(m_clusters, 0);
  
  for(int i = 0; i < n; i++)
  {
    //既に割り当てられている場合はスキップ
    if(m_node[(int)array[i][1]].GetCluster() > -1) continue;
    
    //現在のノードが既存のクラスタに隣接しているかどうかを確認する
    int r = clnh.loop((int)array[i][1], m_node);
    if(r > -1) //近傍はすでにクラスタに属しています
    {
      m_node[(int)array[i][1]].SetCluster(r);
    }
    else //新しいクラスターが必要
    {
      ArrayResize(m_clusters, (count + 1) * m_dimension);
      
      double vector[];
      m_node[(int)array[i][1]].GetCodeVector(vector);
      ArrayCopy(m_clusters, vector, count * m_dimension, 0, m_dimension);
      
      m_node[(int)array[i][1]].SetCluster(count++);
    }
  }
}

このアルゴリズムは、上記で説明されている言語の擬似コードを実質的に完全に従います: 2 次元配列 (最初の次元の数式からの値と2番目のニューロンインデックス) をインプットし、並べ替え、ループ内のすべてのニューロンを参照します。

インタラクションの品質は、もちろん、実際に評価されるべきです。 しかし、古典的なインタラクション法のほとんどが問題を抱えており、提案されたものに対して容易に劣っていることを考えると、新しい解決策は魅力的に見えます。

この実現の利点の中で、クラスタが重要性によって調整されるという事実があり (上記の K 平均、クラスタは等しい)、形はランダムであり、数は事前に定義される必要はありません。 直近のものは、逆側があることに留意すべきです。 すなわち、クラスターの数はかなり大きくすることができます。 沿って、コンテンツ類似性の度合いと最小誤差によるクラスタの配置は、実質的に最初の5-10 クラスタのみを考慮し、他のものを「舞台裏」に残すことを可能にします。

任意のオープンソースで同様のインタラクションメソッドを見つけていないので、U マトリクスと量子化誤差 (QE) に基づいて、Korotky インタラクション、またはより長いが、まともなショートパスインタラクションに名前をつけることを提案します。

先に実行して、多くのテストにおいて、アルゴリズム K 平均によって発見されたクラスターセンターが代替インタラクションよりも悪い結果を提供した (少なくとも最適化結果の分析の問題において) ことを実質的に強化したと言うべきです。 したがって、インタラクションのその方法のみを以下に適用します。

テスト

さて、理論から実践に移り、ネットワークがどのように動作するかをテストしましょう。 基本的な関数を実証するオプションを備えた、シンプルで普遍的なEAを作成しましょう。 SOM-Explorerという名前にします。

上記のクラスのヘッダーファイルを含めてみましょう。 インプットを定義します。

Group —ネットワーク構造とデータ設定

• DataFileName —ティーチングまたはテスト用のデータを含むテキストファイルの名前。クラス CSOM は csv 形式をサポートしていますが、他のEAの設定を最適化する分析は「賭け」であるため、EA自体にセットファイルの読み取りを追加します。インプットを含むファイルが指定されている場合、その名前は、ネットワークを保存するためにも使用しますが、別の拡張子 (下記参照)。csv 拡張子を示すかしないことができます。そして、名前は MQL5/ファイル内のフォルダを含むことができます。
  
  
• NetFileName —拡張 som を持つ独自の形式のバイナリファイルの名前。クラス CSOM では、このようなファイルのネットワークを保存して読み取ることができます。格納するデータの構造を変更する必要がある場合は、ファイルの先頭に記述されている署名のバージョン番号を変更します。NetFileName が空の場合、EAは学習モードで動作し、ネットワークが指定されている場合はテストモードです。 すなわち、インプットを ready ネットワークに表示します。som 拡張子を指定することもできます。そして、名前は MQL5/ファイル内のフォルダを含むことができます。
  
  
• DataFileName と NetFileName の両方が空の場合、EAはランダムな3d データのデモンストレーションセットを生成し、その上で学習を行います。
  
  
• NetFileName 内のネットワーク名が正しい場合は、「?」文字だけなど、既存でないファイルの名前を DataFileName に指定することができ、EAはネットワークファイルに保存されている定義範囲のテストデータのランダムサンプルを生成します (ネットワークが動作モードで未知のデータを正しく正規化するために、この情報が必要であること。定義の別の範囲からの値でネットワークインプットを供給することは、もちろん、結果を信頼できません。たとえば、ドローダウンの負の値または取引の数が提供される場合、ネットワークが正常に動作することを期待することは困難です。
  
  
• CellsX —グリッドの水平サイズ (ニューロンの数)、デフォルトでは10.
  
  
• CellsY —グリッド (ニューロンの数) の場合は垂直サイズ、デフォルトでは10.
  
  
• HexagonalCell —六角形のグリッドを使用する関数は、デフォルトでは「真」です。長方形のグリッドの場合は、「false」に切り替えます。
  
  
• UseNormalization —インプットの正規化を有効または無効にします。デフォルトでは ' true ' であり、無効にしないことをお勧めします。
  
  
• EpochNumber —学習エポックの数。デフォルトでは100.
  
  
• ValidationSetPercent —インプットの合計数に対する検証選択のサイズ (パーセンテージ)。デフォルトでは0です。 すなわち、検証が無効になっています。使用する場合、推奨値は約10です。
  
  
• ClusterNumber —クラスターの数。デフォルトで1で、アダプティブインタラクションを意味します。値0はインタラクションを無効にします。0より上の値は、K-平均法を使用してインタラクションを起動します。インタラクションは学習直後に行われます。クラスタはネットワークファイルに保存されます。

Group - ビジュアライゼーション

• ImageW —デフォルトでは、各マップ (プレーン) のピクセル単位の水平サイズ500.
  
  
• ImageH —デフォルトでは、各マップ (プレーン) のピクセル単位の垂直サイズ500.
  
  
• MaxPictures —行内のマップの数。デフォルトでは0で、スクロールオプションを使用して連続した行にマップを表示するモードを意味します (大きな画像が許可されています)。MaxPictures が0より上にある場合、平面のセット全体が複数の行に表示され、それぞれがマップの MaxPictures が配置されます (小さな縮尺ですべてのマップを同時に表示する場合に便利です)。
  
  
• ShowBorders —ニューロン間の境界線の描画を有効/無効にします。デフォルトでは ' false ' です。
  
  
• ShowTitles —有効化/無効化ニューロン特性を持つテキストの表示は、デフォルトでは「真」です。
  
  
• ColorScheme —4つの配色のいずれかを選択します。デフォルトでは Blue_Green_Red (最もカラフルなもの) です。
  
  
• ShowProgress —学習中にネットワークイメージを動的に更新することを有効/無効にします。1秒ごとに実行されます。デフォルトでは ' true ' です。

Group - オプション

• RandomSeed —乱数ジェネレーターを初期化するための整数。デフォルトでは0です。
• SaveImages —完了時にネットワークイメージを保存するオプション。また、学習後と最初の起動後に使用することができます。デフォルトでは ' false ' です。

基本的な設定だけです。 問題を解決し続けるように、他の特定のパラメータを追加します。

注意! このEAは、現在のチャートの設定を変更します—このEAのみを扱うための専用の新しいチャートを開きます。

CSOMDisplay クラスオブジェクトは、EA内のすべてのタスクを実行します。

CSOMDisplay KohonenMap;

初期化中に、マウス移動イベント処理を有効にすることを忘れないでください-クラスは、ポップアップヒントを表示し、スクロールするために使用します。

void OnInit()
{
  ChartSetInteger(0, CHART_EVENT_MOUSE_MOVE, true);
  EventSetMillisecondTimer(1);
}

void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
{
  KohonenMap.OnChartEvent(id, lparam, dparam, sparam);
}

ニューラルネットワークアルゴリズム (学習またはテスト) は、EAでタイマーによって一度だけ起動され、その後タイマーは無効になります。

void OnTimer()
{
  EventKillTimer();
  
  MathSrand(RandomSeed);
  
  bool hasOneTestPattern = false;
  
  if(NetFileName != "")
  {
    if(!KohonenMap.Load(NetFileName)) return;
    KohonenMap.DisplayInit(ImageW, ImageH, MaxPictures, ColorScheme, ShowBorders, ShowTitles);

    Comment("Map ", NetFileName, " is loaded; size: ", KohonenMap.GetWidth(), "*", KohonenMap.GetHeight(), "; features: ", KohonenMap.GetFeatureCount());

ネットワークの準備ができているファイルが指定されている場合、ロードし、視覚的な設定に従ってディスプレイを準備します。

    if(DataFileName != "")
    {
      if(!KohonenMap.LoadPatterns(DataFileName))
      {
        Print("Data loading error, file: ", DataFileName);

        //ランダムなテストベクトルを生成する
        int n = KohonenMap.GetFeatureCount();
        double min, max;
        double v[];
        ArrayResize(v, n);
        for(int i = 0; i < n; i++)
        {
          KohonenMap.GetFeatureBounds(i, min, max);
          v[i] = (max - min) * rand() / 32767 + min;
        }
        KohonenMap.AddPattern(v, "RANDOM");
        Print("Random Input:");
        ArrayPrint(v);
        double y[];
        CSOMNode *node = KohonenMap.GetBestMatchingFeatures(v, y);
        Print("Matched Node Output (", node.GetX(), ",", node.GetY(), "); Hits:", node.GetHitsCount(), "; Error:", node.GetMSE(),"; Cluster N", node.GetCluster(), ":");
        ArrayPrint(y);
        KohonenMap.CalculateOutput(v, true);
        hasOneTestPattern = true;
      }
    }

テストの詳細を含むファイルが指定されている場合は、ロードします。 動作しない場合は、ログにメッセージを表示し、ランダムテストデータサンプル v を生成します。数 (ベクトルの寸法) とその許容範囲は、GetFeatureCount と GetFeatureBounds を用いて定義されなければならない。 次に、AddPattern を呼び出すことによって、サンプルはランダムの名前でワーキングデータセットに追加されます。

この方法は、データベースなどのサポートされていない形式を持つデータソースからの学習選択を形成し、インジケータから直接埋めるのに適します。 原則として、この特定のケースでは、ワーキングセットにサンプルを追加する必要があるのは、後でマップ上で視覚化するためだけです (下図) が、ネットワーク内で最も適したニューロンを見つけるには1つの call GetBestMatchingFeatures だけで十分です。 利用可能な GetBestMatchingXYZ の中からこのメソッドは、配列 y でウィニングニューロンの特徴の関連する値を取得することができます。 最後に、CalculateOutput を使用して、テストサンプルへのネットワーク応答を追加の平面で表示します。

引き続きEAコードに従います。

  }
  else //net ファイルが提供されていないため、トレーニングが想定されています
  {
    if(DataFileName == "")
    {
      //スケーリングされの値を使用して3-d デモベクトルを生成します{[0,+1000], [0,+1], [-1,+1]}。
      //正規化の有無にかかわらず結果を比較するために
      //Nb。 NB. タイトルは BMP の有効なファイル名でなければなりません
      string titles[] = {"R1000", "R1", "R2"};
      KohonenMap.AssignFeatureTitles(titles);
      double x[3];
      for(int i = 0; i < 1000; i++)
      {
        x[0] = 1000.0 * rand() / 32767;
        x[1] = 1.0 * rand() / 32767;
        x[2] = -2.0 * rand() / 32767 + 1.0;
        KohonenMap.AddPattern(x, StringFormat("%f %f %f", x[0], x[1], x[2]));
      }
    }

学習ネットワークが指定されていない場合は、学習モードを想定します。 インプットがあるかどうかを確認します。 そうでない場合は、最初の成分が [0, + 1000] の範囲内にあり、2番目のコンポーネントが [ゼロ、+ 1]、3番目の要素が [-1, + 1] 内にあるランダムな3次元ベクトルのセットを生成します。 コンポーネントの名前は AssignFeatureTitles を使用してネットワークに渡され、データは AddPattern を使用して既に知られています。

    else //データファイルが提供されます。
    {
      if(!KohonenMap.LoadPatterns(DataFileName))
      {
        Print("Data loading error, file: ", DataFileName);
        return;
      }
    }

ファイルからのインプットの場合は、このファイルをロードします。 エラーが発生した場合は、ネットワークまたはデータがないため、タスクを終了します。

さらに、ティーチングとインタラクションを行います。

    KohonenMap.Init(CellsX, CellsY, ImageW, ImageH, MaxPictures, ColorScheme, HexagonalCell, ShowBorders, ShowTitles);
    
    if(ValidationSetPercent > 0 && ValidationSetPercent < 50)
    {
      KohonenMap.SetValidationSection((int)(KohonenMap.GetDataCount() * (1.0 - ValidationSetPercent / 100.0)));
    }

    KohonenMap.Train(EpochNumber, UseNormalization, ShowProgress);

    if(ClusterNumber > 1)
    {
      KohonenMap.Clusterize(ClusterNumber);
    }
    else
    {
      KohonenMap.Clusterize();
    }
  }

個々のテストサンプルの分析が指定されていない場合 (特に、学習直後)、デフォルトではゼロを持つベクトルに対するネットワーク応答を形成します。

  if(!hasOneTestPattern)
  {
    double vector[];
    ArrayResize(vector, KohonenMap.GetFeatureCount());
    ArrayInitialize(vector, 0);
    KohonenMap.CalculateOutput(vector);
  }

次に、グラフィカルリソースの内部バッファ (最初の色) にすべてのマップを描画します。

  KohonenMap.Render(); //内部 BMP バッファへのマップの描画

そして、キャプション:

  if(hasOneTestPattern)
    KohonenMap.ShowAllPatterns();
  else
    KohonenMap.ShowAllNodes(); //BMP バッファ内のセルにラベルを描画する

クラスターのマーキング:

  if(ClusterNumber != 0)
  {
    KohonenMap.ShowClusters(); //クラスターのマーク
  }

チャート上のバッファを表示し、必要に応じて、画像をファイルに保存します。

  KohonenMap.ShowBMP(SaveImages); //チャート上のビットマップ画像としてファイルを表示し、オプションでファイルに保存

このファイルは、ネットワークファイルと同じ名前 (指定されている場合)、またはデータを含むファイル (指定されている場合) の別のフォルダに配置されます。 データファイルが指定されておらず、ランダムに生成されたデータでネットワークが学習した場合、SOMファイルの名前とイメージを含むフォルダは、SOMプレフィックスと現在の日付と時刻を使用して形成されます。

最後に、学習されたネットワークをファイルに保存します。 ネットワーク名がすでに NetFileName で指定されている場合は、EAがテストモードで動作していることを意味するため、ネットワークを再度保存することはありません。

  if(NetFileName == "")
  {
    KohonenMap.Save(KohonenMap.GetID());
  }
}

テストランダムデータを生成してEAを開始します。 すべてのプレーンがスクリーンショット、ImageW = 230、ImageH = 230、MaxPictures = 3 に取得することを確認するために使用するイメージソリューション以外のすべてのデフォルトの設定では、次の画像を取得します。

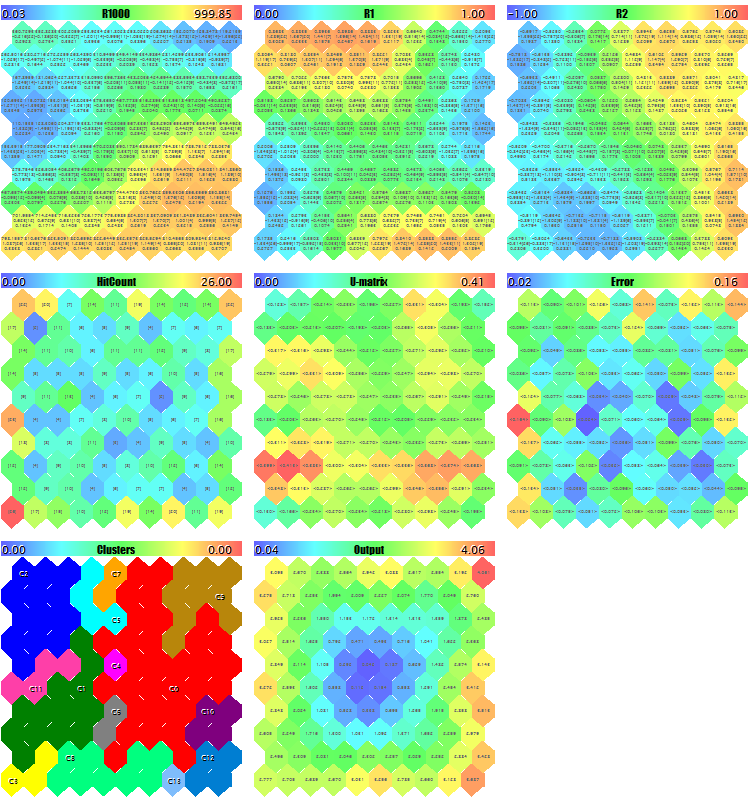
ランダム3D ベクトルのサンプル Kohonen マップ

ここでは、各ニューロンにサービスデータが表示され (マウスカーソルをポイントすることで詳細を見ることができます)、見つかったクラスターがマークされています。

このプロセスでは、次の情報 (クラスター情報は5つによって制限されますが、ソースコードで変更できます) はログに表示されます。

Pass 0 from 1000 0%
Pass 78 from 1000 7%
Pass 157 from 1000 15%
Pass 232 from 1000 23%
Pass 310 from 1000 31%
Pass 389 from 1000 38%
Pass 468 from 1000 46%
Pass 550 from 1000 55%
Pass 631 from 1000 63%
Pass 710 from 1000 71%
Pass 790 from 1000 79%
Pass 870 from 1000 87%
Pass 951 from 1000 95%
Overall NMSE=0.09420336270396877
Training completed at pass 1000, NMSE=0.09420336270396877
Clusters [14]:
"R1000" "R1"    "R2"   
N0
754.83131   0.36778   0.25369
N1
341.39665   0.41402  -0.26702
N2
360.72925   0.86826  -0.69173
N3
798.15569   0.17846  -0.37911
N4
470.30648   0.52326   0.06442
Map file SOM-20181205-134437.som saved

ここで、パラメータ NetFileName にネットワークを持つ作成された SOM-20181205-134437 ファイルの名前とパラメータ DataFileName の '? ' を指定した場合、学習セットからではなくランダムサンプルのテスト実行の結果を取得します。 マップをよりよく見るには、サイズを大きくして、MaxPictures を0に設定します。 

ランダムな3次元ベクトルの最初の2つの要素の Kohonen マップ

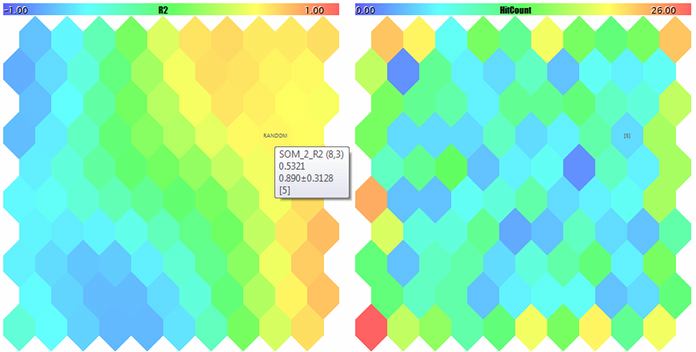
ランダム3次元ベクトルの3成分の Kohonen マップとヒットカウンタ

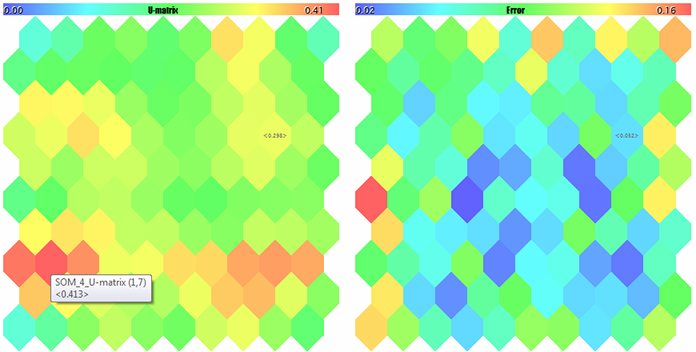
U マトリクスと量子化エラー

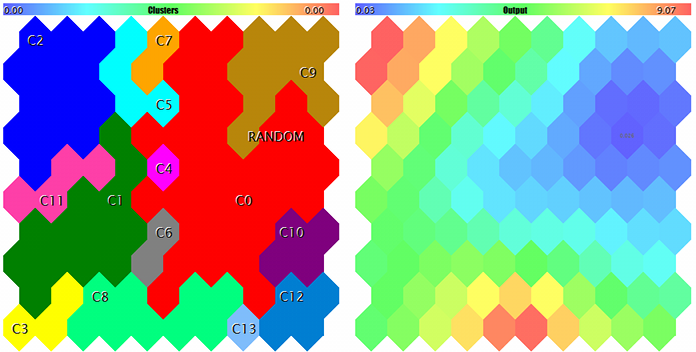
クラスターと Kohonen テストサンプルへのネットワーク応答

サンプルはランダムでマークされています。マウスカーソルをポイントすると、ニューロンのヒントがポップアップ表示されます。 ログには次のようなものが表示されます。

FileOpen error ?.csv : 5004
Data loading error, file: ?
Random Input:
457.17510   0.29727   0.57621
Matched Node Output (8,3); Hits:5; Error:0.05246704285146882; Cluster N0:
497.20453   0.28675   0.53213

そのため、Kohonen ネットワークを操作するためのツールが用意されています。 これで適用される問題に行くことができます。 2番目の記事でやるつもりです。

結論

すでに MetaTrader ユーザーにKohonen ニューラルネットワークは利用されています。 エラーを修正し、有用なツールで補完しました。そして、特別なデモEAを使用して、その動作をテストしました。 ソースコードを使用すると、独自のタスクにクラスを適用できます。関連する例は今後さらに検討します—