Грокаем "память" рынка через дифференцирование и энтропийный анализ

Мотивация применения подхода и краткая предыстория

Известно, что наличие большого количества участников на ликвидных рынках, работающих с различными инвестиционными горизонтами, продуцируют много рыночного шума. Другими словами, рынки обладают низким отношением сигнала к шуму. Ситуацию усугубляют попытки целочисленного дифференцирования временного ряда, которое стирает остатки памяти, приводя котировки к ряду со свойством стационарности. 

Ценовые ряды имеют память, поскольку каждое значение зависит от длинной истории ценовых уровней. Трансформации временного ряда, такие, как логарифм приращений, вырезают память, потому что строятся на ограниченной длине окна. Когда преобразования к стационарности уничтожают рыночную память, статистики применяют сложные математические методы для извлечения её остатков. Неудивительно, что применение таких классических статистических подходов к рынкам приводит к ложным выводам.

Понятие долгосрочной зависимости

Долгосрочная зависимость, так же называемая долгой памятью или долгосрочной персистентностью, наблюдается при анализе финансовых временных рядов. Это выражается в скорости затухания статистической зависимости между двумя ценами, с увеличением временного интервала (или расстояния между ними). Считается, что явление имеет дальнодействующую зависимость, когда зависимость затухает медленнее, чем экспоненциальный спад. Долгосрочную зависимость также часто ассоциируют с самоподобными процессами. Подробную информацию о LRD (long-range dependence) можно найти в Википедии.

Проблема стационарности и наличия памяти

Общая черта ценовых диаграмм — это наличие нестационарности, то есть длинной истории ценовых уровней, которые смещают среднюю цену во времени. Для того что бы провести статистический анализ, исследователям необходимо работать с приращениями цен (или логарифмами приращений), изменениями доходностей или волатильности. Эти преобразования делают временной ряд стационарным, удаляя всю память из ценовых последовательностей. Несмотря на то, что стационарность является необходимым свойством для статистических выводов, не всегда необходимо удалять всю память, поскольку она является основой для предсказательных свойств моделей. Например, равновесные (стационарные) модели должны содержать некоторое количество памяти для оценки того, как далеко цена удалилась от своего ожидаемого значения.

Проблема состоит в том, что приращения цен стационарны, но не содержат памяти о прошлом, тогда как ценовой ряд содержит весь объем доступной памяти, но нестационарен. Возникает вопрос: как необходимо дифференцировать временной ряд, что бы он стал стационарным и, в то же время, содержал максимально возможное количество памяти. Соответственно, мы хотели бы обобщить понятие ценовых приращений для рассмотрения стационарных рядов, где стирается не вся память. В этом ключе ценовые приращения не являются оптимальным решением трансформации цен среди других прочих методов.

Таким образом, будет введено понятие дробного дифференцирования. Существует большой диапазон возможностей между двумя крайностями: единичным и нулевым дифференцированием. Полностью дифференцированные цены с одной стороны, и не дифференцированные с другой.

Область применения дробного дифференцирования достаточно широка. Например, алгоритмы машинного обучения, обычно, принимают дифференцированный ряд на вход. Проблема в том, что необходимо вывести новые данные в соответствии с имеющейся историей, чтобы модель машинного обучения смогла распознать их. В случае нестационарного ряда новые данные могут лежать вне известного диапазона значений, что приведет к неправильной работе модели.

Экскурс в историю дробного дифференцирования

Практически все методы анализа и прогнозирования финансовых временных рядов, описанные в литературе и научных статьях, дают представление о целочисленном дифференцировании.

Возникает пара вопросов:

• почему целочисленное дифференцирование (скажем, с единичным лагом) является оптимальным?    
• не является ли такое гипердифференцирование одной из причин, что экономическая теория так склонна к гипотезе эффективных рынков?

Понятие дробного дифференцирования, применительно к анализу и прогнозированию временных рядов, восходит, по крайней мере, к Хоскингу. В той статье семейство процессов ARIMA было обобщено, позволяя степени дифференцирования принимать дробные значения. Это имело смысл, поскольку процесс дробного дифференцирования выявлял долгосрочную персистентность или антиперсистентность, увеличивая прогнозирующую способность по сравнению со стандартным ARIMA. Эта модель получила название ARFIMA (autoregressive fractionally integrated moving average) или FARIMA. После этой статьи дробное дифференцирование иногда упоминалось в статьях других авторов, в основном, в части ускорения методов расчетов.

Такие модели полезны при моделировании временных рядов с долгой памятью, то есть в тех случаях, когда отклонения от долгосрочного среднего затухают медленнее экспоненциального спада.

Понятие дробного дифференцирования

Рассмотрим оператор обратного смещения (или лаговый оператор) B, примененный к матрице реальных значений  {Xt}, где B^kXt = Xt−k, для любого целого k ≥ 0. Например, (1 − B)^2 = 1 − 2B + B^2, где  B^2Xt = Xt−2, следовательно, (1 − B)^2Xt = Xt − 2Xt−1 + Xt−2. 

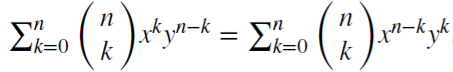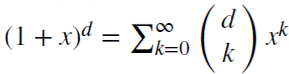Обратим внимание, что (x + y)^n =  , для каждого положительного целого n. Для действительного числа d,  , является биномиальным рядом. В дробной модели показатель d может быть действительным числом, со следующим формальным расширением биномиального ряда:

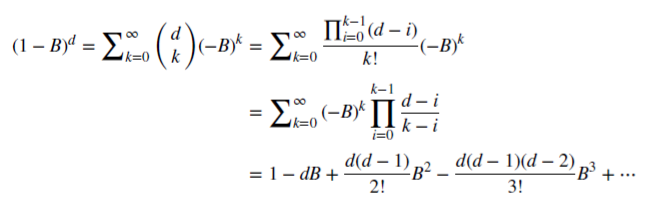
Сохранение памяти рынка в случае дробного дифференцирования

Посмотрим, как рациональное неотрицательное d сохраняет память. Данная арифметическая серия состоит из скалярного произведения:

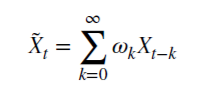
с весами 𝜔

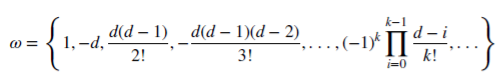
и значениями Х

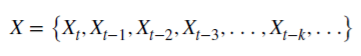
Когда d является положительным целым, 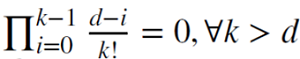 , то память в этом случае отсекается.

Например, d = 1 используется для вычисления приращений, где 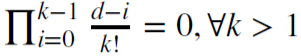  и 𝜔 = {1,−1, 0, 0,…}.

Дробное дифференцирование для фиксированного окна наблюдений

Обычно дробное дифференцирование применяется для всей последовательности временного ряда, что имеет большую вычислительную сложность и отрицательное смещение трансформированного ряда. Marcos Lopez De Prado в своей книге " Advances in Financial Machine Learning" предложил метод фиксированного окна, в котором последовательность коэффициентов отбрасывается, когда их модуль  (|𝜔k|) становится меньше заданного порогового значения (𝜏). Эта процедура дает преимущество перед классическим методом расширяющегося окна, поскольку позволяет иметь одинаковые веса для любой последовательности исходного ряда, снижает сложность вычислений и избавляет от отрицательного смещения. Результатом такого преобразования является сохранение памяти о ценовых уровнях плюс шум. Распределение такого преобразования не является нормальным (Гауссовским) из-за наличия памяти, асимметрии и избыточного эксцесса , однако, оно может быть стационарным.

Демонстрация процесса дробного дифференцирования

Напишем скрипт, который позволит визуально оценить эффект, получаемый от дробного дифференцирования временного ряда. Создадим две функции: для получения весов  𝜔 и для расчета новых значений ряда:

//+------------------------------------------------------------------+
void get_weight_ffd(double d, double thres, int lim, double &w[]) {
    ArrayResize(w,1); 
    ArrayInitialize(w,1.0);
    ArraySetAsSeries(w,true);
    
    int k = 1;
    int ctr = 0;
    double w_ = 0;
    while (ctr != lim - 1) {
        w_ = -w[ctr] / k * (d - k + 1);
        if (MathAbs(w_) < thres) break;  
        ArrayResize(w,ArraySize(w)+1); 
        w[ctr+1] = w_;      
        k += 1;
        ctr += 1;
    }
}
//+------------------------------------------------------------------+
void frac_diff_ffd(double &x[], double d, double thres, double &output[]) {
   double w[];
   get_weight_ffd(d, thres, ArraySize(x), w);

   int width = ArraySize(w) - 1;
   
   ArrayResize(output, width);
   ArrayInitialize(output,0.0);
   ArraySetAsSeries(output,true);
   ArraySetAsSeries(x,true);
   ArraySetAsSeries(w,true);
   
   int o = 0;
   for(int i=width;i<ArraySize(x);i++) {
      ArrayResize(output,ArraySize(output)+1);
      
      for(int l=0;l<ArraySize(w);l++)       
         output[o] += w[l]*x[i-width+l];      
      o++; } 
   ArrayResize(output,ArraySize(output)-width);
}

Отобразим анимированный график, меняющийся в зависимости от параметра  0<d<1:

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   for(double i=0.05; i<1.0; plotFFD(i+=0.05,1e-5))     
  }
//+------------------------------------------------------------------+
void plotFFD(double fd, double thresh) {
   double prarr[], out[];
   CopyClose(_Symbol, 0, 0, hist, prarr);
   
   for(int i=0; i < ArraySize(prarr); i++)
      prarr[i] = log(prarr[i]);
    
   frac_diff_ffd(prarr, fd, thresh, out);
   GraphPlot(out,1); Sleep(500);
}

Посмотрим, что получилось в итоге:

  

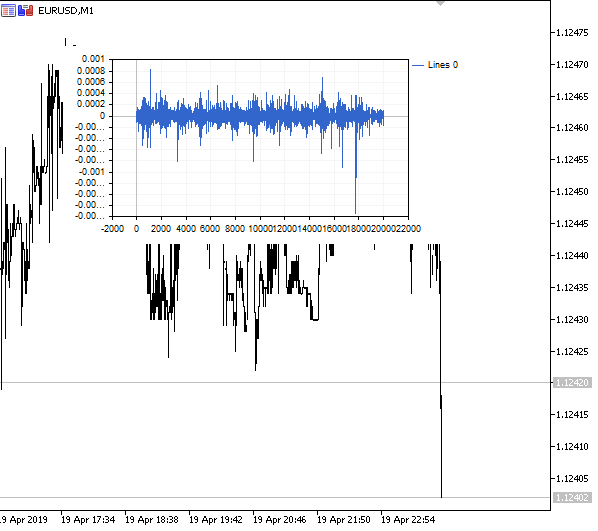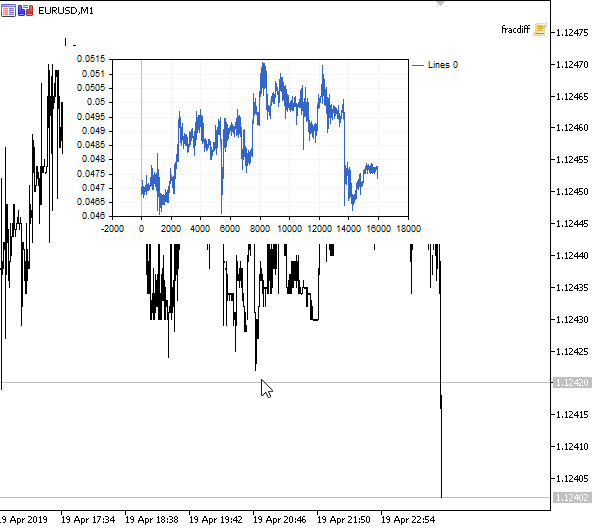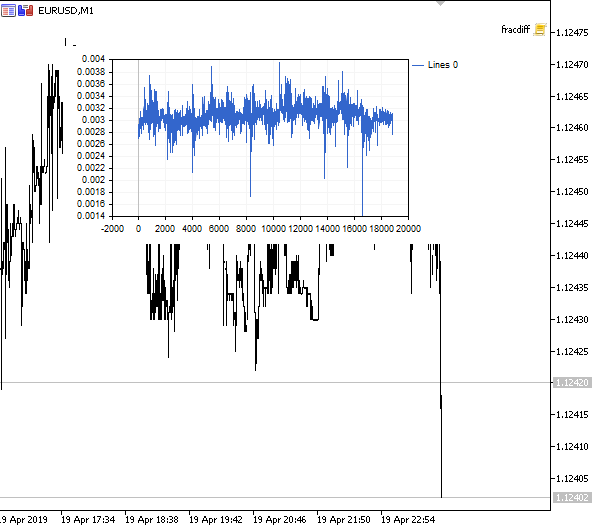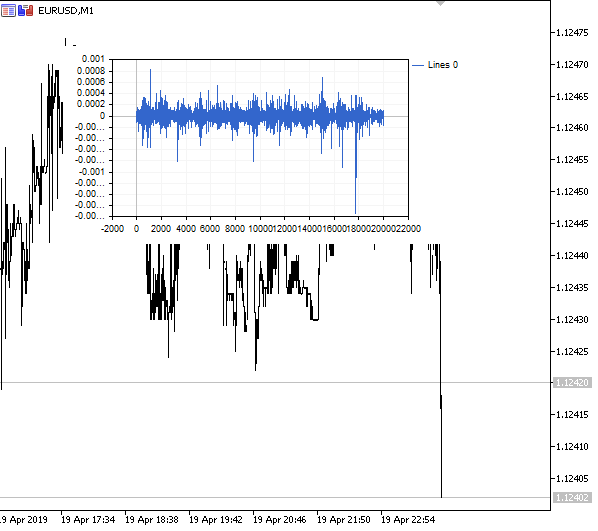
Рис 1. Дробное дифференцирование 0<d<1

Как и предполагалось, при увеличении степени дифференцирования d, график становится более стационарным, постепенно утрачивая "память" о прошлых уровнях. Причем, веса для ряда (ф-ии скалярного произведения весов на значения цен) остаются неизменными для всей последовательности и не нуждаются в перерасчете. 

Создание индикатора на основе дробного дифференцирования

Для удобного использования в советниках напишем индикатор, который можно будет подключать, указывая различные настройки: степень дифференцирования, размер порога для отсечения лишних весов и глубину отображаемой истории. Здесь я не стану приводить полный код индикатора, его можно посмотреть в исходнике.

Укажу лишь, что функция подсчета весов осталась прежней, а для расчета значений индикаторного буфера используется функция:

frac_diff_ffd(weights, price, ind_buffer, hist_display, prev_calculated !=0);  

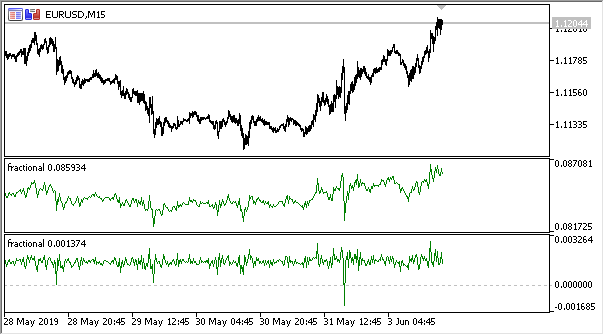
Рис 2. Дробное дифференцирование со степенями 0.3 и 0.9

У нас появился индикатор, который вполне точно эксплицирует динамику изменения количества информации во временном ряде. При увеличении степени дифференцирования, информация утрачивается и ряд принимает более стационарный вид. Однако, утрачивается информация только о ценовых уровнях, но могут оставаться периодические циклы, которые будут опорной точкой для прогнозирования. Так мы приближаемся к методам информационной теории, а именно — информационной энтропии, которая поможет с оценкой количества информации.

Понятие информационной энтропии

Информационная энтропия — это концепция из теории информации, которая показывает, сколько информации содержится в событии. В целом, чем более определенное или детерминированное событие, тем меньше информации оно будет содержать. Более конкретно, информация — это увеличение неопределенности. Данная концепция была введена Клодом Шенноном.

Так, энтропию случайной величины можно определить, введя понятие распределения случайной величины X, принимающей конечное число значений:

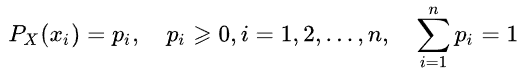
Тогда собственная информация события (или временного ряда) определяется как:

А оценку энтропии можно записать следующим образом:

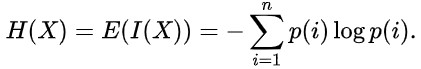
От основания логарифма зависит единица измерения количества информации и энтропии, например: бит, нат, трит или хартли.

Не станем подробно описывать энтропию Шеннона. Отметим лишь, что данный метод плохо подходит для оценки коротких и зашумленных временных рядов, в связи с чем, Стив Пинкус и Рудольф Калман предложили метод под названием " ApEn" (approximate entropy) применительно к финансовым тайм-сериям, который подробно был изложен в статье "Irregularity, volatility, risk and financial market time series".

В этой статье они предположили две формы отклонения цен от постоянства (описание волатильности), которые принципиально различны:

• первая описывает большое стандартное отклонение
• вторая — это крайняя нерегулярность и непредсказуемость

Эти две формы совершенно разные и такое разделение не является избыточным: стандартное отклонение остается хорошей оценкой отклонения от меры центральности, тогда как ApEn дает оценку нерегулярности. Более того, степень изменчивости не является настолько критичной, в то время как нерегулярность и непредсказуемость являются проблемой.

Приведем простой пример с двумя тайм-сериями:

• серия (10,20,10,20,10,20,10,20,10,20,10,20...) с чередующимися 10 и 20
• серия (10,10,20,10,20,20,20,10,10,20,10,20...) где 10 и 20 выбираются случайно, с вероятностью 1/2

Моменты статистики, такие как среднее и дисперсия, не покажут различий между двумя тайм-сериями. В то же время, первая серия совершенно регулярна, то есть всегда можно предсказать следующее значение, зная предыдущее. Вторая же абсолютно случайна и любая попытка предсказания обречена на провал.

Джошуа Ричман и Рэндэлл Моэрманн подвергли критике метод "ApEn" в своей статье "Physiological time-series analysis using approximate entropy and sample entropy", предложив улучшенный "SampEn" метод. В частности, критике были подвергнуты зависимость показателя энтропии от длины выборки, а также несогласованности показателей для различных но связанных временных рядов. Также, новый метод вычислительно менее сложен. Будем использовать этот метод и опишем особенности применения.

Sample entropy метод для определения регулярности ценовых приращений

Итак, SampEn метод — это модификация ApEn метода, использующийся для оценки сложности (нерегулярности) сигнала (временного ряда). Для заданного размера вложения m, допуска r и количества рассчитываемых значений N, SampEn — это логарифм вероятности того, что если две серии одновременных точек длины m имеют дистанцию < r, тогда две серии одновременных точек длины m + 1 также имеют дистанцию < r. 

Теперь предположим, что у нас есть набор данных временных рядов длины   с константным временным интервалом между ними. Определим шаблон вектора длины m, такой что   и функцию расстояния  (i≠j) по Чебышеву, которое является максимумом модуля разности компонент этих  векторов (но может быть иной функцией расстояния), и определим SampEn как:

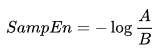
Где:

• A = количеству пар шаблонных векторов, имеющих 
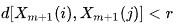
• B = количеству пар шаблонных векторов, имеющих 

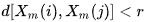
Из определения понятно, что A будет всегда <= B, следовательно, значение SampEn будет всегда нулевым или положительным числом. Меньшее значение также указывает на большее самоподобие в наборе данных или меньше шума.

В основном используются значения m = 2 и r = 0.2 * std, где std означает стандартное отклонение, которое должно приниматься для очень большого набора данных.

Я нашел быструю имплементацию метода, предложенную в листинге ниже, и переписал ее на MQL5:

double sample_entropy(double &data[], int m, double r, int N, double sd)
{
  int Cm = 0, Cm1 = 0;
  double err = 0.0, sum = 0.0;
  
  err = sd * r;
  
  for (int i = 0; i < N - (m + 1) + 1; i++) {
    for (int j = i + 1; j < N - (m + 1) + 1; j++) {      
      bool eq = true;
      //m - length series
      for (int k = 0; k < m; k++) {
        if (MathAbs(data[i+k] - data[j+k]) > err) {
          eq = false;
          break;
        }
      }
      if (eq) Cm++;
      
      //m+1 - length series
      int k = m;
      if (eq && MathAbs(data[i+k] - data[j+k]) <= err)
        Cm1++;
    }
  }
  
  if (Cm > 0 && Cm1 > 0)
    return log((double)Cm / (double)Cm1);
  else
    return 0.0; 
}

В дополнение, предлагаю вариант расчета cross-sample entropy (cross-SampEn) для случаев, когда следует получить оценку энтропии для двух рядов (два входных вектора), но можно также использовать для расчетов sample entropy:

// Calculate the cross-sample entropy of 2 signals
// u : signal 1
// v : signal 2
// m : length of the patterns that compared to each other
// r : tolerance
// return the cross-sample entropy value
double cross_SampEn(double &u[], double &v[], int m, double r) {
    double B = 0.0;
    double A = 0.0;
    if (ArraySize(u) != ArraySize(v))
        Print("Error : lenght of u different than lenght of v");
    int N = ArraySize(u);
    
    for(int i=0;i<(N-m);i++)
      {
         for(int j=0;j<(N-m);j++)
           {   
               double ins[]; ArrayResize(ins, m); double ins2[]; ArrayResize(ins2, m);
               ArrayCopy(ins, u, 0, i, m); ArrayCopy(ins2, v, 0, j, m);
               B += cross_match(ins, ins2, m, r) / (N - m);
               ArrayResize(ins, m+1); ArrayResize(ins2, m+1);
               ArrayCopy(ins, u, 0, i, m + 1); ArrayCopy(ins2, v, 0, j, m +1);
               A += cross_match(ins, ins2, m + 1, r) / (N - m);
           }
      }
    
    B /= N - m;
    A /= N - m;
    return -log(A / B);
}
// calculation of the matching number
// it use in the cross-sample entropy calculation
double cross_match(double &signal1[], double &signal2[], int m, double r) {
    // return 0 if not match and 1 if match
    double darr[];
    for(int i=0; i<m; i++)
      {
         double ins[1]; ins[0] = MathAbs(signal1[i] - signal2[i]);
         ArrayInsert(darr, ins, 0, 0, 1);
      }    
    if(darr[ArrayMaximum(darr)] <= r)  return 1.0; else return 0.0;
}

Нам достаточно первого метода расчетов, поэтому будем использовать его.

Персистентность и модель дробного броуновского движения

Если значение приращения ценового ряда увеличивается в текущий момент, какова вероятность того, что на следующем отсчете оно тоже будет расти? Так мы подошли к пониманию персистентности, или устойчивости. Измерение показателя устойчивости может представлять большую пользу. В этом разделе мы рассмотрим приложение метода SampEn к оценке персистентности приращений в скользящем окне. Данный метод оценки был предложен в уже упоминавшейся выше статье " Irregularity, volatility, risk and financial market time series".

У нас уже есть продифференцированный ряд, согласно теории дробного броуновского движения (термин "дробное дифференцирование" исходит оттуда). Определим крупнозернистый двоичный инкрементальный ряд 

BinInci:= +1, if di+1 – di > 0, –1. Проще говоря, бинаризуем приращения в диапазон +1, -1. Таким образом мы оценим непосредственно распределение четырех возможных вариантов поведения приращений:

• Вверх, Вверх
• Вниз, Вниз
• Вверх, Вниз
• Вниз, Вверх

Независимость оценок и статистическая мощь метода проистекают из того свойства, что практически все процессы имеют чрезвычайно малые уровни ошибок SampEn для Binlnci ряда. Что более важно, эта оценка не предполагает и не требует, чтобы данные были марковскими и не требует априорных знаний каких-либо характеристик, кроме стационарности. Если данные удовлетворяют свойству марковости первого порядка, то SampEn(1) = SampEn(2), из чего можно будет сделать дополнительные выводы.

Дробное броуновское движение представляет собой хорошую модель и восходит к Бенуа Мандельброту, который моделировал явления, которые демонстрировали как дальнодействующую зависимость или "память", так и "тяжелые хвосты". Это также привело к появлению новых статистических приложений, таких как показатель Херста и R/S анализ. Как мы уже знаем, ценовые приращения иногда демонстрируют дальнодействующую зависимость и тяжелые хвосты.

Таким образом, мы можем напрямую оценить персистентность временного ряда, где наименьшие значения SampEn будут соответствовать наибольшим значениям устойчивости и наоборот.

Реализация оценки персистентности для дифференцированного ряда

Перепишем наш индикатор, то есть добавим в него возможность работы в режиме оценки устойчивости. Поскольку оценка энтропии работает для дискретных величин, нормализуем значения приращений с точностью до 2-х знаков.

Полную реализацию смотрите в предложенном индикаторе "fractional entropy", здесь я опишу настройки индикатора:

input bool   entropy_eval = true; // выводить показания энтропии или приращения
input double diff_degree = 0.3;   // степень дифференцирования временного ряда
input double treshhold = 1e-5;    // порог для отсечения лишних весов (можно оставить по умолчанию)
input int    hist_display = 5000; // глубина отображаемой истории
input int    entropy_window = 50; // скользящее окно для оценки энтропии процесса

В итоге индикатор в двух режимах выглядит следующим образом (сверху энтропия, снизу стандартизированные приращения):

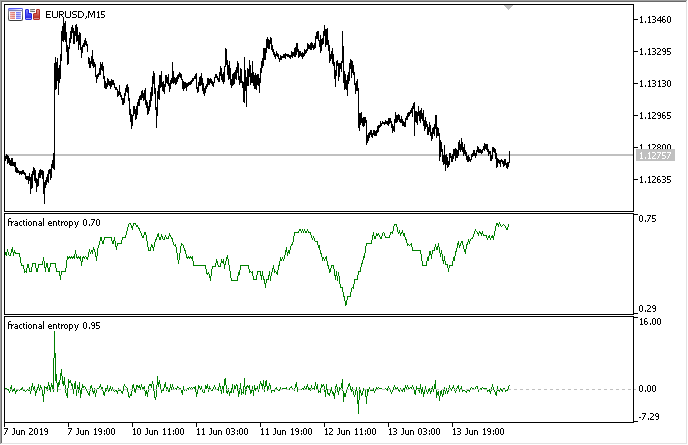
Рис 3. Показания энтропии для скользящего окна 50 (сверху) и дробное дифференцирование для со степенью 0.8

Заметно, что показания обеих оценок не коррелируют, что является хорошим знаком для модели машинного обучения (отсутствие мультиколлинеарности), которая будет рассмотрена в следующем разделе.

Оптимизация эксперта на лету с использованием машинного обучения: логит регрессия

Итак, у нас есть подходящий продифференцированный временной ряд, который можно использовать для получения торговых сигналов. Выше было упомянуто, что он является более стационарным и удобоваримым для моделей машинного обучения. Также у нас есть оценка персистентности этого ряда. Встает вопрос о выборе оптимальной модели машинного обучения. Поскольку эксперт должен оптимизироваться сам внутри себя, то предъявляется требование к скорости обучения — оно должно быть очень быстрым, с минимальными задержками. Из этих соображений я выбрал логистическую регрессию.

Логистическая регрессия применяется для прогнозирования вероятности какого-либо события по значениям множества признаков x1, x2, x3 ... xN, которые также называются предикторами или регрессорами. Признаками в нашем случае будут являться показания индикатора. Также необходимо ввести зависимую переменную y, которая обычно принимает одно из двух значений — 0 или 1. Несложно догадаться, что это может быть сигнал на покупку и на продажу. На основе показаний регрессоров вычисляется вероятность принадлежности зависимой переменной к тому или иному классу.

Делается предположение о том, что вероятность наступления события y = 1 равна:   где  - векторы значений независимых переменных 1, x1, x2 ... xN и коэффициентов регрессии соответственно, а f(z) - логистическая функция, или сигмоид: 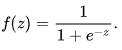  В итоге функцию распределения y при заданном x можно записать как: 

Рис 4. Логистическая кривая (сигмоид). Источник: Википедия.

Мы не будем подробно описывать алгоритм логистической регрессии, поскольку он широко известен, а воспользуемся готовым классом CLogitModel из библиотеки Alglib.

Создание класса автооптимизатора

Напишем отдельный класс CAuto_optimizer, который будет представлять из себя простейший виртуальный тестер и логит регрессию в одном флаконе:

//+------------------------------------------------------------------+
//|Auto optimizer class                                              |
//+------------------------------------------------------------------+
class CAuto_optimizer
  {
private:
// Logit regression model |||||||||||||||
   CMatrixDouble     LRPM;
   CLogitModel       Lmodel;
   CLogitModelShell  Lshell; 
   CMNLReport        Lrep;
   int               Linfo;
   double            Lout[];
//||||||||||||||||||||||||||||||||||||||||
   int               number_of_samples, relearn_timout, relearnCounter;
   virtual void      virtual_optimizer();
   double            lVector[][2];
   int               hnd, hnd1;
   
public:
                     CAuto_optimizer(int number_of_sampleS, int relearn_timeouT, double diff_degree, int entropy_window) {                                      
                             this.number_of_samples = number_of_sampleS;
                             this.relearn_timout = relearn_timeouT;
                             relearnCounter = 0;
                             LRPM.Resize(this.number_of_samples, 5);
                             hnd = iCustom(NULL, 0, "fractional entropy", false, diff_degree, 1e-05, number_of_sampleS, entropy_window);
                             hnd1 = iCustom(NULL, 0, "fractional entropy", true, diff_degree, 1e-05, number_of_sampleS, entropy_window);
                            }
                     ~CAuto_optimizer() {};
   double            getTradeSignal();
  };

Здесь в секции //Logit regression model// создается матрица для значений x и y, сама логит модель Lmodel и ее вспомогательные классы. Массив Lout[] после обучения модели будет принимать вероятности отнесения сигнала к тому или иному классу 0:1. 

Конструктор, соответственно, принимает размер обучающего окна number_of_samples, период, после которого модель будет переоптимизироваться relearn_timout, и степень дробного дифференцирования для индикатора diff_degree, а также окно для расчета энтропии entropy_window.

Остановимся подробнее на методе virtual_optimizer():

//+------------------------------------------------------------------+
//|Virtual tester                                                    |
//+------------------------------------------------------------------+
CAuto_optimizer::virtual_optimizer(void) {
   double indarr[], indarr2[];
   CopyBuffer(hnd, 0, 1, this.number_of_samples, indarr);
   CopyBuffer(hnd1, 0, 1, this.number_of_samples, indarr2);
   ArraySetAsSeries(indarr, true); ArraySetAsSeries(indarr2, true);
   
   for(int s=this.number_of_samples-1;s>=0;s--) {
      LRPM[s].Set(0, indarr[s]);
      LRPM[s].Set(1, indarr2[s]);
      LRPM[s].Set(2, s);
     
      if(iClose(NULL, 0, s) > iClose(NULL, 0, s+1)) { 
         LRPM[s].Set(3, 0.0);
         LRPM[s].Set(4, 1.0);
      }
      else {
         LRPM[s].Set(3, 1.0);
         LRPM[s].Set(4, 0.0);
      }  
    }
     
    CLogit::MNLTrainH(LRPM, LRPM.Size(), 3, 2, Linfo, Lmodel, Lrep);
    
    double profit[], out[], prof[1];
    ArrayResize(profit,1); ArraySetAsSeries(profit, true); profit[0] = 0.0;
    int pos = 0, openpr = 0;
    
    for(int s=this.number_of_samples-1;s>=0;s--) {
      double in[3];
      in[0] = indarr[s]; in[1] = indarr2[s]; in[2] = s;
      CLogit::MNLProcess(Lmodel, in, out);
      
      if(out[0] > 0.5 && !pos) {pos = 1; openpr = s;};
      if(out[0] < 0.5 && !pos) {pos = -1; openpr = s;};
      
      if(out[0] > 0.5 && pos == 1) continue;
      if(out[0] < 0.5 && pos == -1) continue;
      
      if(out[0] > 0.5 && pos == -1) {
         prof[0] = profit[0] + (iClose(NULL, 0, openpr) - iClose(NULL, 0, s)); 
         ArrayInsert(profit, prof, 0, 0, 1); pos = 0; }
         
      if(out[0] < 0.5 && pos == 1) {
         prof[0] = profit[0] + (iClose(NULL, 0, s) - iClose(NULL, 0, openpr)); 
         ArrayInsert(profit, prof, 0, 0, 1); pos = 0; }
    }
 GraphPlot(profit);
}

Совершенно очевидно, что он очень прост, и поэтому быстр. В цикле первый столбец матрицы LRPM заполняется значениями индикаторов + значение линейного тренда (было решено добавить). Затем в следующем цикле проводится сравнение текущей цены закрытия с предыдущей, чтобы уточнить вероятность сделки: на покупку или продажу. Если текущее значение больше предыдущего, значит был сигнал на покупку, в ином случае на продажу. Соответственно, следующие  столбцы заполняются значениями 0 и 1.

Таким образом, это очень простой тестер, который не претендует на оптимальный подбор сигналов, а просто берет их с каждого нового бара. Он может быть усовершенствован путем перегрузки метода, что выходит за рамки данной статьи.

После этого происходит обучение логит регрессии посредством метода MNLTrain(), который принимает матрицу, ее размер, количество переменных x (у нас передается только одна переменная для каждого случая), объект класса Lmodel для сохранения в него обученной модели и вспомогательные классы.

После обучения модели проводится ее тестирование и отображается в окне оптимизатора в виде графика баланса. Это сделано для наглядности, чтобы посмотреть как модель обучилась на обучающей выборке, и никак не анализируется алгоритмически.

Виртуальный оптимизатор вызывается из следующего метода:

//+------------------------------------------------------------------+
//|Get trade signal                                                  |
//+------------------------------------------------------------------+
double CAuto_optimizer::getTradeSignal() {
   if(this.relearnCounter==0)
      this.virtual_optimizer();
   relearnCounter++;
   if(this.relearnCounter>=this.relearn_timout) this.relearnCounter=0;
   
   double in[], in1[];
   CopyBuffer(hnd, 0, 0, 1, in); CopyBuffer(hnd1, 0, 0, 1, in1);
   double inn[3]; inn[0] = in[0]; inn[1] = in1[0]; inn[2] = relearnCounter + this.number_of_samples - 1;         
   CLogit::MNLProcess(Lmodel, inn, Lout);
   return Lout[0];
}

Он проверяет количество баров, прошедших с момента последнего обучения. И если оно превышает установленный в настройках порог, то модель заново переобучается. После этого копируется последнее значение индикаторов и единиц времени, прошедших после последнего обучения и подается в модель через метод MNLProcess(), который возвращает принадлежность к определенному классу 0:1, что является торговым сигналом.

Создание эксперта для проверки работы библиотеки

Осталось подключить библиотеку к торговому эксперту и прописать обработчик сигналов:

#include <MT4Orders.mqh>
#include <Math\Stat\Math.mqh>
#include <Trade\AccountInfo.mqh>
#include <Auto optimizer.mqh>

input int       History_depth = 1000;
input double    FracDiff = 0.5;
input int       Entropy_window = 50;
input int       Recalc_period = 100;
sinput double   MaximumRisk=0.01;
sinput double   CustomLot=0;
input int       Stop_loss = 500;           //Stop loss, positions protection
input int       BreakEven = 300;           //Break even
sinput int      OrderMagic=666;

static datetime last_time=0;

CAuto_optimizer *optimizer = new CAuto_optimizer(History_depth, Recalc_period, FracDiff, Entropy_window);
double sig1;

Настройки эксперта очень просты — это размер скользящего окна History_depth, то есть количество обучающих примеров для автооптимизатора. Степень дифференцирования FracDiff и количество пришедших баров Recalc_period, после которого модель будет заново переобучена. Также добавлена настройка Entropy_window, позволяющая регулировать окно для расчета энтропии.

Оставшаяся функция принимает сигнал от обученной модели и совершает торговые операции:

void placeOrders(){
   if(countOrders(0)!=0 || countOrders(1)!=0)   {
      for(int b=OrdersTotal()-1; b>=0; b--)
         if(OrderSelect(b,SELECT_BY_POS)==true) {
          if(OrderType()==0 && sig1 < 0.5) if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {};
          if(OrderType()==1 && sig1 > 0.5) if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {};
      }
    }
   
   if(countOrders(0)!=0 || countOrders(1)!=0) return;
   if(sig1 > 0.5 && (OrderSend(Symbol(),OP_BUY,lotsOptimized(),SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN)>0)) { return; }
   if(sig1 < 0.5 && (OrderSend(Symbol(),OP_SELL,lotsOptimized(),SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0,0,NULL,OrderMagic,INT_MIN)>0)) {}
  }

 Если вероятность покупки больше 0.5 то это сигнал на покупку и/или сигнал на закрытие шортов. И наоборот.

Тестирование самооптимизирующегося эксперта и выводы

Переходим к самому интересному — к тестам. 

Эксперт был запущен с указанными гиперпараметрами без генетической оптимизации, то есть почти наугад, на паре EURUSD 15 минут, по ценам открытия.

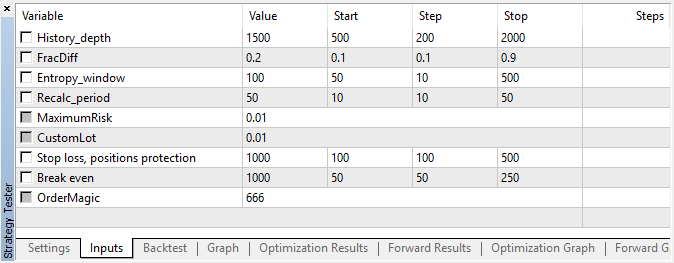
Рис 5. Настройки тестируемого советника

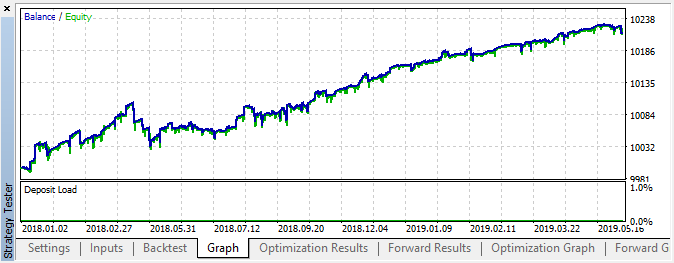
Рис 6. Результат тестирования с указанными настройками

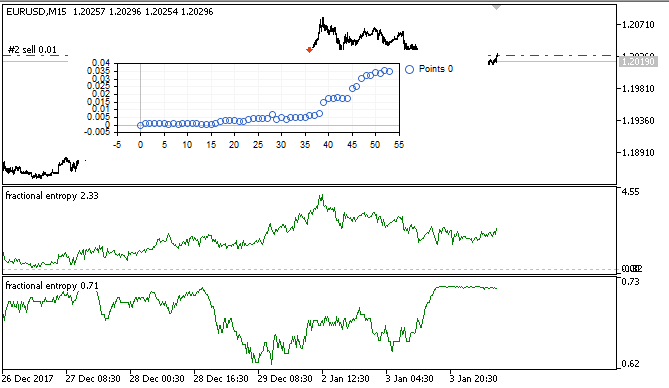
Рис 7. Отображение результатов виртуального тестера на обучающей выборке

На этом участке данная реализация показала достаточно устойчивый рост, что говорит о том, что в целом подход может быть интересным для дальнейших исследований.

В результате мы постарались убить трех зайцев в одной статье:

• получили понимание рыночной "памяти",
• научились ее оценивать в терминах энтропии,
• и писать самооптимизирующихся экспертов.