Создание прибыльной торговой системы (Часть 1): Количественный подход

Введение

Стабильно прибыльная торговая система основана на взаимодействии трех основных компонентов:

1. Win Rate (процент прибыльных сделок)
2. Соотношение риска и прибыли (Risk-Reard Ratio, RRR)
3. Объём риска (через размер позиции)

Эти три переменные являются основополагающими факторами ключевых показателей эффективности, таких как коэффициент прибыли, фактор восстановления и просадки. Однако многие трейдеры совершают ошибку, уделяя внимание только прибыльным сделкам, упуская из виду критическую важность доходности/риска и размера позиции при оценке эффективности своих (автоматических) торговых систем.

Чтобы в конечном итоге добиться успеха и оставаться активными на рынках, трейдеры должны понимать динамику своей торговой стратегии, в частности, Win Rate, Risk/Reward, а также оптимальный размер позиции, соответствующий этим двум показателям.

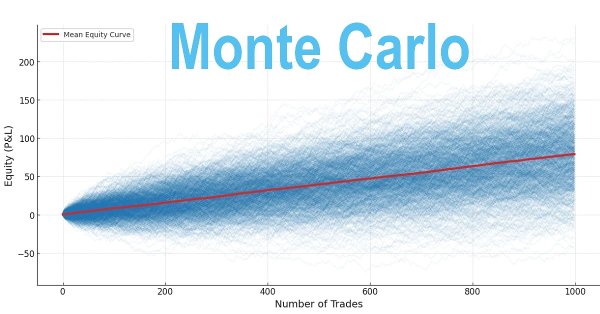
Данная статья призвана помочь трейдерам оценить свои стратегии в долгосрочной перспективе путем включения статистических результатов тестирования на истории в метод Монте-Карло. Такой подход генерирует широкий спектр возможных результатов и обеспечивает дополнительный уровень уверенности, помогая трейдеру определить, следует ли продолжать использовать систему, улучшать ее или отказываться от нее.

Ожидание: математика прибыльности

Прибыльность количественно определяется ожиданием — функцией винрейта и соотношения доходности к риску. Положительное ожидание определяет прибыльную систему. Отрицательное ожидание означает убыточную систему в долгосрочной перспективе, даже если сам винрейт в отдельности выглядит хорошо. Однако даже при положительном ожидании неправильный размер позиции может увеличить просадку.

Какие темы обсуждаются в данной статье:

• Математические основы прибыльных торговых систем
• Минимальные пороговые значения, необходимые для достижения прибыльности
• Проверка эффективности стратегии по методу Монте-Карло на Python

Целью является предоставить трейдерам фреймворк для оценки статистической жизнеспособности системы. Например, если Win Rate трейдера не превышает минимально необходимого порогового значения для заданного RRR, то нельзя ожидать долгосрочной  даже при многообещающем тестировании на истории.

Моделирование по методу Монте-Карло позволяет трейдерам моделировать тысячи синтетических результатов на основе различных комбинаций показателей Win Rate, RRR и размера позиции. Это позволяет лучше оптимизировать стратегию еще до начала реального или исторического тестирования.

Трейдеры, у которых уже есть результаты тестирования на истории, могут использовать моделирование для указания фактических значений Win Rate, RRR и размера позиций для прогнозирования потенциальных будущих результатов по ряду сделок. Эти статистические данные обеспечивают большую ясность и уверенность в том, стоит ли полагаться на систему.

Определения и математические концепции

1. Win Rate

Win Rate, или процент прибыльных сделок, определяется как отношение прибыльных сделок к общему количеству за определенный период, выраженная в процентах или как вероятность успешных сделок за определенный период. Здесь Win Rate сделок обозначается как P. 

Пример: если из 100 сделок 40 успешных, то коэффициент успешных сделок составит 40%.

2. Соотношение риска и прибыли (Risk-Reward Ratio, RRR)

Соотношение прибыли (тейк-профит) к риску  (стоп-лосс):

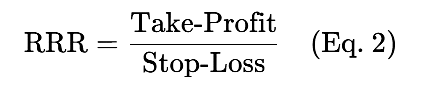
Пример: Если тейк-профит составляет 100 пипсов, а стоп-лосс — 50 пипсов, то RRR = 2.

3. Размер позиции

Размер позиции определяет размер риска по капиталу на сделку. Его можно рассчитать следующим способом:

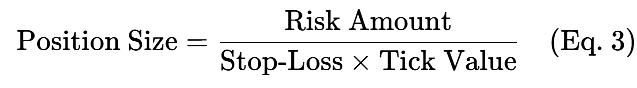
Пример: риск $200 с 50-пипсовым стоп-лоссом и значением тика $10/пипс,

размер позиции= 0,4 лота

4. Ожидание 

Ожидание, обозначенное как Ev, представляет собой ожидаемую доходность на сделку и рассчитывается следующим образом

Ev >0 — потенциально прибыльная система 

Ev <0 — потенциально убыточная система

Минимальный Win Rate или RRR для создания прибыльной системы

Взаимозависимость винрейта и RRR является математическим фактом. При любом заданном винрейте существует минимальный RRR, необходимый для достижения прибыльности. Аналогично, когда известен RRR, для получения прибыли требуется минимальный процент прибыльных сделок. Высокое значение Win Rate само по себе не подтверждает эффективность автоматизированной системы, если он не сопровождается четко определенным соотношением риска и прибыли (RRR).

Система с предопределенными настройками стоп-лосса и тейк-профита имеет фиксированный RRR. Если соответствующий коэффициент успешных сделок ниже требуемого минимума, система не сможет поддерживать долгосрочную прибыльность, даже если генерирует краткосрочные прибыли, способные вводить трейдеров в заблуждение. Это часто приводит к полному сливу счета.

Вывод условия прибыльности

Для лучшего понимания разберем математическую концепцию

Из формулы ожидания: 

Ev = (Win Rate*Reward) - (1 - Win Rate)*Risk

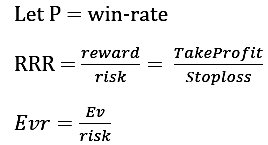
Чтобы система была прибыльной, Ev > 0.

Из уравнения 5:

если известно RRR, то минимальный винрейт (P) для прибыльной системы определяется как:

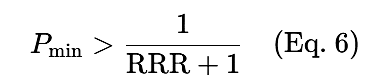
Если винрейт (P) известен, то минимальное RRR для прибыльной системы определяется как:

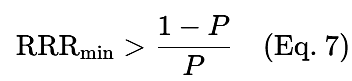
Таблица 1. Минимальный коэффициент успешных сделок для заданного RRR

RRR	минимальный P
1.0	>50.00%
1.5	>40.00%
2.0	>33.33%
2.5	>28.57%
3.0	>25.00%

Из Таблицы 1 следует, что если у системы RRR = 1, то для того, чтобы она приносила прибыль в долгосрочной перспективе, необходимо, чтобы значение Win Rate было более 50%. Также, если RRR системы = 3,0, то для долгосрочной прибыльности ей потребуется винрейт более 25,00%.  Из таблицы 1 можно увидеть, что по мере увеличения RRR минимальный процент успешных сделок уменьшается. Если RRR торговой системы превышает ее минимальный Win Rate, система будет прибыльной в долгосрочной перспективе.

Таблица 2. Минимальное RRR, необходимое для заданного Win Rate

	минимальное RRR
30%	>2.333
40%	>1.50
50%	>1.00
60%	>0.667
70%	>0.429

Win Rate системы в большинстве случаев неизвестен, если не провести бэктестирование стратегии на исторических данных с определенным RRR. Таблица 2 дает нам представление о минимальном показателе RRR, при котором определенный Win Rate становится прибыльным. При Win Rate в 30%, чтобы достичь прибыльности в долгосрочной перспективе RRR должен быть больше 2,333. Аналогично, при значении 70%, чтобы обеспечить прибыльность в долгосрочной перспективе RRR должен превышать 0,429. По мере увеличения винрейта минимум RRR уменьшается.

Вот почему трейдерам не следует слепо гнаться за высоким значением Win Rate, не принимая во внимание RRR, и наоборот.

Поскольку Win Rate — это просто отношение общего числа успешных сделок к общему числу сделок, прежде чем делать выводы об истинном показателе системы, чтобы собрать достаточно данных о сделках, важно дать ей поработать достаточно долго. Например, автоматизированная система, совершающая всего 30 сделок за 6 месяцев из которых 20 успешных, будет иметь процент успешных сделок в 60%. Однако если той же системе без каких-либо изменений позволить торговать в течение 18 месяцев, совершив 200 сделок с 90 случаями успеха, процент прибыльных сделок упадет до 45%. Чем больше сделок совершает система, тем надежнее и репрезентативнее становится Win Rate.

Размер позиции и управление рисками

Используемая для определения размера позиции величина обычно выражается в процентах от баланса счета. Этот показатель имеет решающее значение, поскольку определяет, сможет ли прибыльная торговая система выдерживать периоды максимальной просадки, избегать слива счета и в конечном итоге достигать торговых целей.

Зачастую трейдеры рискуют слишком большой частью своего счета в погоне за быстрой прибылью, что может привести к тому, что даже прибыльная система сольет их депозит. Когда это происходит, трейдер может обвинить разработчика системы, обозвав систему мошенничеством. Правда в том, что какой бы хорошей или прибыльной ни была система, если Win Rate не составляет 100%, она будет терпеть убытки. Если вы рискуете больше, чем может выдержать ваш счет, вы столкнетесь с маржин-коллами и, возможно, полной потерей депозита, если для его поддержки не будет дополнительных средств.

В данном разделе мы рассмотрим, как применять правильный размер позиции, оставаясь в безопасной зоне риска, чтобы вы могли пережить полосы убытков и продолжать двигаться к своим целям по прибыли. В этом суть разумного управления рисками и деньгами. Углубимся в математику:

Определения:

•  f: фиксированная доля текущего счета, подверженная риску на сделку.
•  RRRmin =  1.50: минимальное соотношение прибыли к риску
•  P = 0.40: Коэффициент успешных сделок (40%)

Результат успешной сделки: 

если сделка успешна, прибыль составляет RRR * Сумма риска

New Balance  = Current Balance + 1.50*(f*Current Balance)

Упрощаем:

Результат убыточной сделки:

в случае убытков по сделке убыток равен сумме риска:

Ожидаемый мультипликативный коэффициент на сделку:

объединяя уравнения 8 и 9, ожидаемый коэффициент роста E[factor] составляет:

Подставив P = 0,4 и упростив, получаем:

Трактовка значений: при RRRmin = 1,50 ожидаемый коэффициент роста равен ровно 1, что означает отсутствие долгосрочного роста (безубыточность).

Условие роста

RRR> RRRmin:   для RRR = 1.70

Для положительного роста (Ef >1); f должно удовлетворять 

 

Расчет оптимальной доли риска (f)

Для достижения цели предположим, что Ef = 1,002:

Из этого следует, что для достижения нашей цели нам необходимо рисковать не менее 2,5% от остатка на счете. Риск менее чем 2,5% позволит счету расти более стабильно с течением времени. Это подчеркивает важную концепцию, которую часто упускают из виду: для любой заданной комбинации коэффициента успешных сделок, соотношения прибыли к риску (RRR) и целевой прибыли всегда существует соответствующий оптимальный риск на сделку.

Ожидаемый коэффициент роста 

Для определения ожидаемого коэффициента роста (Ef) трейдер должен сначала определить три ключевых параметра:

1. Целевая прибыль (P_target)
2. Количество сделок для достижения цели (x)
3. Начальный баланс счета (Ini_bal)

Ef  выводится из составного уравнения роста

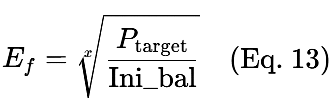
Например, учитывая следующее:

• Целевая прибыль (P_target) = $10 000
• Количество сделок (x) = 300
• Начальный баланс счета (Ini_bal) = $1 000

Подставив числа, получаем:

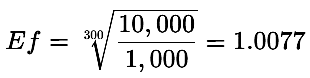
Ожидаемый коэффициент роста отражает ваш стиль торговли (являетесь ли вы консервативным или агрессивным трейдером), поскольку он определяет требуемый риск на сделку для достижения вашей цели.

Пример:

предположим, что торговая система имеет:

коэффициент успешных сделок = 40%

соотношение риска и прибыли (RRR) = 1,7

Целью трейдера или  автоматизированной системы  является превращение 1000 долларов в 10 000 долларов за 300 сделок. Требуемый риск на сделку (f) из уравнения 12 рассчитывается следующим образом:

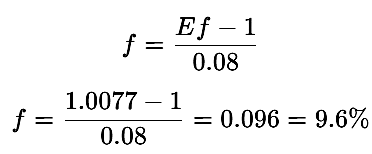
В этом случае трейдер или автоматизированная система должны рисковать не менее 9,6% на сделку, чтобы достичь цели, что является крайне агрессивным подходом.

Теперь, если количество сделок для достижения цели увеличить до x = 700:

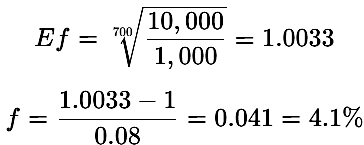
При 700 сделках система или сделка становятся менее агрессивными, требуя всего 4,1% риска на сделку для достижения той же цели.

Важно отметить, что при более высоком коэффициенте успешных сделок и более высоком показателе RRR цель становится более достижимой.

Пример: если RRR = 2,0 (при P = 40%), Ef = 1 + 0,2*f, что снижает f до 1,54%  для Ef = 1,0077

Из этой математической модели можно сделать вывод, что даже прибыльные системы требуют оптимизации как ожидания, так и размера позиции. В следующем разделе  мы проиллюстрируем это более подробно, используя метод Монте-Карло, чтобы обеспечить долгосрочную перспективу для потенциала системы.

Моделирование по методу Монте-Карло

Подтверждение долгосрочной надежности торговой системы зависит от оптимизированного RRR, коэффициента успешных сделок и размера позиции. Метод Монте-Карло позволит смоделировать диапазон возможных результатов для тысяч рандомизированных торговых последовательностей. Параметры для оптимизации:

1. Коэффициент успешных сделок
2. RRR 
3. Размер позиции  

Это позволит учитывать:

• Полосы убытков
• Максимальные просадки
• Пути ожидаемой доходности
• Вероятность выживания счёта

Однако цель состоит в том, чтобы проверить ожидаемую доходность и вероятность выживания счета при различных сценариях. 

Метод Монте-Карло создан с использованием программирования на Python.

import numpy as np
import matplotlib.pyplot as plt

# Parameters
win_rate = 0.40
reward_risk_ratio = 1.5  # 1.5:1
risk_per_trade = 1  # Risk $1 per trade (normalized)
num_trades = 1000  # Total number of trades to simulate
num_simulations = 1000  # Number of Monte Carlo simulations

# Monte Carlo simulation
equity_curves = []

Мы импортируем математические функции, многомерные массивы и матрицы, необходимые для вычислений, с помощью библиотеки NumPy и назначаем их как np.

Мы также импортируем графические функции для построения графиков наших моделированных результатов с использованием модуля pyplot из Matplotlib и называем его plt.

Затем мы инициализируем наш коэффициент успешных сделок, соотношение прибыли и риска, риск на сделку, количество сделок на каждое моделирование и количество итераций. Результаты сохраняются в кривых капитала. Количество итераций можно уменьшить или увеличить в зависимости от предпочтений пользователя.

for _ in range(num_simulations):
    equity = 0
    curve = [equity] # Start curve with initial equity (0)
    peak = equity # Track peak equity for drawdown calculation
   # max_drawdown = 0 # Track max drawdown for this simulation

    for _ in range(num_trades):
        if np.random.rand() < win_rate:
            pnl = risk_per_trade * reward_risk_ratio
        else:
            pnl = -risk_per_trade
        equity += pnl
        curve.append(equity)

    equity_curves.append(curve)

# Convert to numpy array for easier analysis
equity_curves = np.array(equity_curves)

При моделировании выполняется 1000 итераций (по 100 сделок в каждой). Результаты сохраняются в виде кривой капитала, которая преобразуется в массив NumPy для анализа.

# Plot results
plt.figure(figsize=(12, 6))
for i in range(min(num_simulations, 100)):
    # Adjust indexing if plotting against trade number (starts from 0)
    plt.plot(range(num_trades + 1), equity_curves[i], alpha=0.2, color='blue')

Результаты каждого моделирования отображаются на графике синим цветом.

# Plot mean curve
mean_curve = equity_curves.mean(axis=0)
plt.plot(range(num_trades + 1), mean_curve, color='red', linewidth=2, label='Mean Equity Curve')

Красная линия отмечает среднее значение моделированных результатов.

plt.title(f'Monte Carlo Simulation: {num_simulations} Simulations, {num_trades} Trades Each\nWin Rate = {win_rate*100:.1f}%, 
R:R = {reward_risk_ratio}:1')
plt.xlabel('Number of Trades')
plt.ylabel('Equity (P&L)')
plt.legend()
plt.grid(True)
plt.tight_layout() 
plt.show()

Этот сегмент выполняет форматирование графика: название, метки осей (метка x, метка y) и активацию сетки (grid=True).

# Summary statistics
# Final equity is now the last element of the curve, which has num_trades + 1 points
final_equity = equity_curves[:, -1]
mean_final_equity = final_equity.mean()
median_final_equity = np.median(final_equity)
std_final_equity = final_equity.std()
percent_profitable = np.mean(final_equity > 0) * 100

print('mean_final_equity:',mean_final_equity, '\nmedian_final_equity:', median_final_equity,
 '\nstd_final_equity:', std_final_equity,'\npercent_profitable:', percent_profitable,'%')

Раздел окончательного кода рассчитывает и выводит: средний итоговый капитал, медианный итоговый капитал, стандартное отклонение итогового капитала и процент прибыльных сделок.

Сценарий А: результат торговой стратегии с 40%-ным Win Rate и RRR, равным 1,5 за 1000 моделирований

В этом сценарии торговая стратегия с процентом успешных сделок 40% и соотношением прибыли к риску (RRR) равным 1,5 тестировалась на 1000 сделках за моделирование. Всего было проведено 1000 отдельных моделирований для оценки эффективности и характеристик риска стратегии. Результаты, представленные на рисунке 1, таковы:

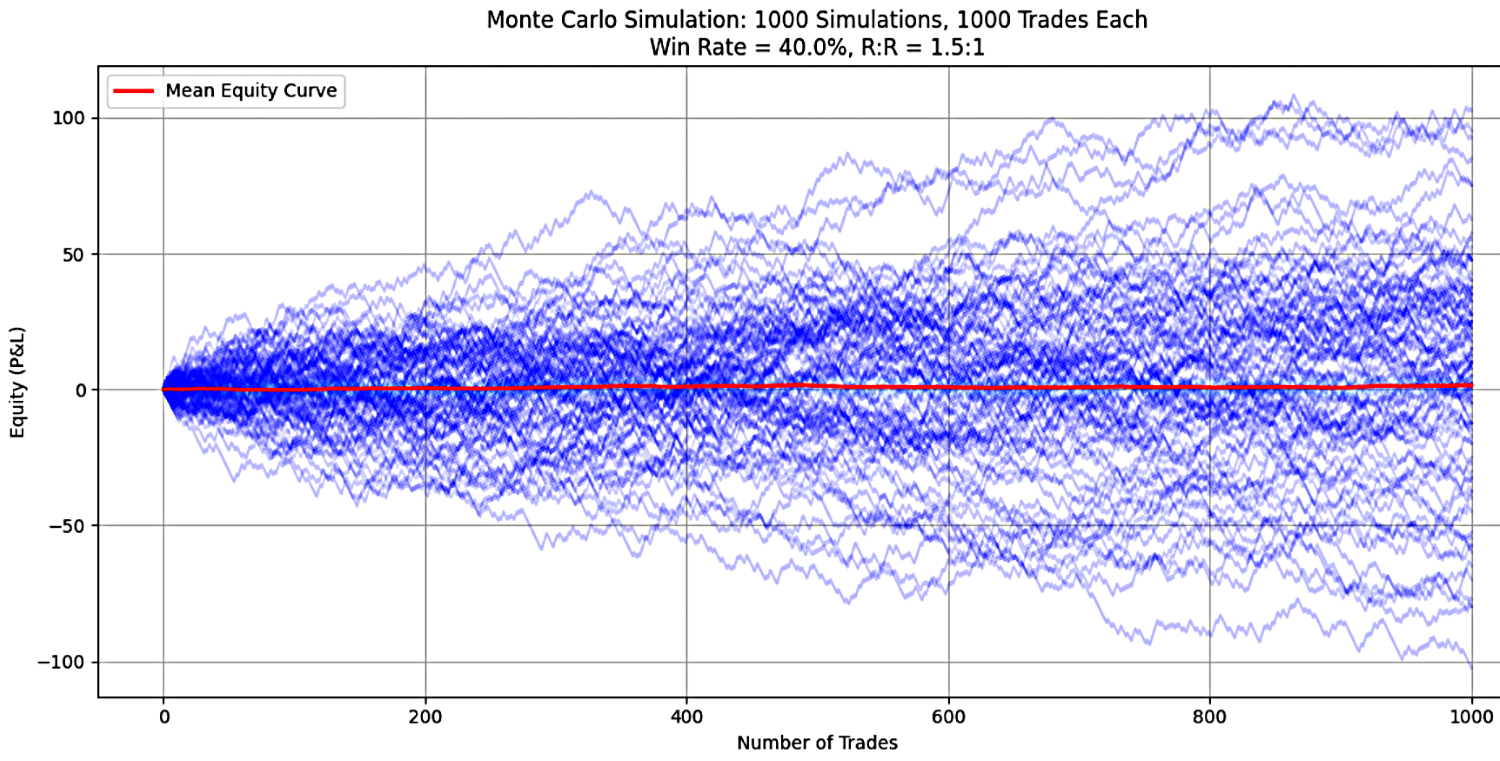
Рисунок 1

Результаты моделирования для коэффициента успешных сделок равного 40% и RRR равного 1,5 приведены ниже:

Параметры	Значения
Средний итоговый капитал	1,44
Медианный итоговый капитал	0,0
Стандартное отклонение итогового капитала	37,91
Процент прибыльных моделирований	49,0%

Трактование результатов

1. Средний итоговый капитал: средний итоговый остаток на счете по всем моделированиям в 1,44 раза превышал первоначальный капитал. Это говорит о том, что в среднем стратегия принесла скромную общую прибыль. Однако на это среднее значение существенное влияние оказывают несколько крайне положительных результатов, показанных на рисунке 1. Наличие этих выбросов искажает среднее значение в сторону увеличения, маскируя частоту плохих результатов.

2. Медианный итоговый капитал: медианный результат составил 0,0, что указывает на то, что по крайней мере половина моделирований привела к полной потере капитала. По крайней мере в 50% случаев моделирования счет был обнулен (вероятно, баланс достигал 0 или имел место маржин-колл). Эта стратегия сопряжена с огромным риском разорения. В половине случаев сценария произошла потеря всего капитала, в то время как другая половина принесла прибыль. Это даёт достаточно искаженную картину, чтобы поднять среднее значение до 1,44. Это показывает, что большинство результатов являются плохими и сигнализируют о неприемлемом риске.

3. Стандартное отклонение: стандартное отклонение, равное 37,91, подчеркивает крайнюю волатильность и непредсказуемость результатов. Стандартное отклонение велико по сравнению со средним значением. Большинство путей группируются вблизи полной потери (среднее значение = 0). Некоторые случаи моделирования закончились большим положительным балансом (что завышает среднее значение), в то время как многие потерпели крах.

4. Процент прибыльных моделирований: только 49% случаев моделирования закончились с прибылью; таким образом, итоговый капитал превысил начальный баланс. В 51% случаев система терпела убытки. Это совпадает со медианным значением = 0,0, что подтверждает, что когда потери происходят, они носят катастрофический характер.

Эти статистические значения отражают несколько ключевых характеристик эффективности торговой системы: 

• Неустойчивая система:

несмотря на то, что средний итоговый капитал является положительным (1,44x), результат обусловлен несколькими «удачными» сериями с высокими заработками. Равная нулю медиана ясно показывает, что большинство случаев показали ужасные результаты — по крайней мере 50% из них завершились опустошением счета.  Это несоответствие между средним значением и медианой указывает на фундаментальную неустойчивость системы — большинство случаев показали очень плохие результаты, и только некоторые из них показали исключительно хорошие результаты.

• Высокий риск разорения:

Равная нулю медиана показала, что если не будут применяться очень строгие меры контроля рисков, данная стратегия с высокой вероятностью приведет к обнулению вашего счета.

• Высокая волатильность:

большое стандартное отклонение (приблизительно 37,9) по сравнению со средним значением (приблизительно 1,44) говорит о том, что результаты чрезвычайно разбросаны. Некоторые из них превосходны, некоторые — катастрофичны.  Такая непоследовательность не позволяет полагаться на эту стратегию для получения стабильной прибыли.

• Слабая прибыльность:

только 49% случаев завершились прибылью, несмотря на положительное среднее значение. Система показала, что не является надежной, несмотря на положительное среднее значение , поскольку стабильная масштабируемая система имела бы гораздо более высокий процент положительных результатов.

Сценарий Б: результат торговой стратегии с 40%-ным Win Rate и RRR, равным 1,7 за 1000 моделирований

В случае сценария Б торговая стратегия сохраняет процент успешных сделок на уровне 40%, но увеличила соотношение прибыли к риску (RRR) до 1,70 и оценивалась на основе более 1000 сделок за моделирование.  Для тщательной оценки характеристик эффективности и риска проведено 1000 отдельных моделирований по методу Монте-Карло. Ключевые результаты, представленные на рисунке 2, таковы:

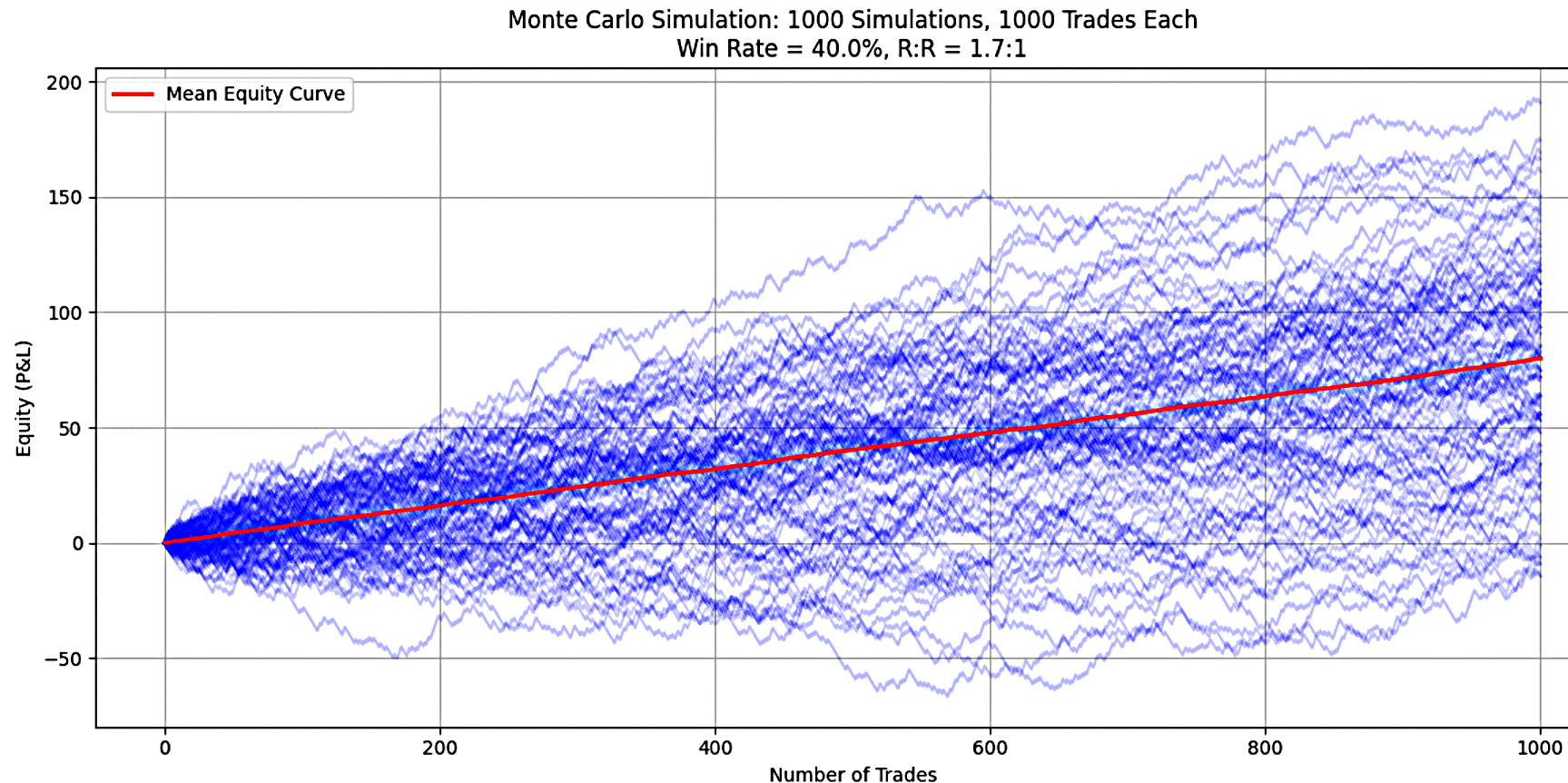
Рисунок 2

Ниже представлены результаты моделирований для Win Rate равного 40% при соотношении риска и прибыли, равном 1,7.

Параметры	Значения
Средний итоговый капитал	80,0
Медианный итоговый капитал	80,0
Стандартное отклонение итогового капитала	45,82
Процент прибыльных моделирований	96,7%

Трактование результатов

1. Средний итоговый капитал: в среднем за период моделирования стратегия увеличила первоначальный капитал в 80 раз. Это отражает исключительный потенциал наращивания и подтверждает высокую прибыльность стратегии в данных условиях. Средняя доходность, в 80 раз превышающая первоначальный баланс, является выдающимся результатом, позволяющим предположить, что система способна обеспечить существенную прибыль.

2.  Медианный итоговый капитал: медианный результат также в 80 раз превышал первоначальный капитал, что означает, что по крайней мере в 50% случаев моделирования достигнута доходность на этом уровне или выше. Близкое соответствие между средним и медианным значениями указывает на симметричное распределение результатов. При этом большинство моделирований группируются около отметки доходности 80x. Этот результат подчеркивает не только высокую прибыльность, но и отличную согласованность при проведении моделирования. 

3.  Стандартное отклонение итогового капитала:  хотя стандартное отклонение в 45,82 указывает на некоторую изменчивость результатов, этот уровень волатильности относительно невелик, если рассматривать его по сравнению со значительным средним значением. Стандартное отклонение составляет приблизительно 57% от среднего значения, указывая на то, что, хотя отдельные результаты могут различаться (например, некоторые запуски дают доходность 40x или 120x), большинство результатов по-прежнему сосредоточены вокруг среднего значения 80x. Это отражает систему с контролируемой волатильностью и надежным функционированием.

4. Процент прибыльных моделирований: впечатляющие 96,7% моделирований закончились с прибылью, и только 3,3% привели к убыткам. Этот очень высокий показатель успеха свидетельствует об исключительной надежности системы и очень низком риске разорения. Подавляющее большинство торговых операций принесли прибыль, что подчеркивает надежность стратегии в этих смоделированных условиях.

Эти статистические значения отражают несколько ключевых характеристик эффективности торговой системы: 

• Высокоприбыльная:

выравнивание среднего и медианного значений при значении 80х в сочетании с плотной кластеризацией результатов показывает, что при протестированных параметрах это высокорентабельная и стабильная система.

• Низкий риск разорения:

поскольку всего 3,3% моделирований оказались убыточными, система демонстрирует значительное повышение надежности по сравнению с предыдущим сценарием с RRR равным 1,5. Теперь риск разорения исключительно низок.

• Контролируемая волатильность:

несмотря на то, что абсолютное стандартное отклонение кажется большим, по сравнению с очень высокой доходностью оно является обоснованным. Результаты показывают, что, хотя некоторые колебания и ожидаются, система стабильно демонстрирует высокие результаты.

• Чувствительность к RRR:

самое поразительное наблюдение заключается в том, как существенно улучшились результаты при простом увеличении RRR с 1,5 до 1,7, при сохранении коэффициента успешных сделок на уровне 40%. Это подчеркивает важность оптимизации соотношения прибыли и риска. Особенно это касается стратегий с низким коэффициентом успешных сделок, где даже небольшие корректировки могут значительно повысить стабильность и прибыльность системы.

Заключение

Настоящий анализ наглядно продемонстрировал как математически, так и с помощью моделирования по методу Монте-Карло, что оптимизация соотношения доходности к риску (RRR) для заданного Win Rate может значительно повысить прибыльность и стабильность торговой системы. Как показано в наших сценариях, даже при сохранении фиксированного винрейта в 40%, увеличение RRR с 1,5 до 1,7 превратило систему из системы с высокой нестабильностью и значительным риском банкротства в приносящую стабильную прибыль систему с низкой вероятностью банкротства счета.

Важно подчеркнуть, что Win Rate сделок и RRR по своей сути взаимозависимы, как показано в уравнениях 6 и 7 настоящей статьи. Усилия по оптимизации RRR, естественно, повлияют на текущий Win Rate, и наоборот. Важно отметить, что каждый винрейт имеет соответствующий минимальный RRR, который необходимо превышать для достижения долгосрочной прибыльности. Например, при винрейте в 40% система, чтобы быть устойчивой, должна превышать пороговое значение RRR, равное 1,5.

Это дополнительно иллюстрируется на примере ожиданий:

При RRR=1,5 ожидание = (0,4*1,50)- (0,6*1) = 0. Предполагаемая безубыточность. Это объясняет сильное расхождение между средним и медианным значениями.

При RRR=1,7 ожидание = (0,4*1,70)- (0,6*1) = 0,08. Положительное ожидание, приводящее к прибыльному результату в 96,7%.

В заключение следует сказать, что многие торговые системы можно преобразовать в стабильно прибыльные стратегии, надлежащим образом сбалансировав Win Rate и Risk/Reward. Главное — не просто добиться высокого показателя прибыльных сделок, а гарантировать, что RRR превысит минимальное пороговое значение, необходимое для формирования положительного ожидания с течением времени.

Когда трейдер определяет и стоп-лосс, и тейк-профит, RRR системы становится фиксированным. Чтобы система была прибыльной во время тестирования на истории, коэффициент успешных сделок должен превышать минимум, требуемый для данного RRR. В данной статье приведены несколько значений RRR вместе с соответствующими минимальными винрейтами. Что касается других комбинаций, уравнения 6 и 7 можно использовать для расчета требуемых пороговых значений прибыльности.

Чтобы оценить долгосрочную жизнеспособность, трейдеры могут использовать метод Монте-Карло для моделирования эффективности на основе статистики бэктестинга.  Анализ по методу Монте-Карло позволяет моделировать тысячи возможных последовательностей сделок с использованием статистики бэктестинга (Win Rate, RRR, размер позиции):

• Прогнозирует вероятность успеха/неудачи на длительные периоды времени.
• Определяет, зависят ли результаты от удачи или статистических преимуществ.
• Дает трейдерам возможность доверять своей стратегии, либо пересматривать ее, прежде чем рисковать капиталом.

Система, стабильно демонстрирующая положительные результаты при моделировании, обеспечивает более высокую степень уверенности, позволяя трейдерам доверять своей стратегии и соблюдать дисциплину.

Наконец, несмотря на то, что в данной статье основное внимание уделяется ожиданию и оптимизации RRR, важно подчеркнуть, что размер позиции является не менее важным столпом эффективности системы. Без разумного управления рисками даже система с положительным ожиданием может потерпеть неудачу. В следующей статье мы рассмотрим, как применять оптимальный размер позиции для повышения восстановительного потенциала системы и обеспечения устойчивого успеха в торговле.