Возможности Мастера MQL5, которые вам нужно знать (Часть 26): Скользящие средние и показатель Херста
719
5
Введение
Мы продолжаем серию статей о методах работы с Мастером MQL5, которые фокусируются на альтернативных методах анализа финансовых временных рядов в интересах трейдеров. В этой статье мы рассмотрим показатель Херста. Это метрика, которая показывает, имеет ли временной ряд высокую положительную автокорреляцию или отрицательную автокорреляцию в долгосрочной перспективе. Применение этой метрики может быть весьма обширным. Как мы можем использовать ее? Во-первых, мы бы рассчитали показатель Херста, чтобы определить, находится ли рынок в тренде (что обычно дает нам значение больше 0,5) или рынок возвращается к среднему значению/колеблется (что дает нам значение меньше 0,5). В этой статье, поскольку мы сейчас рассматриваем скользящие средние, мы объединим показатель Херста с относительным положением текущей цены по отношению к скользящей средней. Относительное положение цены относительно скользящей средней может указывать на следующее направление цены, но с одной важной оговоркой.
Нам необходимо знать, находятся ли рынки в тренде или колеблются (возвращаются к среднему значению). Поскольку для ответа на этот вопрос мы можем использовать показатель Херста, то нам просто нужно посмотреть, где находится цена относительно среднего значения, а затем совершить сделку. Однако даже это может оказаться немного поспешным, учитывая, что колеблющиеся рынки, как правило, лучше изучаются на более коротких временных периодах, чем трендовые рынки, которые более очевидны при рассмотрении на гораздо более длительных временных периодах. Именно по этой причине нам понадобятся две отдельные скользящие средние, чтобы взвесить относительное положение цены, прежде чем можно будет оценить окончательное состояние. Это будет быстрая скользящая средняя для рынков, находящихся во флэте или возвращающихся к среднему значению, и медленно скользящая средняя для трендовых рынков, определяемая показателем Херста. Таким образом, каждый тип рынка, заданный экспонентой, будет иметь свою собственную скользящую среднюю. В этой статье мы рассмотрим анализ масштабированного диапазона (Rescaled Range Analysis) как средство оценки показателя Херста. Мы рассмотрим процесс оценки шаг за шагом и реализуем класс сигналов советников, реализующий эту экспоненту.
Разделение временного ряда
Согласно Википедии, формула показателя Херста имеет вид:
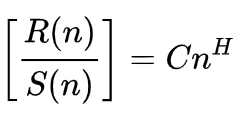
где
- n — размер анализируемой выборки
- R() — это повторно масштабированный диапазон выборки
- S() — стандартное отклонение выборки
- C — константа
- H — показатель Херста
Эта формула по сути представляет нам 2 неизвестных. Обход этого ограничения для поиска как константы C, так и искомого показателя H заключается в регрессии нескольких сегментов отобранного множества. H — это степень, из которой мы берем средние арифметические с обеих сторон уравнения, чтобы найти H, и это наш последний шаг, как мы увидим ниже. Итак, самый первый шаг — это определение сегментов в выборке данных.
Минимальное количество сегментов, которое мы можем получить из любой выборки, равно 2. Максимум, который мы можем получить из выборки, зависит от ее размера, а элементарная формула — это размер выборки, деленный на 2. Теперь мы ищем две неизвестные, то есть нам нужно больше, чем пара точек, чтобы иметь минимум два уравнения, как это и происходит на практике. Количество уравнений или пар точек, которые мы можем сгенерировать из выборки, определяется как половина размера выборки минус 1. Таким образом, размер выборки из 4 точек данных сгенерирует только одну пару точек для регрессии, чего будет явно недостаточно для нахождения показателя Херста и константы C.
Однако выборка с 6 точками данных может сгенерировать минимум 2 пары точек, которые можно использовать для оценки показателя степени и константы. На практике мы хотим, чтобы размер выборки был как можно больше, поскольку, как указано в определении, показатель Херста является "долгосрочным" свойством. Кроме того, приведенная выше формула из Википедии применима к выборкам, когда n стремится к бесконечности. Поэтому важно, чтобы размер выборки был как можно больше, чтобы оценить более репрезентативный показатель Херста.
Разделение выборки на сегменты, где каждый набор сегментов/разделений генерирует одну пару точек, является самым "первым шагом". Я использую "первый шаг", поскольку в подходе, который мы используем в этой статье, как показано в исходном коде ниже, мы не разделяем данные в одностороннем порядке и не определяем все сегменты сразу перед переходом к следующему шагу, а вместо этого для каждого разделения вычисляем пару точек, которые отображаются из этого выборочного разделения. Ниже приведена соответствующая часть исходного кода:
//+------------------------------------------------------------------+ // Function to Estimate Hurst Exponent & Constant C //+------------------------------------------------------------------+ void CSignalHurst::Hurst(vector &Data, double &H, double &C) { matrix _points; double _std = Data.Std(); if(_std == 0.0) { printf(__FUNCSIG__ + " uniform sample with no standard deviation! "); return; } int _t = Fraction(Data.Size(), 2); if(_t < 3) { printf(__FUNCSIG__ + " too small sample size, cannot generate minimum 2 regression points! "); return; } _points.Init(_t - 1, 2); _points.Fill(0.0); for (int t = 2; t <= _t; t++) { matrix _segments; int _rows = Fraction(Data.Size(), t); _segments.Init(_rows, t); int _r = 0, _c = 0; for(int s = 0; s < int(Data.Size()); s++) { _segments[_r][_c] = Data[s]; _c++; if(_c >= t) { _c = 0; _r++; if(_r >= _rows) { break; } } } ... } ... }
Поэтому на каждом этапе мы задействуем матрицу для регистрации непересекающихся сегментов из выборки данных. В общей итерации мы начинаем с наименьшего размера сегмента 2, а затем увеличиваем его до половины размера выборки данных. Вот почему у нас есть этап проверки размера выборки данных, на котором мы проверяем и видим, составляет ли половина ее размера не менее 3. Если значение меньше трех, то нет смысла вычислять показатель Херста, так как мы не сможем получить хотя бы две пары точек, необходимые для регрессии на последнем шаге.
Другой шаг проверки, который мы выполняем для выборки данных, заключается в том, чтобы убедиться в наличии изменчивости среди данных, поскольку нулевое стандартное отклонение приводит к недействительному значению или делению на ноль.
Корректировка среднего
После того как у нас есть набор сегментов на заданной итерации (где общее количество итераций ограничено половиной размера выборки), нам нужно найти среднее значение каждого сегмента. Поскольку наши сегменты находятся в матрице по строкам, каждую строку можно получить как вектор. Используя вектор каждой строки, мы можем легко получить среднее значение благодаря встроенной функции вектора mean, что избавляет от необходимости писать много кода. Затем среднее значение каждого сегмента вычитается из каждой точки данных в соответствующем сегменте. Это то, что называется корректировкой среднего (mean adjustment). Это важно в анализе масштабированного диапазона по ряду причин.
Во-первых, корректировка нормализует все данные по каждому сегменту, что гарантирует, что анализ будет сосредоточен на колебаниях относительно среднего значения, а не будет зависеть от абсолютных значений каждой точки данных в сегменте. Во-вторых, эта нормализация действительно служит цели уменьшения смещения в сторону искажений и выбросов, которые могут помешать достижению более репрезентативного масштаба диапазона.
Это также обеспечивает согласованность во всех сегментах, благодаря чему они становятся более сопоставимыми, чем если бы абсолютные значения рассматривались без этой нормализации. Мы проводим эту корректировку в MQL5 с помощью следующего исходного кода:
//+------------------------------------------------------------------+ // Function to Estimate Hurst Exponent & Constant C //+------------------------------------------------------------------+ void CSignalHurst::Hurst(vector &Data, double &H, double &C) { matrix _points; ... _points.Init(_t - 1, 2); _points.Fill(0.0); for (int t = 2; t <= _t; t++) { ... vector _means; _means.Init(_rows); _means.Fill(0.0); for(int r = 0; r < _rows; r++) { vector _row = _segments.Row(r); _means[r] = _row.Mean(); } ... } ... }
Матричные и векторные типы данных оказываются незаменимыми не только для поиска средних значений, но и для ускорения нормализации.
Накопленное отклонение
После того как мы получаем сегменты со скорректированным средним значением, нам необходимо просуммировать эти отклонения от среднего значения для каждого сегмента, чтобы получить накопленные отклонения (cumulative deviations) каждого сегмента. Это можно рассматривать как форму снижения размерности, которая служит основой анализа масштабированного диапазона. Мы делаем это следующим образом в нашем исходном коде:
//+------------------------------------------------------------------+ // Function to Estimate Hurst Exponent & Constant C //+------------------------------------------------------------------+ void CSignalHurst::Hurst(vector &Data, double &H, double &C) { matrix _points; ... _points.Init(_t - 1, 2); _points.Fill(0.0); for (int t = 2; t <= _t; t++) { matrix _segments; ... matrix _deviations; _deviations.Init(_rows, t); for(int r = 0; r < _rows; r++) { for(int c = 0; c < t; c++) { _deviations[r][c] = _segments[r][c] - _means[r]; } } vector _cumulations; _cumulations.Init(_rows); _cumulations.Fill(0.0); for(int r = 0; r < _rows; r++) { for(int c = 0; c < t; c++) { _cumulations[r] += _deviations[r][c]; } } ... } ... }
Итак, кратко подведем итог: для каждого значения t мы создаем группу сегментов, которые разделяют нашу выборку данных. Из каждой выборки мы получаем ее среднее значение и вычитаем среднее значение из точек данных в соответствующем сегменте. Это вычитание служит формой нормализации, и после его выполнения мы по сути получаем матрицу точек данных, где каждая строка представляет собой сегмент исходной выборки данных. В качестве метода уменьшения размерности сегментов мы суммируем эти отклонения от их соответствующих средних значений, так что многомерный сегмент дает нам единое значение. Это означает, что после того, как мы выполнили накопление отклонений в матрице, у нас остался вектор сумм, и этот вектор в нашем коде выше обозначен как _cumulations.
Масштабированный диапазон и логарифмический график
После того как мы получим накопления отклонений по всем сегментам вектора, следующим шагом будет простое нахождение диапазона, который представляет собой разницу между наибольшим и наименьшим общим отклонением. Имейте в виду, что когда мы регистрировали отклонения каждой точки данных в сегментах выше, мы не регистрировали абсолютное значение. Мы просто записали значение сегмента за вычетом его среднего значения. Это означает, что наши накопления очень легко могут в сумме дать ноль. Это то, что необходимо проверить перед тем, как приступить к вычислению показателя Херста, поскольку это может легко привести к недействительному результату. Эта проверка не выполняется в прилагаемом исходном коде, и читатели могут свободно вносить изменения. Этот предпоследний шаг мы выполняем в следующем коде:
//+------------------------------------------------------------------+ // Function to Estimate Hurst Exponent & Constant C //+------------------------------------------------------------------+ void CSignalHurst::Hurst(vector &Data, double &H, double &C) { matrix _points; ... _points.Init(_t - 1, 2); _points.Fill(0.0); for (int t = 2; t <= _t; t++) { ... ... _points[t - 2][0] = log((_cumulations.Max() - _cumulations.Min()) / _std); _points[t - 2][1] = log(t); } LinearRegression(_points, H, C); }
Как видно из приведенной выше части исходного кода, мы получаем накопленные диапазоны, а также их натуральные логарифмы, поскольку мы ищем показатель степени, а логарифмы помогают его вычислить. Из уравнения выше следует, что размер выборки находится на одной стороне уравнения, поэтому мы также получаем его натуральный логарифм, который служит нашим графиком по оси Y, а график по оси X представляет собой натуральный логарифм масштабированного диапазона, поделенного на стандартное отклонение выборки данных. Эти пары точек, x и y, уникальны для каждого размера сегмента. Другой размер сегмента в выборке данных представляет другую пару точек x и y, и чем больше их у нас, тем более репрезентативным является наш показатель Херста. Как упоминалось выше, общее количество возможных пар точек x-y, которые мы можем иметь, ограничено половиной размера выборки данных.
Итак, наша матрица _points представляет собой логарифмический график, полученный при анализе масштабированного диапазона. Именно этот график служит входными данными для расчетов линейной регрессии.
Линейная регрессия
Линейная регрессия выполняется функцией, отдельной от метода Херста. Ниже приведен ее простой код:
//+------------------------------------------------------------------+ // Function to perform linear regression //+------------------------------------------------------------------+ void CSignalHurst::LinearRegression(matrix &Points, double &Slope, double &Intercept) { double _sum_x = 0.0, _sum_y = 0.0, _sum_xy = 0.0, _sum_xx = 0.0; for (int r = 0; r < int(Points.Rows()); r++) { _sum_x += Points[r][0]; _sum_y += Points[r][1]; _sum_xy += (Points[r][0] * Points[r][1]); _sum_xx += (Points[r][0] * Points[r][0]); } Slope = ((Points.Rows() * _sum_xy) - (_sum_x * _sum_y)) / ((Points.Rows() * _sum_xx) - (_sum_x * _sum_x)); Intercept = (_sum_y - (Slope * _sum_x)) / Points.Rows(); }
Линейная регрессия - это процесс, при котором мы получаем ключевые коэффициенты в уравнении y = mx + c для заданного набора точек. Предоставленные коэффициенты определяют уравнение для наилучшей линии соответствия этих входных точек x-y. Это уравнение важно для нас, поскольку наклон этой линии наилучшего соответствия является показателем Херста, а y-пересечение служит константой C. Функция LinearRegression принимает в качестве опорных входных данных два значения типа double, которые служат показателем Херста и заполнителем константы C, и, как и функция Херста, она возвращает void.
В этой статье нашей основной целью является вычисление показателя Херста, однако часть выходных данных, которые мы получаем в результате этого процесса, как уже упоминалось выше, представляет собой C-константу. Какой же цели служит эта C-константа? Это метрика изменчивости выборки данных. Рассмотрим сценарий, в котором ценовые ряды двух активов имеют одинаковый показатель Херста, но разные константы C, где у одного C равен 7, а у другого C равен 21.
Одинаковое значение показателя указывает на то, что два актива имеют схожие характеристики "устойчивости", то есть, если показатель Херста для обоих активов ниже 0,5, то оба актива, как правило, часто возвращаются к прежнему уровню, а если показатель больше 0,5, то они, как правило, часто демонстрируют тенденцию к тренду в долгосрочной перспективе. Однако их различные константы C, несмотря на схожее ценовое поведение, явно указывают на различные профили риска. Это связано с тем, что C-константу можно рассматривать как показатель волатильности. Активы с более высокой C-константой будут иметь более широкие колебания цен по сравнению со средними значениями в отличие от активов с меньшей C-константой. Это может означать различные режимы определения размера позиции по двум активам, при условии что все остальные факторы остаются неизменными.
Компиляция в класс сигнала
Мы используем сгенерированные нами значения показателя Херста для определения условий на покупку и продажу торгуемого символа в рамках пользовательского класса сигналов. Показатель Херста предназначен для отражения долгосрочных тенденций, поэтому по определению он имеет тенденцию быть более точным, когда размер выборки стремится к бесконечности. Однако для практических целей нам необходимо измерять его на основе определенного размера исторических цен на ценные бумаги. Мы будем рассматривать одну из двух различных скользящих средних при оценке наших условий на покупку и продажу, поэтому определенный размер истории, используемый при вычислении показателя Херста, принимается равным сумме двух периодов, используемых при вычислении этих двух средних.
Этого может быть недостаточно, поскольку, как уже упоминалось, чем длиннее период выборки данных, тем по определению надежнее показатель Херста, поэтому читатель может внести необходимые изменения, чтобы получить более репрезентативный для него размер истории. Как всегда, полный исходный код прилагается. Итак, для каждой из функций условия (на покупку и продажу) мы начинаем с копирования цен закрытия в вектор размером до размера нашей выборки данных. Размер нашей выборки данных представляет собой сумму длинных и коротких периодов.
После этого мы вычисляем показатель Херста, вызывая функцию Херста, а затем оцениваем возвращенное значение, чтобы определить, как оно соотносится с 0,5. Возможны вариации этой реализации, в которых пороговое значение добавляется к значению выше и ниже 0,5, чтобы сузить точки входа или принятия решения. Если наш коэффициент Херста выше 0,5, то наблюдается инерционность, и поэтому для долгосрочного условия мы будем смотреть, находимся ли мы выше скользящей средней медленного периода (долгосрочной). Если это так, то это может указывать на возможность бычьей позиции. Аналогично, для условия на продажу мы бы посмотрели, находимся ли мы ниже скользящей средней медленного периода, и если это так, это будет означать открытие короткой позиции.
Если показатель Херста ниже 0,5, это будет означать, что мы находимся на флэтовом рынке или рынке, возвращающемся к среднему значению. В этом случае мы сравним текущую цену bid со скользящей средней быстрого периода. При условии на покупку, если цена ниже быстрой скользящей средней, это будет указывать на бычью позицию. И наоборот, при условии на продажу, если цена выше скользящей средней быстрого периода, то это указывает на короткую позицию. Реализация этих двух условий представлена ниже:
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalHurst::LongCondition(void) { int result = 0; vector _data; if(_data.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period + m_slow_period)) { double _hurst = 0.0, _c = 0.0; Hurst(_data, _hurst, _c); vector _ma; if(_hurst > 0.5) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period)) { if(m_symbol.Bid() > _ma.Mean()) { result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } else if(_hurst < 0.5) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period)) { if(m_symbol.Bid() < _ma.Mean()) { result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } } return(result); } //+------------------------------------------------------------------+ //| "Voting" that price will fall. | //+------------------------------------------------------------------+ int CSignalHurst::ShortCondition(void) { int result = 0; vector _data; if(_data.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period + m_slow_period)) { double _hurst = 0.0, _c = 0.0; Hurst(_data, _hurst, _c); vector _ma; if(_hurst > 0.5) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period)) { if(m_symbol.Bid() < _ma.Mean()) { result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } else if(_hurst < 0.5) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period)) { if(m_symbol.Bid() > _ma.Mean()) { result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } } return(result); }
Тестирование стратегии и отчеты
Тесты на 4-часовом таймфрейме для пары GBPCHF за 2023 год дали следующие результаты:
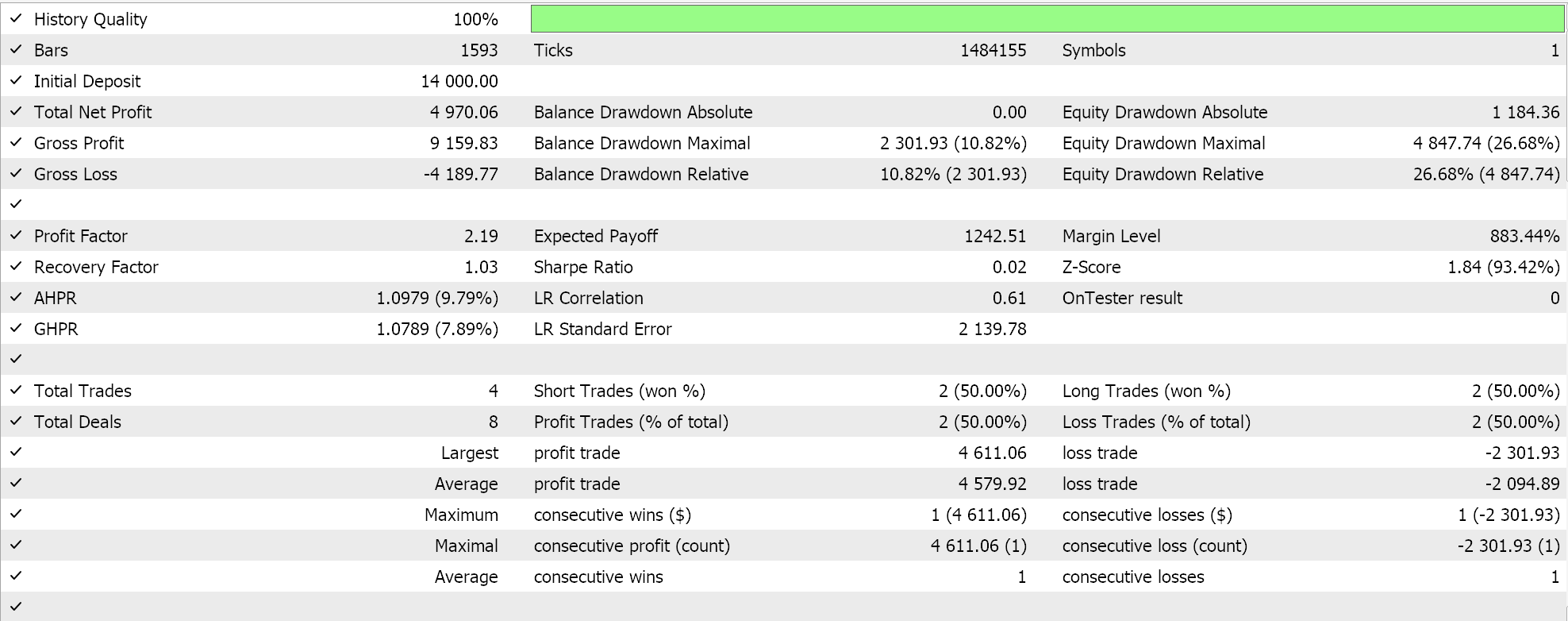
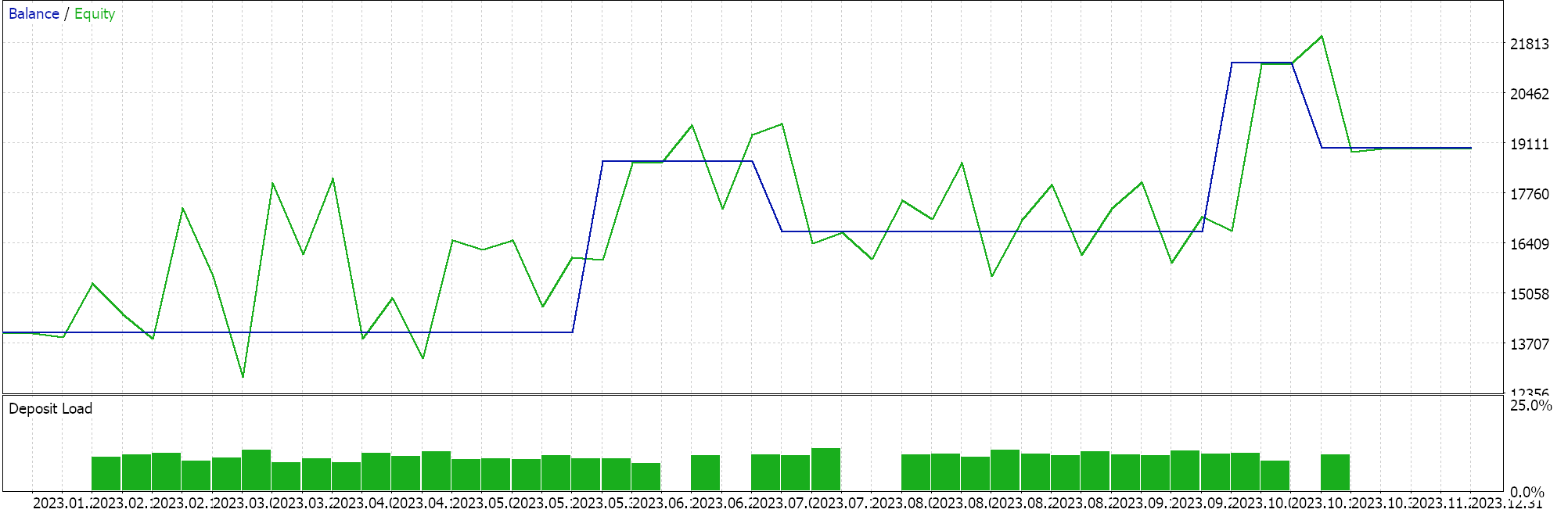
Сделок относительно немного. Это может быть хорошим знаком, поскольку указывает на дискриминантный советник. Однако, как всегда, прежде чем принимать какие-либо решения об эффективности советника, необходимо провести тестирование на более длительных периодах, особенно с использованием форвард-тестов.
Необработанная автокорреляция как инструмент контроля
Показатель Херста, как утверждается, способен оценить, имеет ли ряд устойчивые признаки (значения выше 0,5) или является неустойчивым (значения ниже 0,5), выступая в качестве метрики автокорреляции. Но если предположить, что мы просто измерили корреляции рядов данных, не утруждая себя вычислением этой экспоненты, и использовали результаты наших фактических измерений корреляций для оценки рыночных условий, насколько по-другому будет работать наш советник?
Мы разрабатываем такой пользовательский класс сигналов, который, как и следовало ожидать, имеет меньше функций и просто сначала оценивает любые положительные корреляции в течение более длительного (медленного) периода усреднения. Если такая положительная корреляция существует, то скользящая средняя за этот более медленный период используется для оценки настроек следования за трендом, где цены выше этой средней являются бычьими, а цены ниже нее — медвежьими. Однако если положительной корреляции за более длительные периоды не наблюдается, то отрицательная корреляция ищется за более короткий (быстрый) период усреднения. В этом случае мы будем искать значения настроек, возвращающиеся к среднему значению, где цена ниже быстрой скользящей средней будет бычьей, а цена выше нее — медвежьей. Код для нашего условия на покупку/продажу выглядит следующим образом:
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalAC::LongCondition(void) { int result = 0; vector _new,_old; if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_slow_period, m_slow_period)) { vector _ma; if(_new.CorrCoef(_old) >= m_threshold) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period)) { if(m_symbol.Bid() > _ma.Mean()) { result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } else if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_fast_period, m_fast_period)) { if(_new.CorrCoef(_old) <= -m_threshold) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period)) { if(m_symbol.Bid() < _ma.Mean()) { result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } } } return(result); } //+------------------------------------------------------------------+ //| "Voting" that price will fall. | //+------------------------------------------------------------------+ int CSignalAC::ShortCondition(void) { int result = 0; vector _new,_old; if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_slow_period, m_slow_period)) { vector _ma; if(_new.CorrCoef(_old) >= m_threshold) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period)) { if(m_symbol.Bid() < _ma.Mean()) { result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } else if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_fast_period, m_fast_period)) { if(_new.CorrCoef(_old) <= -m_threshold) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period)) { if(m_symbol.Bid() > _ma.Mean()) { result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } } } return(result); }
Мы провели почти аналогичные тестовые прогоны для той же пары GBPCHF на 4-часовом временном интервале за 2023 год. Результаты лучших прогонов представлены ниже:
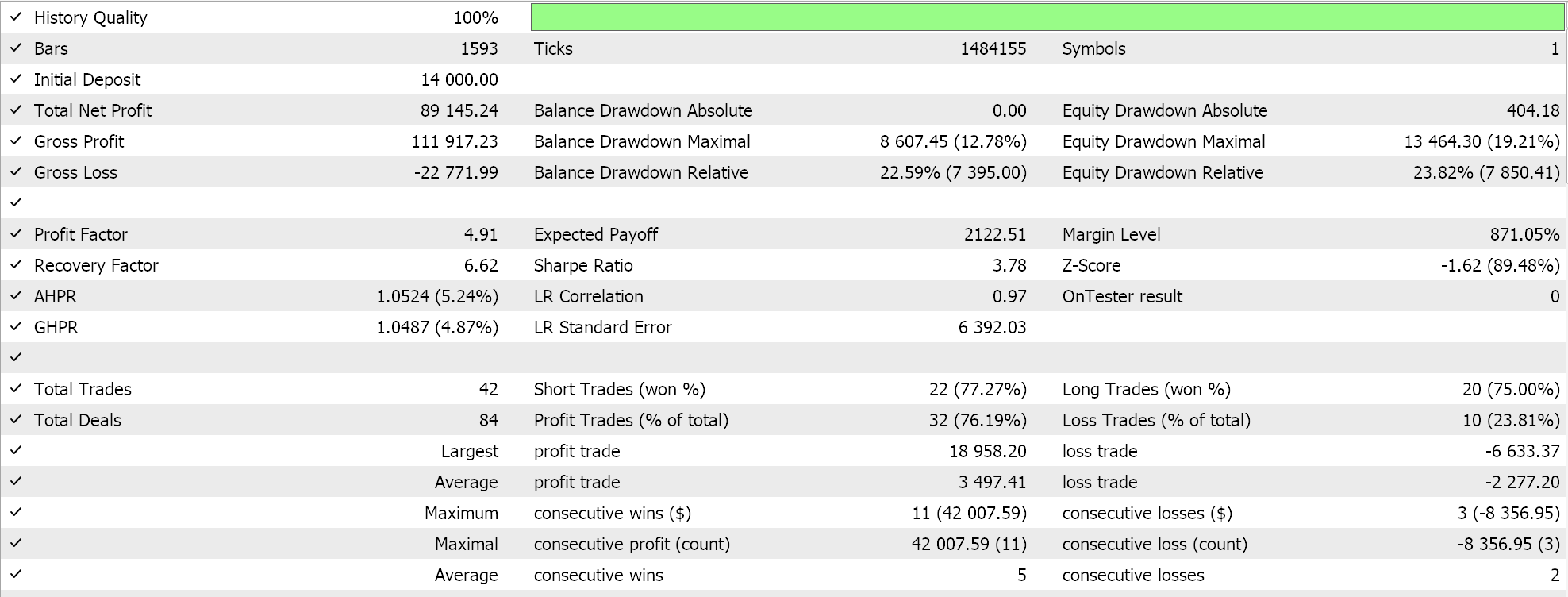
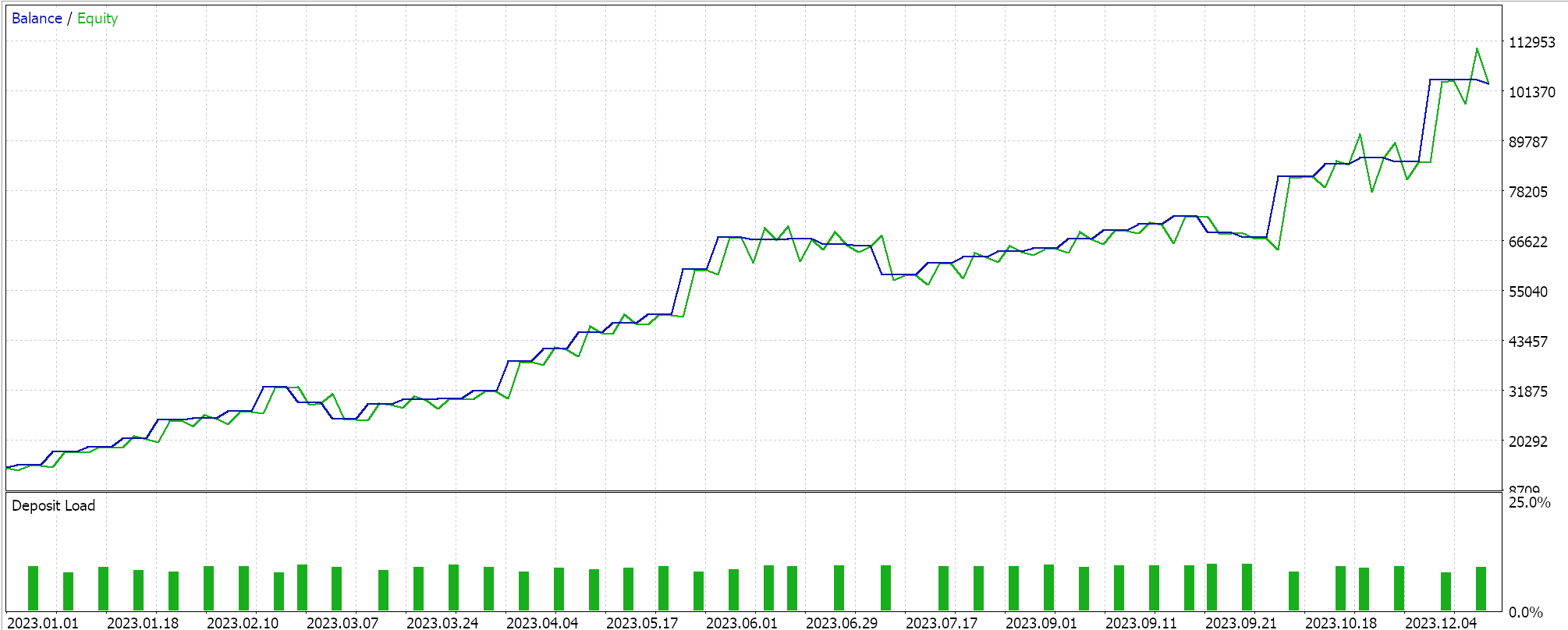
Очевидно, что между этим сигналом и сигналом показателя Херста наблюдается разница в производительности.
Заключение
Показатель Херста был разработан в начале прошлого века в первую очередь как инструмент для потенциального прогнозирования приливов и отливов реки Нил на основе данных об отметках уровня воды. С тех пор он был принят на вооружение во многих отраслях, среди которых — анализ финансовых временных рядов. В этой статье мы объединили показатель временного ряда со скользящими средними, чтобы лучше отличать трендовые рынки от рынков, возвращающихся к среднему, и создать пользовательский класс сигналов.
Несмотря на то, что, судя по первым же проведенным нами тестам, у него явно есть определенный потенциал, очевидно, что его использование ЕЩЕ не обосновано, учитывая его относительную производительность по сравнению с нашим необработанным сигналом автокорреляции. Он требует больших вычислительных ресурсов, чрезмерно фильтрует сделки, а его лучшие прогоны проходят со слишком большой просадкой, что вызывает беспокойство, учитывая относительно небольшое тестовое окно, используемое для этих прогонов. Как всегда, независимые тестовые прогоны могут дать иные и даже более многообещающие результаты. При желании вы можете провести такие тесты. Сборка и компиляция прилагаемого исходного кода в советник выполняется в соответствии с рекомендациями, приведенными здесь и здесь. Дальнейшие тесты рекомендуется проводить с использованием реальных данных брокера и на достаточно продолжительном периоде времени.
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/15222
Разработка системы репликации (Часть 57): Анализируем тестовый сервис
Переосмысливаем классические стратегии на языке Python: Пересечения скользящих средних
Нейросети в трейдинге: Модели с использованием вейвлет-преобразовании и многозадачного внимания
Нейросети в трейдинге: Гибридный торговый фреймворк с предиктивным кодированием (Окончание)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Привет, Стивен,
Я получил огромное удовольствие от Ваших статей. Статья Hurst представила результаты автокорреляции, которые были особенно интересны. Я скачал Ваши исходники, скомпилировал и запустил тест советника Hurst CTL. Результаты оказались весьма разочаровывающими - убыток 3108 против Вашего выигрыша 89 145.
Я сравнил исходные тексты с вашим оригиналом, и единственные изменения были внесены в операторы include. В качестве источника данных я использовал Forex.com.
Возможно, вы сможете определить, почему эти два результата так кардинально отличаются.
Будьте здоровы,
CapeCoddah
Привет, Стивен,
Мне очень понравились ваши статьи о волшебнике. В статье о Херсте были представлены результаты автокорреляции, которые были особенно интересны. Я скачал ваши исходники, скомпилировал и провел тест советника Hurst CTL. Результаты оказались весьма неутешительными - убыток 3108 против вашего выигрыша 89 145.
Я сравнил исходники с вашим оригиналом, и единственные изменения коснулись операторов включения. В качестве источника данных я использовал Forex.com.
Возможно, вы сможете определить, почему эти два результата так сильно отличаются.
Будьте здоровы,
CapeCoddah
Здравствуйте,
Только что увидел это. Результаты, которые вы получаете в тестере стратегий, зависят от входов в советник. Обычно, но не всегда, я использую лимитные ордера с целями по тейк-профиту без стоплосса. Такая настройка не будет идеальной, если рассматривать эти идеи дальше, так как необходимо будет установить стоплосс или максимальный период удержания, или какую-то стратегию, которая смягчит ваш минус.
Идеи, представленные здесь, носят исключительно ознакомительный характер и не являются торговыми советами, но воспроизведение отчетов тестера моих стратегий должно быть легким, если вы точно настроите свои входные данные.
Спасибо за чтение.
Спасибо за ответ.
Я предположил, что для получения прибыли, показанной в BackTest, использовались входные данные советника, указанные в загруженном zip-файле. Я пересмотрю входные данные и скорректирую их в соответствии с вашими значениями по умолчанию.