Merkmalsauswahl und Dimensionenreduktion mit Hilfe von Hauptkomponenten

Einführung

Bei der Vorhersage von Finanzzeitreihen werden häufig zahlreiche Merkmale analysiert, von denen viele stark korreliert sein können. Techniken zur Dimensionenreduzierung wie die Hauptkomponentenanalyse (Principal Component Analysis, PCA) können zu einer kompakteren Darstellung dieser Merkmale beitragen. Die PCA hat jedoch ihre Grenzen, insbesondere bei stark korrelierten Variablen. In solchen Fällen neigt die PCA dazu, den Gruppierungseffekt zu zeigen, bei dem eine Reihe von hoch korrelierten Variablen gemeinsam zu einer bestimmten Hauptkomponente beiträgt. Anstatt eine einzelne Variable hervorzuheben, verteilt die PCA den Einfluss relativ gleichmäßig auf alle Variablen in der korrelierten Gruppe.

Diese gleichmäßige Verteilung kann für die Rauschunterdrückung von Vorteil sein, da die Hauptkomponenten gemeinsame Muster hervorheben und nicht die zufälligen Schwankungen, die für einzelne Variablen typisch sind. Diese Rauschunterdrückung hat jedoch ihren Preis: Sie verwässert häufig den Beitrag der einzelnen Variablen zu jeder Hauptkomponente. Variablen, die für sich genommen bedeutsam sein könnten, können im transformierten Raum weniger wichtig erscheinen, da ihr Einfluss in der breiteren Struktur, die von der Gruppe erfasst wird, absorbiert wird. Dies kann bei Aufgaben wie der Variablenauswahl, bei der es darum geht, die einflussreichsten Merkmale zu ermitteln, oder bei der Ursachenanalyse, bei der das Verständnis der direkten Auswirkungen bestimmter Variablen entscheidend ist, ein erheblicher Nachteil sein.

Außerdem erschwert dieses Merkmal die Interpretation des Modells. Da jede Hauptkomponente eine Kombination aller ursprünglichen Variablen darstellt, kann es schwierig sein, den Beitrag dieser Komponenten in den Kontext der ursprünglichen Variablen zurück zu übertragen. Für Praktiker kann es schwierig sein, klare Erkenntnisse aus den Hauptkomponenten zu ziehen, da es schwierig ist zu bestimmen, welche ursprünglichen Variablen die beobachteten Muster bestimmen. Um dieses Problem anzugehen, stellen wir eine Implementierung der Forward Selection Component Analysis (FSCA) vor, eine Methode, die von der Arbeit von Luca Puggini und Sean McLoone inspiriert ist und die darauf abzielt, die Fallstricke der PCA zu vermeiden, wenn es um stark korrelierte Merkmale geht.

Forward Selection Component Analysis

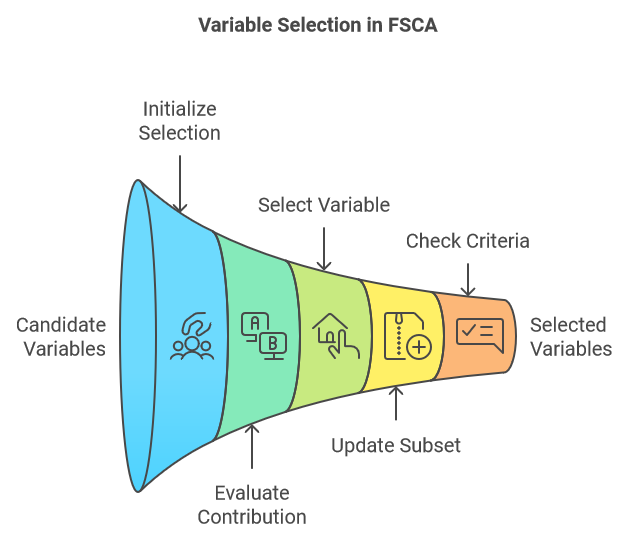
Die Forward Selection Component Analysis (FSCA), zu deutsch Komponentenanalyse der Vorwärtsauswahl, ist eine Technik zur Dimensionenreduktion, die Dimensionenreduktion und Merkmalsauswahl kombiniert, indem sie die informativsten Variablen zur Erklärung der ursprünglichen Daten ermittelt. FSCA verwendet einen gierigen Ansatz, bei dem eine Variable nach der anderen auf der Grundlage ihrer Fähigkeit, die verbleibende Varianz in den Daten zu erfassen, ausgewählt wird. Im Folgenden werden die wichtigsten Schritte des FSCA-Verfahrens beschrieben:

1. Initialisierung:
   
   • Beginnen wir mit einer leeren Menge ausgewählter Variablen und einer vollständigen Menge von Kandidatenvariablen.
   • Wir berechnen die Gesamtvarianz des Datensatzes
   • und beginnen den iterativen Prozess, indem wir die Variable auswählen, die die Werte aller anderen Variablen am besten vorhersagt, und stellen sicher, dass diese Wahl den maximalen Anteil der erklärten Varianz erfasst.
     
2. Iterative Auswahl:
   
   • Bei jedem Schritt wird der Beitrag jeder verbleibenden Kandidatenvariable zur Erklärung der Varianz bewertet, wenn sie zur aktuellen Gruppe der ausgewählten Variablen hinzugefügt wird.
   • Es werden die Variable ausgewählt, die den größten Anstieg der Erklärung der Varianz bewirkt, wenn sie der Teilmenge hinzugefügt wird.
     
3. Aktualisierung:
   
   • Die ausgewählte Variable wird der zur Untergruppe der ausgewählten Variablen hinzugefügt.
   • Die ausgewählte Variable wird aus der Menge der Kandidatenvariablen ausgeschieden.
   • Die Restvarianz bzw. die verbleibende, unerklärte Varianz wird nach Berücksichtigung der Beiträge der ausgewählten Variablen neu berechnet.
     
4. Stopp-Kriterien:
   
   • Der Prozess wird fortgesetzt, bis ein vorher festgelegtes Abbruchkriterium erfüllt ist. Dabei kann es sich um eine bestimmte Anzahl ausgewählter Variablen, einen Zielanteil an der erklärten Gesamtvarianz oder einen Schwellenwert für die zusätzliche Varianz handeln, die durch das Hinzufügen einer neuen Variablen erklärt wird.

     
     

Bei einer Reihe von Rohvariablen ordnen wir diese in einer Matrix an, wobei jede Spalte für ein bestimmtes Merkmal und jede Zeile für eine einzelne Stichprobe steht. Die Rohwerte werden zunächst durch eine Normierung transformiert. Von diesem Zeitpunkt an bezieht sich jede Bezugnahme auf die ursprünglichen Variablen auf die Menge der standardisierten Variablen, die wir als Matrix X bezeichnen werden. Diese Matrix X hat v Spalten (Variablen). Der FSCA-Algorithmus erzeugt mindestens drei neue Sätze von Variablen:

• Matrix Z: Diese Matrix besteht aus einer Teilmenge k (mit k<v) der Spalten von X, die danach geordnet sind, wie gut sie zur Rekonstruktion von X beitragen. Diese Spalten werden als Forward Selection Variables (FSV) bezeichnet.
• Matrix M: Die Spalten dieser Matrix werden als Forward Selection Components (FSC) bezeichnet. Jede Komponente ist eine Funktion der entsprechenden Spalte in Z sowie gegebenenfalls der vorangehenden Spalten.
• Matrix U: Diese Matrix enthält die Koeffizienten oder Ladungen, die in Kombination mit den FSV die FSC ergeben.
  

Ziel des Algorithmus ist es, eine optimale Teilmenge von Variablen zu erhalten, die die einzigartige Variation in X am besten repräsentiert. Dies ist jedoch ein anspruchsvolles Optimierungsproblem. Bei FSCA ist nicht immer gewährleistet, dass die optimale Teilmenge von Variablen gemäß den festgelegten Optimierungskriterien gefunden wird. Bei großen Datensätzen kann es unpraktisch sein, alle möglichen Teilmengen zu durchsuchen, daher bietet FSCA einen pragmatischeren Ansatz. Dennoch gelingt es manchmal nicht, die optimale Teilmenge zu finden, weil die in frühen Iterationen ausgewählten Variablen redundant werden können, wenn zusätzliche Variablen hinzugefügt werden. Um diese Einschränkung zu beheben, schlagen die Autoren des eingangs erwähnten Forschungspapiers vor, einen Schritt der Rückwärtsverfeinerung (backward refinement) in das FSCA-Verfahren einzuführen.

FSCA mit Rückwärtsverfeinerung

Die Rückwärtsverfeinerung ist ein Verfahren, das das Entfernen und Ersetzen von zuvor ausgewählten Variablen ermöglicht. Bei diesem Prozess wird der Beitrag jeder ausgewählten Variable zur erklärten Gesamtvarianz neu bewertet und es werden alternative Variablen in Betracht gezogen, die eine bessere Übereinstimmung bieten könnten. Dadurch kann zwar die Qualität des endgültigen Variablensatzes verbessert werden, doch wird die strenge Reihenfolge der Wichtigkeit, die bei der reinen Vorwärtsauswahl beibehalten wird, geopfert.

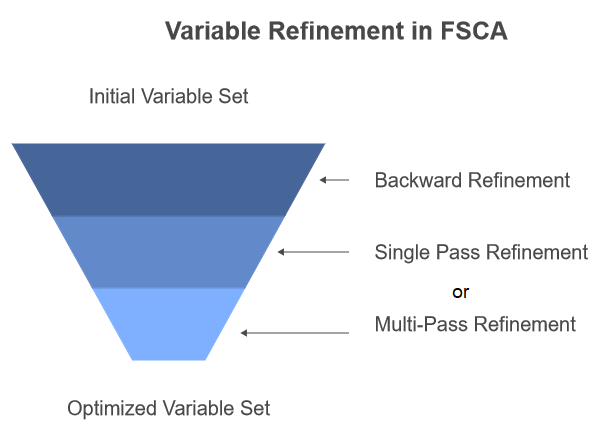
Das Forschungspapier skizziert zwei Ansätze für die Einbeziehung der Rückwärtsverfeinerung. Beim ersten Ansatz wird die Rückwärtsverfeinerung nach Abschluss aller Schritte der FSCA als Nachbearbeitungsschritt angewendet. Beim zweiten Ansatz, der rekursiven Rückwärtsverfeinerung, wird jedes Mal eine Rückwärtsverfeinerung durchgeführt, wenn am Ende von Schritt 3 des FSCA-Algorithmus eine neue Variable zu Z hinzugefügt wird. Dieser Ansatz ist in dem Code implementiert, der in einem späteren Abschnitt dieses Textes vorgestellt wird.

Es gibt auch zwei Varianten für den Verfeinerungsschritt selbst. Bei der ersten Methode, dem Single Pass Backward Refinement (SPBR), wird die Relevanz jeder Variablen der Reihe nach bewertet, und zwar von der ältesten zur neuesten. Die zweite Methode, das Multi-Pass Backward Refinement (MPBR), trägt der Tatsache Rechnung, dass ursprünglich als relevant erachtete Variablen irrelevant werden können, wenn später in der Sequenz Anpassungen an Variablen vorgenommen werden. Bei MPBR wird der Prozess so lange wiederholt, bis ein vollständiger Durchlauf ohne weitere Verfeinerungen erfolgt. Beachten Sie, dass der später in diesem Artikel vorgestellte Code nur SPBR implementiert.

In den folgenden Abschnitten werden wir die einzelnen Schritte des FSCA-Algorithmus anhand von Mathematik und Code genauer beschreiben. Alle referenzierten Codeschnipsel stammen aus der Datei fsca.mqh, die am Ende dieses Artikels angehängt ist.

Hauptkomponenten

Der FSCA-Algorithmus stützt sich auf die Verwendung von Hauptkomponenten, um zunächst die eindeutigen Variationsquellen im Datensatz X zu identifizieren. Dieser Schritt liefert auch einen Hinweis auf die maximale Anzahl von Komponentenvariablen für die Z-Matrix, indem er den Wert von k (wie zuvor definiert) bestimmt. In dem Forschungspapier verwendet der Algorithmus einen vom Nutzer festgelegten k-Wert. In unserer Implementierung wird k jedoch immer gleich der Anzahl der Hauptkomponenten gesetzt. Die Hauptkomponenten werden durch Zerlegung der Eigenwerte der Korrelationsmatrix von X ermittelt. Das folgende Listing zeigt die Routine zur Berechnung der Faktorenstruktur mit Hilfe der Funktion compute_factor_structure().

//+------------------------------------------------------------------+
//| computes the factor structure of a correlation matrix            |
//+------------------------------------------------------------------+
matrix            compute_factor_structure(matrix &covar,matrix &eigenvectors,vector &eigenvalues,vector &cumeigenvalues)
  {
   if(!covar.EigenSymmetricDC(EIGVALUES_V,eigenvalues,eigenvectors))
     {
      Print(__FUNCTION__, " error ", GetLastError());
      return matrix::Zeros(1,1);
     }
   double sum = 0.0;


   if(!np::reverseVector(eigenvalues) ||  !np::reverseMatrixCols(eigenvectors))
     {
      Print(__FUNCTION__, " reverse operation error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   double cumulate[];
   for(ulong i=0 ; i<eigenvalues.Size() ; i++)
     {
      if(eigenvalues[i]>1.e-8)
        {
         sum += eigenvalues[i] ;
         if(!cumulate.Push(sum))
           {
            Print(__FUNCTION__," error adding element ", GetLastError());
            return matrix::Zeros(1,1);
           }
        }
     }

   if(!cumeigenvalues.Assign(cumulate))
     {
      Print(__FUNCTION__," vector assignment error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   cumeigenvalues/=cumeigenvalues[cumeigenvalues.Size()-1];

   cumeigenvalues*=100.0;

   matrix structmat=eigenvectors;

   for(ulong i = 0; i<structmat.Cols(); i++)
      if(!structmat.Col(eigenvectors.Col(i)*sqrt(eigenvalues[i]>=0.0?eigenvalues[i]:0.0),i))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return matrix::Zeros(1,1);
        }

   if(!structmat.Clip(-1.0,1.0))
     {
      Print(__FUNCTION__, "error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   return structmat;
  }

//+------------------------------------------------------------------+
//| computes the factor structure of a correlation matrix            |
//+------------------------------------------------------------------+
matrix compute_factor_structure(matrix &covar, matrix &eigenvectors, vector &eigenvalues, vector &cumeigenvalues) {
    if (!covar.EigenSymmetricDC(EIGVALUES_V, eigenvalues, eigenvectors)) {
        Print(__FUNCTION__, " error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    double sum = 0.0;

    if (!np::reverseVector(eigenvalues) || !np::reverseMatrixCols(eigenvectors)) {
        Print(__FUNCTION__, " reverse operation error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    double cumulate[];
    for (ulong i = 0; i < eigenvalues.Size(); i++) {
        if (eigenvalues[i] > 1.e-8) {
            sum += eigenvalues[i];
            if (!cumulate.Push(sum)) {
                Print(__FUNCTION__, " error adding element ", GetLastError());
                return matrix::Zeros(1, 1);
            }
        }
    }

    if (!cumeigenvalues.Assign(cumulate)) {
        Print(__FUNCTION__, " vector assignment error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    cumeigenvalues /= cumeigenvalues[cumeigenvalues.Size() - 1];
    cumeigenvalues *= 100.0;

    matrix structmat = eigenvectors;

    for (ulong i = 0; i < structmat.Cols(); i++) {
        if (!structmat.Col(eigenvectors.Col(i) * sqrt(eigenvalues[i] >= 0.0 ? eigenvalues[i] : 0.0), i)) {
            Print(__FUNCTION__, "error ", GetLastError());
            return matrix::Zeros(1, 1);
        }
    }

    if (!structmat.Clip(-1.0, 1.0)) {
        Print(__FUNCTION__, "error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    return structmat;
}

Diese Funktion nimmt eine Korrelationsmatrix, covar, als Eingabe und gibt eine Matrix mit den Faktorladungen zurück. Sie führt eine Eigenwertzerlegung der Korrelationsmatrix mit Hilfe der Funktion EigenSymmetricDC durch. Die sich daraus ergebenden Eigenwerte werden im Eigenwertvektor gespeichert, während die Eigenvektoren in der Eigenvektor-Matrix gespeichert werden. Die Funktion kehrt dann die Reihenfolge der Eigenwerte und Eigenvektoren um, um sicherzustellen, dass sie in absteigender Reihenfolge sortiert sind. Sie berechnet die kumulativen Eigenwerte durch iterative Summierung und speichert diese im Vektor der kumulativen Eigenwerte. Die kumulativen Eigenwerte werden normalisiert, um den Prozentsatz der Gesamtvarianz darzustellen.

Anschließend berechnet die Funktion die Faktorladungen, indem sie jeden Eigenvektor mit der Quadratwurzel des entsprechenden Eigenwerts multipliziert und das Ergebnis in der Strukturmatrix speichert. Um sicherzustellen, dass die Faktorladungen in einem vernünftigen Bereich bleiben, werden sie zwischen -1 und 1 abgeschnitten. Schließlich gibt die Funktion die Matrix structmat zurück, die die berechneten Faktorwerte enthält.

Die aus der Korrelationsmatrix abgeleitete Faktorenstruktur besteht aus Faktorwerte, die die Beziehungen zwischen den Variablen und den zugrunde liegenden latenten Faktoren darstellen. Diese Werte helfen, die Bedeutung der latenten Faktoren zu interpretieren und die Bedeutung der einzelnen Variablen für die Erklärung der Varianz in den Daten zu bewerten.

Die Ausgabe von compute_factor_structure() wird in der Funktion compute_principal_components() zur Berechnung der Hauptkomponenten verwendet.

//+------------------------------------------------------------------+
//|   calculates the principal components                            |
//+------------------------------------------------------------------+
matrix compute_principal_components(void) {
    matrix out(m_data.Rows(), ulong(m_num_comps));
    vector drow, eigcol, nv;
    double sum;

    for (ulong i = 0; i < m_data.Rows(); i++) {
        drow = m_data.Row(i);
        for (ulong j = 0; j < m_num_comps; j++) {
            sum = 0.0;
            for (ulong k = 0; k < m_data.Cols(); k++) {
                sum += drow[k] * m_eigvectors[k][j] / sqrt(m_eigvalues[j]);
            }
            out[i][j] = sum;
        }
    }

    return out;
}

Die Funktion compute_principal_components() benötigt keine Eingabeparameter und gibt eine Matrix mit den Hauptkomponenten zurück. Zur Speicherung der Hauptkomponenten wird eine Ausgabematrix out initialisiert, deren Dimensionen der Anzahl der Zeilen in den Eingabedaten und der Anzahl der gewünschten Hauptkomponenten entsprechen. Die Funktion iteriert über jede Zeile der Eingabedatenmatrix und berechnet jede Hauptkomponente, indem sie das Punktprodukt der Zeile mit dem entsprechenden Eigenvektor der Kovarianzmatrix bildet, geteilt durch die Quadratwurzel des zugehörigen Eigenwerts. Die resultierende Hauptkomponente wird in der Out-Matrix gespeichert. Diese Funktion berechnet die Hauptkomponenten unter Verwendung der Standardformel für die Projektion von Datenpunkten auf den Hauptkomponenten-Unterraum.

Das grundlegende Konzept, das den Hauptkomponenten zugrunde liegt, ist die Annäherung an die ursprüngliche Datenmatrix X, die viele Variablen enthält, durch einen reduzierten Satz von Komponentenvariablen. Diese Annäherung wird durch eine lineare Transformation erreicht.

Wir können den Fehler in dieser Annäherung bewerten, indem wir die Summe der quadrierten Differenzen zwischen X und seiner Annäherung berechnen.

Alternativ können wir die Qualität der Annäherung bewerten, indem wir den Anteil der Gesamtvarianz von X berechnen, der durch die Komponentenvariablen erklärt wird.

Um eine optimale Annäherung zu erreichen, müssen wir strategisch eine Teilmenge von Spalten aus X auswählen, um Z zu bilden, das zur Berechnung der Komponentenvariablen verwendet wird. Es ist wichtig zu beachten, dass die Hauptkomponenten und die endgültigen Komponentenvariablen, die durch die Matrix M dargestellt werden, unterschiedlich sind.

Maximierung der erklärten Varianz

Einer der wichtigsten Schritte im FSCA-Algorithmus ist die Auswahl der optimalen Variablen, die der bestehenden Teilmenge hinzugefügt werden soll. Zu diesem Zweck weisen wir jeder potenziellen Variablen eine Punktzahl zu und wählen diejenige mit der höchsten Punktzahl aus. Die Berechnung dieses Kriteriums (Punktzahl) ist, wie in dem Forschungspapier beschrieben, relativ komplex. Die Autoren liefern jedoch einen mathematischen Beweis dafür, dass die Rangfolge dieses Kriteriums für konkurrierende Variablen mit der Rangfolge ihrer erklärten Varianz übereinstimmt. Das bedeutet, dass die Variable mit der höchsten Punktzahl auch die erklärte Varianz maximiert.

Eine einfachere Möglichkeit, die Berechnung der Punktzahl für jede potenzielle Variable zu beschreiben, ist die unten stehende Gleichung. Leser, die an der mathematischen Herleitung der Formel interessiert sind, können diese in der Forschungsarbeit nachlesen.

Z(i) ist die Matrix Z, zu der die Spalte i von X hinzugefügt wird.
Die Variable x(j) ist Spalte j von X
Der Term v ist die Anzahl der Variablen (Spalten) in X
Der Zwischenterm q ist ein Spaltenvektor mit k Elementen Länge

Nachfolgend finden Sie den Code, der die Berechnung des Kriteriums durchführt.

//+------------------------------------------------------------------+
//|  calculates the criterion for assessing a component              |
//+------------------------------------------------------------------+
double compute_criterion(matrix &covar, ulong &keptcols[], ulong nkept, ulong trial_col) {
    ulong i, j, k, irow, new_kept;
    double sum, crit, dtemp;
    new_kept = nkept + 1;
    matrix mt(new_kept, new_kept);

    for (i = 0; i < new_kept; i++) {
        if (i < nkept)
            irow = keptcols[i];
        else
            irow = trial_col;

        for (j = 0; j < nkept; j++)
            mt[i][j] = covar[irow][keptcols[j]];

        mt[i][nkept] = covar[irow][trial_col];
    }

    matrix mtinv = mt.Inv();
    vector vec(new_kept);

    crit = 0.0;
    for (j = 0; j < m_preds; j++) {
        for (i = 0; i < nkept; i++)
            vec[i] = covar[j][keptcols[i]];

        vec[nkept] = covar[j][trial_col];

        sum = 0.0;
        for (i = 0; i < new_kept; i++)
            sum += vec[i] * vec[i] * mtinv[i][i];

        crit += sum;

        sum = 0.0;
        for (i = 1; i < new_kept; i++) {
            dtemp = vec[i];
            for (k = 0; k < i; k++)
                sum += dtemp * vec[k] * mtinv[i][k];
        }

        crit += 2.0 * sum;
    }

    return crit;
}

Die Funktion compute_criterion() berechnet ein Kriterium für die Bewertung einer Komponente im Merkmalsauswahlprozess. Als Eingabe dient eine Korrelationsmatrix, covar, ein Array ausgewählter Variablen, keptcols, die Anzahl der ausgewählten Variablen, nkept, und der Index der auszuwertenden Versuchsvariablen.

Die Funktion beginnt mit der Erstellung einer neuen Matrix, mt, die den bestehenden Satz ausgewählter Variablen um die Versuchsvariable ergänzt. Anschließend wird die Inverse dieser erweiterten Matrix, mt, berechnet. Die Funktion iteriert über alle Variablen im Originaldatensatz und berechnet für jede Variable ein Kriterium, das auf der Kovarianz zwischen dieser Variable und den ausgewählten Variablen basiert und mit der Inversen der mt-Matrix gewichtet ist. Das berechnete Kriterium wird in der Variablen crit akkumuliert.

Der Zweck dieser Funktion besteht darin, die Auswirkungen des Hinzufügens einer neuen Variable zur Menge der ausgewählten Variablen zu bewerten. Ein höherer Kriteriumswert zeigt an, dass die neue Variable die Leistung des Modells wahrscheinlich verbessert, während ein niedrigerer Kriteriumswert darauf hindeutet, dass sie möglicherweise nicht von Vorteil ist. Diese Funktion kann innerhalb eines Merkmalsauswahlalgorithmus verwendet werden, um die informativsten Variablen für ein bestimmtes Modell zu ermitteln.

Rekursive Rückwärtsverfeinerung

Die Rückwärtsverfeinerung ist eine Abwandlung der Vorwärtsauswahl, wie das nachstehende Codeprotokoll backward_refinement() zeigt.

//+------------------------------------------------------------------+
//| backward refinement routine                                      |
//+------------------------------------------------------------------+
ulong backward_refinement(matrix &covar, ulong &kept_columns[], ulong nkept, double &best_crit) {
    ulong i, old_col, new_col, best_col, refined;
    double crit;

    best_crit = substvar(covar, kept_columns, nkept, 0, kept_columns[0]);
    refined = 0;

    for (old_col = 0; old_col < nkept; old_col++) {

        if (old_col == nkept - 1 && !refined)
            break;

        best_col = ULONG_MAX;
        for (new_col = 0; new_col < m_preds; new_col++) {

            for (i = 0; i < nkept; i++) {
                if (new_col == kept_columns[i])
                    break;
            }

            if (i < nkept)
                continue;

            crit = substvar(covar, kept_columns, nkept, old_col, new_col);

            if (crit > best_crit) {
                best_crit = crit;
                best_col = new_col;
            }
        }

        if (best_col != ULONG_MAX && best_col >= 0) {
            // Print(__FUNCTION__,"  Replaced predictor at column ",kept_columns[old_col], " with ",best_col," to get criterion = ", best_crit);
            kept_columns[old_col] = best_col;
            refined = 1;
        }
    }
    return refined;
}

Dieser MQL5-Code implementiert einen Algorithmus der Rückwärtsverfeinerung für die Merkmalsauswahl. Dabei werden die Auswirkungen des Entfernens jeder ausgewählten Variablen auf ein bestimmtes Kriterium bewertet. Durch die Berechnung des Kriteriums ohne jede Variable ermittelt die Funktion, welche Variable die geringste Veränderung des Kriteriums zur Folge hat. Liegt die Änderung unter einem vordefinierten Schwellenwert, wird die Variable aus der Auswahlmenge entfernt, und der Vorgang wird so lange wiederholt, bis keine weiteren Verfeinerungen mehr möglich sind. Die Funktion gibt 1 zurück, wenn eine Verfeinerung vorgenommen wurde, und sonst 0.

Die Routine substvar(), die innerhalb der Funktion backward_refinement() aufgerufen wird, implementiert einen Mechanismus zur Variablensubstitution, der ein Kriterium auf der Grundlage der Korrelationsmatrix und einer Reihe ausgewählter Variablen berechnet. Diese Routine wird in einem Algorithmus zur Merkmalsauswahl verwendet, um die Auswirkungen des Ersetzens einer Variablen durch eine andere zu bewerten.

//+------------------------------------------------------------------+
//| variable substitution routine                                    |
//+------------------------------------------------------------------+
double substvar(matrix &covar, ulong &keptcols[], ulong nkept, ulong old_col, ulong new_col) {
    ulong i, j, k, irow, saved_col;
    double sum, crit, dtemp;
    matrix mt(nkept, nkept);

    saved_col = keptcols[old_col];
    keptcols[old_col] = new_col;

    for (i = 0; i < nkept; i++) {
        irow = keptcols[i];
        for (j = 0; j < nkept; j++) {
            mt[i][j] = covar[irow][keptcols[j]];
        }
    }

    matrix mtinv = mt.Inv();
    vector vec(nkept);

    crit = 0.0;
    for (j = 0; j < m_preds; j++) {

        for (i = 0; i < nkept; i++) {
            vec[i] = covar[j][keptcols[i]];
        }

        sum = 0.0;
        for (i = 0; i < nkept; i++) {
            sum += vec[i] * vec[i] * mtinv[i][i];
        }
        crit += sum;

        sum = 0.0;
        for (i = 1; i < nkept; i++) {
            dtemp = vec[i];
            for (k = 0; k < i; k++) {
                sum += dtemp * vec[k] * mtinv[i][k];
            }
        }
        crit += 2.0 * sum;
    }

    keptcols[old_col] = saved_col;

    return crit;
}

Die Funktion nimmt als Eingabe eine Korrelationsmatrix, covar, ein Array ausgewählter Variablen, keptcols, die Anzahl ausgewählter Variablen, nkept, und die Indizes der zu ersetzenden alten und neuen Variablen. Es wird eine temporäre Matrix, mt, erstellt, um die Untermatrix von covar zu speichern, die den ausgewählten Variablen entspricht. Die Funktion berechnet dann die Inverse der mt-Matrix mit Hilfe der Funktion Inv(). Es durchläuft alle Variablen des ursprünglichen Datensatzes und berechnet für jede Variable ein Kriterium, das auf der Kovarianz zwischen der Variable und den ausgewählten Variablen basiert und mit der Inversen der mt-Matrix gewichtet wird. Das berechnete Kriterium wird in der Variablen crit akkumuliert. Nach der Berechnung des Kriteriums stellt die Funktion die ursprüngliche Variable im Array keptcols wieder her und gibt das berechnete Kriterium zurück.

Der Zweck dieser Funktion besteht darin, die Auswirkungen des Ersetzens einer Variablen durch eine andere auf das Gesamtmodell zu bewerten. Ein höherer Kriteriumwert zeigt an, dass die Ersetzung wahrscheinlich die Leistung des Modells verbessert, während ein niedrigerer Kriteriumwert darauf hindeutet, dass sie möglicherweise nicht von Vorteil ist. Diese Funktion kann in einen Algorithmus zur Merkmalsauswahl integriert werden, um die optimale Kombination von Variablen für ein bestimmtes Modell zu ermitteln.

Orthogonalisierung von Komponenten

Bei der Auswahl von Variablen durch eine reine Vorwärtsselektion ohne Rückwärtsverfeinerung wird eine hierarchische Reihenfolge auf der Grundlage ihrer Bedeutung erstellt, beginnend mit der einflussreichsten und mit abnehmender Bedeutung. Diese Reihenfolge ist in der Praxis oft von unschätzbarem Wert. Während Rohwerte direkt verwendet werden können, bieten orthogonale Komponentenvariablen - die als lineare Kombinationen der ursprünglichen Variablen konstruiert werden - deutliche Vorteile. Diese Komponenten sind unkorreliert, was das Modelltraining erleichtert und die Redundanz minimiert. Außerdem kann das Fehlen von Redundanzen innerhalb dieser Variablen die Interpretation ihrer Beiträge vereinfachen.

Um orthogonale Komponentenvariablen unter Beibehaltung der ursprünglichen Reihenfolge zu erhalten, eignet sich die Gram-Schmidt-Orthogonalisierungsmethode. Dieses Verfahren beginnt mit der Definition der Anfangskomponente als skalierte erste ausgewählte Variable. Bei den nachfolgenden Komponenten werden die Projektionen auf die bestehenden Komponenten subtrahiert. Durch systematische Subtraktion dieser Projektionen und Normierung auf eine Längeneinheit wird die Orthogonalität der Komponenten sichergestellt. Schließlich wird durch die Umskalierung auf eine Standardabweichung die Konsistenz gewahrt. Im Wesentlichen wandelt die Gram-Schmidt-Orthogonalisierung die ausgewählten Variablen in einen Satz orthogonaler Komponenten um, die die ursprüngliche Reihenfolge der Wichtigkeit beibehalten, was potenzielle Vorteile für die Interpretierbarkeit und Effizienz des Modells bietet.

Es folgt eine Implementierung der Gram-Schmidt-Transformation. Das Ergebnis der Funktion ist eine neue Matrix, in der jede Spalte einen orthogonalisierten Vektor darstellt.

//+------------------------------------------------------------------+
//|   Gram Schmidt routine                                           |
//+------------------------------------------------------------------+
matrix gram_schmidt(matrix &input_) {
    ulong irow, icol, inner;
    double dtemp, sum;
    ulong nrows = input_.Rows();
    ulong ncols = input_.Cols();
    matrix output = input_;

    sum = 0.0;

    vector colsum = output.Col(0);
    colsum = MathPow(colsum, 2.0);
    sum = colsum.Sum();
    sum = sqrt(sum);

    if (sum == 0.0) {
        Print(__FUNCTION__, " sum == 0.0 ");
        return matrix::Zeros(0, 0);
    }

    if (!output.Col(output.Col(0) / sum, 0)) {
        Print(__FUNCTION__, " failed column insertion ", GetLastError());
        return matrix::Zeros(0, 0);
    }

    for (icol = 1; icol < ncols; icol++) {
        for (inner = 0; inner < icol; inner++) {
            sum = 0.0;
            for (irow = 0; irow < nrows; irow++)
                sum += (output[irow][icol] * output[irow][inner]);

            for (irow = 0; irow < nrows; irow++)
                output[irow][icol] -= (sum * output[irow][inner]);
        }

        sum = 0.0;
        for (irow = 0; irow < nrows; irow++) {
            dtemp = output[irow][icol];
            sum += dtemp * dtemp;
        }

        sum = sqrt(sum);

        if (sum == 0.0) {
            Print(__FUNCTION__, " sum == 0.0 ");
            return matrix::Zeros(0, 0);
        }

        if (!output.Col(output.Col(icol) / sum, icol)) {
            Print(__FUNCTION__, " failed column insertion ", GetLastError());
            return matrix::Zeros(0, 0);
        }
    }

    return output;
}

Der Algorithmus funktioniert durch iterative Orthogonalisierung jeder Spalte der Eingabematrix in Bezug auf die zuvor orthogonalisierten Spalten. Dies geschieht durch Projektion der aktuellen Spalte auf den von den vorherigen Spalten aufgespannten Unterraum und Subtraktion dieser Projektion von der aktuellen Spalte. Der resultierende Vektor wird dann so normiert, dass er eine Einheitslänge hat. Der Code enthält mehrere Optimierungen zur Verbesserung der Effizienz, wie die Verwendung von Vektoroperationen für Berechnungen und die Vermeidung unnötiger Berechnungen. Darüber hinaus enthält die Funktion eine Fehlerbehandlung, um mögliche Probleme wie Vektoren mit einer Länge von Null oder fehlgeschlagene Spalteneinfügungen zu erkennen.

Nachdem alle Kernroutinen für die Durchführung der Vorwärtsauswahl mit optionaler Rückwärtsverfeinerung behandelt wurden, wird im nächsten Abschnitt gezeigt, wie diese Routinen in der vollständigen Implementierung des FSCA-Algorithmus verwendet werden.

Die Klasse CFsca

Die Klasse CFsca kapselt die Funktionalität für die Durchführung der Vorwärtsselektionskomponentenanalyse auf einem Datensatz. Die vollständige Klasse ist in fsca.mqh definiert, zusammen mit einer einfachen Standardisierungstransformationsroutine namens stdmat(). Diese Funktion nimmt eine Matrix als Eingabe und gibt eine standardisierte Matrix zurück.

//+------------------------------------------------------------------+
//| standardize a matrix                                             |
//+------------------------------------------------------------------+
matrix stdmat(matrix &in) {
    vector mean = in.Mean(0);
    vector std = in.Std(0);
    std += 1e-10;
    matrix out = in;

    for (ulong row = 0; row < out.Rows(); row++) {
        if (!out.Row((in.Row(row) - mean) / std, row)) {
            Print(__FUNCTION__, " error ", GetLastError());
            return matrix::Zeros(in.Rows(), in.Cols());
        }
    }

    return out;
}

Die Funktion stdmat() berechnet den Mittelwert und die Standardabweichung jeder Spalte der Eingabematrix mit Hilfe der Funktionen Mean und Std. Anschließend wird eine Ausgabematrix mit denselben Abmessungen wie die Eingabematrix erstellt. Die Funktion iteriert über jede Zeile der Eingabematrix und standardisiert sie, indem sie den Mittelwert der entsprechenden Spalte subtrahiert und durch die Standardabweichung der Spalte dividiert. Die normierte Zeile wird in der Ausgabematrix out gespeichert, die am Ende der Funktion zurückgegeben wird. Diese Funktion ist außerhalb der Klasse CFsca platziert, um eine unabhängige Nutzung zu ermöglichen.

Die Klasse CFsca beginnt mit der Definition ihrer privaten Mitglieder, die zur Speicherung von Zwischenergebnissen und den für FSCA erforderlichen Datenstrukturen verwendet werden.

//+------------------------------------------------------------------+
//| fsca class implementation                                        |
//+------------------------------------------------------------------+
class CFsca
  {
private:
   bool              m_fitted;              //flag showing if principal factors were extracted
   matrix m_corrmat,             //correlation matrix
          m_covar,               //altered correlation matrix
          m_data,                //standardized data is here
          m_eigvectors,          //matrix of eigen vectors of m_corrmat matrix
          m_structmat,           //factor loading matrix of m_corrmat matrix
          m_principal_components,             //principal components
          m_fscv_struct,        //fsca factor structure
          m_fscv_eigvects,      //fsca eigen structure
          m_Fsca,        //ordered fsca variables
          m_coeffs,      //fsca component coefficients
          m_Fscv;        //refined fsca variables
   vector m_eigvalues,           //vector of eigen values of m_corrmat matrix
          m_sqcorr,              //mean squared correlation matrix
          m_fscv_eigvals,        //fsca eigen values
          m_fscv_cumeigvals,     //fsca cumulative variance contribution
          m_cumeigvalues;        //cumulative variance contributions of m_corrmat matrix
   ulong             m_num_comps;           //unique instances of redundent variation in m_data
   ulong             m_preds;               //number of variables (columns) in dataset (m_data)
   ulong  m_keptorderedcolumns[],//indices of columns upon which components are calculated for ordered fsca
          m_keptrefinedcolumns[],//indices of columns upon which components are calculated for backward refined fsca
          m_keptcolumns[],
          m_bestcolumn;          //index of first selected column in analysis
   double            m_best_crit;           //best criterion value

Als Nächstes folgen die privaten Methoden der Klasse CFsca, von denen wir einige bereits in früheren Abschnitten dieses Textes behandelt haben. Andere Methoden werden kurz erwähnt, wenn wir die öffentlichen Methoden der Klasse besprechen.

Die öffentlichen Methoden werden am Ende der CFsca-Klasse definiert. Die fit()-Methode sollte zuerst aufgerufen werden, nachdem eine Instanz der Klasse initialisiert wurde. Bei dieser Methode wird der Rohdatensatz einer Komponentenanalyse der Vorwärtsselektion unterzogen. Sie nimmt als Eingabe eine Matrix mit den ursprünglichen Rohdaten und gibt einen booleschen Wert zurück, der angibt, ob der Anpassungsprozess erfolgreich war.

//+------------------------------------------------------------------+
//| perform forward selection component analysis on a raw dataset    |
//+------------------------------------------------------------------+
bool fit(matrix &data) {
    m_preds = data.Cols();
    m_fitted = false;
    m_sqcorr = vector::Zeros(m_preds);

    m_data = stdmat(data);
    m_corrmat = m_data.CorrCoef(false);

    m_structmat = compute_factor_structure(m_corrmat, m_eigvectors, m_eigvalues, m_cumeigvalues);

    if (m_structmat.Rows() == 1)
        return false;

    m_num_comps = m_cumeigvalues.Size();

    if (ArrayResize(m_keptorderedcolumns, int(m_num_comps)) < 0 || 
        ArrayResize(m_keptrefinedcolumns, int(m_num_comps)) < 0 ||
        ArrayResize(m_keptcolumns, int(m_num_comps)) < 0 || 
        ArrayInitialize(m_keptcolumns, ULONG_MAX) < 0) {
        Print(__FUNCTION__, " array error ", GetLastError());
        return false;
    }

    m_principal_components = compute_principal_components();

    for (ulong i = 0; i < m_preds; i++)
        m_sqcorr[i] = (compute_criterion(m_corrmat, m_keptcolumns, 0, i) - 1.0) / double(m_preds - 1);

    vector evd_vals = m_eigvalues;
    while (evd_vals[m_preds - 1] <= 0.0) {
        for (ulong j = 1; j < m_preds; j++) {
            for (ulong k = 0; k < j; k++) {
                m_corrmat[j][k] *= 0.99999;
                m_corrmat[k][j] = m_corrmat[j][k];
            }
        }

        matrix empty;
        if (!m_corrmat.EigenSymmetricDC(EIGVALUES_N, evd_vals, empty)) {
            Print(__FUNCTION__, " failed eig decomp ", GetLastError());
            return false;
        }
    }

    m_Fsca = compute_fsca_components(m_data);
    m_Fscv = compute_fscv_components(m_data);

    m_fitted = (m_Fsca.Rows() > 1 && m_Fscv.Rows() > 1);

    return m_fitted;
}

Die Funktion fit() initialisiert verschiedene Variablen und Matrizen, die im FSCA-Prozess verwendet werden. Zunächst wird die Eingabedatenmatrix standardisiert, sodass sie einen Mittelwert von Null und eine Einheitsvarianz aufweist. Die Funktion berechnet dann die Korrelationsmatrix der standardisierten Daten und speichert sie in m_corrmat. Anschließend wird die Faktorenstruktur der Korrelationsmatrix mit der Funktion compute_factor_structure berechnet. Diese Faktorenstruktur umfasst die Eigenvektoren (m_eigvectors), Eigenwerte (m_eigvalues) und kumulativen Eigenwerte (m_cumeigvalues) der Korrelationsmatrix. Die Funktion prüft, ob die Faktorenstrukturmatrix (m_structmat) nur eine Zeile hat; ist dies der Fall, weist dies auf einen Fehler bei der Auswertung der Faktorenstruktur hin, und die Funktion gibt false zurück.

Die Anzahl der Komponenten (m_num_comps) wird gleich der Anzahl der Eigenwerte ungleich Null gesetzt. Die Funktion initialisiert dann verschiedene Arrays, die im FSCA-Prozess verwendet werden. Sie berechnet die Hauptkomponenten der standardisierten Daten mit der Funktion compute_principal_components und berechnet die quadrierten Korrelationen zwischen jeder Variablen und der ersten Hauptkomponente. Zusätzlich prüft die Funktion, ob negative Eigenwerte vorhanden sind. Werden welche gefunden, werden die Korrelationsmatrix leicht angepasst und die Eigenwerte neu berechnet, bis alle positiv sind. Schließlich berechnet die Funktion die FSCA-Komponenten mit der Funktion compute_fsca_components und die FSCV-Komponenten mit der Funktion compute_fscv_components. Wenn sowohl die FSCA- als auch die FSCV-Komponente erfolgreich berechnet wurden, setzt die Funktion das Flag m_fitted auf true.

Den Abschluss der Definition der Klasse CFsca bilden Getter-Funktionen, die den Zugriff auf verschiedene Aspekte der analytischen Berechnungen ermöglichen, die während des FSCA-Prozesses durchgeführt werden.

//+------------------------------------------------------------------+
//| get the principal components                                     |
//+------------------------------------------------------------------+
matrix get_principal_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_principal_components;
}

//+------------------------------------------------------------------+
//| get the ordered fsca components                                  |
//+------------------------------------------------------------------+
matrix get_fsca_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_Fsca;
}

//+------------------------------------------------------------------+
//| get the backward refined fsca components                         |
//+------------------------------------------------------------------+
matrix get_fscv_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_Fscv;
}

//+------------------------------------------------------------------+
//| get indices of variables defining the ordered fsca components    |
//+------------------------------------------------------------------+
bool get_fsca_var_indices(ulong &indices[]) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    return (ArrayCopy(indices, m_keptorderedcolumns, 0, 0, int(m_num_comps)) > 0);
}

//+---------------------------------------------------------------------------+
//| get indices of variables defining the backward refined fsca components    |
//+---------------------------------------------------------------------------+
bool get_fscv_var_indices(ulong &indices[]) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    return (ArrayCopy(indices, m_keptrefinedcolumns, 0, 0, int(m_num_comps)) > 0);
}

//+-------------------------------------------------------------------+
//| get cumulative variance contribution based on principal components|
//+-------------------------------------------------------------------+
vector get_principal_components_cumulative_variance_contribution(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_cumeigvalues;
}

//+-------------------------------------------------------------------+
//| get cumulative variance contribution based on fscv components     |
//+-------------------------------------------------------------------+
vector get_fscv_cumulative_variance_contribution(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_fscv_cumeigvals;
}

//+-------------------------------------------------------------------+
//| get eigen structure of principal components                       |
//+-------------------------------------------------------------------+
bool get_principal_components_eigstructure(matrix &vectors, vector &values) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    vectors = m_eigvectors;
    values = m_eigvalues;

    return true;
}

//+-------------------------------------------------------------------+
//| get eigen structure of backward refined FSCs                      |
//+-------------------------------------------------------------------+
bool get_fscv_eigstructure(matrix &vectors, vector &values) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    vectors = m_fscv_eigvects;
    values = m_fscv_eigvals;

    return true;
}

//+-------------------------------------------------------------------+
//| get principal components factor structure                         |
//+-------------------------------------------------------------------+
matrix get_principal_components_factorstructure(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_structmat;
}

//+-------------------------------------------------------------------+
//| get the factor structure of FSC with backward refinement          |
//+-------------------------------------------------------------------+
matrix get_fscv_factorstructure(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_fscv_struct;
}

//+------------------------------------------------------------------+
//| get mean squared correlations                                    |
//+------------------------------------------------------------------+
vector get_avg_correlations(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_sqcorr;
}

//+-------------------------------------------------------------------+
//| get forward selection component coefficients matrix               |
//+-------------------------------------------------------------------+
matrix get_fsca_component_coeffs(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_coeffs;
}

Mit diesen Funktionen können die Nutzer wichtige Ergebnisse abrufen, z. B. die standardisierten Daten, die Korrelationsmatrix, die Faktorenstruktur, die Hauptkomponenten und die Komponentenvariablen, was die weitere Analyse und Interpretation der Ergebnisse erleichtert. Wir schließen diese Ausführungen mit einer Demonstration, wie die CFsca-Klasse eingesetzt werden kann.

Ein Beispiel

Das nachstehende Code-Listing definiert ein MQL5-Skript mit dem Namen FSCA_Demo.mq5, das eine Forward Selection Component Analysis (FSCA) auf einem zufällig generierten Datensatz durchführt. Das Skript enthält die Header-Datei fsca.mqh, die die Definition der für die FSCA-Analyse verwendeten CFsca-Klasse enthält.

//+------------------------------------------------------------------+
//|                                                    FSCA_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<fsca.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   MathSrand(120);
//---
   matrix mat(100,9);
//---
   mat.Random(0.0,1.0);
//---
   vector var1 = mat.Col(0) + mat.Col(1);
// ---
   vector var2 = mat.Col(2) + mat.Col(3);
//---
   vector var3 = var1 + var2;
//---
   if(!mat.Col(var1,6) || !mat.Col(var2,7) || !mat.Col(var3,8))
     {
      Print("failed column assignment ", GetLastError());
      return;
     }
//---
   CFsca fsca;
//---
   if(!fsca.fit(mat))
      return;
//---
   ulong index[];
   Print("Principal components cumulative variance conributions \n", fsca.get_principal_components_cumulative_variance_contribution());
   Print(" Principal components factor structure \n", fsca.get_principal_components_factorstructure());
   Print("Mean squared correlation of each variable with all others \n", fsca.get_avg_correlations());
//---
   if(fsca.get_fsca_var_indices(index))
     {
      Print(" Ordered FSCA components based on variables located in column indices ");
      ArrayPrint(index);
     }
//---
   Print(" Ordered FSCA component coefficients matrix \n", fsca.get_fsca_component_coeffs());
//---
   if(fsca.get_fscv_var_indices(index))
     {
      Print(" Backward refined FSCA components based on variables located in column indices ");
      ArrayPrint(index);
     }
//---
   matrix vects;
   vector vals;
//---
   if(fsca.get_fscv_eigstructure(vects,vals))
     Print("Backward refined fsca component eigenvalues \n", vals);
//---
   Print(" Backward refined cumulative variance contributions \n", fsca.get_fscv_cumulative_variance_contribution());
//---
   Print(" Backward refined fsca components factor structure \n", fsca.get_fscv_factorstructure());
  }
//+------------------------------------------------------------------+

Zunächst wird ein Zufallswert festgelegt und eine Matrix mit Zufallswerten erstellt. Drei neue Vektoren werden durch Summierung der vorhandenen Spalten in der Matrix erstellt. Das Skript versucht dann, die Matrixdaten an das FSCA-Modell anzupassen und ruft verschiedene FSCA-Ergebnisse ab, darunter den kumulativen Varianzbeitrag, die Faktorenstruktur und die mittleren quadratischen Korrelationen. Außerdem führt es sowohl die Standard-FSCA als auch die rückwärts verfeinerte FSCA durch und druckt die Indizes der geordneten Variablen und die Koeffizienten der Komponenten aus. Sowie die Faktorenstruktur der rückwärts verfeinerten FSCA-Komponenten. Das Skript erzeugt einfach einen Datensatz von Zufallsvariablen mit 100 Stichproben und 9 Merkmalen. Die letzten 3 Variablen des Datensatzes sind so angelegt, dass sie von anderen Variablen abhängig sind, während die übrigen Variablen unabhängig sind. 

Wenn wir das Skript ausführen und die Merkmale der Hauptkomponenten analysieren, stellen wir fest, dass es nur sechs von neun einzigartigen Variationsquellen gibt.

DG      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   Principal components cumulative variance conributions 
RM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [31.72121326219056,54.98374706330443,70.21399790786099,82.34742379766755,91.9067775629936,100]
CM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Principal components factor structure 
MH      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [[-0.5430877600903072,0.4698851388299595,-0.02139789374204959,0.5468988095320395,-0.4254498037566715,-0.06082703269184352,-1.3842452210817e-09,-7.527559895073524e-10,0]
RH      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5283294988376427,0.4246506210338227,-0.1190026606589024,-0.6285471675075863,0.3351428244532062,0.1377893424956133,-1.351333204556555e-09,-7.34858353171856e-10,0]
ES      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5563230307728618,-0.3632156082945803,0.4770295070287525,0.3051596297191441,0.4575827252246154,-0.1688715686919785,-1.694159101189325e-09,2.164855665400724e-10,0]
NF      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.2379617600470182,-0.6943076552356867,-0.4580766878219635,-0.2737307249578351,-0.4112051990027778,0.08636320534609224,-1.769139142521297e-09,2.260667780777343e-10,0]
DO      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [0.02487447101754412,-0.08203927651647476,-0.6079889924620585,0.4701685445643955,0.3604839483405348,0.5215295442601863,1.313244252124911e-25,1.228203109452781e-25,0]
IP      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.07016546285360215,-0.110242984252018,0.7306990214221818,-0.07491798042552207,-0.2276538908363994,0.6257501374625694,4.158606798395552e-25,-7.369218656716687e-26,0]
NE      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.7598477338270035,0.6346843827822741,-0.09872272409405579,-0.04786755450396145,-0.0705236166963274,0.05287812507625003,-1.359967783374346e-10,1.333715775589249e-09,0]
NO      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5934182368659159,-0.8024046895986707,-0.000973814713973191,0.01424096330384607,0.02077689502375221,-0.05801790712583575,2.667167815186452e-10,-1.355042254629964e-11,0]
RM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.9897757278036692,-0.1138316306178367,-0.07343616940955985,-0.02494592427830717,-0.03690113231990194,-0.0030829919659495,2.802923111601039e-09,-3.865027968054199e-10,0]]

Dies ist zu erwarten, da drei der Variablen Kombinationen der anderen sind. Betrachtet man die kumulierten Varianzbeiträge der einzelnen Variablen, so stellt man fest, dass die erste Komponente etwa ein Drittel der Gesamtvariation ausmacht. Die Faktorenstruktur deutet auf eine mäßige bis starke umgekehrte Korrelation zwischen der ersten Hauptkomponente und den Variablen in den Spalten 0 bis 3 und 6 bis 8 hin, während die Variablen in den Spalten 4 und 5 einen entgegengesetzten Trend aufweisen. Die zweite Komponente zeigt die Unterschiede zwischen den Variablen 0 und 1 und 2 und 3. Zusammen erklären die ersten beiden Komponenten über 55 Prozent der Gesamtvariation.

QK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   Mean squared correlation of each variable with all others 
GK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [0.09874555673359317,0.09196664871445229,0.09678803260182336,0.08640965168371836,0.009232616218980055,0.01341075732654295,0.1892345119240549,0.1695472310064176,0.2291509382521983]

Der Vektor der mittleren quadratischen Korrelationen der einzelnen Variablen mit der kombinierten Sammlung aller Variablen listet die Korrelationen in der Reihenfolge auf, in der die Variablen im ursprünglichen Datensatz erscheinen. Die letzten drei Variablen weisen die höchsten durchschnittlichen Korrelationen auf, während die Variablen in den Spalten 4 und 5 die niedrigsten Werte aufweisen.

LR      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Ordered FSCA components based on variables located in column indices 
QQ      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   8 6 2 4 1 5

Als Nächstes betrachten wir die vorausgewählten Werte, die durch den Aufruf von get_fscv_var_indices() ermittelt werden. Sie zeigt die Indizes der Variablen, die den Großteil der Variation im Datensatz am besten erfassen, in absteigender Reihenfolge, je nachdem, welche Variable am meisten zur Gesamtvariation in den Daten beiträgt. Hier sehen wir, dass die letzte Variable die größte Variation in den Daten erfasst, da sie zuerst erscheint.

QJ      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Ordered FSCA component coefficients matrix 
DM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [[0.9999999989356357,-0.9551778313323678,-1.196676438579672,-0.163265209103464,-0.1301792726137802,0.0741114239785734]
IR      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [7.62883988565579e-10,1.382882745177175,0.7080052470472653,0.1327136589445282,-0.8962870520067646,-0.01038862969019799]
LF      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [6.044914586250671e-10,-1.162965671680505e-09,1.327736785211269,0.1291890234653878,0.1244453203448803,-0.2315140872599129]
EM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [5.84342504938995e-11,-9.115276242144255e-11,-1.685031073006549e-10,1.005785752630206,0.08917398176616295,0.2288955899392838]
JM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [6.626278020206711e-11,8.05911615654048e-10,2.135397240976555e-10,-3.939133914887538e-11,1.404086244047662,0.03569800251260542]
KK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-2.859616016204214e-11,3.48387846349496e-11,2.600743786995707e-10,-1.479500966183878e-10,-3.333024481411151e-11,1.048952273510343]]

Als Nächstes untersuchen wir die Tabelle der Koeffizienten, die für die Berechnung der sechs Komponenten erforderlich sind. Die Variablen werden in der gleichen Reihenfolge dargestellt, wie sie sich aus den Indizes des soeben untersuchten Arrays ergibt. Hier sehen wir, dass die letzte Variable die wichtigste ist und der entsprechende Koeffizient sehr nahe bei 1 liegt. In dieser Matrix werden die Koeffizienten so klein, dass sie praktisch Null sind.

CM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Backward refined FSCA components based on variables located in column indices 
ND      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   3 0 2 4 1 5

Schließlich untersuchen wir die Indizes der Variablen, die durch eine Kombination aus Vorwärtsauswahl und Rückwärtsverfeinerung ausgewählt wurden. Es ist wichtig zu beachten, dass bei dieser Variante der FSCA die Reihenfolge der ausgewählten Variablen nicht von Bedeutung ist. Die sich daraus ergebende Menge ausgewählter Variablen ist jedoch aussagekräftiger als der strenge Ordnungsansatz, da er nur die unabhängigen Zufallsvariablen beibehält und diejenigen, die eine gewisse Abhängigkeit aufweisen, verwirft. Dies wird deutlich, wenn man die Ergebnisse der Standardvorwärtsauswahl und der rückwärts verfeinerten Vorwärtsauswahl vergleicht.

Schlussfolgerung

Abschließend haben wir eine Implementierung der Forward Selection Component Analysis in MQL5 vorgestellt, die ihre Wirksamkeit als Werkzeug sowohl für die Dimensionenreduktion als auch für die Merkmalsauswahl unter Beweis gestellt hat. Das Tool kann auch für die explorative Datenanalyse verwendet werden. Eines der Nebenprodukte des Algorithmus ist die Faktorenstruktur des Datensatzes, die nützlich sein kann, wenn man versucht, die zugrunde liegenden Effekte zu verstehen. Der gesamte Code, auf den in diesem Artikel verwiesen wird, ist unten angefügt.

Datei Name	Beschreibung
MQL5/include/np.mqh	Header-Datei mit allgemeinen Vektor- und Matrix-Hilfsfunktionen
MQL5/include/fsca.mqh	Header-Datei mit der Definition der CFsca-Klasse, die die Vorwärtsselektions-Komponentenanalyse implementiert
MQL5/Skripte/FSCA_Demo.mq5	ein MetaTrader 5-Skript, das die Verwendung der CFsca-Klasse demonstriert