Selección de características y reducción de dimensionalidad mediante componentes principales

Introducción

La predicción de series temporales financieras a menudo implica el análisis de numerosas características, muchas de las cuales pueden estar altamente correlacionadas. Las técnicas de reducción de dimensionalidad, como el análisis de componentes principales (Principal Component Analysis, PCA), pueden ayudar a crear una representación más compacta de estas características. Sin embargo, el PCA tiene limitaciones, especialmente en presencia de variables altamente correlacionadas. En tales casos, el PCA tiende a mostrar el efecto de agrupamiento, en el que un conjunto de variables altamente correlacionadas contribuye colectivamente a un componente principal determinado. En lugar de destacar una sola variable, el PCA distribuye la influencia de manera relativamente uniforme entre todas las variables del grupo correlacionado.
Esta distribución uniforme puede ser beneficiosa para la supresión del ruido, ya que los componentes principales enfatizan los patrones comunes en lugar de las fluctuaciones aleatorias propias de las variables individuales. Sin embargo, esta supresión del ruido tiene un coste: a menudo diluye la contribución de las variables individuales a cada componente principal. Las variables que pueden ser significativas por sí mismas pueden parecer menos importantes dentro del espacio transformado, ya que su influencia se absorbe en la estructura más amplia capturada por el grupo. Esto puede suponer un inconveniente importante en tareas como la selección de variables, cuyo objetivo es identificar las características más influyentes, o en el análisis de causas raíz, en el que es fundamental comprender el impacto directo de variables específicas.

Además, esta característica complica la interpretación del modelo. Dado que cada componente principal representa una combinación de todas las variables originales, traducir la contribución de estos componentes al contexto de las variables originales puede resultar complicado. Los profesionales pueden tener dificultades para extraer conclusiones claras de los componentes principales, ya que resulta complicado determinar qué variables originales determinan los patrones observados. Para abordar este problema, presentamos una implementación del análisis de componentes de selección hacia adelante (Forward Selection Component Analysis, FSCA), un método inspirado en el trabajo de Luca Puggini y Sean McLoone, cuyo objetivo es evitar los inconvenientes del PCA cuando se trata de características altamente correlacionadas.

Análisis de componentes con selección hacia adelante

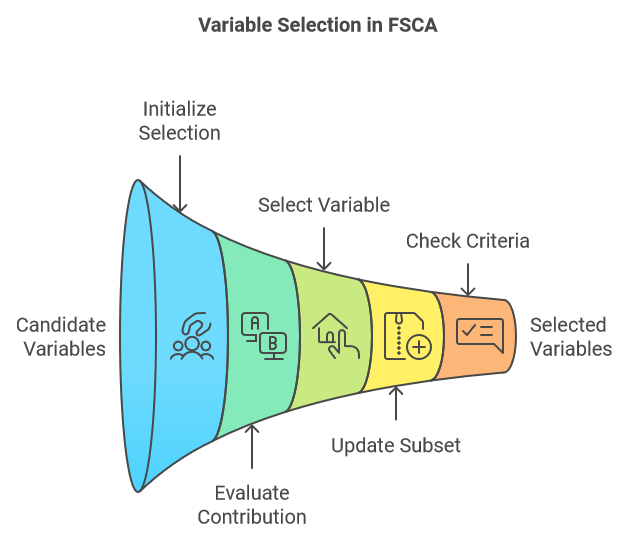
El análisis de componentes de selección hacia adelante (FSCA) es una técnica de reducción de dimensionalidad que combina la reducción de dimensionalidad y la selección de características mediante la identificación de las variables más informativas para explicar los datos originales. FSCA utiliza un enfoque codicioso, seleccionando las variables una por una en función de su capacidad para capturar la varianza restante en los datos. A continuación se presenta un resumen de los pasos fundamentales que componen el procedimiento de la FSCA:

1. Inicialización:
   
   • Comience con un conjunto vacío de variables seleccionadas y un conjunto completo de variables candidatas.
   • Calcula la varianza total del conjunto de datos.
   • Comience el proceso iterativo seleccionando la variable que mejor predice los valores de todas las demás variables, asegurándose de que esta elección capture la máxima cantidad de varianza explicada.
     
2. Selección iterativa:
   
   • En cada paso, evalúe la contribución de cada variable candidata restante a la varianza explicada cuando se añade al conjunto actual de variables seleccionadas.
   • Seleccione la variable que da lugar al mayor aumento de la varianza explicada cuando se añade al subconjunto.
     
3. Actualización:
   
   • Añadir la variable seleccionada al subconjunto de variables elegidas.
   • Elimine la variable seleccionada del conjunto de variables candidatas.
   • Recalcular la varianza residual, o la varianza restante sin explicar, después de tener en cuenta las contribuciones de las variables seleccionadas.
     
4. Criterios de detención:
   
   • Continúe el proceso hasta que se cumpla un criterio de detención predeterminado. Esto podría ser un número específico de variables seleccionadas, una proporción objetivo de la varianza total explicada o un umbral para la varianza incremental explicada al añadir una nueva variable.

     
     

Dado un conjunto de variables sin procesar, las organizamos en una matriz, en la que cada columna representa una característica distinta y cada fila representa una sola muestra. Los valores brutos se transforman primero mediante la estandarización. A partir de este momento, cualquier referencia a las variables originales se refiere al conjunto de variables estandarizadas, que denominaremos matriz X. Esta matriz X tiene "v" columnas (variables). El algoritmo FSCA produce al menos tres nuevos conjuntos de variables:

• Matriz Z: Esta matriz consiste en un subconjunto k (donde k<v) de las columnas de X, clasificadas según su contribución a la reconstrucción de X. Estas columnas se conocen como variables de selección directa (FSV).
• Matriz M: Las columnas de esta matriz se denominan componentes de selección progresiva (FSC). Cada componente es una función de la columna correspondiente en Z, así como de las que la preceden, si las hay.
• Matriz U: Esta matriz contiene los coeficientes o cargas que, cuando se combinan con los FSV, producen los FSC.
  

El objetivo del algoritmo es obtener un subconjunto óptimo de variables que represente mejor la variación única en X. Sin embargo, se trata de un problema de optimización complejo. No siempre se garantiza que el FSCA encuentre el subconjunto óptimo de variables según los criterios de optimización definidos. Cuando se trabaja con conjuntos de datos de gran tamaño, puede resultar poco práctico buscar en todos los subconjuntos posibles, por lo que FSCA ofrece un enfoque más pragmático. Cuando se trabaja con conjuntos de datos de gran tamaño, puede resultar poco práctico buscar en todos los subconjuntos posibles, por lo que FSCA ofrece un enfoque más pragmático. Para abordar esta limitación, los autores del artículo de investigación mencionado al principio de este artículo proponen introducir un paso de refinamiento hacia atrás en el procedimiento FSCA.

FSCA con refinamiento hacia atrás

El refinamiento hacia atrás es un procedimiento que permite eliminar y sustituir variables seleccionadas previamente. Este proceso implica reevaluar la contribución de cada variable seleccionada a la varianza total explicada y considerar variables alternativas que podrían proporcionar un mejor ajuste. Si bien esto puede mejorar la calidad del conjunto final de variables, sacrifica el orden estricto de importancia que mantiene la selección hacia adelante pura.
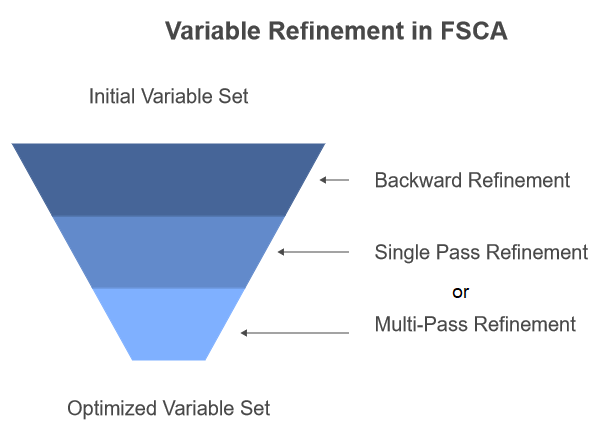
El artículo de investigación describe dos enfoques para incorporar el refinamiento hacia atrás. El primer enfoque aplica el refinamiento hacia atrás una vez completados todos los pasos del FSCA, como paso de posprocesamiento. El segundo enfoque, denominado refinamiento recursivo hacia atrás, consiste en realizar un refinamiento hacia atrás cada vez que se añade una nueva variable a Z al final del paso 3 del algoritmo FSCA. Este enfoque es el que se implementa en el código que se presentará en una sección posterior de este texto.

También hay dos variaciones del paso de refinamiento en sí. El primero, denominado Refinamiento hacia atrás de una sola pasada (Single Pass Backward Refinement, SPBR), evalúa la relevancia de cada variable en secuencia, pasando de la más antigua a la más reciente. El segundo, el refinamiento hacia atrás multipaso (Multi-Pass Backward Refinement , MPBR), reconoce que las variables que inicialmente se consideraban relevantes pueden dejar de serlo a medida que se realizan ajustes en variables posteriores de la secuencia. En MPBR, el proceso se repite hasta que se produce una pasada completa sin más refinamientos. Tenga en cuenta que el código que se proporciona más adelante en este artículo solo implementa SPBR.Tenga en cuenta que el código que se proporciona más adelante en este artículo solo implementa SPBR.

En las secciones siguientes, describiremos los pasos del algoritmo FSCA con más detalle, utilizando algunas matemáticas y código. Todos los fragmentos de código a los que se hace referencia se han extraído de fsca.mqh, que se encuentra adjunto al final de este artículo.

Componentes principales

El algoritmo FSCA se basa en el uso de componentes principales para identificar inicialmente las fuentes únicas de variación en el conjunto de datos X. Este paso también proporciona una indicación del número máximo de variables componentes para la matriz Z, determinando el valor de k (tal y como se ha definido anteriormente). En el artículo de investigación, el algoritmo utiliza un valor k especificado por el usuario. Sin embargo, en nuestra implementación, k siempre se establece igual al número de componentes principales. Los componentes principales se obtienen descomponiendo los valores propios de la matriz de correlación de X. La siguiente lista muestra la rutina que calcula la estructura factorial utilizando la función compute_factor_structure().

//+------------------------------------------------------------------+
//| computes the factor structure of a correlation matrix            |
//+------------------------------------------------------------------+
matrix            compute_factor_structure(matrix &covar,matrix &eigenvectors,vector &eigenvalues,vector &cumeigenvalues)
  {
   if(!covar.EigenSymmetricDC(EIGVALUES_V,eigenvalues,eigenvectors))
     {
      Print(__FUNCTION__, " error ", GetLastError());
      return matrix::Zeros(1,1);
     }
   double sum = 0.0;


   if(!np::reverseVector(eigenvalues) ||  !np::reverseMatrixCols(eigenvectors))
     {
      Print(__FUNCTION__, " reverse operation error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   double cumulate[];
   for(ulong i=0 ; i<eigenvalues.Size() ; i++)
     {
      if(eigenvalues[i]>1.e-8)
        {
         sum += eigenvalues[i] ;
         if(!cumulate.Push(sum))
           {
            Print(__FUNCTION__," error adding element ", GetLastError());
            return matrix::Zeros(1,1);
           }
        }
     }

   if(!cumeigenvalues.Assign(cumulate))
     {
      Print(__FUNCTION__," vector assignment error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   cumeigenvalues/=cumeigenvalues[cumeigenvalues.Size()-1];

   cumeigenvalues*=100.0;

   matrix structmat=eigenvectors;

   for(ulong i = 0; i<structmat.Cols(); i++)
      if(!structmat.Col(eigenvectors.Col(i)*sqrt(eigenvalues[i]>=0.0?eigenvalues[i]:0.0),i))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return matrix::Zeros(1,1);
        }

   if(!structmat.Clip(-1.0,1.0))
     {
      Print(__FUNCTION__, "error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   return structmat;
  }

//+------------------------------------------------------------------+
//| computes the factor structure of a correlation matrix            |
//+------------------------------------------------------------------+
matrix compute_factor_structure(matrix &covar, matrix &eigenvectors, vector &eigenvalues, vector &cumeigenvalues) {
    if (!covar.EigenSymmetricDC(EIGVALUES_V, eigenvalues, eigenvectors)) {
        Print(__FUNCTION__, " error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    double sum = 0.0;

    if (!np::reverseVector(eigenvalues) || !np::reverseMatrixCols(eigenvectors)) {
        Print(__FUNCTION__, " reverse operation error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    double cumulate[];
    for (ulong i = 0; i < eigenvalues.Size(); i++) {
        if (eigenvalues[i] > 1.e-8) {
            sum += eigenvalues[i];
            if (!cumulate.Push(sum)) {
                Print(__FUNCTION__, " error adding element ", GetLastError());
                return matrix::Zeros(1, 1);
            }
        }
    }

    if (!cumeigenvalues.Assign(cumulate)) {
        Print(__FUNCTION__, " vector assignment error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    cumeigenvalues /= cumeigenvalues[cumeigenvalues.Size() - 1];
    cumeigenvalues *= 100.0;

    matrix structmat = eigenvectors;

    for (ulong i = 0; i < structmat.Cols(); i++) {
        if (!structmat.Col(eigenvectors.Col(i) * sqrt(eigenvalues[i] >= 0.0 ? eigenvalues[i] : 0.0), i)) {
            Print(__FUNCTION__, "error ", GetLastError());
            return matrix::Zeros(1, 1);
        }
    }

    if (!structmat.Clip(-1.0, 1.0)) {
        Print(__FUNCTION__, "error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    return structmat;
}

Esta función toma como entrada una matriz de correlación, covar, y devuelve una matriz que contiene las cargas factoriales. Realiza la descomposición en valores propios de la matriz de correlación utilizando la función EigenSymmetricDC. Los valores propios resultantes se almacenan en el vector de valores propios, mientras que los vectores propios se almacenan en la matriz de vectores propios. A continuación, la función invierte el orden de los valores propios y los vectores propios para garantizar que estén ordenados en orden descendente. Calcula los valores propios acumulativos sumándolos iterativamente y los almacena en el vector cumeigenvalues. Los valores propios acumulativos se normalizan para representar el porcentaje de la varianza total.

A continuación, la función calcula las cargas factoriales multiplicando cada vector propio por la raíz cuadrada de su valor propio correspondiente y almacenando el resultado en la matriz structmat. Para garantizar que las cargas factoriales se mantengan dentro de un rango razonable, se recortan entre -1 y 1. Por último, la función devuelve la matriz structmat que contiene las cargas factoriales calculadas.

La estructura factorial derivada de la matriz de correlación consiste en cargas factoriales que representan las relaciones entre las variables y los factores latentes subyacentes. Estas cargas ayudan a interpretar el significado de los factores latentes y a evaluar la importancia de cada variable a la hora de explicar la varianza en los datos.

El resultado de compute_factor_structure() se utiliza en la función compute_principal_components() para calcular los componentes principales.

//+------------------------------------------------------------------+
//|   calculates the principal components                            |
//+------------------------------------------------------------------+
matrix compute_principal_components(void) {
    matrix out(m_data.Rows(), ulong(m_num_comps));
    vector drow, eigcol, nv;
    double sum;

    for (ulong i = 0; i < m_data.Rows(); i++) {
        drow = m_data.Row(i);
        for (ulong j = 0; j < m_num_comps; j++) {
            sum = 0.0;
            for (ulong k = 0; k < m_data.Cols(); k++) {
                sum += drow[k] * m_eigvectors[k][j] / sqrt(m_eigvalues[j]);
            }
            out[i][j] = sum;
        }
    }

    return out;
}

La función compute_principal_components() no toma parámetros de entrada y devuelve una matriz que contiene los componentes principales. Se inicializa una matriz de salida out para almacenar los componentes principales, con dimensiones iguales al número de filas de los datos de entrada y al número de componentes principales deseados. La función recorre cada fila de la matriz de datos de entrada y calcula cada componente principal tomando el producto escalar de la fila con el vector propio correspondiente de la matriz de covarianza, dividido por la raíz cuadrada del valor propio asociado. El componente principal resultante se almacena en la matriz out. Esta función calcula los componentes principales utilizando la fórmula estándar para proyectar puntos de datos en el subespacio de componentes principales.

El concepto fundamental que subyace a los componentes principales es la aproximación de la matriz de datos original X, que contiene muchas variables, utilizando un conjunto reducido de variables componentes. Esta aproximación se consigue mediante una transformación lineal.

Podemos evaluar el error en esta aproximación calculando la suma de las diferencias al cuadrado entre X y su aproximación.

Alternativamente, podemos evaluar la calidad de la aproximación calculando la fracción de la varianza total de X que se explica por las variables componentes.

Para lograr una aproximación óptima, debemos seleccionar estratégicamente un subconjunto de columnas de X para formar Z, que se utilizará para calcular las variables componentes. Es importante señalar que los componentes principales y las variables componentes finales, representadas por la matriz M, son distintos.

Maximización de la varianza explicada

Uno de los pasos clave del algoritmo FSCA es seleccionar la variable óptima para añadir al subconjunto existente. Para ello, asignamos una puntuación a cada variable potencial y seleccionamos la que tiene la puntuación más alta. El cálculo de este criterio (puntuación), tal y como se describe en el artículo de investigación, es relativamente complejo. Sin embargo, los autores proporcionan una prueba matemática de que el orden de clasificación de este criterio para variables competitivas coincide con el orden de clasificación de su varianza explicada. Esto significa que la variable con la puntuación más alta también maximiza la varianza explicada.

Una forma más sencilla de describir el cálculo de la puntuación para cada variable potencial es mediante la ecuación que se proporciona a continuación. Los lectores interesados en la derivación matemática de la fórmula pueden consultar el artículo de investigación.

Z(i) es la matriz Z con la columna i de X añadida a ella.
La variable x(j) es la columna j de X.
El término v es el número de variables (columnas) en X.
El término intermedio q es un vector columna de k elementos de longitud.

A continuación se muestra el código que implementa el cálculo del criterio.

//+------------------------------------------------------------------+
//|  calculates the criterion for assessing a component              |
//+------------------------------------------------------------------+
double compute_criterion(matrix &covar, ulong &keptcols[], ulong nkept, ulong trial_col) {
    ulong i, j, k, irow, new_kept;
    double sum, crit, dtemp;
    new_kept = nkept + 1;
    matrix mt(new_kept, new_kept);

    for (i = 0; i < new_kept; i++) {
        if (i < nkept)
            irow = keptcols[i];
        else
            irow = trial_col;

        for (j = 0; j < nkept; j++)
            mt[i][j] = covar[irow][keptcols[j]];

        mt[i][nkept] = covar[irow][trial_col];
    }

    matrix mtinv = mt.Inv();
    vector vec(new_kept);

    crit = 0.0;
    for (j = 0; j < m_preds; j++) {
        for (i = 0; i < nkept; i++)
            vec[i] = covar[j][keptcols[i]];

        vec[nkept] = covar[j][trial_col];

        sum = 0.0;
        for (i = 0; i < new_kept; i++)
            sum += vec[i] * vec[i] * mtinv[i][i];

        crit += sum;

        sum = 0.0;
        for (i = 1; i < new_kept; i++) {
            dtemp = vec[i];
            for (k = 0; k < i; k++)
                sum += dtemp * vec[k] * mtinv[i][k];
        }

        crit += 2.0 * sum;
    }

    return crit;
}

La función compute_criterion() calcula un criterio para evaluar un componente en el proceso de selección de características. Toma como entrada una matriz de correlación, covar, una matriz de variables seleccionadas, keptcols, el número de variables seleccionadas, nkept, y el índice de la variable de prueba que se va a evaluar.

La función comienza creando una nueva matriz, mt, que amplía el conjunto existente de variables seleccionadas con la variable de prueba. A continuación, calcula la inversa de esta matriz aumentada, mt. La función recorre todas las variables del conjunto de datos original y calcula un criterio para cada variable basado en la covarianza entre esa variable y las variables seleccionadas, ponderada por la inversa de la matriz mt. El criterio calculado se acumula en la variable crit.

El objetivo de esta función es evaluar el impacto de añadir una nueva variable al conjunto de variables seleccionadas. Un valor de criterio más alto indica que es probable que la nueva variable mejore el rendimiento del modelo, mientras que un valor de criterio más bajo sugiere que puede que no sea beneficiosa. Esta función se puede utilizar dentro de un algoritmo de selección de características para identificar las variables más informativas para un modelo determinado.

Refinamiento recursivo hacia atrás

El refinamiento hacia atrás es una variante de la selección hacia adelante, como se ilustra en el código backward_refinement() que se muestra a continuación.

//+------------------------------------------------------------------+
//| backward refinement routine                                      |
//+------------------------------------------------------------------+
ulong backward_refinement(matrix &covar, ulong &kept_columns[], ulong nkept, double &best_crit) {
    ulong i, old_col, new_col, best_col, refined;
    double crit;

    best_crit = substvar(covar, kept_columns, nkept, 0, kept_columns[0]);
    refined = 0;

    for (old_col = 0; old_col < nkept; old_col++) {

        if (old_col == nkept - 1 && !refined)
            break;

        best_col = ULONG_MAX;
        for (new_col = 0; new_col < m_preds; new_col++) {

            for (i = 0; i < nkept; i++) {
                if (new_col == kept_columns[i])
                    break;
            }

            if (i < nkept)
                continue;

            crit = substvar(covar, kept_columns, nkept, old_col, new_col);

            if (crit > best_crit) {
                best_crit = crit;
                best_col = new_col;
            }
        }

        if (best_col != ULONG_MAX && best_col >= 0) {
            // Print(__FUNCTION__,"  Replaced predictor at column ",kept_columns[old_col], " with ",best_col," to get criterion = ", best_crit);
            kept_columns[old_col] = best_col;
            refined = 1;
        }
    }
    return refined;
}

Este código MQL5 implementa un algoritmo de refinamiento hacia atrás para la selección de características. Evalúa de forma iterativa el impacto de eliminar cada variable seleccionada en un criterio específico. Al calcular el criterio con cada variable eliminada, la función identifica qué variable, al eliminarla, produce el cambio menos significativo en el criterio. Si el cambio es inferior a un umbral predefinido, la variable se elimina del conjunto seleccionado y el proceso se repite hasta que no se puedan realizar más ajustes. La función devuelve 1 si se ha realizado un refinamiento y 0 en caso contrario.

La rutina substvar(), llamada dentro de la función backward_refinement(), implementa un mecanismo de sustitución de variables que calcula un criterio basado en la matriz de correlación y un conjunto de variables seleccionadas. Esta rutina se utiliza en un algoritmo de selección de características para evaluar el impacto de sustituir una variable por otra.

//+------------------------------------------------------------------+
//| variable substitution routine                                    |
//+------------------------------------------------------------------+
double substvar(matrix &covar, ulong &keptcols[], ulong nkept, ulong old_col, ulong new_col) {
    ulong i, j, k, irow, saved_col;
    double sum, crit, dtemp;
    matrix mt(nkept, nkept);

    saved_col = keptcols[old_col];
    keptcols[old_col] = new_col;

    for (i = 0; i < nkept; i++) {
        irow = keptcols[i];
        for (j = 0; j < nkept; j++) {
            mt[i][j] = covar[irow][keptcols[j]];
        }
    }

    matrix mtinv = mt.Inv();
    vector vec(nkept);

    crit = 0.0;
    for (j = 0; j < m_preds; j++) {

        for (i = 0; i < nkept; i++) {
            vec[i] = covar[j][keptcols[i]];
        }

        sum = 0.0;
        for (i = 0; i < nkept; i++) {
            sum += vec[i] * vec[i] * mtinv[i][i];
        }
        crit += sum;

        sum = 0.0;
        for (i = 1; i < nkept; i++) {
            dtemp = vec[i];
            for (k = 0; k < i; k++) {
                sum += dtemp * vec[k] * mtinv[i][k];
            }
        }
        crit += 2.0 * sum;
    }

    keptcols[old_col] = saved_col;

    return crit;
}

La función toma como entrada una matriz de correlación, covar, una matriz de variables seleccionadas, keptcols, el número de variables seleccionadas, nkept, y los índices de las variables antiguas y nuevas que se van a sustituir. Crea una matriz temporal, mt, para almacenar la submatriz de covar correspondiente a las variables seleccionadas. A continuación, la función calcula la inversa de la matriz mt utilizando la función Inv(). Itera sobre todas las variables del conjunto de datos original, calculando un criterio para cada variable basado en la covarianza entre la variable y las variables seleccionadas, ponderado por la inversa de la matriz mt. El criterio calculado se acumula en la variable crit. Después de calcular el criterio, la función restaura la variable original en la matriz keptcols y devuelve el criterio calculado.

El objetivo de esta función es evaluar el impacto que tiene la sustitución de una variable por otra en el modelo global. Un valor de criterio más alto indica que es probable que la sustitución mejore el rendimiento del modelo, mientras que un valor de criterio más bajo sugiere que puede que no sea beneficiosa. Esta función se puede integrar en un algoritmo de selección de características para identificar la combinación óptima de variables para un modelo determinado.

Ortogonalización de componentes

La selección de variables mediante selección estrictamente ascendente, sin incorporar el refinamiento descendente, establece un orden jerárquico basado en su importancia, comenzando por las más influyentes y disminuyendo progresivamente en importancia. Este orden suele ser muy valioso en aplicaciones prácticas. Si bien los valores brutos se pueden utilizar directamente, las variables de componentes ortogonales (construidas como combinaciones lineales de las variables originales) ofrecen ventajas claras. Estos componentes no están correlacionados, lo que facilita el entrenamiento del modelo y minimiza la redundancia. Además, la ausencia de redundancia dentro de estas variables puede simplificar la interpretación de sus contribuciones.

Para lograr variables de componentes ortogonales conservando el orden original, es adecuado el método de ortogonalización de Gram-Schmidt. Este procedimiento comienza definiendo el componente inicial como la primera variable seleccionada escalada. Para los componentes posteriores, se restan las proyecciones sobre los componentes existentes. Restando sistemáticamente estas proyecciones y normalizándolas a la longitud unitaria, se asegura la ortogonalidad de los componentes. Por último, el reescalado a la desviación estándar de la unidad mantiene la consistencia. En esencia, la ortogonalización de Gram-Schmidt transforma las variables seleccionadas en un conjunto de componentes ortogonales que conservan el orden original de importancia, lo que ofrece beneficios potenciales en la interpretabilidad y la eficiencia del modelo.

La siguiente es una implementación de la transformación de Gram-Schmidt. La salida de la función es una nueva matriz donde cada columna representa un vector ortogonalizado.

//+------------------------------------------------------------------+
//|   Gram Schmidt routine                                           |
//+------------------------------------------------------------------+
matrix gram_schmidt(matrix &input_) {
    ulong irow, icol, inner;
    double dtemp, sum;
    ulong nrows = input_.Rows();
    ulong ncols = input_.Cols();
    matrix output = input_;

    sum = 0.0;

    vector colsum = output.Col(0);
    colsum = MathPow(colsum, 2.0);
    sum = colsum.Sum();
    sum = sqrt(sum);

    if (sum == 0.0) {
        Print(__FUNCTION__, " sum == 0.0 ");
        return matrix::Zeros(0, 0);
    }

    if (!output.Col(output.Col(0) / sum, 0)) {
        Print(__FUNCTION__, " failed column insertion ", GetLastError());
        return matrix::Zeros(0, 0);
    }

    for (icol = 1; icol < ncols; icol++) {
        for (inner = 0; inner < icol; inner++) {
            sum = 0.0;
            for (irow = 0; irow < nrows; irow++)
                sum += (output[irow][icol] * output[irow][inner]);

            for (irow = 0; irow < nrows; irow++)
                output[irow][icol] -= (sum * output[irow][inner]);
        }

        sum = 0.0;
        for (irow = 0; irow < nrows; irow++) {
            dtemp = output[irow][icol];
            sum += dtemp * dtemp;
        }

        sum = sqrt(sum);

        if (sum == 0.0) {
            Print(__FUNCTION__, " sum == 0.0 ");
            return matrix::Zeros(0, 0);
        }

        if (!output.Col(output.Col(icol) / sum, icol)) {
            Print(__FUNCTION__, " failed column insertion ", GetLastError());
            return matrix::Zeros(0, 0);
        }
    }

    return output;
}

El algoritmo funciona ortogonalizando iterativamente cada columna de la matriz de entrada con respecto a las columnas ortogonalizadas previamente. Esto se logra proyectando la columna actual sobre el subespacio abarcado por las columnas anteriores y restando esta proyección de la columna actual. Luego, el vector resultante se normaliza para que tenga una longitud unitaria. El código incluye varias optimizaciones para mejorar la eficiencia, como el uso de operaciones vectoriales para los cálculos y evitar cálculos innecesarios. Además, la función incorpora manejo de errores para verificar problemas potenciales, como vectores de longitud cero o inserciones de columnas fallidas.

Habiendo cubierto todas las rutinas principales para realizar la selección hacia adelante con refinamiento hacia atrás opcional, la siguiente sección demostrará cómo se utilizan estas rutinas en la implementación completa del algoritmo FSCA.

La clase CFsca

La clase denominada CFsca encapsula la funcionalidad para realizar análisis de componentes de selección avanzada en un conjunto de datos. La clase completa se define en fsca.mqh, junto con una rutina de transformación de estandarización simple llamada stdmat(). Esta función toma una matriz como entrada y devuelve una matriz estandarizada.

//+------------------------------------------------------------------+
//| standardize a matrix                                             |
//+------------------------------------------------------------------+
matrix stdmat(matrix &in) {
    vector mean = in.Mean(0);
    vector std = in.Std(0);
    std += 1e-10;
    matrix out = in;

    for (ulong row = 0; row < out.Rows(); row++) {
        if (!out.Row((in.Row(row) - mean) / std, row)) {
            Print(__FUNCTION__, " error ", GetLastError());
            return matrix::Zeros(in.Rows(), in.Cols());
        }
    }

    return out;
}

La función stdmat() calcula la media y la desviación estándar de cada columna de la matriz de entrada utilizando las funciones Mean y Std. Luego crea una matriz de salida con las mismas dimensiones que la matriz de entrada. La función itera sobre cada fila de la matriz de entrada, estandarizándola restando la media de la columna correspondiente y dividiéndola por la desviación estándar de la columna. La fila estandarizada se almacena en la matriz de salida out, que se devuelve al final de la función. Esta función se coloca fuera de la clase CFsca para permitir su utilización independiente.

La clase CFsca comienza definiendo sus miembros privados, que se utilizan para almacenar resultados intermedios y las estructuras de datos necesarias para FSCA.

//+------------------------------------------------------------------+
//| fsca class implementation                                        |
//+------------------------------------------------------------------+
class CFsca
  {
private:
   bool              m_fitted;              //flag showing if principal factors were extracted
   matrix m_corrmat,             //correlation matrix
          m_covar,               //altered correlation matrix
          m_data,                //standardized data is here
          m_eigvectors,          //matrix of eigen vectors of m_corrmat matrix
          m_structmat,           //factor loading matrix of m_corrmat matrix
          m_principal_components,             //principal components
          m_fscv_struct,        //fsca factor structure
          m_fscv_eigvects,      //fsca eigen structure
          m_Fsca,        //ordered fsca variables
          m_coeffs,      //fsca component coefficients
          m_Fscv;        //refined fsca variables
   vector m_eigvalues,           //vector of eigen values of m_corrmat matrix
          m_sqcorr,              //mean squared correlation matrix
          m_fscv_eigvals,        //fsca eigen values
          m_fscv_cumeigvals,     //fsca cumulative variance contribution
          m_cumeigvalues;        //cumulative variance contributions of m_corrmat matrix
   ulong             m_num_comps;           //unique instances of redundent variation in m_data
   ulong             m_preds;               //number of variables (columns) in dataset (m_data)
   ulong  m_keptorderedcolumns[],//indices of columns upon which components are calculated for ordered fsca
          m_keptrefinedcolumns[],//indices of columns upon which components are calculated for backward refined fsca
          m_keptcolumns[],
          m_bestcolumn;          //index of first selected column in analysis
   double            m_best_crit;           //best criterion value

A continuación, están los métodos privados de la clase CFsca, algunos de los cuales hemos cubierto en secciones anteriores de este texto. Se mencionarán brevemente otros métodos cuando analicemos los métodos públicos de la clase.

Los métodos públicos se definen al final de la clase CFsca. El método fit() debe llamarse primero después de inicializar una instancia de la clase. Este método realiza un análisis de componentes de selección hacia adelante en el conjunto de datos sin procesar. Toma como entrada una matriz que contiene los datos originales sin procesar y devuelve un valor booleano que indica si el proceso de ajuste fue exitoso.

//+------------------------------------------------------------------+
//| perform forward selection component analysis on a raw dataset    |
//+------------------------------------------------------------------+
bool fit(matrix &data) {
    m_preds = data.Cols();
    m_fitted = false;
    m_sqcorr = vector::Zeros(m_preds);

    m_data = stdmat(data);
    m_corrmat = m_data.CorrCoef(false);

    m_structmat = compute_factor_structure(m_corrmat, m_eigvectors, m_eigvalues, m_cumeigvalues);

    if (m_structmat.Rows() == 1)
        return false;

    m_num_comps = m_cumeigvalues.Size();

    if (ArrayResize(m_keptorderedcolumns, int(m_num_comps)) < 0 || 
        ArrayResize(m_keptrefinedcolumns, int(m_num_comps)) < 0 ||
        ArrayResize(m_keptcolumns, int(m_num_comps)) < 0 || 
        ArrayInitialize(m_keptcolumns, ULONG_MAX) < 0) {
        Print(__FUNCTION__, " array error ", GetLastError());
        return false;
    }

    m_principal_components = compute_principal_components();

    for (ulong i = 0; i < m_preds; i++)
        m_sqcorr[i] = (compute_criterion(m_corrmat, m_keptcolumns, 0, i) - 1.0) / double(m_preds - 1);

    vector evd_vals = m_eigvalues;
    while (evd_vals[m_preds - 1] <= 0.0) {
        for (ulong j = 1; j < m_preds; j++) {
            for (ulong k = 0; k < j; k++) {
                m_corrmat[j][k] *= 0.99999;
                m_corrmat[k][j] = m_corrmat[j][k];
            }
        }

        matrix empty;
        if (!m_corrmat.EigenSymmetricDC(EIGVALUES_N, evd_vals, empty)) {
            Print(__FUNCTION__, " failed eig decomp ", GetLastError());
            return false;
        }
    }

    m_Fsca = compute_fsca_components(m_data);
    m_Fscv = compute_fscv_components(m_data);

    m_fitted = (m_Fsca.Rows() > 1 && m_Fscv.Rows() > 1);

    return m_fitted;
}

La función fit() inicializa varias variables y matrices utilizadas en el proceso FSCA. En primer lugar, estandariza la matriz de datos de entrada, garantizando que tenga media cero y varianza unitaria. Luego, la función calcula la matriz de correlación de los datos estandarizados y la almacena en m_corrmat. A continuación, calcula la estructura factorial de la matriz de correlación utilizando la función compute_factor_structure. Esta estructura factorial incluye los vectores propios (m_eigvectors), los valores propios (m_eigvalues) y los valores propios acumulativos (m_cumeigvalues) de la matriz de correlación. La función verifica si la matriz de estructura factorial (m_structmat) tiene solo una fila; si es así, esto indica un error en la evaluación de la estructura factorial y la función devuelve falso.

El número de componentes (m_num_comps) se establece igual al número de valores propios distintos de cero. Luego, la función inicializa varias matrices utilizadas en el proceso FSCA. Calcula los componentes principales de los datos estandarizados utilizando la función compute_principal_components y calcula las correlaciones al cuadrado entre cada variable y el primer componente principal. Además, la función comprueba si existen valores propios negativos. Si se encuentra alguno, realiza pequeños ajustes en la matriz de correlación y recalcula los valores propios hasta que todos sean positivos. Finalmente, la función calcula los componentes FSCA utilizando la función compute_fsca_components y los componentes FSCV utilizando la función compute_fscv_components. Si los componentes FSCA y FSCV se calculan correctamente, la función establece el indicador m_fitted en verdadero.

Para concluir la definición de la clase CFsca se encuentran las funciones getter que proporcionan acceso a varios aspectos de los cálculos analíticos realizados durante el proceso FSCA.

//+------------------------------------------------------------------+
//| get the principal components                                     |
//+------------------------------------------------------------------+
matrix get_principal_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_principal_components;
}

//+------------------------------------------------------------------+
//| get the ordered fsca components                                  |
//+------------------------------------------------------------------+
matrix get_fsca_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_Fsca;
}

//+------------------------------------------------------------------+
//| get the backward refined fsca components                         |
//+------------------------------------------------------------------+
matrix get_fscv_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_Fscv;
}

//+------------------------------------------------------------------+
//| get indices of variables defining the ordered fsca components    |
//+------------------------------------------------------------------+
bool get_fsca_var_indices(ulong &indices[]) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    return (ArrayCopy(indices, m_keptorderedcolumns, 0, 0, int(m_num_comps)) > 0);
}

//+---------------------------------------------------------------------------+
//| get indices of variables defining the backward refined fsca components    |
//+---------------------------------------------------------------------------+
bool get_fscv_var_indices(ulong &indices[]) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    return (ArrayCopy(indices, m_keptrefinedcolumns, 0, 0, int(m_num_comps)) > 0);
}

//+-------------------------------------------------------------------+
//| get cumulative variance contribution based on principal components|
//+-------------------------------------------------------------------+
vector get_principal_components_cumulative_variance_contribution(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_cumeigvalues;
}

//+-------------------------------------------------------------------+
//| get cumulative variance contribution based on fscv components     |
//+-------------------------------------------------------------------+
vector get_fscv_cumulative_variance_contribution(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_fscv_cumeigvals;
}

//+-------------------------------------------------------------------+
//| get eigen structure of principal components                       |
//+-------------------------------------------------------------------+
bool get_principal_components_eigstructure(matrix &vectors, vector &values) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    vectors = m_eigvectors;
    values = m_eigvalues;

    return true;
}

//+-------------------------------------------------------------------+
//| get eigen structure of backward refined FSCs                      |
//+-------------------------------------------------------------------+
bool get_fscv_eigstructure(matrix &vectors, vector &values) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    vectors = m_fscv_eigvects;
    values = m_fscv_eigvals;

    return true;
}

//+-------------------------------------------------------------------+
//| get principal components factor structure                         |
//+-------------------------------------------------------------------+
matrix get_principal_components_factorstructure(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_structmat;
}

//+-------------------------------------------------------------------+
//| get the factor structure of FSC with backward refinement          |
//+-------------------------------------------------------------------+
matrix get_fscv_factorstructure(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_fscv_struct;
}

//+------------------------------------------------------------------+
//| get mean squared correlations                                    |
//+------------------------------------------------------------------+
vector get_avg_correlations(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_sqcorr;
}

//+-------------------------------------------------------------------+
//| get forward selection component coefficients matrix               |
//+-------------------------------------------------------------------+
matrix get_fsca_component_coeffs(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_coeffs;
}

Estas funciones permiten a los usuarios recuperar resultados importantes, como datos estandarizados, matriz de correlación, estructura factorial, componentes principales y variables componentes, lo que facilita un mayor análisis e interpretación de los resultados. Concluimos esta exposición con una demostración de cómo emplear la clase CFsca.

Un ejemplo

La siguiente lista de códigos define un script MQL5 llamado FSCA_Demo.mq5 que realiza un análisis de componentes de selección avanzada (FSCA) en un conjunto de datos generado aleatoriamente. El script incluye el archivo de encabezado fsca.mqh, que contiene la definición de la clase CFsca utilizada para el análisis FSCA.

//+------------------------------------------------------------------+
//|                                                    FSCA_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<fsca.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   MathSrand(120);
//---
   matrix mat(100,9);
//---
   mat.Random(0.0,1.0);
//---
   vector var1 = mat.Col(0) + mat.Col(1);
// ---
   vector var2 = mat.Col(2) + mat.Col(3);
//---
   vector var3 = var1 + var2;
//---
   if(!mat.Col(var1,6) || !mat.Col(var2,7) || !mat.Col(var3,8))
     {
      Print("failed column assignment ", GetLastError());
      return;
     }
//---
   CFsca fsca;
//---
   if(!fsca.fit(mat))
      return;
//---
   ulong index[];
   Print("Principal components cumulative variance conributions \n", fsca.get_principal_components_cumulative_variance_contribution());
   Print(" Principal components factor structure \n", fsca.get_principal_components_factorstructure());
   Print("Mean squared correlation of each variable with all others \n", fsca.get_avg_correlations());
//---
   if(fsca.get_fsca_var_indices(index))
     {
      Print(" Ordered FSCA components based on variables located in column indices ");
      ArrayPrint(index);
     }
//---
   Print(" Ordered FSCA component coefficients matrix \n", fsca.get_fsca_component_coeffs());
//---
   if(fsca.get_fscv_var_indices(index))
     {
      Print(" Backward refined FSCA components based on variables located in column indices ");
      ArrayPrint(index);
     }
//---
   matrix vects;
   vector vals;
//---
   if(fsca.get_fscv_eigstructure(vects,vals))
     Print("Backward refined fsca component eigenvalues \n", vals);
//---
   Print(" Backward refined cumulative variance contributions \n", fsca.get_fscv_cumulative_variance_contribution());
//---
   Print(" Backward refined fsca components factor structure \n", fsca.get_fscv_factorstructure());
  }
//+------------------------------------------------------------------+

Comienza estableciendo una semilla aleatoria y creando una matriz de valores aleatorios. Se crean tres nuevos vectores sumando las columnas existentes en la matriz. Luego, el script intenta ajustar los datos de la matriz al modelo FSCA y recupera varios resultados de FSCA, incluida la contribución de la varianza acumulada, la estructura factorial y las correlaciones cuadráticas medias. También realiza tanto FSCA estándar como FSCA refinado hacia atrás, imprimiendo los índices de las variables ordenadas y los coeficientes de los componentes. Así como la estructura factorial de los componentes FSCA refinados hacia atrás. El script simplemente genera un conjunto de datos de variables aleatorias con 100 muestras y 9 características. Las últimas 3 variables del conjunto de datos están configuradas para depender de otras variables, mientras que el resto son independientes. 

Cuando ejecutamos el script y analizamos las características de los componentes principales, encontramos que solo hay seis fuentes únicas de variación de las nueve.

DG      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   Principal components cumulative variance conributions 
RM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [31.72121326219056,54.98374706330443,70.21399790786099,82.34742379766755,91.9067775629936,100]
CM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Principal components factor structure 
MH      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [[-0.5430877600903072,0.4698851388299595,-0.02139789374204959,0.5468988095320395,-0.4254498037566715,-0.06082703269184352,-1.3842452210817e-09,-7.527559895073524e-10,0]
RH      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5283294988376427,0.4246506210338227,-0.1190026606589024,-0.6285471675075863,0.3351428244532062,0.1377893424956133,-1.351333204556555e-09,-7.34858353171856e-10,0]
ES      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5563230307728618,-0.3632156082945803,0.4770295070287525,0.3051596297191441,0.4575827252246154,-0.1688715686919785,-1.694159101189325e-09,2.164855665400724e-10,0]
NF      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.2379617600470182,-0.6943076552356867,-0.4580766878219635,-0.2737307249578351,-0.4112051990027778,0.08636320534609224,-1.769139142521297e-09,2.260667780777343e-10,0]
DO      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [0.02487447101754412,-0.08203927651647476,-0.6079889924620585,0.4701685445643955,0.3604839483405348,0.5215295442601863,1.313244252124911e-25,1.228203109452781e-25,0]
IP      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.07016546285360215,-0.110242984252018,0.7306990214221818,-0.07491798042552207,-0.2276538908363994,0.6257501374625694,4.158606798395552e-25,-7.369218656716687e-26,0]
NE      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.7598477338270035,0.6346843827822741,-0.09872272409405579,-0.04786755450396145,-0.0705236166963274,0.05287812507625003,-1.359967783374346e-10,1.333715775589249e-09,0]
NO      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5934182368659159,-0.8024046895986707,-0.000973814713973191,0.01424096330384607,0.02077689502375221,-0.05801790712583575,2.667167815186452e-10,-1.355042254629964e-11,0]
RM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.9897757278036692,-0.1138316306178367,-0.07343616940955985,-0.02494592427830717,-0.03690113231990194,-0.0030829919659495,2.802923111601039e-09,-3.865027968054199e-10,0]]

Esto es esperado porque tres de las variables son combinaciones de las otras. Al observar las contribuciones de la varianza acumulada de cada variable, vemos que el primer componente representa aproximadamente un tercio de la variación total. La estructura factorial indica una correlación inversa moderada a fuerte entre el primer componente principal y las variables en las columnas 0 a 3 y 6 a 8, inclusive, mientras que las variables en las columnas 4 y 5 muestran la tendencia opuesta. El segundo componente representa las diferencias entre las variables 0 y 1 versus 2 y 3. Juntos, los dos primeros componentes explican más del 55 por ciento de la variación total.

QK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   Mean squared correlation of each variable with all others 
GK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [0.09874555673359317,0.09196664871445229,0.09678803260182336,0.08640965168371836,0.009232616218980055,0.01341075732654295,0.1892345119240549,0.1695472310064176,0.2291509382521983]

Pasando al vector de correlaciones cuadráticas medias de cada variable con la colección combinada de todas las variables, este vector enumera las correlaciones en el orden en que aparecen las variables en el conjunto de datos original. Las últimas tres variables tienen las correlaciones promedio más grandes, mientras que las variables en las columnas 4 y 5 tienen las más bajas.

LR      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Ordered FSCA components based on variables located in column indices 
QQ      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   8 6 2 4 1 5

A continuación, observamos los valores seleccionados hacia adelante, que se obtienen llamando a get_fscv_var_indices(). Muestra los índices de las variables que mejor capturan la mayor parte de la variación en el conjunto de datos, organizados en orden descendente en términos de qué variable contribuye más a la variación general de los datos. Aquí, vemos que la última variable captura la mayor variación en los datos, ya que aparece primero.

QJ      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Ordered FSCA component coefficients matrix 
DM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [[0.9999999989356357,-0.9551778313323678,-1.196676438579672,-0.163265209103464,-0.1301792726137802,0.0741114239785734]
IR      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [7.62883988565579e-10,1.382882745177175,0.7080052470472653,0.1327136589445282,-0.8962870520067646,-0.01038862969019799]
LF      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [6.044914586250671e-10,-1.162965671680505e-09,1.327736785211269,0.1291890234653878,0.1244453203448803,-0.2315140872599129]
EM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [5.84342504938995e-11,-9.115276242144255e-11,-1.685031073006549e-10,1.005785752630206,0.08917398176616295,0.2288955899392838]
JM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [6.626278020206711e-11,8.05911615654048e-10,2.135397240976555e-10,-3.939133914887538e-11,1.404086244047662,0.03569800251260542]
KK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-2.859616016204214e-11,3.48387846349496e-11,2.600743786995707e-10,-1.479500966183878e-10,-3.333024481411151e-11,1.048952273510343]]

A continuación, estudiamos la tabla de coeficientes necesarios para calcular los seis componentes. Las variables se representan en el mismo orden de importancia dado por los índices de la matriz que acabamos de examinar. Aquí vemos que, siendo la última variable la más importante, el coeficiente correspondiente está muy cerca de 1. Al desplazarse hacia abajo por esta matriz, observe cómo los coeficientes se vuelven tan pequeños que son prácticamente cero.

CM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Backward refined FSCA components based on variables located in column indices 
ND      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   3 0 2 4 1 5

Por último, examinamos los índices de las variables seleccionadas mediante una combinación de selección hacia adelante y refinamiento hacia atrás. Es importante tener en cuenta que en esta variación de FSCA, el orden de las variables seleccionadas no tiene importancia. Sin embargo, el conjunto resultante de variables seleccionadas es más significativo que el enfoque de ordenamiento estricto, ya que sólo conserva las variables aleatorias independientes y descarta aquellas que muestran cierta dependencia. Esto se demuestra claramente al comparar los resultados tanto de la selección hacia adelante estándar como de la selección hacia adelante refinada hacia atrás.

Conclusión

En conclusión, hemos presentado una implementación del análisis de componentes de selección avanzada en MQL5, mostrando su eficacia como herramienta tanto para la reducción de dimensionalidad como para la selección de características. La herramienta también se puede utilizar para el análisis exploratorio de datos. Uno de los subproductos del algoritmo es la estructura factorial del conjunto de datos, que puede ser útil cuando se intenta comprender los efectos en juego. Todo el código al que se hace referencia en este artículo se adjunta a continuación.

Nombre del archivo	Descripción
MQL5/include/np.mqh	Archivo de encabezado de funciones de utilidad genéricas de vectores y matrices.
MQL5/include/fsca.mqh	Archivo de encabezado que contiene la definición de la clase CFsca que implementa el análisis de componentes de selección avanzada.
MQL5/scripts/FSCA_Demo.mq5	Un script de MetaTrader 5 que demuestra el uso de la clase CFsca.